Metamaterial Absorber Comprised of Butt-Facing U-Shaped Nanoengineered Gold Metasurface

Abstract

The paper reports spectral features of the absorbed electromagnetic (EM) waves in a new kind of multilayered plasmonic metamaterial thin film comprised of homogenous layers of copper and silicon as the bottom and the middle sections (of the thin film), respectively, and the inhomogeneous U-shaped nanoengineered gold layer as the top. Each unit cell of the top metasurface consists of one upside and one downside U-shaped (butt-facing) structure. The absorbance of EM waves is simulated in the wavelength range of 200−1500 nm under different incidence angles considering the wave as being transmitted from the metasurface side. The low-order TE and TM modes are taken into account for the estimation of wave absorbance under varying metasurfaces as well as silicon layer thicknesses. It has been found that the nanoengineered gold layer causes higher confinement of power in silicon, which can be further controlled by suitably adjusting its thickness. Further, the increased thickness of metasurface results in shifts in absorption peak along with the existence of dual-absorption maxima in the visible spectral range. The obtained spectral features reveal possible application of the proposed structure as a prudent metamaterial absorber, which can be exploited for EM heating purposes.

1. Introduction

Micro- and nanoengineered metamaterials are very interesting as these find many absorption-based applications viz. plasmonic sensor [1,2], broadband terahertz resonator [3], heat generation [4] and selective thermal emitters [5]. The impact of engineered metamaterial structures on negative index metamaterial absorbers (MAs) allows us to govern absorption peaks in specific spans of the electromagnetic (EM) spectrum [6]. The resonance condition of MAs relies on geometrical properties of metamaterial that include the number of layers and the thickness of each layer. The interaction of microwaves with nanoscale periodic MAs results in completely different responses compared to the situation when the waves in the terahertz region are taken into account. Exotic spectral behaviors of EM waves as a function of MA size have been reported in the context of some other applications including different structural resonators, e.g., LC resonator [7], ring resonator [8] and E-shaped dielectric resonators [9], fishnet [10] and thermal switching [11].

The fabrication of MA exploits the use of different types of metals such as silver, copper or aluminum. Among the other metals, however, gold remains the most prudent one in plasmonic applications owing to its noble properties of prefect electrical conductivity and high corrosion resistance [12].

The technique of crystal growth based on epitaxial methods is one of the most promising ways to form a metamaterial layer over the host thin film. The exemplary successful fabrication work reported by Fedorov et al. [13] makes use of lithium fluoride as a highly transparent substrate that can be exploited in the epitaxial growth process. The authors described in their work the growth of gold monocrystals as two arches of metamaterial split ring with different angles of arch, and experimentally investigated the reflection and transmission plasmonic resonance spectra.

The phenomenon of surface plasmon polariton exhibits exotic effects under the situation where EM waves interact with a metamaterial that is a few tens of nano-meters thick [14]. The major application of metamaterials with high absorptivity in the visible spectral range remains in solar thermal energy harvesting. Furthermore, in the higher spectral band, the metamaterial prefect absorber (MPA) can be suitably exploited for short range transfer of power [15].

The present paper investigates absorption characteristics of specially designed metasurface based absorber structure under various dimensional as well as operational conditions. In particular, the metasurface is comprised of butt-facing U-shaped nanoengineered structure of gold formed over a layer of Si, which is backed by a reflector made of copper nanolayer. The U-kind of structure is actually parabolic in shape, and the two ends of a parabola are mounted with semi-rectangular horns. Further, two such U-shaped structures are arranged in a way that the semi-rectangular horns of neighboring U-shapes face each other. Taking into account such a kind of MA configuration, the absorption spectra are obtained for a wide range of wavelength from 200 nm to 1500 nm. It has been found that the proposed MPA would yield over 99% absorbance under certain dimensional and/or operational conditions. The proposed nanoengineered thin film can be experimentally realized by the technique of advanced electron beam lithography. The present paper, however, focuses more on the expected results and the efficacy of the use of this kind of metasurface design in EM applications.

2. Theory and Model Specifications

The metamaterial nanostructure includes two main butt-facing U-shapes of nanoscaled gold structure, which are inversely positioned up-facing towards each other. Combination of both the U-shapes serves as only a one unit cell, as shown in Figure 1a. However, the curvature of U-shape is closely similar to a circular ring, and symmetrical parabolic shapes having 2 nm width perform as a ring. The total dimension of butt-facing U-shape within the unit cell is much smaller than the excitation wavelength—this remains of great importance since the plasma frequency is related to the electron density of metasurface within the MPA structure through the equation [16],

$${\mathsf{\omega }}_{\mathrm{p}}=\frac{N{\mathrm{e}}^2}{m{\mathsf{\epsilon }}_0}$$

(1)

where $N$, $m$ and $e$ and ${\mathsf{\epsilon }}_0$ represent electron density, electronic mass, electronic charge and free-space permittivity, respectively. The light beam, which is the external EM field, causes free-electrons (plasma) to oscillate towards the direction in which it is applied. These free-electrons, confined inside the U-shaped nanostructure, move in the $–z$-direction as the incident light impinges from the $+z$-direction. As a result, the whole metamaterial structure would not take part in the movement of charge.

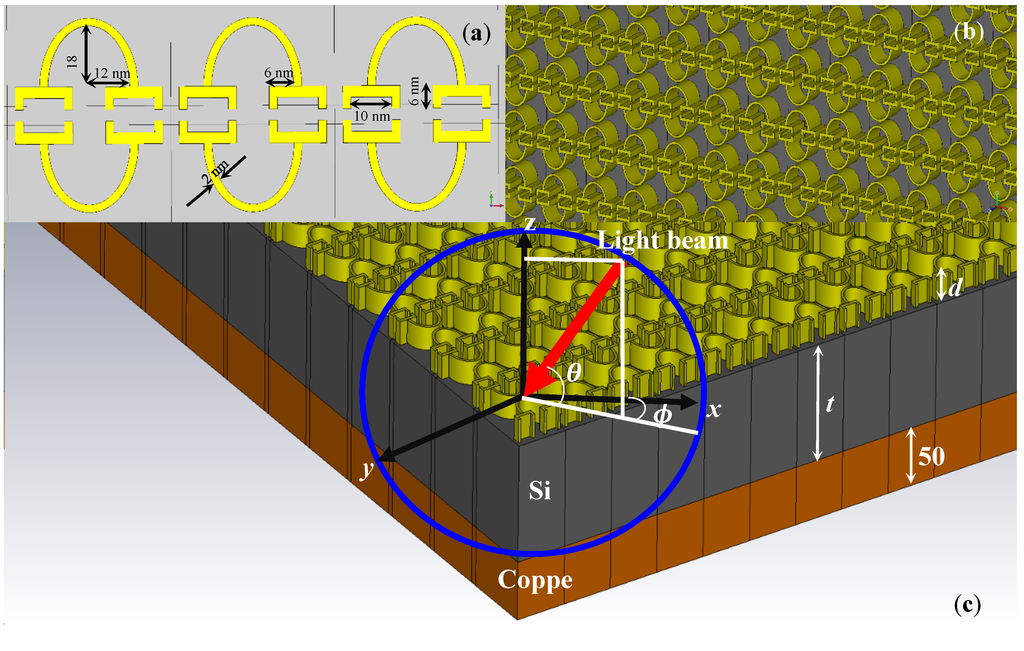
Figure 1. (a) Dimensional specifications of the butt-facing U-shaped resonator structure within the unit cell; (b) perspective view of the metasurface and (c) 3D schematic of multilayer metamaterial prefect absorber (MPA).

The effective electron density $N_{eff}$, developed due to the fraction of free-electrons participating in resonance (due to the effect of external incident light beam), is directly related to the size and the effective mass of the butt-facing U-shaped structure within each unit cell, and inversely related to the distance between neighboring U-shapes. Thus, the effective electron density of U-shape due to asymmetrical properties (of the structure) is mainly related to the distance of separation between the up- and the down-vertex points of each U-shape. Moreover, the width of the U-shape also plays an important role in enhancing the effective electron density of the structure. Generally, $N_{eff}$ can be expressed as:

$$N_{eff}\propto N\frac{S_{u-d}}{d_{eff}}$$

(2)

where $S_{u-d}$ is the size of the up- and the down-shaped U-shape, and $d_{eff}$ is the effective distance between two U-shapes.

Figure 1a shows dimensional features of the metamaterial structure within the unit cell that constitutes the top metasurface (as illustrated in Figure 1b). The values of the thickness $d$ of (the gold) metasurface are taken as typically 50 nm and 100 nm. The case of $d=0$ will essentially yield a simple metal loaded planar guide configuration—this situation is also considered in this paper, in order to compare the results. Further, small values of $d$ would contribute to the generation of surface plasmonic waves, the effects of which are primarily discussed in the present work. Figure 1c shows the schematic of MPA that incorporates the lower layers as Si and copper. The Si layer thickness $t$ is typically chosen as 100 nm and 500 nm, in order to evaluate the effect on the absorption characteristics due to the variation in thickness of the wave confinement section; the (lowest) copper layer thickness remains fixed at 50 nm. It is noteworthy that the Si and the copper layers perform as the light trapper and prefect light reflector, respectively.

The spherical coordinate in Figure 1c is purposely illustrated to feature the trace of the incoming light beam along with the $\mathsf{\theta }$-direction. The importance of it lies in that the metasurface is essentially an anisotropic medium, and the spectral behavior (of MPA) is analyzed when the incident angle $\mathsf{\theta }$ sweeps a wide range under transverse electric (TE) and transverse magnetic (TM) polarizations (of the incidence excitation). Also, in some cases, the results are obtained corresponding to the two different values of the azimuthal angle $\mathsf{\varphi }$ (viz. $0°$ and $90°$), in order to illustrate the effect of $\mathsf{\varphi }$ on the absorption characteristics. The scattering matrix, developed by the CST simulator, is used to analyze the frequency-dependent absorption of the MPA structure; the detector is essentially considered as placed below the copper nanolayer.

3. Results and Discussion

Figure 2 illustrates the refractive index (RI) dependence of gold and copper on the wavelength $\lambda$ in the NUV and NIR regions (200–1500 nm) of the EM spectrum. Since the RI values remain complex in nature, we represent those in the cases of gold (Au) and copper (Cu) as $n_{Au}\left(\mathsf{\lambda }\right)=n_{Au}^{\prime }\left(\mathsf{\lambda }\right)+j{n}_{Au}^{\prime \prime }\left(\mathsf{\lambda }\right)$ and $n_{Cu}\left(\mathsf{\lambda }\right)=n_{Cu}^{\prime }\left(\mathsf{\lambda }\right)+j{n}_{Cu}^{\prime \prime }\left(\mathsf{\lambda }\right)$, respectively. Further the RI value of Si is taken as $3.45+j6.4\times {10}^{-5}$. It is clear from Figure 2 that gold and copper both exhibit decrease in RI with increasing wavelength, and for higher wavelengths, the RI values become almost independent (of wavelength). Also, the imaginary part of RI remains larger for higher wavelengths.

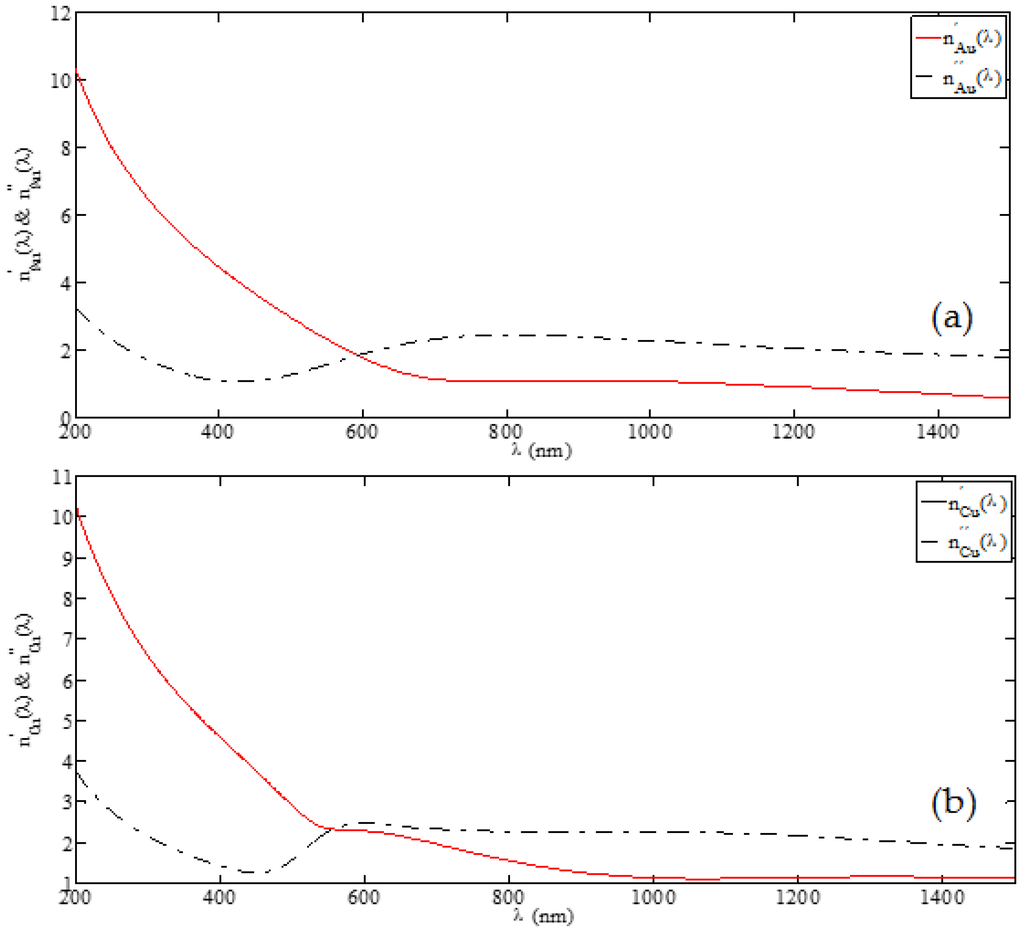
Figure 2. RI dependence on wavelength for (a) gold Au and (b) copper Cu.

Figure 3 and Figure 4 illustrate absorption patterns for the MPA structure under consideration. In these plots, the behavioral features of the absorption coefficient $A$ are shown against the wavelength $\mathsf{\lambda }$ in the NUV and NIR regions (as described above) corresponding to the different incident angles $\mathsf{\theta }$ (keeping the azimuthal angle as $\mathsf{\varphi }=0°$), metasurface thickness $d$, Si layer thickness $t$ and the polarization states of the incident light (i.e., TE or TM). The angle of incidence is varied from $30°$ to $70°$ in a step of $10°$. The incident angles below $30°$ and above $70°$ yield absorption characteristics in the lower and the higher spectral bands, wherein alterations have been observed to be less significant as compared to those obtained for the angular range between $30°$ and $70°$, and therefore, those portions of absorption spectra are not taken into account. It must be noted down at this point that the EM waves are generally allowed to sweep across the target with various angles of incidence $\mathsf{\theta }$, and therefore, the azimuthal angle $\mathsf{\varphi }$ is kept fixed to $0°$ in this case.

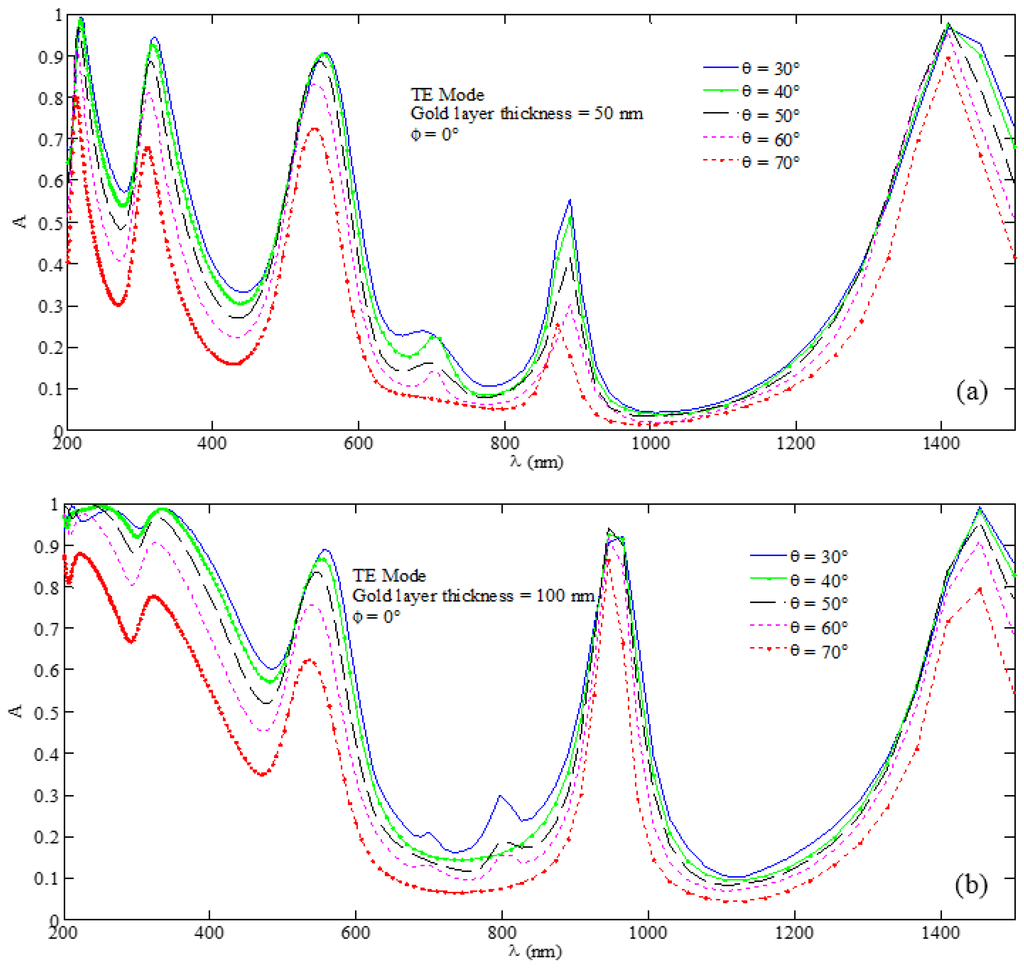
Figure 3. Absorption spectra for the butt-facing U-shaped MPA nanostructure under the TE wave excitation with $\mathsf{\varphi }=0°$ incidence and corresponding to the cases of (a) $d=50$ nm and (b) $d=100$ nm with $t=100$ nm.

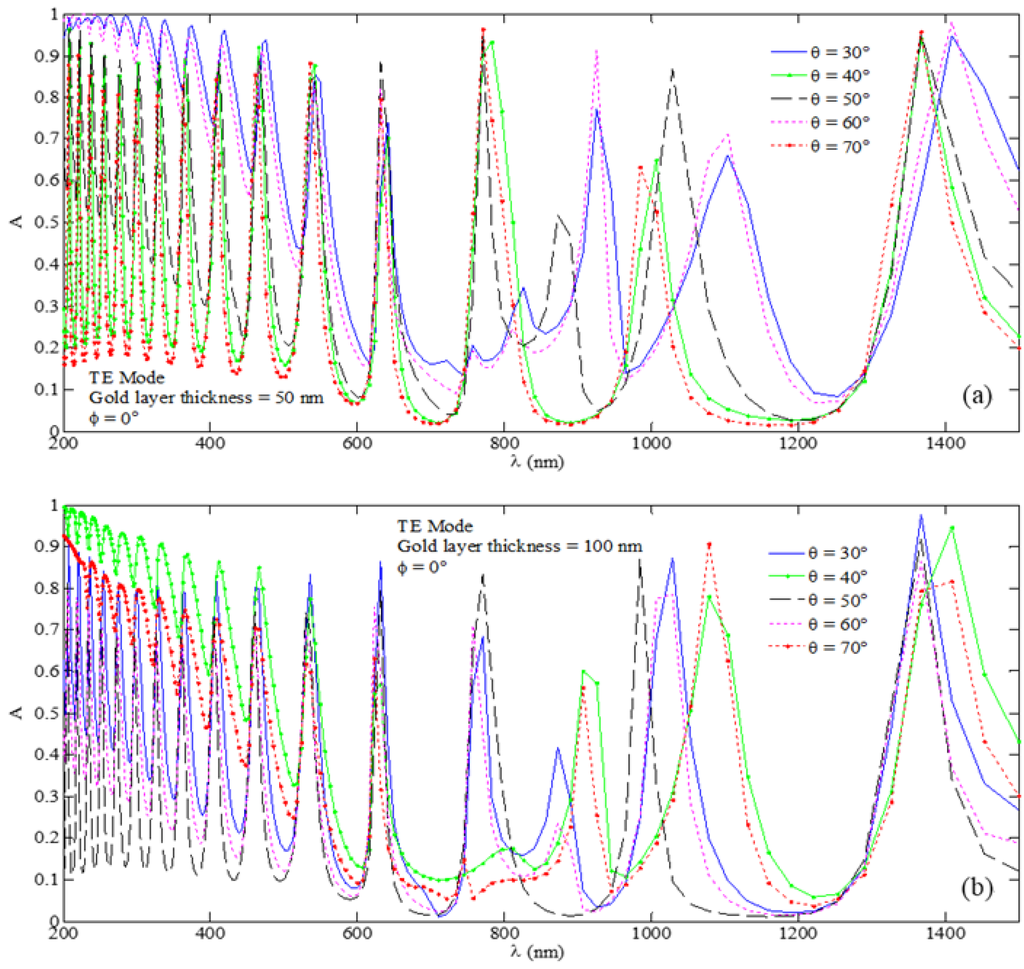
Figure 4. Absorption spectra for the butt-facing U-shaped MPA nanostructure under the TE wave excitation with $\mathsf{\varphi }=0°$ incidence and corresponding to the cases of (a) $d=50$ nm and (b) $d=100$ nm with $t=500$ nm.

Figure 3a shows absorption spectra under the TE polarization state of incident light when the thickness $d$ of the metasurface is 50 nm. It can be observed that, among the other peaks at different wavelengths, the MPA structure exhibits the highest absorptivity $(~0.992$) at the angle $\mathsf{\theta }=30°$ corresponding to the wavelength $~$219.08 nm. The first plasmonic peak appears between 200 and 325 nm, and the lowest peak in this range appears corresponding to $\mathsf{\theta }=70°$ at the wavelength $~$212 nm. The increase in incidence angle form $\mathsf{\theta }=30°$ to $\mathsf{\theta }=70°$ causes small blue-shifts in the absorption peak. The second and the third plasmonic peaks, that yield more than 96% absorption, appear in the visible regime with wavelength spans $~$309.0–319.76 nm and $~$536.3–555.8 nm, respectively. This briefly shows that the angle of incidence of the incoming wave would effectively lead to wider blue-shift at the upper band of the NUV class.

Besides these, Figure 3a depicts that there are two more peaks located at the lower and the upper bands of the NIR class. The first peak is less significant owing to low absorptivity (which is less than 60%) at $\mathsf{\lambda }\approx 900$ nm, but the second peak at $\mathsf{\lambda }\approx 1400$ nm possesses different characteristics, as compared to the rest of the peaks. It can be clearly noticed from Figure 3a that the MPA shows very high absorptivity ($A\approx 0.9817$) corresponding to $\mathsf{\theta }=50°$, as compared to the other values of incident angles. More importantly, the effect of blue-shifts in absorption spectra almost vanishes for all incidence angles when the absorption peaks remain centered at $\mathsf{\lambda }\approx 1408$ nm with the absorptivity value as $A\approx 0.98$.

Results corresponding to the TE wave incidence excitation for $d=100$ nm show different absorptivity conditions (Figure 3b). This case clearly indicates that the wavelength range $~$200–370 nm is considerable since, at the incidence angles $\mathsf{\theta }=30°$ and $\mathsf{\theta }=40°$, absorptivity remains above 90%. Further, the absorption peaks in this range are not enough sharp; the maximum sharpness is achieved near $\mathsf{\lambda }\approx 370$ nm. In Figure 3b, the actual plasmonic peaks in the visible range appear in the wavelength span $~$539–555 nm, and similar to the situation for $d=50$ nm, the highest absorption peak appears at $\mathsf{\lambda }\approx 555.8$ nm corresponding to $\mathsf{\theta }=30°$ incidence.

The most important feature of spectral behavior corresponding to the TE-polarized incident wave is that, while using the metamaterial thickness $d=50$ nm, the absorption peaks are weak in terms of sharpness, whereas the choice of $d=100$ nm makes the peaks strongly magnified and centered at $\mathsf{\lambda }\approx 940$ nm. In Figure 3b as well, the blue-shifts in absorption peak, as a result of variation in incidence angle, remain strongly obvious. In this figure, the peak amplitude of absorption corresponding to $\mathsf{\theta }=30°$ and $\mathsf{\lambda }\approx 964.45$ nm is almost 92%, whereas for $\mathsf{\theta }=70°$ and $\mathsf{\lambda }\approx 944.62$ nm, it is nearly 86%. This clearly indicates a shift of $~$20 nm due to the$40°$ rotation of incidence angle of the wave.

The last set of peaks in Figure 3b, in contrast to the case of $d=50$ nm (Figure 3a), indicates that $\mathsf{\theta }=30°$ is the incidence angle where the highest peak (with 99.1% absorption) appears at $\mathsf{\lambda }\approx 1452.5$ nm. Further, similar to the case of Figure 3a, the choice of $d=100$ nm eliminates blue-shifts of plasmonic peaks in the wavelength range in the vicinity of $\mathsf{\lambda }\approx 1400$ nm.

In order to see the effect of the Si layer, the thickness $t$ (of this region) is increased to 500 nm, and the absorption spectra are shown in Figure 4. Comparing the results with those obtained with the 100 nm thick Si layer (Figure 3), it can be observed that the number of absorption peaks is now significantly enhanced, and the structure behaves as comb filter [14]. The reason for this is very obvious: the enlarged thickness of wave trapping section will essentially allow proliferation of modes, thereby causing the existence of more absorption peaks. A comparative look at Figure 4a,b leaves impression that the increase of metasurface thickness results in a little more absorption peaks—the feature that has been observed to some extent in Figure 4 too, corresponding to the case of 100 nm Si layer thickness. However, it is the combinational effect of both the metasurface thickness and the wave confinement section thickness that ultimately enhances (or manipulates) absorption peaks of the MPA. This is further justified from Figure 4 which demonstrates over 99% absorption in the short wavelength span with 50 nm metasurface thickness.

The cases discussed in Figure 3 and Figure 4 correspond to the situation when the azimuthal angle $\mathsf{\varphi }$ assumes $0°$ value. As the metasurface is anisotropic in nature, it would be interesting to observe the effect of $\mathsf{\varphi }$ on the absorption characteristics. Figure 5 illustrates the case when the TE wave incidence happens with $\mathsf{\varphi }=90°$; the sweeping values of the angle $\mathsf{\theta }$ are taken similarly as in the afore-discussed situations. Further, we choose the illustrative cases of metasurface layer thickness $d=50$ nm (Figure 5a) and $d=100$ nm (Figure 5b), keeping the Si layer thickness fixed to $t=100$ nm.

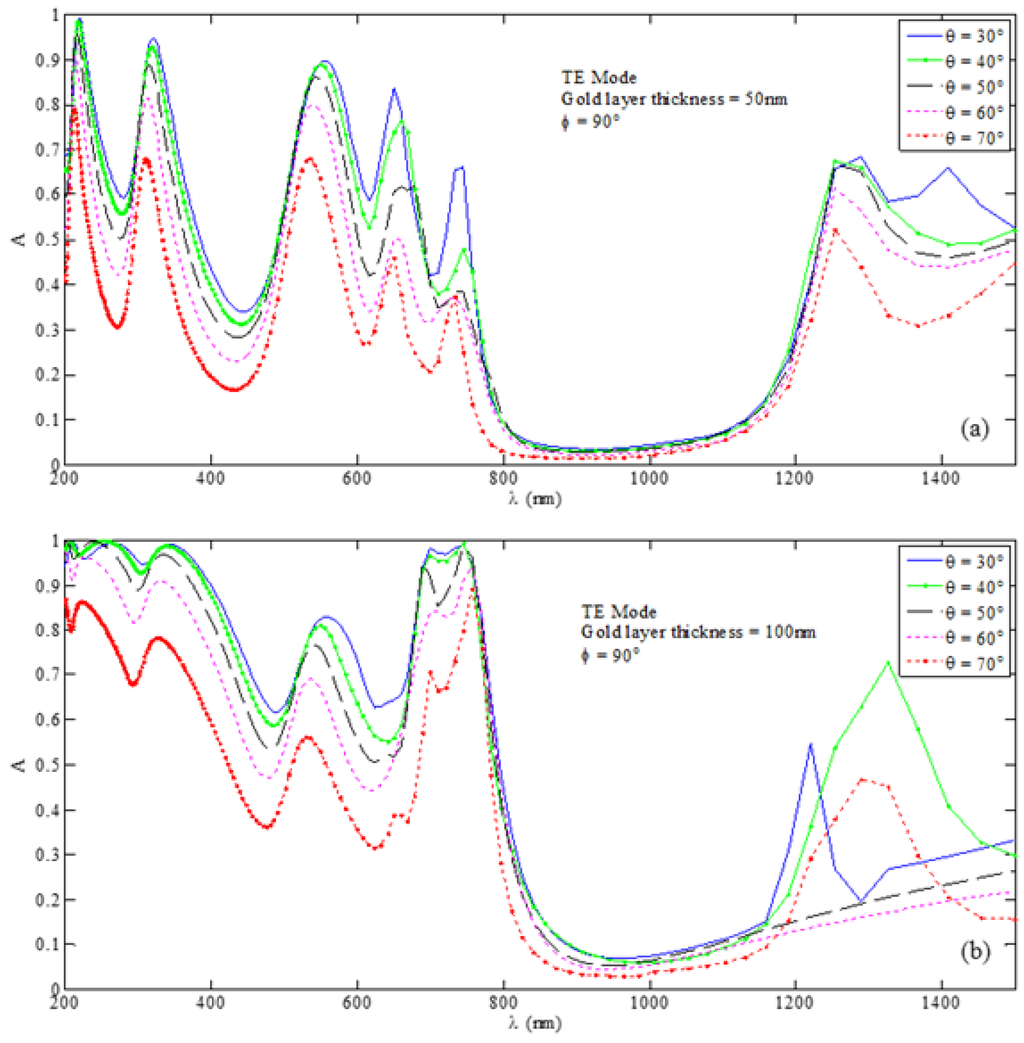
Figure 5. Absorption spectra for the U-shaped MPA nanostructure under the TE wave excitation with $\mathsf{\varphi }=90°$ incidence and corresponding to the cases of (a) $d=50$ nm and (b) $d=100$ nm with $t=100$ nm.

We observe in Figure 5 that, in both the situations, the patterns of absorption features are significantly altered, and the positions of absorption peaks are less prominently defined, as compared to that in Figure 3. This happened in the entire range of wavelength under consideration. As such, the choice of $\mathsf{\varphi }=90°$ may not be that appropriate for the usage of the metasurface-based device for the absorber kinds of applications.

Absorption patterns corresponding to the TM-polarized incident waves (Figure 6) are almost similar to that obtained for the TE excitation (Figure 3). However, enhanced sharpness and amplification of absorption peaks, as observed for both the values of metasurface thickness (i.e., $d=50$ nm (Figure 6a) and $d=100$ nm (Figure 6b)), are the primary advantages of using the TM-polarized incident field over the TE-polarized one (Figure 3). It is clear from Figure 6a that the use of metasurface thickness as 50 nm would yield almost 99.9% absorption at $\mathsf{\lambda }\approx 1440$ nm under the situation of $\mathsf{\theta }=30°$ incidence. Figure 6b shows that the same incidence angle would provide $~99.9\%$ absorption at $\mathsf{\lambda }\approx 955$ nm when the metasurface assumes 50 nm thickness. It is clear from Figure 3 and Figure 6 that such a high amount of absorption is rarely achieved with the TE-polarized incidence excitation except in the long wavelength range ($\mathsf{\lambda }\approx 1415$ nm), taking into account 100 nm metasurface thickness (Figure 3b) and $30°$ incidence angle. It can thus be remarked that Figure 6a,b exhibit a $30°$ angle of incidence as promising to achieve the highest absorptivity in this case, which is similar to the situation of Figure 3 corresponding to the case of TE incidence excitation.

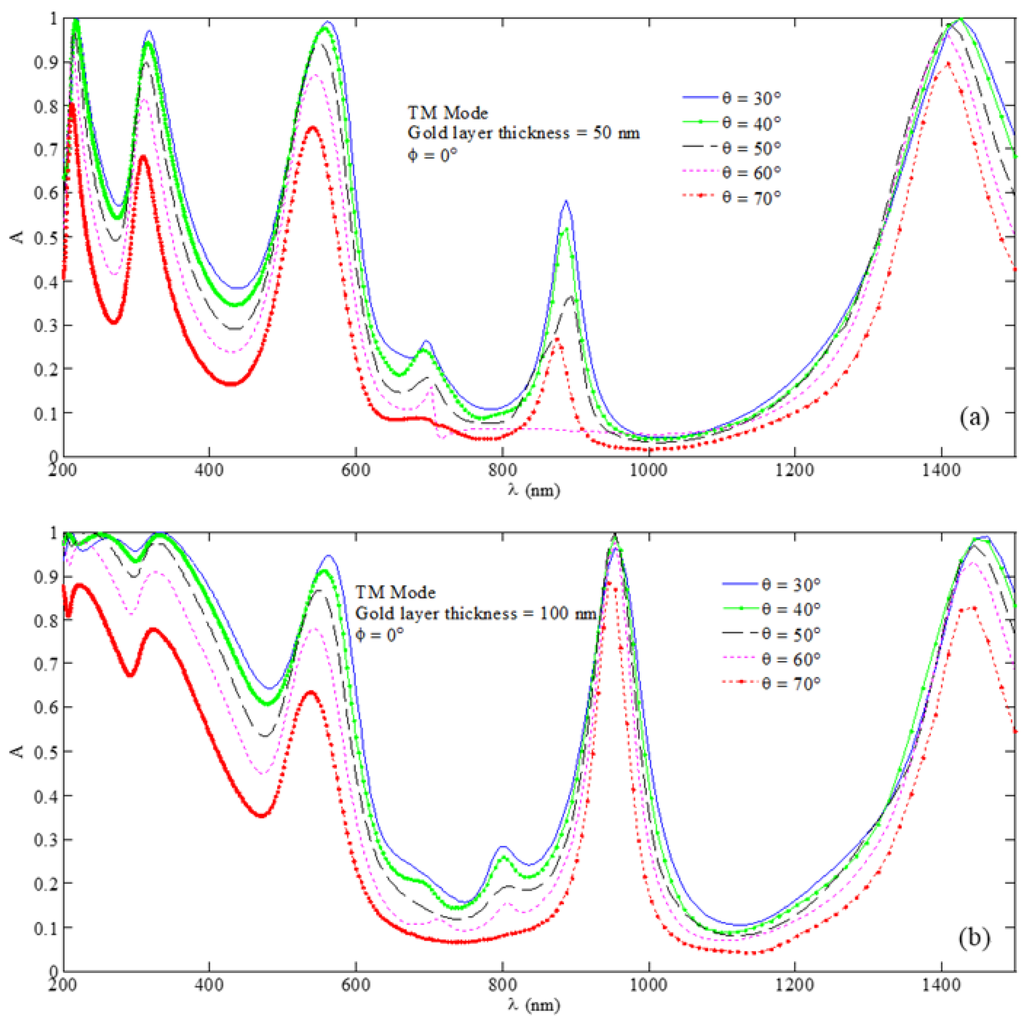
Figure 6. Absorption spectra for the butt-facing U-shaped MPA nanostructure under the TM wave excitation with $\mathsf{\varphi }=0°$ incidence and corresponding to the cases of (a) $d=50$ nm and (b) $d=100$ nm with $t=100$ nm.

Figure 7 shows absorption spectra of the MPA structure when the Si layer assumes 500 nm thickness. The trend of absorption patterns is observed to be similar to the case of TE-polarized incidence, i.e., the increase of Si layer thickness enhances the number of sustained modes within the light trapping medium, thereby causing enhancement of absorption peaks. As such, a proper adjustment of the thicknesses of metasurface and wave confinement regions would yield the desired absorption in a particular wavelength span; indeed, the polarization state and the angle of incidence also play very important roles in this regard.

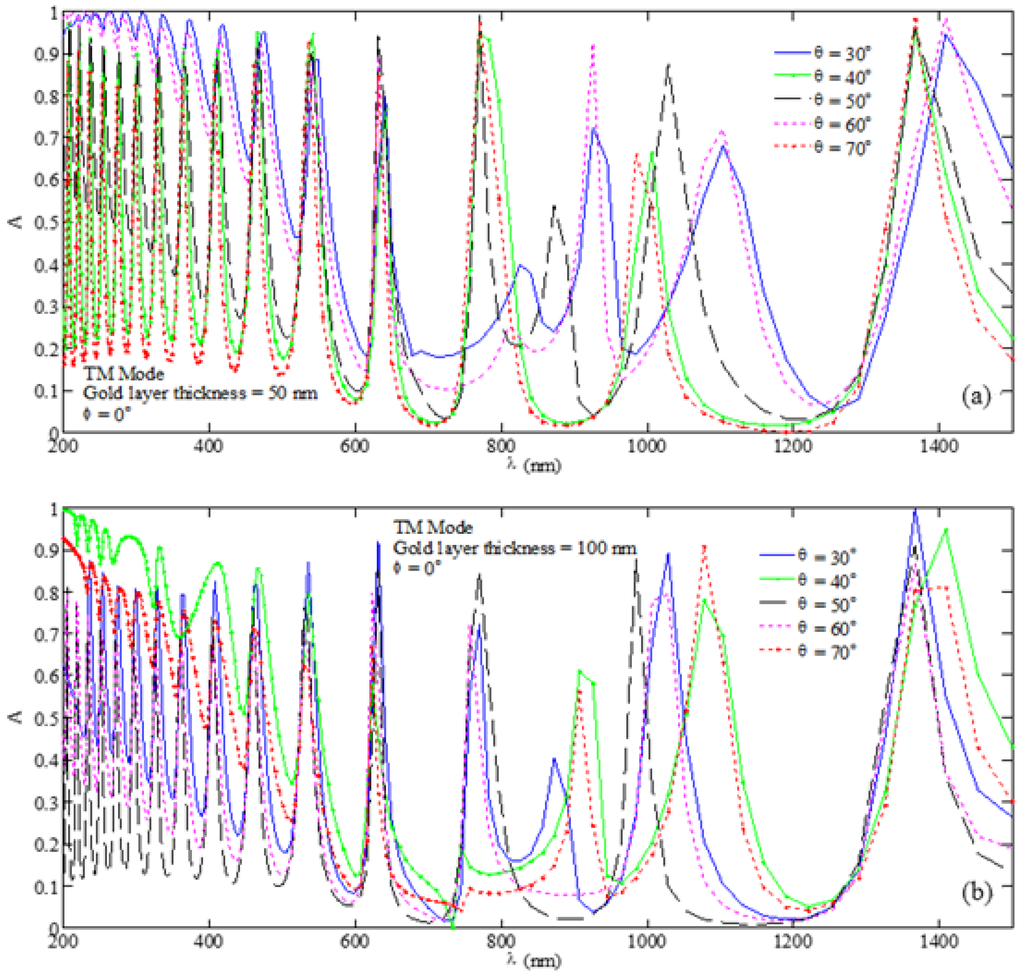
Figure 7. Absorption spectra for the butt-facing U-shaped MPA nanostructure under the TM wave excitation with $\mathsf{\varphi }=0°$ incidence and corresponding to the cases of (a) $d=50$ nm and (b) $d=100$ nm with $t=500$ nm.

Figure 8 exhibits the plots of absorption under the TM wave excitation with $\mathsf{\varphi }=90°$. The other parametric values are chosen in the same way as those in the case of Figure 5, i.e., keeping the Si layer thickness $t$ fixed to 100 nm, the metasurface layer thickness $d$ to 50 nm and 100 nm, and sweeping angle $\mathsf{\theta }$ as $30°$, $40°$, $50°$, $60°$ and $70°$. We find that, also in this case, the absorption peaks are not prominent enough (in comparison with those in Figure 6) for particular usage, and therefore, the choice of $\mathsf{\varphi }=90°$ would not be appropriate enough to obtain significantly application oriented results. In the present paper, however, such results are shown just in order to observe the anisotropic features of the metasurface in use.

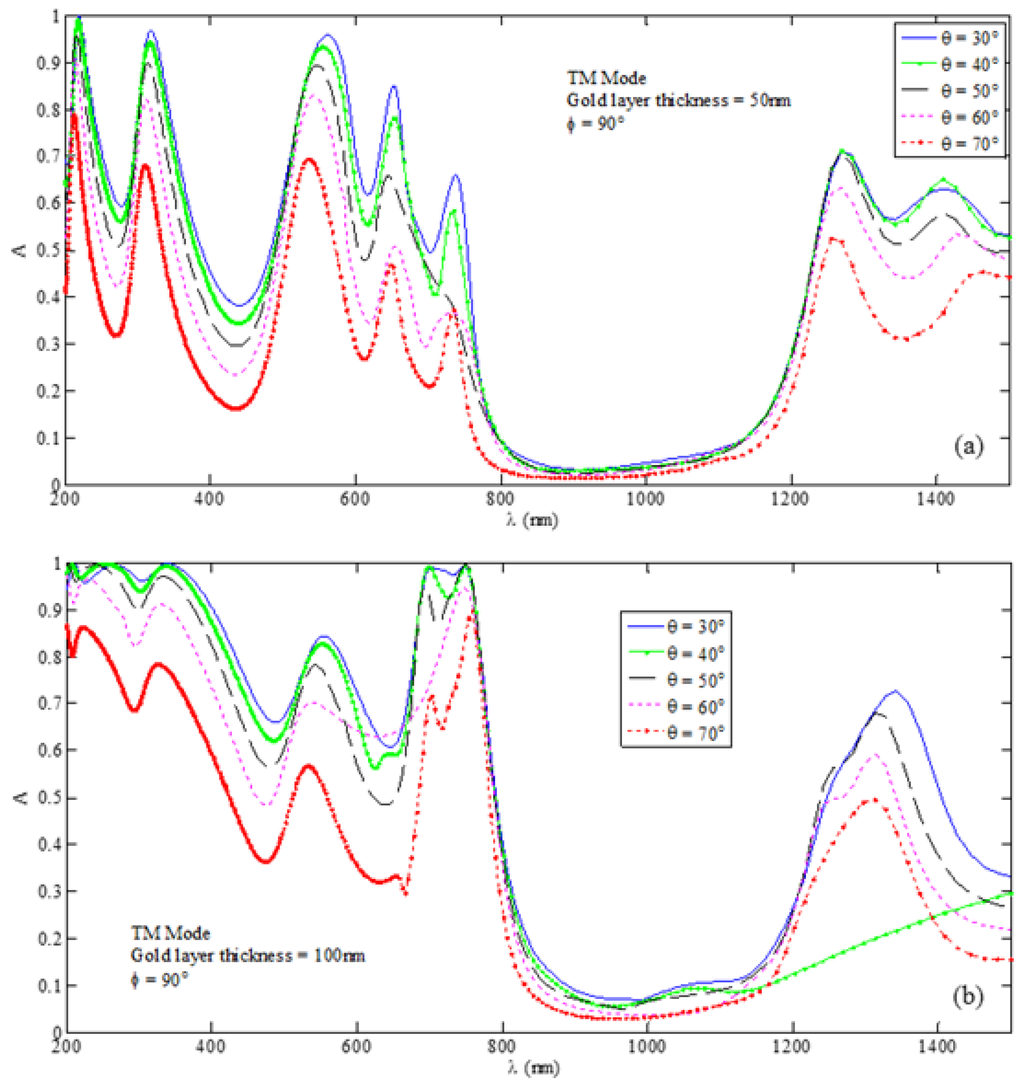
Figure 8. Absorption spectra for the U-shaped MPA nanostructure under the TM wave with $\mathsf{\varphi }=90°$ excitation incidence and corresponding to the cases of (a) $d=50$ nm and (b) $d=100$ nm with $t=100$ nm.

The absorption characteristics of the MPA structure having different dimensional features are further investigated by incorporating the electric field patterns. However, it must be noted that the presence of multiple peaks in absorption spectra essentially corresponds to different resonant conditions. As such, some of the absorption peaks are chosen that typically exhibit the minimum and the maximum values of absorption under certain dimensional features, incident angles and polarization states of the incidence excitation.

In this context, Figure 9 and Figure 10, respectively, illustrate the electric field distribution patterns for the MPA structure with the thickness $d$ (of metasurface) as 50 nm and 100 nm; in both the cases, the thickness $t$ of light trapping medium is taken as 100 nm and the incidence excitation as the TE-polarized one. However, for other dimensional features (of the MPA) and excitation as well, field patterns may be obtained, but those are not incorporated into the text. Instead, typical field distributions for a particular value of the angle of incidence $\mathsf{\theta }$, as evolved corresponding to the absorption maxima and minima, are considered.

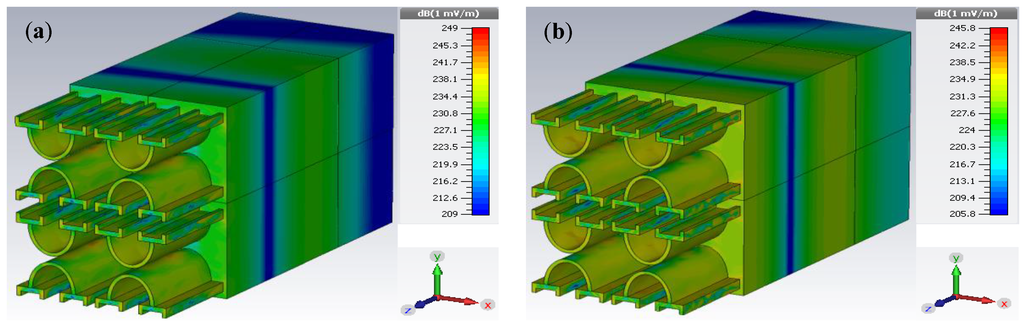
Figure 9. Electric field distributions under the TE-polarized incidence excitation corresponding to (a) $\mathsf{\lambda }=565.11$ nm, $\mathsf{\theta }=30°$ and (b) $\mathsf{\lambda }=541.2$ nm, $\mathsf{\theta }=70°$, taking into account $d=50$ nm and $t=100$ nm.

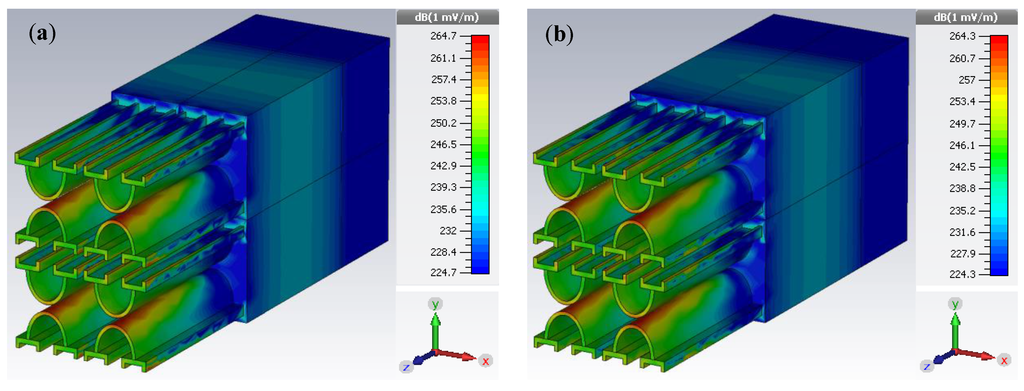
Figure 10. Electric field distributions under the TE-polarized incidence excitation corresponding to (a) $\mathsf{\lambda }=953.5$ nm, $\mathsf{\theta }=30°$ and (b) $\mathsf{\lambda }=945.6$ nm, $\mathsf{\theta }=70°$, taking into account $d=100$ nm and $t=100$ nm.

It can be observed from Figure 3a that, corresponding to the metasurface thickness $d$ as 50 nm, the TE-polarized wave excitation gives the maximum absorbance of 98.8% at $\mathsf{\theta }=30°$ for wavelength $\mathsf{\lambda }=565.11$ nm, and the minimum absorbance of 74.2% at $\mathsf{\theta }=70°$ for $\mathsf{\lambda }=541.2$ nm. These situations are, respectively, depicted in Figure 9a,b, emphasizing the field distributions. Figure 9a shows that the field is highly concentrated in the Si section (of the MPA structure), and the intensity of field (in this section) is higher than that observed in Figure 9b (corresponding to the case of lower absorptivity)—the theme which is very much justified from the absorption spectra of Figure 3a.

Figure 10a,b respectively, depict the field distributions obtained corresponding to the TE-polarized incidence excitation with the incidence angles $30°$ and $70°$, and when the metasurface thickness $d$ is increased to 100 nm. Similar to Figure 9, also in this case, the field configurations are obtained for the wavelength values that yield the maximum (for $\mathsf{\lambda }=953.5$ nm, $\mathsf{\theta }=30°$) and the minimum (for $\mathsf{\lambda }=945.6$ nm, $\mathsf{\theta }=70°$) absorption. It can be noticed that the increase of metasurface thickness causes the electric field to extend to the lower edges of nanostructured resonator, except for its confinement in the Si layer. In the case of larger thickness of metasurface, the electric field exhibits significant coupling with the edges of the metamaterial structure. The absorption of incident waves happens due to the confinement of electric field on the edges of metallic resonator. With the increase in incidence angle, the field starts entering the substrate region, thereby reducing the absorbance.

Along with the afore-discussed issues of the absorption characteristics of the device, one may think of the features of absorbance that may be achieved in the absence of nanoengineered gold metasurface (shown in Figure 1). With this view point, the results are obtained corresponding to the excitations of TE (Figure 11) and TM (Figure 12) modes with the sweep in $\mathsf{\theta }$ as $30°$, $40°$, $50°$, $60°$ and $70°$. As the upper layer is now isotropic in nature, the angle $\mathsf{\varphi }$ will essentially have no effect on the results. Further, similar to the previously discussed cases, we consider two values of the Si layer thickness, viz. $t=100$ nm and $t=500$ nm.

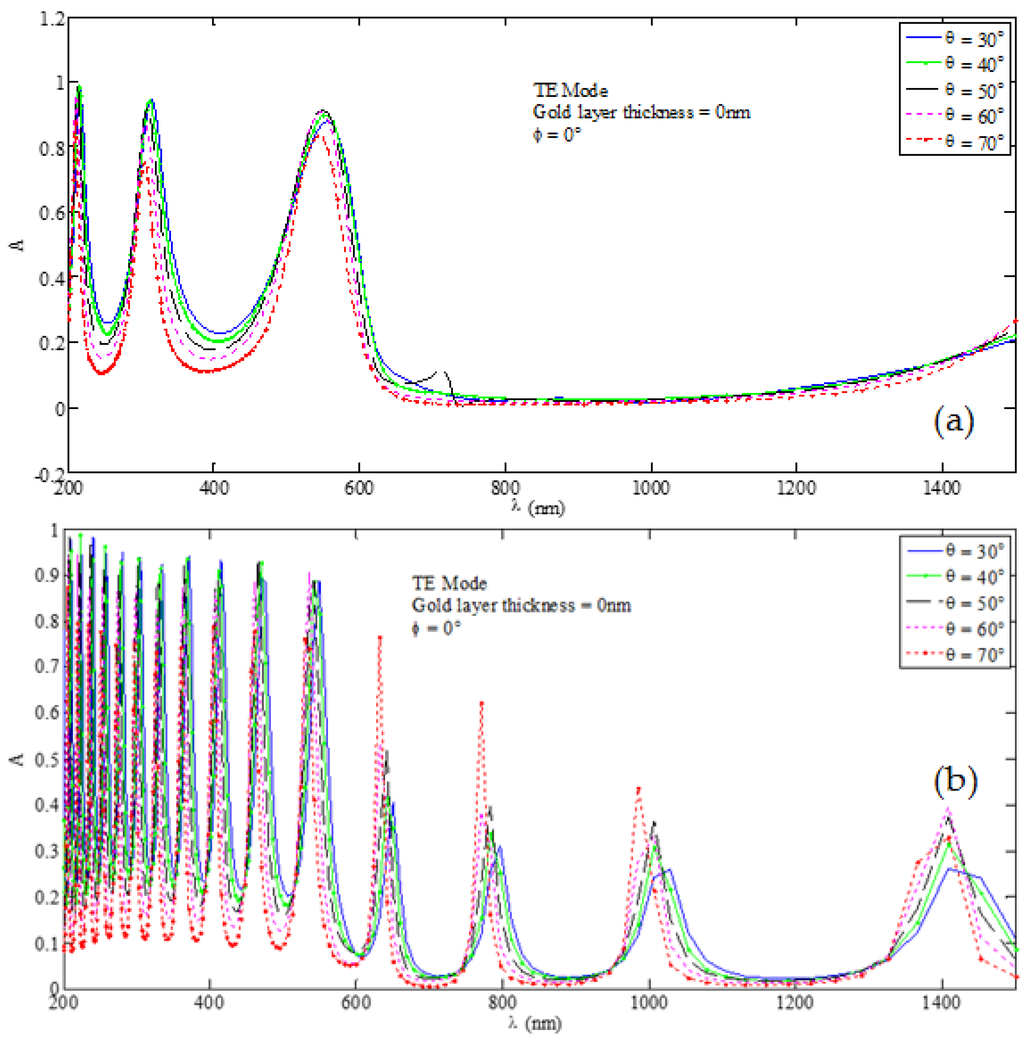
Figure 11. Absorption spectra obtained for $d=0$ under the TE wave excitation incidence and corresponding to (a) $t=100$ nm and (b) $t=500$ nm.

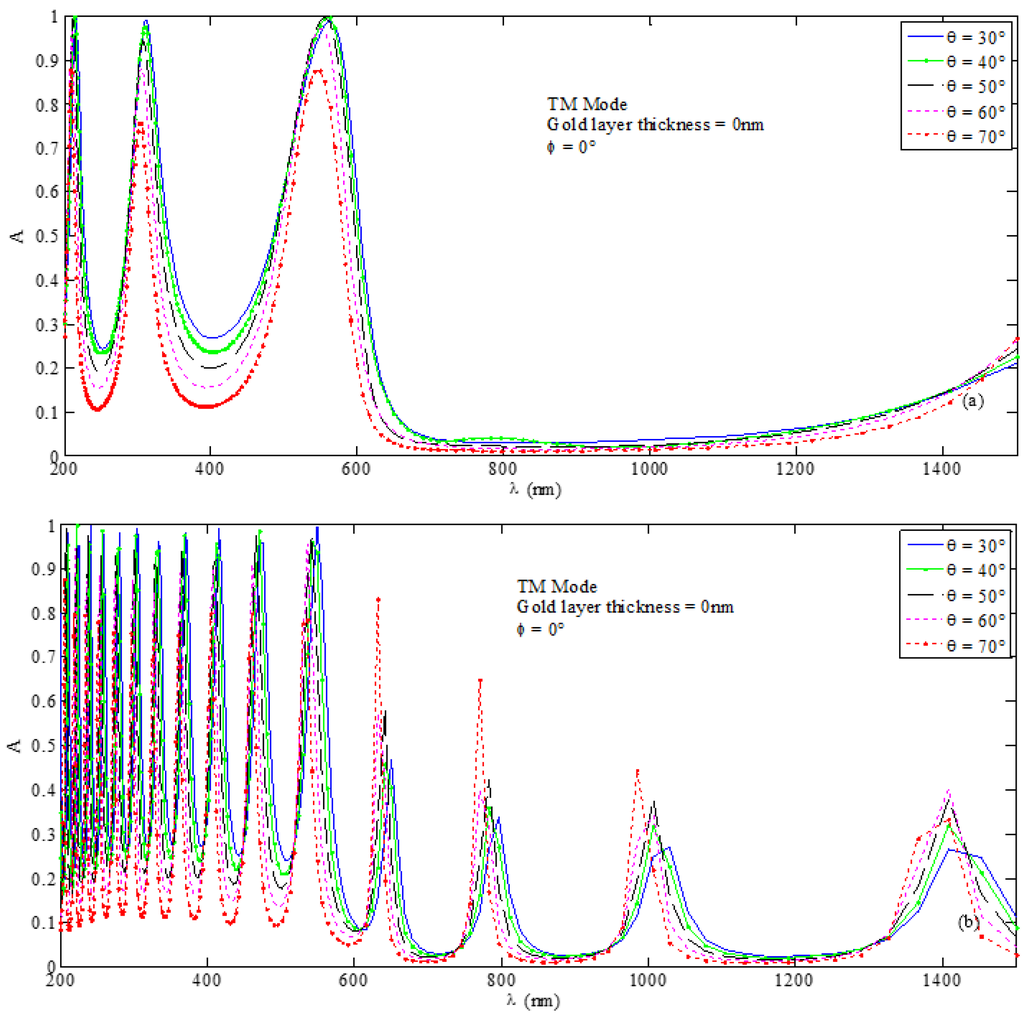
Figure 12. Absorption spectra obtained for $d=0$ under the TM wave excitation incidence and corresponding to (a) $t=100$ nm and (b) $t=500$ nm.

Figure 11a,b, respectively, illustrate the absorption characteristics corresponding to the Si layer thickness as 100 nm and 500 nm, and in the absence of metasurface layer (i.e., $d=0$). Comparing the results in Figure 3 and Figure 11a, we observe that, under the TE mode excitation, the presence of metasurface enhances the number of absorption peaks particularly in the longer wavelength range. Clearly, the peaks in regions with $\mathsf{\lambda }\approx 900$ nm and $\mathsf{\lambda }\approx 1400$ nm vanish in the absence of gold metasurface. Also, the variation in $\mathsf{\theta }$ has more profound impact on the absorbance in the presence of metasurface, which is essentially due to the plasmonic effect. Further, the increase of the Si layer thickness to 500 nm certainly enhances the number of peaks (Figure 11b), but the comparison of these results with that in Figure 4 clearly indicates the enhancement of absorption in the mid to the longer wavelength ranges of operation. As such, the efficacy of the presence of gold metasurface is justified as the device can then exhibit significantly improved features of absorption.

Similar characteristics can be observed corresponding to the TM mode excitation as well, upon comparing the results of Figure 12 with those in Figure 6 (for $t=100$ nm) and 7 (for $t=500$ nm). We notice that the elimination of gold metasurface greatly affects the absorption patterns in the form of reducing/eliminating absorbance in the longer wavelength range, irrespective of the chosen values of the Si layer thickness. Angular variations also result in a similar way to that described above.

Finally, the novelty of the proposed MPA design lies in that the device would yield nearly 100% absorption of the incidence waves in the visible region of the EM spectrum—the feature that would find potential applications in miniaturized EM energy harvesting gadgets. Apart from this, the device would also be useful in filtering applications in a wide range of wavelengths, as evidenced by the absorption spectra.

4. Conclusions

Studies have been performed of the butt-facing U-shaped metamaterial nanostructure (of gold) to achieve multi-plasmonic peaks at the visible and the NUV spectral bands. The emphasis has been given on the performance of MPA under varying thicknesses of the metasurface as well as the light trapping Si layer, and the TE and TM polarizations of the incidence excitation fields. It has been observed that, upon changing the angle of incidence (of the incoming light), absorptivity of the proposed MPA efficiently reaches above 99% over the short wavelength span, and, moreover, this feature happens with both the TE- and the TM-polarized incident light. Such a value of absorptivity has also been noticed in the long wavelength regime as well with almost vanishing blue-shift under varying angle of incidence. With these remarks, the obtained results indicate usefulness of the proposed MPA structure as an efficient metamaterial absorber.