Abstract
With the development of wave energy, a promising renewable resource, oscillating water column (OWC) devices, has been extensively studied for its potential in harnessing this energy. However, traditional OWC devices face challenges such as corrosion and damage from prolonged exposure to harsh marine environments, limiting their long-term viability and efficiency. To address these limitations, this paper proposes a novel U-tube type dual chamber OWC wave energy conversion device integrated within a marine vehicle. The research involves the design of a U-tube dual-chamber OWC device, which utilizes the pitch motion of a marine vehicle to drive the oscillation of water columns within the U-tube, generating reciprocating airflow that drives an air turbine. Numerical simulations using computational fluid dynamics (CFD) were conducted to analyze the effects of various structural dimensions, including device length, width, air chamber height, U-tube channel width, and bottom channel height, on the aerodynamic power output. The simulations considered real sea conditions, focusing on low-frequency waves prevalent in China’s sea areas. Simulation results reveal that increasing the device’s length and width substantially boosts aerodynamic power, while air chamber height and U-tube channel width have minor effects. These findings provide valuable insights into the optimal design of U-tube dual-chamber OWC devices for efficient wave energy conversion, laying the foundation for future physical prototype development and experimental validation.
1. Introduction
The field of marine renewable energy encompasses various forms of energy derived from the ocean, including tidal, marine current, wave, ocean thermal and salinity gradient resources [1,2,3]. Among these energy sources, wave energy stands out for its high energy density and relatively low environmental impact [4,5]. As one of the most promising marine energy sources, wave energy has garnered significant attention due to its wide spatial distribution and abundant reserves. It is estimated that the global wave energy reserves amount to approximately 2 terawatts (TW), with a technical potential of up to 90% availability throughout the year [6,7]. Due to climate change, renewable energy sources such as solar, wave, and tidal power are being actively explored worldwide for electricity generation [8]. Therefore, research on wave energy holds significant importance.
Over the past years, various innovative wave energy converters (WECs) have been developed and tested [9,10]. Based on deployment location, WECs may be classified into floating and shore-fixed configurations [11,12,13]. Among all existing WEC technologies, oscillating water column (OWC) devices have received extensive research attention [10]. OWC technology is widely recognized as a promising wave energy conversion system with substantial resource potential [9]. As shown in Figure 1, OWC devices have already been applied in practical applications, including, for instance, the Limpet Wave Energy Converter [14], the REWEC3 [15], OE Buoy [16]. However, existing OWC designs require direct contact with seawater, making them highly susceptible to damage under extreme sea conditions and corrosion during prolonged exposure. To address this limitation, this paper proposes an OWC device integrating into the interior of marine vessel, aiming to significantly reduce the impact of extreme sea conditions and prevent corrosion caused by direct exposure to seawater.

Figure 1.
OWC devices: (a) the Limpet WEC, (b) the REWEC3, (c) OE Buoy, (d) Jida.4th.
The development of the sloshing tank experimental apparatus traces its origins to the pioneering investigations of William Froude. The central challenge of Froude’s research was to mitigate the inherent rolling motion encountered by ships navigating through rough seas [17]. In recent decades, research on the performance characteristics of sloshing tank systems has stimulated extensive investigation within the marine engineering community. Early numerical modeling studies of fluid motion in U-tube tanks were initiated by Stigte [18]. Subsequently, Lloyd [19] developed a simplified one-dimensional model based on the Euler momentum equation to study rolling oscillations in U-tube tanks. With significant advancements in computational capabilities, Zhong [20] conducted more in-depth research using the finite element method for two-dimensional computational fluid dynamics (CFD) simulations. Their approach implemented a finite element discretization of the Navier–Stokes equations via the Galerkin weighted residual formulation. This method was also applied by Van Daalen et al. [21] and Bhushnan et al. [22] when studying the performance of U-shaped water tanks through fully three-dimensional (3D) CFD simulations and validated by experimental results.
Traditionally, U-shaped tank research focused on ship roll stabilization [23]. In contrast, this study proposes an integrated solution embedding a WEC device within a ship’s hull to provide backup power for navigational instruments. By coupling vessel roll motion to an OWC wave energy converter integrated with a U-tank system, this approach expands U-tank applications beyond conventional stabilization.
Inspired by U-shaped roll stabilization tanks [24,25], this paper proposes a U-tube dual-chamber oscillating water column device (U-OWC). The U-OWC structure eliminates the need for direct contact with seawater, avoiding direct wave action. Similar to conventional OWC devices, the air turbine of the U-OWC is installed in the passage connecting the air chamber to the atmosphere. Crucially, unlike typical OWC deployments, the novelty of this converter lies in its placement inside a ship, isolated from seawater. The vessel’s motion during navigation causes the internal water column to oscillate, continuously compressing and expanding the air within the two air chambers. The resulting pressure difference drives reciprocating airflow through the turbine. When the airflow passes through the air turbine, it drives the turbine’s rotation, thereby powering a generator to produce electricity.
The remainder of this paper is organized as follows: Section 2 introduces the proposed U-OWC; Section 3 presents the numerical model; Section 4 describes the simulation setup for the newly proposed U-tube dual-chamber oscillating water column device; Section 5 details the numerical simulation calculations for the same; and Section 6 presents the results and discussions.
2. The Design of U-Tube Dual Chamber OWC
Most conventional OWC devices operate through direct interaction with seawater, where waves directly impinge upon the device, inducing vertical oscillations in the internal water column as a result of external wave forces [26]. This motion periodically compresses and releases the air within the air chamber, generating bidirectional airflow. The airflow is then converted into unidirectional rotation by a turbine (typically a Wells turbine or an impulse turbine) [27,28].
In contrast, the proposed U-tube dual-chamber OWC is installed inside a marine vessel. When waves act upon the vessel, they induce oscillatory motions (e.g., roll, pitch, or heave), which are transmitted to the U-OWC. This design converts wave energy into mechanical energy and ultimately electricity through its unique structure (as shown in Figure 2).
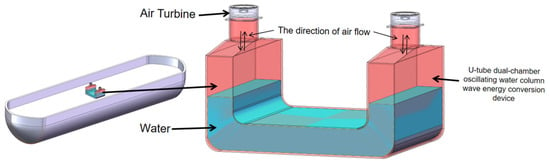
Figure 2.
Structural design of a novel U-tube dual-chamber oscillating water column wave energy conversion device.
The U-OWC (Figure 2) consists of a hollow U-tube with two identical rectangular air chambers at its ends. Each chamber has a cylindrical outlet of a uniform cross-sectional area. Two air turbines are installed separately in the duct connecting each air chamber to the atmosphere, housed in the cylindrical channels above each chamber in the simulated configuration.
3. Numerical Model
For this research, the thermodynamic behavior of the gaseous medium within the computational framework is governed by the ideal gas equation of state. Given that airflow velocities in the chamber remain below Mach 0.3 (approximately 102 m/s), a threshold permitting treatment as an incompressible fluid, air compressibility effects are consequently neglected throughout the simulations [29]. The aerodynamic power of the air chambers is calculated as follows [30]:
where is the aerodynamic power of one of the two air chambers, ΔP is defined as the differential pressure between the internal chamber pressure and atmospheric pressure, is the real-time air flow rate through the chamber’s top opening, is the real-time vertical air velocity through the orifice, and S is the cross-sectional area of the orifice.
The generation of air flow caused by pressure changes in the air chamber originates from the rising and falling movement of the free liquid surface within the air chamber. The gas flow rate can be derived based on the movement of the liquid level or changes in the air chamber volume [31]:
where is the air turbine coefficient and is the pressure drop in the air chamber, Q indicates the air volume flow rate, and V indicates the air chamber volume that changes with the rise and fall of the liquid level.
In the U-OWC, the two pneumatic chambers operate independently. Consequently, the total efficiency of the dual-chamber OWC system equals the arithmetic sum of the individual efficiencies of each chamber:
The continuity and momentum equations in incompressible flows are defined as in Equation (4) and Equation (5), respectively [32]:
where , t, P, , p, and t are velocity components, time, static pressure, body force density, dynamic viscosity, and turbulence viscosity, respectively. In this study, t is calculated using the standard k-ε model.
The Volume of Fluid (VOF) model tracks two or more immiscible fluids by solving a unified set of momentum equations and monitoring the volume fraction of each fluid across the computational domain. Typical applications include predicting jet breakup, large bubble dynamics in liquids, post-dam-break liquid motion, and steady/transient liquid-gas interface tracking. In the VOF approach, each computational cell is assigned a volume fraction for each phase to delineate their spatial distribution. The interfacial flow dynamics exhibit convective interactions between the phases, quantified by the volume fraction α (as defined in Equation (6)) [32].
If the fluid’s volume fraction in the cell is denoted, then the following three conditions are possible:
α = 0, The cell is empty (of the fluid);
α = 1, The cell is full (of the fluid);
0 < α < 1, The cell contains the interface between the fluid and one or more other fluids.
The local volume fraction α dictates the assignment of material properties and variables to each control volume within the computational domain.
With respect to dynamic meshes, the integral form of the conservation equation for a general scalar on an arbitrary control volume whose boundary is moving can be written as
V:
where is the fluid density, is the flow velocity vector, is the mesh velocity of the moving mesh, is the diffusion coefficient, is the source term of p.
4. Simulation Settings
To assess the impact of structural dimensions on aerodynamic power output at the device’s air chamber outlet, numerical simulations were conducted for models with the following parameters (as shown in Figure 3): Total device length (L): 1100 mm, 1200 mm, 1300 mm, 1400 mm; Total device width (W): 800 mm, 1000 mm, 1200 mm, 1400 mm; Air chamber height (H): 200 mm, 300 mm, 400 mm, 500 mm; U-tube channel width (T): 300 mm, 400 mm, 500 mm, 600 mm; Bottom channel height (D): 100 mm, 200 mm, 300 mm, 400 mm. During simulations, the air turbine was replaced with an orifice plate, and its influence on system behavior was disregarded. Optimal wave energy conversion efficiency in OWC systems is achieved at orifice ratios (orifice area/water column area) of 0.5–2.0%, where the damping characteristics are most favorable. Consequently, the orifice configuration in this work was set at 1% of the air chamber cross-section [33]. The still water depth within the device was consistently maintained at 150 mm above the bottom channel height to minimize interference with other variables.
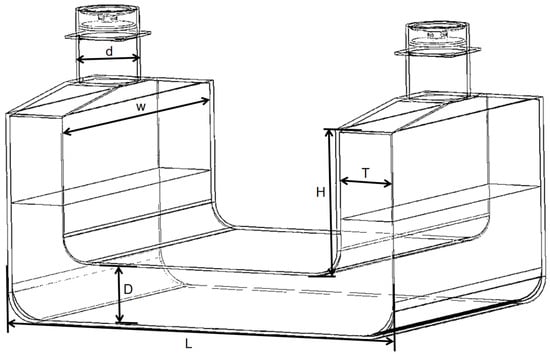
Figure 3.
Three-dimansional model.
The final device performance was determined through systematic parameter variations. To investigate the impact of individual parameters on equipment performance, a single-variable optimization strategy was employed. Each parameter’s range was configured based on actual equipment constraints. Our approach accelerates convergence to near-optimal solutions while significantly reducing computational time. Due to computational and time limitations, this study did not account for potential coupling effects between multiple parameters. Each marine region across the globe has distinct wave patterns and energy levels [34]. In real marine environments, ocean waves predominantly exhibit low-frequency characteristics. Across China’s coastal waters, the dominant wave periods range from 3 s to 6 s [35], with significant wave heights typically spanning 0.5 m to 4 m. Under such sea states, over 80% of the total wave energy is concentrated within this spectral band [36].
The external excitation forces acting on the described device primarily originate from vessel roll motion. As the device is rigidly affixed within the ship’s hull with no relative displacement, the ship’s oscillatory motion directly induces equivalent forced oscillations in the device. The roll period and roll amplitude serve as kinematic input conditions for the device rather than resulting from direct wave impacts. Consequently, no investigations were conducted regarding wave height or wave period parameters. Under head sea conditions (χ = 0° or 180°), vessels exhibit minimal roll motion. Conversely, beam sea encounters (χ = 90°) induce substantial roll amplitudes exceeding 10°. To facilitate unambiguous parametric sensitivity analysis of the wave energy converter (WEC), simulations in this study adopted a standardized 10° roll amplitude [37]. These parameters align with motion characteristics documented in the China Classification Society *R001-2024 Rules for Classification of Sea-going Steel Ships*, where typical roll response ranges for small vessels are quantified as follows: Roll amplitude range: 0° to 30°; Roll period: 3 to 6 s; Corresponding roll frequency: 0.167 Hz to 0.333 Hz.
This research specifically addresses how internal configuration parameters of U-OWC systems influence their operational efficiency. Analyses pertaining to wave-induced structural loads and hydrodynamic responses of vessels are explicitly excluded from the present investigation. In this study, the oscillation angle was fixed at 10°, and the oscillation period was varied between 3 s and 6 s to simulate realistic sea conditions. The fluid domain within the device was extracted in ANSYS Fluent 2023R1, with simulation boundaries defined as no-slip walls and the two outlets set as pressure inlet conditions. Initializing the pressure differential at the orifice to 0 Pa establishes a pressure baseline referenced to atmospheric pressure, which dynamically fluctuates in synchronization with pneumatic chamber pressure variations during simulations. This configuration enables bidirectional gas exchange dynamics throughout the liquid oscillation cycle, where gas ingestion and expulsion processes periodically alternate in a phase-locked manner. During meshing, the grid near the orifices was refined to improve data accuracy, using structured quadrilateral elements to ensure convergence in subsequent transient dynamic mesh simulations (as shown in Figure 4).
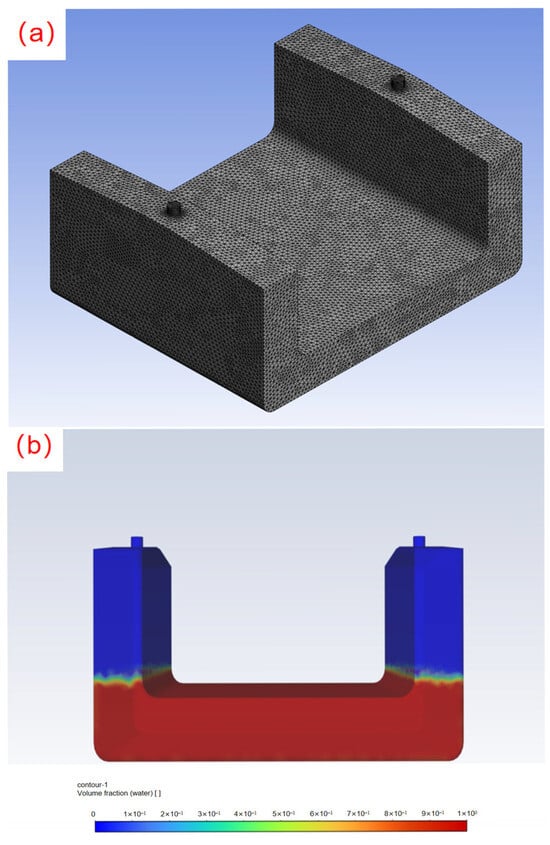
Figure 4.
Model for CFD simulation analysis: (a) Mesh Generation, (b) Model Initialization.
5. Simulation Analysis
5.1. Mesh Effect of the Numerical Model
To mitigate computational costs while preserving accuracy, a grid independence study was conducted to assess mesh parameter sensitivity. Insufficient mesh density compromises solution accuracy, whereas excessive elements incur prohibitive computational overhead [38]. Three models with 0.3 M, 0.6 M, and 0.9 M cells were simulated. As illustrated in Figure 5, the air mass flow rate curves exhibit consistent trends across all resolutions, with the 0.6 M and 0.9 M models demonstrating negligible divergence (<2%). Given the 0.6 M mesh’s superior computational efficiency and minimal accuracy loss relative to the 0.9 M case, it was selected as the optimal configuration. In addition, the symmetry of inflow and outflow volume rates within each oscillation cycle confirms that the constructed model strictly adheres to the principles of mass conservation.
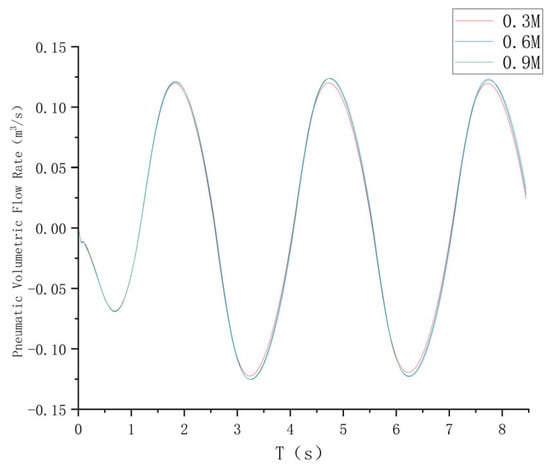
Figure 5.
Comparison of pneumatic volumetric flow rates across simulation models with varying mesh resolutions.
5.2. The Effect of the Overall Device Length on the Aerodynamic Power
The impact of variations in the overall device length on the overall aerodynamic power was investigated. Table 1 shows the cross-sectional area of the air chamber outlet channel and the corresponding maximum aerodynamic power for four different device lengths. When the length was set to 1400 mm, the device achieved optimal performance, with a peak aerodynamic power of 26.8 W. Longer device lengths correlated with increased maximum power output.

Table 1.
Length parameters and research results.
Figure 6 illustrates the overall aerodynamic power curves of the device, generated via simulation software, for varying device lengths. Notably, the curve for the 1100 mm device exhibits minimal fluctuations. As device length increases, the aerodynamic power curve demonstrates a more pronounced upward trend. Significant disparities in power output were observed among the four lengths within the 3 s to 4.5 s oscillation period range. Beyond 4.5 s, the power outputs converged. Comparative analysis confirmed that the 1400 mm (L1400) configuration delivered the best performance.
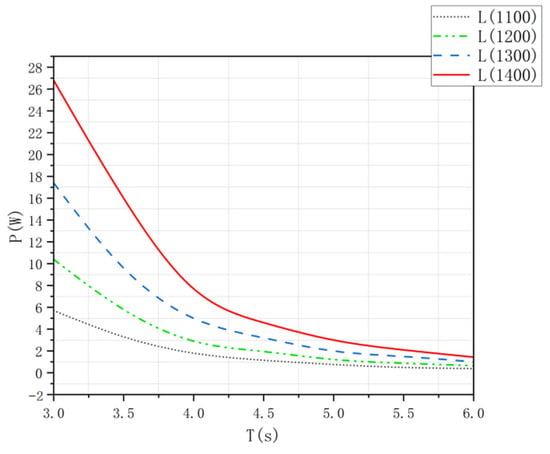
Figure 6.
Aerodynamic power under different lengths in numerical analysis.
Increasing the conduit length prolongs hydraulic transit time, amplifying phase-opposition oscillations in the vertical water columns and enhancing pneumatic throughput. Numerical analysis of the impact of device length variations reveals that length adjustments significantly influence the overall aerodynamic power output. Notably, a device length of 1400 mm yields the highest aerodynamic power, offering critical insights for optimizing device width in future studies.
5.3. The Impact of the Overall Width of the Device on Aerodynamic Power
The analysis was conducted to assess the impact of varying device width on the overall aerodynamic power output. Table 2 summarizes the cross-sectional area of the air chamber outlet channel and the corresponding maximum aerodynamic power for four device widths. A width of 1400 mm yields the optimal performance, achieving a peak aerodynamic power of 27.6 W. However, compared to length adjustments, varying the width resulted in smaller power improvements.

Table 2.
Width parameters and research results.
Figure 7 presents the simulated power curves for different widths. Aerodynamic power increased with wider configurations, with the 1400 mm (W1400) design outperforming others.
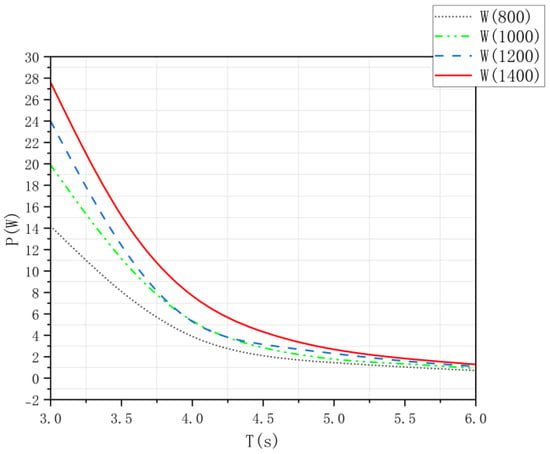
Figure 7.
Aerodynamic power under different widths in numerical analysis.
Wider conduits strengthen inertial coupling between water columns, promoting phase-opposition synchronization and maximizing pneumatic flux. Numerical analysis further validates that device width variations substantially influence aerodynamic power. Specifically, the 1400 mm width maximizes power output, providing critical insights for optimizing the air chamber height in future studies.
5.4. The Impact of the Overall Height of the Device on Aerodynamic Power
Table 3 summarizes four air chamber heights, their corresponding outlet cross-sectional areas, and the associated maximum aerodynamic power. Notably, an air chamber height of 500 mm yields the highest performance, achieving a peak aerodynamic power of 27.4 W. Increasing the air chamber height beyond this point does not proportionally enhance aerodynamic power, indicating a plateau in efficiency.

Table 3.
Height parameters and research results.
Figure 8 depicts the simulated aerodynamic power curves for the four air chamber heights. The data show minimal variation in the power curves across height adjustments, suggesting that air chamber height has a negligible impact on the final aerodynamic power output. A comprehensive comparison confirms that the 500 mm (H500) configuration is optimal.
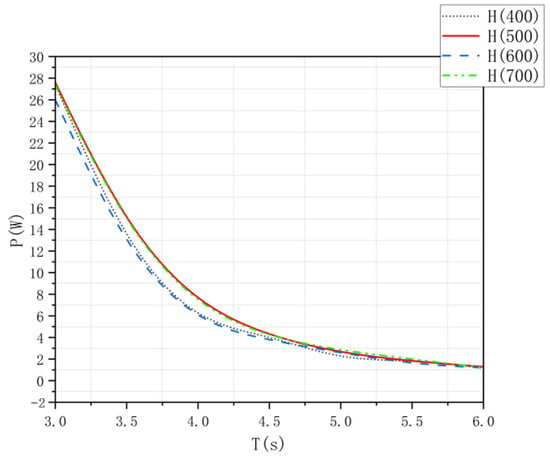
Figure 8.
Aerodynamic power under different heights in numerical analysis.
Variations in air chamber height exhibit negligible direct influence on the displacement amplitudes of the flanking water columns. However, when chamber height exceeds the optimal design value, the differential pressure gradient across the chamber boundary diminishes, impairing pneumatic energy transfer efficiency. Numerical analysis reinforces these findings: air chamber height variations exert little influence on overall aerodynamic power. The 500 mm height maximizes power generation, providing critical insights for optimizing internal channel heights in future designs.
5.5. The Impact of the Channel Width Inside the Device on the Aerodynamic Power
Table 4 summarizes the cross-sectional area of the air chamber outlet channel and the corresponding maximum aerodynamic power for four U-tube channel widths. A width of 400 mm achieves the highest performance, delivering a peak aerodynamic power of 32 W.

Table 4.
Channel width parameters and research results.
Figure 9 shows the simulated aerodynamic power curves for the four U-tube channel widths. The data reveal minimal variations in the power curves across width adjustments, though differences are more pronounced at lower oscillation periods. At higher oscillation periods, the curves converge, indicating negligible impact of channel width on aerodynamic power. However, the 400 mm design consistently outperformed others, especially at lower periods.
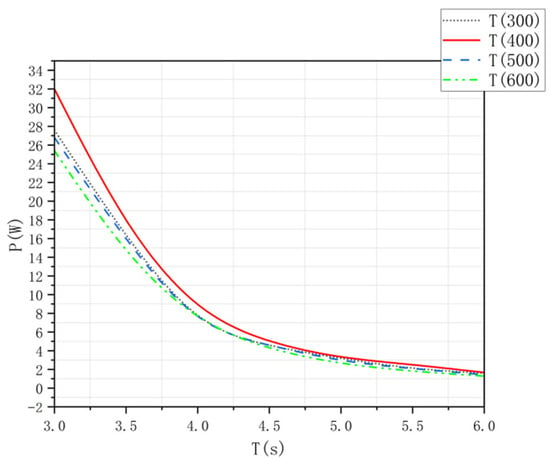
Figure 9.
Aerodynamic power under different U-tube channel widths in numerical analysis.
While wider U-tube channel width increases the airflow rate within the air chambers, it concurrently reduces the differential pressure between the chambers and the external environment. This trade-off ultimately diminishes the net pneumatic power output, as established through hydrodynamic scaling laws. Numerical analysis validates these findings: setting the U-tube channel width to 400 mm maximizes aerodynamic power output, providing critical insights for optimizing the air chamber angle in future designs.
5.6. The Impact of the Channel Height Inside the Device on the Aerodynamic Power
Table 5 summarizes four bottom channel heights, corresponding air chamber outlet cross-sectional areas and the associated maximum aerodynamic power. Notably, a bottom channel height of 100 mm yields the highest performance, achieving a peak aerodynamic power of 40 W.

Table 5.
Channel height parameters and research results.
Figure 10 displays the simulated aerodynamic power curves for the four bottom channel heights. The data reveal that reducing the bottom channel height significantly enhances aerodynamic power at lower oscillation periods, while the 100 mm configuration consistently outperforms the others across all conditions. A comprehensive comparison confirms that D100 is optimal.
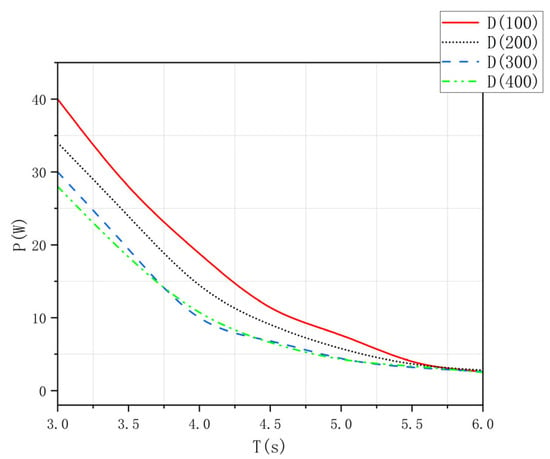
Figure 10.
Aerodynamic power under different bottom channel height conditions in numerical analysis.
The reduction in bottom channel height accelerates the water flow velocity within the conduit, resulting in more pronounced vertical displacements of the flanking water columns. This intensified oscillation enhances pneumatic power generation during the operational cycle. Numerical analysis validates these findings: setting the bottom channel height to 100 mm maximizes aerodynamic power output, particularly at lower oscillation periods.
5.7. The Impact of Sloshing Angle on the Aerodynamic Power of the Device
For vessels with wave incidence angles of 45° or 135° (χ = 45° or 135°), the roll angle of the vessel tends to be approximately 5 degrees. Table 6 presents two different oscillation angles, the corresponding cross-sectional area of the air chamber outlet channel of the device, and the corresponding maximum aerodynamic power. As shown in Table 6, when the oscillation angle of the device is 10°, the overall aerodynamic power generated by the device is higher than that generated when the oscillation angle is 5°.

Table 6.
Oscillation angle parameters and research results.
Figure 11 presents a curve diagram of the overall aerodynamic power of the device calculated by simulation software under different oscillation angles. By observing the overall curve diagram, it can be seen that higher aerodynamic power can be generated when the oscillation angle is larger, while the curve tends to be flatter when the oscillation angle is smaller.
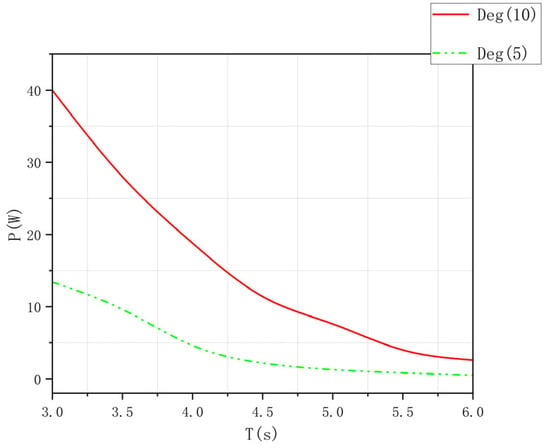
Figure 11.
Aerodynamic power under different sloshing angle conditions in numerical analysis.
The larger the oscillation angle, the greater the swing amplitude of the water column relative to the equilibrium position inside the device, and the faster the speed at which the water column rises and falls, thus generating more aerodynamic power. Through numerical calculation and analysis of the influence of the oscillation angle, it is found that when the oscillation angle is larger, the device can generate higher aerodynamic power.
5.8. Simulation Conclusions
Based on the analysis of multiple sets of data through simulation and modeling, the following conclusions can be drawn:
- (1)
- The numerical simulation results show that changing the length, width of the device, and the height of the bottom channel of the device has a significant impact on the generated aerodynamic power. Specifically, increasing the length and width of the device can increase the generated aerodynamic power; reducing the height of the bottom channel of the device can also increase the generated aerodynamic power. Adjusting these three groups of variables also has a relatively obvious effect on the change of aerodynamic power.
- (2)
- Numerical simulations indicate that modifying the air chamber height and U-tube width has minimal effect on aerodynamic power. However, subtle refinements to the U-tube width may yield marginal improvements in power generation under specific conditions.
6. Conclusions
This paper introduces a U-tube dual-chamber oscillating water column wave energy conversion device designed to expand application scenarios for OWC-based wave energy harvesting. Through numerical simulations, the study analyzes the device’s aerodynamic power output to identify optimal structural parameters and their corresponding efficiency, providing a foundational design framework for practical wave energy systems. The main achievements of this paper include:
- (1)
- A novel U-tube dual-chamber OWC device is proposed, targeting enhanced adaptability and efficiency in wave energy conversion, thereby broadening the operational scope of existing OWC technologies.
- (2)
- Fluid dynamics modeling and simulations were conducted to evaluate the device’s structural and operational dynamics. By systematically varying parameters such as length, width, and bottom channel height, the study quantifies their impact on aerodynamic power efficiency, establishing data-driven design guidelines.
Future work will focus on manufacturing a physical prototype for semi-physical experimental verification on a six-degree-of-freedom platform. Due to computational constraints and time limitations, this study did not take into account the possible coupled and varying relationships among multiple parameters. The parameters of the practical prototype will be optimized by optimization algorithms such as particle swarm optimization (PSO) to achieve better power conversion efficiency.
The prototype will incorporate an air turbine system to measure actual power generation, enabling iterative refinement of the device’s structural and operational parameters. The influence of the ship’s roll angle under different wave incidence directions will also be verified in our future research.
Author Contributions
Conceptualization, S.Y. and Y.T.; Methodology, S.Y.; Software, S.Y. and H.L.; Validation, H.L.; Formal analysis, Y.H., Y.T. and B.L.; Investigation, J.F., Z.D. and Y.T.; Resources, J.F. and Y.T.; Data curation, J.F. and C.L.; Writing–original draft, S.Y., H.L. and Y.H.; Writing–review & editing, S.Y., H.L. and Y.H.; Visualization, J.F. and Z.D.; Supervision, Y.H., Z.D. and B.L.; Project administration, C.L. and B.L.; Funding acquisition, C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by following projects: Fujian Provincial Natural Science Youth Funding (Funder: Fujian Science and Technology Bureau, Grant Number: 2022J05155), Xiamen Science and Technology Bureau Nature Funding (Funder: Xiamen Science and Technology Bureau, Grant Number: 3502Z20227057, 3502Z202471046); National Natural Science Foundation (Funder: National Natural Science Foundation of China, Grant Number: 42476225); Fujian Province University Industry University Cooperation Project (Funder: Fujian Science and Technology Bureau, Grant Number: 2023H61010068); Fujian Provincial Natural Science funding (Funder: Fujian Science and Technology Bureau, Grant Number: 2023J01791, 2023J01146, 2024J01112); Fujian Province Young and Middle-aged Teacher Education Research Project (Science and Technology) Key Project: (Funder: Fujian Education Department, Grant Number: JZ230027, JAT210236).
Data Availability Statement
The original contributions presented in the study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pennock, S.; Noble, D.R.; Vardanyan, Y.; Delahaye, T.; Jeffrey, H. A modelling framework to quantify the power system benefits from ocean energy deployments. Appl. Energy 2023, 347, 12. [Google Scholar] [CrossRef]
- Rehman, S.; Alhems, L.M.; Alam, M.M.; Wang, L.J.; Toor, Z. A review of energy extraction from wind and ocean: Technologies, merits, efficiencies, and cost. Ocean Eng. 2023, 267, 38. [Google Scholar] [CrossRef]
- Wan, L.; Moan, T.; Gao, Z.; Shi, W. A review on the technical development of combined wind and wave energy conversion systems. Energy 2024, 294, 19. [Google Scholar] [CrossRef]
- Drew, B.; Plummer, A.R.; Sahinkaya, M.N. A review of wave energy converter technology. Proc. Inst. Mech. Eng. Part J. Power Energy 2009, 223, 887–902. [Google Scholar] [CrossRef]
- Ozkop, E.; Altas, I.H. Control, power and electrical components in wave energy conversion systems: A review of the technologies. Renew. Sust. Energ. Rev. 2017, 67, 106–115. [Google Scholar] [CrossRef]
- Chen, P.H.; Wu, D.W. A review of hybrid wave-tidal energy conversion technology. Ocean Eng. 2024, 303, 14. [Google Scholar] [CrossRef]
- Shi, X.L.; Liang, B.C.; Li, S.W.; Zhao, J.C.; Wang, J.H.; Wang, Z.L. Wave energy resource classification system for the China East Adjacent Seas based on multivariate clustering. Energy 2024, 299, 23. [Google Scholar] [CrossRef]
- Adibzade, M.; Akbari, H. Spectral approach to evaluate multi-body floating wave energy converters in complex sea states. Ocean Eng. 2023, 286, 115567. [Google Scholar] [CrossRef]
- Falcao, A.F.O.; Henriques, J.C.C. Oscillating-water-column wave energy converters and air turbines: A review. Renew. Energy 2016, 85, 1391–1424. [Google Scholar] [CrossRef]
- Falcão, A.F.O. Developments in oscillating water column wave energy converters and air turbines. In Renewable Energies Offshore; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Çelik, A.; Altunkaynak, A. Experimental and analytical investigation on chamber water surface fluctuations and motion behaviours of water column type wave energy converter. Ocean Eng. 2018, 150, 209–220. [Google Scholar] [CrossRef]
- Çelik, A.; Altunkaynak, A. Determination of hydrodynamic parameters of a fixed OWC by performing experimental and numerical free decay tests. Ocean Eng. 2020, 204, 106827. [Google Scholar] [CrossRef]
- Mandev, M.B.; Çelik, A.; Altunkaynak, A. Maximizing oscillating water column efficiency: The impact of vertical plate and guide vane. Energy 2024, 308, 132901. [Google Scholar] [CrossRef]
- Heath, T. The development and installation of the LIMPET wave energy converter. In World Renewable Energy Congress VI; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Arena, F.; Romolo, A.; Malara, G.; Fiamma, V.; Laface, V.L.A. The first worldwide application at full-scale of the REWEC3 device in the Port of Civitavecchia: Initial energetic performances. In Proceedings of the 2nd International Conference on Renewable Energies Offshore (RENEW2016), Lisbon, Portugal, 24–26 October 2016. [Google Scholar]
- Liu, Z.; Zhang, X.; Ding, L.; Han, Z.; Ni, H. Hydrodynamic and energy-harvesting performances of a compact-array OWC device: An experimental study. Energy 2024, 310, 133209. [Google Scholar] [CrossRef]
- Froude, W. On the rolling of Ships. Available online: http://books.google.com/books?id=xDMDAAAAQAAJ&printsec=frontcover&hl=zh-CN#v=onepage&q&f=false (accessed on 24 December 2024).
- Stigter, C. The performance of U-tanks as a passive anti-rolling device. Int. Shipbuild. Prog. 1966, 13, 249–275. [Google Scholar] [CrossRef]
- Holder, L.A. Seakeeping–Ship Behaviour in Rough Weather. A. R. J. M. Lloyd. 486 pages, 17 × 24.5 cm, Ellis Horwood, 1989. £59.50. J. Navig. 1990, 43, 140. [Google Scholar] [CrossRef]
- Zhong, Z.Y.; Falzarano, M.; Fithen, R. A Numerical Study of U-Tube Passive Anti-Rolling Tanks. In Proceedings of the Eighth International Offshore and Polar Engineering Conference, Montreal, QC, Canada, 24–29 May 1998. [Google Scholar]
- Daalen, E.V.; Kleefsman, K.M.T.; Gerrits, J.; Luth, H.R.; Veldman, A.E.P. Anti-Roll Tank Simulations with a Volume of Fluid (VOF) Based Navier-Stokes Solver; University of Groningen, Johann Bernoulli Institute for Mathematics and Computer Science: Groningen, The Netherlands, 2001. [Google Scholar]
- Taskar, B.U.; DasGupta, D.; Nagarajan, V.; Chakraborty, S.; Chatterjee, A.; Sha, O.P. CFD aided modelling of anti-rolling tanks towards more accurate ship dynamics. Ocean Eng. 2014, 92, 296–303. [Google Scholar] [CrossRef]
- Fontana, M.; Giorgi, G.; Accardi, M.; Giorcelli, E.; Brizzolara, S.; Sirigu, S.A.; Dos Santos, E.D.; Isoldi, L.A. Numerical and Experimental Investigation of the Dynamics of a U-Shaped Sloshing Tank to Increase the Performance of Wave Energy Converters. J. Mar. Sci. Eng. 2023, 11, 2339. [Google Scholar] [CrossRef]
- Gawad, A.F.A.; Ragab, S.; Nayfeh, A.H.; Mook, D.T. Roll stabilization by anti-roll passive tanks. Ocean Eng. 2001, 28, 457–469. [Google Scholar] [CrossRef]
- Moaleji, R.; Greig, A. On the development of ship anti-roll tanks. Ocean Eng. 2007, 34, 103–121. [Google Scholar] [CrossRef]
- Yang, S.; Zhu, W.; Tu, Y.; Cao, G.; Chen, X.; Du, Z.; Fan, J.; Huang, Y. Study on the influence of heave plate on energy capture performance of central pipe oscillating water column wave energy converter. Energy 2024, 312, 133517. [Google Scholar] [CrossRef]
- Guo, P.; Zhang, Y.; Chen, W. Numerical analysis on a self-rectifying impulse turbine with U-shaped duct for oscillating water column wave energy conversion. Energy 2023, 274, 127359. [Google Scholar] [CrossRef]
- Licheri, F.; Ghisu, T.; Cambuli, F.; Puddu, P. Experimental reconstruction of the local flow field in a Wells turbine using a three-dimensional pressure probe. Energy 2024, 296, 131062. [Google Scholar] [CrossRef]
- Gato, L.M.C.; Maduro, A.R.; Carrelhas, A.A.D.; Henriques, J.C.C.; Ferreira, D.N. Performance improvement of the biradial self-rectifying impulse air-turbine for wave energy conversion by multi-row guide vanes: Design and experimental results. Energy 2021, 216, 119110. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Y. Numerical investigation on the wave power extraction for a 3D dual-chamber oscillating water column system composed of two closely connected circular sub-units. Appl. Energy 2021, 295, 117009. [Google Scholar] [CrossRef]
- Fleming, A.; Macfarlane, G. In-situ orifice calibration for reversing oscillating flow and improved performance prediction for oscillating water column model test experiments. Int. J. Mar. Energy 2017, 17, 147–155. [Google Scholar] [CrossRef]
- ANSYS. ANSYS Fluent Theory Guide 17.2; ANSYS: Canonsburg, PA, USA, 2016. [Google Scholar]
- Sheng, W.; Alcorn, R.; Lewis, A.W. Primary wave energy conversions of oscillating water columns. In Proceedings of the 10th European Wave and Tidal Energy Conference, Aalborg, Denmark, 2–5 September 2013. [Google Scholar]
- Adibzade, M.; Akbari, H. Fully spectral approach to evaluate the performance of floating wave energy converters in directional complex sea states. Ocean Eng. 2024, 306, 117999. [Google Scholar] [CrossRef]
- Zheng, C.; Li, X.; Sun, C.; Su, S.; Chen, X. In Meticulous Simulation of Seasonal Characteristics of the China Sea Wave Period. Adv. Mar. Sci. 2014, 1, 44–49. [Google Scholar] [CrossRef]
- Wan, Y.; Zhang, J.; Meng, J.M.; Wang, J. A wave energy resource assessment in the China’s seas based on multi-satellite merged radar altimeter data. Acta Oceanol. Sin. 2015, 34, 115–124. [Google Scholar] [CrossRef]
- Youn, D.H.; Choi, L.K.; Kim, J. Motion Response Characteristics of Small Fishing Vessels of Different Sizes among Regular Waves. J. Ocean. Eng. Technol. 2023, 37, 1–7. [Google Scholar] [CrossRef]
- Yu, T.; He, S.; Shi, H.; Chen, X.; Guo, Q. Numerical investigation of hydrodynamic performance and efficiency of a dual-chamber oscillating water column under different damping and chamber breadth ratio combination. Ocean Eng. 2022, 266, 113008. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).