Energy and Exergy Analysis of Conventional Automobile Engines: Evaluation of Waste Heat Recovery Potential to Drive Parasitic Loads
Abstract
1. Introduction
- (1)
- To perform energy and exergy analyses of the exhaust gases from ICEs commonly used in conventional automobiles.
- (2)
- To propose a retrofit E-turbine design for recovering waste heat and replacing ICE-driven parasitic loads.
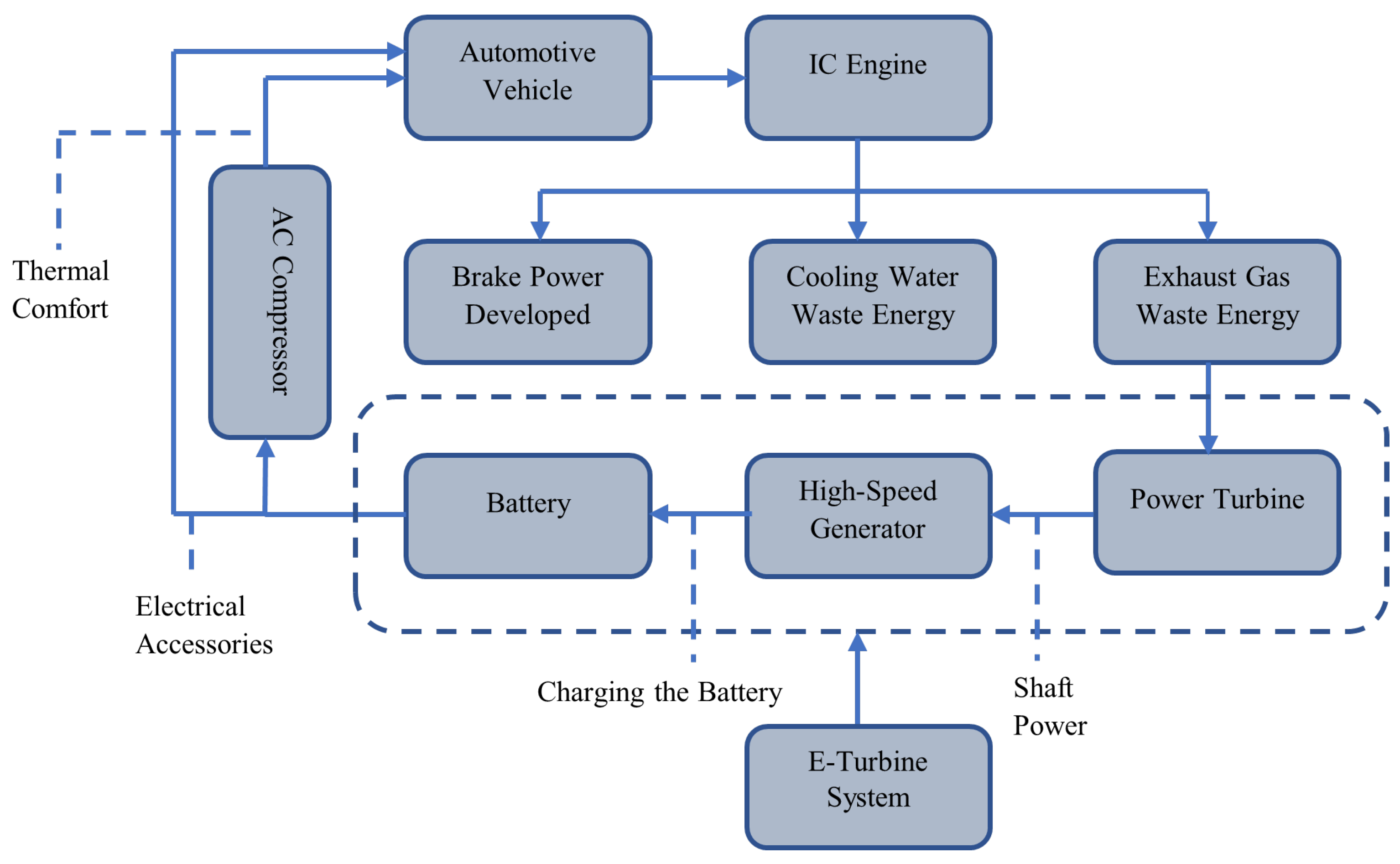
2. E-Turbine System Description
3. E-Turbine System Governing Models and Implementation
3.1. ICE Governing Models
3.2. Power Turbine Governing Models
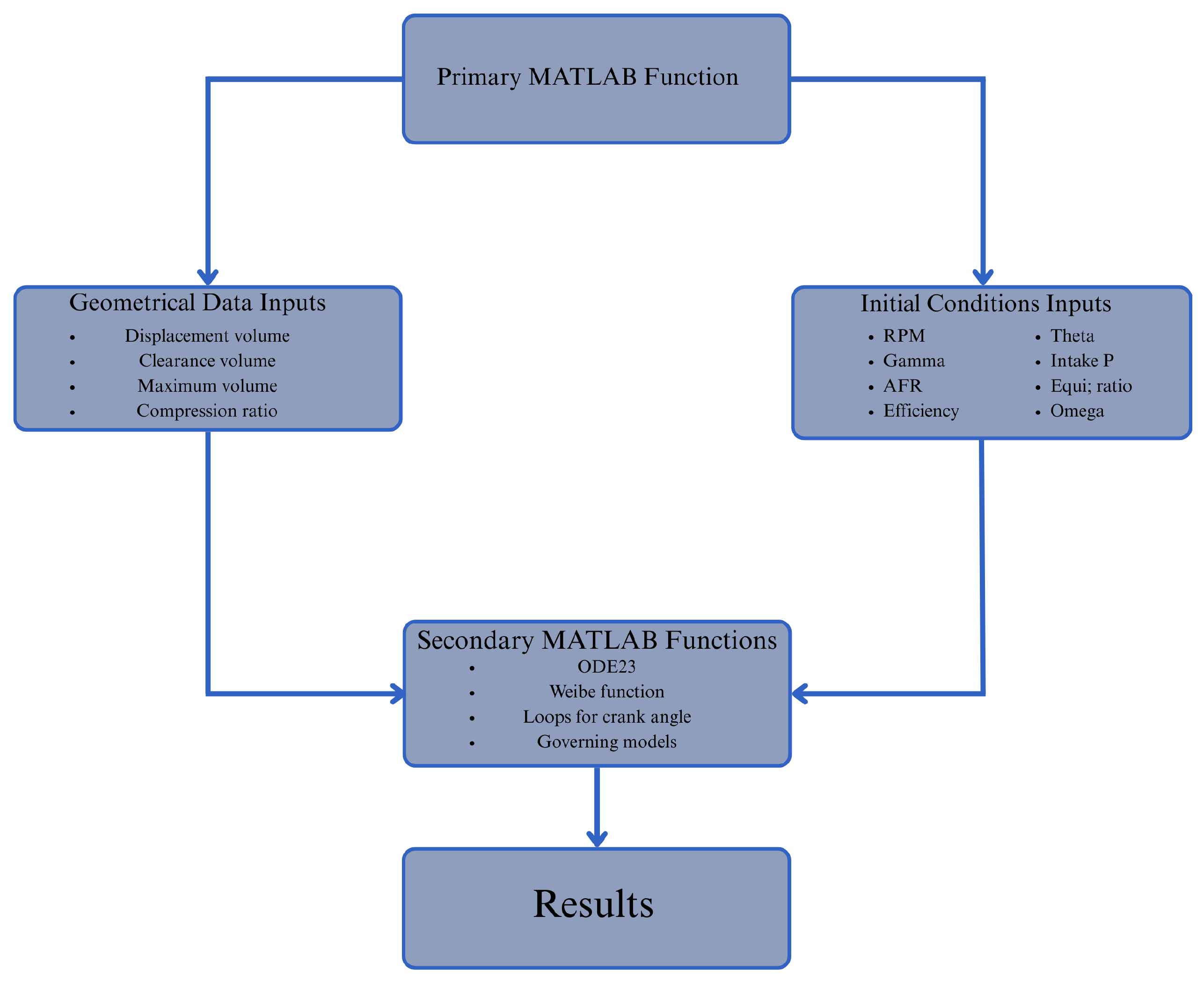
3.3. MATLAB® Model
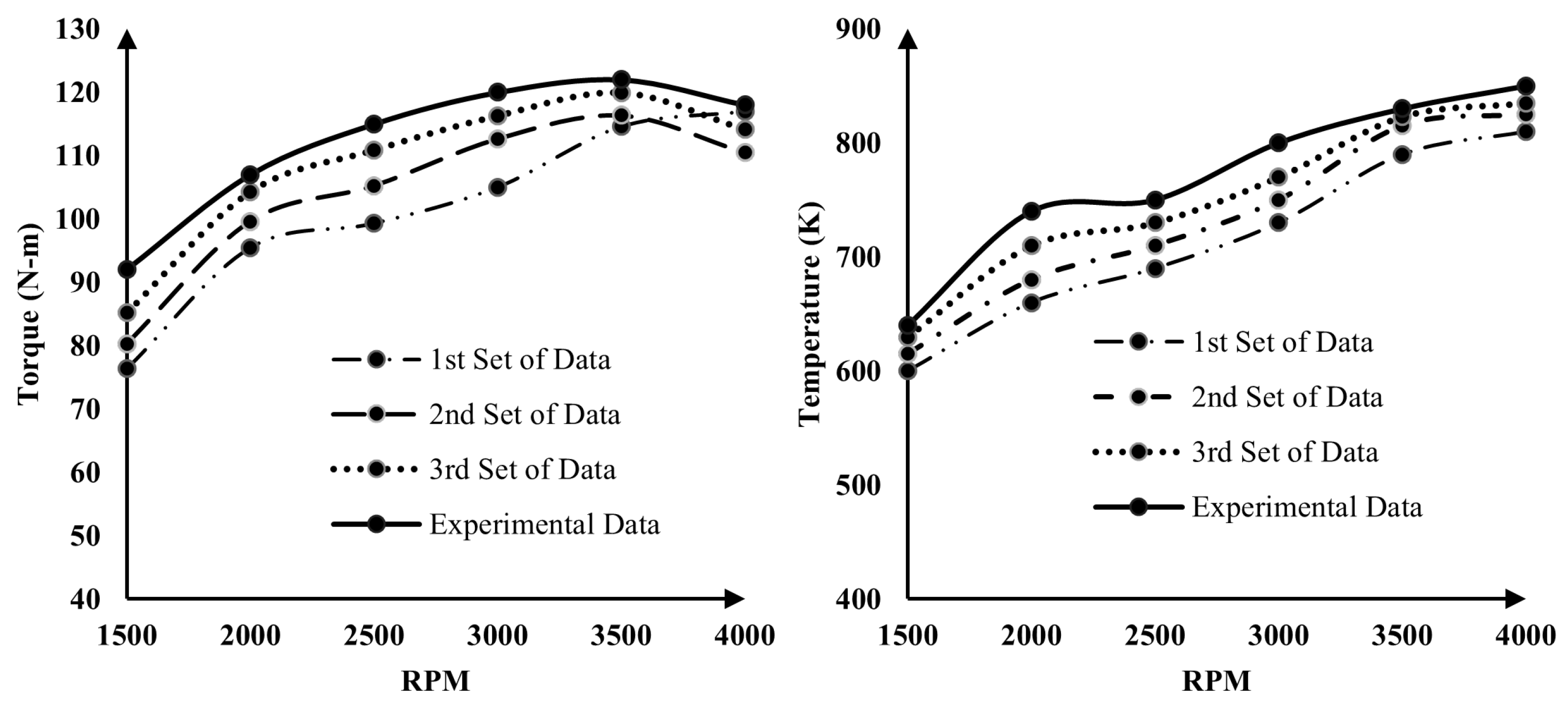
3.4. Validation of MATLAB® Model
4. Results and Discussion
4.1. Energy and Exergy Analysis of Exhaust Gases
4.2. Design of E-Turbine System
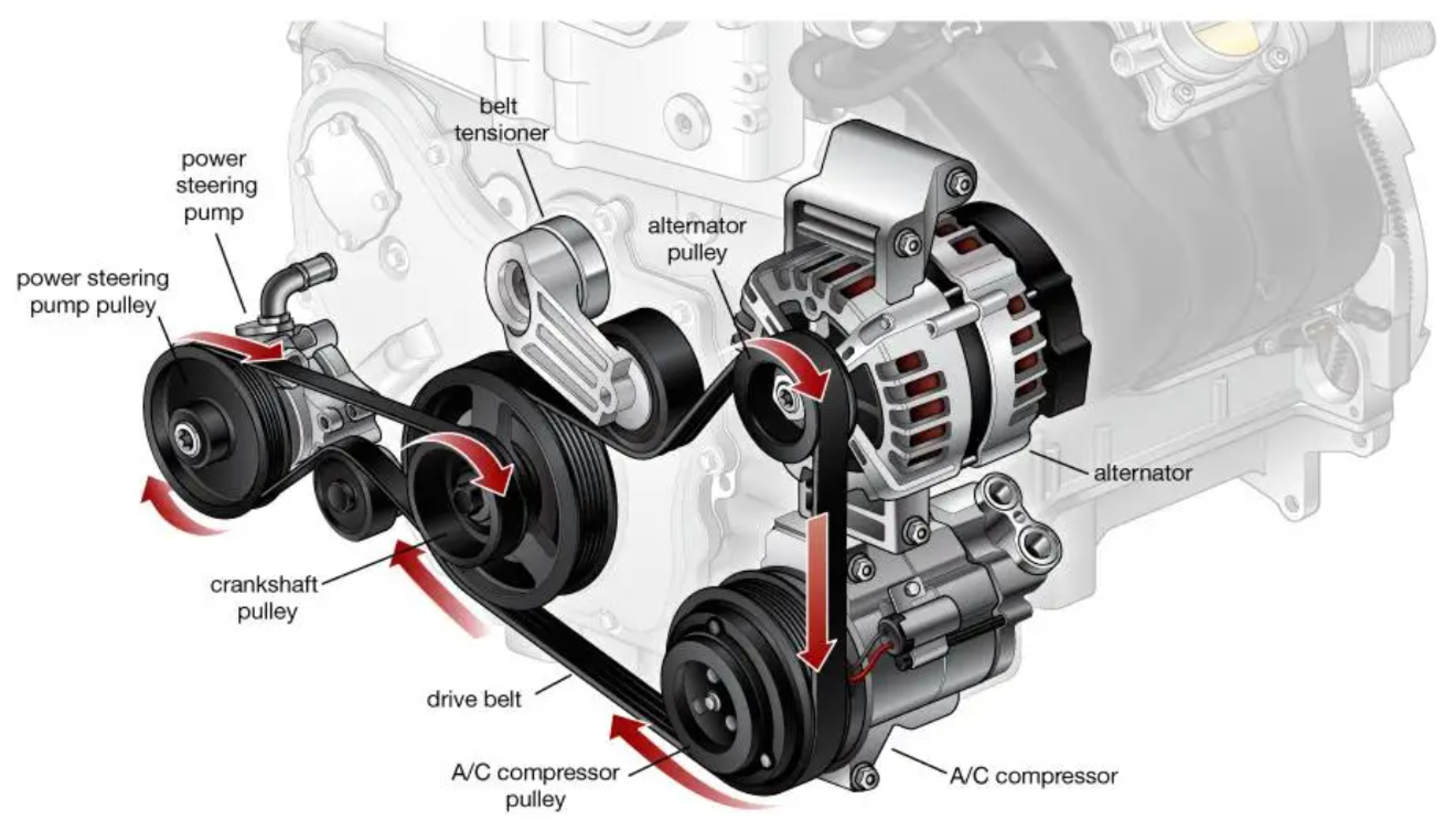
4.2.1. AC Compressor
4.2.2. Design Point Selection
4.2.3. Preliminary Turbine Sizing
4.2.4. High-Speed Permanent Magnet Synchronous Generator (PMSG)
4.2.5. Battery Sizing
4.2.6. Limitations in the Integration of an E-Turbine as a Retrofit System
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International Energy Agency. Energy Consumption in Transport by Fuel in the Net Zero Scenario, 1975–2030; IEA: Paris, France, 2023; Available online: https://www.iea.org/data-and-statistics/charts/energy-consumption-in-transport-by-fuel-in-the-net-zero-scenario-1975-2030 (accessed on 17 May 2025).
- International Energy Agency. World Energy Outlook 2024; IEA: Paris, France, 2024; Available online: https://www.iea.org/reports/world-energy-outlook-2024 (accessed on 17 May 2025).
- International Energy Agency. Global CO2 Emissions from Transport by Sub-Sector in the Net Zero Scenario, 2000–2030; IEA: Paris, France, 2023; Available online: https://www.iea.org/data-and-statistics/charts/global-co2-emissions-from-transport-by-sub-sector-in-the-net-zero-scenario-2000-2030-2 (accessed on 17 May 2025).
- Heidrich, P.; Krisch, T. Assessment of waste heat recovery options in passenger car applications by various Rankine cycles. Heat Transf. Eng. 2015, 36, 1321–1331. [Google Scholar] [CrossRef]
- Chammas, R.; Clodic, D. Combined Cycle for Hybrid Vehicles; SAE Technical Paper number 2005-01-1171; SAE International: Warrendale, PA, USA, 2005. [Google Scholar]
- Nashville Performance. Impact of Air Conditioning on Fuel Efficiency. 2023. Available online: https://nashvilleperformance.com/impact-of-air-conditioning-on-fuel-efficiency (accessed on 17 May 2025).
- Welstand, J.S.; Haskew, H.H.; Gunst, R.F.; Bevilacqua, O.M. Evaluation of the Effects of Air Conditioning Operation and Associated Environmental Conditions on Vehicle Emissions and Fuel Economy; Technical Report 2003-01-2247; SAE International: Warrendale, PA, USA, 2003. [Google Scholar]
- Heywood, J.B. Internal Combustion Engine Fundamentals; McGraw-Hill Education: New York, NY, USA, 1988. [Google Scholar]
- National Research Council. Cost, Effectiveness, and Deployment of Fuel Economy Technologies for Light-Duty Vehicles; The National Academies Press: Washington, DC, USA, 2015. [Google Scholar]
- Armstead, J.R.; Miers, S.A. Review of waste heat recovery mechanisms for internal combustion engines. J. Therm. Sci. Eng. Appl. 2014, 6, 014001. [Google Scholar] [CrossRef]
- Schwitzer. Introduction to Turbochargers; Schwitzer Turbochargers: Indianapolis, IN, USA, 1991. [Google Scholar]
- Baines, N.C. Fundamentals of Turbocharging; Concepts NREC: White River Junction, VT, USA, 2005. [Google Scholar]
- He, W.; Zhang, G.; Zhang, X.; Zhao, X.; Xu, J.; Li, G. Recent development and application of thermoelectric generator and cooler. Appl. Energy 2015, 143, 1–25. [Google Scholar] [CrossRef]
- Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Demir, M.; Dincer, I. Performance assessment of a thermoelectric generator applied to exhaust waste heat recovery. Appl. Therm. Eng. 2017, 120, 694–707. [Google Scholar] [CrossRef]
- Shi, L.; Shu, G.; Tian, H.; Deng, S. A review of modified Organic Rankine cycles (ORCs) for internal combustion engine waste heat recovery (ICE-WHR). Renew. Sustain. Energy Rev. 2017, 68, 638–658. [Google Scholar] [CrossRef]
- Sprouse, C.; Depcik, C. Review of Organic Rankine Cycles for Internal Combustion Engine Exhaust Waste Heat Recovery. Appl. Therm. Eng. 2013, 51, 711–722. [Google Scholar] [CrossRef]
- Xie, J.; Wang, L. Waste heat recovery technologies in internal combustion engines: A review. Energy 2012, 38, 8–16. [Google Scholar]
- Moore, S. The Current State of the Global Automotive Manufacturing Market. AZoM 2022. Available online: https://www.azom.com/article.aspx?ArticleID=22236 (accessed on 14 May 2025).
- Hedges Company. How Many Cars Are There in the World in 2023? 2023. Available online: https://hedgescompany.com/blog/2021/06/how-many-cars-are-there-in-the-world/ (accessed on 14 May 2025).
- International Energy Agency. Global EV Outlook 2023; IEA: Paris, France, 2023. [Google Scholar]
- Rowe, D.M. (Ed.) Thermoelectrics and Its Energy Harvesting; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Snyder, G.J. Small Thermoelectric Generators. Electrochem. Soc. Interface 2008, 17, 54–56. [Google Scholar] [CrossRef]
- Quoilin, S.; Van Den Broek, M.; Declaye, S.; Dewallef, P.; Lemort, V. Techno-economic Survey of Organic Rankine Cycle (ORC) Systems. Renew. Sustain. Energy Rev. 2013, 22, 168–186. [Google Scholar] [CrossRef]
- Tchanche, B.F.; Lambrinos, G.; Frangoudakis, A.; Papadakis, G. Low-grade Heat Conversion into Power Using Organic Rankine Cycles—A Review of Various Applications. Renew. Sustain. Energy Rev. 2011, 15, 3963–3979. [Google Scholar] [CrossRef]
- Ghojel, J.I. Review of the Development and Applications of the Wiebe Function: A Tribute to the Contribution of Ivan Wiebe to Engine Research. Int. J. Engine Res. 2010, 11, 297–312. [Google Scholar] [CrossRef]
- Stobart, R.K. An availability approach to thermal energy recovery in vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2007, 221, 1011–1021. [Google Scholar] [CrossRef]
- Yadav, R.M.; Berwal, A.K. Availability Analysis in the Exhaust of Multi Cylinder Gasoline Engine. IAETSD J. Adv. Res. Appl. Sci. 2018, 5, 122–128. [Google Scholar]
- Moran, M.J.; Shapiro, H.N.; Boettner, D.D.; Bailey, M.B. Fundamentals of Engineering Thermodynamics, 7th ed.; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Dincer, I.; Rosen, M.A. Exergy: Energy, Environment and Sustainable Development; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Szargut, J.; Morris, D.R.; Steward, F.R. Exergy Analysis of Thermal, Chemical, and Metallurgical Processes; Hemisphere Publishing: New York, NY, USA, 1988. [Google Scholar]
- Dixon, S.L.; Hall, C.A. Fluid Mechanics and Thermodynamics of Turbomachinery, 6th ed.; Butterworth-Heinemann: Oxford, UK, 2005. [Google Scholar]
- The MathWorks Inc. ODE23-Solve Differential Equations Using 2nd and 3rd Order Runge-Kutta. 2025. Available online: https://www.mathworks.com/help/matlab/ref/ode23.html (accessed on 24 April 2025).
- Peng, Z.; Wang, T.; He, Y.; Yang, X.; Lu, L. Analysis of environmental and economic benefits of integrated Exhaust Energy Recovery (EER) for vehicles. Appl. Energy 2013, 105, 238–243. [Google Scholar] [CrossRef]
- Sanden International (Singapore) Pte Ltd. Sanden Singapore SD7 Series Compressor Catalogue; Sanden International (Singapore) Pte Ltd.: Singapore, 2011. [Google Scholar]
- Akhave, A.; Chrysakis, G.; Gupta, A. Design and evaluation of a turbo-generator as an auxiliary power unit for hybrid vehicles. In Proceedings of the 5th IET Hybrid and Electric Vehicles Conference (HEVC 2014), London, UK, 5–6 November 2014; pp. 1–7. [Google Scholar]
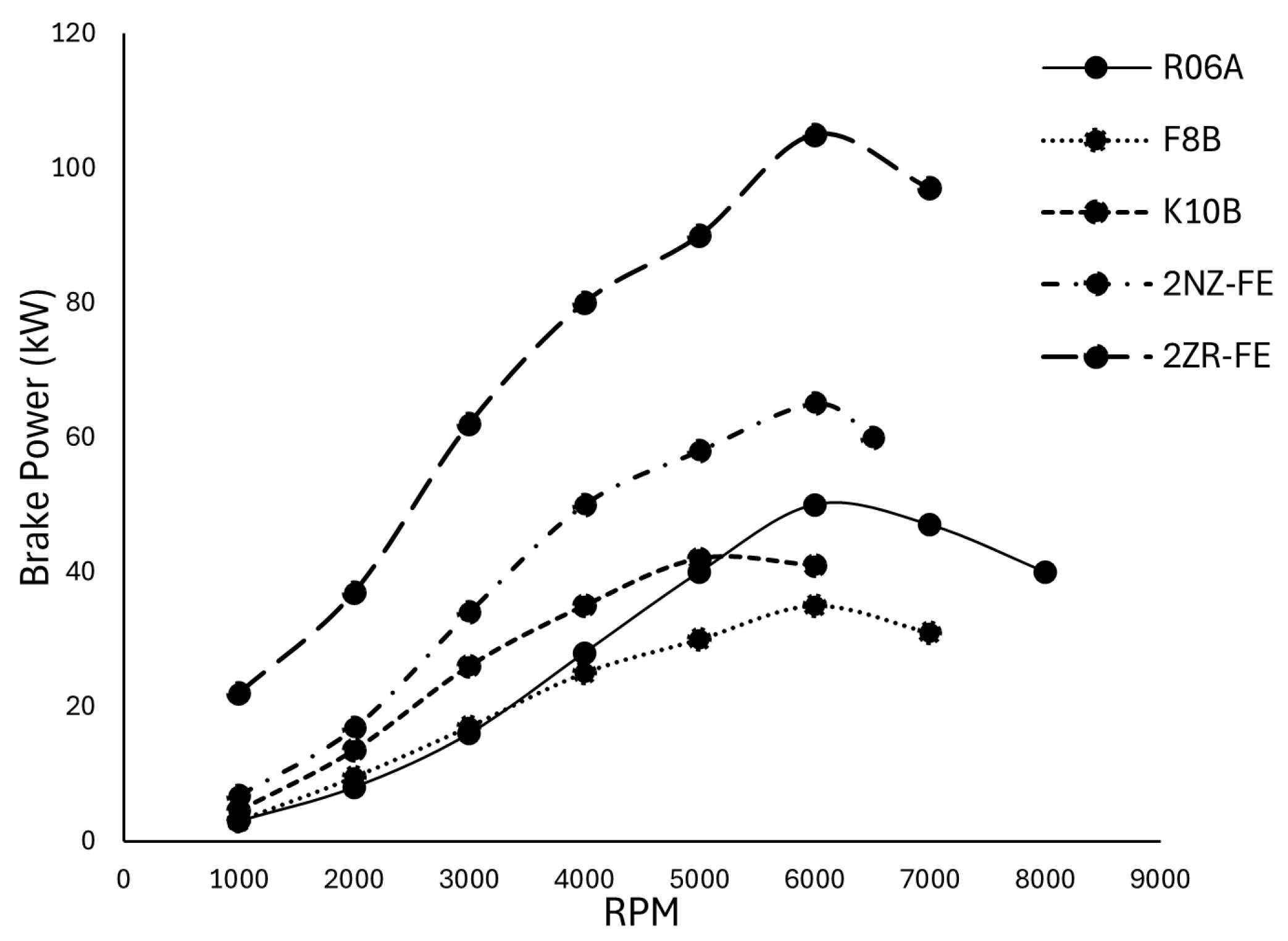
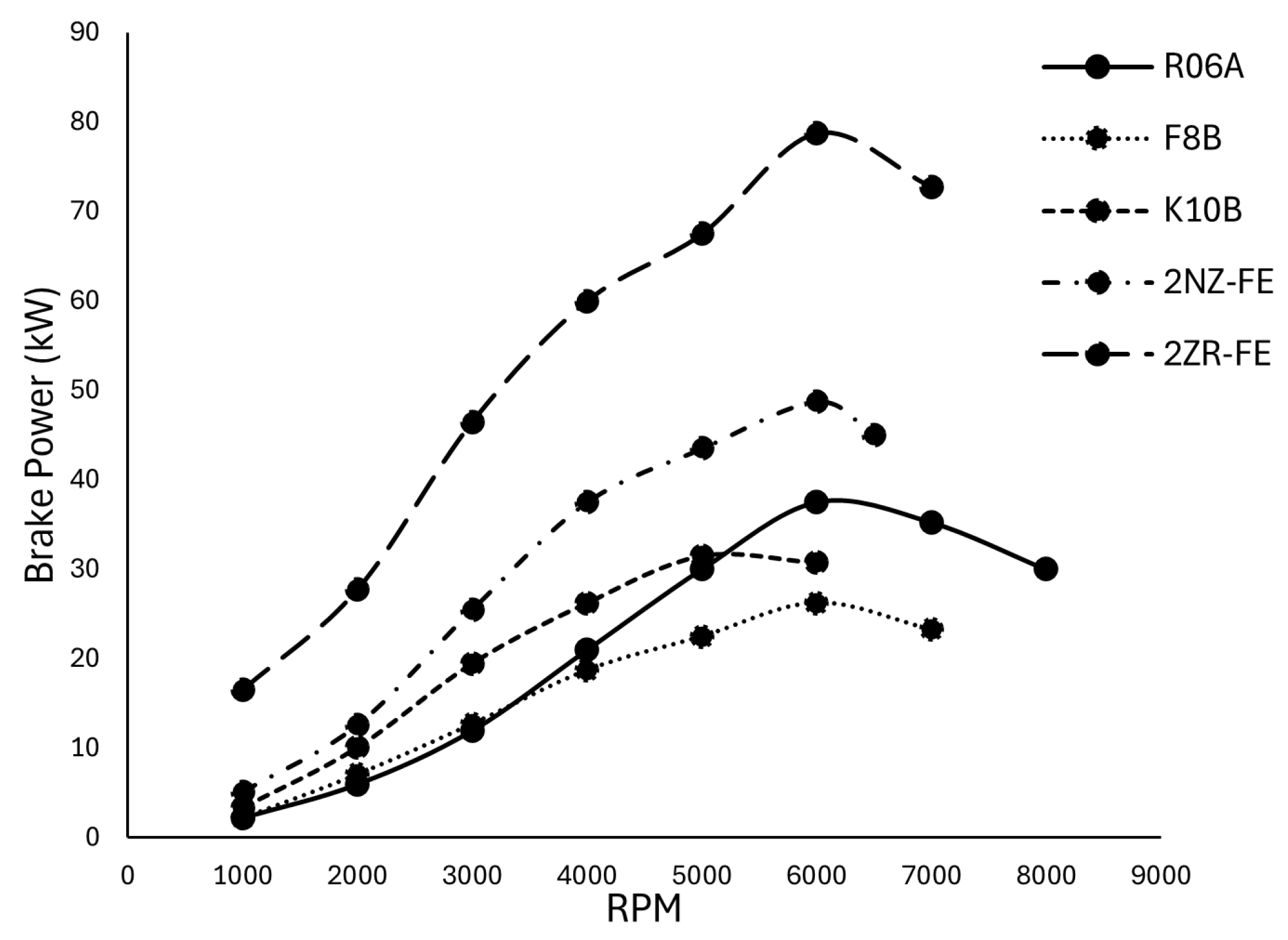
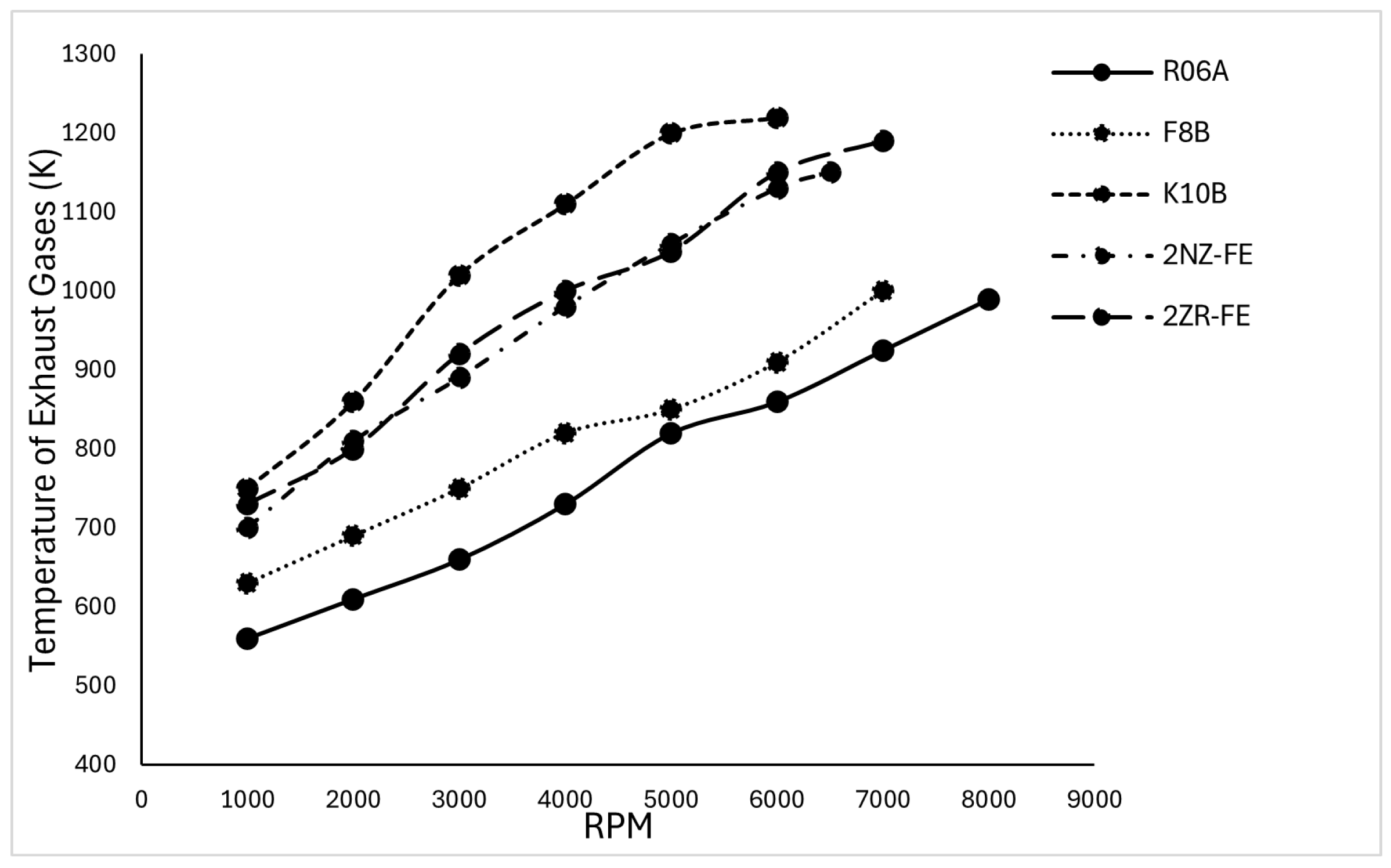

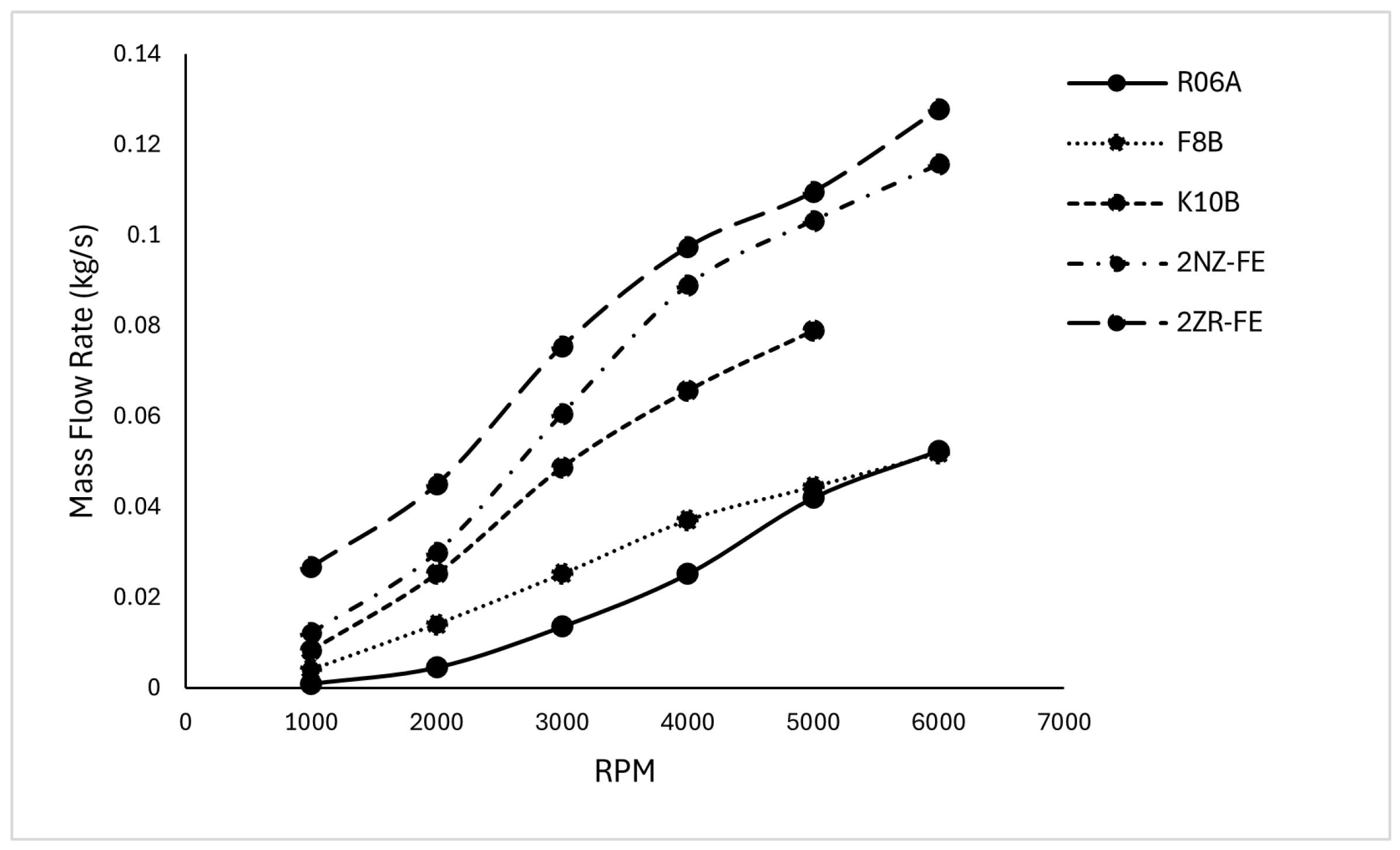
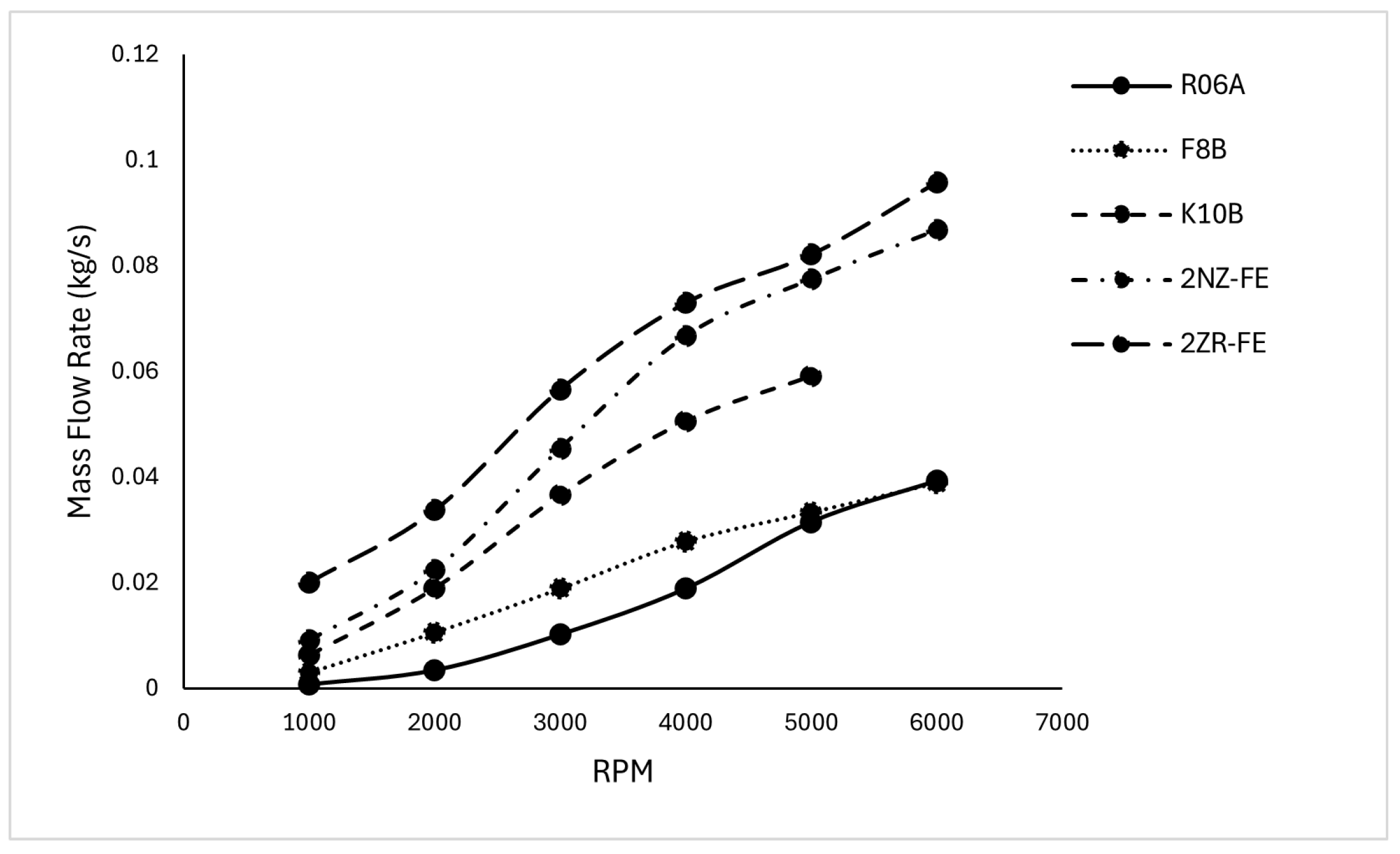
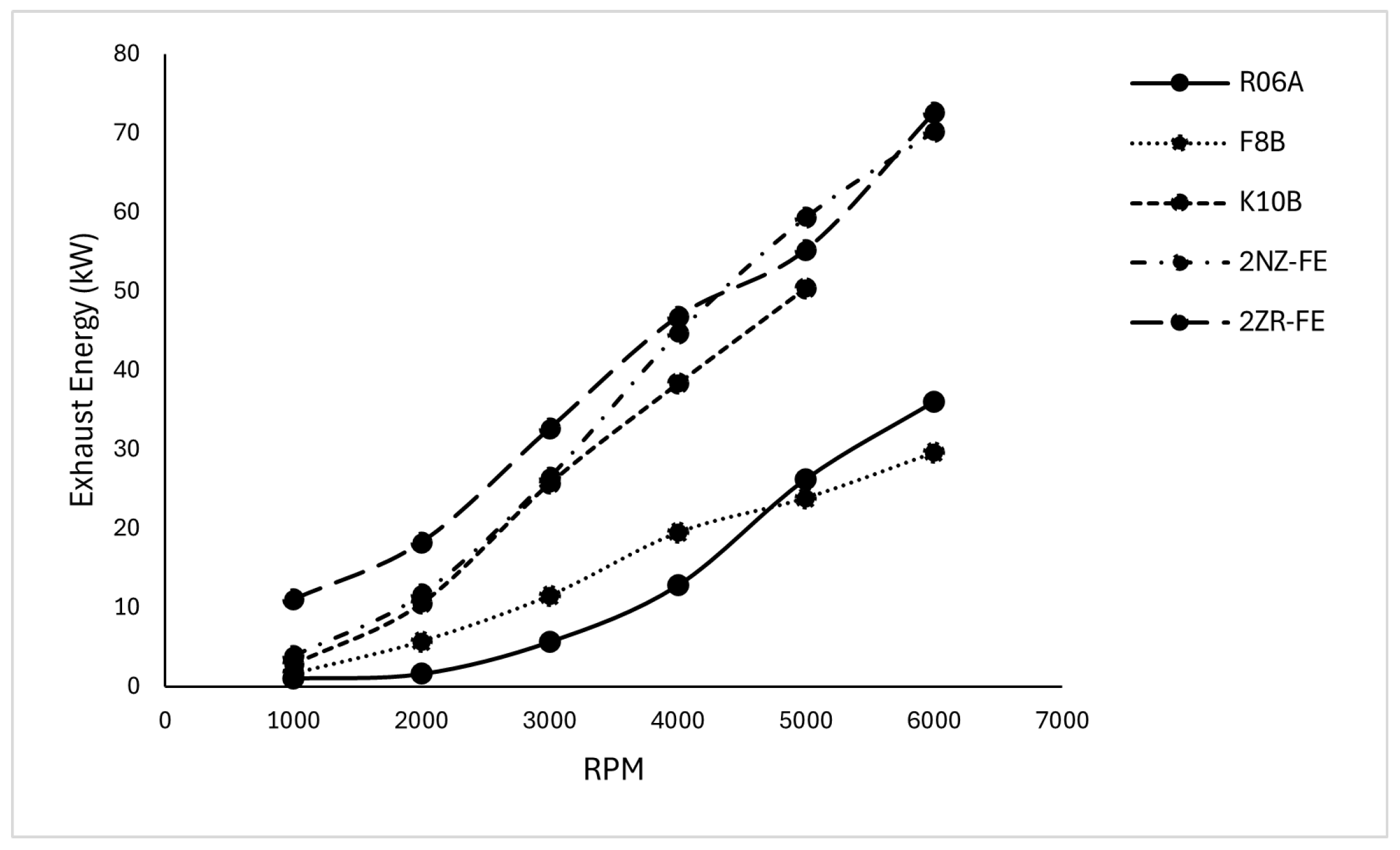
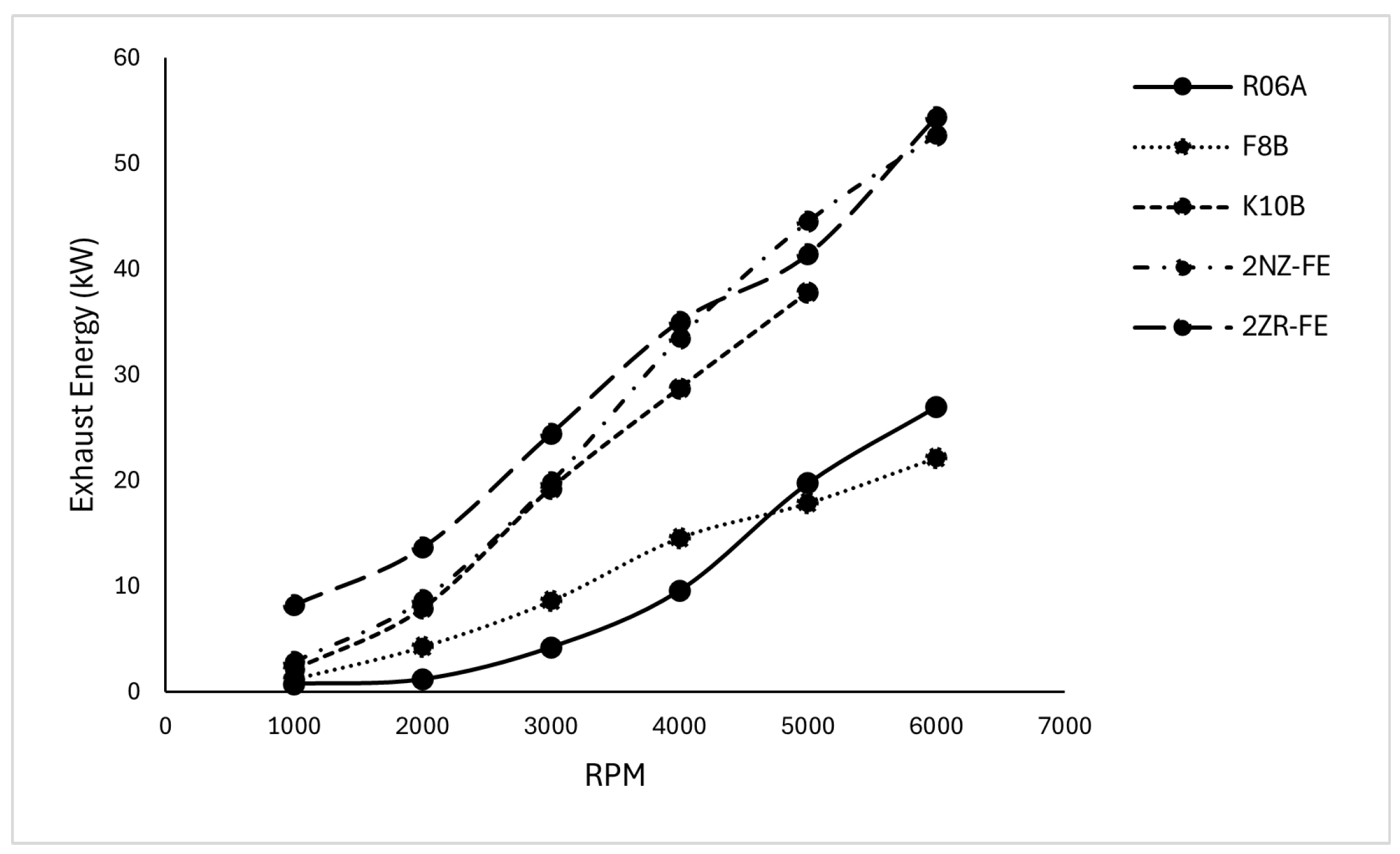

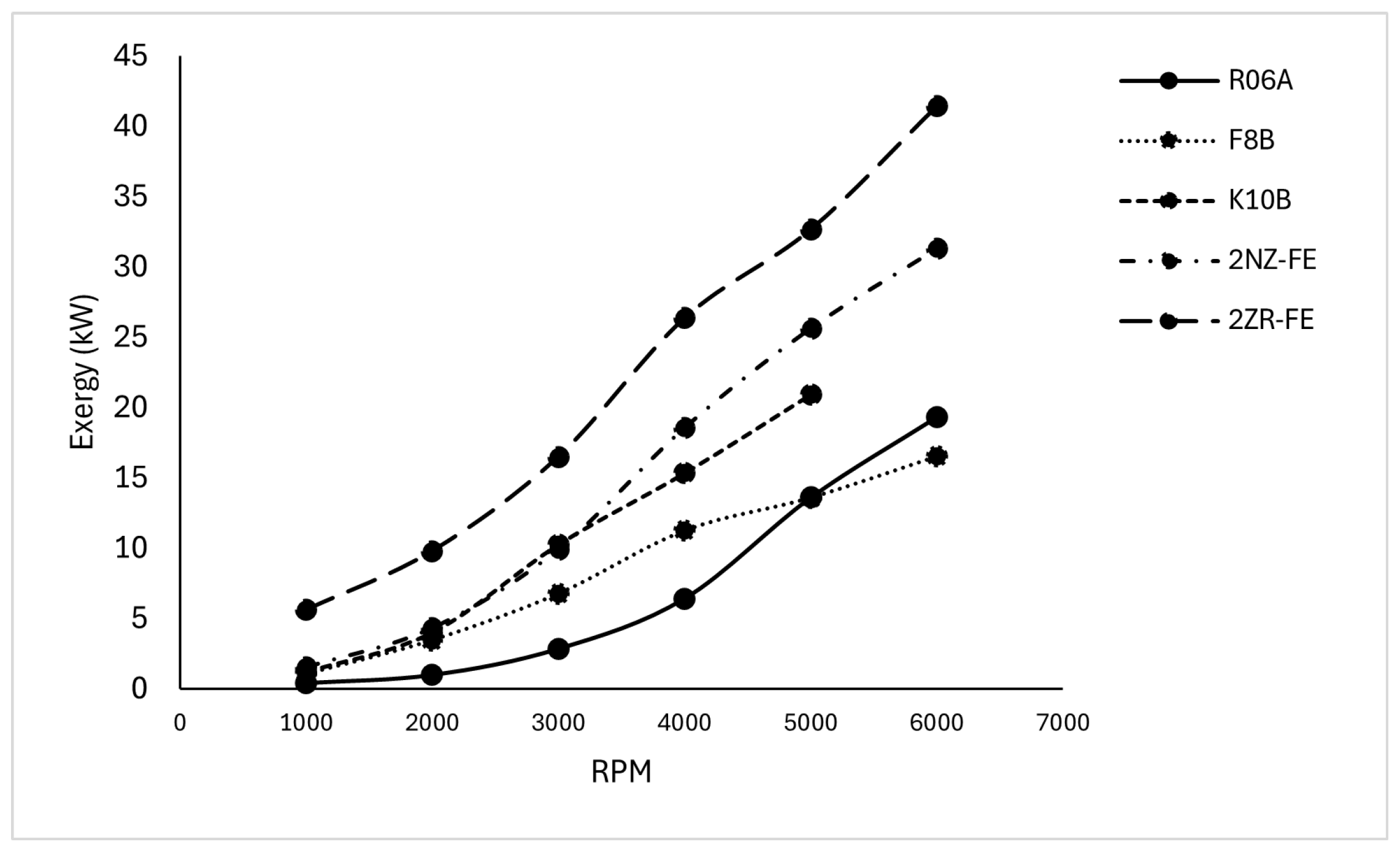


| ICE | R06A | F8B | K10B | 2NZ-FE | 2ZR-FE |
|---|---|---|---|---|---|
| No. of cylinders | 3 | 3 | 4 | 4 | 4 |
| Bore × stroke (mm) | 64 × 68.5 | 68.5 × 72 | 67 × 70 | 75 × 73.5 | 80.5 × 88.3 |
| Displacement volume (L) | 0.6 | 0.8 | 1 | 1.3 | 1.8 |
| Compression ratio | 11.5 | 11 | 9 | 10.5 | 10 |
| No. of valves | 12 | 6 | 16 | 16 | 16 |
| Power (kW/rpm) | 40/6000 | 29/5500 | 50/6200 | 63/6000 | 173/6400 |
| Torque (Nm/rpm) | - | 59/3000 | 90/3200 | 121/4400 | 173/4000 |
| Fuel | Gasoline | Gasoline | Gasoline | Gasoline | Gasoline |
| Working cycle | Natural | Natural | Natural | Natural | Natural |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishaq Khan, M.; Maccioni, L.; Concli, F. Energy and Exergy Analysis of Conventional Automobile Engines: Evaluation of Waste Heat Recovery Potential to Drive Parasitic Loads. Energies 2025, 18, 3264. https://doi.org/10.3390/en18133264
Ishaq Khan M, Maccioni L, Concli F. Energy and Exergy Analysis of Conventional Automobile Engines: Evaluation of Waste Heat Recovery Potential to Drive Parasitic Loads. Energies. 2025; 18(13):3264. https://doi.org/10.3390/en18133264
Chicago/Turabian StyleIshaq Khan, Muhammad, Lorenzo Maccioni, and Franco Concli. 2025. "Energy and Exergy Analysis of Conventional Automobile Engines: Evaluation of Waste Heat Recovery Potential to Drive Parasitic Loads" Energies 18, no. 13: 3264. https://doi.org/10.3390/en18133264
APA StyleIshaq Khan, M., Maccioni, L., & Concli, F. (2025). Energy and Exergy Analysis of Conventional Automobile Engines: Evaluation of Waste Heat Recovery Potential to Drive Parasitic Loads. Energies, 18(13), 3264. https://doi.org/10.3390/en18133264










