Operational Energy Consumption Map for Urban Electric Buses: Case Study for Warsaw
Abstract
1. Introduction
- No study to date has produced probabilistic section-level maps of both energy consumption and 30 s peak power demand for an entire urban bus network; existing analyses instead aggregate data over whole routes or rely on standardised driving cycles;
- Analyses often use average values, neglecting the probabilistic nature of urban driving;
- Few works offer spatially resolved energy demand maps at the inter-stop level;
- There is limited integration of such maps with charger deployment and route planning.
- Leveraging a unique dataset of two years of real-world operational data from onboard recorders on all bus lines in Warsaw, enabling unprecedented scale and granularity;
- Applying classical kinematic models and vehicle drive system loss maps to compute instantaneous power waveforms, energy use, and probabilistic distributions at the inter-stop section level;
- Producing intuitive energy and peak power demand maps that serve as practical tools for urban planners, transport operators, and energy providers to optimise route design, charger placement, and vehicle specification;
- Demonstrating the method’s scalability and generalisability, and outlining how it can be adapted to other cities by recalibrating with local data and extending to future scenarios such as new vehicle technologies and evolving traffic patterns.
2. Materials and Methods
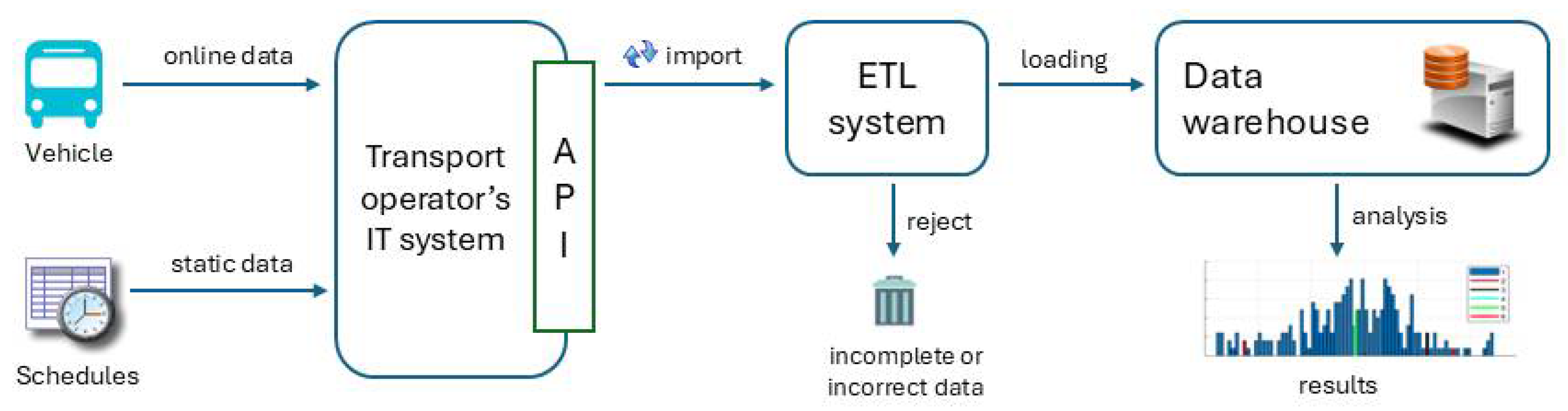
2.1. Materials
- Mistaken random recording of latitude or longitude;
- Interruption in data transmission;
- Vehicle time recording error (clock not turned on or faulty);
- Change in the transmission time step;
- No record of the timing of the stop.
- The routes of the individual lines;
- The timetables of the individual lines;
- The coordinates of the stops for each line;
- The length and location of the inter-stop sections.
2.2. Methods
3. Results
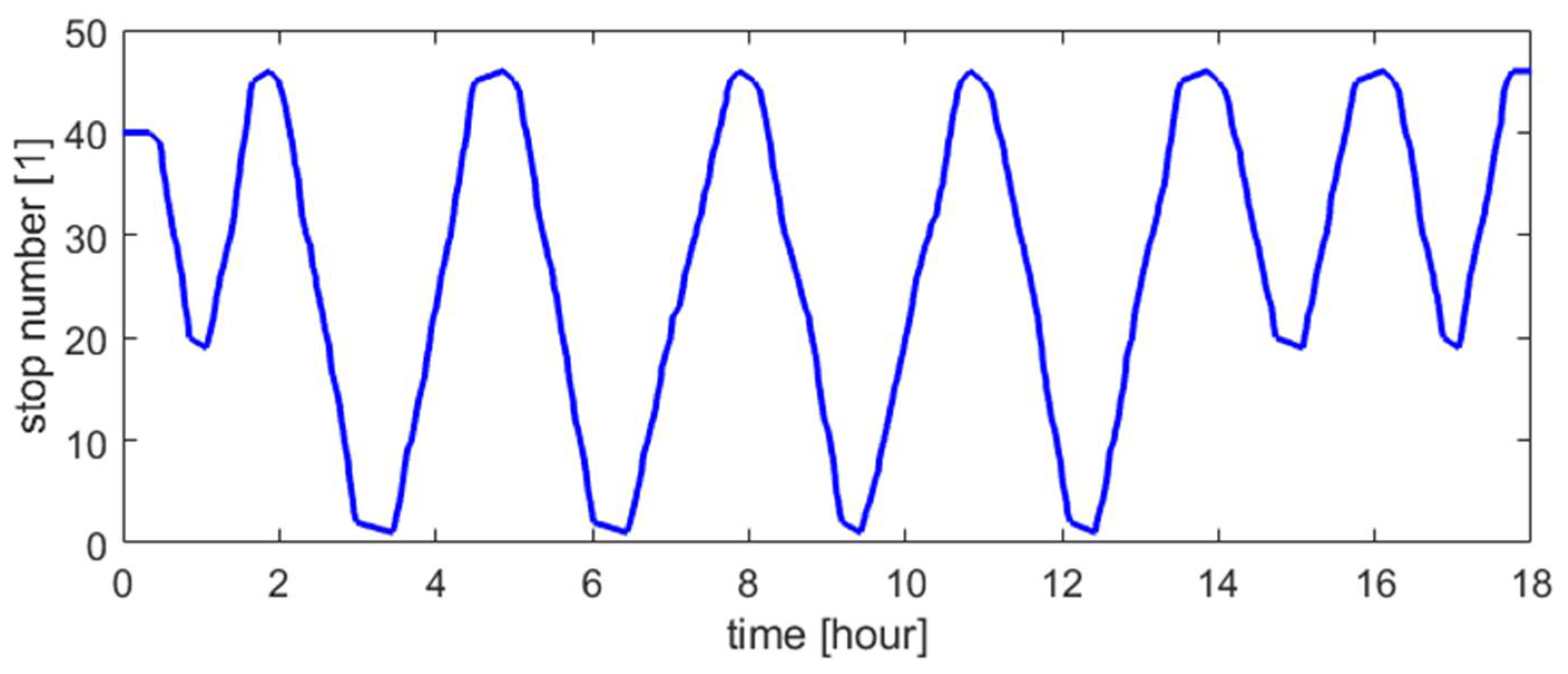
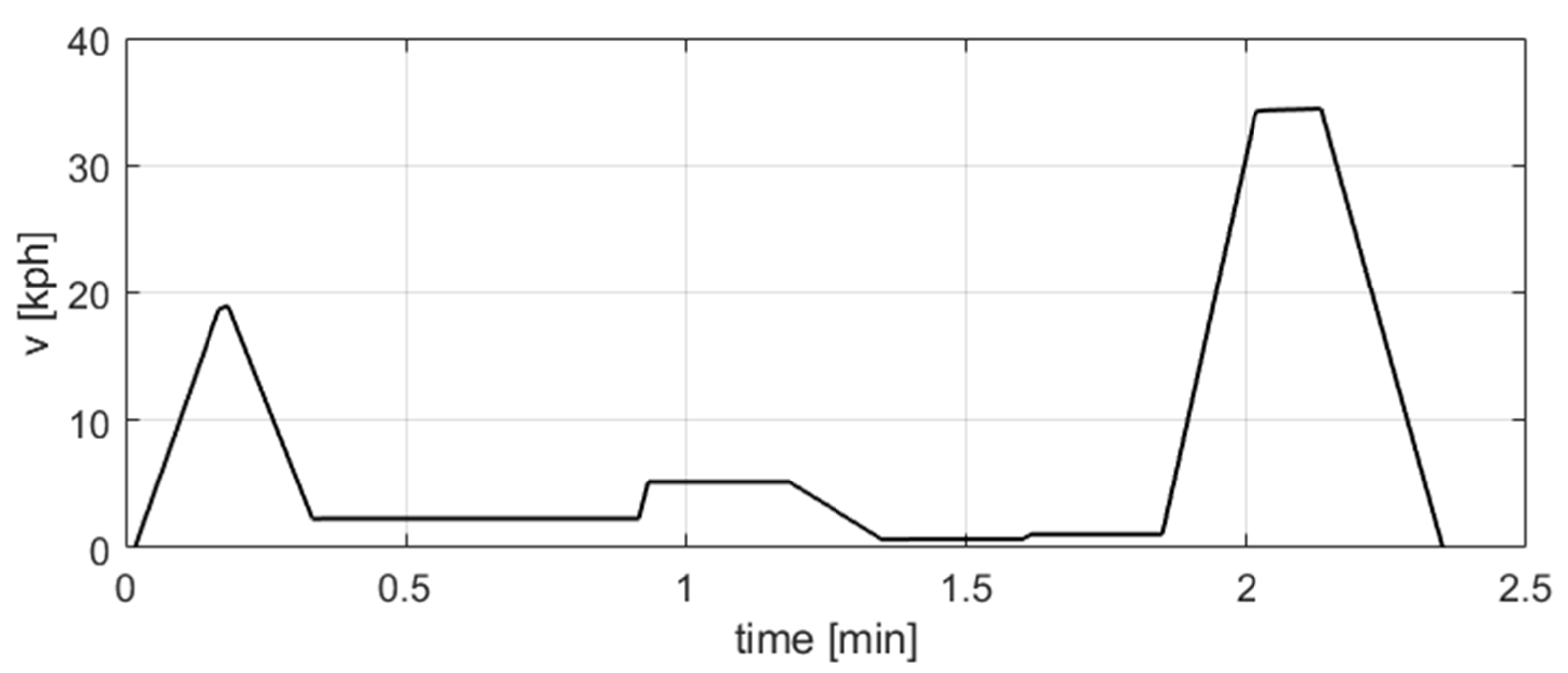
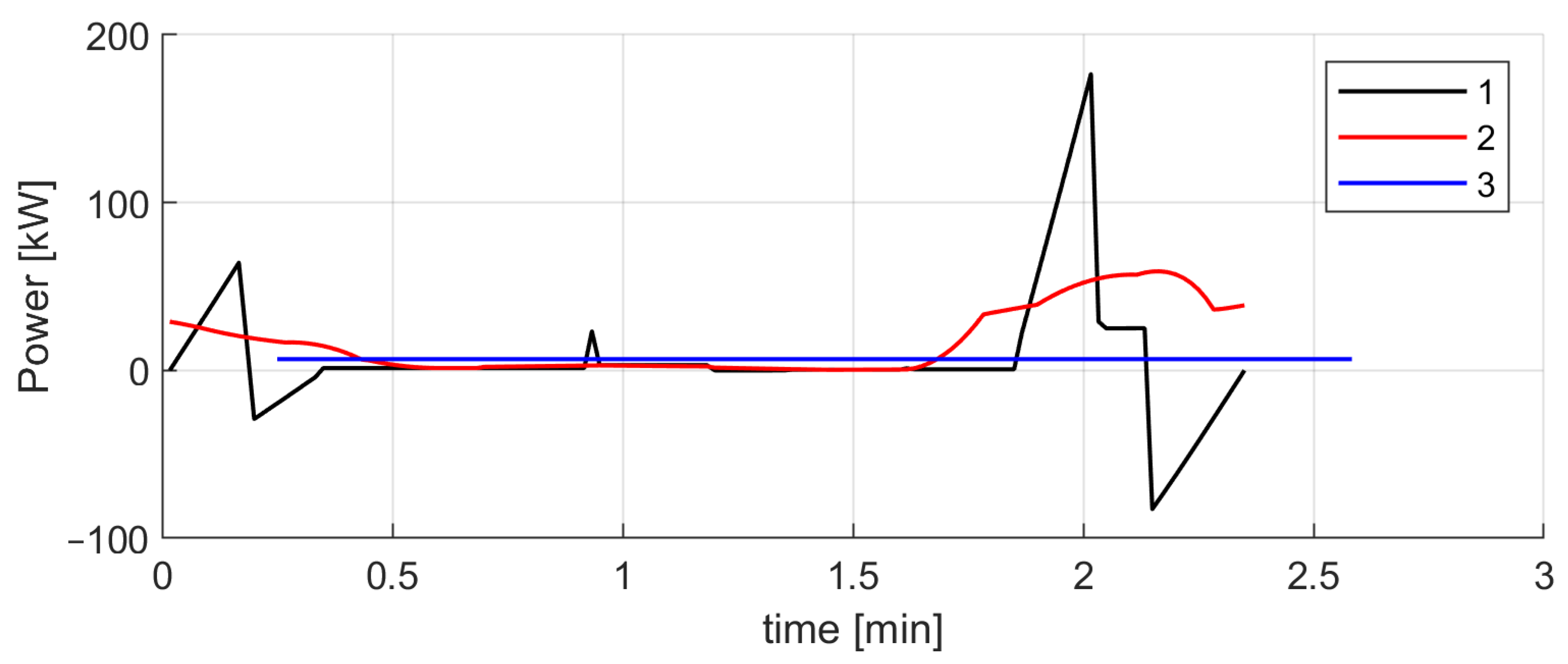
3.1. Results of the Analysis of Selected Route’s Section
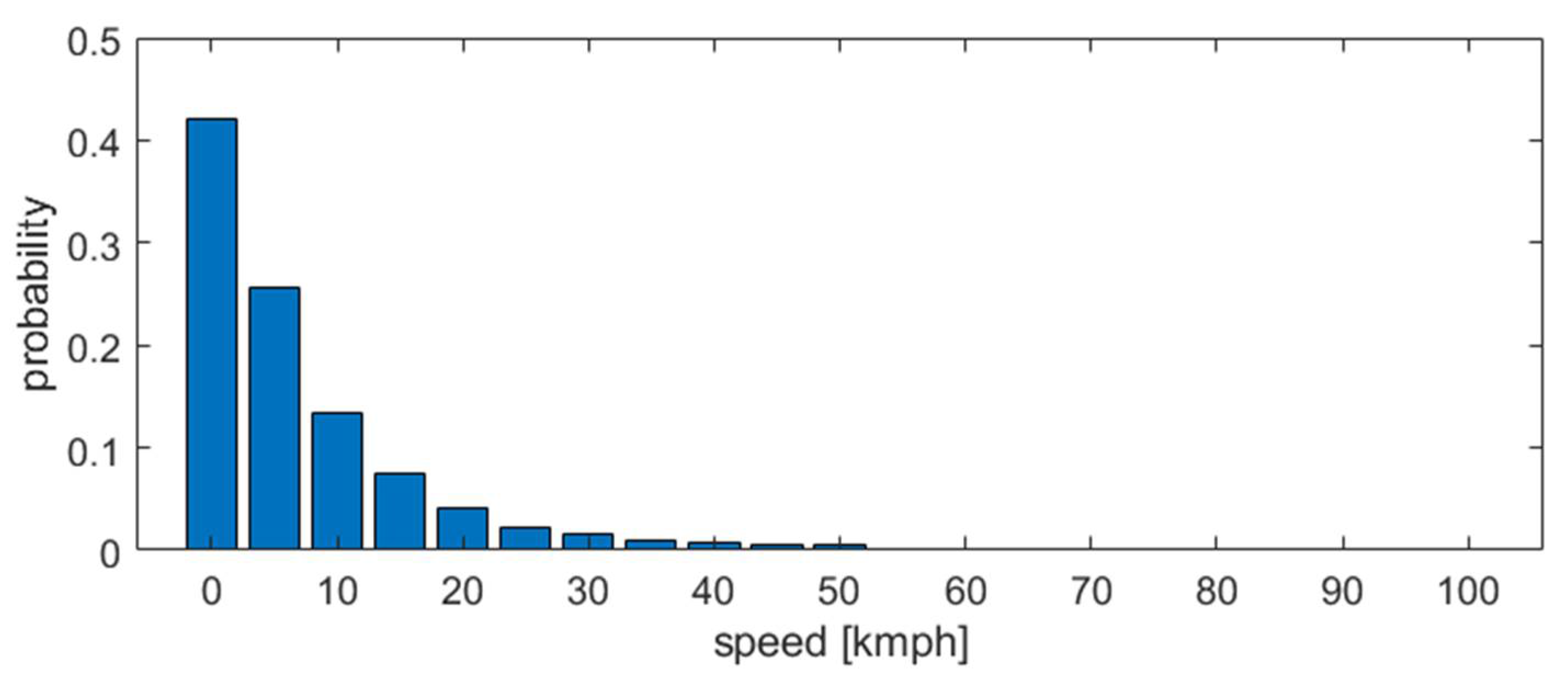
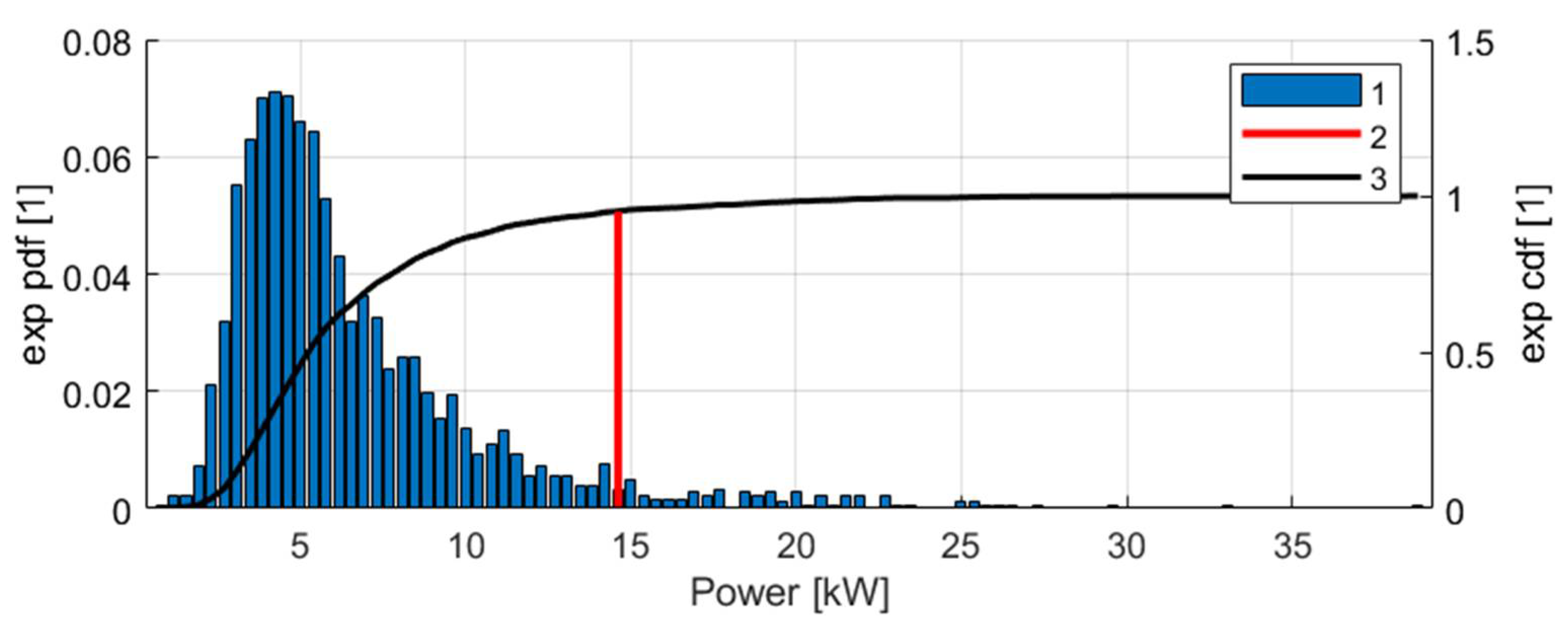
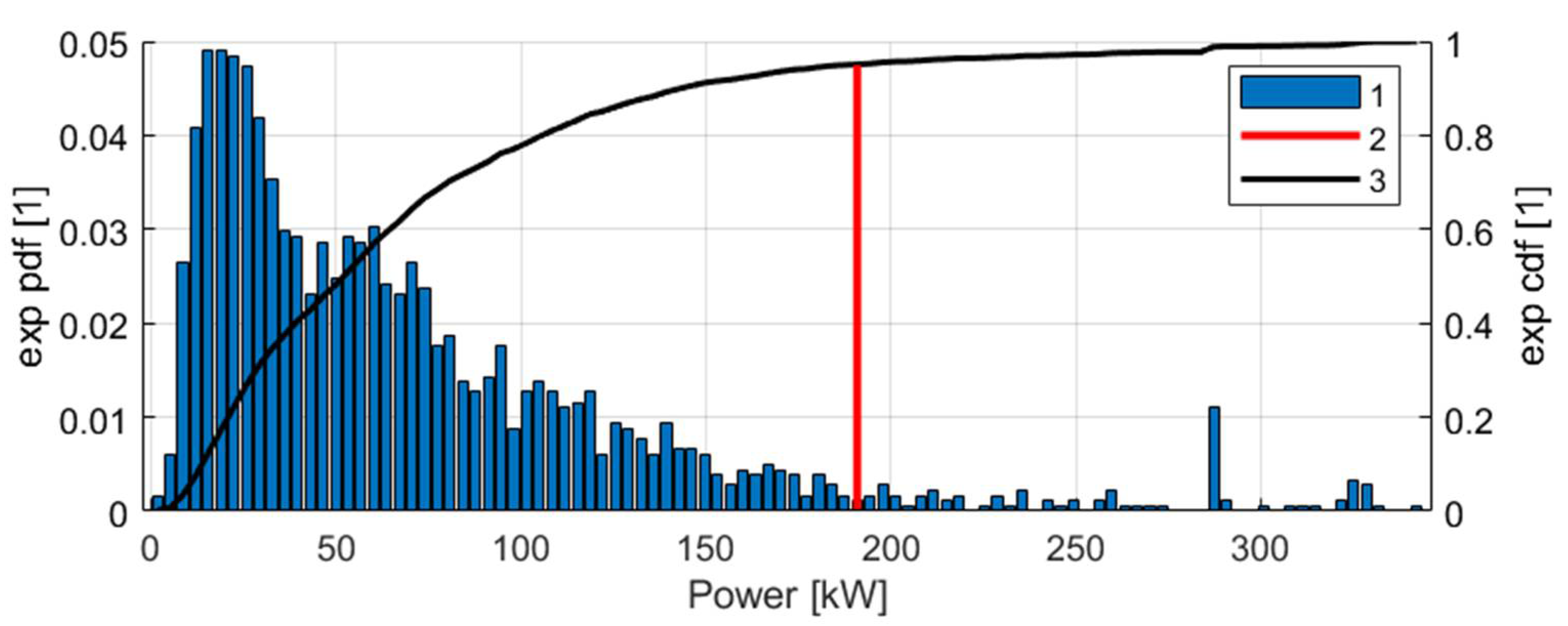
3.2. Results of the Analysis of Service Trips
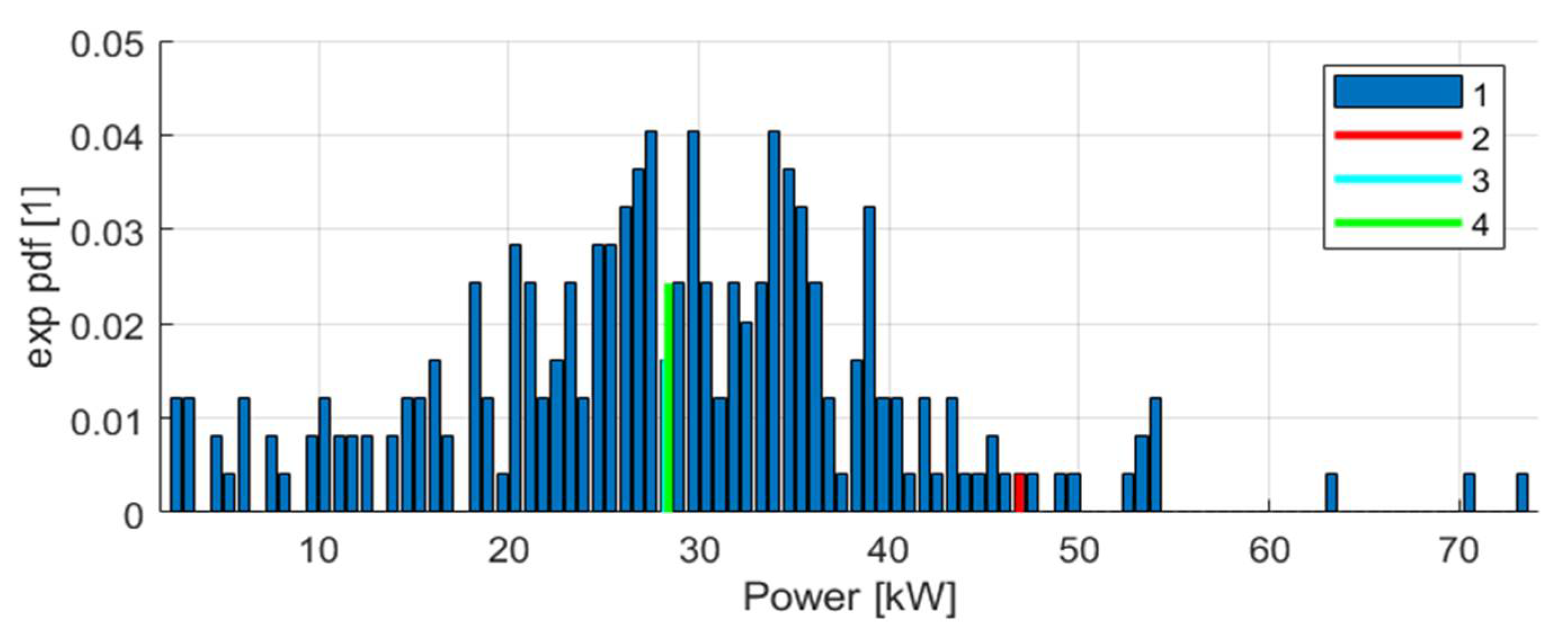
3.3. Estimated Incremental Increase in Electricity
3.4. Energy Demand Map
4. Discussion
5. Conclusions
- Availability of two years of high-resolution operational data from onboard bus recorders, accessed via the transport operator’s IT system;
- Use of classical “theoretical trip” models (kinematic equations) to derive instantaneous traction forces and power waveforms from recorded speed profiles;
- Application of detailed inverter motor loss maps to convert mechanical traction power into electrical energy demand.
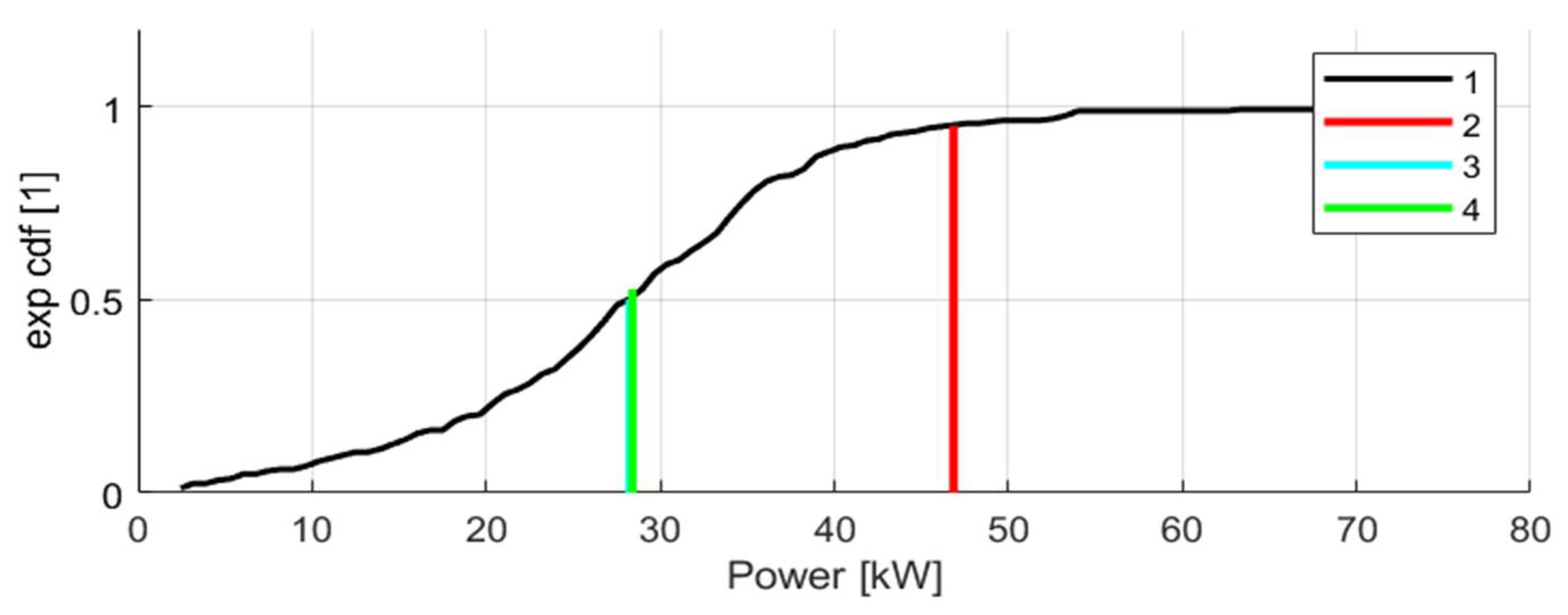
- A large discrepancy between continuous and peak power demands, with the 95th percentile of peak power exceeding that of continuous power by a factor of approximately five;
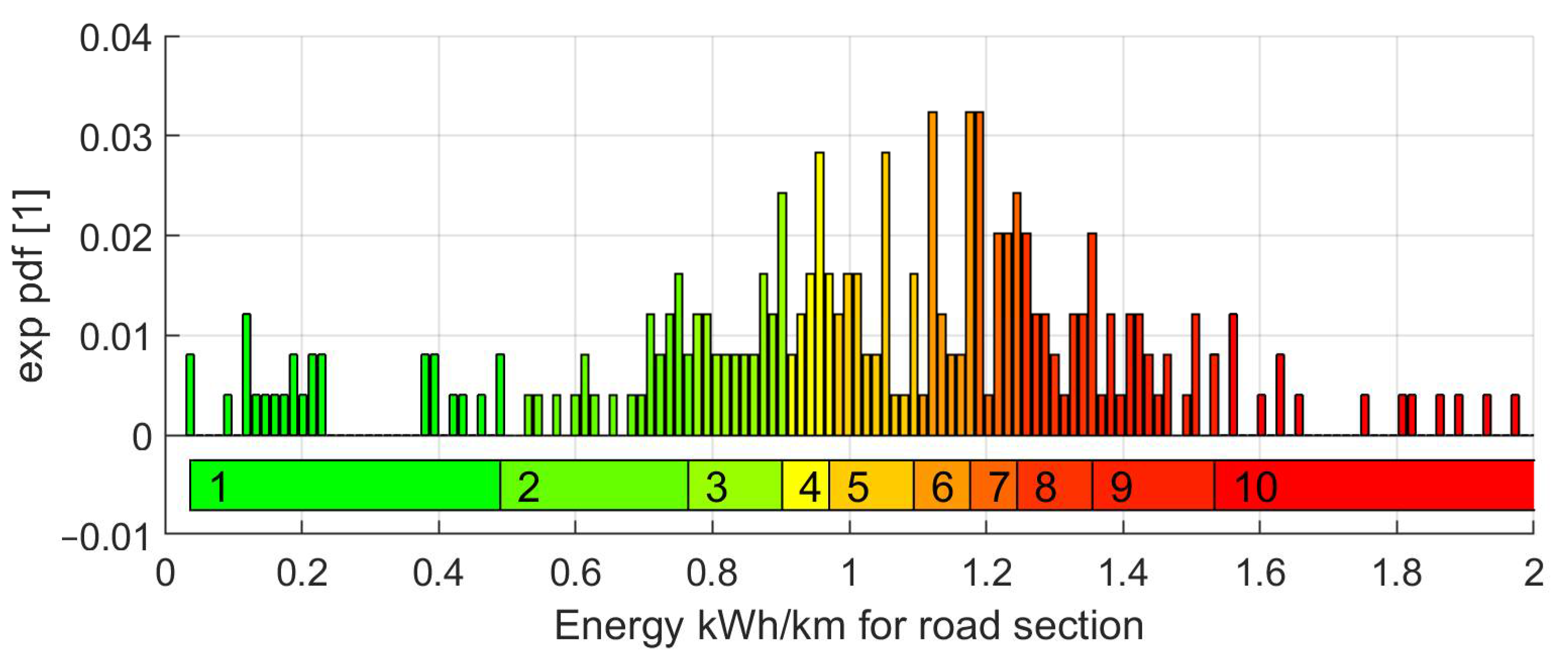
- High variability of energy use and power requirements across different route sections, underscoring the importance of section-level analysis rather than aggregated averages.
- Strategic charger placement and sizing along routes, by identifying “hot spots” of high energy or power demand;
- Rational dimensioning of battery capacity and traction motor power, ensuring reliable operation under real-world conditions;
- Route planning and verification, by providing pre-computed energy estimates for existing and newly configured routes.
- Integration of our maps with charger location models to optimise both siting and power ratings under budgetary and operational constraints (charger network optimisation);
- Combine our probabilistic energy profiles with battery ageing models to predict life-cycle costs and replacement schedules (advanced battery analysis);
- Incorporation of ambient temperature, precipitation (rain/snow), and other weather variables to enrich our profiling, enabling energy demand maps that vary by weather conditions (integration of meteorological data);
- Exploration of how network parameters (route length, stop frequency, service intervals) impact energy use, in collaboration with established bus network design heuristics (network design implications);
- Leveraging the same dataset to build statistical and machine-learning models (e.g., Kruskal–Wallis clustering, post hoc tests, and future LSTM networks) that predict bus arrival delays and inform timetable resilience (delay prediction and punctuality).
- Access to similarly detailed operator data;
- Recalibration of vehicle and loss model parameters to match local bus specifications and driving conditions;
- Management of massive datasets (tens to hundreds of millions of records), which, while uncountable in practice, lend themselves to probabilistic independence assumptions—almost any section-level difference will be statistically significant under tests like Kruskal–Wallis with post hoc analysis.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Indumathi, R. Electric Vehicles and Environmental Sustainability. ANWESH Int. J. Manag. Inf. Technol. 2020, 5, 5. [Google Scholar]
- Mo, T.; Li, Y.; Lau, K.; Poon, C.K.; Wu, Y.; Luo, Y. Trends and Emerging Technologies for the Development of Electric Vehicles. Energies 2022, 15, 6271. [Google Scholar] [CrossRef]
- Majumder, S.; De, K.; Kumar, P. Zero Emission Transportation System. In Proceedings of the 2016 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Trivandrum, India, 14–17 December 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar]
- Brdulak, A.; Chaberek, G.; Jagodziński, J. Development Forecasts for the Zero-Emission Bus Fleet in Servicing Public Transport in Chosen EU Member Countries. Energies 2020, 13, 4239. [Google Scholar] [CrossRef]
- Stec, S. Assessment of the Economic Efficiency of the Operation of Low-Emission and Zero-Emission Vehicles in Public Transport in the Countries of the Visegrad Group. Energies 2021, 14, 7706. [Google Scholar] [CrossRef]
- Rizza, V.; Torre, M.; Tratzi, P.; Fazzini, P.; Tomassetti, L.; Cozza, V.; Naso, F.; Marcozzi, D.; Petracchini, F. Effects of Deployment of Electric Vehicles on Air Quality in the Urban Area of Turin (Italy). J. Environ. Manag. 2021, 297, 113416. [Google Scholar] [CrossRef]
- Marotta, A.; Lodi, C.; Julea, A.; Gómez Vilchez, J.J. European Governments’ Electromobility Plans: An Assessment with a Focus on Infrastructure Targets and Vehicle Estimates until 2030. Energy Effic. 2023, 16, 92. [Google Scholar] [CrossRef]
- Electromobility and Alternative Fuels Act. Available online: https://sip.lex.pl/akty-prawne/dzu-dziennik-ustaw/elektromobilnosc-i-paliwa-alternatywne-18683445 (accessed on 13 April 2024).
- Polish Automotive Industry Association 2024 Year of Stagnation in Electric Car Market, Infrastructure on the Upside. Available online: https://www.pzpm.org.pl/pl/Elektromobilnosc/Licznik-Elektromobilnosci/Rok-2024/Grudzien-2024 (accessed on 15 April 2025).
- Zeng, Z.; Wang, S.; Qu, X. On the Role of Battery Degradation in En-Route Charge Scheduling for an Electric Bus System. Transp. Res. Part E Logist. Transp. Rev. 2022, 161, 102727. [Google Scholar] [CrossRef]
- Tepe, B.; Jablonski, S.; Hesse, H.; Jossen, A. Lithium-Ion Battery Utilization in Various Modes of e-Transportation. eTransportation 2023, 18, 100274. [Google Scholar] [CrossRef]
- Perumal, S.S.G.; Lusby, R.M.; Larsen, J. Electric Bus Planning & Scheduling: A Review of Related Problems and Methodologies. Eur. J. Oper. Res. 2022, 301, 395–413. [Google Scholar] [CrossRef]
- Avenali, A.; Catalano, G.; Giagnorio, M.; Matteucci, G. Factors Influencing the Adoption of Zero-Emission Buses: A Review-Based Framework. Renew. Sustain. Energy Rev. 2024, 197, 114388. [Google Scholar] [CrossRef]
- Brozovsky, J.; Gustavsen, A.; Gaitani, N. Zero Emission Neighbourhoods and Positive Energy Districts—A State-of-the-Art Review. Sustain. Cities Soc. 2021, 72, 103013. [Google Scholar] [CrossRef]
- Tsoi, K.H.; Loo, B.P.Y.; Li, X.; Zhang, K. The Co-Benefits of Electric Mobility in Reducing Traffic Noise and Chemical Air Pollution: Insights from a Transit-Oriented City. Environ. Int. 2023, 178, 108116. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhao, A.; Tang, C. Integrated Optimization of Mixed Bus Fleet Replacement and Scheduling with Emission and Budget Constraints. Preprint 2025. [Google Scholar]
- Gairola, P.; Nezamuddin, N. Determining Battery and Fast Charger Configurations to Maximize E-Mileage of Electric Buses under Budget. J. Transp. Eng. Part A Syst. 2022, 148, 04022100. [Google Scholar] [CrossRef]
- Wenz, K.-P.; Serrano-Guerrero, X.; Barragán-Escandón, A.; González, L.G.; Clairand, J.-M. Route Prioritization of Urban Public Transportation from Conventional to Electric Buses: A New Methodology and a Study of Case in an Intermediate City of Ecuador. Renew. Sustain. Energy Rev. 2021, 148, 111215. [Google Scholar] [CrossRef]
- Czerepicki, A.; Choromański, W.; Kozłowski, M.; Kazinski, A. Analysis of the Problem of Electric Buses Charging in Urban Transport. Sci. Tech. 2020, 19, 349–355. [Google Scholar] [CrossRef]
- Zhou, Y.; Meng, Q.; Ong, G.P. Electric Bus Charging Scheduling for a Single Public Transport Route Considering Nonlinear Charging Profile and Battery Degradation Effect. Transp. Res. Part B Methodol. 2022, 159, 49–75. [Google Scholar] [CrossRef]
- Olsen, N.; Kliewer, N. Location Planning of Charging Stations for Electric Buses in Public Transport Considering Vehicle Scheduling: A Variable Neighborhood Search Based Approach. Appl. Sci. 2022, 12, 3855. [Google Scholar] [CrossRef]
- Szilassy, P.Á.; Földes, D. Consumption Estimation Method for Battery-Electric Buses Using General Line Characteristics and Temperature. Energy 2022, 261, 125080. [Google Scholar] [CrossRef]
- Zhang, X.; Nie, S.; He, M.; Wang, J. Charging System Analysis, Energy Consumption, and Carbon Dioxide Emissions of Battery Electric Buses in Beijing. Case Stud. Therm. Eng. 2021, 26, 101197. [Google Scholar] [CrossRef]
- Li, P.; Jiang, M.; Zhang, Y.; Zhang, Y. Cooperative Optimization of Bus Service and Charging Schedules for a Fast-Charging Battery Electric Bus Network. IEEE Trans. Intell. Transp. Syst. 2023, 24, 5362–5375. [Google Scholar] [CrossRef]
- Behnia, F.; Schuelke-Leech, B.-A.; Mirhassani, M. Optimizing Sustainable Urban Mobility: A Comprehensive Review of Electric Bus Scheduling Strategies and Future Directions. Sustain. Cities Soc. 2024, 108, 105497. [Google Scholar] [CrossRef]
- Weiss, M.; Winbush, T.; Newman, A.; Helmers, E. Energy Consumption of Electric Vehicles in Europe. Sustainability 2024, 16, 7529. [Google Scholar] [CrossRef]
- Lee, G.; Song, J.; Lim, Y.; Park, S. Energy Consumption Evaluation of Passenger Electric Vehicle Based on Ambient Temperature under Real-World Driving Conditions. Energy Convers. Manag. 2024, 306, 118289. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Liu, P.; Zhang, Z. Energy Consumption Analysis and Prediction of Electric Vehicles Based on Real-World Driving Data. Appl. Energy 2020, 275, 115408. [Google Scholar] [CrossRef]
- Jonas, T.; Wilde, T.; Hunter, C.D.; Macht, G.A. The Impact of Road Types on the Energy Consumption of Electric Vehicles. J. Adv. Transp. 2022, 2022, 1436385. [Google Scholar] [CrossRef]
- Ou, X.; Zhang, X.; Chang, S. Alternative Fuel Buses Currently in Use in China: Life-Cycle Fossil Energy Use, GHG Emissions and Policy Recommendations. Energy Policy 2010, 38, 406–418. [Google Scholar] [CrossRef]
- Skrúcaný, T.; Kendra, M.; Stopka, O.; Milojević, S.; Figlus, T.; Csiszár, C. Impact of the Electric Mobility Implementation on the Greenhouse Gases Production in Central European Countries. Sustainability 2019, 11, 4948. [Google Scholar] [CrossRef]
- Borghetti, F.; Carra, M.; Besson, C.; Matarrese, E.; Maja, R.; Barabino, B. Evaluating Alternative Fuels for a Bus Fleet: An Italian Case. Transp. Policy 2024, 154, 1–15. [Google Scholar] [CrossRef]
- Warsaw City Administration. Open Data. Available online: https://api.um.warszawa.pl/# (accessed on 13 April 2024).
- Warsaw Public Transport Timetables. Available online: https://www.ztm.waw.pl/pliki-do-pobrania/dane-rozkladowe/ (accessed on 16 April 2025).
- General Transit Feed Specification. Available online: https://gtfs.org/documentation/overview/ (accessed on 16 April 2025).
- Basma, H.; Mansour, C.; Haddad, M.; Nemer, M.; Stabat, P. Energy Consumption and Battery Sizing for Different Types of Electric Bus Service. Energy 2022, 239, 122454. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Y.; Sun, R. Data-Driven Estimation of Energy Consumption for Electric Bus under Real-World Driving Conditions. Transp. Res. Part D Transp. Environ. 2021, 98, 102969. [Google Scholar] [CrossRef]
- Lim, L.K.; Muis, Z.A.; Ho, W.S.; Hashim, H.; Bong, C.P.C. Review of the Energy Forecasting and Scheduling Model for Electric Buses. Energy 2023, 263, 125773. [Google Scholar] [CrossRef]
- Fiori, C.; Montanino, M.; Nielsen, S.; Seredynski, M.; Viti, F. Microscopic Energy Consumption Modelling of Electric Buses: Model Development, Calibration, and Validation. Transp. Res. Part D Transp. Environ. 2021, 98, 102978. [Google Scholar] [CrossRef]
- Kozłowski, M.; Czerepicki, A. Quick Electrical Drive Selection Method for Bus Retrofitting. Sustainability 2023, 15, 10484. [Google Scholar] [CrossRef]
- OpenStreet Map. Available online: https://www.openstreetmap.org/ (accessed on 10 June 2024).





| Route | Vehicle | Crew No. | Latitude | Longitude | Time | |
|---|---|---|---|---|---|---|
| Data type | string | string | int | float | float | datetime |
| Sample value | 112 | 3489 | 6 | 52.39210 | 20.94418 | 10 February 2024 19:21:43 |
| Route | Stops | Length, [km] |
|---|---|---|
| 112 (Regular line) | 45/48 | 24.76/25.78 |
| 180 (Tourist line) | 42/45 | 19.60/19.80 |
| 523 (Express line) | 35/33 | 20.67/20.45 |
| Symbol | Definition | Unit |
|---|---|---|
| Cumulative distance travelled by vehicle | m | |
| Time | s | |
| Instantaneous vehicle speed | m/s | |
| Instantaneous rate of change of distance (speed) | m/s | |
| Instantaneous acceleration | m/s2 | |
| Traction force at the wheels | N | |
| Substitute vehicle mass (empty vehicle + battery + average payload) | kg | |
| Motion resistance force (rolling + aerodynamic), approximated by a quadratic function of speed | N | |
| W | ||
| J | ||
| W | ||
| 30 s peak mechanical power | W | |
| Electrical input power (mechanical power ± losses) | W | |
| Power loss in reduction gear | W | |
| Power loss in machine inverter assembly | W | |
| Reduction gear efficiency (constant) | – | |
| Function of the traction machine power loss map as a function of the operating point | – | |
| Motor torque | kN·m | |
| Motor angular speed | rpm | |
| Rated (continuous) electric machine power | W | |
| – |
| 0.1580 | −0.2733 | −0.2278 | 0.7812 | 1.4745 | 1.1305 | −0.2249 | −1.9670 |
| −1.0319 | −0.3290 | 0.0198 | 0.4836 | 0.8965 | −0.0003 | 0.1103 |
| Stop Id1 | Stop Id2 | Mean | Sigma | Q95 | Dist., km | EE, kWh/100 km |
|---|---|---|---|---|---|---|
| 101,303 | 613,304 | 2.6255 | 0.4791 | 3.4193 | 2.23 | 153 |
| 101,304 | 115,902 | 1.3394 | 0.3654 | 1.9373 | 0.76 | 255 |
| 108,503 | 108,505 | 0.4400 | 0.2080 | 0.9047 | 0.35 | 258 |
| 108,504 | 108,510 | 0.3813 | 0.2890 | 0.8600 | 0.35 | 246 |
| 108,505 | 116,101 | 0.5909 | 0.2882 | 1.1413 | 0.31 | 368 |
| 108,510 | 115,002 | 0.2780 | 0.1766 | 0.6075 | 0.28 | 217 |
| 114,601 | 114,704 | 0.4439 | 0.2063 | 0.8840 | 0.38 | 233 |
| 114,602 | 114,606 | 0.4562 | 0.2434 | 0.9603 | 0.25 | 384 |
| 114,606 | 131,902 | 0.6367 | 0.3288 | 1.1194 | 0.54 | 207 |
| 114,702 | 114,602 | 0.4717 | 0.3309 | 0.8775 | 0.47 | 187 |
| 114,704 | 115,303 | 0.0855 | 0.2436 | 0.3736 | 0.40 | 93 |
| 115,001 | 108,503 | 0.2347 | 0.1887 | 0.4967 | 0.37 | 134 |
| Class | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.04 | 0.49 | 0.76 | 0.90 | 0.97 | 1.09 | 1.18 | 1.25 | 1.35 | 1.53 | |
| 0.49 | 0.76 | 0.90 | 0.97 | 1.09 | 1.18 | 1.25 | 1.35 | 1.53 | 3.41 | |
| 5 | 114 | 154 | 184 | 214 | 234 | 253 | 273 | 303 | 343 | |
| 114 | 154 | 184 | 214 | 234 | 253 | 273 | 303 | 343 | 500 | |
| Colour | 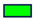 | 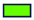 |  |  |  |  |  |  |  |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozłowski, M.; Czerepicki, A. Operational Energy Consumption Map for Urban Electric Buses: Case Study for Warsaw. Energies 2025, 18, 3281. https://doi.org/10.3390/en18133281
Kozłowski M, Czerepicki A. Operational Energy Consumption Map for Urban Electric Buses: Case Study for Warsaw. Energies. 2025; 18(13):3281. https://doi.org/10.3390/en18133281
Chicago/Turabian StyleKozłowski, Maciej, and Andrzej Czerepicki. 2025. "Operational Energy Consumption Map for Urban Electric Buses: Case Study for Warsaw" Energies 18, no. 13: 3281. https://doi.org/10.3390/en18133281
APA StyleKozłowski, M., & Czerepicki, A. (2025). Operational Energy Consumption Map for Urban Electric Buses: Case Study for Warsaw. Energies, 18(13), 3281. https://doi.org/10.3390/en18133281








