Abstract
In this paper, we propose a concise but general two-dimensional model based on the penetration model in order to simulate the heat and mass transfer and drying kinetics of sludge in the paddle dryer. The sludge control equations were developed to simulate the heat and mass transfer of sludge and the penetration model was introduced to describe the mixing of sludge. Compared to the experimental results in the existing literature, the drying kinetics simulated simulated by the present model were in good agreement with the experimental data under various operation conditions. The effects of four key parameters on drying kinetics in the paddle dryer were studied. The results showed that the water content increased with the increase of sludge flowrate and the decrease of wall temperature and sludge density. Furthermore, the stirring velocity had little effect on the drying kinetics of the sludge. The present study contributes to the better understanding of the sludge drying kinetics and provides guidance for the optimal design of industrial paddle dryers.
1. Introduction
Sludge is a sort of solid waste which is a byproduct of municipal and industrial waste water treatment processes and is of great harm to human life [1]. With the development of the national industrial economy and the acceleration of urbanization in China, the discharge of sludge is also increasing. According to statistics, China’s sludge output with a water content of 80% has exceeded 65 million tons in 2020, and it is expected that China’s annual sludge output will exceed 90 million tons in 2025. Improper sludge disposal seriously pollutes the surrounding environment, which has become a common problem in many localities.
Sludge treatment technologies mainly include concentration, fermentation, drying and so on. Drying technology is safe and stable and has strong adaptability to different kinds of sludges; therefore, it is one of the most widely used and mature technologies in the sludge treatment field. Sludge drying refers to the process of evaporating water in sludge by heating, which can be divided into direct drying and indirect drying according to whether the sludge is in contact with the heat source medium. A paddle dryer is an indirect drying technology, which is one of the most mature and widely used sludge drying devices. The drying process of sludge in the paddle dryer belongs to the dividing wall-type heating and drying process. Steam or heat transfer oil are usually used as the hot medium in paddle dryers. While the dryer is operating, steam or heat transfer oil flows into the cavities inside the dryer housing interlayer and paddles, transferring heat to the sludge by heat conduction though the wall of interlayer and paddles. The sludge is cut and stirred by the rotation of paddles during the moving process and dried by the heat conduction with the water evaporation [2].
In order to realize the rational design and optimization of the paddle dryer, it is of great significance to develop a computational model which can accurately describe the heat and mass transfer of sludge in a paddle dryer. However, the heat and mass transfer behavior, and the movement process of sludge in a paddle dryer, are very complex and are mainly affected by the geometric structure, the mechanical operating parameters, the physical and chemical characteristics of the sludge itself, the heat source, the carrier gas and so on. To simplify the complex physical phenomena, the sludge drying process in a paddle dryer can be decomposed into the heat transfer, mass transfer and mixing process of sludge in time, as well as the movement behavior of sludge in space.
To accurately simulate the heat and mass transfer behavior of sludge in a paddle dryer, a series of research has been carried out by worldwide scholars in the past decades. Schlünder and his group members [3,4,5] developed the so-called penetration model, which was used to simulate the indirect drying process of non-porous granular materials under vacuum and inert gas atmosphere. In the penetration model, it is assumed that the mass transfer resistance and heat transfer resistance of a single particle in the particle layer are zero, and only the contact thermal resistance between the bottom layer of the particle layer and the heating surface and the thermal resistance of the material layer are considered. The continuous mixing of the material by mechanical agitation in the drying process can be divided into many discontinuous mixing processes. In the single discontinuous mixing process, mixing of the material is assumed to be completed in an instant. The penetration model has been proven to simulate the drying process in mechanically agitated devices such as a paddle dryer. To develop a new method for the thermal design of paddle dryers, Arlabosse et al. [6,7] developed a simple model to simulate the drying kinetics of sludge in the lab-scale paddle dryer. In this method, the drying process is divided into two parts according to the sludge consistency: first, a constant evaporating flow rate is assumed in the pasty zone and, second, a linear decrease with the moisture content is taken into account in the granular zone. The calculation results are in agreement with the experimental data. Arlabosse and Chitu [8] also used the penetration model to simulate the drying characteristics of sludge in a batch agitated dryer with steam used as the hot side working medium. They found that the model could describe the sludge drying kinetics well. Milhé et al. [9] developed a model based on the theory of Markov chains to predict the residence time distribution (RTD) of sewage sludge in a paddle dryer. In this model, the flow process of sludge was described by a chain of n perfectly mixed cells, with n corresponding to the number of paddles installed the shaft. They found that the model could describe the sludge flow well in a continuous lab-scale paddle dryer. After that, Milhé et al. [10] also coupled the one-dimensional Markov chain model with the penetration model, thus establishing a one-dimensional penetration model used to simulate the drying characteristics of sludge in a uniaxial continuous paddle dryer. The modified model can better simulate the water content distribution of sludge in the dryer. Chen et al. [11,12] presented a series of experiments on drying characteristics in a continuous paddle dryer and developed a coupled model of the penetration model and the Markov chain in order to study the drying behavior. The simulation results of the new model showed good agreement with the experimental results. The impact of various drying parameters on the sludge drying kinetics were also investigated in their study. Lyu et al. [13] developed a two-dimensional model based on the theory of Markov chain to predict the Residence Time Distribution (RTD) of sludge in the continuous paddle dryer. The results showed that the two-dimensional model demonstrated its ability to describe the sludge flow in the paddle dryer based on the comparison between calculation and experiment results. The thermal and mass transfer properties of sludge are the important input parameters to model the sludge drying. Layth et al. [14] carried out a series of experiments to determine the thermo-physical properties of sludge such as shrinkage coefficient, density, apparent moisture diffusivity, effective thermal conductivity and heat capacity. The mathematical relationships between sludge properties and the water content/temperature are established, and they could be applied in a numerical drying model.
According to the literature, it has been found that many studies on sludge model development have been presented. However, most of the existing models for heat and mass transfer simulation of sludge are complex, and the relevant studies were still in the lab stage. The applicability of a model for practical engineering design required further improvement. Meanwhile, the heat transfer in the paddle dryer is a coupled heat transfer process between the hot side and the sludge side. There are few reports on a bilateral coupled model for heat and mass transfer simulation in the paddle dryer. Therefore, to accurately predict the heat transfer and drying behavior of sludge in a paddle dryer, it is necessary to continue to make efforts on the heat and mass transfer model development of sludge, which lays a theoretical foundation for the performance optimization design of industrial paddle dryers.
2. Model Description
2.1. Basic Equation
The heat and mass transfer process of sludge in a paddle dryer is very complex. On the one hand, when the sludge enters the dryer, the sludge temperature will rise and the water in the sludge will begin to evaporate owing to the heating effect of high-temperature steam or heat transfer oil. On the other hand, due to the arrangement of several wedge-shaped paddles inside the dryer, the sludge will be driven to stir by paddles, making the heat and mass transfer process more complex and difficult to describe with precise mathematical equations. The temperature and the water content evolve continuously during drying, not only along the radial direction but also along the axial direction.
According to the features of the drying process of sludge in the paddle dryer, in the present model, we divided the drying of sludge in the paddle dryer into two processes: heat and mass transfer and mixing. For the model development, the sludge is assumed to be a porous water-contained media. The physical quantities describing the state of the sludge are water content (X) and temperature (T). To simplify the physical process, we make the following assumptions:
- (1)
- The movement of sludge in the axial direction in the dryer is assumed to be a uniform linear motion.
- (2)
- The mixing phenomenon of sludge in the vertical and axial directions is described based on the penetration theory, which will be introduced in detail in the next section.
- (3)
- The water in the sludge becomes gaseous after evaporation after heating and leaves the sludge directly without heat and mass transfer with the sludge.
- (4)
- Physical properties are functions of water content.
Based on the above assumptions, the sludge control equations can be given. First, the water content equation is as follows:
where X is water content. X0 is the initial water content. D is the apparent diffusivity coefficient. u is the sludge movement velocity. Under defined operating conditions, the sludge movement velocity is constant, depending on the sludge flowrate. is the evaporation mass rate, which is defined as [15]:
where stands for the initial sludge mass. ρ is the density of sludge. T is the temperature of sludge. r is an empirical coefficient.
Meanwhile, the energy equation can be defined as:
where is density of the sludge. T is temperature of the sludge. is the effective thermal conductivity. is the total evaporation heat, which is determined by the following equation [16]:
is the water’s latent heat of evaporation, which is 2256.43 kJ/kg at standard atmospheric pressure. is the binding energy of water. A TGA-DSC method and curve fitting was used to calculate the sludge water binding energy [11]:
2.2. Boundary Conditions
The boundary conditions of the above model are determined according to the actual situation of the paddle dryer. First, sludge flows from the inlet. Due to the stable inlet conditions, the inlet boundary condition is defined as a Dirichlet boundary condition for T and X:
For the outlet boundary condition, a homogeneous Neumann condition on T and X can be defined as:
For the heating wall, heat is transferred from steam to sludge through the paddle wall. Since the heat transfer coefficient on the steam side is much greater than that of the sludge side, the boundary conditions on the sludge side can be simplified to a constant temperature boundary (Saturation Temperature of steam). The boundary condition for X remains Neumann condition, given as:
For the upper wall (unheated wall), we simplify the boundary condition to the Neumann boundary condition, given as:
As a summary, the boundary conditions for the two-dimensional sludge model are shown in Figure 1.
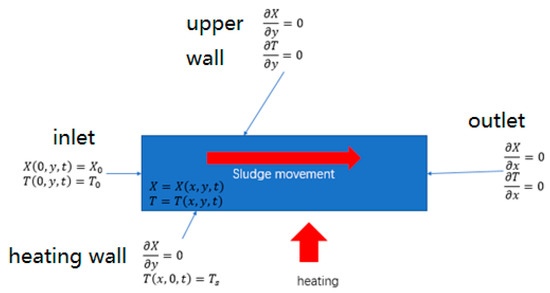
Figure 1.
Schematic diagram of the two-dimensional model of sludge.
2.3. Penetration Theory
The above heat and mass transfer model was suitable for simulating sludge drying processes under a static condition. In the actual paddle dryer, the sludge is mixed at the same time and the heat and mass transfer process is accelerated owing to the stirring effect of the paddles on the sludge. In order to describe the mixing of sludge, the penetration theory [3,4,5] has been used for reference in the present model.
As mentioned before, the penetration model is a theory model to describe the contact drying of mechanically agitated particulate material by a hot surface. The basic idea of the penetration model is to decompose the continuous macroscopic mixing characteristics of sludge into several discontinuous mixing processes. In the penetration model, a time interval is firstly defined as the contact time, during which the material is assumed to be at rest and heat is transferred to the material by heat conduction. After this, the material immediately finishes the macro and uniform mixing processes with the time interval considered as 0. By repeating the process above, a new heat transfer and mixing cycle is formed until the material dries.
Based on the penetration theory, the contact time can be calculated as follows:
where and n are the mixing number and the stirrer velocity, respectively. is defined as a function of Froud number:
where is the Froud number:
Figure 2 shows the difference in calculation results of whether the penetration model was applicable to describe sludge mixing in the dryer. As shown in the figure, when the penetration model was used, the temperature and water content of sludge could be fully mixed along the radial direction, which is consistent with the physical phenomenon in the actual paddle dryer. Hence, it is believed that the penetration model can describe the mixing process of sludge in the paddle dryer. Coupled with the two-dimensional sludge model proposed in this paper, the complex heat and mass transfer process in the paddle dryer is expected to be accurately described.
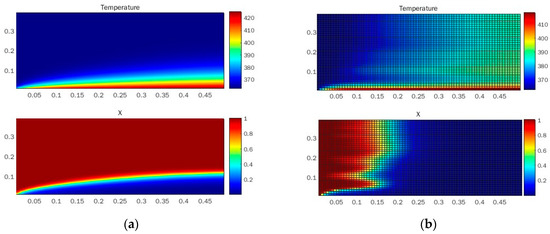
Figure 2.
Temperature and water content distribution w/wo penetration model. (a) Without penetration model. (b) With penetration model.
3. Numerical Method and Validation
3.1. Implementation of Heat and Mass Transfer Model
Due to the coupling nature of the heat and mass transfer equations in the present model, we plan to use a coupled solution method to solve X and T simultaneously. First, we discretize the water content equation and the energy equation, respectively. The equations are discretely formatted in an implicit format to guarantee the stability of the algorithm, shown as:
Sort out the system of linear equations:
where x is a vector of unknowns, given as:
A is the coefficient matrix, which is a sparse matrix of the form shown in Figure 3. The system of linear equations was solved using the Bi-CGSTAB algorithm. Since an implicit algorithm was used in our study, the time step had no significant effect on the calculation results.
Figure 3.
Coefficient matrix A.
3.2. Implementation of the Penetration Model
According to the definition of the penetration model, we add a judgment statement between the time step cycles. When the time reaches the contact time , the sludge is thoroughly mixed once. That is, the penetration model is realized. The schematic diagram is shown in Figure 4.
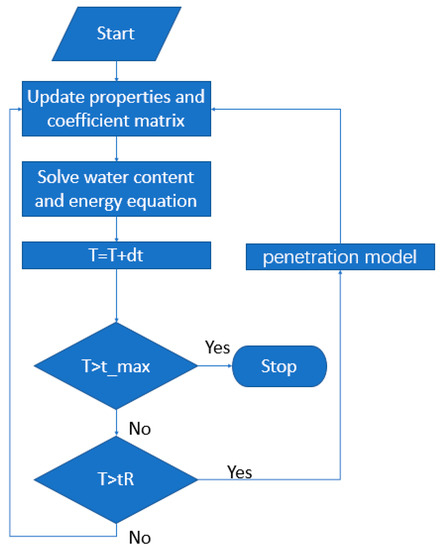
Figure 4.
Schematic diagram of program.
3.3. Sludge Properties
The sludge properties is very important to model the sludge drying. In the present study, the new model was validated by the experimental data from Chen et al.’s study [11,12,13] obtained by the drying experiment in a lab-scale continuous paddle dryer. Therefore, the thermal properties of the sludge used in the model validation calculation were also from Chen et al.’s study.
The calculation of sludge density was based on the method proposed in the previous study [10,17]. When the water content of sludge is higher than this critical value (Xcr = 1.5 in Chen’s study), the shrinkage volume of the sludge drying process is basically equal to the shrinkage volume of evaporated water. Based on this, the density is calculated by the following equation:
where is sludge density. and are the density of water and the density of dry sludge, respectively.
The constant-pressure specific heat of the sludge is determined as:
cp = ((1040 + 2.72 × (T − 273.15)) + 4187 × X)/(1 + X)
The equivalent thermal conductivity of sludge is calculated as:
where is the constant-pressure specific heat of the sludge. keff and kb are the equivalent thermal conductivity and the thermal diffusion coefficient of the sludge, respectively.
3.4. Model Validation
As mentioned before, the experimental data from Chen et al.’s study obtained by the drying experiment in a lab-scale continuous paddle dryer was used to compare and verify the proposed heat and mass transfer model of sludge in the present study. In order to investigate the sludge drying characteristics in the double-axis continuous paddle dryer, Chen et al. designed a lab-scale sludge drying system [11,12,13]. Based on the experimental system, Chen et al. carried out an experimental study on the drying characteristics of a double-axis continuous paddle dryer. The experimental data of water content at different axial positions were measured by a sampling method. A total of 12 sets of experimental data were obtained. In the present study, in view of the variables considered in the model, 6 sets of experimental data were selected for model verification, which took into account the variations of sludge inlet flow, heat source temperature and rotational velocity, respectively. The operation condition is listed in Table 1.

Table 1.
Operation conditions of experiments.
Figure 5 presents the comparison between the calculated results by the new two-dimensional heat and mass transfer model of sludge and the experimental results. It was found that the new model developed in the present study was generally in good agreement with the experimental results and could correctly reflect the variation trend of sludge water content along the axial direction of the paddle dryer, especially in the range of medium water content (X is about 0.4–0.6). Although there is some deviation compared to some experimental data points, the deviation between the calculated results and the experimental results is still within an acceptable range, by considering the complexity of the sludge drying process and the large uncertainty of the sampling method adopted in the experimental study. Therefore, it can be concluded that the new two-dimensional heat and mass transfer model in the present study could accurately describe the heat transfer and drying behavior of sludge in the paddle dryer, which also lays a foundation for the parametric sensitivity analysis and optimal design of the paddle dryer.
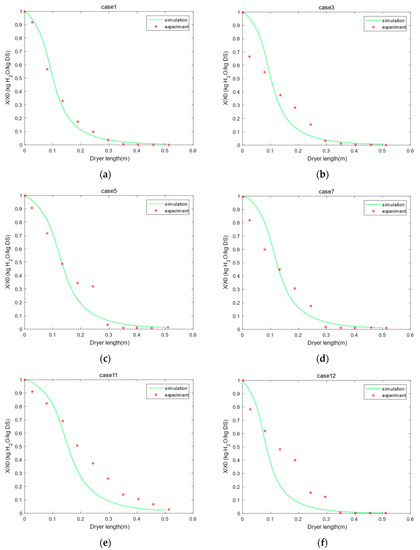
Figure 5.
Comparison of experimental and simulation of water content along the paddle dryer in different operating conditions. (a) Case 1, (b) Case 3, (c) Case 5, (d) Case 7, (e) Case 11, (f) Case 12.
4. Parametric Analysis and Discussion
4.1. Effect of Sludge Flow Rate
To further analyze the application capability of the present two-dimensional heat and mass transfer model and study the sludge drying characteristics inside the paddle dryer, parametric analysis was carried out by using the model, focusing on the effects of four key parameters, i.e., sludge inlet flow rate, stirring velocity, wall temperature and sludge density. The analysis results provided guidance on the design and performance optimization of the paddle dryer.
In order to study the effect of sludge inlet flowrate on sludge drying characteristics, the water content variations during drying were calculated by the present model at three different sludge flow rates, i.e., 0.727 kg/h, 1.212 kg/h and 1.818 kg/h, respectively. The stirring velocity and heat source temperature remained at 19 rpm and 433.15 K, respectively, for all the cases. The water content results are shown in Figure 6. It was found that the water content of the sludge decreased along the sludge moving direction. With the increase in the sludge flow rate, the water content increased and the evaporation rate slowed down at the same axial positions, which was consistent with the phenomena observed in the experiment [13]. The reason for this trend was that the sludge stayed for a longer time in the paddle dryer when the sludge flow rate became small and other boundary conditions remained unchanged, resulting in more water being evaporated at the same axial position.
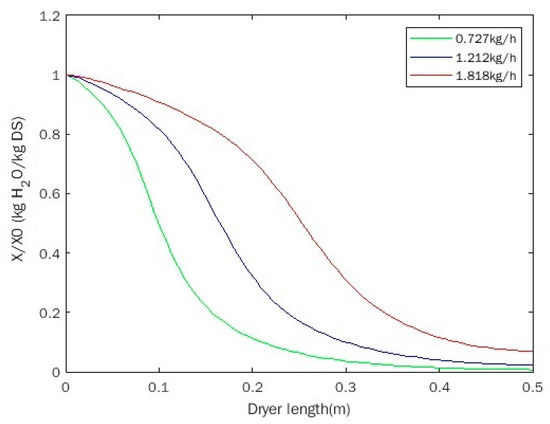
Figure 6.
Effect of sludge flowrate on water content.
4.2. Effect of Stirring Velocity
The stirring effect of shaft rotation on sludge is one of the key factors that significantly affected the drying behavior of sludge. Figure 7 shows the water content variations under conditions of different stirring velocities. Three different stirring velocities of 10 rpm, 19 rpm and 28 rpm were selected. The wall temperature was fixed at 433.15 K and the sludge flow rates were 0.727 kg/h and 1.818 kg/h in Figure 7a and Figure 7b, respectively. In Figure 7a, the results showed that the water content of sludge did not change significantly at relatively low sludge flow rate when the stirring velocity changed. With the increase in stirring velocity, the decreased rate of water content increased slightly, which was consistent with the experimental results [13]. At a relatively high sludge flow rate in Figure 7b, it was found that the decreased rate of water content increased when the stirring velocity changed from 10 rpm to 19 rpm, but it barely changed when the stirring velocity changed from 19 rpm to 28 rpm. Combined with Figure 2, it could be seen that the stirring of sludge caused by the rotating paddles has a significant effect on the sludge drying behavior, but there was a certain limit of the stirring effect on the enhancement of sludge drying. Higher sludge flow rates would result in the larger limit value in which the drying process is not affected by stirring velocity. That is to say, when the sludge flow rate remained unchanged, the further increase in the stirring velocity after reaching a certain value had little effect on the water content of the sludge.
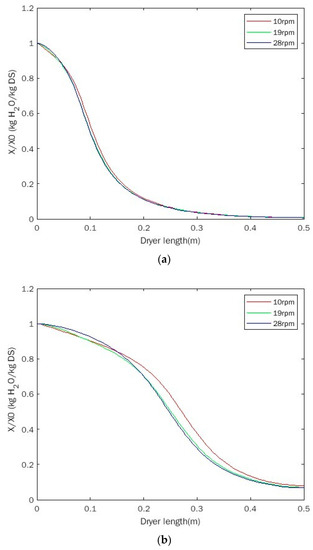
Figure 7.
Effect of stirring velocity on water content. (a) The sludge flow rate of 0.727 kg/h, (b) the sludge flow rate of 1.818 kg/h.
4.3. Effect of Wall Temperature
The effect of wall temperature on sludge drying behavior was analyzed under the conditions of wall temperatures from 413.15 K to 453.15 K. The stirring velocity and sludge inlet flow rate was kept at 19 rpm and of 0.727 kg/h, respectively. Figure 8 presents the variations of water content along the axial direction at different wall temperatures. As can be seen from this figure, the water content of the sludge at the same axial position decreased correspondingly with the increase in wall temperature. It indicated that the higher wall temperature was conducive to the sludge drying in the paddle dryer. The increase in wall temperature lead to a larger heat transfer temperature difference, which was consistent with our physical understanding of the heat transfer process as well as the experimental results. However, it should be noted that heat source temperature or wall temperature could not be increased without any limit in the actual design of the paddle dryer. On the one hand, the increase in the temperature of the hot working medium required more energy consumption, resulting in an increase in the overall cost. On the other hand, according to previous experimental studies, the excessive wall temperature might cause the phenomenon of “sticky crust” on the inner surface of the paddles in the drying process, resulting in the heat transfer being sharply decreased [18]. Because the present model can only predict the heat and mass transfer on the sludge side, the effect of hot source temperature on the drying characteristics of the sludge will be further analyzed and studied in more detail after the bilateral coupled model for the whole dryer is developed in the future.
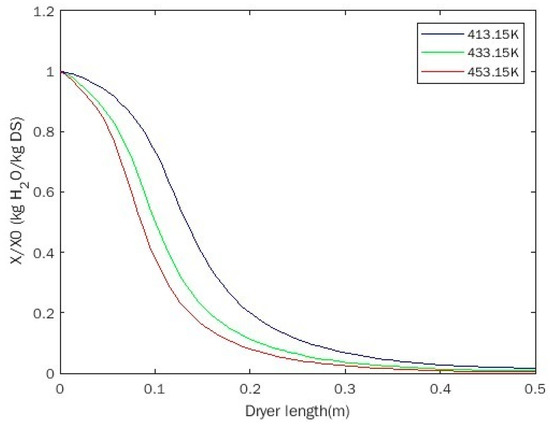
Figure 8.
Effect of wall temperature on water content.
4.4. Effect of Sludge Density
In view of the large differences in the sludge produced at different cities or factories, the influence of sludge density on the sludge drying characteristics was investigated in this section. With the stirring velocity and the sludge flow rate stayed at 19 rpm and 0.727 kg/h, respectively, the variation of water content along the axial of the paddle dryer was compared at three different densities of 400 kg/m3, 820 kg/m3 and 2000 kg/m3, shown in Figure 9. It could be seen that the increase in sludge density lead to the decrease in the water content of sludge at the same axial position. Although the sludge density multiplied in our calculation, the decrease in water content was not very significant. The possible reason for this phenomenon might be that the increase in the sludge density resulted in a higher evaporation rate. However, owing to the lack of the comparison with experimental results, the reliability of the above conclusion needed to be further verified.
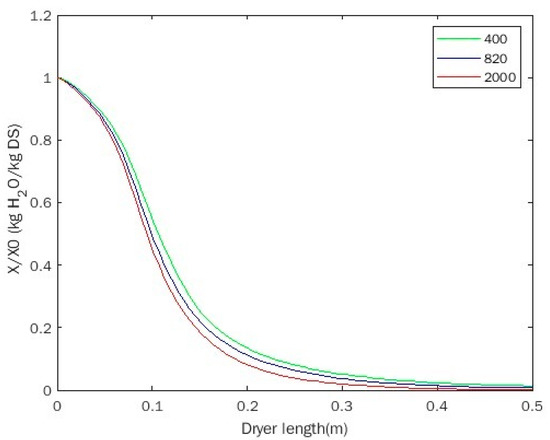
Figure 9.
Effect of sludge density on water content.
4.5. Drying Characteristics Calculation of the Industrial Paddle Dryer
To further demonstrate its industrial application capacity, an industrial paddle dryer designed by the GREEN WATER CO., LTD. (Lishui City, China) was simulated by the present model. The geometrical model of the paddle dryer is given in Figure 10. The dryer adopted a semi-drying scheme, in which the wet sludge with a water content of 60–80% was dried to the water content of 30–35% at the outlet. When treated, the weight of sludge was reduced by about 70%. The paddle dryer had a diameter of 0.65 m, a length of 6.9 m and a stirring velocity of 12 rpm. Saturated steam with the pressure of 0.4 MPa was used as the hot working medium to provide heat for drying the sludge.

Figure 10.
Schematic diagram of the paddle dryer designed by GREEN WATER CO., LTD. (Lishui City, China).
The water content curve along the axial direction in the paddle dryer was obtained by using the present model, shown in Figure 11. Due to the evaporation of water in sludge, the water content decreased along the axial direction in the paddle dryer. According to a previous study [12], the drying process of sludge can be divided into three phases: the decrease in water content, i.e., the pasty phase, the sticky phase, and the complete-granular phase. When the water content was relatively high, the state of the sludge was in the pasty phase. At this time, most of the heat was used to heat the sludge and water since the temperature of the sludge was still less than the saturated temperature. The water content decreased slowly at this stage correspondingly. With the increase in the sludge temperature, the variation rate of water content began to increase, and maintained at a relatively large value in the sticky phase for continuous drying. As the water content was further reduced, the sludge state came to the complete-granular phase. At this phase, surface bound water and intracellular water mainly existed in the sludge. Since the binding energy of water was very high, the evaporation of this part of water required more energy. Meanwhile, with the decrease in the effective contact area of sludge and the increase in the sludge density, the variation rate of the water content decreased significantly.
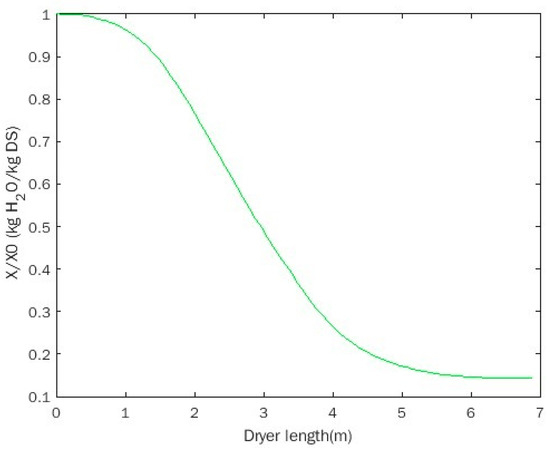
Figure 11.
Water content variation along the axial direction in the paddle dryer.
Figure 12 shows the distribution of temperature and water content along the axial direction in the paddle dryer. The temperature and water content were almost uniformly distributed along the radial direction. It indicated that the mixing effect on sludge caused by the agitation of the shaft and paddles could be affected by the present model.
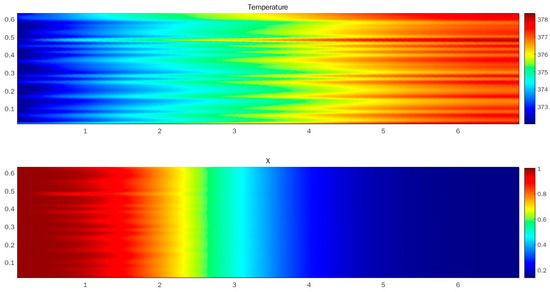
Figure 12.
Temperature and water content distributions along the axial direction in the paddle dryer.
5. Conclusions
In this paper, a concise but general two-dimensional model was proposed based on the penetration model in order to simulate the heat and mass transfer and drying kinetics of sludge in the paddle dryer. Experimental data from the existing study was used to validate the new model. The parametric study on sludge drying kinetics was also presented. The main conclusions can be summarized as follows.
The drying process of sludge in the paddle dryer was divided into heat and mass transfer and mixing, and sludge was assumed as a porous water-contained media. The sludge control equations, including the water content equation and the energy equation, were proposed to simulate the heat and mass transfer of sludge, and the penetration model was introduced to describe the mixing of sludge. Compared to the experimental results in the existing literature, the drying kinetics simulated by the present model were in good agreement with the experimental data under various operation conditions.
The effects of four key parameters, including sludge inlet flow rate, stirring velocity, wall temperature and sludge density, on drying kinetics in the paddle dryer were studied by using the present model. The results showed that the water content increased with the increase of sludge flowrate and the decrease of wall temperature and sludge density. Meanwhile, the stirring velocity had little effect on the drying kinetics of the sludge.
The present study can contribute to the understanding of sludge drying kinetics in a paddle dryer and it provides guidance for the optimal design of industrial paddle dryers.
Author Contributions
Conceptualization, W.L. and M.G.; Validation, F.Z., Y.Z. and Z.L.; Formal analysis, W.L. and M.G.; Investigation, W.L., M.G., F.Z. and Y.Z.; Resources, M.G.; Writing—original draft, W.L.; Writing—review & editing, M.G., F.Z., Y.Z. and Z.L.; Supervision, Z.L.; Funding acquisition, W.L. and M.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The submitted version has been read and approved by all authors and no conflict of interest exits in this manuscript. We guarantee that our manuscript had not been published previously and was not under consideration for publication elsewhere.
References
- Lyu, L.; Chen, S.; Wang, F. Research on Sludge Drying Characteristics in a Double-Axis Paddle Dryer by Coupling Markov Chain and Penetration Theory. Waste Biomass Valorization 2022, 13, 3403–3421. [Google Scholar] [CrossRef]
- Cao, T. Study on the Drying and Reutilization of Industrial Sludge; North China Electric Power University: Beijing, China, 2016. [Google Scholar]
- Schlünder, E.U.; Mollekopf, N. Vacuum Contact Drying of Free Flowing Mechanically Agitated Particulate Material. Chem. Eng. Process. Process Intensif. 1984, 18, 93–111. [Google Scholar] [CrossRef]
- Tsotsas, E.; Schlünder, E.U. Contact Drying of Mechanically Agitated Particulate Material in the Presence of Inert Gas. Chem. Eng. Process. Process Intensif. 1986, 20, 277–285. [Google Scholar] [CrossRef]
- Tsotsas, E.; Schlünder, E.U. Vacuum Contact Drying of Mechanically Agitated Beds: The Influence of Hygroscopic Behaviour on the Drying Rate Curve. Chem. Eng. Process. Process Intensif. 1987, 21, 199–208. [Google Scholar] [CrossRef]
- Arlabosse, P.; Chavez, S.; Lecomte, D. Method for Thermal Design of Paddle Dryers: Application to Municipal Sewage Sludge. Dry. Technol. 2004, 22, 2375–2393. [Google Scholar] [CrossRef]
- Arlabosse, P.; Chavez, S.; Prevot, C. Drying of Municipal Sewage Sludge: From a Laboratory Scale Batch Indirect Dryer to the Paddle Dryer. Braz. J. Chem. Eng. 2005, 22, 227–232. [Google Scholar] [CrossRef]
- Arlabosse, P.; Chitu, T. Identification of the Limiting Mechanism in Contact Drying of Agitated Sewage Sludge. Dry. Technol. 2007, 25, 557–567. [Google Scholar] [CrossRef]
- Milhé, M.; Charlou, C.; Sauceau, M.; Arlabosse, P. Modeling of Sewage Sludge Flow in a Continuous Paddle Dryer. Dry. Technol. 2015, 33, 1061–1067. [Google Scholar] [CrossRef]
- Milhé, M.; Sauceau, M.; Arlabosse, P. Modeling of a Continuous Sewage Sludge Paddle Dryer by Coupling Markov Chains with Penetration Theory. Appl. Math. Model. 2016, 40, 8201–8216. [Google Scholar] [CrossRef]
- Chen, S. Modelling and Experimental Research of Sludge Drying in Paddle Dryers; Zhejiang University: Hangzhou, China, 2018. [Google Scholar]
- Chen, S.; Wang, F.; Milhé, M.; Arlabosse, P.; Liang, F.; Chi, Y.; Nzihou, A.; Yan, J. Experimental and Theoretical Research on Agitated Contact Drying of Sewage Sludge in a Continuous Paddle Dryer. Dry. Technol. 2016, 34, 1979–1990. [Google Scholar] [CrossRef]
- Lyu, L.; Chen, S.; Wang, F. Two Dimensional Modeling of Sewage Sludge Flow in a Double-Axis Continuous Paddle Dryer. Waste Manag. 2021, 124, 63–71. [Google Scholar] [CrossRef] [PubMed]
- Layth, A.A.; Christelle, L.; Delphine, H.; Denise, B.; Marc, C. Thermal and Mass Transfer Properties of a Shrinkable Industrial Sludge: Experimental Determination and Modeling Approach. Environ. Technol. 2022, 43, 2230–2240. [Google Scholar] [CrossRef] [PubMed]
- Ji, W.T.; Mao, S.F.; Chong, G.H.; Zhao, C.Y.; Zhang, H.; Tao, W.Q. Numerical and Experimental Investigation on the Condensing Heat Transfer of R134a Outside Plain and Integral-Fin Tubes. Appl. Therm. Eng. 2019, 159, 113878. [Google Scholar] [CrossRef]
- Manara, P.; Zabaniotou, A. Towards Sewage Sludge Based Biofuels via Thermochemical Conversion—A Review. Renew. Sustain. Energy Rev. 2012, 16, 2566–2582. [Google Scholar] [CrossRef]
- Ruiz, T.; Wisniewski, C. Correlation between Dewatering and Hydro-Textural Characteristics of Sewage Sludge during Drying. Sep. Purif. Technol. 2008, 61, 204–210. [Google Scholar] [CrossRef]
- Yan, J.H.; Deng, W.Y.; Li, X.D.; Wang, F.; Chi, Y.; Lu, S.Y.; Cen, K.F. Experimental and Theoretical Study of Agitated Contact Drying of Sewage Sludge under Partial Vacuum Conditions. Dry. Technol. 2009, 27, 787–796. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).