Abstract
In this paper, dual-rotor counter-rotating (CR) configurations of vertical axis wind turbines (VAWTs) are briefly inspected and divided into three types. This investigation was focused on one of these types—the CR-VAWT with co-axial rotors, in which two equal rotors are placed on the same shaft, displaced from each other along it and rotated in opposite directions. For this CR-VAWT with three-blade H-Darrieus rotors, the properties of the design in terms of aerodynamics, mechanical transmission and electric generator, as well as control system, are analyzed. A new direct-driven dual-rotor permanent magnet synchronous generator was proposed, in which two built-in low-power PM electric machines have been added. They perform two functions—starting-up and overclocking of the rotors to the angular velocity at which the lifting force of the blades is generated, and stabilizing the CR-VAWT work as wind gusts act on the two rotors. Detailed in this paper is the evaluation of the aerodynamic performance of the CR-VAWT via 3D computational fluid dynamics simulations. The evaluation was conducted using the CONVERGE CFD software with the inclusion of the actuator line model for the rotor aerodynamics, which significantly reduces the computational effort. Obtained results show that both rotors, while they rotate in opposite directions, had a positive impact on each other. At the optimal distance between the rotors of 0.3 from a rotor height, the power coefficients of the upper and lower rotors in the CR-VAWT increased, respectively, by 5.5% and 13.3% simultaneously with some increase in their optimal tip-speed ratio compared to the single-rotor VAWT.
1. Introduction
The exigencies of environmental sustainability and rising energy consumption worldwide determine the demand for finding new sustainable ways to generate energy or to make pre-existing methods more effective, for instance, wind and solar power generation systems. Because of the availability of distributed renewables, humanity now has the ability to generate green energy at home, in offices or in residential buildings, and then, if necessary, share it within the “energy internet” [1]; this could potentially provide a more stable delivery of energy in places where frequent electrical network failures or large power fluctuations are common.
In recent years, small-scale wind energy conversion systems (WECSs) have become more popular since they can produce energy for stand-alone households that are located far from the electrical network on a daily basis [2]. One of the downsides of mounting wind turbines next to houses is that they are typically located in areas with low-potential wind speeds. In such conditions, vertical axis wind turbines (VAWTs) are advantageous compared to horizontal axis wind turbines (HAWTs), as Johari et al. [3] observed. Of the many types of different VAWT constructions, the high-speed H-shape Darrieus wind rotor is the best in terms of compromising between efficiency and complexity of manufacture [4]. Not only are VAWTs well designed to extract energy from winds with low potential, but they also have several other advantages over HAWTs [2,3,4,5]:
- The ability to accept wind from any direction, eliminating the need for the rotational mechanisms for turning the wind turbine to the upcoming wind, thus reducing the cost of the turbine;
- Better performance in turbulent wind conditions;
- Low noise operation, which is a topical issue in densely populated areas;
- The ability to mount the generator and electromechanical transmission at the bottom part of the wind turbine installation, which is closely linked to the cost-effectiveness and ease of maintenance;
- Ease of installation (roofs of buildings, yards, gas stations, decks of ships);
- Simplicity of production of blades with a constant aerodynamic profile in comparison with blades for HAWTs, which should be conical and twisted to achieve the desired optimal productivity.
However, the disadvantages of VAWTs also cannot be ignored. Most high-speed VAWTs have low self-starting capabilities [6]. To facilitate starting, they need to be brought to an optimal rotational velocity by external means. For instance, this could be accomplished by switching the generator to motor mode. The motor will drive the rotor to the desired optimal rotational velocity, so with the specific incoming wind velocity the maximum possible energy from the wind will be extracted. Another way to bring the rotor to the desired rotational velocity is to use an additional rotor such as the Savonius one. The latter should be attached to the shaft of the main rotor, as carried out by Sharma et al. [7]. The usage of helical blades [8] might also improve the starting characteristics. However, the process of their manufacturing is complicated and more expensive than the straight blades.
Another disadvantage of VAWTs is that during operation, each blade produces vortices, so the rotor always operates in unsteady turbulent flow. This causes a reduction in the effectiveness of the VAWT [3,8].
It is known that the maximum aeromechanical efficiency of any rotor, both HAWTs and VAWTs, is limited by the theoretical limit, named after one of its authors Betz, which is equal to 16/27 = 0.593 [2,3]. However, almost 40 years ago, a radically different idea of increasing the energy efficiency of HAWTs was proposed—to deploy two rotors in one WT, each of which rotates in one or opposite directions to the other [9]. Installing a second rotor on the same axis as the first rotor allows utilization of that part of the wind power that remains in the wake of the first rotor and thus increases the theoretical limit of the counter-rotating (CR) HAWT to 0.64 [10]. Numerous model and experimental studies have demonstrated the higher efficiency of CR-HAWTs for a number of configurations with different rotors diameter ratios and optimal axial distances for their installation [11,12]. Another area of research for CR-HAWTs is the configuration of the drivetrain, which can include different types of mechanical transmission [13,14] or provide a direct drive when each of the rotors is directly connected to the inductor and armature of a dual-rotor (DR) electric generator (EG) [15]. The latter option is the simplest and most reliable but is characterized by only one control channel, which is not enough to ensure optimal control of the angular velocities of the two rotors. Therefore, as a rule, at least one rotor in CR-HAWTs has an additional channel for pitch control [15,16].
Recently, the idea of using two rotors has spread to VAWTs [17,18,19]. Dual-rotor CR-VAWTs can have different degrees of aerodynamic interaction between the two rotors and different variants of their drivetrains. The potential efficiency increase in VAWTs by means of dual-rotor design of VAWTs is worth further investigation. Additionally, while the aerodynamic effects of VAWTs are well documented, the aerodynamics of CR-VAWTs are not well understood yet.
In this paper, an attempt to classify CR-VAWTs is made, and design features and numerical modeling of one of the least studied types of these VAWTs, namely the CR-VAWT with co-axial rotors displaced from each other along the axis of rotation, are conducted. The limited interest of researchers in this type of CR-VAWT is explained by the apparent patterns of its operation, when two rotors interact almost independently with the wind flow. However, if we consider the whole WECS, previously unexpected effects are manifested. These effects take place in different parts of the system—aerodynamic, electromechanical and control system, and their nature can be both positive and negative. In this work, the design features of this type of CR-VAWT, which ensure its effective operation, are consistently considered—aerodynamic design, drivetrain and EG design, and control system design. A significant part of the work is devoted to the numerical modeling of this CR-VAWT via CFD. There is no study yet for how far the rotors should be spread apart in the CR-VAWT so as to not negatively affect each other during operation. Accordingly, the paper tries to find the aforementioned optimal ratio of displacement for the rotors.
The paper is organized as follows. An overview and classification of dual-rotor CR-VAWT are in Section 2. Section 3 presents the design features of the CR-VAWT with co-axial rotors displaced from each other along the axis of rotation, including the rotor, drivetrain, special DR-EG and control system design. Actuator line modeling (ALM) for CR-VAWT simulations, especially the aerodynamic theory of the VAWTs, is shown in Section 4. Section 5 has two sub-sections of simulation results and their discussions—single-rotor VAWT and a sample of CR-VAWT. Lastly, conclusions and some discussions are delineated in Section 6.
2. Overview of Dual-Rotor CR-VAWTs
Unlike the CR-HAWT, the CR-VAWT can have a large number of configurations that are fundamentally different. The analysis of a relatively small number of studies on the development of CR-VAWTs, allowed dividing all configurations into three types: (i) dual-axis CR-VAWT, (ii) CR-VAWT with co-axial rotors of different sizes when one rotor covers the other, and (iii) CR-VAWT with co-axial rotors displaced from each other along the axis of their rotation (Figure 1).
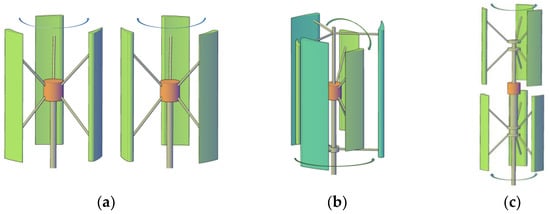
Figure 1.
Three types of CR-VAWT: (a) dual-axis CR-VAWT; (b) CR-VAWT with co-axial rotors when one rotor covers the other; (c) CR-VAWT with co-axial rotors displaced from each other along the axis of rotation.
2.1. Dual-Axis CR-VAWT
As can be seen from Figure 1a, this type of CR-VAWT is actually two separate VAWTs, which rotate in opposite directions around their own parallel axes. Due to the aerodynamic interaction between these VAWTs, it allows a higher power density in a wind farm.
Wind farms based on HAWTs require significant turbine separation to avoid aerodynamic interference, because the latter reduces the efficiency of wind flow interaction with downstream rotors. In contrast, the aerodynamic interaction of VAWTs provides higher power per unit of land area because of their smaller footprint [20]. Some investigations have shown that additional benefits can be obtained by optimizing the placement of VAWTs and choosing the direction of rotation. Comparative 3D studies were performed for an isolated VAWT and for co- and counter-rotating pairs of VAWTs with varying wind direction and turbine spacing. These investigations have shown an average 14% increase in performance for the most optimal array configuration studied at over approximately a 50° range of wind direction [21]. The power coefficient of each rotor can increase by more than 10% when the turbines are oriented in such a way that a line connecting their centers of rotation is perpendicular to the wind direction. When the VAWTs are oriented in a doublet-like configuration and their blades move upwind in the interior area between the rotors, the power coefficient of each rotor can increase up to 15% [22]. However, such positive results quickly decrease if the wind direction deviates from the specified one.
2.2. CR-VAWT with Co-Axial Rotors When One Rotor Covers the Other
This type of CR-VAWT, also called a multi-stage VAWT, is similar in construction to CR-HAWTs, where two rotors are installed in series. As can be seen from Figure 1b, two rotors are located on the same axis, and the primary (outer) rotor completely covers the secondary (inner) rotor. In this case, the Darrieus-type H-rotor is used in which the blades are straight and parallel to their axis of rotation. As mentioned above, VAWT blades interact with the disturbed wind flow much more than a HAWT during its rotation, which is one of the reasons for VAWTs’ lower efficiency. In the case of the CR-VAWT type discussed in this subsection, the aerodynamic interaction of two rotors is very high, as the smaller rotor operates with wind flow completely perturbed by the larger rotor. In addition, the smaller rotor’s work further disrupts the wind flow for the larger rotor, as the latter now partially operates in the wake of the smaller rotor. This can reduce the aeromechanical efficiency of both rotors. However, the development of this type of CR-VAWT is dedicated to solving another important problem for high-speed and efficient VAWTs—ensuring their self-start at low wind speeds.
In [23], the authors performed 2D simulations for the flow-induced rotation of coupled and uncoupled versions of multi-stage VAWTs. Studies have shown that placing the second rotor with the same blades but a twice-smaller diameter inside the primary rotor provided approximately a twice-fast CR-VAWT overclocking as a single rotor, with better dynamic properties obtained in the coupled version.
In [24], both the starting behavior and power performance of a CR-VAWT with co-axial aerodynamically coupled rotors are outlined by comparing with an equivalent single-rotor VAWT by large eddy simulation (LES). The numerical results showed that the CR-VAWT offers self-start capabilities at a low tip-speed ratio (TSR) simultaneously with an improvement of the power coefficient at a high TSR. The authors set “the effect of drag dynamic stall induced by successive flow-blade collisions” [24]. This effect provided an increase in power coefficient at a low TSR. Because of the lift dynamic stall at the TSR value near 2, the power coefficient was increased by more than 10% compared with the single-rotor VAWT. In [25], similar theoretical results were also confirmed experimentally.
2.3. CR-VAWT with Co-Axial Rotors Displaced from Each Other along the Axis of Rotation
This type of CR-VAWT is basically a dual-rotor system where two rotors rotate opposite to each other on the same axis, but the rotors are displaced by each other along the axis of rotation so that they do not interact aerodynamically with each other in a negative way (see Figure 1c). It should be worth noting that the CR-VAWT of this type in comparison with the previous type of CR-VAWT and CR-HAWT is more efficient, because both rotors receive an equal amount of kinetic energy from a uniform free-stream wind.
The expediency of developing this type of CR-VAWT is also due to other positive qualities. Dual-rotor designs of CR-VAWTs out-perform those of single-rotor VAWTs of the same swept area in the following areas:
- Because the two rotors rotate in opposite directions, the relative angular velocity of the generator with two rotated parts, inductor and armature, would be a sum of both rotor’s angular velocities, so the size of the generator could be much smaller to generate the same power as a single VAWT with the same rated output power;
- It is easier to manufacture and transport two smaller rotors than one bigger;
- Single-rotor blades are bigger, so the blade surface stresses, vibratory loads and loading noises are also bigger, which, accordingly, require stronger and more expensive supports for VAWT installation.
In a number of studies, the aerodynamic properties of CR-VAWTs of this type were compared with the corresponding properties of single-rotor VAWTs by both computer simulation and experimentally. In most cases, the CR-VAWTs consist of two identical Savonius rotors [26,27,28], but there are studies that use H-Darrieus rotors [17,19,29] or even a combination of these two types [30].
Experimental studies of CR-VAWTs based on Savonius rotors have shown very low starting wind speeds starting at 1.744 m/s [26], as well as higher efficiency of the upper rotor compared to the lower [28]. The same was confirmed by a computational fluid dynamics (CFD) study conducted in ANSYS Fluent using the k–ω turbulence model [29].
In Didane et al.’s experimental and 3D simulation studies of CR-VAWTs based on H-Darrieus rotors [17,29], to help the blade to self-start, they used semicircular polyvinyl chloride pipes mounted at each arm of the two rotors, by which the blades were joined to the central shaft. However, this decision led to an increase in drag forces reducing the optimal TSR of the rotors to 0.38–0.55, reducing their power coefficient and thus losing all the benefits of high-speed H-Darrieus-type rotors. The simulation results demonstrate a significant increase in conversion efficiency for both power and torque compared to a single-rotor VAWT system of a similar type. The results also indicate an increase in this performance with a reduction of the axial distance between the rotors. As is indicated in the conclusion of [29], “further improvements should be made including blade design, appropriate generator and static geometrical parameters such as relative size of the main and auxiliary rotors, optimum distance between the two rotors, airfoil profile type, aspect ratio etc.”.
Poguluri et al. [19] conducted systematic a 3D CFD simulation and analytical investigation of a high-power CR-VAWT, where two-blade H-Darrieus rotors for the CR-VAWT were obtained from a conventional single-rotor VAWT by splitting its blade length into two equal parts separated by a small distance. The results showed a close agreement of output power between the CR-VAWT and the single-rotor VAWT at low wind speed, but at high speeds, there was a lower power generation by the CR-VAWT. The authors explained this by the strong interaction of the tip vortices between the upper and lower rotors. To improve the performance of the CR-VAWT, the authors identified the need for the study and optimization of some parameters such as the blade length, the rotor diameter, the number of blades in a rotor, and the distance between two rotors.
2.4. Drivetrains for CR-VAWT
The design features of CR-VAWTs determine the special design of their drivetrains. In the first type, dual-axis CR-VAWTs, two separate EGs have been used due to the significant distance between the axes of rotation of two rotors. In the other two types, CR-VAWT with co-axial rotors, the designs of their drivetrains may be the same, because from a mechanical point of view, these types differ only in the relative position of their rotors. Therefore, we will further analyze the possible implementations of drivetrains for such CR-VAWTs.
The design of the CR-VAWT drivetrain depends on the design and number of EGs used, as well as the ratio of the rated speeds of the rotors and EG. Chong et al. [31] proposed two designs of the CR-VAWT drivetrain. The first presents two rotors mounted on their co-axial shafts rotating in opposite directions; each has its own EG for transducing mechanical energy into electrical energy. The design is simple and allows individual optimization of the load of each rotor; however, two EGs complicate the design of the CR-VAWT, increase its cost and might cause additional load on the shaft due to their weight. In another design, the shaft of one rotor is coupled with the rotor of the EG, and the shaft of the other rotor is coupled with the armature of the EG. Their counter-rotating movement increases the relative angular velocity of the DR-EG and decreases its size and weight. Another investigation in this area was carried out by Ramos et al. [27], which concluded that the starting torque of a CR-VAWT with the DR-EG doubled that of a single VAWT. This improved the breaking inertia level and thus the self-starting capability of the turbine. A similar solution has been used in other studies in recent years, which indicates its effectiveness [15,32].
Shchur and Klymko [33] have performed one more investigation related to a CR-VAWT with co-axial rotors displaced from each other along the axis of rotation. The authors have studied by computer simulation operation of a CR-VAWT with three types of mechanical transmissions: rigid with a bevel gearbox [13,26], semi-rigid with a differential [14] and soft gearless with the dual-rotor PMSG (DR-PMSG) [15,33]. According to the results obtained, the rigid transmission has an advantage over the other two for start and stabile operation and disadvantages that are related to the existence of backlash between the gears, which causes significant ripples with springy torques. Instead, the gearless transmission is the simplest of all and reliable. In the case of long and elastic rotor shafts, the gearless transmission effectively dampens mechanical vibrations. However, it is vulnerable to the differences in the rotor’s moments of inertia and gusts of wind speeds, acting differently on each rotor. The differential transmission provides better work stability in similar cases than the gearless transmission. Because of these observations, it was concluded that the gearless transmission is promising to use in a CR-VAWT, but it is expedient to develop a new means for stabilization of WECS operation.
3. Design Features of CR-VAWT with Co-Axial Rotors Displaced from Each Other along the Axis of Rotation
3.1. Aerodynamic Design
In our investigation, we are focused on the CR-VAWT composed of Darrieus rotors, in particular straight-bladed H-rotors, which offer relatively high values of power coefficient Cp. Because of the straight blades, the H-rotor is easy to manufacture and reliable during operation. Studies have shown that when the H-rotor has three blades, its starting and working characteristics for low wind speeds are optimal [34]. In addition, three-bladed H-rotors operate at much higher TSR values compared to Savonius rotors; this is why EGs could be directly linked with rotors forming a direct drive. This simplifies the construction and installation of the CR-VAWT, improves the starting characteristics and increases the reliability during operation.
To evaluate the energy efficiency of a specific WT, its output power and torque are to be calculated according to the following equations [35]:
where ρa is the air density; A = 2RH is the rotor’s swept area (R is the rotor radius; H is the rotor blade height); Cp(λ) is the power coefficient of a specific rotor, which depends on the TSR λ and the rotor construction; and Vw is the wind speed.
The TSR is a non-dimensional characteristic of the rotor angular velocity—the ratio between the linear speed of the blade and the incoming wind speed. It can be evaluated as follows [35]:
where ω is the angular velocity of the rotor.
For each rotor, there is a specific Cp(λ) characteristic, which is evaluated experimentally or numerically using a computational model. The optimal point Cp.max(λopt) is depicted in Figure 2, at which the rotor extracts the maximum possible amount of power from the wind. For each wind speed, there is an optimal value of the rotor angular velocity ω, which is provided by the control system of the WT. It is crucial to maintain that optimal angular velocity value for the duration of the wind turbine’s operation to extract the maximum possible amount of power from the wind. The system ensures this is the maximum power point tracking (MPPT) system.
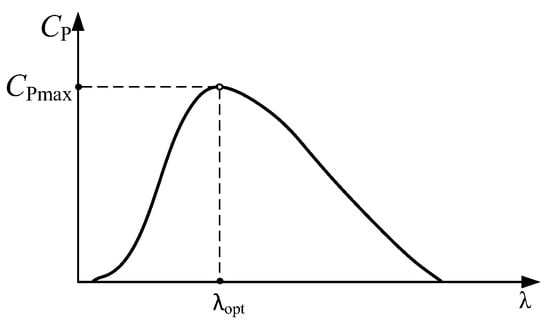
Figure 2.
Cp(λ) characteristic.
Because the rotor is driven by the wind that sweeps the rotor blades, the output power directly depends on the shape of the blades. Most often, NACA airfoils are chosen for H-rotor blades [35], which have very good aerodynamic characteristics. These NACA blades could be symmetric or asymmetric [35,36]. The usage of asymmetric blades for a rotor improves the starting characteristics of that rotor; however, the Cp value might be reduced in this case [37].
When it comes to design, one of the critical parameters of rotors is the solidity σ, which can be evaluated as follows [37]:
where nb is the number of the rotor’s blades, and c is the blade chord length.
Starting and operating characteristics of the rotors directly depend on the solidity. With a higher solidity value, starting characteristics are better, so the rotor will start to rotate at lower wind speeds. However, the working characteristics will suffer—the Cp will be decreased [38]. Therefore, there is an issue with the optimal combinations of the starting and working characteristics of H-rotors [39].
Another key parameter in the process of wind turbine design is the aspect ratio (AR)—the ratio between a rotor’s height H and its diameter D. It is shown [40] that an optimal AR not only has a positive effect on the starting characteristics of the rotor, but also increases the Cp. The optimal AR for each unique rotor is different, so to estimate the correct AR, CFD or experimental modeling should be performed.
Considering the specified regularities of VAWTs, to build an aerodynamically effective CR-VAWT of the chosen type, it is advisable to use rotors of the Darrieus type, especially H-rotors with three blades [34]. The symmetrical aerodynamic profile of the airfoil is recommended, such as the widely used NACA 0018 [39]. To achieve a compromise between starting and operating characteristics of rotors, it is advised to choose the solidity (4) from the range of σ = 0.1 to 0.4 [38,40]. Small values of solidity ensure a higher optimal TSR of WT λopt; however, for VAWT of the Darrieus type, the zone of low TSR with a low or even negative value of Cp expands. This impairs the VAWT’s starting capabilities, i.e., the wind speed increases at which the rotor is able to spin up to the angular velocity at which the lift force of the blades develops and the VAWT heads towards the point of maximum power generation. Larger values of solidity, on the contrary, sharply reduce λopt of WT, contributing to an increase in the starting capabilities of VAWT but a decrease in Cp. In the case of applying additional measures to ensure VAWT startup, which will be recommended in this work, it is advisable to apply a small value of solidity while maintaining high values of the power coefficient. Taking this into account, for a CR-VAWT of this type with rotors based on straight blades with a NACA 0018 airfoil, it is possible to select σ = 0.15, which provides Cp.max = 0.4–0.45 at λopt = 4.8–5 in the entire operating range of Reynolds number Re. Note the Cp.max decreases with smaller Re [37].
Regarding the geometric proportions of rotors, to ensure a compromise between the optimal values of the rotors’ rotation speed and the corresponding values of Re, according to the results of the studies conducted in [40], a value of AR close to unity is recommended for the three-bladed rotors with the NACA 0018 airfoil. Compared to the single-rotor VAWT of the same power and the same optimal AR as a CR-VAWT, the rated angular velocity of the DR-PMSG significantly increases (approximately 2.8 times) [41]. This increase is due to two factors. First, the relative speed between the inductor and armature of the DR-PMSG is obtained by adding the angular velocities of the two rotors. Second, in the case of the same optimal value of the AR, the rated angular velocity of each rotor in the CR-VAWT, according to Equations (1) and (3), is √2 times larger compared to the single-rotor VAWT of the same total power.
3.2. Drivetrain and EG Design
As shown in a number of studies [31,32], the best configuration of the drivetrain for the CR-VAWT with co-axial rotors displaced from each other along the axis of rotation is a direct drive with the DR-PMSG. This configuration provides a small-size DR-PMSG, the easiest self-start, gently extinguishes vibrations caused by gusts of wind and provides high reliability due to the absence of mechanical transmissions.
However, as shown by computer simulations [33], this configuration of the drivetrain for a CR-VAWT is characterized by worse stability in the presence of differences in the parameters of the two rotors and/or actions on them with different wind disturbances compared to configurations that use mechanical gears. This is due to the presence of two independent perturbation channels from the side of each rotor and only one common for the CR-VAWT load control channel—the PMSG electric load with the inability to distribute the load torque between the axes of two rotors. All this, together with the obvious nonlinearity of the mechanical characteristics of rotors TWT(ω) obtained from (2) and (3), can lead to a loss of mechanical stability of CR-VAWT, when the angular velocity of one rotor increases and the other stops altogether.
To eliminate this shortcoming, as well as to ensure the start of rotors, a new design of the DR-PMSG has been proposed with a corresponding control system, which ensures the stability of the gearless co-axial CR-VAWT operation. This generator can be considered as an improved version of the standard DR-PMSG, in which the inductor with permanent magnets 1 is connected to the shaft 2 of one rotor, and the armature 3 is connected to the shaft 4 of another rotor (Figure 3). Two shafts can rotate in their own casing 5. The slip rings 6 supply power to the main armature winding 3. In this new DR-PMSG concept, two additional built-in low-power electric machines are added. They ensure the electromagnetic coupling of the moving two rotors of the generator with their own casing 5. Each of these additional machines is a synchronous type with PMs. Their permanent magnets 7 and 8 are placed on each rotor of the DR-PMSG, and armatures 9 and 10 are placed on the casing. By controlling additional electric generator/motor machines, we can create small torques with different signs between the axes of two rotors and the common fixed casing. Thus, we add two more load control channels separately for each rotor. Stabilization of the CR-VAWT, i.e., the alignment of the angular velocities of two rotors, is achieved by adding extra torque to the axis of one rotor and subtracting the extra torque from the axis of another rotor. These torques can be equal in magnitude, i.e., one additional electric machine must operate in motor mode and the other at this time will operate as a generator. Thus, in CR-VAWT stabilization modes, these machines can feed each other and their external power supply will cover only the energy losses in these machines, which ensures high efficiency. In addition, these motors/generators can perform an initial overclocking of the two rotors for startup. Studies [41] have shown that, for a CR-VAWT at the rated power of 10 kW, each of the additional electric machines has a rated power requirement of no more than 500 W.
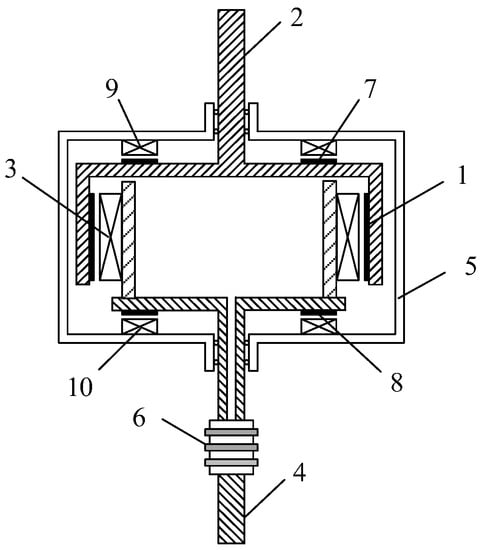
Figure 3.
Sketch of a new design of the DR-PMSG: 1—inductor with permanent magnets, 2—shaft of the first rotor, 3—armature, 4—shaft of the second rotor, 5—casing, 6—slip rings, 7 and 8—permanent magnets of the additional machines, 9 and 10—armatures of the additional machines.
3.3. Control System Design
The control system of the investigated CR-VAWT should provide the next main functions [41]: (i) startup of the rotors at a cut-in wind speed, (ii) optimal loading of the main ED for the two rotors at their maximum power points work, (iii) stabilization of the rotor’s power at their reference points by the two additional PM machines.
Figure 4 shows that the structure of the control system of the CR-VAWT includes three control channels for the adjustment of electromagnetic torques of the three PM electric machines. The main electromagnetic part forms the electromagnetic torque of the PMSG TG.e, and the auxiliary electromagnetic parts 1 and 2 form the electromagnetic torques Tk1 and Tk2 of the additional small PM machines. Because the additional PM machines provide the function of rotor startup, the main PMSG should operate only as a generator. It significantly simplifies the load control system, which can be realized by a DC-DC converter. In Figure 4, the Control system consists of two inverters I1 and I2 to provide the bidirectional control of the additional small PM machines and a diode bridge with the DC-DC converter to provide unidirectional control of the main PMSG providing an MPPT of the CR-VAWT.
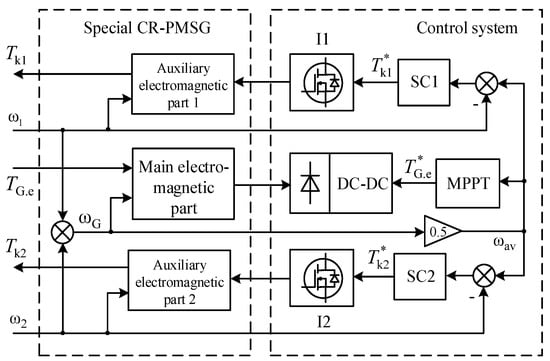
Figure 4.
Structure of the control system for CR-VAWT with the new DR-PMSG.
To start the rotors, the control subsystem forms the reference of the electromagnetic torques for the additional PM machines at the maximum values but with opposite signs. After rotor startup, with the purpose of stabilization of their operation, the reference torques for these PM machines are formed by the corresponding PI speed controllers SC1 and SC2 as follows:
where KP and KI are the proportional and integral coefficients of the speed controllers, respectively; ω1 and ω2 are the angular velocities of the first and second rotors; and ωav = 0.5(ω1 + ω2) is the average angular velocity of these rotors of the DR-PMSG.
To simplify and reduce the cost, winding commutation systems for the additional PM machines might be the brushless DC method with Hall sensors.
In small WECS, sensor-less strategies (without a wind speed sensor) have an advantage in application for MPPT [42]. The optimal torque control (OTC) strategy is the most common among them [43]. It forms the reference of the electromagnetic torque of the EG loading in proportion to the square of the average angular velocity of the WT:
where kT = 0.5ρa A Cp.max (R/λopt)3 in the case of direct-drive transmission.
For the WECS based on the CR-VAWT with the proposed DR-PMSG, the OTC strategy (7) is equivalent to the optimal current control (OCC) strategy—forming the reference of the load DC current for the DC-DC converter based on the average angular velocity of the rotors (rotors of DR-PMSG) at the set load voltage, e.g., the battery voltage. Such a strategy can be expressed as a polynomial dependency:
where ai are the coefficients.
In a previously conducted investigation [41], the OCC strategy (8) for such a WECS was used and shown as effective stability MPPT control in the system, per the structure shown in Figure 4.
4. Method of Numerical Modeling of VAWT
4.1. Numerical Modeling of Rotor Operation
Numerical modeling of rotor operation is based on the calculation of the distribution of forces, which act on the rotor blades during their rotation. According to [8], these forces depend on two variables: (1) the resultant wind speed Vr, which is the vector sum of the axial wind speed Va and the linear velocity of the rotor’s blade Vl = ωR; (2) the angle of attack of the blade β (Figure 5). The resultant wind speed and the angle of attack β constantly change during the blade rotation due to the change of the azimuthal angle ψ of the blade.
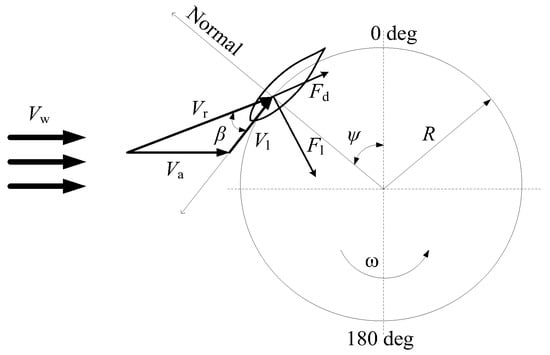
Figure 5.
Velocity vectors diagram of a single blade of the rotor during its rotation.
In addition, during the blade rotation, the distribution of the lift force Fl and drag force Fd changes, in reference to [44]. The resultant of these forces is a thrust force Fr, which can be divided into two components—normal Fn and tangential Ft (Figure 6). The latter creates the torque on the rotor shaft, so the shaft starts to rotate together with the blades.
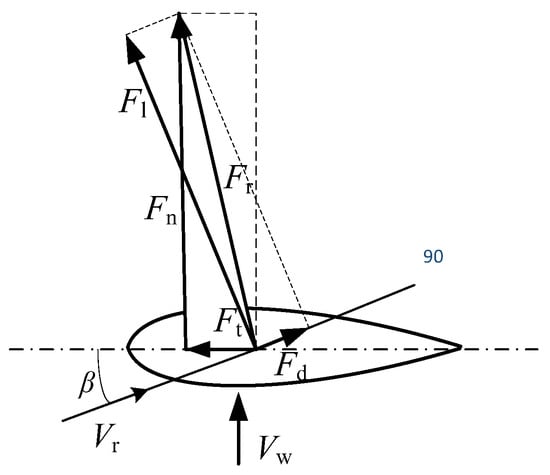
Figure 6.
Force distribution on the rotor blade during rotor rotation.
The angle of attack β can be estimated as follows in accordance with [45]:
The value of β is positive in the range of the azimuthal angle of the blade from 0° to 180° and takes its maximum value when ψ equals 90°. When the angle of attack β exceeds the critical value, the breakdown of the attached boundary layer occurs near the trailing edge of the blade and the appearing vortices slow down the blade. This phenomenon explains the maximum possible peak rotor performance characteristic Cp(λ) when the TSR is in the range of 2.5–4.0—the linear velocity of the blade significantly exceeds the oncoming wind speed. As can be seen from the typical dependencies (Figure 7), for each value of the Reynolds number Re, there is a critical value of angle of attack, at which the coefficient of lift force Cl drops down and the coefficient of drag force Cd rises.
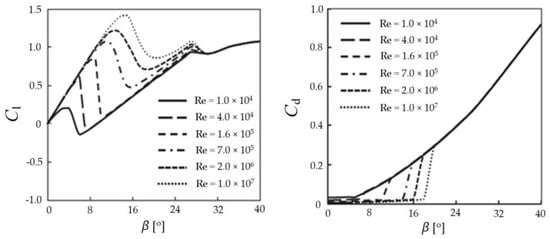
Figure 7.
Typical dependencies of the lift (Cl) and drag (Cd) coefficients on the angle of attack β for the NACA airfoil [46].
Dependencies, which are depicted in Figure 7, can be obtained either experimentally or with the use of CFD. Knowing these data, the coefficients of the tangential Ct and normal Cn forces can be evaluated as follows [45]:
The values of the normal and tangential forces, which act on the blade, can be estimated using these expressions:
where Ab is the blade area.
The normal and tangential forces in Equations (12) and (13) are obtained for each azimuthal position of the blade ψ. Having the instantaneous value of Ft(ψ) for a rotor with radius R and the number of blades of nb, it is possible to estimate the instantaneous torque during rotation as
4.2. Actuator Line Modeling for VAWT Simulations
To choose the optimal design of the rotor and to test the rotor to best meet the desired level of effectiveness, a real field test or physical experiment with the use of an aerodynamic tunnel could be used. However, this is usually a very expensive and slow method. Thus, numerical modeling with the usage of the CFD is the first step in choosing the optimal parameters for the rotor of the CR-VAWT. Therefore, the CFD software CONVERGE is used in this research to investigate the drag and lift forces that act on the rotor blades during their rotation. The value of Cp is then estimated for the chosen wind turbine. The boundary conditions (BC) of the setup vary and are shown for each of the cases.
In this study, 3D Reynolds-averaged Navier–Stokes (RANS) simulation is integrated with the actuator line model (ALM) to study the working characteristics of the WT, for instance, the Cp(λ) characteristic. To best depict the physical processes that take place while the VAWT rotates, the k–ω shear stress transport (SST) turbulence model is implemented [27,47].
ALM is a method that combines a 3D flow solver with a model in which aerodynamic forces are distributed radially along lines and these lines represent the blades of the WT [48]. The loading on the blades is determined using tabulated data for the lift and drag coefficients of a specific airfoil shape. In other words, this method treats each blade of the turbine as an actuator line, which comprises a series of airfoil elements along the spanwise direction [49]. This method is widely used because it significantly reduces the computational effort compared with blade-resolved CFD, as well as being able to capture some key flow features due to the rotation of the turbine. It is recommended by Shamsoddin et al. [48] that for numerical simulation of the wake, the ALM method is seen as the most feasible and practical way of considering the effects of the turbine on the flow. ALM is a good alternative to resolving the full rotor geometry, since it requires fewer grid cells and allows larger time steps [50]. However, the drawback could be the lack of resolution of the blade boundary layer, which can be important to some fine-scale, local effects.
To determine the aerodynamic force per unit span length acting on the rotor blades, the following equation is used for each airfoil element [51]:
where Cl = Cl(β, Re) and Cd = Cd(β, Re) are the dependencies of the lift and drag coefficients from the blade angle of attack and Reynolds number, Vr is the relative wind velocity at the element, and e1 and ed are the unit vectors in the directions of lift and drag, respectively.
The forces are then projected from the blades back to the flow. They must be distributed smoothly on several mesh points to avoid singular behavior. The projection is performed in a 3D Gaussian manner by taking the convolution of the computed local load f and a regularization kernel , as shown below [52]:
where is the distance between cell-centered grid points with coordinate vector x and points at the i-th actuator line, and ε is the projection width that serves to adjust the concentration of the regularized load.
In this work, is used following Xie and Archer [53], where c is the chord length, and Δ is the size of the grid containing the blade section. Therefore, the regularized force per unit volume becomes:
where B is the number of actuator lines.
In this work, the tabulated data of the drag and lift coefficients were obtained from the database of Sheldahl and Klimas [54] developed for the VAWTs, which contains values over a wide range of Reynolds numbers. Although this dataset might have some limitations—data for some airfoil/Reynolds numbers were derived numerically based on the results of other measurements—it is likely the most comprehensive source due to the variety of profiles and range of Reynolds numbers [49]. In addition, the blades were fixed in the wind tunnel measurements. However, during each cycle of VAWT rotation, the blades encounter the wakes shed from other blades [55], which is missed in the wind tunnel measurements. Furthermore, due to the rapid change of the angle of attack β, a dynamic stall will occur and will affect the instantaneous drag and lift force predictions. Therefore, corrections of the dynamic stall effects must be performed to mitigate the limitation of using static lift and drag coefficient data. In this work, the modified Massachusetts Institute of Technology dynamic stall model is used following Shamsoddin and Porté-Agel [56].
In summary, at each time step, the locations of the blades are updated. For each blade section, the angle of attack β and the local Reynolds number are determined. The latter is defined for the local relative velocity, the chord length of the blade section, and the kinematic viscosity of the dry air at 300 K. For a specific combination of β and the local Reynolds number, the lift and drag coefficients, which are interpolated from the Sheldahl database by a 2D bilinear scheme, are used to calculate the blade forces as in (15), and the forces are then distributed to the neighboring CFD points by (17). The ALM module is coupled within the CONVERGE CFD solver via a user-defined function (UDF), which has been well validated for both HAWT and VAWT simulations in previous studies [57,58].
5. Results and Discussion
5.1. Single-Rotor VAWT Sample Simulation
The characteristics of the chosen rotor sample are presented in Table 1. As discussed earlier, a straight-bladed H-rotor with three NACA0018 blades was used in this study. Having a diameter D = 0.9 m and a height of the rotor blade H = 1.0 m, it can be easily calculated that the aspect ratio AR is 1.1. This value is optimal for the VAWTs as a literature review shows [59]. Note that there is no resolved geometry of the rotor during simulation; however, the dimensions of the rotor will be used in the ALM parameterization.

Table 1.
Features of the rotor sample.
The computational domain is a rectangular box with dimensions 15 × 12 × 7 (m), respectively, in the streamwise (x), lateral (y) and vertical (z) directions (Figure 8). The boundary conditions of the domain are chosen to be as follows: the inlet—Inflow (Neumann pressure BC with Dirichlet velocity BC), the outlet and sides—Outflow (Dirichlet pressure equals 101,325 Pa), the bottom side—Wall with a wall model based on the log law. The k–ω SST model is used for turbulence modeling, considering its good performance for turbulent swirling flows. The flow is driven by a fixed streamwise wind of speeds 4, 7 and 10 m/s from the inlet. The rotor is represented only via blades modeled by ALM.
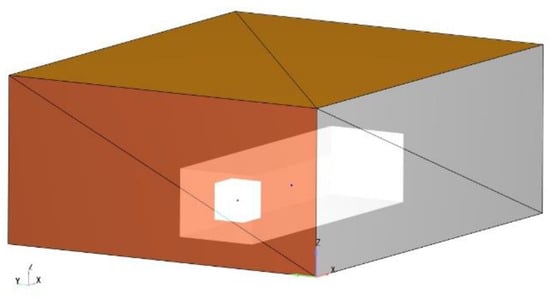
Figure 8.
Domain setup: BC for the single-rotor VAWT sample case. The inner box represents the region of embedding of scale 3, the middle box represents the region of embedding of scale 1 and the outer box is the domain.
As for the rotor placement, its center is located at 8 m (~10D from the inlet) in the x-direction, 6 m in the y-direction and 1.5 m in the z-direction, which gives enough space for the flow to be well-developed. The base grid size of 0.24 m is used away from the rotor and the wake region, while grid embedding is added near with scale n = 3 around the rotor and n = 1 in the wake. The grid embedding is performed as , where and are the local and base grid sizes, respectively.
The grid sensitivity test is performed first. Here, the base grid size is constant, but the embedding levels change for the rotor and wake. The time-averaged power coefficients at different grid resolutions are shown in Figure 9. Here, the inflow wind speed is 7 m/s. The value of Cp approaches roughly 0.27 asymptotically with the increase in the grid resolution, meaning that grid convergence is achieved. On the other hand, Figure 9 shows how significantly the number of cells increases when the value of relationship in Figure 9 grows. The values of this relationship, 0.58, 2.35 and 4.7, correspond to the embedding levels 1, 2 and 3, respectively. It also indicates that embedding levels 1, 2 and 3 correspond almost to the same number of cells owing to the fact that the embedding is performed locally. In the upcoming simulations, the embedding level 3 is chosen, considering that it keeps a good balance between the numerical accuracy and the numerical cost.
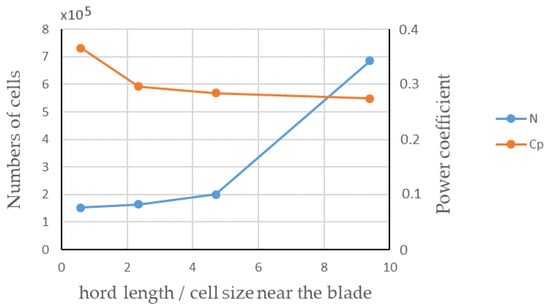
Figure 9.
Dependencies of the number of cells and Cp value as a function of the chord length/cell size ratio near the blade.
Next, the obtained Cp(λ) characteristics for a single-rotor VAWT sample with different wind speeds of 4, 7 and 10 m/s are depicted in Figure 10. In the figure, the characteristics are nearly parabolic in shape, which shows similarity with those presented in the literature [55,60]. The highest value of Cp is obtained for the value of TSR around 2.5. Note that due to the poor starting possibilities of the VAWT, the values of Cp are low for the TSR of 0.25–0.5, even at the wind speed of 10 m/s.
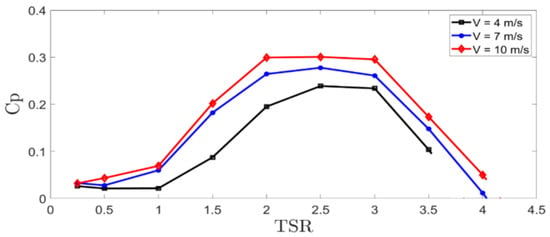
Figure 10.
Cp(λ) characteristics of a single-rotor VAWT sample for the wind speeds of 4, 7 and 10 m/s.
In Figure 11, the Q criterion shows how vortical structures progress in the wake of the investigated single-rotor VAWT at the free-stream velocity of 7 m/s. In the near-wake region, the vortical structures are well organized corresponding to the rotor motion, while they start to break up after some distance in the downstream due to instability of velocity shear at the wake edges (Figure 12a), which causes relatively large turbulence kinetic energy (TKE), as shown in Figure 12b. From Figure 12, it is also observed that the wake lasts through the whole computational domain downstream of the turbine and is still strong at the outlet (~10D). A noticeable velocity increase is observed above and below the rotor, which will have an important influence on the power efficiency of the CR-VAWT, which will be discussed later.

Figure 11.
Isosurface of the Q criterion colored by streamwise velocity component for the investigated single-rotor VAWT sample at free-stream velocity of 7 m/s.
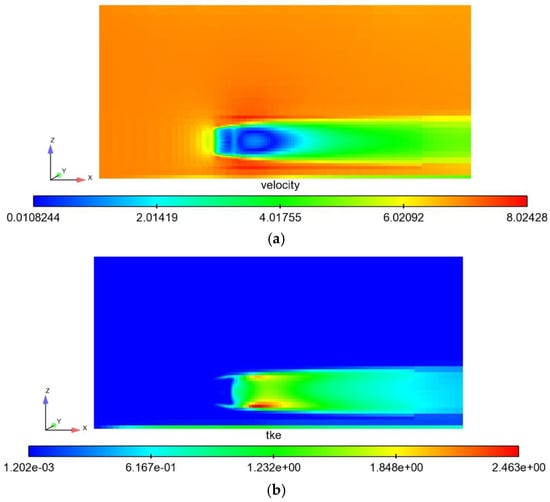
Figure 12.
Time-averaged streamwise velocity component field (a) and TKE field (b) at the vertical central plane of a single-rotor VAWT at a free-stream velocity of 7 m/s. Only part of the computational domain is shown here.
5.2. CR-VAWT Simulation
In this section, the effects of counter rotation for two VAWTs aligned in the vertical direction are investigated. In the simulations, the rotors rotated in opposite directions—the lower rotor rotated clockwise, and the upper one rotated counter-clockwise from the top view.
The BC for modeling the CR-VAWT sample was the same as for the single-rotor VAWT sample. The sizes of the domain in the x- and y-directions were also the same; however, the size in the z-direction varied from 8.1 to 8.5 m due to the added second rotor and the distance between rotors. Figure 13 presents the idea of counter-rotating rotors. Note, in this study, ALM is also applied, and no rotor blade geometry is resolved.
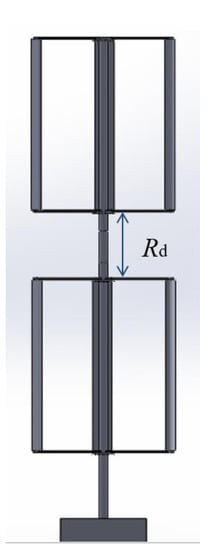
Figure 13.
The 3D geometry of the CR-VAWT.
The time-averaged streamwise velocity field and the TKE field at the vertical central plane are shown in Figure 14. Compared to the single-rotor VAWT case, the wake in the CR-VAWT case has a similar strength in both velocity and TKE at the same location downstream, which means that their influence on the downstream turbines in a wind farm will be also similar, although the CR-VAWT’s wake is more than two times wider in the vertical direction. Moreover, the wake shape in terms of the velocity deficit of each individual rotor is much less symmetric in the CR-VAWT case than that in the single-rotor case. In the CR-VAWT case, the velocity deficit of each individual rotor is skewed towards the gap between the two rotors, which is due to the acceleration of the velocity between the two rotors producing a low-pressure zone that sucks the flow from the upper and lower parts. Accordingly, due to the acceleration and large shear at the gap, the maximum TKE also happens there.
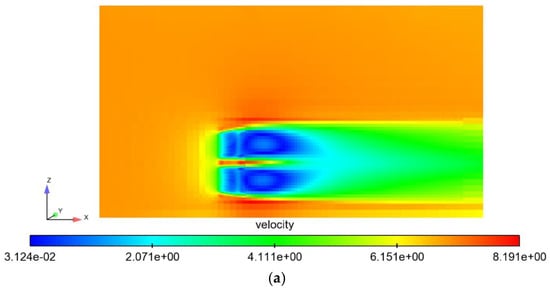
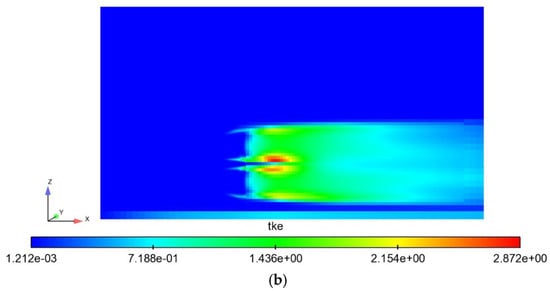
Figure 14.
Time-averaged streamwise velocity field (a) and TKE field (b) at the vertical central plane of a CR-VAWT at free-stream velocity of 7 m/s. Only part of the computational domain is shown here.
To study the effect of the distance Rd between the two rotors, five different values were chosen for the simulations—0.1H, 0.2H, 0.3H, 0.4H and 0.5H, where H is the blade length. The power coefficient results of the CR-VAWT with varying Rd and TSR are presented in Figure 15 and Figure 16. As shown, regardless of Rd, the power coefficient of the upper rotor in the CR-VAWT increased by roughly 5.5% and the lower rotor by 13.3% compared to the same single rotor. It also can be seen from the figures that both rotors benefit from the counter rotation, especially for the lower one at Rd between (0.3 and 0.4)H. The lower rotor has slightly better Cp in the range of TSR from 2.0 to 3.5 than the upper one. This increase can be explained by the stronger channeling effect between the ground and the lower level of the upper rotor where the velocity accelerates due to mass conservation, as shown in Figure 12a. A smaller, but still noticeable, velocity increase above the lower rotor accounts for the slight increase in Cp of the upper rotor. Moreover, the distance Rd does not seem to have a significant influence on the overall power efficiency for the design discussed in this paper. Individually, the Cp of the lower rotor increases slightly with the reduction of Rd due to the stronger channeling effect, but the upper rotor displays an opposite trend since it faces stronger wind speed at higher locations. It is expected that, eventually, the overall Cp will increase with the further increase in Rd when the gain of the upper rotor from higher wind speeds aloft dominates over the loss of the lower rotor from the weaker channeling effect, but it is less practical and thus beyond the scope of this work. In the cases comprising the present work, Rd = 0.3H seems to be a good compromise between efficiency and expense.
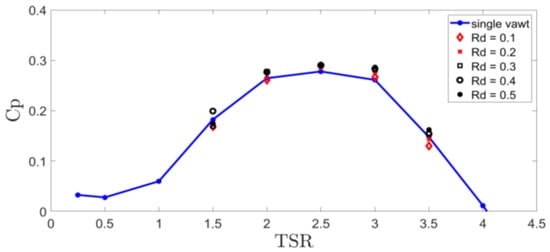
Figure 15.
Comparison of time-averaged Cp(λ) characteristics of the upper rotor of CR-VAWT sample between the single-rotor VAWT sample and cases with various Rd at free-stream velocity of 7 m/s.
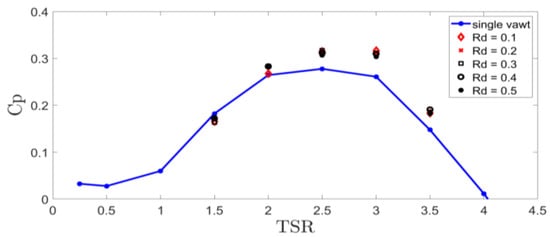
Figure 16.
Comparison of time-averaged Cp(λ) characteristics of the lower rotor of CR-VAWT sample between the single-rotor VAWT sample and cases with various Rd at free-stream velocity of 7 m/s.
Next, the performance of the CR-VAWT is compared with a single-rotor VAWT with the swept area doubled. Therefore, the total swept area of the CR-VAWT is the same as the single-rotor VAWT. Having the same AR of 1.1 (as the individual rotor of the CR-VAWT) and the swept area of 1.8 m2, a new size of the single-rotor VAWT was found: D = 1.28 m and H = 1.4 m. The Cp of the original single-rotor VAWT, the double-sized single-rotor VAWT, and the CR-VAWT are plotted in Figure 17. These results indicate two observations. First, simply increasing the rotor swept area is almost ineffective to increase the power coefficient, although the power increases with the swept area. Secondly, with the same swept area, the CR-VAWT achieves higher Cp at higher TSR, compared to the single-rotor VAWT. The Cp of the CR-VAWT increases by 10.2% at λ = 2.5 and increases by 13% at λ = 3. This increase in the power efficiency is mainly caused by the local velocity increase due to the interactions between the two rotors, as explained earlier.
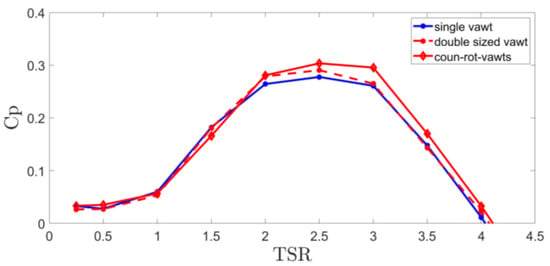
Figure 17.
Comparison of time-averaged CP(λ) characteristics of the CR-VAWT sample and single-rotor VAWT samples of different swept areas at free-stream velocity of 7 m/s.
Another possible benefit of the dual-rotor design, especially with counter-rotating rotors, is that the oscillation in the total mechanical power can be depressed significantly compared to the single-rotor VAWT, as compared in Figure 18. The individual VAWT rotor is known to have a distinctive oscillation with the frequency three times its RPM, i.e., every 120 degrees. In a counter-rotating dual-rotor system, such as the CR-VAWT design studied in this work, the power oscillation of each individual rotor is always at different phases. When they are superimposed, they will partially cancel each other so that the total power is much less oscillatory.
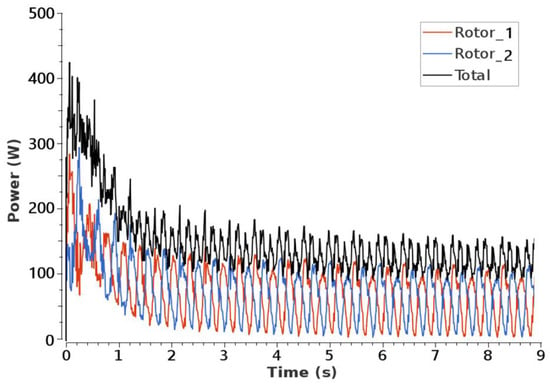
Figure 18.
Temporal rotors power of investigated CR-VAWT at free-stream velocity of 7 m/s.
6. Conclusions
In this work, the concept of a CR-VAWT with two co-axial three-blade H-Darrieus rotors has been studied from different aspects, including drivetrain design, electric generator, control system design and rotor aerodynamic analysis. The results show a number of advantages of such CR-VAWT both in terms of technical implementation, reliability and cost, and aerodynamics.
To improve the rotor’s self-start characteristics, a new direct-driven DR-PMSG design has been proposed for the CR-VAWT, in which two built-in low-power PM electric machines have been added. They perform two functions—starting-up and overclocking the rotors to the angular velocity at which the lifting force of the blades is generated, and stabilizing the CR-VAWT to work in different wind gusts acting on two rotors. To perform these functions, the control system for the operation of the proposed DR-PMSG has been developed.
To study and optimize the aerodynamic characteristics of the CR-VAWT, a set of CFD simulations was conducted using the CONVERGE CFD software with ALM for the rotor modeling, which significantly reduces the computational effort in comparison to the blade-resolved CFD. Based on the CFD results, it was determined that both rotors have positive interactions with each other while rotating in opposite directions. As a result of the mutual interaction, the power coefficient of the upper and especially lower rotor in the CR-VAWT increased compared to the same single-rotor VAWT. This effect provided an increase in the average value of the power coefficient in the CR-VAWT sample by 10–13% compared to the single-rotor VAWT of the same swept area as the CR-VAWT and the same aspect ratio as its rotor. At the same time, the optimal TSR also increases somewhat, which in the final case will lead to a decrease in the size of the generator. The optimal separation distance between the upper and lower rotors was found to be 0.3 of the rotor height. One more aerodynamic advantage of the CR-VAWT of this type was that the total mechanical power of both rotors oscillated less than for individual rotors. In terms of technical analysis, if the output power oscillates less, there will be more stable electricity generation.
A promising direction for further work, in our opinion, is to study a system consisting of a CR-VAWT and a stationary wind flow concentrator. The latter will make it possible to increase the speed of the incoming wind flow (or the flow in the rotor area) and improve the efficiency of the CR-VAWT, especially when working in low-speed winds [61].
7. Patent
Shchur, I.; Klymko, V. Electric Generator for Dual-Rotor Counter-Rotating Wind Turbine. UA Patent #125404, 11 November 2019.
Author Contributions
Conceptualization, I.S. and D.S.; methodology, S.X.; software, V.K. and S.X.; validation, I.S., V.K. and S.X.; formal analysis, V.K.; investigation, I.S., V.K. and S.X.; resources, S.X.; data curation, S.X.; writing—original draft preparation, V.K.; writing—review and editing, I.S. and D.S.; visualization, V.K.; supervision, I.S.; project administration, I.S. and D.S.; funding acquisition, D.S. All authors have read and agreed to the published version of the manuscript.
Funding
The Fulbright Association supported this research (Grantee ID: E0579594). Convergent Science Inc. Computing resources were provided by the University of Massachusetts, Amherst, Department of Industrial and Mechanical Engineering and by the San Diego Supercomputer Center through XSEDE. This work used the Extreme Science and Engineering Discovery Environment (XSEDE) funded by National Science Foundation Grant No.ACI-1548562.
Data Availability Statement
The data are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Acronyms | |
| ALM | actuator line modeling |
| AR | aspect ratio |
| BC | boundary conditions |
| CFD | computational fluid dynamics |
| CR | counter rotating |
| DR | double rotor |
| EG | electric generator |
| HAWT | horizontal axis wind turbine |
| LES | large eddy simulation |
| MPPT | maximum power point tracking |
| OCC | optimal current control |
| OTC | optimal torque control |
| PM | permanent magnet |
| PMSG | permanent magnet synchronous generator |
| SST | shear stress transport |
| TSR | tip-speed ratio |
| UDF | user-defined function |
| VAWT | vertical axis wind turbine |
| WECS | wind energy conversion system |
| WT | wind turbine |
| Latin symbols | |
| A | rotor swept area (m2) |
| B | number of actuator lines |
| Cl, Cd | lift and drag blade coefficients |
| Cp | power coefficient |
| H | rotor blade height (m) |
| reference load DC current of PMSG (A) | |
| KP, KI | proportional and integral coefficients of speed controllers |
| PWT | WT power (W) |
| R | rotor radius (m) |
| Re | Reynolds number |
| reference electromagnetic torque of PMSG (Nm) | |
| reference electromagnetic torque of the first and second additional PM machines (Nm) | |
| TWT | WT torque (Nm) |
| Vw | wind speed (m/s) |
| c | blade chord length (m) |
| d | distance between cell-centered grid points and points at the i-th actuator line (m) |
| e1, ed | unit vectors in the directions of lift and drag, respectively |
| f | computed local load (N) |
| f2d | vector of aerodynamic force per unit span length acting on the rotor blade (N/m) |
| nb | number of rotor blades |
| s | Laplace operator |
| Greek symbols | |
| Δ | size of grid containing the blade section (m) |
| β | angle of attack of blade (degree) |
| ε | width of regularized load (m) |
| ηε | regularization kernel |
| λ | tip-speed ratio |
| ρa | air density (kg/m3) |
| σ | rotor solidity |
References
- Rifkin, J. Third Industrial Revolution: How Lateral Power is Transforming Energy, the Economy, and the World; St. Martin’s Press: New York, NY, USA, 2011. [Google Scholar]
- Malinowski, M.; Milczarek, A.; Kot, R.; Goryca, Z.; Szuster, J.T. Optimized energy-conversion systems for small wind turbines: Renewable energy sources in modern distributed power generation systems. IEEE Power Electr. Mag. 2015, 2, 16–30. [Google Scholar] [CrossRef]
- Johari, M.K.; Jalil, M.A.; Shariff, M.F. Comparison of horizontal axis wind turbine (HAWT) and vertical axis wind (VAWT). Int. J. Eng. Technol. 2018, 7, 74–80. [Google Scholar] [CrossRef]
- Bhutta, M.; Hayat, N.; Farooq, A.; Ali, Z.; Jamil, S.; Hussain, Z. Vertical axis wind turbine—A review of various configurations and design techniques. Renew. Sustain. Energy Rev. 2012, 16, 1926–1939. [Google Scholar] [CrossRef]
- Mollerstrom, E.; Larsson, S.; Ottermo, F.; Hylander, J.; Baath, L. Noise propagation from a vertical axis wind turbine. In Proceedings of the 43rd Internet Congress on Noise Control Engineering, Melbourne, Australia, 16–19 November 2014. [Google Scholar]
- Malael, I.; Dumitrescu, H.; Cardos, V. Numerical simulation of vertical axis wind turbine at low speed ratios. Glob. J. Res. Eng. I Numer. Methods 2014, 14, 8–20. [Google Scholar]
- Sharma, K.; Biswas, A.; Gupta, R. Performance measurement of a three-bladed combined Darrieus-Savonius rotor. Int. J. Renew. Energy Res. 2013, 3, 885–891. [Google Scholar]
- Alaimo, A.; Esposito, A.; Messineo, A.; Orlando, C.; Tumino, D. 3D CFD analysis of a vertical axis wind turbine. Energies 2015, 8, 3013. [Google Scholar] [CrossRef]
- Oprina, G.C.; Chihaia, R.A.; El-Leathey, A.; Nicolaie, S.; Babutanu, C.; Voina, A. A review on counter-rotating wind tur-bines development. J. Sustain. Energy 2016, 7, 91–98. [Google Scholar]
- Vasel-Be-Hagh, A.; Archer, C.L. Wind farms with counter-rotating wind turbines. Sustain. Energy Technol. Assess. 2017, 24, 19–30. [Google Scholar] [CrossRef]
- Faisal, M.; Zhao, X.; Kang, M.-H.; You, K. Aerodynamic performance and flow structure investigation of contra-rotating wind turbines by CFD and experimental methods. IOP Conf. Ser. Mater. Sci. Eng. 2020, 926, 012017. [Google Scholar] [CrossRef]
- Rosenberg, A.; Selvaraj, S.; Sharma, A. A novel dual-rotor turbine for increased wind energy capture. J. Phys. Conf. Ser. 2014, 524, 012078. [Google Scholar] [CrossRef]
- Cho, W.; Lee, K.; Choy, I.; Back, J. Development and experimental verification of counter-rotating dual rotor/dual generator wind turbine: Generating, yawing and furling. Renew. Energy 2017, 114B, 644–654. [Google Scholar] [CrossRef]
- San, D.G.; Pastor, B.; Nalianda, D.; Sethi, V.; Midgley, R.; Rolt, A.; Block, A. Preliminary design framework for the power gearbox in a contra-rotating open rotor. J. Eng. Gas Turbines Power 2021, 143, 041022. [Google Scholar]
- Erturk, E.; Sivrioglu, S.; Bolat, F.C. Analysis model of a small scale counter-rotating dual rotor wind turbine with double rotational generator armature. Int. J. Renew. Energy Res. 2018, 8, 1849–1858. [Google Scholar]
- Moghadassian, B.; Rosenberg, A.; Sharma, A. Numerical investigation of aerodynamic performance and loads of a novel dual rotor wind turbine. Energies 2016, 9, 571. [Google Scholar] [CrossRef]
- Didane, D.H.; Rosly, N.; Zulkafli, M.F.; Shamsudin, S.S. Performance evaluation of a novel vertical axis wind turbine with coaxial contra-rotating concept. Renew. Energy 2018, 115, 353–361. [Google Scholar] [CrossRef]
- Tahani, M.; Razavi, M.; Mirhosseini, M.; Razi Astaraei, F. Unsteady aerodynamic performance of dual-row H-darrieus vertical axis wind turbine. Energy Equip. Syst. 2020, 8, 55–80. [Google Scholar]
- Poguluri, S.K.; Lee, H.; Bae, Y.H. An investigation on the aerodynamic performance of a CO-AXIAL contra-rotating vertical-axis wind turbine. Energy 2020, 42, 119547. [Google Scholar] [CrossRef]
- Duraisamy, K.; Lakshminarayan, V. Flow physics and performance of vertical axis wind turbine arrays. In Proceedings of the 32nd AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 16–20 June 2014; pp. 1–17. [Google Scholar]
- Brownstein, I.D.; Wei, N.J.; Dabiri, J.O. Aerodynamically interacting vertical-axis wind turbines: Performance enhancement and three-dimensional flow. Energies 2019, 12, 2724. [Google Scholar] [CrossRef]
- Kanner, S.; Wang, L.; Persson, P.-O. Implicit Large-Eddy Simulation of 2D counter-rotating vertical-axis wind turbines. In Proceedings of the 34th Wind Energy Symposium, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Asr, M.T.; Osloob, R.; Mustapha, F. Double-stage H-Darrieus wind turbine-rotor aerodynamics. Appl. Mech. Mater. 2016, 829, 21–26. [Google Scholar]
- Dumitrescu, H.; Dumitrache, A.; Malael, I.; Bogateanu, R. The standard and counter-rotating VAWT performances with LES. In Recent Advances in CFD for Wind and Tidal Offshore Turbines; Springer Nature: Cham, Switzerland, 2019; pp. 117–127. [Google Scholar]
- Malael, I.; Dragan, V. Numerical and experimental efficiency evaluation of a counter-rotating vertical axis wind turbine. Eng. Technol. Appl. Sci. Res. 2018, 8, 3282–3286. [Google Scholar] [CrossRef]
- Chaichana, T.; Chaitep, S. Performance evaluation of co-axis counter-rotation wind turbine. Energy Procedia 2015, 79, 149–156. [Google Scholar] [CrossRef]
- Ramos, D.; Carvajal, D. CFD study of a vertical axis counter-rotating wind turbine. In Proceedings of the 2017 IEEE 6th International Conference on Renewable Energy Research and Applications (ICRERA), San Diego, CA, USA, 5–8 November 2017. [Google Scholar]
- Didane, D.H.; Kudam, D.; Zulkafli, M.F.; Mohd, S.; Batcha, M.F.M.; Khalid, A. Development and performance investigation of a unique dual-rotor Savonius-type counter-rotating wind turbine. Int. J. Integr. Eng. 2021, 13, 89–98. [Google Scholar] [CrossRef]
- Didane, D.H.; Rosly, N.; Zulkafli, M.F.; Shamsudin, S.S. Numerical investigation of a novel contra-rotating vertical axis wind turbine. Sustain. Energy Technol. Assess 2019, 31, 43–53. [Google Scholar] [CrossRef]
- Didane, D.H.; Maksud, S.M.; Zulkafli, M.F.; Rosly, N.; Shamsudin, S.S.; Khalid, A. Performance investigation of a small Savonius-Darrius counter-rotating vertical-axis wind turbine. Int. J. Energy Res. 2019, 44, 9309–9316. [Google Scholar] [CrossRef]
- Chong, W.; Fazlizan, A.; Poh, S.; Pan, K.; Ping, H. Early development of an innovative building integrated wind, solar, and rain water harvester for urban high rise application. Energy Build. 2012, 47, 201–207. [Google Scholar] [CrossRef]
- Kutt, F.; Blecharz, K.; Karkosiński, D. Axial-flux permanent-magnet dual-rotor generator for a counter-rotating wind turbine. Energies 2020, 13, 2833. [Google Scholar] [CrossRef]
- Shchur, I.; Klymko, V. Comparison of different types of electromechanical systems for creating of counter-rotating VAWT. In Proceedings of the 2017 IEEE First Ukraine Conference on Electrical and Computer Engineering (UKRCON), Kyiv, Ukraine, 29 May–2 June 2017. [Google Scholar]
- Castelli, M.R.; Betta, S.; Benini, E. Effect of blade number on a straight-bladed vertical-axis Darreius wind turbine. Int. J. Aerosp. Mech. Eng. 2012, 6, 68–74. [Google Scholar]
- Li, Y.; Zheng, Y.; Zhao, S.; Feng, F.; Li, J.; Wang, N.; Bai, R. A review on aerodynamic characteristics of straight-bladed vertical axis wind turbine. Acta Aerodyn. Sin. 2017, 35, 368–382. [Google Scholar]
- Chiarelli, M.; Massai, A.; Atzeni, D.; Bianco, F. A new configuration of vertical axis wind turbine: An overview on efficiency and dynamic behavior. J. Energy Chall. Mech. 2015, 2, 23–28. [Google Scholar]
- Singh, M.; Biswas, A.; Misra, R. Investigation of self-starting and high rotor solidity on the performance of a three S1210 blade H-type Darrieus rotor. Renew. Energy 2015, 76, 381–387. [Google Scholar] [CrossRef]
- Mohamed, M. Impacts of solidity and hybrid system in small wind turbines performance. Energy 2013, 57, 495–504. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Z.; Huang, W.; Ingham, D.; Ma, L.; Pourkashanian, M. A numerical study on choosing the best configuration of the blade for vertical axis wind turbines. J. Wind Eng. Ind. Aerodyn. 2020, 201, 104162. [Google Scholar] [CrossRef]
- Bruska, S.; Lanzafame, R.; Messina, M. Design of a vertical-axis wind turbine: How the aspect ratio affects the turbine’s performance. Int. J. Energy Environ. Eng. 2014, 5, 333–340. [Google Scholar] [CrossRef]
- Shchur, I.; Klymko, V. Stabilization of the coaxial counter-rotating vertical axis wind turbine via torque balancing by special double rotor PMSG. In Proceedings of the IEEE 2nd Ukraine Conference Electrical and Computer Engineering (UKRCON), Lviv, Ukraine, 2–6 July 2019. [Google Scholar]
- Muteanu, I.; Bratcu, A.I.; Cutululis, N.A.; Ceangă, E. Optimal Control of Wind Energy Systems; Springer: London, UK, 2008. [Google Scholar]
- Nasiri, M.; Milimonfared, J.; Fathi, S.H. Modeling, analysis and comparison of TSR and OTC methods for MPPT and power smoothing in permanent magnet synchronous generator-based wind turbines. Energy Convers. Manag. 2014, 86, 892–900. [Google Scholar] [CrossRef]
- Islam, M.; Ting, D.; Fartaj, A. Aerodynamic models for Darrieus-type straight-bladed vertical axis wind turbines. Renew. Sustain. Energy Rev. 2008, 12, 1087. [Google Scholar] [CrossRef]
- Wekesa, D.; Wang, C.; Wei, Y.; Danao, L. Influence of operating conditions on unsteady wind performance of vertical axis wind turbines operating within a fluctuating free-stream: A numerical study. J. Wind Eng. Ind. Aerodyn. 2014, 135, 76. [Google Scholar] [CrossRef]
- Melo, R.; Neto, A. Integral analysis of rotors of a wind generator. Renew. Sustain. Energy Rev. 2012, 16, 4809. [Google Scholar] [CrossRef]
- Bai, C.; Lin, Y.; Lin, S.; Wang, W. Computational fluid dynamics analysis of the vertical axis wind turbine blade with tubercle leading edge. J. Renew. Sustain. Energy 2015, 7, 033124. [Google Scholar] [CrossRef]
- Shamsoddin, S.; Porte-Agel, F. Large eddy simulation of vertical axis wind turbine wakes. Energies 2014, 7, 890–912. [Google Scholar] [CrossRef]
- Bachant, P.; Goude, A.; Wosnik, M. Actuator line modeling of vertical-axis turbine. Wind Energy 2016, 1, 1–21. [Google Scholar]
- Martinez-Tossas, L.; Churchfield, M.; Leonardi, S. Large eddy simulations of the flow past wind turbines: Actuator line and disk modeling. Wind Energy 2015, 18, 1047–1060. [Google Scholar] [CrossRef]
- Sorensen, J.; Shen, W. Numerical modeling of wind turbine wakes. J. Fluids Eng. 2002, 124, 393–399. [Google Scholar] [CrossRef]
- Troldborg, N.; Sorensen, J.; Mikkelsen, R. Numerical simulations of wake characteristics of a wind turbine in uniform inflow. Wind Energy 2010, 13, 86–99. [Google Scholar] [CrossRef]
- Xie, S.; Archer, C. Self-similarity and turbulence characteristics of wind turbine wakes via large-eddy simulation. Wind Energy 2015, 18, 1815–1838. [Google Scholar] [CrossRef]
- Sheldahl, R.; Klimas, P. Aerodynamic Characteristics of Seven Symmetrical Airfoil Sections through 180-Degree Angle of Attack for Use in Aerodynamic Analysis of Vertical Axis Wind Turbines; Technical Report Number SAND-80-2114; Sandia National Labs.: Albuquerque, NM, USA, 1981. [Google Scholar]
- Hezaveh, S.; Bou-Zeid, E.; Lohry, M.; Martinelli, L. Simulation and wake analysis of a single vertical axis wind turbine. Wind Energy 2017, 20, 713–730. [Google Scholar] [CrossRef]
- Shamsoddin, S.; Porté-Agel, F. A Large-eddy simulation study of vertical axis wind turbine wakes in the atmospheric boundary layer. Energies 2016, 9, 366. [Google Scholar] [CrossRef]
- Xie, S. An actuator-line model with Lagrangian-averaged velocity sampling and piecewise projection for wind turbine simulations. Wind Energy 2021, 24, 1095–1106. [Google Scholar] [CrossRef]
- Papi, F.; Melani, P.F.; Xie, S.; Perrone, C.; Scienza, P.; Balduzzi, F.; Bianchini, A. Development and validation of an advanced actuator line model for wind turbines. In Proceedings of the E3S Web of Conference, Proceedings of the 76th Italian National Congress ATI (ATI 2021), Rome, Italy, 15–17 September 2021; EDP Sciences: Les Ulis, France, 2021; Volume 312. [Google Scholar]
- Qingan, L.; Maeda, T.; Kamada, Y.; Shimizu, K.; Ogasawara, T.; Nakai, A.; Kasuya, T. Effect of rotor aspect ratio and solidity on a straight-bladed vertical axis wind turbine in three-dimensional analysis by the panel method. Energy 2017, 121, 1–9. [Google Scholar]
- Almohammadi, K.; Ingham, D.; Ma, L.; Pourkashan, M. Computational fluid dynamics (CFD) mesh independency techniques for a straight blade vertical axis wind turbine. Energy 2013, 58, 483–493. [Google Scholar] [CrossRef]
- Chong, W.; Fazlizan, A.; Poh, S.; Pan, K.; Hew, W.; Hsiao, F. The design, simulation and testing of an urban vertical axis wind turbine with the omni-direction-guide-vane. Appl. Energy 2013, 112, 601–609. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).