Abstract
Massive growth in global electrical energy demand has necessitated a genuine exploration and integration of solar and wind energy into the electrical power mix. This incorporation goes a long way in improving the cumulative generated power capacity of the power system. However, wind and solar photovoltaic (PV) are intermittent in nature, making the provisioning of a good maximum power tracking (MPPT) scheme necessary. Furthermore, the integration is characterized by synchronization challenges and introduces various modes of power system oscillations as it is converter-driven. This greatly affects the overall stability of the integrated power mix. Consequently, various technological models have been designed to address these challenges ranging from MPPT schemes, phase-lock loop (PLL), virtual synchronous generator (VSG), power system stabilizers (PSS), flexible AC transmission system (FACTS), coordinated control and artificial intelligence (AI). In this work, a multi-machine power system model is reviewed for integration stability studies. Various technical solutions associated with the integration are also reviewed. MPPT, PLL, VSG, PSS, FACTS, coordinated control, and various optimization technique schemes used for damping controller design are discussed.
1. Introduction
International demand for electric power is growing phenomenally due to the continuous growth in the world population. The pursuit for improved power energy production and its reliable delivery to end users have mandated the need for exploring hygienic and renewable energy sources, particularly solar and wind, to augment and in some cases replace the conventional fossil-based electrical energy generation systems [1,2]. Consequently, ensuring that this thriving energy demand is met from safe, secure, and environment-friendly resources has become one of the top priorities for world leaders, researchers, and energy investors. Thus, evaluating the exploration and integration of non-conventional renewable sources into the electrical power mix is receiving the desired global attention [3,4]. In terms of international installed capacity, the three leading renewable energy competitors are hydro, solar, and wind energy [5]. However, penetration of renewable energy into the grid cannot take the place of conventional power generation as there are maximal allowable limits. In [6], an analysis of stability effects and limits of high penetration of renewables using two case studies was conducted. In case one, 70% of the power supply was from the conventional grid and 30% from renewables, here rotor angle stability was maintained. In case two, 72% of the power supply was from renewables and 28% from the conventional grid and it resulted in high angular instability.
Solar photovoltaic (PV) power generating system is an established and financially viable renewable energy solution that is postulated to attain a status of fulfilling almost about 28% of the world’s total energy demand by 2040 [7]. It is a hygienic, noise-free, profuse, and eco-friendly energy source that has attained mind-blowing satisfactoriness in personal and commercial applications [5,8,9]. Accordingly, momentous technological advances and cost reductions in solar photovoltaic (PV) modules have led to the large-scale adoption of PV-based power generators. Thus, it is widely considered a viable, striking, and promising solution to be espoused in meeting the global energy demand [10]. The two major implementations of a solar PV system are the off-grid and on-grid PV systems [5]. The former is a power generating system that operates in isolation from the main power grid while the latter is normally integrated into the main grid system. The topology for an on-grid PV system consisting of arrays of PV modules, LC filters, step-up transformers, and power electronics converters is shown in Figure 1.
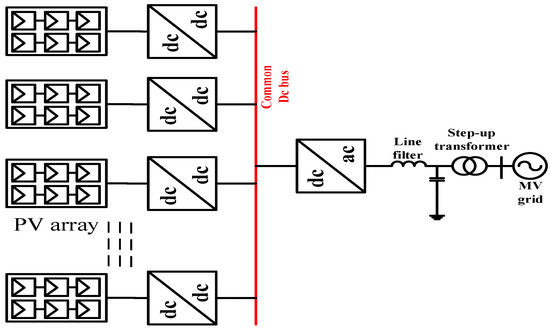
Figure 1.
Topology of solar PV grid-connected system [10].
Power electronic converters play a central role in the integration of PV-based generators into AC power grid systems. They are required for converting the DC output of the PV modules to AC power for reliable incorporation. Furthermore, a transformer is used in stepping up the low AC voltage into a medium AC voltage to feed power into a medium-voltage power transmission line. Additionally, a good photovoltaic (PV) system is equipped with a maximum power point tracker (MPPT) for tracking the maximum power point [11,12,13,14]. Depending on the solar design, the power output from the system is fed to the load while the excess power if available is willed to the grid for an increase in the power installed capacity.
With respect to wind energy systems, it is one of the most widely utilized and readily available non-conventional renewable energy sources available for both individual and commercial exploitation. Its high energy conversion rate, economic viability, and other social benefits make it a virtuous energy solution for large-scale applications [15]. The wind energy system generates electricity through a wind energy conversion system. It entails the usage of the mechanical force of the fast-moving wind to drive a wind turbine connected to an induction generator for electrical power production. Generally, wind turbines are complex machines in which numerous technologies are assembled and combined. They are specifically designed to operate in challenging environmental and operating conditions including unpredictable loads due to gust wind, humidity, air pressures, and so on [16]. Based on the induction generator selection and configuration of the wind generating systems, they can be broadly classified into four categories. The squirrel cage induction generators are categorized as type I, while the wound rotor induction generators are type II. Control resistors, gearboxes, and slip rings are some of the major components of Type I and Type II systems. Capacitors are also incorporated for reactive power supply to the induction generator and the grid. In Type III wind energy systems, a doubly fed induction generator (DFIG), gearbox, an inverter (DC/AC), and a rectifier (AC/DC) constitute the power generating system. A permanent synchronous generator (PMSG), a rectifier (AC/DC), an inverter (DC/AC), or grid-side converter, and a gearbox make up the type IV wind-based power generating system [17,18,19,20,21].
Currently, doubly fed induction generator (DFIG)-based wind turbines are gradually displacing the traditional synchronous generators in various power system applications [22]. According to [17], high wind energy grid integration requires a thorough consideration of established grid codes, policies, monitoring strategies, and energy storage systems. For reliable grid–wind synchronization, a phase-lock loop (PLL) is employed in tracking the phase of the voltage terminal of a grid-connected wind turbine to achieve a good connection [23].
However, wind energy installation can be either onshore (land) or offshore (ocean). Owing to the vast land required to implement onshore wind farms and the development of an HVDC-adopted transmission system, the offshore wind system is gaining momentum [24]. Figure 2 shows a parallel connected HVDC offshore wind system.
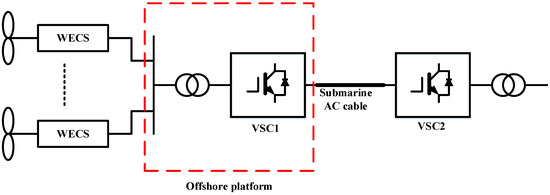
Figure 2.
HVDC offshore wind connected in parallel [24].
Renewable energy sources (RESs) are often used in integrated systems at their maximum power points and are connected to the grid through converters [25]. High-tech advancements in power electronic converters have greatly influenced the large-scale adoption of grid–wind-integrated energy systems [26]. Nonetheless, integrating this converter-driven renewable energy solution into the electrical grid causes several technical issues, particularly power system oscillations, which generally impair the overall power transmission capability of already-installed transmission lines [27,28]. These oscillations are basically of various electromechanical modes based on their frequency range of occurrence. The local mode (0.7–2.0 Hz) and inter-area modes (0.1–0.8 Hz) have been extensively studied [29]. Consequently, the overall stability of the integrated power system is affected owing to the numerous nonlinear dynamic devices and components involved in the renewable energy system (RES) grid integration [30]. In this regard, electrical power grid system stability can be seriously threatened if the resultant oscillations caused are not properly dampened [28]. Thus, solving power system oscillation problems is of great interest to the electrical power industry.
Power system stabilizers (PSSs) are the most often used technology in electrical power systems to dampen electromechanical oscillations and increase the stability of the power system. By modifying the voltage reference of the automatic voltage regulator (AVR) in response to the feedback of rotor speed or frequency deviation from the rated value, power system stabilizers inject a stabilizing signal into the generator’s excitation system. The goal of this stabilizer is to restore the rotor speed of the generators to their rated value [31]. The PSS may not always in some cases provide appropriate damping for the inter-area modes. Thus flexible AC transmission systems (FACTSs) introduced by Hingorani are an intriguing alternative because, when used in conjunction with a power oscillation damping (POD) controller system, they can add extra damping to the inter-area oscillation modes in addition to improving the performance of the power system [29]. Due to the robust nature of RES-integrated electric power systems, robust damping controller like FACTS controller, and PSS are combined and coupled to grid synchronous generators [27].
Power system oscillations can be extremely severe and difficult to manage. This calls for a robust design of damping controllers that can effectively address the various oscillation modes to achieve the desired stability. However, damping controller design is an optimization-centered process that requires the exploitation of various optimization algorithms [32]. The damping of power system oscillations with damping controllers mostly depends on the tuning strategy adopted in obtaining the optimal parameters [33]. Time integral performance criteria for calculating the integral error of the damping controller [32] and the eigenvalue-based stability analysis on the multi-machine test system are employed to evaluate the performance of damping controllers.
Furthermore, with the evolution of artificial intelligence and the continuous penetration of RESs into the electric power grid, artificial intelligence damping controller systems have been proposed by [34,35,36]. These intelligent controllers are capable of learning and adapting to any system they are applied to, and improving the system’s performance. However, applying several damping controller combinations ineffectively in power systems may further disrupt the system. This is because of the interaction of the controllers which might create system destabilization. Normally, a transient stability study for various system disturbances can be used to evaluate the design. Therefore, the stability issues in RES-integrated power systems may be resolved by properly designing damping controllers. The formulation of the objective function, which makes use of a variety of power system indicators, is crucial in efficiently damping oscillations in the power system. Creating an objective function that effectively moves the eigenvalues into a more stable region of the complex s-plane is essential for stability analysis. Angular stability is measured using the damping ratio and damping factor that is calculated from the real and imaginary eigenvalues of complex power systems. The eigenvalues are moved to the left of the complex s-imaginary plane’s axis to increase stability [37]. A time integral performance criterion for figuring out the integral error of damping controllers can also be used in stability analysis [32]. The time error objective functions are used to decrease the rotor speed deviation error for angular stability.
Over the years, several controller design studies have been carried out [38,39,40,41]. The objective function was formulated using a variety of approaches by the authors. A crucial component of controller design is the objective function which must be appropriately designed to ensure that the damping achieved by the applied damping scheme is suitable and sufficient. Prior to this work, there has been no research that has critically evaluated objective function formulation for the design of a damping controller in a RESs-integrated power grid system. It is crucial to find the best objective function approach for a reliable design that guarantees stability in a multi-machine-integrated renewable energy source power system. The widely acknowledged optimization technique for designing damping controllers is the application of metaheuristic, heuristic, and other artificial intelligent techniques [42,43,44]. These methods perform well for the PSS design problems. Considering renewable sources, the overall optimal solution can have a big impact and the solution might be limited to local optimal points.
The application of damping controllers to these renewable energy sources is not yet governed by grid codes. However, because RESs are now more widely used, it is critical to assess how well damping controllers work with RESs. The majority of inverters need a phase-lock loop (PLL) to synchronize with the grid. A PLL is unable to reduce oscillations in the power system since it is dependent on the frequency produced by the synchronous generators. As a result, system instability and a loss of synchronism with the grid are frequently the results. Research has established the virtual synchronous generator (VSG) concept as a means of addressing the stability issue while supporting the inertia of the power system. A VSG imitates the dynamic behavior of an actual synchronous generator [45]. The study in [46] proposed that to improve system stability, the inverter output is controlled using pulse width modulation with the frequency and voltage of an infinite bus as input signals.
This review provides a thorough overview of power system oscillation to advance future work on developing effective damping controllers for RESs-integrated power systems. Detailed explanations are provided for the overview of developments in solar and wind renewable energy sources. Further described are the types of power system oscillations and their basic principles. Different damping controllers are shown, and the controller design is streamlined using two alternative approaches for formulating the design objective functions. A review of optimization methods taken into account by earlier researchers is also discussed. This study concludes with some recommendations for enhancing the effectiveness of future damping controller design in an integrated RES power system, as well as suggestions for additional research.
2. Review Methodology
The focus of this review is on the application of optimization techniques in damping controller design for a multi-machine power system with solar, wind, and hydro renewable energy sources. In line with the review focus, books, journals, and conference proceedings on Scopus scientific database were adopted. After examining the title, abstract, keywords, paper’s contents, and findings of the searched works of literature, relevant ones were chosen. The choice was based on the impact factor, citations, and the review process. To also carry out a recent review, articles published from the year 2016 to date were prioritized for citation.
Findings were organized into sections: the review starts with the review of synchronous machine modeling and a summary of recent developments in renewable energy sources, such as solar and wind. In section two, maximum power tracking and integration to the grid are discussed. Power system stability and oscillations, also known as electromechanical oscillation, are explained in section three. The stability study of various damping systems is discussed in the fourth section. In Section five, the construction of damping controllers for linearizing non-linear systems is discussed, also a thorough analysis of the eigenvalue-based objective function is provided. In the sixth section, a comparison of single and multiple objective functions is presented. Discussions on the advantages and limitations of some optimization techniques used for damping controller design are explained, and the review provides key recommendations for future development on oscillation damping in RES-integrated power systems.
3. Solar, Wind, and Their Hybridization Integration for Multi-Machine Power System Controllers Optimization
3.1. Renewable Energy Sources (RESs) and Integration with Multi-Machine Power System
3.1.1. Synchronous Machine Modeling
A multi-machine test system has synchronous machines interconnected with each other. The test system in this review is a reference benchmark model for analyzing and controlling oscillation dynamics in power systems. The synchronous machine modeling involves representation with Differential Algebraic Equations (DAEs) as follows:
For m number of machines representing the synchronous grid machine, its voltage regulator, known as an automatic voltage regulator, is modeled as described in Equations (1)–(19) [47]:
where
The notation meaning of the various parameters as seen in [47]:
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- = q-axis component of generator terminal voltage;
- ;
- ;
- ;
- ;
- .
In Equation (4), electrical torque is used;
Algebraic equations of a synchronous machine stator are:
Algebraic equations of all stators in the synchronous machines of a power system in matrix form are:
where
Considering an infinite bus system, m number of machines and n number of loads, the power system network equations are as follows:
with m machines, the loads in the power system can be described as constant impedance, hence keeping the load impedance zero. Reduction order reduces the elements that are load related from the admittance matrix of the lines network.
Equations (17) and (18) interface the machine and the network:
the above differential algebra equation determines the power system’s nonlinear behavior, and the ordinary differential equations use a solution loop to solve the DAEs presented using the ordinary differential equations (ODEs), as shown in Figure 3.
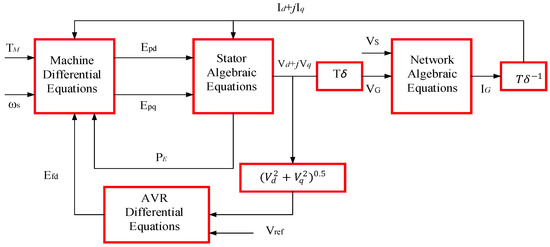
Figure 3.
Diagrammatic representation of algebraic equations using ordinary differential equations [47].
3.1.2. SOLAR
Solar thermal collectors or photovoltaic (PV) solar systems can be used to harness solar energy, which is a form of renewable energy [48,49]. Harnessing solar energy through thermal collectors is performed by concentrating sunlight in a solar thermal power system which results in a temperature rise of the heat sinks, and causes them to produce steam. The steam is used in turbines to generate power. However, substantial installations are required for the solar thermal power system to generate enough power. In a photovoltaic (PV) solar system, photons from the sunlight are used to energize the semiconductor-embedded free electrons and leads to the production of electrical energy. PV solar systems are harnessed through solar panels that operate on various conditions and are frequently employed on roofs or in a large land mass to form solar farms or mini-grids [50]. Figure 4 shows a Solar PV Conversion system.
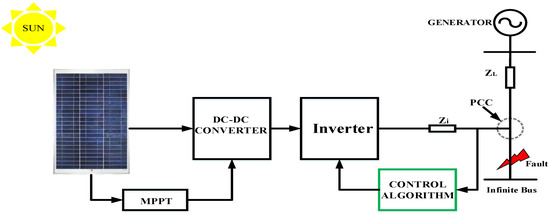
Figure 4.
A Solar PV Conversion system [51].
Solar energy generation depends on solar irradiance, that is the radiant energy the sun emits in the form of electromagnetic radiation. Solar irradiance has the strongest association with PV power production and is directly correlated with the amount of solar energy that can be harnessed [50]. Solar irradiance of a particular area can only be forecasted due to variations in solar radiation. Moreover, natural variation in solar irradiance at ground level presents a substantial barrier to the widespread use of solar energy [52]. To successfully manage solar energy production operations, a reliable forecast approach is needed. Recently, researchers have deployed various artificial intelligent approaches [53,54] to forecast solar energy generation.
PV solar system installation has increased massively over the years, particularly in 2020. PV solar system installations globally were estimated at 139 GW, and this increased the global total installed capacity to 760 GW, for both on-grid PV solar systems and off-grid PV solar systems [55]. Figure 5 presents the solar PV installations globally from 2010 to 2020.
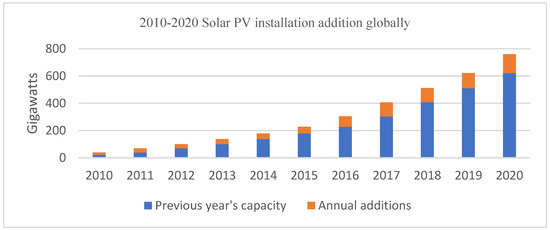
Figure 5.
Solar PV global capacity and Annual Additions [55].
3.1.3. WIND
Wind energy is one of the most developed and rapidly expanding forms of renewable energy worldwide. It is also one of the most sustainable energy sources capable of ensuring alternative energy security [56,57]. Due to increased adoption, research is ongoing in different areas of wind energy systems. However, wind energy generation relies on the installed location’s topography, weather conditions, and wind speed. Thus, wind energy may not always provide the same amount of electricity as conventional energy sources such as hydro and gas due to the inconsistent nature of wind speed. Therefore, wind energy systems are integrated into the power grid system. The stability of the power grid system can be affected by the integration of the wind energy system [57,58,59]. Wind energy generation is achieved through a wind energy conversion system (WECS), the four categories of generators used for variable wind speed conversion in wind energy systems are electrically excited synchronous generators (EESG), squirrel-cage induction generators (SCIG), permanent magnet synchronous generators (PMSG), and doubly fed induction generators (DFIG) [60]. However, compared with EESG and SCIG, DFIG and PMSG have gained greater attention due to their higher energy conversion efficiency and quick control capability. Both systems occupy almost equal market shares in global wind energy installed systems [61]. The DFIG wind energy system consists of a gearbox that connects a wind turbine to the DFIG wind energy system and converts mechanical energy from the turbine to electrical power [62]. Figure 6 shows the DFIG system. The three-phase winding rotor used in DFIG allows for a wide range of variable speeds. Thus, variable speed control changes the converter’s active and reactive power rotor current flow. However, frequent maintenance of brushes and multiple-stage gearbox in the DFIG system is required to reduce the possibility of machine failure.
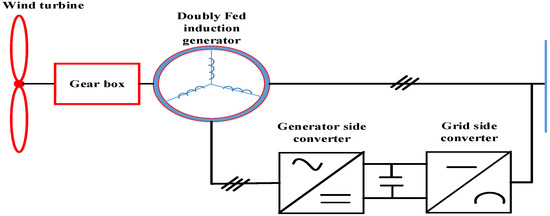
Figure 6.
A doubly fed induction generator (DFIG) wind energy conversion system [63].
The permanent magnet synchronous generator (PMSG) creates an excitation field using permanent magnets rather than coils. Moreover, because PMSG has fewer moving parts than electrically excited generators and DFIG, PMSG requires less attention. Due to its superior energy conversion efficiency and a longer lifespan than EESG and SCIG, PMSG with a fully rated power converter is one of the best options for variable-speed generation, even though it has a high capital cost [63]. The synchronous generators (SGs) require controllers to efficiently maximize the amount of wind energy from wind to meet grid integration requirements. Thus, before sending electricity to the grid, PMSG is connected to a frequency converter that comprises a converter for the machine (rotor-side converter) and one for the grid (grid-side converter). The rotor-side converter regulates the operation of the PMSG. This converter can either be a diode-based rectifier or a pulse-width modulated voltage source converter. On the other hand, the grid-side converter controls the direct current link voltage by exporting active power to the grid network and can only be a pulse-width modulated voltage source converter. Figure 7 shows the PMSG wind energy conversion system.
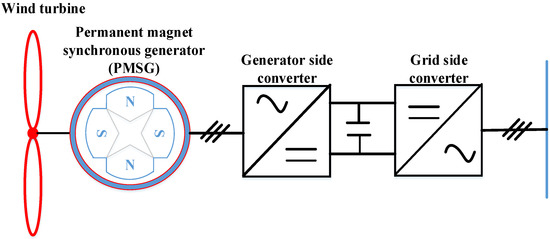
Figure 7.
A permanent magnet synchronous generator (PMSG) wind energy conversion system [63].
Depending on where they exist, wind energy systems can be classified as either onshore (on land) or offshore (at sea). Due to higher uniform wind speeds in deep oceans, offshore technology has been slowly gaining traction in recent years. Compared with the onshore wind energy system, offshore wind energy system often has higher capacity ratings [64]. The integration of offshore wind energy systems can be justified as a benefit of renewable energies of ocean and wind because the oceans cover more than 70% of the Earth’s surface.
In terms of global wind energy installed capacity, a tremendous achievement was recorded in the year 2020. About 93 GW of the wind energy system was installed globally with more than 86.9 GW of the installed wind energy capacity onshore and about 6.1 GW offshore. This 93 GW addition brought the total installed wind energy system close to 743 GW worldwide [55]. Figure 8 presents wind power global capacity and annual additions for 2010 to 2020
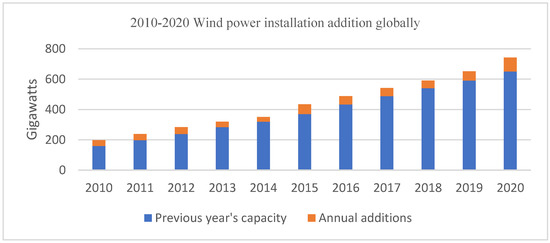
Figure 8.
Wind power global capacity and annual additions [55].
Conventionally, siting of wind energy systems is majorly onshore due to the ease of construction and maintenance compared with offshore wind energy systems [65]. These days, interest in the offshore wind energy system is increasing due to strong and steady sea winds [66]. Europe is presently leading in offshore wind power plant development. As of 2018 total global installed offshore wind capacity was 22,045 MW, with about 80% concentrated in Europe [67]. The electrical power generated from offshore wind energy systems is transmitted from the offshore substations to the onshore grid substations. A direct high-voltage current (HVDC) or high-voltage alternating current transmission line connects wind energy systems to offshore grid substations [68]. These offshore grid substations usually run at a medium voltage and low frequency. The electrical power is transferred from the offshore grid substations to the power system grid network using high-voltage AC transmission cables [68].
For reduced transmission cost and improved efficiency, the study in [65] proposed a rectifier (AC/DC) interfaced converter for medium voltage direct current to displace the conventional AC transmission. This DC high-temperature superconducting cable can transmit around three times as much power as an equivalent AC cable [69]. Moreover, improved efficiency is due to several DC operation characteristics, such as high dc critical current and dielectric material. DC cable’s electrical breakdown strength is almost twice that of an AC cable and its electrical resistance is more than 100 times lower than that of a traditional AC cable. Consequently, it results in a very low electrical loss [69].
3.1.4. Hybrid
In various countries, there has been a significant transformation in the power sector over the years due to increased wind and solar power penetration. In 2020, about 20% of at least nine countries’ total electricity generation was from solar and wind energy. Table 1 shows the total electricity generation distribution of the top countries with a high share of solar and wind energy.

Table 1.
Top countries in 2020 with a high share of solar and wind energy in their total electricity generation [55].
3.2. Wind–PV Maximum Power Tracking and Integration to the GRID
3.2.1. Maximum Power Point Tracking (MPPT)
Generated power from renewable energy sources such as wind and solar is intermittent and inexact [70]. For improved efficiency, a maximum power point tracking (MPPT) control algorithm is incorporated into the system to track down the maximum available power from renewable energy sources [71]. Different MPPT algorithms for reliable power tracking to extract maximum power from PV and wind energy sources were analyzed and studied in [72,73].
In PV-based grid integration, the MPPT control scheme implements an algorithm to extract the desired power from the PV arrays [74]. The control scheme allows an adaptation between the PV and the loads so that the electrical energy generated corresponds to its maximum value and is transferred directly to the grid [8]. Depending on the control algorithm of the solar MPPT design, its major operation entails taking the PV array’s measured voltage, current, and adjusting the pulse width modulation (PWM) duty cycle for the PV side controller switching devices via a voltage controller. The perturb and observe (P and O) control technique is the most widely implemented solar MPPT algorithm because of the ease of its execution and the appropriate convergence it offers. However, the P and O-based MPPT approach has a delayed response time under abrupt changes in solar irradiation and poor tracking effectiveness, resulting in a decreased ability to harvest energy. Hence, other solar MPPT control algorithms are investigated in [75,76].
In wind-based energy systems, the indirect speed controller is used to track wind speed peaks. The objective of such control is to maximize the power obtained by the wind when wind speed fluctuates, either below or surpassing its rated value. Consequently, a good control algorithm is required to maintain a good balance between the maximum extraction of wind power and the overall safety of the system [77]. A pitch control system interfaces the wind control strategy and the wind turbine to tap the maximum wind speed [78].
In a hybrid power system consisting of PV and wind, the complexity in the implementation of reliable control is greatly affected by the MPPT control algorithm adopted, as each of the algorithms has exclusive boundaries. A well-designed MPPT control system for monitoring wind speed from wind, solar sources, and also the convergence time, is discussed in [79]. However, individual MPPTs for each wind speed source are needed, affecting the cost and size of implementing a hybrid control system for MPPT. Therefore, an artificial neural network (ANN) single MPPT control strategy called the Radial Basis Function Network is considered a reliable MPPT solution for overcoming the above drawbacks. It offers increased maximum power tracking [80].
3.2.2. Phase-Lock Loop (PLL)
One of the most crucial difficulties in managing power converters connected to the grid is synchronization. PLL synchronizes the energy transfer between the grid and the power converter and evaluates the phase angle of the basic vector of the AC mains voltage in real-time. Recently, some proposed control algorithms use phase-locked loops to track the utility voltage phase angle and frequency [80]. Functionally, a PLL links the renewable energy source to the grid-connected power system. Hence, the PLL’s phase-tracking performance affects the power system’s overall dynamic performance [81].
The PLL performs phase and frequency tracking to synchronize the reference signal with the grid voltage and reduce unwanted frequency changes. This loop reacts swiftly and precisely to re-synchronize the two signals each time it notices a difference in angle [82]. Various PLL control techniques have been proposed in converter-based power-generating systems such as PV and wind [83]. Proportional resonant controllers and stationary frame proportional integral regulators are some of the standard PLL techniques used for grid synchronization. Practically, the dynamic interaction with the Voltage Source Converters lead to inaccurate PLL synchronization as the grid-side voltage and phase angle are always required [84]. Figure 9 and Figure 10 show the conventional synchronous reference frame PLL and the proposed PLL-based controller, respectively.
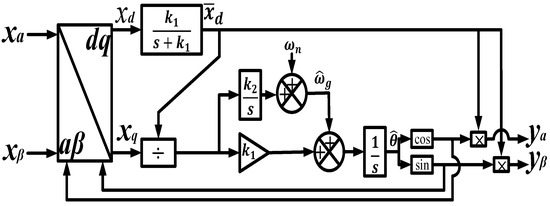
Figure 9.
Conventional synchronous reference frame PLL [83].
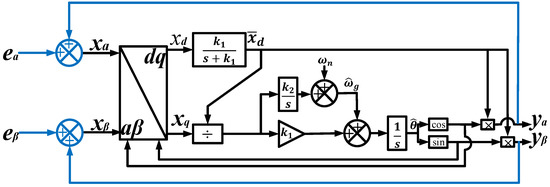
Figure 10.
Proposed PLL-based controller [83].
3.2.3. Converters
The grid-side converter (GSC) regulates the reactive power flux between the converter, the electrical grid, and the DC-link voltage. In DFIG-based wind energy system, the rotor-side converter (RSC) controls the active and reactive power flow between the stator and grid. To achieve the desired result, the operation of these converters control is by a cascaded control loop, as shown in Figure 11 and Figure 12 [85].
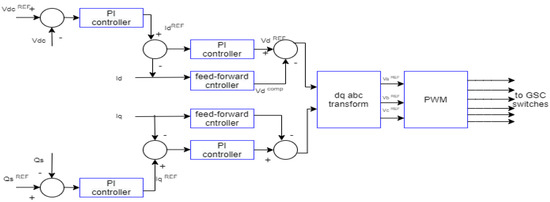
Figure 11.
Grid-side converter control structure [85].
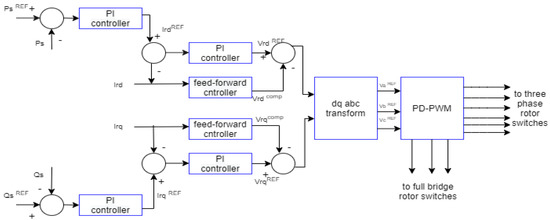
Figure 12.
Rotor-side converter control structure [85].
3.3. Power System Stability and Oscillations
Significant work has been carried out in recent years to increase the power stability of electrical power systems. A stable electrical power system maintains equilibrium and is mostly disrupted by load, disturbances, and power generation changes [86]. Generally, an increase in installed solar and wind energy affects the rotor angle, frequency, voltage, resonance, and converter-associated stability of the power system as shown in Figure 13 [87].
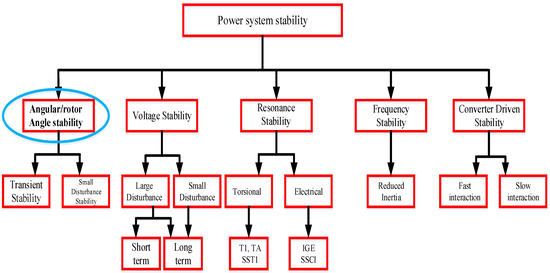
Figure 13.
Classification of power system stability considering converters [90].
With respect to power system oscillations, integrating renewable energies has brought about spontaneous low-frequency oscillations [88].
Rotor angle and voltage stability are of two categories small signal and transient stability. The first oscillations in the system following a significant disruption, such as transmission network short circuits or the loss of a generating unit, are classified as transient stability [89]. Small-signal stability on the other hand is confined to restoring steady-state operation following the appearance of minor disruptions due to slight variations in loads. This review focuses on rotor angle stability issues caused by power system oscillations.
Power system oscillations or electromechanical oscillation occurrences have always been a challenge in renewable-integrated power systems, which affect the stable operation of the integrated power grid. Analysis of electromechanical oscillation involves two categories, i.e., the frequency and damping performance [91]. Electromechanical oscillation frequency can reflect its potential causes and type. At the same time, the electromechanical oscillation’s damping performance is a characteristic of its damping rate [92]. In a power system grid with a weak damping rate, damping controllers improve the system’s damping performance.
In RESs with converter-interfaced generation such as solar PV, its lack of inertia reduces the power system inertia, in proposing several techniques to provide such inertia services power system oscillations need consideration [93]. These techniques involve two approaches. In the first approach, the converter is synchronized to the grid using a phase-locked loop (PLL), thus exchanging additional power, proportional to the time derivative and frequency [94]. The converter in the second approach emulates the inertia property of a synchronous generator (e.g., virtual synchronous generators VSGs) [95].
3.4. Stability Analysis of Different Damping Schemes
Power system oscillation incidents occur spontaneously. Thus, the system is designed with automated control and appropriate detecting systems to dampen these oscillations. This review discusses different types and modeling approaches to improve system oscillation damping. Earlier studies on various damping schemes have been used to reduce power system oscillations, damping controller scheme classification into five main types including virtual synchronous generator damping, PSS damping, FACTS damping, coordinated damping, and most recently, artificial intelligence (machine learning)-based damping. Figure 14 shows the different classification schemes and damping controller devices under different schemes while Table 2 Provides a summary of the fundamental purpose of various damping schemes and their limitations.
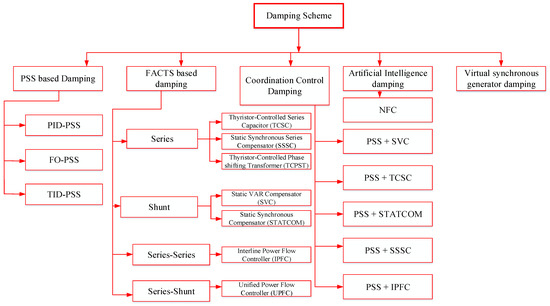
Figure 14.
Damping schemes for power system oscillation [10].

Table 2.
Provides a summary of the fundamental purpose of various damping schemes and their limitations.
3.4.1. Damping Schemes
The total power system inertia reduces when more renewable energy sources (RESs) are integrated and fewer conventional generators are used [96]. Virtual synchronous generation is an important concept geared towards frequency stabilization as it injects appropriate active power into the grid when required to balance the inertia requirement of the power system [97]. Whether inertia energy is obtained from extra sources or the capacitors in the VSC, the VSG depends on the energy storage system (ESS) to provide the required inertia support [98]. The VSG is a promising solution to the problem, and many research efforts have been devoted to this area. Power oscillation of a PMSG-based virtual synchronous generator was studied in [98] where both the machine-side and the grid-side converters of the PSMG are controlled as a VSG. However, parameter alternating methods are suggested to update the key parameters of VSG following the operational status of power systems to enhance the dynamic performance of VSG in real-time. Figure 15 shows a schematic of a virtual synchronous generator (VSG).
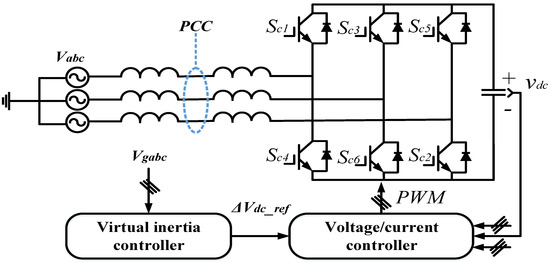
Figure 15.
Schematic diagram of VSG [99].
PSS-Based Damping
De Mello and Concordia established the PSS concept in 1969 as a crucial power system component to tackle the power oscillation challenge. According to the synchronous machine theory, the excitation system can adjust and vary the output power generated. PSS adds an input signal to the synchronous generator’s excitation system [100,101], and an extra phase-locked synchronization torque to the speed deviation of the generator, thereby controlling the system’s stability by dampening the power system oscillations. In addition to effectively damping local oscillations, a correctly designed PSS can also dampen inter-area oscillations [28]. Previous research explained oscillation damping by designing PSS for a single machine [102,103,104], for multi-machine systems [105,106,107], and a RES-integrated power system [108,109]. Figure 16 shows the internal structure of a lead–lag PSS.
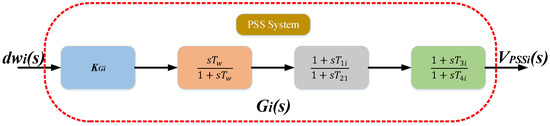
Figure 16.
A lead–lag PSS [35].
FACTS-Based Damping
Power electronic converters’ voltage, current, and switching frequency have increased considerably over the past few decades. This increase in switching frequency, voltage, and current led to the development of several FACTS devices [110]. FACTS devices, as its name suggests, allow for a voltage or reactive power injection at a bus while providing flexibility on otherwise inflexible network parameters of a transmission line. The primary use of FACTS is not to dampen oscillations but to improve the transmission line’s power transfer capability [111]. Although its damping function has drawn attention from researchers and industry. Since then, various research has been conducted on FACTS-based damping [112,113,114,115,116] in power systems.
FACTS device classification is according to the way they are connected to the power system which includes: (i) shunt-connected examples are static VAR compensator (SVC), and STATic COMpensator (STATCOM); (ii) series-connected devices examples are thyristor-controlled series compensator (TCSC), Static synchronous series compensator (SSSC), and gate-controlled series capacitor (GCSC); (iii) shunt- and series-connected devices examples are unified power flow controller (UPFC) and (iv) series–series connected devices example interline power flow controller (IPFC). Various FACTS devices have been used as damping controllers in a renewable-integrated system to dampen oscillations, Figure 17 shows the distribution of FACTS-based damping controllers used in a renewable-integrated system.
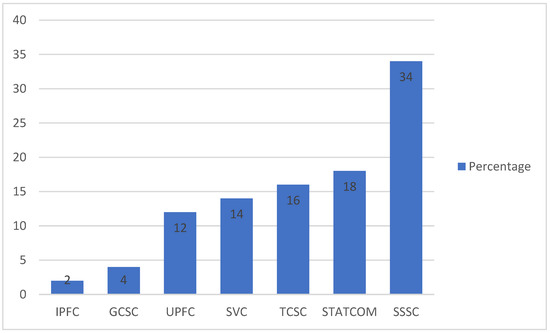
Figure 17.
FACTS utilized damping controllers in a renewable grid-integrated system based on publications.
Figure 17 Shows the distribution of FACTS-utilized damping controllers in a renewable grid-integrated system from the year 2014 to 2022.
As shown in the figure, SSSC usage is approximately 34% and has the highest application as a series FACTS-based damping controller. STATCOM recorded 18% usage, which represents the highest application as a shunt FACTS-based damping controller. Figure 18 shows the functional diagram of SSSC, STATCOM, and IPFC.
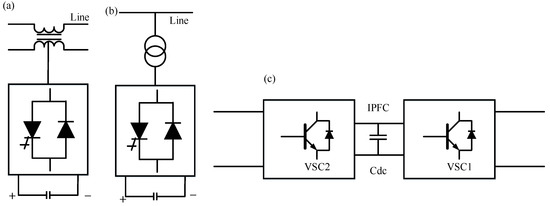
Figure 18.
(a) SSSC, (b) STATCOM, (c) IPFC [44].
Coordination Control Damping
PSS and FACTS are combined to dampen various electromechanical oscillation modes effectively. However, this combination of damping controllers needs precision; otherwise, the entire power system stability may be negatively affected [117,118]. The collaborative design of PSS and FACTS has been the subject of numerous studies [119,120,121,122,123]. Designing a reliable damping scheme to address oscillations is the goal of damping controller coordination schemes.
Artificial Intelligence
The damping strategy for artificial intelligence (AI) has been the subject of recent research [124,125,126,127]. These intelligent controllers can learn from the system where there are deployed and adapt to improve the system’s overall performance in damping oscillations. A neuro-fuzzy controller (NFC) in form of a fuzzy logic controller (FLC) and artificial neural network (ANN) was employed in [35] to replace PSS, and it offered superior features to the traditional PSS and FACTS damping controllers. The learning and adaptation properties of FLC and ANN were combined to create the NFC structure. The simplicity of this controller structure and model-free design is its primary feature. A Sugeno type two input NFC structure is shown in Figure 19 and its coupling to an ST1A excitation system is shown in Figure 20.
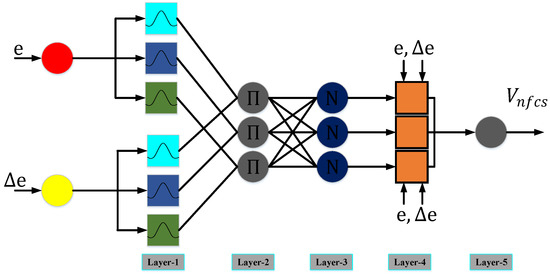
Figure 19.
Sugeno type two input NFC structure [44].
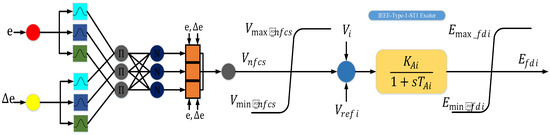
Figure 20.
Two-input Sugeno-type NFC structure connected to STIA IEEE excitation system [44].
3.5. Damping Controllers
The oscillation damping controller is the major component in the damping schemes of an integrated renewable system. The damping controller decides the switching control in the damping scheme. In the previous literature, researchers have proposed different types of damping controllers. FACTS- and PSS-based damping schemes were proposed [128] and [129], respectively, while neural networks and fuzzy controllers were discussed in [130,131].
3.5.1. Trimming and Linearization of a Nonlinear Power System
Though the power system is nonlinear, the design of the damping controller follows the linear control theory. Thus, the trimming and linearization of the power system are reviewed by modeling them using ordinary differential equations (ODE) [132]. Nonlinear ODE determines the dynamics of a power system as discussed in Equations (20)–(25) [131]:
where and = nonlinear parameter functions;
- = output vector;
- = the input vector;
- = state vector, represented as:
The system states at equilibrium and the input vectors are as follows:
The small deviation following a perturbation from the system equilibrium and expanding using Taylor’s series around the equilibrium and input vectors, the final linearized state space equations can is:
- = state matrix;
- = input matrix;
- = output matrix;
- = feedback matrix.
A linear time-invariant system state is obtained by forming nonlinear ordinary differential equations about a set point. Linearization is carried out to check local stability and understand power system dynamics and speed up power system simulation. Figure 21 presents the procedure of trimming and linearization. Moreover, there are toolboxes in MATLAB®/SIMULINK® for linear controller design, for example the power system toolbox (PST) developed by Rogers [132], PSAT [133], MatDyn [134], Matpower, and MatSim [47]. Researchers use these toolboxes in damping controller design to analyze power system oscillation.
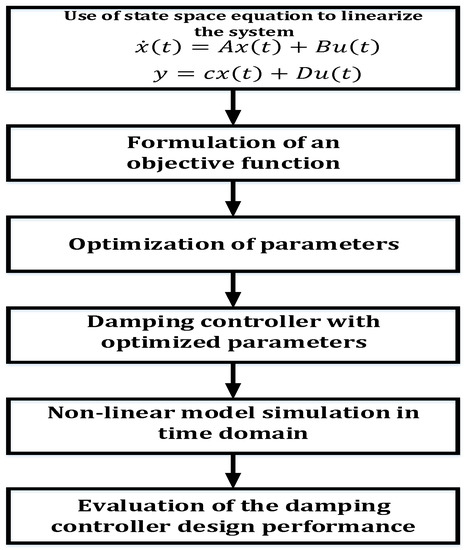
Figure 21.
Procedure of trimming and linearization [28].
3.5.2. Eigenvalues
In linearized systems, the locations of eigenvalues on the s-plane, are used to evaluate the stability of a system and are represented in Equation (26):
where represents the real part and represents the imaginary part of eigenvalues.
The above equation is the state matrix A from the linearized model.
Where can represent the eigenvalues of a linearized system, i.e., the state matrix (A). In MATLAB®, a function calculates the eigenvalues. Figure 22 shows stability criteria for eigenvalues are represented in the s-plane
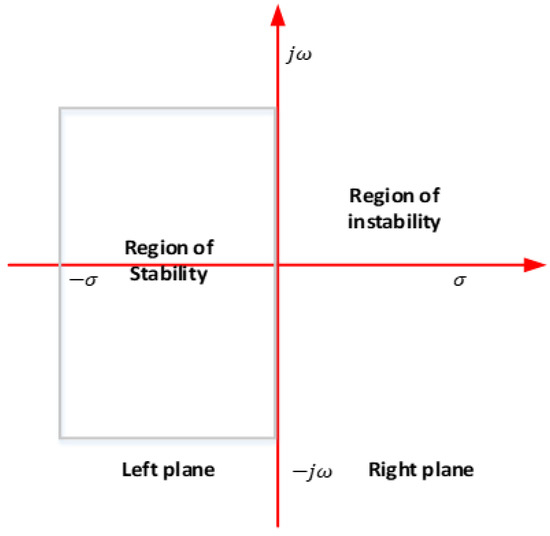
Figure 22.
Stability criteria for eigenvalues are represented in the s-plane [102].
If all the eigenvalues are on the left side of the s-plane, then the system is deemed stable. In contrast, if there is any eigenvalue on the right side of the s-plane, then the system is not stable. Shifting the eigenvalues to the left side of the s-plane is the major function of optimization algorithms in the design of damping controllers.
3.6. Review of Objective Function Formulation
Robust damping controller design involves the application of objective functions with different formulations. In the integral time error-based function the objective function is to minimize the rotor speed deviation error (Δω) using the various integral error functions. The index value should either be a positive or zero value and the system with the lowest index should be regarded as the best.
In eigenvalue analysis, shifting the eigenvalues to the left side of the s-plane is the main focus of the objective function, singular objective function and multiple objective functions are the two major classifications used in defining the objective function. Thus, these objective functions are represented by damping factors and ratios which are the real () and imaginary () parts of eigenvalues. Equations (27) and (28) show the mathematical expression for the damping factor and damping ratio, respectively.
Figure 23a–c show the objective function definition approaches in terms of damping ratio and factor.
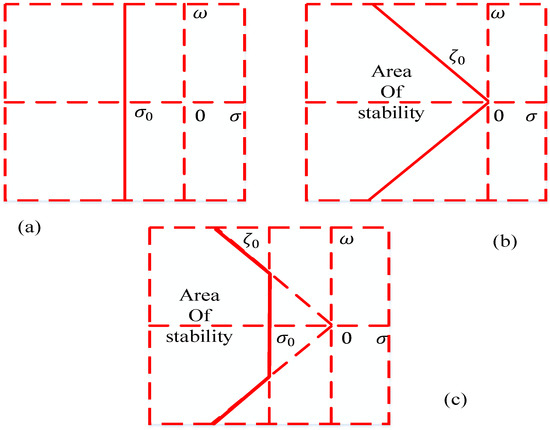
Figure 23.
Approaches for objective function formulation: (a) formulation based on damping factor, (b) formulation based on damping ratio, (c) formulation based on both damping factor and damping ratio (D-shape) [28].
3.6.1. Singular Objective Function
When defining a singular objective function, the target of the mathematical formulation is to achieve either minimization or maximization of the damping ratio or damping factor in various oscillation modes [135,136,137]. The damping ratio determines the oscillation decay rate and thus is maximized for faster oscillation attenuation through optimization of the controller parameters.
3.6.2. Multiple Objective Function
Multiple objective function combines the damping factor and ratio in its definition. Oscillation settling time is increased through damping ratio maximization while reduction in oscillation overshoot is achieved via the damping factor. Thus, combining both in the definition is termed multiple objective function. This combination forms a D-shaped stability area, and the goal of this multiple objective function is to relocate the eigenvalues to the D-shape area. Mathematical details of singular and multiple objective function definition approaches are presented in Table 3.

Table 3.
Objective function definition approaches.
3.7. Optimization Techniques for Damping Controller Design
Over the years, many optimization algorithms have been evaluated and adopted in the design of damping controllers [138,139]. These algorithms may be grouped into (i) traditional, (ii) meta-heuristic (heuristic), (iii) or a combination of two or more techniques. In this regard, researchers studying electrical power systems are increasingly embracing the application of heuristic and meta-heuristic techniques in damping controller design.
Natural behaviors serve as the basis for heuristic algorithms. The techniques employ a stochastic method to find the best solutions based on a defined objective function. Comparatively, meta-heuristic algorithms also mirror natural behaviors and are formulated by further enhancing heuristic algorithms for more effective performance. In diverse research efforts, these strategies have been categorized in a variety of ways. Figure 24 represents shows a broad classification of some meta-heuristic algorithms.
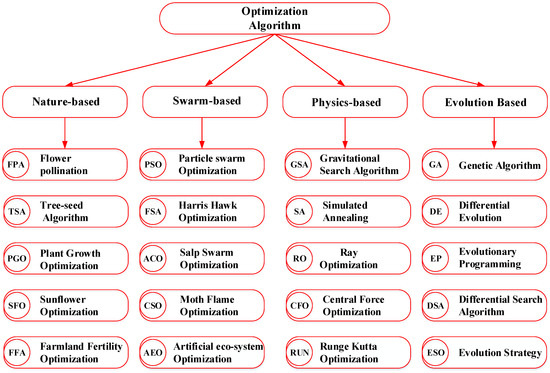
Figure 24.
Broad classification of some meta-heuristic algorithms.
Nevertheless, some of the prevalently explored meta-heuristic algorithms in powers system stability studies are discussed in this sub-section.
3.7.1. Particle Swarm Optimization Meta-Heuristic Algorithm
This is a swarm-based meta-heuristic technique that imitates the behaviors of swarming organisms such as fish or birds. This optimization technique mimics the fish schooling and bird flocking behavior and has been used in damping controller design [105,140,141]. Nevertheless, one of the major challenges with particle swarm optimization (PSO) is its stagnation in the local minima [142]. An improved PSO is presented in [142,143,144] for tackling the local minima trials.
3.7.2. Genetic Algorithms
Genetic Algorithm (GA) is an evolutionary-based meta-heuristic algorithm that imitates the evolution of living things in an ecosystem. This technique explores genetic mutations and crossover. GA is explored in [145] to enhance oscillation damping by tuning the PSS and STATCOM parameters. However, this optimization approach has some drawbacks, including performance degradation and pre-convergence, especially when used to solve multi-dimensional engineering problems.
3.7.3. Tabu Search Algorithm (TS)
Tabu search algorithm (TSA) employs a local search approach by exploring different areas in the search space. It uses artificial intelligence via adaptive memory and iterative methods to solve the given problem. In [146], this algorithm is used for tuning PSS controllers in a three-machine nine-bus system. For effective damping, all parameters must be precisely tuned. Which can be quite large in an integrated power system. The efficiency of TS is low for global search as compared with other algorithms [147].
3.7.4. Salp Swarm Algorithm
This is a population-based metaheuristic optimization method that is based on the behavioral feature of marine organisms. The behavior of the Salp Swarm Algorithm (SSA) can be convincible by computing it with the salp chain searching for optimal food sources, i.e., the target of this swarm is a food source in the search space [148]. A comparative effect of SSA tuning of SVC and TCSC in damping oscillations was performed in [149]. The main limitation of SSA is the no-free launch theorem which states that no optimization algorithm can solve all optimization problems.
3.7.5. Moth-Flame Algorithm
This is a population-based metaheuristic algorithm. Its optimization procedure begins by creating moths at random within the solution space, then calculating each moth’s position and marking the ideal place with a flame. The moth position is then updated and the process is repeated until pre-set termination criteria are met [150]. In [151], moth-flame algorithm (MFO) is applied to three controllers, PID, PSS, and TCSC, for damping oscillation. However, this algorithm suffers from a slow speed convergence which leads to being stuck at local optima [150]. Using a new selection scheme as proposed in [152] provides an enhanced version of this population-based metaheuristic algorithm.
3.7.6. Sine Cosine Algorithm
Sine cosine algorithm (SCA) is a population-based optimization algorithm introduced for solving several optimization problems. Using a mathematical model based on sine and cosine functions, it generates a variety of starting random solutions and moves them in the direction of the optimal solution [147]. Optimal tuning of PSS was carried out in [153] using the Sine cosine algorithm (SCA). However, its low ability to handle the complexities of multi-modal search problems is its major limitation [154]. In [155], a hybrid sine cosine algorithm was proposed to address the aforementioned limitation.
3.7.7. Harris Hawk Algorithm
Harris hawk algorithm (HHA) is a swarm-based metaheuristic optimization. It mimics the behavior of a hawk’s team in a collaborative hunting strategy when looking for prey. Verily, it is a very recent algorithm that is yet to be fully explored particularly in large cross-modal optimization [156]. The singular objective problem is defined and the algorithm was applied in [156]. In [157], it was applied for the optimization of PSS parameters.
3.7.8. Other Algorithms
A kidney-inspired algorithm which is a meta-heuristic algorithm was used in [158] for PSS design. In [101], the farmland fertility algorithm was used for PID–PSS controller design. Presently, there are extensive applications of various metaheuristic algorithms in designing damping controllers. Some researchers have gone further to apply hybrid (two or more) algorithms or improve existing algorithms [43] for robust damping controller design.
3.7.9. Hybrid Algorithms
The major aim of a hybrid algorithm is to achieve robust design, different algorithms have some advantages and disadvantages over others. Therefore, combining two algorithms can improve the damping controller performance. Harris hawk and particle swarm optimization (HHO–PSO) was applied to PSS and STATCOM in [159] to damp power system oscillations. The combination of algorithms may successfully address some limitations. However, it increases the computational complexities of the optimization process.
4. Discussion
4.1. Controller Design limitations in Existing Methods
Various research has demonstrated appropriate damping controller design by combining different definitions of the objective function and applying optimization algorithms. However, it is observed that there are notable limitations in damping controller design. Meta-heuristic algorithm convergence curve is a critical factor used to validate the performance of a designed damping controller. Different researchers validate their designed damping controller by comparing it with other meta-heuristic techniques using the convergence curves [160] and conclude that their designed damping controller is more efficient based on the comparison. However, the meta-heuristic technique is a randomization process. Therefore, this means of validation is not sufficient for justifying the solution convergence. Incorporating statistical analysis can help make this validation a robust one.
Various researchers have ignored the time constant parameters T2 and T4 in optimizing PSS to reduce design complexities [161] and improve the optimization algorithm’s efficiency by reducing the parameters for optimization. However, it is only when all parameters (K, T1, T2, T3, and T4) are optimized that the effectiveness of the designed damping controller can be justified.
4.2. Challenges and Trending Issues
To date, various types of research publications on efficient damping controller design in a renewable energy-integrated system are in place. From the various publications, the following challenges are notable:
4.2.1. Performance and Design of Damping Controller
The proper damping controller design is a big issue in the power system. For an integrated renewable energy system, the design of a damping controller and the optimization process is even more complex [162,163,164]. Therefore, optimal designs are complicated, limiting the damping controller performance.
4.2.2. Objective Function
Over the years, research has been carried out in designing damping controllers [165,166,167]. In these studies, [167,168,169] different methods to define the objective function are considered. Defining the objective function is an integral part of designing the damping controller. Therefore, improper definition may result in poor damping performance in the designed damping controller. Prior to this review, no research has compared the performances of different objective function formulations in a renewable grid-integrated system. Thus, it is essential to determine the best method to define an objective function for effective design in a renewable-integrated grid power system.
4.2.3. Implementation of the Meta-Heuristic Algorithm
Meta-heuristic algorithm application is one of the widely accepted approaches to designing a damping controller, meta-heuristic algorithms determine its optimum solution using a stochastic approach to problem-solving. Researchers have adopted meta-heuristic algorithms for designing different damping controller schemes [121,169,170,171]. However, evaluating the variation in design performance in a renewable-integrated grid system is essential with increased solar and wind energy penetration.
4.3. Future Outlook
The effect of high penetration of Wind–PV into electrical power systems on overall system stability requires more extensive analysis. The design of the damping controller should be further enhanced as it is a constraint-based multimodal optimization problem. The future outlook of power system oscillation damping will be shaped by coordinated damping schemes and a thorough exploration of artificial intelligence-based optimization approaches is required.
4.4. Conclusions and Recommendations
Power system oscillation is a problem that leads to blackouts and the collapse of a renewable-integrated power grid system. Furthermore, it limits power transfer capacity and causes safety issues in the system. Hence it is necessary to have an adequate automated damping controller in the system to mitigate this problem. The design of damping controllers involves two basic steps; objective function definition, and application of optimization algorithms which are applied to the defined objective function. This is carried out to achieve a robust damping controller design for power system stability and to enhance power transfer capacity. Nevertheless, designing a damping controller for a RES-integrated multi-machine system is a cross-modal optimization problem that sometimes limits optimal design using conventional optimization algorithms.
This review tends to solve this problem by presenting renewable energy sources and their integration into the multi-machine power system. The synchronous machine model, which represents the machines (generators) in the power system is discussed, then solar, wind, and hybrid (solar, wind, and hydro) renewable energy sources are presented. For optimum power tracking in solar and wind renewable energy due to its intermittent nature, MPPT is discussed. Moreover, power electronic converters that convert direct current to alternating current are presented, followed by grid synchronizers in form of the phase-lock loop (PLL). In an integrated system, power system oscillation is a major concern as it affects the stability of the entire power system; therefore, the basic concepts of power system oscillation are introduced. To mitigate the power system oscillation, damping schemes and various damping controllers which are incorporated into the system are evaluated. After a thorough evaluation, it is noted that SSSC and STATCOM damping controllers are the regularly employed FACTS damping controllers in the design of power oscillation damper in a RES-integrated system. It is also observed that lead–lag type controllers such as lead–lag PSS are often preferred in PSS-based damping design owing to their adequate performance. The review also introduced the artificial intelligence damping scheme and virtual synchronous generator damping scheme (VSG), which researchers are exploring for robust damping controller design. The linearization of nonlinear systems and the recent toolbox for power system dynamic oscillation analysis in MATLAB® in form of Matsim and Matpower are noted. The eigenvalue approach for defining the objective function is also presented. The discussion concludes with a comparative study of different formulation methods. Furthermore, this review discussed various optimization algorithms employed in the damping controller design. Lastly, the limitations of existing damping controller design methods are discussed.
Conclusively, challenges and current issues are noted. Amidst these issues, suggestions for effective design of damping controllers as renewable energy penetration keeps increasing are as follows:
- ▪
- Artificial intelligent damping type of controller scheme needs to be further explored as there are signs of improved oscillation damping compared with PSS and FACTS;
- ▪
- The objective function definition is a critical part of damping controller design and thus, should be appropriately defined;
- ▪
- Researchers should apply statistical analysis together with the single convergence curve for proper validation in optimizing the parameters of a proposed damping controller which will provide sufficient validation of the convergence curve.
Author Contributions
Conceptualization, A.S.; V.V. and N.I.A.W.; methodology, software, valid ation, formal analysis, investigation, data curation, and writing—original draft preparation, B.Y.K.; T.E.O. and M.D. Reviewing and editing, A.S.; V.V.; B.Y.K.; T.E.O.; M.D. and N.I.A.W., visualization, A.S.; B.Y.K. and T.E.O., supervision, A.S., V.V. and N.I.A.W. All authors have read and agreed to the published version of the manuscript.
Funding
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was supported by Advanced Lightning and Power Energy System, Universiti Putra Malaysia under UPM Grant No. 9630000.
Data Availability Statement
All data are contained within this article.
Conflicts of Interest
The author(s) declare no potential conflict of interest with respect to the research, authorship, and/or publication of this article.
References
- Singh, B.; Murshid, S. A Grid-Interactive Permanent-Magnet Synchronous Motor-Driven Solar Water-Pumping System. IEEE Trans. Ind. Appl. 2018, 54, 5549–5561. [Google Scholar] [CrossRef]
- Camacho Ballesta, J.A.; da Silva Almeida, L.; Rodríguez, M. An analysis of the main driving factors of renewable energy consumption in the European Union. Environ. Sci. Pollut. Res. 2022, 29, 35110–35123. [Google Scholar] [CrossRef]
- Liang, X.; Karim, C.A.-B. Harmonics and Mitigation Techniques Through Advanced Control in Grid-Connected Renewable Energy Sources: A Review. IEEE Trans. Ind. Appl. 2018, 54, 3100–3111. [Google Scholar] [CrossRef]
- Shafiullah, M.; Ahmed, S.D.; Al-Sulaiman, F.A. Grid Integration Challenges and Solution Strategies for Solar PV Systems: A Review. IEEE Access 2022, 10, 52233–52257. [Google Scholar] [CrossRef]
- Zeb, K.; Uddin, W.; Khan, M.A.; Ali, Z.; Ali, M.U.; Christofides, N.; Kim, H.J. A comprehensive review on inverter topologies and control strategies for grid connected photovoltaic system. Renew. Sustain. Energy Rev. 2018, 94, 1120–1141. [Google Scholar] [CrossRef]
- Collados-Rodriguez, C.; Cheah-Mane, M.; Prieto-Araujo, E.; Gomis-Bellmunt, O. Stability and operation limits of power systems with high penetration of power electronics. Int. J. Electr. Power Energy Syst. 2022, 138, 107728. [Google Scholar] [CrossRef]
- Shah, R.; Mithulananthan, N.; Bansal, R.C.; Ramachandaramurthy, V.K. A review of key power system stability challenges for large-scale PV integration. Renew. Sustain. Energy Rev. 2015, 41, 1423–1436. [Google Scholar] [CrossRef]
- Ram, J.P.; Manghani, H.; Pillai, D.S.; Babu, T.S.; Miyatake, M.; Rajasekar, N. Analysis on solar PV emulators: A review. Renew. Sustain. Energy Rev. 2018, 81, 149–160. [Google Scholar] [CrossRef]
- Campanhol, L.B.G.; da Silva, S.A.O.; de Oliveira, A.A.; Bacon, V.D. Power Flow and Stability Analyses of a Multifunctional Distributed Generation System Integrating a Photovoltaic System With Unified Power Quality Conditioner. IEEE Trans. Power Electron. 2019, 34, 6241–6256. [Google Scholar] [CrossRef]
- Islam, M.R.; Mahfuz-Ur-Rahman, A.M.; Muttaqi, K.M.; Sutanto, D. State-of-the-Art of the Medium-Voltage Power Converter Technologies for Grid Integration of Solar Photovoltaic Power Plants. IEEE Trans. Energy Convers. 2019, 34, 372–384. [Google Scholar] [CrossRef]
- Sangwongwanich, A.; Blaabjerg, F. Mitigation of interharmonics in PV systems with maximum power point tracking modification. IEEE Trans. power Electron. 2019, 34, 8279–8282. [Google Scholar] [CrossRef]
- Kermadi, M.; Salam, Z.; Ahmed, J.; Berkouk, E.M. An effective hybrid maximum power point tracker of photovoltaic arrays for complex partial shading conditions. IEEE Trans. Ind. Electron. 2018, 66, 6990–7000. [Google Scholar] [CrossRef]
- Pervez, I.; Shams, I.; Mekhilef, S.; Sarwar, A.; Tariq, M.; Alamri, B. Most valuable player algorithm based maximum power point tracking for a partially shaded PV generation system. IEEE Trans. Sustain. Energy 2021, 12, 1876–1890. [Google Scholar] [CrossRef]
- Kermadi, M.; Salam, Z.; Ahmed, J.; Berkouk, E.M. A high-performance global maximum power point tracker of PV system for rapidly changing partial shading conditions. IEEE Trans. Ind. Electron. 2020, 68, 2236–2245. [Google Scholar] [CrossRef]
- Peng, X.; Liu, Z.; Jiang, D. A review of multiphase energy conversion in wind power generation. Renew. Sustain. Energy Rev. 2021, 147, 111172. [Google Scholar] [CrossRef]
- Rezamand, M.; Kordestani, M.; Carriveau, R.; Ting, D.S.-K.; Orchard, M.E.; Saif, M. Critical Wind Turbine Components Prognostics: A Comprehensive Review. IEEE Trans. Instrum. Meas. 2020, 69, 9306–9328. [Google Scholar] [CrossRef]
- Ahmed, S.D.; Al-Ismail, F.S.M.; Shafiullah, M.; Al-Sulaiman, F.A.; El-Amin, I.M. Grid Integration Challenges of Wind Energy: A Review. IEEE Access 2020, 8, 10857–10878. [Google Scholar] [CrossRef]
- Zhang, C.; Cai, X.; Molinas, M.; Rygg, A. On the impedance modeling and equivalence of AC/DC-side stability analysis of a grid-tied type-IV wind turbine system. IEEE Trans. Energy Convers. 2018, 34, 1000–1009. [Google Scholar] [CrossRef]
- Zou, W.; Li, C.; Chen, P. An inter type-2 FCR algorithm based T–S fuzzy model for short-term wind power interval prediction. IEEE Trans. Ind. Inform. 2019, 15, 4934–4943. [Google Scholar] [CrossRef]
- Xie, X.; Liu, W.; Liu, H.; Du, Y.; Li, Y. A system-wide protection against unstable SSCI in series-compensated wind power systems. IEEE Trans. Power Deliv. 2018, 33, 3095–3104. [Google Scholar] [CrossRef]
- Bahrami, S.; Amini, M.H.; Shafie-Khah, M.; Catalao, J.P.S. A decentralized renewable generation management and demand response in power distribution networks. IEEE Trans. Sustain. Energy 2018, 9, 1783–1797. [Google Scholar] [CrossRef]
- Tang, W.; Hu, J.; Chang, Y.; Liu, F. Modeling of DFIG-Based Wind Turbine for Power System Transient Response Analysis in Rotor Speed Control Timescale. IEEE Trans. Power Syst. 2018, 33, 6795–6805. [Google Scholar] [CrossRef]
- Du, W.; Dong, W.; Wang, H.F. Small-Signal Stability Limit of a Grid-Connected PMSG Wind Farm Dominated by the Dynamics of PLLs. IEEE Trans. Power Syst. 2020, 35, 2093–2107. [Google Scholar] [CrossRef]
- Guo, G.; Song, Q.; Zhao, B.; Rao, H.; Xu, S.; Zhu, Z.; Liu, W. Series-Connected-Based Offshore Wind Farms With Full-Bridge Modular Multilevel Converter as Grid- and Generator-side Converters. IEEE Trans. Ind. Electron. 2020, 67, 2798–2809. [Google Scholar] [CrossRef]
- Chen, J.; Liu, M.; O’Loughlin, C.; Milano, F.; O’Donnell, T. Modelling, simulation and hardware-in-the-loop validation of virtual synchronous generator control in low inertia power system. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; pp. 1–7. [Google Scholar]
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. An Overview of Assessment Methods for Synchronization Stability of Grid-Connected Converters Under Severe Symmetrical Grid Faults. IEEE Trans. Power Electron. 2019, 34, 9655–9670. [Google Scholar] [CrossRef]
- Darabian, M.; Bagheri, A.; Behzadpoor, S. A UPFC-based robust damping controller for optimal use of renewable energy sources in modern renewable integrated power systems. IET Gener. Transm. Distrib. 2022, 16, 4115–4131. [Google Scholar] [CrossRef]
- Hannan, M.A.; Islam, N.N.; Mohamed, A.; Lipu, M.S.H.; Ker, P.J.; Rashid, M.M.; Shareef, H. Artificial intelligent based damping controller optimization for the multi-machine power system: A review. IEEE Access 2018, 6, 39574–39594. [Google Scholar] [CrossRef]
- Martins, L.F.B.; de Araujo, P.B.; de Vargas Fortes, E.; Macedo, L.H. Design of the PI–UPFC–POD and PSS Damping Controllers Using an Artificial Bee Colony Algorithm. J. Control. Autom. Electr. Syst. 2017, 28, 762–773. [Google Scholar] [CrossRef]
- Sabo, A.; Wahab, N.I.A.; Othman, M.L.; Jaffar, M.Z.A.M.; Beiranvand, H. Farmland fertility optimization for designing of interconnected multi-machine power system stabilizer. Appl. Model. Simul. 2020, 4, 183–201. [Google Scholar]
- Tu, G.; Li, Y.; Xiang, J.; Ma, J. Distributed power system stabiliser for multimachine power systems. IET Gener. Transm. Distrib. 2019, 13, 603–612. [Google Scholar] [CrossRef]
- Hassan, M.; Abido, M.A.; Aliyu, A. Design of Power System Stabilizer Using Phase Based Objective Function and Heuristic Algorithm. In Proceedings of the 2019 8th International Conference on Modeling Simulation and Applied Optimization (ICMSAO), Manama, Bahrain, 15–17 April 2019; pp. 1–6. [Google Scholar]
- Pathan, M.I.H.; Rana, M.J.; Shahriar, M.S.; Shafiullah, M.; Zahir, M.H.; Ali, A. Real-time LFO damping enhancement in electric networks employing PSO optimized ANFIS. Inventions 2020, 5, 61. [Google Scholar] [CrossRef]
- Sabo, A.; Wahab, N.I.A.; Othman, M.L.; Jaffar, M.Z.A.B.M.; Acikgoz, H.; Nafisi, H.; Shahinzadeh, H. Artificial Intelligence-Based Power System Stabilizers for Frequency Stability Enhancement in Multi-machine Power Systems. IEEE Access 2021, 9, 166095–166116. [Google Scholar] [CrossRef]
- Sabo, A.; Wahab, N.I.; Othman, M.L.; Mohd Jaffar, M.Z.; Acikgoz, H.; Beiranvand, H. Application of Neuro-Fuzzy Controller to Replace SMIB and Interconnected Multi-Machine Power System Stabilizers. Sustainability 2020, 12, 9591. [Google Scholar] [CrossRef]
- Sambariya, D.K.; Prasad, R. A novel fuzzy rule matrix design for fuzzy logic-based power system stabilizer. Electr. Power Compon. Syst. 2017, 45, 34–48. [Google Scholar] [CrossRef]
- Khawaja, A.W.; Kamari, N.A.M.; Zainuri, M.A.A.M. Design of a damping controller using the sca optimization technique for the improvement of small signal stability of a single machine connected to an infinite bus system. Energies 2021, 14, 2996. [Google Scholar] [CrossRef]
- Bento, M.E.C. Design of a Resilient Wide-Area Damping Controller Using African Vultures Optimization Algorithm. In Proceedings of the 2021 31st Australasian Universities Power Engineering Conference (AUPEC), Virtual, 26–30 September 2021. [Google Scholar] [CrossRef]
- Maity, S.; Ramya, R. A comprehensive review of damping of low frequency oscillations in power systems. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 133–138. [Google Scholar]
- Zhang, C.; Ke, D.; Sun, Y.; Chung, C.Y.; Xu, J.; Shen, F. Coordinated Supplementary Damping Control of DFIG and PSS to Suppress Inter-Area Oscillations with Optimally Controlled Plant Dynamics. IEEE Trans. Sustain. Energy 2018, 9, 780–791. [Google Scholar] [CrossRef]
- Nahak, N.; Mallick, R.K. Investigation and damping<? show [AQ ID= Q1]?> of low-frequency oscillations of stochastic solar penetrated power system by optimal dual UPFC. IET Renew. Power Gener. 2019, 13, 376–388. [Google Scholar]
- El-Dabah, M.A.; Kamel, S.; Khamies, M.; Shahinzadeh, H.; Gharehpetian, G.B. Artificial Gorilla Troops Optimizer for Optimum Tuning of TID Based Power System Stabilizer. In Proceedings of the 2022 9th Iranian Joint Congress on Fuzzy and Intelligent Systems (CFIS), Bam, Iran, 2–4 March 2022; pp. 1–5. [Google Scholar]
- Davut, I.Z.C.I. A novel modified arithmetic optimization algorithm for power system stabilizer design. Sigma J. Eng. Nat. Sci. 2022, 40, 529–541. [Google Scholar]
- Sabo, A.; Abdul Wahab, N.I.; Othman, M.L.; Mohd Jaffar, M.Z.A.; Beiranvand, H.; Acikgoz, H. Application of a neuro-fuzzy controller for single machine infinite bus power system to damp low-frequency oscillations. Trans. Inst. Meas. Control 2021, 43, 3633–3646. [Google Scholar] [CrossRef]
- El-Kareem, A.; Hesham, A.; Abd Elhameed, M.; Elkholy, M.M. Effective damping of local low frequency oscillations in power systems integrated with bulk PV generation. Prot. Control Mod. Power Syst. 2021, 6, 1–13. [Google Scholar] [CrossRef]
- Nogami, S.; Yokoyama, A.; Amano, H.; Daibu, T. Virtual synchronous generator model based control of PV for power system stability improvement in a large-scale power system with a massive integration of PVs. J. Int. Counc. Electr. Eng. 2018, 8, 112–118. [Google Scholar] [CrossRef]
- Beiranvand, H.; Rokrok, E.; Shakarami, M.R.; Kumar, A.; Gopalakrishna, S.; Mohanty, S. MatSim: A Matpower and Simulink based tool for power system dynamics course education. In Proceedings of the 31th Power System Conference, Tehran, Iran, 24–26 October 2016; pp. 1–6. [Google Scholar]
- Naves, A.X.; Barreneche, C.; Fernández, A.I.; Cabeza, L.F.; Haddad, A.N.; Boer, D. Life cycle costing as a bottom line for the life cycle sustainability assessment in the solar energy sector: A review. Sol. Energy 2019, 192, 238–262. [Google Scholar] [CrossRef]
- Molaei, M.J. The optical properties and solar energy conversion applications of carbon quantum dots: A review. Sol. Energy 2020, 196, 549–566. [Google Scholar] [CrossRef]
- Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M.D. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar] [CrossRef]
- Koutroulis, E.; Yang, Y.; Blaabjerg, F. Co-Design of the PV Array and DC/AC Inverter for Maximizing the Energy Production in Grid-Connected Applications. IEEE Trans. Energy Convers. 2019, 34, 509–519. [Google Scholar] [CrossRef]
- Pazikadin, A.R.; Rifai, D.; Ali, K.; Malik, M.Z.; Abdalla, A.N.; Faraj, M.A. Solar irradiance measurement instrumentation and power solar generation forecasting based on Artificial Neural Networks (ANN): A review of five years research trend. Sci. Total Environ. 2020, 715, 136848. [Google Scholar] [CrossRef]
- Li, G.; Xie, S.; Wang, B.; Xin, J.; Li, Y.; Du, S. Photovoltaic power forecasting with a hybrid deep learning approach. IEEE Access 2020, 8, 175871–175880. [Google Scholar] [CrossRef]
- Zhen, Z.; Liu, J.; Zhang, Z.; Wang, F.; Chai, H.; Yu, Y.; Lu, X.; Wang, T.; Lin, Y. Deep learning based surface irradiance mapping model for solar PV power forecasting using sky image. IEEE Trans. Ind. Appl. 2020, 56, 3385–3396. [Google Scholar] [CrossRef]
- REN21 Renewables Now. Renewables in Cities 2021 Global Status Report. REN21 Secr. Paris Fr. 2021. Available online: https://www.ren21.net/reports/global-status-report/ (accessed on 24 October 2022).
- Muisyo, I.N.; Muriithi, C.M.; Kamau, S.I. Enhancing low voltage ride through capability of grid connected DFIG based WECS using WCA-PSO tuned STATCOM controller. Heliyon 2022, 8, e09999. [Google Scholar] [CrossRef] [PubMed]
- Bhukya, J.; Mahajan, V. Optimization of damping controller for PSS and SSSC to improve stability of interconnected system with DFIG based wind farm. Int. J. Electr. Power Energy Syst. 2019, 108, 314–335. [Google Scholar] [CrossRef]
- Ali, M.A.S.; Mehmood, K.K.; Baloch, S.; Kim, C.-H. Modified rotor-side converter control design for improving the LVRT capability of a DFIG-based WECS. Electr. Power Syst. Res. 2020, 186, 106403. [Google Scholar] [CrossRef]
- Alsakati, A.A.; Vaithilingam, C.A.; Alnasseir, J.; Jagadeeshwaran, A. Simplex search method driven design for transient stability enhancement in wind energy integrated power system using multi-band PSS4C. IEEE Access 2021, 9, 83913–83928. [Google Scholar] [CrossRef]
- Ang, T.-Z.; Salem, M.; Kamarol, M.; Das, H.S.; Nazari, M.A.; Prabaharan, N. A comprehensive study of renewable energy sources: Classifications, challenges and suggestions. Energy Strateg. Rev. 2022, 43, 100939. [Google Scholar] [CrossRef]
- Jin, J.X.; Yang, R.H.; Zhang, R.T.; Fan, Y.J.; Xie, Q.; Chen, X.Y. Combined low voltage ride through and power smoothing control for DFIG/PMSG hybrid wind energy conversion system employing a SMES-based AC-DC unified power quality conditioner. Int. J. Electr. Power Energy Syst. 2021, 128, 106733. [Google Scholar] [CrossRef]
- Mwaniki, J.; Lin, H.; Dai, Z. A Condensed Introduction to the Doubly Fed Induction Generator Wind Energy Conversion Systems. J. Eng. 2017, 2017, 2918281. [Google Scholar] [CrossRef]
- Bonfiglio, A.; Delfino, F.; Gonzalez-Longatt, F.; Procopio, R. Steady-state assessments of PMSGs in wind generating units. Int. J. Electr. Power Energy Syst. 2017, 90, 87–93. [Google Scholar] [CrossRef]
- Sadhana, S.G.; Ashok, S.; Kumaravel, S. Small signal stability analysis of grid connected renewable energy resources with the effect of uncertain wind power penetration. Energy Procedia 2017, 117, 769–776. [Google Scholar] [CrossRef]
- Bezerra, M.A.A.; Oliveira, J.L.W.; Praça, P.P.; Oliveira, D.S.; Barreto, L.H.S.C.; de Almeida, B.R. Isolated AC-DC Interleaved Converter for MVDC Collection Grid in HVDC Offshore Wind Farm. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 1926–1933. [Google Scholar]
- Li, Z.; Song, Q.; An, F.; Zhao, B.; Yu, Z.; Zeng, R. Review on DC transmission systems for integrating large-scale offshore wind farms. Energy Convers. Econ. 2021, 2, 1–14. [Google Scholar] [CrossRef]
- Abeynayake, G.; Li, G.; Liang, J.; Cutululis, N.A. A review on MVdc collection systems for high-power offshore wind farms. In Proceedings of the 2019 14th Conference on Industrial and Information Systems (ICIIS), Kandy, Sri Lanka, 18–20 December 2019; pp. 407–412. [Google Scholar]
- Islam, M.R.; Rahman, M.A.; Muttaqi, K.M.; Sutanto, D. A new magnetic-linked converter for grid integration of offshore wind turbines through MVDC transmission. IEEE Trans. Appl. Supercond. 2019, 29, 1–5. [Google Scholar] [CrossRef]
- Kou, P.; Liang, D.; Wu, Z.; Ze, Q.; Gao, L. Frequency support from a dc-grid offshore wind farm connected through an hvdc link: A communication-free approach. IEEE Trans. Energy Convers. 2018, 33, 1297–1310. [Google Scholar] [CrossRef]
- Kumar, K.; Babu, N.R.; Prabhu, K.R. Design and analysis of RBFN-based single MPPT controller for hybrid solar and wind energy system. IEEE access 2017, 5, 15308–15317. [Google Scholar] [CrossRef]
- Li, S.; Li, J. Output predictor-based active disturbance rejection control for a wind energy conversion system with PMSG. IEEE Access 2017, 5, 5205–5214. [Google Scholar] [CrossRef]
- Ram, J.P.; Rajasekar, N.; Miyatake, M. Design and overview of maximum power point tracking techniques in wind and solar photovoltaic systems: A review. Renew. Sustain. Energy Rev. 2017, 73, 1138–1159. [Google Scholar] [CrossRef]
- Tiwari, R.; Babu, N.R. Recent developments of control strategies for wind energy conversion system. Renew. Sustain. Energy Rev. 2016, 66, 268–285. [Google Scholar] [CrossRef]
- Abdul Basit, B.; Nguyen, A.T.; Ryu, S.; Park, H.; Jung, J. A state-of-the-art comprehensive review of modern control techniques for grid-connected wind turbines and photovoltaic arrays distributed generation systems. IET Renew. Power Gener. 2022, 16, 2191–2222. [Google Scholar] [CrossRef]
- Mao, M.; Cui, L.; Zhang, Q.; Guo, K.; Zhou, L.; Huang, H. Classification and summarization of solar photovoltaic MPPT techniques: A review based on traditional and intelligent control strategies. Energy Reports 2020, 6, 1312–1327. [Google Scholar] [CrossRef]
- Premkumar, M.; Sowmya, R. An effective maximum power point tracker for partially shaded solar photovoltaic systems. Energy Reports 2019, 5, 1445–1462. [Google Scholar] [CrossRef]
- Azar, A.T.; Serrano, F.E. Design and modeling of anti wind up PID controllers. In Complex System Modelling and Control through Intelligent Soft Computations; Springer: Cham, Switzerland, 2015; pp. 1–44. [Google Scholar]
- Ghoudelbourk, S.; Dib, D.; Omeiri, A.; Azar, A.T. MPPT control in wind energy conversion systems and the application of fractional control (PIα) in pitch wind turbine. Int. J. Model. Identif. Control 2016, 26, 140–151. [Google Scholar] [CrossRef]
- Fathabadi, H. Novel fast and high accuracy maximum power point tracking method for hybrid photovoltaic/fuel cell energy conversion systems. Renew. Energy 2017, 106, 232–242. [Google Scholar] [CrossRef]
- Huang, L.; Xin, H.; Li, Z.; Ju, P.; Yuan, H.; Lan, Z.; Wang, Z. Grid-synchronization stability analysis and loop shaping for PLL-based power converters with different reactive power control. IEEE Trans. Smart Grid 2019, 11, 501–516. [Google Scholar] [CrossRef]
- Du, W.; Chen, X.; Wang, H. Parameter tuning of the PLL to consider the effect on power system small-signal angular stability. IET Renew. Power Gener. 2018, 12, 1–8. [Google Scholar] [CrossRef]
- Verma, A.K.; Jarial, R.K.; Rao, U.M.; Roncero-Sánchez, P. A Robust Three-Phase Prefiltered Phase Locked-Loop for the Subcycle Estimation of Fundamental Parameters. IEEE Trans. Ind. Appl. 2021, 57, 6155–6166. [Google Scholar] [CrossRef]
- Golestan, S.; Guerrero, J.M.; Vasquez, J.C. A PLL-based controller for three-phase grid-connected power converters. IEEE Trans. Power Electron. 2017, 33, 911–916. [Google Scholar] [CrossRef]
- Karimi-Ghartemani, M.; Khajehoddin, S.A.; Piya, P.; Ebrahimi, M. Universal controller for three-phase inverters in a microgrid. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1342–1353. [Google Scholar] [CrossRef]
- Simonetti, D.S.L.; Amorim, A.E.A.; Oliveira, F.D.C. Doubly fed induction generator in wind energy conversion systems. In Advances in Renewable Energies and Power Technologies; Elsevier: Amsterdam, The Netherlands, 2018; pp. 461–490. [Google Scholar]
- Khawaja, A.W.; Kamari, N.A.M.; Zainuri, M.A.A.M. Design of a Damping Controller Using a Metaheuristic Algorithm for Angle Stability Improvement of an MIB System. Appl. Sci. 2022, 12, 589. [Google Scholar] [CrossRef]
- Sabo, A.; Wahab, N.I.A. Rotor angle transient stability methodologies of power systems: A comparison. In Proceedings of the 2019 IEEE Student Conference on Research and Development (SCOReD), Bandar Seri Iskandar, Malaysia, 15–17 October 2019; pp. 1–6. [Google Scholar]
- Nazari, V.; Mousavi, M.H.; Cheshmehbeigi, H.M. Reduction of Low Frequency Oscillations Using an Enhanced Power System Stabilizer via Linear Parameter Varying Approach. J. Renew. Energy Environ. 2022, 9, 59–74. [Google Scholar]
- Vargas, E.D.; Macedo, L.H.; Bueno, P.; Araujo, D.; Romero, R. Electrical Power and Energy Systems A VNS algorithm for the design of supplementary damping controllers for small-signal stability analysis. Int. J. Electr. Power Energy Syst. 2018, 94, 41–56. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Milanovic, J.; Rahmann, C.; Ajjarapu, V.; Canizares, C.; Erlich, I.; Hill, D.; Hiskens, I.; Kamwa, I.; Pal, B. Definition and classification of power system stability–revisited & extended. IEEE Trans. Power Syst. 2020, 36, 3271–3281. [Google Scholar]
- Zheng, Z.; An, Z.; Shen, C. Evaluation method for equivalent models of PMSG-based wind farms considering randomness. IEEE Trans. Sustain. Energy 2018, 10, 1565–1574. [Google Scholar] [CrossRef]
- Hu, Y.; Bu, S.; Yi, S.; Zhu, J.; Luo, J.; Wei, Y. A Novel Energy Flow Analysis and Its Connection With Modal Analysis for Investigating Electromechanical Oscillations in Multi-Machine Power Systems. IEEE Trans. Power Syst. 2021, 37, 1139–1150. [Google Scholar] [CrossRef]
- Mauricio, J.M.; Leon, A.E. Improving small-signal stability of power systems with significant converter-interfaced generation. IEEE Trans. Power Syst. 2020, 35, 2904–2914. [Google Scholar] [CrossRef]
- Du, W.; Chen, X.; Wang, H. PLL-induced modal resonance of grid-connected PMSGs with the power system electromechanical oscillation modes. IEEE Trans. Sustain. Energy 2017, 8, 1581–1591. [Google Scholar] [CrossRef]
- Ying, J.; Yuan, X.; Hu, J.; He, W. Impact of inertia control of DFIG-based WT on electromechanical oscillation damping of SG. IEEE Trans. Power Syst. 2018, 33, 3450–3459. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, D.; Blaabjerg, F. Modelling, implementation, and assessment of virtual synchronous generator in power systems. J. Mod. Power Syst. Clean Energy 2020, 8, 399–411. [Google Scholar] [CrossRef]
- Othman, M.H.; Mokhlis, H.; Mubin, M.; Talpur, S.; Ab Aziz, N.F.; Dradi, M.; Mohamad, H. Progress in control and coordination of energy storage system-based VSG: A review. IET Renew. Power Gener. 2020, 14, 177–187. [Google Scholar] [CrossRef]
- Wang, Y.; Meng, J.; Zhang, X.; Xu, L. Control of PMSG-based wind turbines for system inertial response and power oscillation damping. IEEE Trans. Sustain. Energy 2015, 6, 565–574. [Google Scholar] [CrossRef]
- Fang, J.; Lin, P.; Li, H.; Yang, Y.; Tang, Y. An improved virtual inertia control for three-phase voltage source converters connected to a weak grid. IEEE Trans. Power Electron. 2018, 34, 8660–8670. [Google Scholar] [CrossRef]
- Sabo, A.; Wahab, N.I.A.; Othman, M.L. Coordinated Design of PSS and IPFC Using FFA to Control Low Frequency Oscillations. In Proceedings of the 2021 IEEE 19th Student Conference on Research and Development (SCOReD), Kota Kinabalu, Malaysia, 23–25 November 2021; 2021; pp. 201–206. [Google Scholar]
- Sabo, A.; Abdul Wahab, N.I.; Othman, M.L.; Mohd Jaffar, M.Z.A.; Beiranvand, H. Optimal design of power system stabilizer for multimachine power system using farmland fertility algorithm. Int. Trans. Electr. Energy Syst. 2020, 30, e12657. [Google Scholar] [CrossRef]
- Tzounas, G.; Sipahi, R.; Milano, F. Damping power system electromechanical oscillations using time delays. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 2725–2735. [Google Scholar] [CrossRef]
- Mujeer, S.A.; Dwarasila, M.K.; Chintala, J.D.; Adimulam, V.S.K. Low frequency oscillations damping by design of power system stabilizer using intelligent controllers. Mater. Today Proc. 2021. In Press. [Google Scholar]
- Tare, A.; Jadhav, S.S.; Pande, V.N.; Ghanegaonkar, S.P. Design of Power System Stabilizer as Second-Order Sliding Mode Controller. In Smart Sensors Measurements and Instrumentation; Springer: Basel, Switzerland, 2021; pp. 295–305. [Google Scholar]
- Verdejo, H.; Pino, V.; Kliemann, W.; Becker, C.; Delpiano, J. Implementation of particle swarm optimization (PSO) algorithm for tuning of power system stabilizers in multimachine electric power systems. Energies 2020, 13, 2093. [Google Scholar] [CrossRef]
- Ghosh, S.; Isbeih, Y.J.; El Moursi, M.S.; El-Saadany, E.F. Cross-gramian model reduction approach for tuning power system stabilizers in large power networks. IEEE Trans. Power Syst. 2019, 35, 1911–1922. [Google Scholar] [CrossRef]
- Chitara, D.; Niazi, K.R.; Swarnkar, A.; Gupta, N. Cuckoo search optimization algorithm for designing of a multimachine power system stabilizer. IEEE Trans. Ind. Appl. 2018, 54, 3056–3065. [Google Scholar] [CrossRef]
- Zhou, J.; Ke, D.; Chung, C.Y.; Sun, Y. A computationally efficient method to design probabilistically robust wide-area PSSs for damping inter-area oscillations in wind-integrated power systems. IEEE Trans. Power Syst. 2018, 33, 5692–5703. [Google Scholar] [CrossRef]
- Shukla, A.; Gupta, A.K. Damping enhancement of DFIG integrated power system by coordinated controllers tuning using marine predators algorithm. In Control Applications in Modern Power System; Springer: Singapore, 2021; pp. 165–176. [Google Scholar]
- Kohan, V.; Conka, Z.; Kolcun, M.; Karabinos, M.; Havran, P.; Stefko, R.; Tailor, R.J. Use of Flexible Alternating Current Transmission System to improve power system operation—Damping oscillation and power flow control. In Proceedings of the 2021 IEEE 4th International Conference and Workshop Óbuda on Electrical and Power Engineering (CANDO-EPE), Budapest, Hungary, 17–18 November 2021; pp. 113–118. [Google Scholar]
- Yu, S.; Chau, T.K.; Fernando, T.; Savkin, A.V.; Iu, H.H.-C. Novel quasi-decentralized SMC-based frequency and voltage stability enhancement strategies using valve position control and FACTS device. IEEE Access 2016, 5, 946–955. [Google Scholar] [CrossRef]
- Shair, J.; Xie, X.; Yang, J.; Li, J.; Li, H. Adaptive damping control of subsynchronous oscillation in DFIG-based wind farms connected to series-compensated network. IEEE Trans. Power Deliv. 2021, 37, 1036–1049. [Google Scholar] [CrossRef]
- Guo, J.; Zenelis, I.; Wang, X.; Ooi, B.-T. WAMS-based model-free wide-area damping control by voltage source converters. IEEE Trans. Power Syst. 2020, 36, 1317–1327. [Google Scholar] [CrossRef]
- Basu, M.; Mahindara, V.R.; Kim, J.; Nelms, R.M.; Muljadi, E. Comparison of active and reactive power oscillation damping with pv plants. IEEE Trans. Ind. Appl. 2021, 57, 2178–2186. [Google Scholar] [CrossRef]
- Alghamdi, S.; Markovic, U.; Stanojev, O.; Schiffer, J.; Hug, G.; Aristidou, P. Wide-area oscillation damping in low-inertia grids under time-varying communication delays. Electr. Power Syst. Res. 2020, 189, 106629. [Google Scholar] [CrossRef]
- Bhattacharyya, B.; Kumar, S. Approach for the solution of transmission congestion with multi-type FACTS devices. IET Gener. Transm. Distrib. 2016, 10, 2802–2809. [Google Scholar] [CrossRef]
- Surinkaew, T.; Ngamroo, I. Two-level coordinated controllers for robust inter-area oscillation damping considering impact of local latency. IET Gener. Transm. Distrib. 2017, 11, 4520–4530. [Google Scholar] [CrossRef]
- Naghshbandy, A.H.; Faraji, A. Coordinated design of PSS and unified power flow controller using the combination of CWT and Prony methods with the help of SPEA II multi-objective optimisation algorithm. IET Gener. Transm. Distrib. 2019, 13, 4900–4909. [Google Scholar] [CrossRef]
- Guesmi, T.; Alshammari, B.M.; Almalaq, Y.; Alateeq, A.; Alqunun, K. New coordinated tuning of SVC and PSSs in multimachine power system using coyote optimization algorithm. Sustainability 2021, 13, 3131. [Google Scholar] [CrossRef]
- Fan, X.; Shu, J.; Zhang, B. Coordinated control of DC grid and offshore wind farms to improve rotor-angle stability. IEEE Trans. Power Syst. 2018, 33, 4625–4633. [Google Scholar] [CrossRef]
- Toolabi Moghadam, A.; Aghahadi, M.; Eslami, M.; Rashidi, S.; Arandian, B.; Nikolovski, S. Adaptive Rat Swarm Optimization for Optimum Tuning of SVC and PSS in a Power System. Int. Trans. Electr. Energy Syst. 2022, 2022, 4798029. [Google Scholar] [CrossRef]
- Khampariya, P.; Panda, S.; Alharbi, H.; Abdelaziz, A.Y.; Ghoneim, S.S.M. Coordinated Design of Type-2 Fuzzy Lead–Lag-Structured SSSCs and PSSs for Power System Stability Improvement. Sustainability 2022, 14, 6656. [Google Scholar] [CrossRef]
- Eshkaftaki, A.A.; Rabiee, A.; Kargar, A.; Boroujeni, S.T. An applicable method to improve transient and dynamic performance of power system equipped with DFIG-based wind turbines. IEEE Trans. Power Syst. 2019, 35, 2351–2361. [Google Scholar] [CrossRef]
- Uddin, W.; Zeb, N.; Zeb, K.; Ishfaq, M.; Khan, I.; Ul Islam, S.; Tanoli, A.; Haider, A.; Kim, H.-J.; Park, G.-S. A neural network-based model reference control architecture for oscillation damping in interconnected power system. Energies 2019, 12, 3653. [Google Scholar] [CrossRef]
- Gupta, P.; Pal, A.; Vittal, V. Coordinated Wide-Area Damping Control Using Deep Neural Networks and Reinforcement Learning. IEEE Trans. Power Syst. 2021, 37, 365–376. [Google Scholar] [CrossRef]
- Ghodsi, M.R.; Tavakoli, A.; Samanfar, A. Microgrid Stability Improvement Using a Deep Neural Network Controller Based VSG. Int. Trans. Electr. Energy Syst. 2022, 2022, 7539173. [Google Scholar] [CrossRef]
- Lee, H.-J.; Jhang, S.-S.; Yu, W.-K.; Oh, J.-H. Artificial neural network control of battery energy storage system to damp-out inter-area oscillations in power systems. Energies 2019, 12, 3372. [Google Scholar] [CrossRef]
- Gomis-Bellmunt, O.; Sau-Bassols, J.; Prieto-Araujo, E.; Cheah-Mane, M. Flexible converters for meshed HVDC grids: From flexible AC transmission systems (FACTS) to flexible DC grids. IEEE Trans. Power Deliv. 2019, 35, 2–15. [Google Scholar] [CrossRef]
- Zhang, G.; Hu, W.; Zhao, J.; Cao, D.; Chen, Z.; Blaabjerg, F. A novel deep reinforcement learning enabled multi-band pss for multi-mode oscillation control. IEEE Trans. Power Syst. 2021, 36, 3794–3797. [Google Scholar] [CrossRef]
- Tan, K.-H.; Lin, F.-J.; Shih, C.-M.; Kuo, C.-N. Intelligent control of microgrid with virtual inertia using recurrent probabilistic wavelet fuzzy neural network. IEEE Trans. Power Electron. 2019, 35, 7451–7464. [Google Scholar] [CrossRef]
- Osipov, D.; Sun, K. Adaptive nonlinear model reduction for fast power system simulation. IEEE Trans. Power Syst. 2018, 33, 6746–6754. [Google Scholar] [CrossRef]
- Rogers, G. Modal analysis for control. In Power System Oscillations; Springer: Boston, MA, USA, 2000; pp. 75–100. [Google Scholar]
- Milano, F. An open source power system analysis toolbox. IEEE Trans. Power Syst. 2005, 20, 1199–1206. [Google Scholar] [CrossRef]
- Cole, S.; Belmans, R. Matdyn, a new matlab-based toolbox for power system dynamic simulation. IEEE Trans. Power Syst. 2010, 26, 1129–1136. [Google Scholar] [CrossRef]
- Zhang, K.; Shi, Z.; Huang, Y.; Qiu, C.; Yang, S. SVC damping controller design based on novel modified fruit fly optimisation algorithm. IET Renew. Power Gener. 2018, 12, 90–97. [Google Scholar] [CrossRef]
- Gheisarnejad, M. An effective hybrid harmony search and cuckoo optimization algorithm based fuzzy PID controller for load frequency control. Appl. Soft Comput. 2018, 65, 121–138. [Google Scholar] [CrossRef]
- Chen, Y.; Xie, Z.; Zhou, L.; Wang, Z.; Zhou, X.; Wu, W.; Yang, L.; Luo, A. Optimized design method for grid-current-feedback active damping to improve dynamic characteristic of LCL-type grid-connected inverter. Int. J. Electr. Power Energy Syst. 2018, 100, 19–28. [Google Scholar] [CrossRef]
- Bramerdorfer, G.; Tapia, J.A.; Pyrhönen, J.J.; Cavagnino, A. Modern electrical machine design optimization: Techniques, trends, and best practices. IEEE Trans. Ind. Electron. 2018, 65, 7672–7684. [Google Scholar] [CrossRef]
- Sun, S.; Cao, Z.; Zhu, H.; Zhao, J. A survey of optimization methods from a machine learning perspective. IEEE Trans. Cybern. 2019, 50, 3668–3681. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Liu, C.; Sun, K.; Shi, D.; Wang, Z. Optimization of battery energy storage to improve power system oscillation damping. IEEE Trans. Sustain. Energy 2018, 10, 1015–1024. [Google Scholar] [CrossRef]
- Morshed, M.J.; Fekih, A. A probabilistic robust coordinated approach to stabilize power oscillations in DFIG-based power systems. IEEE Trans. Ind. Informatics 2019, 15, 5599–5612. [Google Scholar] [CrossRef]
- Dziwiński, P.; Bartczuk, Ł. A new hybrid particle swarm optimization and genetic algorithm method controlled by fuzzy logic. IEEE Trans. Fuzzy Syst. 2019, 28, 1140–1154. [Google Scholar] [CrossRef]
- Wang, D.; Ma, N.; Wei, M.; Liu, Y. Parameters tuning of power system stabilizer PSS4B using hybrid particle swarm optimization algorithm. Int. Trans. Electr. Energy Syst. 2018, 28, e2598. [Google Scholar] [CrossRef]
- Latif, S.; Irshad, S.; Ahmadi Kamarposhti, M.; Shokouhandeh, H.; Colak, I.; Eguchi, K. Intelligent Design of Multi-Machine Power System Stabilizers (PSSs) Using Improved Particle Swarm Optimization. Electronics 2022, 11, 946. [Google Scholar] [CrossRef]
- Bhukya, J.; Mahajan, V. Parameter tuning of PSS and STATCOM controllers using genetic algorithm for improvement of small-signal and transient stability of power systems with wind power. Int. Trans. Electr. Energy Syst. 2021, 31, e12912. [Google Scholar] [CrossRef]
- Verdejo, H.; Torres, R.; Pino, V.; Kliemann, W.; Becker, C.; Delpiano, J. Tuning of Controllers in Power Systems Using a Heuristic-Stochastic Approach. Energies 2019, 12. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A. Advances in Sine Cosine Algorithm: A comprehensive survey. Artif. Intell. Rev. 2021, 54, 2567–2608. [Google Scholar] [CrossRef]
- Abualigah, L.; Shehab, M.; Alshinwan, M.; Alabool, H. Salp swarm algorithm: A comprehensive survey. Neural Comput. Appl. 2020, 32, 11195–11215. [Google Scholar] [CrossRef]
- Dey, P.; Mitra, S.; Bhattacharya, A.; Das, P. Comparative study of the effects of SVC and TCSC on the small signal stability of a power system with renewables. J. Renew. Sustain. Energy 2019, 11, 33305. [Google Scholar] [CrossRef]
- Shehab, M.; Abualigah, L.; Al Hamad, H.; Alabool, H.; Alshinwan, M.; Khasawneh, A.M. Moth–flame optimization algorithm: Variants and applications. Neural Comput. Appl. 2020, 32, 9859–9884. [Google Scholar] [CrossRef]
- Agrawal, N.; Gowda, M. Comparison of Damping Control Performance of PID, PSS and TCSC Controllers by Moth Flame Optimization Algorithm. INFOCOMP J. Comput. Sci. 2022, 21. Available online: https://infocomp.dcc.ufla.br/index.php/infocomp/article/view/2089 (accessed on 20 October 2022).
- Shehab, M.; Alshawabkah, H.; Abualigah, L.; AL-Madi, N. Enhanced a hybrid moth-flame optimization algorithm using new selection schemes. Eng. Comput. 2021, 37, 2931–2956. [Google Scholar] [CrossRef]
- Devarapalli, R.; Bhattacharyya, B. Optimal controller parameter tuning of PSS using sine-cosine algorithm. In Metaheuristic and Evolutionary Computation: Algorithms and Applications; Springer: Singapore, 2021; pp. 337–360. [Google Scholar]
- Gupta, S.; Deep, K. A hybrid self-adaptive sine cosine algorithm with opposition based learning. Expert Syst. Appl. 2019, 119, 210–230. [Google Scholar] [CrossRef]
- Gupta, S.; Deep, K. A novel hybrid sine cosine algorithm for global optimization and its application to train multilayer perceptrons. Appl. Intell. 2020, 50, 993–1026. [Google Scholar] [CrossRef]
- Alabool, H.M.; Alarabiat, D.; Abualigah, L.; Heidari, A.A. Harris hawks optimization: A comprehensive review of recent variants and applications. Neural Comput. Appl. 2021, 33, 8939–8980. [Google Scholar] [CrossRef]
- Chaib, L.; Choucha, A.; Arif, S.; Zaini, H.G.; El-Fergany, A.; Ghoneim, S.S.M. Robust design of power system stabilizers using improved harris hawk optimizer for interconnected power system. Sustainability 2021, 13, 11776. [Google Scholar] [CrossRef]
- Ekinci, S.; Demiroren, A.; Hekimoglu, B. Parameter optimization of power system stabilizers via kidney-inspired algorithm. Trans. Inst. Meas. Control 2019, 41, 1405–1417. [Google Scholar] [CrossRef]
- Devarapalli, R.; Kumar, V. Power system oscillation damping controller design: A novel approach of integrated HHO-PSO algorithm. Arch. Control Sci. 2021, 31, 553–591. [Google Scholar]
- Ibrahim, N.M.A.; Elnaghi, B.E.; Ibrahim, H.A.; Talaat, H.E.A. Performance assessment of bacterial foraging based power system stabilizer in multi-machine power system. Int. J. Intell. Syst. Appl. 2019, 11, 43. [Google Scholar] [CrossRef]
- Mou, Q.; Ye, H.; Liu, Y. Nonsmooth Optimization-Based WADC Tuning in Large Delayed Cyber-Physical Power System by Interarea Mode Tracking and Gradient Sampling. IEEE Trans. Power Syst. 2019, 34, 668–679. [Google Scholar] [CrossRef]
- Khalilpourazari, S.; Khalilpourazary, S. Optimization of production time in the multi-pass milling process via a Robust Grey Wolf Optimizer. Neural Comput. Appl. 2018, 29, 1321–1336. [Google Scholar] [CrossRef]
- Khalilpourazari, S.; Khalilpourazary, S. SCWOA: An efficient hybrid algorithm for parameter optimization of multi-pass milling process. J. Ind. Prod. Eng. 2018, 35, 135–147. [Google Scholar] [CrossRef]
- Devarapalli, R.; Bhattacharyya, B.; Sinha, N.K. An intelligent EGWO-SCA-CS algorithm for PSS parameter tuning under system uncertainties. Int. J. Intell. Syst. 2020, 35, 1520–1569. [Google Scholar] [CrossRef]
- Singh, B.; Singh, S. GA-based optimization for integration of DGs, STATCOM and PHEVs in distribution systems. Energy Reports 2019, 5, 84–103. [Google Scholar] [CrossRef]
- Peres, W.; da Costa, N.N. Comparing strategies to damp electromechanical oscillations through STATCOM with multi-band controller. ISA Trans. 2020, 107, 256–269. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Diwania, S.; Singh, R.; Ashfaq, H.; Khetrapal, P.; Singh, S. An intelligent Hybrid Wind–PV farm as a static compensator for overall stability and control of multimachine power system. ISA Trans. 2022, 123, 286–302. [Google Scholar] [CrossRef] [PubMed]
- Prakash, A.; Kumar, K.; Parida, S.K. Energy capacitor system based wide-area damping controller for multiple inter-area modes. IEEE Trans. Ind. Appl. 2022, 58, 1543–1553. [Google Scholar] [CrossRef]
- Rout, B.; Pati, B.B.; Panda, S. Modified SCA algorithm for SSSC damping controller design in power system. ECTI Trans. Electr. Eng. Electron. Commun. 2018, 16, 46–63. [Google Scholar] [CrossRef][Green Version]
- Zhang, T.; Mao, C.; Zhang, J.; Tian, J.; Yu, M.; Wu, K.; Xiong, H.; Wu, L.; Yu, H. Design and field application of flexible excitation system damping controllers. IEEE Trans. Ind. Electron. 2020, 68, 949–959. [Google Scholar] [CrossRef]
- Kasilingam, G.; Pasupuleti, J.; Bharatiraja, C.; Adedayo, Y. Single machine connected infinite bus system tuning coordination control using biogeography: Based optimization algorithm. FME Trans. 2019, 47, 502–510. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).