Abstract
Commercial buildings are a significant consumer of energy worldwide. Logistics facilities, and specifically warehouses, are a common building type which remain under-researched in the demand-side energy forecasting literature. Warehouses have an idiosyncratic profile when compared to other commercial and industrial buildings with a significant reliance on a small number of energy systems. As such, warehouse owners and operators are increasingly entering energy performance contracts with energy service companies (ESCOs) to minimise environmental impact, reduce costs, and improve competitiveness. ESCOs and warehouse owners and operators require accurate forecasts of their energy consumption so that precautionary and mitigation measures can be taken. This paper explores the performance of three machine learning models (Support Vector Regression (SVR), Random Forest, and Extreme Gradient Boosting (XGBoost)), three deep learning models (Recurrent Neural Networks (RNNs), Long Short-Term Memory (LSTM), and Gated Recurrent Unit (GRU)), and a classical time series model, Autoregressive Integrated Moving Average (ARIMA) for predicting daily energy consumption. The dataset comprises 8040 records generated over an 11-month period from January to November 2020 from a non-refrigerated logistics facility located in Ireland. The grid search method was used to identify the best configurations for each model. The proposed XGBoost models outperformed other models for both very short-term load forecasting (VSTLF) and short-term load forecasting (STLF); the ARIMA model performed the worst.
1. Introduction
Logistics operations consume significant energy resources worldwide through service processes, transportation, and buildings. Indeed, research by McKinsey suggested that as much as 90% of firm-level environmental impact comes from firm supply chains [1]. Unsurprisingly, there is an increasing focus on reducing energy consumption in the global supply chain system and a shift towards so-called ’green logistics’ and ’green supply chain management’ [2]. Indeed, meeting the United Nations (UN) Sustainable Development Goals and European Union (EU) targets will require the sector to reduce fossil fuel use and CO emissions by over 50% by 2050 [3]. To achieve such targets requires energy efficiencies across the entire logistics system including procurement, warehousing, transportation, production, sales, and information systems [2].
This study concerns one aspect of the logistics system, warehouse logistics, and specifically the design and management of energy consumption in warehouse buildings. The world’s stock of warehouses was estimated at 150,000 warehouses in 2020, approximately 2.3 billion square metres of space [4]. Driven by growing global e-commerce consumption, the number of units is set to grow to 180,000 warehouses by 2025 [4]. Warehouses have a distinct energy consumption profile concentrated in a few key systems—lighting (71%), heating and ventilation (16%), battery charging (7%), and other miscellaneous energy consumption [5]. Warehouses are not only an important part of the commercial building sector but are embedded elements of supply chains; thus, there is a wide range of drivers of greater energy efficiency including corporate social responsibility, legal, competitive, and cost factors [6]. While the relative percentage of greenhouse gases (GHGs) from logistics facilities is small at 0.55%, this still represents over 300 megatonnes of GHG emissions per year [7]. This is particularly salient because electricity costs and usage can be dramatically reduced through a number of small interventions [5]. For example, the Carbon Trust estimates that non-refrigerated warehouses operating with legacy lighting can typically reduce electricity costs by 70% by moving to light emitting diode (LED), while an investment in solar photovoltaic (PV) has an estimated payback of 8.8 years [5]. As such, green warehousing can be a significant first step towards both net zero warehousing and supply chain decarbonisation.
Energy load forecasting techniques are essential for effective energy management in both residential and commercial buildings [8,9]. Energy load forecasting applications can be categorised into four main categories based on the time length of the prediction (forecasting horizon): (i) very short-term load forecasting (VSTLF) (minutes to hours); (ii) short-term load forecasting (STLF) (hours to days); (iii) medium-term load forecasting (weeks to months); and (iv) long-term load forecasting (months to years) [9,10]. Similarly, load forecasting applications can be classified as either supply- or demand-side-based in function of whether the focus is on energy production or consumption [11]. This paper specifically focuses on short- and very short-term demand-side load forecasting. While load forecasting has been one of the main research topics in electrical engineering for more than three decades [10], STLF and VSTLF have only become possible in recent years thanks to the widespread adoption of the advanced metering infrastructure (AMI) and connected sensors that are able to capture electrical consumption at a high level of granularity [9,12]. This real-time, fine-grain consumption data at the point of use in buildings and associated analysis, can be used by building energy managers and end users for planning and end-user behaviour change [13].
The optimisation of energy consumption is not only an important design factor in warehouse operations and intralogistics [6], but it is also a critical element in energy performance contracting (EPC)-based business models, a key strategy in combating climate change [14,15]. EPC involves the outsourcing of one or more energy-related services to a third party, typically an ESCO [15,16]. Under an EPC arrangement, the ESCO “implements a project to deliver energy savings, or a renewable energy project, and uses the stream of income from the expense reduction, or the renewable energy produced, to repay the whole or part of the costs of the project, including the costs of the investment” [15]. Through EPC, the ESCO establishes a link between contract payments and equipment performance during a long-term period, typically based on energy performance and associated energy and cost savings [15,16]. Warehouses are an ideal target for ESCOs and energy service contracts due to the concentration of energy consumption in a small number of systems, ideally placed for outsourcing, i.e., lighting and heating, but also due to their suitability for solar PV installations. While lighting and heating are predictable, energy demand management may be required to mitigate the impact of other elements, e.g., plug-in electric vehicles and other energy storage units. Near-term electricity load forecasting can help in the design of energy performance contracts, building a business case for green warehousing, controlling building energy systems, and managing the charging/discharging or energy storage units in an energy-efficient and cost-effective way.
Extant literature on STLF and VSTLF has typically (i) focused on supply-side perspectives; (ii) one forecasting horizon; (iii) aggregated energy costs; and (iv) failed to recognise the idiosyncrasies of warehouses. The use of STLF and VSTLF has not been considered from an EPC perspective. We argue that more accurate load forecasting allows warehouse operators and ESCOs to make better decisions to inform their investment decisions with respect to equipment and renewable energy systems. Prior studies on STLF and VSTLF have adopted a wide range of methodologies and techniques depending on the type of data available to researchers and the length of the forecast horizon [17]. Fallah et al. [17] classified existing methodologies into four categories, namely (i) similar pattern; (ii) variable selection; (iii) hierarchical forecasting; and (iv) weather station selection [17]. While most models adopt a variable selection methodology, similar pattern approaches are also widely adopted, particularly for short and very short forecast horizon and when data other than energy load are not available to researchers. Other studies have provided an overview of different techniques that have been implemented in prior studies. Mogharm et al. [18] and Daut et al. [19], for example, reviewed and compared conventional statistical approaches with more recent techniques that are based on computational intelligence (CI). Both studies concluded that CI-based techniques tend to provide more accurate forecasts. Notwithstanding this, there is a dearth of studies on demand-side firm-level (V) STLF specifically using machine learning and deep learning for warehouses. Those few studies that have been published do not compare the performance of the proposed deep learning models against commonly used machine learning models, classical time series models, or other approaches used in practice. Similarly, few articles have compared performance between STLF and VSTLF. In addition to proposing prediction models for STLF and VSTLF, we also address this gap.
In this paper, we focus on performance analyses of deep learning and machine learning models for building-level STLF and VSTLF in a non-refrigerated logistics facility. We use energy consumption data from a real multinational warehouse located in Ireland. We propose three deep learning models—simple Recurrent Neural Networks (RNN), Long Short-Term Memory (LSTM) networks, and Gated Recurrent Unit (GRU)—and three machine learning models—Support Vector Regression (SVR), Random Forest, and Extreme Gradient Boosting—for predicting hourly and daily energy consumption. We use the grid search method to identify the best model configurations. We compare the performance of the deep learning and machine learning models for predicting the energy consumption of the next hour using data from the previous 48 h (VSTLF) using (i) common metrics—root mean squared error (RMSE), mean absolute percentage error (MAPE), and mean absolute error (MAE); and (ii) a classical time series model, Autoregressive Integrated Moving Average (ARIMA). The best performing models for VSTLF, XGBoost-5-100 and XGBoost-7-100, were further evaluated for predicting energy consumption over longer time horizons, i.e., 12 h and 24 h.
The remainder of this paper is organised as follows. Section 2 presents the description of the data, pre-processing, and the evaluation metrics used in our work. Section 4 presents the results of our analysis. Section 3 presents the models identified for evaluation. Section 5 discusses related works in the field of STLF and VSTLF using machine learning and deep learning for warehouse facilities. The paper concludes with a summary of the paper and future avenues for research in Section 6.
2. Materials and Methods
2.1. Dataset
The data used in this study were sourced from an ESCO that offers services to warehouse owners and operators worldwide. Specifically, this ESCO specialises in the replacement of legacy lighting systems with LED lighting and intelligent controls and the installation and generation of electricity through solar PV. The ESCO operates an EPC arrangement with customers and thus generates its income from reducing the energy consumption and energy costs of client facilities. The dataset comprises 8040 records of hourly energy consumption from an 11-month period from 1 January 2020 to 30 November 2020 for a non-refrigerated logistics facility located in Ireland. Figure 1 presents the time series of the dataset used in this work while Table 1 presents some descriptive and quantile statistics.
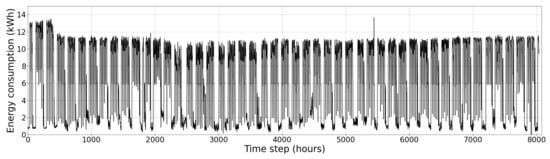
Figure 1.
Time series overview of the energy consumption of the focal site (January–November 2020).

Table 1.
Quantile and descriptive statistics.
2.2. Data Preprocessing
An initial analysis of the dataset revealed that there were no missing values or measurement errors; thus, it was not necessary to perform any data cleaning. However, it was necessary to normalise the data so that all inputs to the model had equal weights and a similar range (i.e., between zero and one [0, 1]). This was also necessary to reduce the forecast errors and training process time [20]. Sklearn’s MinMaxScaler function was used to normalise the data in this study as presented in Equation (1):
where is the rescaled value; is the original value; min(x) is the minimum value of feature x; max(x) is the maximum value of feature x.
2.3. Evaluation Metric
In this study, we adopted the root mean squared error (RMSE), mean absolute percent error (MAPE), and mean absolute error (MAE) to evaluate and compare the performances of different models as they are the most commonly metrics used to evaluate the accuracy of energy consumption models [21].
RMSE is defined as the square root of the mean squared error (MSE) [22]. This is calculated as presented in Equation (2) where represents the predicted value, represents the real (observed) value (Equation (2)), and n represents the sample size. As RMSE considers the squared value of the difference between the predicted value and the observed value, it is particularly sensitive to outliers. RMSE presents error values in the same scale as the original variable [22] and has been widely applied in time series analysis [23]:
MAPE is widely used to evaluate models when a high-quality forecast is required as well as in energy forecasting research [24,25,26,27,28,29]. MAPE was calculated as presented in Equation (3) [24], measuring the error as a percentage. MAPE is relatively intuitive to interpret as a metric but it can only be calculated when observed values in the dataset are not equal to zero [30]:
MAE is defined as per Equation (4) [26,31]. In contrast to RMSE and MAPE, MAE depends on the scale of the data and it is not sensitive to outliers as it treats all errors (both positive and negative) in the same way. In this study, we used MAE to quantify a model’s ability to predict energy consumption:
These metrics have been commonly used in previous studies related to load forecasting (for example, [11,25,32,33]) and specifically in relation to short-term load forecasting at commercial building levels [9,34].
3. Model Identification
As mentioned previously, Fallah et al. [17] pointed out that a number of different methodologies have been implemented for VSTLF and STLF. As the dataset adopted in this study only contains energy consumption data, we adopted a similar pattern methodology. Fallah et al. [17] also highlighted that “both methods and techniques are important when it comes to accurate estimation”.
The forecasting techniques used to perform VSTLF and STLF mainly come from the statistics and computational intelligence domains [8]. Regression methods belong to the former and typically assume that a linear relationship exists between load prediction and selected explanatory variables. These models have attracted attention as they are relatively easy to implement and interpret but they return large forecasting errors when an unexpected change in the input variables occurs [18]. Other statistical approaches that have been used for STLF include traditional and adaptive autoregressive moving average [35,36,37] and stochastic time series [38,39] but they are all subject to the same limitations as regression models.
Machine learning techniques perform significantly better than statistical techniques, particularly when non-linear trends and patterns are present in the data as in the dataset used in this study (see Figure 1). Traditional machine learning models include, for example, Regression Trees [40], Support Vector Regression (SVR) [41,42,43], random forest [44], Extreme Gradient Boosting (XGBoost) [45,46] and Artificial Neural Networks (ANNs) [47,48]. More recently, the development of deep learning methods has yielded further performance improvements thanks to their capacity to extract a variety of features from large datasets [9]. These models include (i) Convolutional Neural Networks (CNNs), which perform particularly well in terms of feature extraction and generalisation [49]; and (ii) Recurrent Neural Networks (RNNs) which use information and patterns embedded in the time series itself to perform tasks that are prohibitive for other ANNs [11]. While deep learning models tend to outperform more traditional machine learning algorithms, they are not without limitations. RNNs, for example, struggle with long-term dependencies because of vanishing and exploding gradient issues during training [50,51]. More recently, alternative RNN models have been developed, namely Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU), which aim to overcome such limitations [52,53,54]. LSTM algorithms are able to store the useful information of long-span states and have achieved significantly better performance than other RNNs when predicting energy demand [29,55]. GRU models are simpler than LSTM models as they only use a single gate named update gate and tend to be faster to train [56]. Similarly to LSTM, GRU models have been used for STLF with excellent performance [57,58].
In this paper, we aimed to assess and compare the accuracy and performance of different machine learning and deep learning models for building-level STLF and VSTLF. More specifically, we will compare SVR, Random Forest and XGBoost models with RNN, LSTM, and GRU. We will also use an Autoregressive Integrated Moving Average (ARIMA) model as our baseline benchmark. Each of these models will be presented in more detail in the following sections. All our models use energy consumption data from the previous 2 days (48 h) as input and have the predicted energy consumption for the next hour as output.
3.1. Machine Learning Models
For this study, we selected SVR, Random Forest and XGBoost as suitable machine learning models as they have been implemented in a number of STLF studies (see, for example, [42,43,44,46]).
While ANNs have become extremely popular in the load forecasting literature over the last decade, they face significant challenges when it comes to STLF and VSTLF real-life applications, mostly due to model overfitting and the exponential increase in complexity associated with high dimensionality [41]. SVR is a regression technique based on Support Vector Machines (SVMs) [59] (a machine-learning technique that leverages statistical learning theory [60]) which has been demonstrated to perform well in forecasting time series [61]. SVR models perform a linear regression in the high-dimensional feature space created by a kernel function using an epsilon-insensitive loss function while also minimising the model coefficients to reduce complexity [59].
Random Forest models were initially proposed by Breiman [62] as a potential solution to the generalisability and overfitting issues typical of decision trees [63]. Random Forest models are based on the Bagging ensemble learning theory [64] and the random subspace method [65]. They integrate a number of weak classification decision trees into a stronger, more accurate classifier. More specifically, each decision tree generates an independent classification and the ultimate outcome is the one that received the majority of the votes among all the decision trees [66,67].
Similarly to Random Forest, XGBoost models are based on ensemble learning theory which combine gradient boosting decision trees models and second-order Taylor expansion on the loss function to speed up the optimisation process while avoiding overfitting [68]. XGBoost models also support parallel processing and are therefore quicker to train and deploy than traditional decision trees.
To configure machine learning models settings, we used the Python scikit-learn library (sklearn.svm.SVR; sklearn.ensemble.RandomForestRegressor); and the XGBoost Python Package. To perform the analysis of the defined metrics (RMSE, MAPE, and MAE), we used the Python NumPy library. In order to identify the best hyperparameters for each model, we performed a grid search. The parameters and levels used for the grid search are listed in Table 2.

Table 2.
Machine learning parameters and levels.
A learning rate of 0.07 was fixed. For SVR, a gamma of 0.002, and the cost and type of kernel were used as parameters. For both Random Forest and XGBoost, the maximum depth of trees and the number of trees were used as parameters. All these parameters were chosen empirically.
We used 80% of the original dataset (1 January 2020 to 24 September 2020) as the training dataset while the remaining 20% (25 September 2020 to 30 November 2020) was used as the test dataset using the holdout process.
Figure 2, Figure 3 and Figure 4 present the results of the grid search for each model based on RMSE, MAPE, and MAE. For SVR, the model with a configuration where the C value is 10 and uses the rbf kernel (SVR-10-rbf) provided the best performance based on RMSE and MAPE; the model configuration with a C value of 10 using the linear kernel (SVR-10-linear), provided the best results based on MAE. With regard to Random Forest, the best configurations across the three metrics were those with a maximum depth of nine and with 200 trees (Random Forest-9-200). For XGBoost, the models with configurations with a maximum depth of 5 and with 100 trees (XGBoost-5-100) provided the best results based on RMSE; the model configuration with a maximum depth of 7 and with 100 trees (XGBoost-7-100) provided the best results based on MAPE and MAE. Consequently, these five model configurations were selected for the benchmark evaluation.
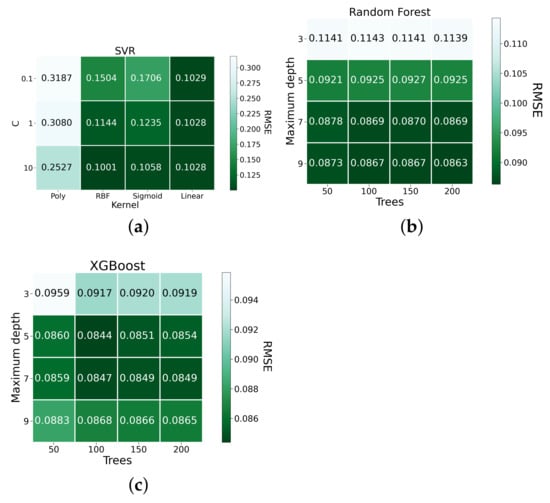
Figure 2.
RMSE grid search result for (a) SVR; (b) Random Forest; and (c) XGBoost.
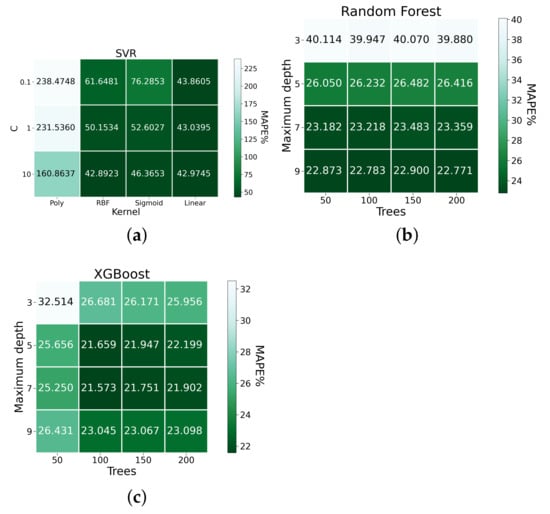
Figure 3.
MAPE grid search result for (a) SVR; (b) Random Forest; and (c) XGBoost.
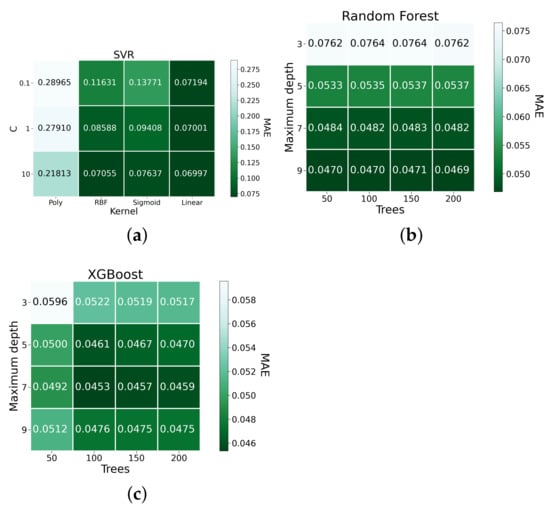
Figure 4.
MAE grid search result for (a) SVR; (b) Random Forest; and (c) XGBoost.
3.2. Deep Learning Models
As mentioned in Section 3, in this study, we implemented three deep learning models: RNN, LSTM, and GRU. RNNs are designed to recognise patterns in time series data. Such models process an input sequence at a time and maintain hidden units in their state vector that contain information about the history of all the past elements of the series [69]. This means that the decision, classification, or learning done at a given time will influence the decision, classification, or learning in the next time step [11]. However, RNNs suffer from gradient vanishing issues which means that the weights propagated forward and backward through the layer tend to decrease, and therefore the algorithm cannot preserve long-range dependencies [50].
LSTM overcomes the main limitation of RNNs by introducing the cell state and gates into RNN cells which preserve weights propagated through time and different layers [70]. More specifically, an LSTM network uses three main gates, namely a forget gate, an input gate, and an output gate. Figure 5 provides an overview of the typical LSTM architecture. The forget gate is responsible for deleting information that is no longer useful in the unit [71]. At each time step, the input and the output from the previous unit are multiplied by the weight matrix. The result then goes through an activation function that generates a binary output that causes the information that is no longer useful to forget . The input gate instead provides useful information to the unit’s status. The information is initially adjusted by the sigmoid function and then the tanh function is used to create a vector whose values range between −1 and +1. Finally, the output gate completes the information extraction from the current state by applying a tanh function to a cell. Through these steps, LSTM models are able accurately predict time series with intervals of unspecified duration [70]. However, LSTM is not without limitations. As LSTM models take a long time to train [72], GRU models are being increasingly used as alternatives.
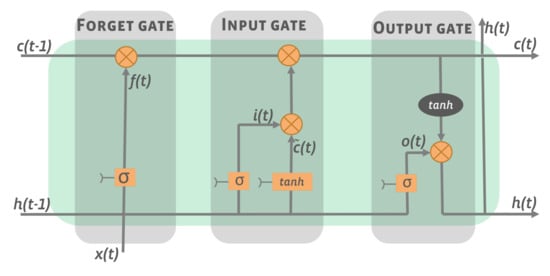
Figure 5.
LSTM architecture (adapted from [73]).
GRUs are quicker to train and are also capable of reaching performance comparable to LSTMs as they are able to capture both long- and short-term dependencies in a time series [56,72]. GRUs are less complex than LSTMs as they only use two gates, namely the update and reset gate [56] (see Figure 6). GRU models transfer time dependencies in the data between different time steps by a single hidden state [11].
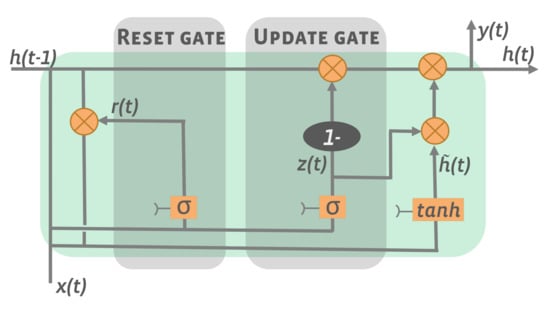
Figure 6.
GRU architecture (adapted from [73]).
To configure deep learning models settings, the keras APIs were used: LSTM class, GRU class, and SimpleRNN class. To perform the analysis of the defined metrics (RMSE, MAPE, and MAE), the Python NumPy library was used. Following the same approach presented in Section 3.1, we adopted a grid search method to identify the configuration of each deep learning model with the best performance [74,75,76,77,78]. The hyperparameters considered in the grid search were (i) the number of layers; and (ii) the number of nodes in each layer as summarised in Table 3. As per the machine learning models, all deep learning models were tested using 80% of the original dataset as the training set while the remaining 20% was used as the test dataset.

Table 3.
Parameters and levels of use in grid search.
The following parameters were fixed across different models: 1000 epochs with early stopping function, a batch size of 256, sigmoid [79] as the activation function, MSE as the loss function, and the Adam method was used for stochastic optimisation. Due to the stochastic nature of the optimisation process, the grid search was performed 30 times using RMSE, MAPE, and MAE as the performance evaluation metrics. In the training stage, the keras API earlying stop function was used. The is equal to EarlyStopping (, mode = auto, verbose = 1, , patience = 10). Table 4 presents the hyperparameters used in the best models.

Table 4.
Hyperparameters of the best deep learning model configuration.
Figure 7 presents the loss convergence during both the training and testing of the deep learning models. It suggests that the models converge after approximately 20 epochs (loss stabilisation); and there is no overfitting.
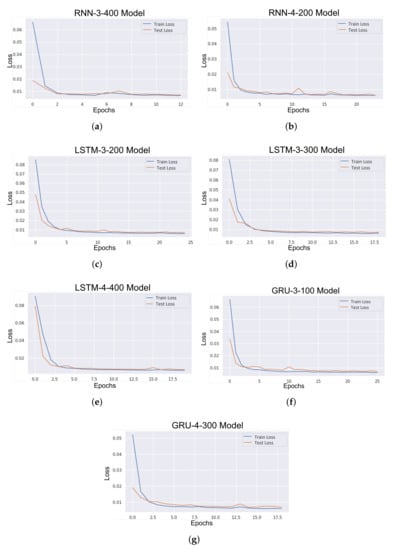
Figure 7.
Convergence results for the (a) Recurrent Neural Network (RNN)-3-400; (b) RNN-4-200; (c) Long Short-Term Memory (LSTM)-3-200; (d) LSTM-3-300; (e) LSTM-4-400; (f) Gated Recurrent Unit (GRU)-3-100; and (g) GRU-4-300.
Figure 8, Figure 9 and Figure 10 present the normalised results of the grid search. For RNN, the model with configuration with four layers and 200 nodes (RNN-4-200) presented the best result based on the MAE average metrics; the model configuration with three layers and 400 nodes (RNN-3-400) presented the best result based on the RMSE average and the MAPE average metrics. For LSTM, the models with configurations (a) with 3 layers and 300 nodes (LSTM-3-300); (b) 4 layers and 400 nodes (LSTM-4-400); and (c) 3 layers and 200 nodes (LSTM-3-200) provided the best results based on RMSE, MAPE, and MAE, respectively. For GRU, the model with the configuration with 3 layers and 100 nodes (GRU-3-100) provided the best result based on the RMSE average and the MAE average metrics; the model configuration with 4 layers and 300 nodes (GRU-4-300) presented the best result based on the MAPE average metrics. Thus, these seven models were considered in the benchmark evaluation.
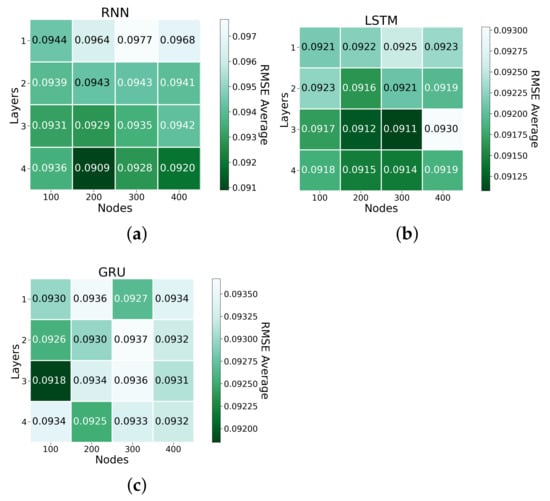
Figure 8.
RMSE grid search result for (a) RNN; (b) LSTM; and (c) GRU.
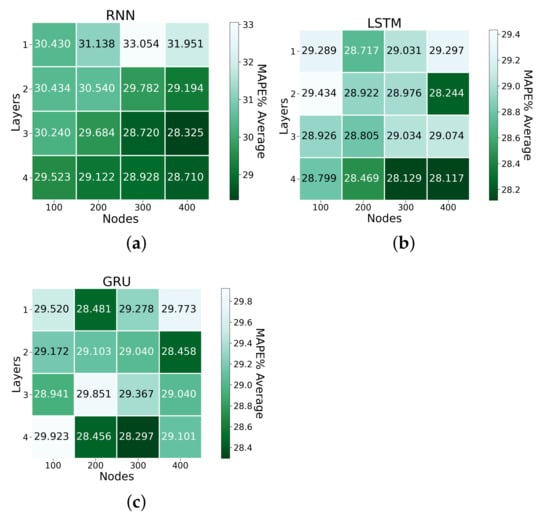
Figure 9.
MAPE grid search result for (a) RNN; (b) LSTM; and (c) GRU.
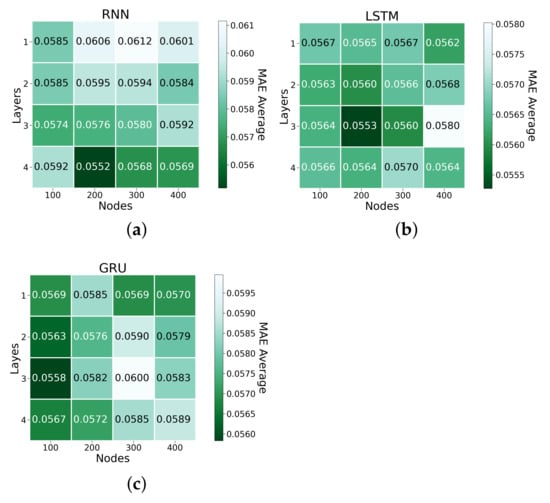
Figure 10.
MAE grid search result for (a) RNN; (b) LSTM; and (c) GRU.
3.3. Benchmarks
An ARIMA model was selected as a benchmark due to its widespread use in building-level energy forecasting (as can be seen, for example, in [34,37,80]). The ARIMA model was deemed a suitable benchmark for this study because of the time-series nature of our dataset. Equation (5) [81] presents how the autoregressive component of the model is calculated:
where t is the index represented by an integer, is the estimated value, p is the number of autoregressive terms, and is the polynomial related to the autoregressive operator of order p.
Equation (6) [81] represents the time dependency of the errors of previous estimates, i.e., past forecast errors that are taken into account when estimating the next value in the time series:
where q is the number of moving average terms, is the polynomial related to the moving average operator of order q, and is the difference between the estimated and observed values of .
Equation (7) [81] combines Equations (5) and (6) and summarises the ARIMA model (p and q) used as a benchmark for this study:
Based on empirical evidence, the ARIMA model used in this study presented the order of the autoregressive (), the degree of differencing (), and the order of the moving average ().
4. Discussion
As described, the models presented in Section 3 were trained to predict the energy consumption of the next hour using data from the previous 48 h. By definition, this prediction is classified as very short-term load forecasting (VSTLF) [82]. For comparison and analysis purposes, we used the same models’ configuration to predict the next 12 and 24 h, in order to explore short-term load forecasting (STLF) performance [82]. This was achieved as follows: once which is the best model to predict the next 1 h (the single-output regression model) is defined, this model will be used to create a chained multi-output regression, that is, a linear sequence of models capable of performing multi-output regression. This means that the first model in the sequence takes an input and predicts the output, then the second model uses the same input as the first model by adding the output of the first model to make a prediction, etc. (A schematic can be seen at Figure 11). This approach is used to define the VSTLF model, to predict the next 12 and 24 h. This technique can end up propagating residual errors throughout the prediction, but despite this, it allows to use of the same trained model to carry out larger predictions, in a simple way and without needing to train new models. Both VSTLF and STLF can be used for the purchase and production of electric power, but STLF has more broad applications, such as the transmission, transfer, and distribution of electric power, the management and maintenance of electric power sources, and the management of daily electric load demand [83]. Furthermore, it can be used by ESCOs to inform energy performance contract design and implementation.

Figure 11.
Chained multi-output regression.
4.1. Short-Term Load Forecasting
Table 5 presents the RMSE, MAPE, and MAE results of the five machine learning models (SVR-10-rbf, SVR-10-linear, Random Forest-9-200, XGBoost-5-100, and XGBoost-7-100) and the seven deep learning models (RNN-3-400, RNN-4-200, LSTM-3-200, LSTM-3-300, LSTM-4-400, GRU-3-100, and GRU-4-300) defined in the previous section. Figure 12 presents the maximum and minimum values for the best deep learning model.

Table 5.
RMSE, MAPE, and MAE results for the selected analysed model.
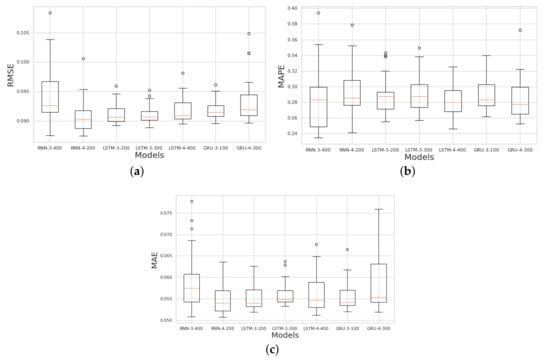
Figure 12.
Boxplot of (a) RMSE, (b) MAPE, and (c) MAE regarding the best deep learning models.
The traditional method for evaluating the performance of prediction models is defined through a comparative analysis of the metrics of each model. Based on this analysis, we concluded that the XGBoost models presented the best results among all analysed models which were generally better than those of all deep learning models. This can be explained by the fact that XGBoost models do better for problems that use tabular data. Furthermore, it is correct to state that most deep learning models require many more experiments to find a better configuration [84]. As seen in Section 3.2, the step of optimising the hyperparameters of DL models required a greater combination of parameters until it was possible to find the ideal configuration, in addition, it was necessary to compare three different types of layers: RNN, GRU, and LSTM. Finally, it would still be possible to create other types of models, such as hybrid models that use more than one type of layer, which would increase the complexity of the models. In certain problems, this greater complexity is justified when deep learning models present better results; however, the results show that in the context presented in this work, XGBoost has advantages over deep learning models, both in terms of accuracy and the complexity of the algorithm used. The ARIMA benchmark model presented the worst RMSE result, and the SVR models presented the worst MAPE result and MAE result among all the analysed models.
Figure 13 and Figure 14 visualise the hourly load forecasts as generated by the machine-learning and deep-learning models in direct comparison with the corresponding observed values. The results clearly show that the predicted values generated by the XGBoost models (Figure 13d,e) are more similar to the corresponding observed values than the ones generated by other models.
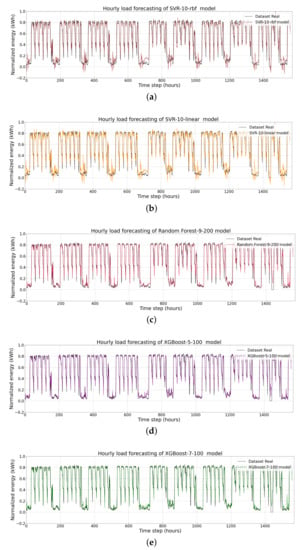
Figure 13.
Hourly load forecasting using (a) the SVR-10-rbf model; (b) the SVR-10-linear model; (c) the Random Forest-9-200 model; (d) the XGBoost-5-100 model; and (e) the XGBoost-7-100 model.
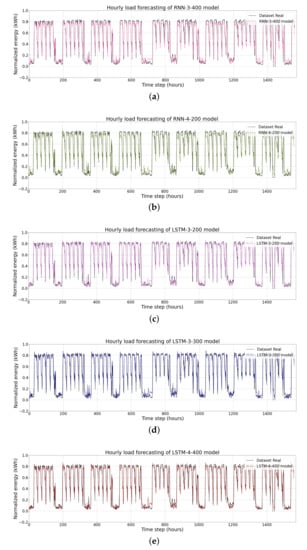
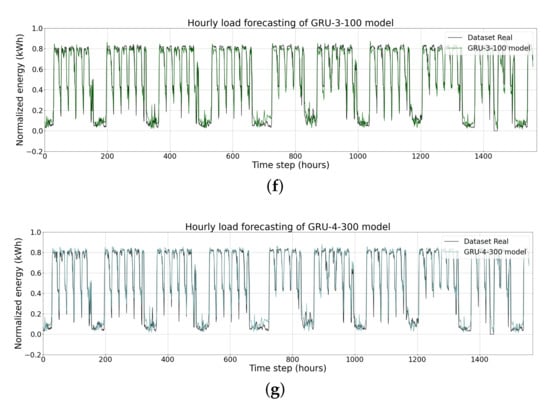
Figure 14.
Hourly load forecasting using (a) the RNN-3-400 model; (b) the RNN-4-200 model; (c) the LSTM-3-200 model; (d) the LSTM-3-300 model; (e) the LSTM-4-400 model; (f) the GRU-3-100 model; and (g) the GRU-4-300 model.
4.2. Very Short-Term Load Forecasting
As per the previous section, XGBoost-5-100 and XGBoost-7-100 were the best-performing models tested. These models were then tested for predicting energy consumption over longer time horizons, i.e., 12 h and 24 h, consistently with STLF. Table 6 presents the RMSE, MAPE, and MAE results of the STLF model (12 h and 24 h) compared with the result of the VSTLF model.

Table 6.
RMSE, MAPE, and MAE results for the VSTLF and STLF models.
When comparing the results obtained with the STLF and VSTLF models, we observed a maximum increase in 177% and 202% in RMSE and MAE, respectively. This increase can be explained by implementing the STLF model since there is a dependency between the outputs.
5. Related Work
There is a substantial and increasing literature base on the use of machine learning and deep learning for load forecasting by forecasting horizon, target use case, and sector [85]. A significant focus of this literature remains supply-side energy consumption and demand forecasting from the perspective of the management and optimisation of power systems and electricity grids, and typically with forecasting horizons longer than minutes and hours. The motivations of warehouse owners and operators, and indeed ESCOs who manage their energy systems, are significantly different to those operating utilities. Furthermore, and as discussed, the energy profile of warehouses is somewhat idiosyncratic compared to other commercial and industrial buildings. Despite this, there are relatively few studies addressing load forecasting in the warehouse context [85]. Similarly, reflecting the focus on power systems and grids, a wider set of parameters (e.g., seasonal weather and special events) and longer forecasting horizons (short-to-long) are typically adopted in studies. Very short-term load forecasting is arguably the least addressed due to the relatively narrow focus on extrapolating recently observed load patterns to the nearest future; modelling the relationship between load, time, weather conditions, special events, and other load affecting factors is less important [86]. At the same time, Guan et al. [87] argued that effective VSTLF is further complicated by a noisy data collection process, the possible malfunctioning of data-gathering devices and complicated load features. Indeed, studies on very short-term horizons are largely absent from reviews [85].
Machine learning and deep learning have been used for building energy predictions in a wide range of studies [85,88]. In their recent review, Gassar et al. [85] noted the most prominent energy prediction techniques for large-scale buildings to be Artificial Neural Network (ANNs), Support Vector Machines (SVMs), Multiple Linear Regression (MLR), Gradient Boosting (GB), and Random Forests (RFs). However, none of the studies studied warehouses as a building type. Similarly, among the fourteen papers identified by Li et al. [88] using LSTM for building energy predictions, none dealt with warehouses.
A number of studies have sought to deploy Artificial Neural Networks (ANNs) for building energy prediction in short time horizons [34,89,90,91]; however, yet again largely warehouses are not addressed. Escriva et al. [89], Gonzalez et al. [91], and Neto et al. [90] all used university-related buildings as a type of commercial building. Chae et al. [34] proposed an ANN for forecasting day-ahead electricity usage of commercial buildings in 15 min resolution. As variables, they selected the day type indicator, time-of-day, Heating, ventilation and air conditioning (HVAC) set temperature schedule, outdoor air dry-bulb temperature, and outdoor humidity as the most important predictors of electricity consumption [34]. The ANN model was a conventional multi-layered feed-forward network using a back-propagation algorithm. The correlation coefficient and co-efficient of variance (CV) (RMSE) were used as metrics to compare against a simple naive model and a variety of machine learning models including SVM, linear regression, Gaussian process, K-star classifier, nearest neighbour ball tree. The ANN outperformed all models and the results suggest that the ANN could provide a day-ahead electricity usage profile with sub-hourly intervals and satisfactory accuracy for daily peak consumption. It is important to note that the specific commercial buildings were not identified by the authors and thus the applicability of these findings to warehouses is uncertain.
In one of the few papers investigating load forecasting for commercial buildings that included warehouses, Chitalia et al. [9] compared nine deep learning algorithms (LSTM, BiLSTM, encoder–decoder, LSTM with attention, BiLSTM with attention, CNN+LSTM, CNN+BiLSTM, ConvLSTM, and ConvBiLSTM) for one-hour-ahead and 24 h-ahead forecasting. The models were tested against peak loads and weather conditions. The algorithms delivered a 20–45% improvement in load forecasting performance compared to benchmarks and found that hybrid deep learning models could deliver satisfactory hour-ahead load prediction with as little as one month of data. The metrics used were RMSE, MAPE, co-efficient of variance (CV). As Chitalia et al. [9] sought to compare different building types, root mean square algorithmic error was also used to allow fair comparison among buildings. A grid search was not employed.
As can be seen from above, there is a dearth of research on demand-side STLF and VSTLF for warehouses in general, and specifically using machine learning and deep learning models. Studies of commercial buildings typically involve universities or office buildings whose energy profiles are significantly different to that of warehouses. Indeed, within the commercial building sector, warehouses are idiosyncratic and consequently require discrete consideration. Even within the small number of studies that could be identified, it is not clear whether one is directly comparable [34] on the basis of building type and the other does not compare performance between machine learning and deep learning models. Finally, none of the identified papers compared the performance of machine learning and deep learning models for both STLF and VSTLF. As such, we seek to address these gaps in the literature.
6. Conclusions and Future Work
This work explored short-term and very short-term electrical load forecasting for an under-researched building type—warehouses. This study compared the performance of machine learning and deep learning models to forecast the energy consumption of the upcoming hour based on data from the previous 48 h, and benchmarked this performance against a classical time series forecasting technique, ARIMA. Unlike existing studies, we considered the data not only from the perspective of a warehouse owner and operator but an ESCO operating under an energy performance contract, and the data available to such a firm. Our results suggest that the XGBoost models outperformed all other machine learning and deep learning models, as well as ARIMA, for very short-term load forecasting. All machine learning and deep learning models outperformed ARIMA when using RMSE as a measure; the SVR models presented the worst MAPE and MAE results. Unsurprisingly, XGBoost was less accurate for a longer time horizons, i.e., 12 h and 24 h.
Accurate local forecasting close to real-time decision making can be used by warehouse owners and operators and ESCOs to design energy performance contracts, build a business case for green warehousing, control building energy systems, and manage the charging/discharging or energy storage units in an energy-efficient and cost-effective way. It can also be used for anomaly detection and proactive plant management, including renewable energy sources such as solar PV, and potentially transacting on future open carbon-trading systems. While this study suggests that machine learning models may be sufficient, ensemble solutions combining machine learning and deep learning may provide better results and are worthy of exploration. This study only examined building energy consumption.The handling, transporting, and storing units change the energy intensity within the wider logistics warehouse management system and are therefore worthy of further research [92]. For example, it may be fruitful for future research to consider the timing of battery charging/discharging and energy consumed by other operating activities. Furthermore, the site of this study did not feature high levels of automation or refrigeration, and was located in a country with a moderate climate—thus negating the need for substantial ventilation and air conditioning. Rudiger et al. [93] provided a useful overview of logistics services activities that contribute to GHG emissions including transshipment activities, the need for cold or ambient storage, and the need for automated or manual order-picking, amongst others. Similarly, Rakhmangulov et al. [2] provided not only a breakdown of the potential warehouse logistics methods and instruments that may inform future research, but also the potential methods and instruments across the supply chain system that could be optimised using machine learning and deep learning. Against this wider supply chain context, it is important to note that warehouses are only one type of logistics facility; transshipment terminals and distribution centres may also prove to be fruitful units of analysis. The addition of parameters that reflect different scenarios would provide the greater robustness and generalisability of the proposed methods against variations in warehouse configuration and use.
Author Contributions
Conceptualization, P.R. and T.L.; methodology, A.M.N.C.R. and P.T.E.; software, A.M.N.C.R. and P.R.X.d.C.; validation, A.M.N.C.R. and P.R.X.d.C.; formal analysis, A.M.N.C.R., P.R.X.d.C. and P.T.E.; investigation, A.M.N.C.R., P.R.X.d.C., P.T.E., P.R. and T.L.; resources, A.M.N.C.R., P.R.X.d.C., P.T.E., P.R. and T.L.; data curation, P.R. and T.L.; writing—original draft preparation, A.M.N.C.R., P.R.X.d.C., P.T.E., P.R. and T.L.; writing—review and editing, A.M.N.C.R., P.R.X.d.C., P.T.E., P.R. and T.L.; visualization, A.M.N.C.R.; supervision, P.T.E.; project administration, P.T.E. and T.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This research was partially supported by the UrbanVolt Inc. and by the Irish Institute of Digital Business. The authors would like to thank the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq); Fundação de Amparo a Ciência e Tecnologia do Estado de Pernambuco (FACEPE); and Universidade de Pernambuco (UPE), an entity of the Government of the State of Pernambuco focused on the promotion of teaching, research, and extension.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ANN | Artificial Neural Networks |
| AMI | Advanced Metering Infrastructure |
| ANN | Artificial Neural Network |
| ARIMA | Autoregressive Integrated Moving Average |
| CV | Co-efficient of Variance |
| EPC | Energy Performance Contract |
| ESCO | Energy Service Company |
| EU | European Union |
| GB | Gradient Boosting |
| GHG | Greenhouse Gas |
| GRU | Gated Recurrent Unit |
| HVAC | Heating, Ventilation and Air Conditioning |
| LED | Light Emitting Diode |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| MLR | Multiple Linear Regression |
| MAPE | Mean Absolute Percent Error |
| MSE | Mean Squared Error |
| PV | Solar Photovoltaic |
| RF | Random Forest |
| RMSE | Root Mean Squared Error |
| RNN | Recurrent Neural Networks |
| STLF | Short-Term Load Forecasting |
| SVM | Support Vector Machines |
| SVR | Support Vector Machine Regression |
| UN | United Nations |
| VSTLF | Very Short-Term Load Forecasting |
| XGBoost | Extreme Gradient Boosting |
References
- Bové, A.T.; Swartz, S. Starting at the Source: Sustainability in Supply Chains. 2016. Available online: https://www.mckinsey.com/business-functions/sustainability/our-insights/starting-at-the-source-sustainability-in-supply-chains (accessed on 10 November 2021).
- Rakhmangulov, A.; Sladkowski, A.; Osintsev, N.; Muravev, D. Green Logistics: A System of Methods and Instruments-Part 2. NAŠE MORE Znanstveni Časopis za More i Pomorstvo 2018, 65, 49–55. [Google Scholar] [CrossRef] [Green Version]
- Smokers, R.; Tavasszy, L.; Chen, M.; Guis, E. Options for Competitive and Sustainable Logistics; Emerald Group Publishing Limited: Bingley, UK, 2014. [Google Scholar]
- Depreaux, J. 28,500 Warehouses To Be Added Globally To Meet E-Commerce Boom. 2021. Available online: https://www.interactanalysis.com/28500-warehouses-to-be-added-globally-to-meet-e-commerce-boom/ (accessed on 13 December 2021).
- Trust, C. Warehousing and Logistics—Energy Opportunities for Warehousing and Logistics Companies. 2019. Available online: https://www.carbontrust.com/resources/warehousing-and-logistics-guide (accessed on 13 December 2021).
- Lewczuk, K.; Kłodawski, M.; Gepner, P. Energy Consumption in a Distributional Warehouse: A Practical Case Study for Different Warehouse Technologies. Energies 2021, 14, 2709. [Google Scholar] [CrossRef]
- World Economic Forum; Accenture. Supply Chain Decarbonisation: The Role of Logistics and Transport in Reducing Supply Chain Carbon Emissions; World Economic Forum and Accenture Geneva: Geneva, Switzerland, 2009. [Google Scholar]
- Dagdougui, H.; Bagheri, F.; Le, H.; Dessaint, L. Neural network model for short-term and very-short-term load forecasting in district buildings. Energy Build. 2019, 203, 109408. [Google Scholar] [CrossRef]
- Chitalia, G.; Pipattanasomporn, M.; Garg, V.; Rahman, S. Robust short-term electrical load forecasting framework for commercial buildings using deep recurrent neural networks. Appl. Energy 2020, 278, 115410. [Google Scholar] [CrossRef]
- Hippert, H.S.; Pedreira, C.E.; Souza, R.C. Neural networks for short-term load forecasting: A review and evaluation. IEEE Trans. Power Syst. 2001, 16, 44–55. [Google Scholar] [CrossRef]
- Ribeiro, A.M.N.; do Carmo, P.R.X.; Rodrigues, I.R.; Sadok, D.; Lynn, T.; Endo, P.T. Short-Term Firm-Level Energy-Consumption Forecasting for Energy-Intensive Manufacturing: A Comparison of Machine Learning and Deep Learning Models. Algorithms 2020, 13, 274. [Google Scholar] [CrossRef]
- Quilumba, F.L.; Lee, W.J.; Huang, H.; Wang, D.Y.; Szabados, R.L. Using smart meter data to improve the accuracy of intraday load forecasting considering customer behavior similarities. IEEE Trans. Smart Grid 2014, 6, 911–918. [Google Scholar] [CrossRef]
- Alahmad, M.; Peng, Y.; Sordiashie, E.; El Chaar, L.; Aljuhaishi, N.; Sharif, H. Information technology and the smart grid-A pathway to conserve energy in buildings. In Proceedings of the 2013 9th International Conference on Innovations in Information Technology (IIT), Abu Dhabi, United Arab Emirates, 17–19 March 2013; pp. 60–65. [Google Scholar]
- Bertoldi, P.; Boza-Kiss, B.; Toleikyté, A. Energy Service Market in the EU; Publications Office of the European Union: Luxembourg, 2019. [Google Scholar]
- European Commission. A Renovation Wave for Europe—Greening Our Buildings, Creating Jobs, Improving Lives. 2020. Available online: https://ec.europa.eu/energy/sites/ener/files/eu_renovation_wave_strategy.pdf (accessed on 12 April 2021).
- Sorrell, S. The economics of energy service contracts. Energy Policy 2007, 35, 507–521. [Google Scholar] [CrossRef]
- Fallah, S.N.; Ganjkhani, M.; Shamshirband, S.; Chau, K.W. Computational intelligence on short-term load forecasting: A methodological overview. Energies 2019, 12, 393. [Google Scholar] [CrossRef] [Green Version]
- Raza, M.Q.; Khosravi, A. A review on artificial intelligence based load demand forecasting techniques for smart grid and buildings. Renew. Sustain. Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
- Daut, M.A.M.; Hassan, M.Y.; Abdullah, H.; Rahman, H.A.; Abdullah, M.P.; Hussin, F. Building electrical energy consumption forecasting analysis using conventional and artificial intelligence methods: A review. Renew. Sustain. Energy Rev. 2017, 70, 1108–1118. [Google Scholar] [CrossRef]
- Sola, J.; Sevilla, J. Importance of input data normalization for the application of neural networks to complex industrial problems. IEEE Trans. Nucl. Sci. 1997, 44, 1464–1468. [Google Scholar] [CrossRef]
- Debnath, K.B.; Mourshed, M. Forecasting methods in energy planning models. Renew. Sustain. Energy Rev. 2018, 88, 297–325. [Google Scholar] [CrossRef] [Green Version]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Kolomvatsos, K.; Papadopoulou, P.; Anagnostopoulos, C.; Hadjiefthymiades, S. Anagnostopoulos, C.; Hadjiefthymiades, S. A Spatio-Temporal Data Imputation Model for Supporting Analytics at the Edge. In Conference on e-Business, e-Services and e-Society; Springer: Berlin/Heidelberg, Germany, 2019; pp. 138–150. [Google Scholar]
- Luo, J.; Hong, T.; Yue, M. Real-time anomaly detection for very short-term load forecasting. J. Mod. Power Syst. Clean Energy 2018, 6, 235–243. [Google Scholar] [CrossRef] [Green Version]
- Ryu, S.; Noh, J.; Kim, H. Deep neural network based demand side short term load forecasting. Energies 2017, 10, 3. [Google Scholar] [CrossRef]
- Berriel, R.F.; Lopes, A.T.; Rodrigues, A.; Varejao, F.M.; Oliveira-Santos, T. Monthly energy consumption forecast: A deep learning approach. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 4283–4290. [Google Scholar]
- Azadeh, A.; Ghaderi, S.; Sohrabkhani, S. Annual electricity consumption forecasting by neural network in high energy consuming industrial sectors. Energy Convers. Manag. 2008, 49, 2272–2278. [Google Scholar] [CrossRef]
- Kuo, P.H.; Huang, C.J. A high precision artificial neural networks model for short-term energy load forecasting. Energies 2018, 11, 213. [Google Scholar] [CrossRef] [Green Version]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar] [CrossRef]
- De Myttenaere, A.; Golden, B.; Le Grand, B.; Rossi, F. Mean absolute percentage error for regression models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, T.J.; Hsiao, H.F.; Yeh, W.C. Forecasting stock markets using wavelet transforms and recurrent neural networks: An integrated system based on artificial bee colony algorithm. Appl. Soft Comput. 2011, 11, 2510–2525. [Google Scholar] [CrossRef]
- Chen, C.; Liu, Y.; Kumar, M.; Qin, J. Energy consumption modelling using deep learning technique—A case study of EAF. Procedia CIRP 2018, 72, 1063–1068. [Google Scholar] [CrossRef]
- Li, C.; Tao, Y.; Ao, W.; Yang, S.; Bai, Y. Improving forecasting accuracy of daily enterprise electricity consumption using a random forest based on ensemble empirical mode decomposition. Energy 2018, 165, 1220–1227. [Google Scholar] [CrossRef]
- Chae, Y.T.; Horesh, R.; Hwang, Y.; Lee, Y.M. Artificial neural network model for forecasting sub-hourly electricity usage in commercial buildings. Energy Build. 2016, 111, 184–194. [Google Scholar] [CrossRef]
- Chen, J.F.; Wang, W.M.; Huang, C.M. Analysis of an adaptive time-series autoregressive moving-average (ARMA) model for short-term load forecasting. Electr. Power Syst. Res. 1995, 34, 187–196. [Google Scholar] [CrossRef]
- Huang, S.J.; Shih, K.R. Short-term load forecasting via ARMA model identification including non-Gaussian process considerations. IEEE Trans. Power Syst. 2003, 18, 673–679. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.; Son, H.g.; Kim, S. Short term electricity load forecasting for institutional buildings. Energy Rep. 2019, 5, 1270–1280. [Google Scholar] [CrossRef]
- Huang, C.M.; Huang, C.J.; Wang, M.L. A particle swarm optimization to identifying the ARMAX model for short-term load forecasting. IEEE Trans. Power Syst. 2005, 20, 1126–1133. [Google Scholar] [CrossRef]
- Chakhchoukh, Y.; Panciatici, P.; Mili, L. Electric load forecasting based on statistical robust methods. IEEE Trans. Power Syst. 2010, 26, 982–991. [Google Scholar] [CrossRef]
- Yang, J.; Stenzel, J. Short-term load forecasting with increment regression tree. Electr. Power Syst. Res. 2006, 76, 880–888. [Google Scholar] [CrossRef]
- Ceperic, E.; Ceperic, V.; Baric, A. A strategy for short-term load forecasting by support vector regression machines. IEEE Trans. Power Syst. 2013, 28, 4356–4364. [Google Scholar] [CrossRef]
- Chen, Y.; Tan, H. Short-term prediction of electric demand in building sector via hybrid support vector regression. Appl. Energy 2017, 204, 1363–1374. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, P.; Chu, Y.; Li, W.; Wu, Y.; Ni, L.; Bao, Y.; Wang, K. Short-term electrical load forecasting using the Support Vector Regression (SVR) model to calculate the demand response baseline for office buildings. Appl. Energy 2017, 195, 659–670. [Google Scholar] [CrossRef]
- Li, Q.; Zhang, L.; Xiang, F. Short-term load forecasting: A case study in Chongqing factories. In Proceedings of the 2019 6th International Conference on Information Science and Control Engineering (ICISCE), Shanghai, China, 20–22 December 2019; pp. 892–897. [Google Scholar]
- Zhu, K.; Geng, J.; Wang, K. A hybrid prediction model based on pattern sequence-based matching method and extreme gradient boosting for holiday load forecasting. Electr. Power Syst. Res. 2021, 190, 106841. [Google Scholar] [CrossRef]
- Zheng, H.; Yuan, J.; Chen, L. Short-term load forecasting using EMD-LSTM neural networks with a Xgboost algorithm for feature importance evaluation. Energies 2017, 10, 1168. [Google Scholar] [CrossRef] [Green Version]
- Grolinger, K.; L’Heureux, A.; Capretz, M.A.; Seewald, L. Energy forecasting for event venues: Big data and prediction accuracy. Energy Build. 2016, 112, 222–233. [Google Scholar] [CrossRef] [Green Version]
- Singh, S.; Hussain, S.; Bazaz, M.A. Short term load forecasting using artificial neural network. In Proceedings of the 2017 Fourth International Conference on Image Information Processing (ICIIP), Shimla, India, 21–23 December 2017; pp. 1–5. [Google Scholar]
- Huang, Q.; Li, J.; Zhu, M. An improved convolutional neural network with load range discretization for probabilistic load forecasting. Energy 2020, 203, 117902. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. Int. Conf. Mach. Learn. PMLR 2013, 28, 1310–1318. [Google Scholar]
- Sundermeyer, M.; Schlüter, R.; Ney, H. LSTM neural networks for language modeling. In Proceedings of the Thirteenth Annual Conference of the International Speech Communication Association, Portland, OR, USA, 9–13 September 2012. [Google Scholar]
- Marino, D.L.; Amarasinghe, K.; Manic, M. Building energy load forecasting using deep neural networks. In Proceedings of the IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 24–27 October 2016; pp. 7046–7051. [Google Scholar]
- Kuan, L.; Yan, Z.; Xin, W.; Yan, C.; Xiangkun, P.; Wenxue, S.; Zhe, J.; Yong, Z.; Nan, X.; Xin, Z. Short-term electricity load forecasting method based on multilayered self-normalizing GRU network. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017; pp. 1–5. [Google Scholar]
- He, F.; Zhou, J.; Feng, Z.k.; Liu, G.; Yang, Y. A hybrid short-term load forecasting model based on variational mode decomposition and long short-term memory networks considering relevant factors with Bayesian optimization algorithm. Appl. Energy 2019, 237, 103–116. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Wang, Y.; Liu, M.; Bao, Z.; Zhang, S. Short-term load forecasting with multi-source data using gated recurrent unit neural networks. Energies 2018, 11, 1138. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.; Liao, W.; Miao, J.; Du, G. Using gated recurrent unit network to forecast short-term load considering impact of electricity price. Energy Procedia 2019, 158, 3369–3374. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1997, 9, 155–161. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995; Volume 10, p. 189. 978p. [Google Scholar]
- Sapankevych, N.I.; Sankar, R. Time series prediction using support vector machines: A survey. IEEE Comput. Intell. Mag. 2009, 4, 24–38. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Huang, N.; Lu, G.; Xu, D. A permutation importance-based feature selection method for short-term electricity load forecasting using random forest. Energies 2016, 9, 767. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar]
- Nadi, A.; Moradi, H. Increasing the views and reducing the depth in random forest. Expert Syst. Appl. 2019, 138, 112801. [Google Scholar] [CrossRef]
- Hammou, B.A.; Lahcen, A.A.; Mouline, S. An effective distributed predictive model with Matrix factorization and random forest for Big Data recommendation systems. Expert Syst. Appl. 2019, 137, 253–265. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, S.; Chen, X.; Zeng, X.; Kong, Y.; Chen, J.; Guo, Y.; Wang, T. Short-term load forecasting of industrial customers based on SVMD and XGBoost. Int. J. Electr. Power Energy Syst. 2021, 129, 106830. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, J.L.; Chang, P.C. A multiple time series-based recurrent neural network for short-term load forecasting. Soft Comput. 2018, 22, 4099–4112. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. In Proceedings of the 1999 Ninth International Conference on Artificial Neural Networks ICANN 99 (Conf. Publ. No. 470), Edinburgh, UK, 7–10 September 1999; Volume 2, pp. 850–855. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Jozefowicz, R.; Zaremba, W.; Sutskever, I. An empirical exploration of recurrent network architectures. Int. Conf. Mach. Learn. 2015, 37, 2342–2350. [Google Scholar]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Liao, J.M.; Chang, M.J.; Chang, L.M. Prediction of Air-Conditioning Energy Consumption in R&D Building Using Multiple Machine Learning Techniques. Energies 2020, 13, 1847. [Google Scholar]
- Yoon, H.; Kim, Y.; Ha, K.; Lee, S.H.; Kim, G.P. Comparative evaluation of ANN-and SVM-time series models for predicting freshwater-saltwater interface fluctuations. Water 2017, 9, 323. [Google Scholar] [CrossRef] [Green Version]
- Kavaklioglu, K. Modeling and prediction of Turkey’s electricity consumption using Support Vector Regression. Appl. Energy 2011, 88, 368–375. [Google Scholar] [CrossRef]
- Samsudin, R.; Shabri, A.; Saad, P. A comparison of time series forecasting using support vector machine and artificial neural network model. J. Appl. Sci. 2010, 10, 950–958. [Google Scholar] [CrossRef] [Green Version]
- Han, J.; Moraga, C. The influence of the sigmoid function parameters on the speed of backpropagation learning. In From Natural to Artificial Neural Computation; Mira, J., Sandoval, F., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; pp. 195–201. [Google Scholar]
- Vaghefi, A.; Jafari, M.A.; Bisse, E.; Lu, Y.; Brouwer, J. Modeling and forecasting of cooling and electricity load demand. Appl. Energy 2014, 136, 186–196. [Google Scholar] [CrossRef] [Green Version]
- Pushp, S. Merging Two Arima Models for Energy Optimization in WSN. arXiv 2010, arXiv:1006.5436. [Google Scholar]
- Hsiao, Y.H. Household electricity demand forecast based on context information and user daily schedule analysis from meter data. IEEE Trans. Ind. Inform. 2014, 11, 33–43. [Google Scholar] [CrossRef]
- Mele, E. A review of machine learning algorithms used for load forecasting at microgrid level. In Sinteza 2019-International Scientific Conference on Information Technology and Data Related Research; Singidunum University: Beograd, Serbia, 2019; pp. 452–458. [Google Scholar]
- Shwartz-Ziv, R.; Armon, A. Tabular data: Deep learning is not all you need. Inf. Fusion 2022, 81, 84–90. [Google Scholar] [CrossRef]
- Gassar, A.A.A.; Cha, S.H. Energy prediction techniques for large-scale buildings towards a sustainable built environment: A review. Energy Build. 2020, 224, 110238. [Google Scholar] [CrossRef]
- Charytoniuk, W.; Chen, M.S. Very short-term load forecasting using artificial neural networks. IEEE Trans. Power Syst. 2000, 15, 263–268. [Google Scholar] [CrossRef]
- Guan, C.; Luh, P.B.; Michel, L.D.; Wang, Y.; Friedland, P.B. Very short-term load forecasting: Wavelet neural networks with data pre-filtering. IEEE Trans. Power Syst. 2012, 28, 30–41. [Google Scholar] [CrossRef]
- Li, G.; Zhao, X.; Fan, C.; Fang, X.; Li, F.; Wu, Y. Assessment of long short-term memory and its modifications for enhanced short-term building energy predictions. J. Build. Eng. 2021, 43, 103182. [Google Scholar] [CrossRef]
- Escrivá-Escrivá, G.; Álvarez-Bel, C.; Roldán-Blay, C.; Alcázar-Ortega, M. New artificial neural network prediction method for electrical consumption forecasting based on building end-uses. Energy Build. 2011, 43, 3112–3119. [Google Scholar] [CrossRef]
- Neto, A.H.; Fiorelli, F.A.S. Comparison between detailed model simulation and artificial neural network for forecasting building energy consumption. Energy Build. 2008, 40, 2169–2176. [Google Scholar] [CrossRef]
- Gonzalez, P.A.; Zamarreno, J.M. Prediction of hourly energy consumption in buildings based on a feedback artificial neural network. Energy Build. 2005, 37, 595–601. [Google Scholar] [CrossRef]
- Zajac, P. Evaluation Method of Energy Consumption in Logistic Warehouse Systems; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Rüdiger, D.; Schön, A.; Dobers, K. Managing greenhouse gas emissions from warehousing and transshipment with environmental performance indicators. Transp. Res. Procedia 2016, 14, 886–895. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).