Design Optimization of Auxetic Structure for Crashworthy Pouch Battery Protection Using Machine Learning Method

Abstract

In 2021, the electric vehicles (EVs) market reached a record-breaking 6.5 million vehicles, and it will continuously grow to USD 31 million in 2030. However, the risk of battery damage should be reduced using a lightweight crashworthy protection system, which can be performed through design optimization to achieve maximum Specific Energy Absorption (SEA). Maximum SEA can be gained by selecting a material with a light weight and high energy absorption properties. An auxetic-shaped cell structure was used since its negative Poisson ratio yields better energy absorption. The research was performed by varying the auxetic cell shape (Re-entrant, Double Arrow, Star-shaped, Double-U), material selection (GFRP, CFRP, aluminum, carbon steel), and geometry variables until the maximum possible SEA was reached. The Finite Element Method (FEM) was used to simulate the impact and obtain the value of the SEA of the varied auxetic cellular structure design samples. The design variation amounted to 100 samples generated using Latin Hypercube Sampling (LHS) to distribute the variables. Finally, the Machine Learning method predicted the design that yielded maximum SEA. The optimization process through Machine Learning consisted of two processes: model approximation using an Artificial Neural Network (ANN) and variable optimization using a Nondominated Sorting Genetic Algorithm-II (NSGA-II). The optimization demonstrated that the maximum SEA resulted from Star-shaped auxetic cells and aluminum material with a thickness of 2.95 mm. This design yielded 1220% higher SEA compared to the baseline model. A numerical simulation was also carried out to validate the result. The prediction error amounted to 6.7%, meaning that the approximation model can successfully predict the most optimum design. After the complete battery system configuration simulation, the design could also prevent excessive battery deformation. Therefore, the optimized structure can protect the battery from failure.

1. Introduction

Within the last 3 years, electric vehicle usage has grown steadily. The accumulated annual sales of battery electric vehicles (BEV) and plug-in hybrid electric vehicles (PHEV) reached two million units in 2019 [1]. Analysis performed by Deloitte predicts that the number will continuously soar and reaches 31.1 million by 2030, while the conventional internal combustion engine (ICE) vehicle will decline.

The growth of electric vehicles, which use a battery, implies the importance of battery application and the urgency of its safety. The Li-Ion type is the most commonly used battery for today’s PHEVs and EVs, which has a high power-to-weight ratio, high energy efficiency, good high-temperature performance, and low self-discharge [2]. However, research and development are continuously ongoing to minimize costs, maximize useful life, and tackle safety concerns regarding overheating [3]. Furthermore, the emergence of the autonomous electric vehicle (AEV) also emphasizes safety and security as one of the Quality of Experience (QoE) parameters [4] to ensure the future AEV is not only autonomous but also has features of safety, security, and comfort. Therefore, designing battery protection will ensure the future application of the electric vehicle is safe and secure.

Concerns are focus on battery-generated heat, which cannot be removed entirely even under regular operation. Heat generation will be quicker at a high temperature or in a large battery pack. A significant increase in the battery temperature would trigger parasitic reactions, leading to thermal runaway or uncontrollable heat production. Thermal runaway will happen at a quicker rate during damage to mechanical (shell casing, compression, punching, and cell twisting), electrical (overcharge/discharge and short circuit), and thermal (thermal shock and local heating) components, which usually occurs during accidents [5].

Given the safety danger imposed by Li-Ion batteries, improving the protection system has become a high-priority task. One of the protective measures is to limit the deformation during an impact to prevent mechanical failure and further incidents. Therefore, a crashworthy battery protector was developed to lower the incident risks. The battery protector must be capable of absorbing the dynamic impact energy and must possess high strength to ensure the battery does not deform excessively. The protector also should be lightweight to conserve vehicle energy.

Various structures have been investigated as lithium-ion battery protectors, including sandwich structures. These structures are lightweight, have high energy absorption capabilities, and are quite common in aerospace and construction [6]. The most important part of a sandwich structure is its core, which is filled with another type of structure, including a meta-structure. The meta-structure is an arrangement of repeated unit cell structures to achieve a light structure with the same strength as a comparable solid structure.

One of the meta-structure types is auxetic, in which each cell structure has a negative Poisson ratio, meaning this structure will become thicker when it is stretched [7]. In recent decades, auxetic materials have become more popular due to their superior mechanical properties. These properties include improved shear and indentation resistance, high fracture toughness, and synclastic curvature, which give the auxetic material potential to be an excellent energy absorber [8]. Moreover, the auxetic structure also features longer plastic deformation along the loading direction; thus, energy absorption can be higher [9]. The auxetic structure also has a lower peak crushing force since the material is drawn to the impact area, reducing the injury and damage to the protected object [9]. Therefore, the auxetic-filled sandwich structure was chosen for this research as a potential battery protection structure due to its high energy absorption, lightweight property, and safety feature.

Studies on the optimization of the auxetic structure as a battery protector have been performed previously by Biharta [10] and Wang et al. [11]. The study by Biharta focused on the optimization of the three-dimensional (3D) auxetic structure to protect the pouch battery from ground impact using the Design for Six Sigma (DFSS) method. The auxetic shapes covered by Biharta included the double-arrow, double-U, Re-entrant A, and Re-entrant B type. Biharta’s design material was set to titanium alloy Ti-6Al-4V. On the other hand, the study by Wang focused on the analysis and optimization of the two-dimensional (2D) Re-entrant auxetic structure to resist the side impact of a battery pack. Wang’s structure was modeled with carbon steel material. The structure model developed by Wang et al. also covered the heat dissipation feature, a significant issue of vehicle batteries which needs to be addressed.

This research was focused on the design optimization of an auxetic structure as a battery protector from ground impact. Moreover, this paper addressed gaps from previous studies in terms of application and design variables. As for application, this research focused on ground impact protection by considering minimum deformation on the battery module with a strategic placement of the battery system in the floor structure of the vehicle platform. With the ground impact loading direction and the location of the battery system in the vehicle platform, a 2D type auxetic structure was chosen to protect the battery system. This research involved the studies on the shape variation of auxetic shapes, geometric density of the core, and materials such as composite and aluminum.

The ground impact load modeling was based on a study by Xia et al. [12], in which the structure experienced an in-plane impact from an impactor moving from the ground. The battery system used in this study was based on the pouch lithium-ion battery, which was modeled and tested experimentally in a study by E. Sahraei et al. [13].

Four auxetic shapes and four materials were combined to create various set of structures, and the combination with highest specific energy absorption (SEA) was determined. The analyzed 2D auxetic shapes were Re-entrant [14], double-arrow [15], Star [16], and double-U [17]. As for the material, this study included glass fiber reinforced polymer (GFRP) [18,19], carbon fiber reinforced polymer (CFRP) [20], carbon steel [11], and aluminum Al6061-T6 [21,22,23]. This study used the finite element method (FEM) [24] to obtain the structural performance through numerical simulation and machine learning (ML) [25] to predict most optimum structural design.

The machine learning optimization study was carried out in three major stages, which were data sampling, data training, and optimization. In the data sampling stage, 100 design samples were generated using Latin Hypercube Sampling (LHS) to create designs with randomly distributed property variables. These samples were then analyzed using FEM to calculate the SEA of each sample. After the complete set of design variables and SEA were obtained, this data set was used as an input for the data training stage. The data training stage refers to regressor model training using the Artificial Neural Network (ANN) [26] which creates a mathematical model to predict the SEA as a function of design variables. Finally, the regressor model was used for the optimization stage, in which the variables were iterated for the maximum SEA using the Non-dominated Sorting Genetic Algorithm II (NSGA-II).

To verify the performance of the optimum battery protection obtained from the machine learning method, the optimum auxetic configuration with highest SEA was implemented in the full battery system analysis using non-linear dynamic finite element method. The full system of battery and optimum protection was evaluated to test whether the optimization result was valid and able to protect the battery from excessive deformation. The battery failure criteria was determined based on Sahraei et al. [13], where the pouch battery failed when it deformed more than 2.9 mm. This criterion was used to check the crashworthiness of the optimized structure.

The optimization and analysis of the structural battery protections is intended to provide an optimum solution for the safety of the lithium-ion battery in the electric vehicle. The potential contributions of this research are detailed as follows:

1.

The design of battery protection to prevent thermal runaway can be implemented for future electric vehicles (EV) applications.

2.

The use of machine learning method to optimize the battery structural protection will provide robust solutions in terms of the energy absorption to weight ratio (specific energy absorption).

2. Numerical Modelling and Validation of Auxetic Structure

2.1. Auxetic Structure Model

2.1.1. Geometry and Numerical Model

Preliminary modeling and simulation of the auxetic structure were conducted to obtain precise settings and validated model. Basic geometry from Wang [11] on the development of negative Poisson’s ratio (NPR) auxetic tube for battery protection was chosen as the preliminary model. The model was constructed using the Re-entrant honeycomb auxetic cell structure with the dimensions specified in Figure 1 and Table 1. The simulation result is shown as well.

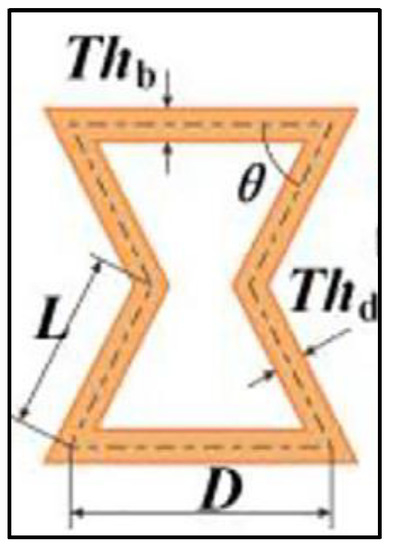
Figure 1. General auxetic honeycomb geometry definition. Th_b and Th_d indicate the cell’s thickness (which assumed to be equal), L and D indicates the cell’s side length, and $\theta$ indicates the cell’s corner angle.

Table 1. Unit cell parameters for the baseline NPR model.

Unit Cell Parameters	Value
D	13.70 mm
L	8.00 mm
Thb, Thd	1.00 mm
$\theta$	55.40

The finite element model of the Re-entrant structure was constructed with a 2-D fully integrated-type shell with a thickness of 2 mm, and the material was defined with the Piecewise Linear Plasticity type, see Figure 2.

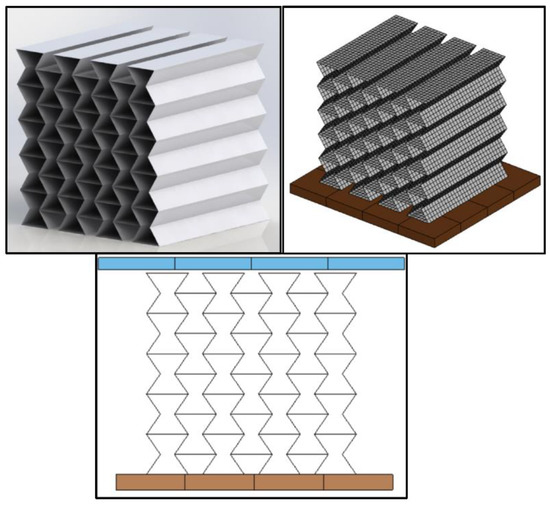
Figure 2. The baseline model from Wang’s study was reconstructed into a 3D model (upper left), then meshed to discretize the model for finite element analysis (upper right), and put together with a solid impactor and floor model on the top and bottom of the model to simulate the impact (bottom).

The impactor was modeled as a solid rigid box with 100 × 100 × 4 mm in dimension, 200 kg in mass, and crushing the structure at a constant velocity of 2 m/s in the direction of Z- (DOF = 3). The velocity as applied to the impactor as a prescribed motion of the rigid body.

The material for auxetic used in experiment by Wang et al. [11] was carbon steel with the properties detailed in Table 2 and Figure 3.

Table 2. Material properties of the baseline model.

Material Properties	Value
Type	Carbon Steel
Density (ρ)	7850.0 kg/m3
Young Mod (E)	210.0 GPa
Yield Strength ($\sigma$)	350.0 MPa
Poisson’s Ratio (ν)	0.3

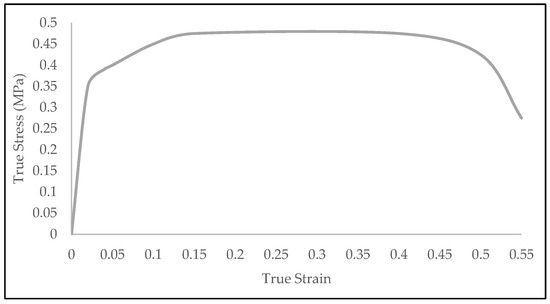
Figure 3. True stress strain curve of carbon steel.

The contact between impactor and cells was modeled using the automatic surface to the surface, and the internal contact between each cell was modeled using the automatic single surface. In Contact keywords, SST = 1.2 was chosen after iterations to generate the most accurate simulation of the reference’s experiment result. The iteration was performed by adjusting the SST value and looking for the closest F(x) curve to the experiment result, as shown in Figure 4.

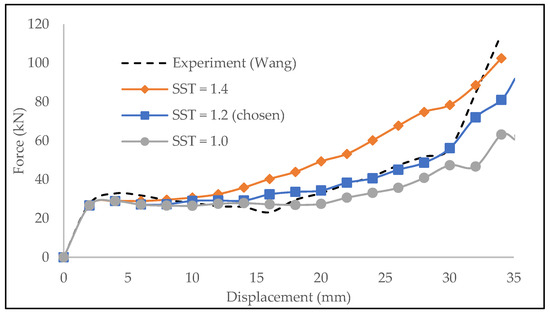
Figure 4. Force vs. displacement curve with SST variation to determine the SST value that provided the most accurate result compared with the baseline experiment. It can be seen that the higher the SST, the higher the force value.

2.1.2. Result Validation

The simulation was performed using non-linear dynamic finite element simulation. The simulation properties (initial condition, boundary condition, and contact definition) were set to imitate the original baseline simulation. The result of the simulation is shown in Figure 5 and Figure 6.

Figure 5. Crushing progression simulation compared with referenced experiment [11].

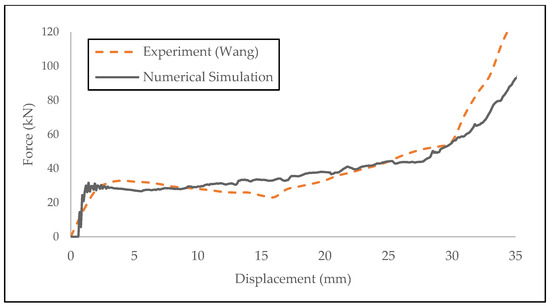
Figure 6. Crushing force vs. displacement from numerical simulation by writer compared with the baseline experiment.

It can be seen that the numerical result on the force and displacement curve from 0–30 mm before densification was similar to the experiment. However, there was a slight deviation after the densification.

Further evaluation on the energy balance from the simulation can be analyzed from Figure 7. The internal structural energy gradually increased as the quasi-static impact occurred, which indicates the ability of the auxetic structure to absorb impact energy during compressive deformation. The hourglass energy and sliding energy also appeared very low, which showed very small error in the numerical computation. Therefore, it can be concluded that the finite element model of the auxetic structure represents the physical experiment.

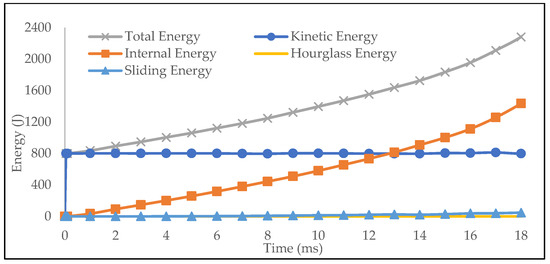
Figure 7. Impact energy plot from the numerical simulation. Total energy is the sum of all energy components. Since the simulation was quasi-static, the kinetic energy was constant. Note that the internal energy was continuously increasing, meaning that the structure absorbed the impact energy. Sliding energy indicates dissipated energy from contact, while hourglass energy is a non-physical energy that generated from numerical element distortion.

3. Modelling of Auxetic Structure and Machine Learning Optimization

3.1. Data Sampling Process

Data sampling was performed to determine the needed sample as input for the Artificial Neural Network (ANN) model. These data were divided into two datasets: the training data and the validation data set. These data were used to build a regressor model to predict output variables from a given input. Two types of data were used: discrete variable (category) and continuous variable (numerical). The variables are presented in Table 3.

Table 3. Variables for the design optimization.

Predictor Variable					Output Variable
	Continuous Variable		Categorical Variable
Geometry Definition	h (inner cell spacing)	4.5–6 mm ($\mathsf{\Delta }$ 0.15 mm)	Cross-section shape	Re-entrant, DAH, Star, DUH	Specific Energy Absorption (SEA)
	$\theta$ (angle of cell’s corner	45–60° ($\mathsf{\Delta }$ 1°)
Material Definition	Material thickness	1–3 mm ($\mathsf{\Delta }$ 0.2 mm)	Composite number of layers	2, 4, 6, 8, 10, 12
	Composite ply orientation	0–180° ($\mathsf{\Delta }$ 15°)

3.1.1. Geometry Definition

Due to the difference in shape and geometrical characteristics, the variables for geometry are normalized/standardized. The normalization is based on a pre-defined input variable called $\theta$ (as “cell corner angle”) and $h$ (as “inner cell spacing”). These variables are the basis for machine learning optimization and are adjusted to each cell shape type. In addition, the auxetic core height and total number of cells are set to constant for all samples. Configurations of the structure are shown in Figure 8 and Figure 9.

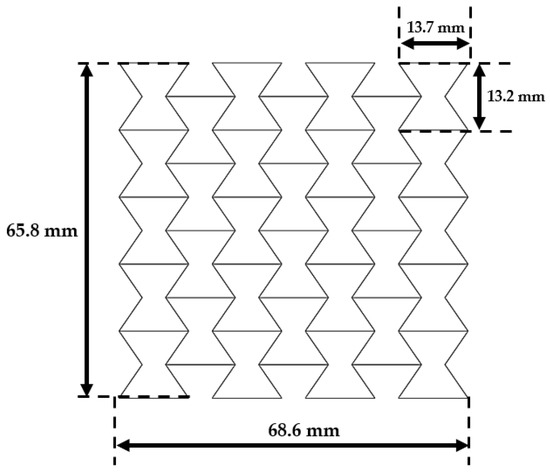
Figure 8. Baseline model height in millimeters (mm).

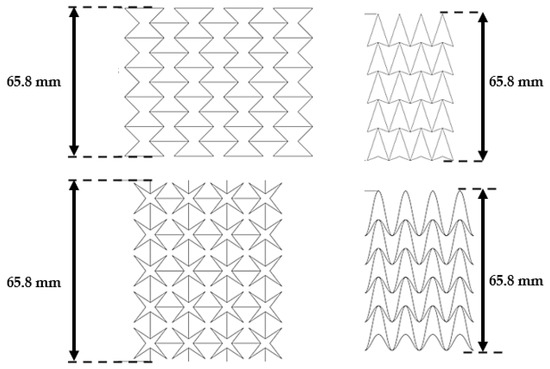
Figure 9. Total cell configuration height for each auxetic type in millimeter (mm), from upper left to lower left (clockwise): Re-entrant, DAH, DUH, Star.

As seen in Figure 9, the auxetic cell configuration is set to be similar to the baseline model. Therefore, the auxetic structure is standardized and comparable. The constraints are (1) total height equals to 65.85 mm and (2) number of cells (horizontal × vertical) equals to 4 × 5.

Meanwhile, there is also variable transformation to define geometrical constraints for each cross-section type. The transformation is made to tackle incompatibility between input variables and unique shapes of the cell. The underlying idea is that the global input variables, h and θ, are proportional to the cell’s density, in a way that as h and θ increase, the cell becomes wider and thus higher density.

The geometrical constraint definition for each cross-section type is explained in Figure 10, Figure 11, Figure 12 and Figure 13, which indicate Re-entrant (Figure 10), DAH (Figure 11), Star (Figure 12), and DUH shape (Figure 13). Note that the numbers indicated in the figure are the geometry variable that is varied in this sampling process.

• Re-entrant honeycomb

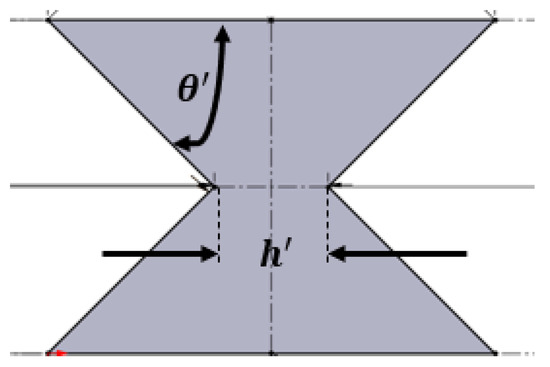
Figure 10. Variable definitions in the Re-entrant cell in millimeters (mm). $h^{\prime }$ and ${\theta }^{\prime }$ indicate the adjusted cell gap width and cell corner angle, respectively.

The geometrical constraints of the Re-entrant cell shape are similar to the input variable; therefore, the variables and its range are:

$$h^{\prime }=h\to 4.5 \mathrm{mm}\le h^{\prime }\le 6.0 \mathrm{mm}$$

(1)

$${\theta }^{\prime }=\theta \to 45°\le {\theta }^{\prime }\le 60°$$

(2)

where $h^{\prime }$ = adjusted inner cell spacing of Re-entrant

• $h$ = global variable of inner cell spacing
• ${\theta }^{\prime }$ = adjusted angle of Re-entrant cell’s corner
• $\theta$ = global variable of cell’s corner angle

2.

Double-arrow honeycomb (DAH)

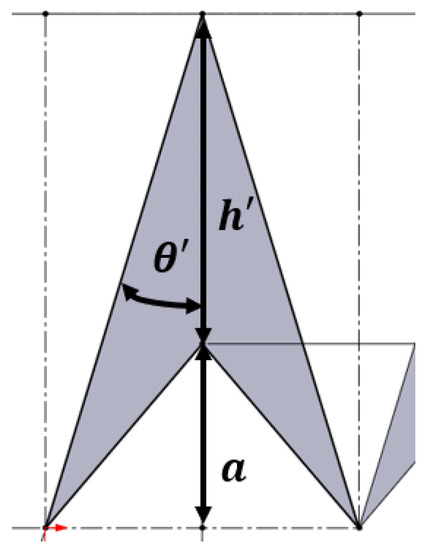
Figure 11. Variable definitions in the DAH cell in millimeters (mm). Variable $h^{\prime }$ and ${\theta }^{\prime }$ indicate the adjusted cell gap width and cell corner angle, respectively. Variable $a$ is the height of the bottom triangle, which was defined to set the constraint of the whole structure height.

The corner angle and inner spacing of DAH were scaled down and up, respectively, to prevent sharp edges and wider sample variations. Therefore, the normalized geometry variables and its range are:

$$h^{\prime }=2.19h\to 7.67 \mathrm{mm}\le h^{\prime }\le 13.14 \mathrm{mm}$$

(3)

$${\theta }^{\prime }=0.36\theta \to 16.47°\le {\theta }^{\prime }\le 22°$$

(4)

where $h^{\prime }$ = adjusted inner cell spacing of DAH

• $h$ = global variable of inner cell spacing
• ${\theta }^{\prime }$ = adjusted angle of DAH cell’s corner
• $\theta$ = global variable of cell’s corner angle

Since the edges of DAH cells are connected vertically, one more constraint must be added to define the height. Note that the number of cells stacked vertically is four cells; therefore, the total structure height is $4h^{\prime }+a$.

$$4h^{\prime }+a=h_{total}=65.8 \mathrm{mm}$$

(5)

$$a=65.85 \mathrm{mm}-4h^{\prime }$$

(6)

where $a$ = height of the bottom triangle within DAH cell

• $h_{total}$ = total height of the stacked DAH cells

3.

Star-shaped

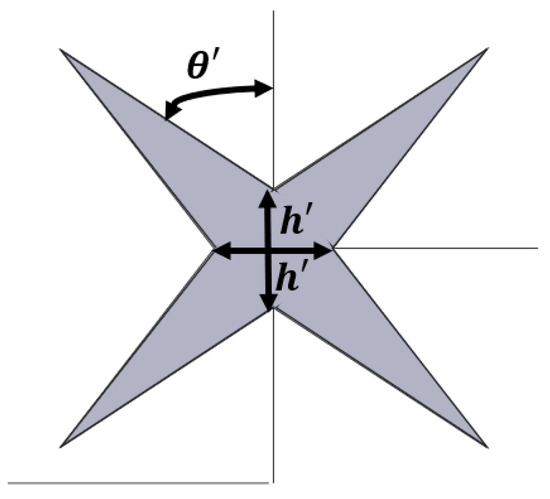
Figure 12. Variable definitions in the Star cell in millimeters (mm), $h^{\prime }$ and ${\theta }^{\prime }$ indicate the adjusted cell gap width and cell corner angle, respectively.

$$h^{\prime }=0.6h\to 2.7 \mathrm{mm}\le h^{\prime }\le 3.6 \mathrm{mm}$$

(7)

$${\theta }^{\prime }=\theta \to 45°\le {\theta }^{\prime }\le 60°$$

(8)

where $h^{\prime }$ = adjusted inner cell spacing of Star

• $h$ = global variable of inner cell spacing
• ${\theta }^{\prime }$ = adjusted angle of Star cell’s corner
• $\theta$ = global variable of cell’s corner angle

Star-shaped cells have a constant cell height, and the inner spacing is scaled down to prevent conflict with the corner angle dimension.

4.

Double-U hierarchical (DUH)

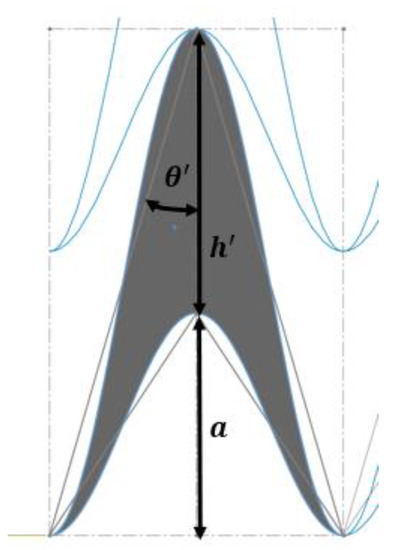
Figure 13. Variable definitions in the DAH cell in millimeters (mm), $h^{\prime }$ and ${\theta }^{\prime }$ indicate the adjusted cell gap width and cell corner angle, respectively. Variable $a$ is the height of the bottom triangle, which is defined to set constraint of the whole structure height.

The underlying geometry of DUH cells is the DAH shape. Therefore, normalization is equivalent to DAH.

$$h^{\prime }=2.19h\to 7.67 \mathrm{mm}\le h^{\prime }\le 13.14 \mathrm{mm}$$

(9)

$${\theta }^{\prime }=0.36\theta \to 16.47°\le {\theta }^{\prime }\le 22°$$

(10)

where $h^{\prime }$ = adjusted inner cell spacing of DAH

• $h$ = global variable of inner cell spacing
• ${\theta }^{\prime }$ = adjusted angle of DAH cell’s corner
• $\theta$ = global variable of cell’s corner angle

3.1.2. Material Definition

The material variations are carbon steel, aluminum, glass fiber reinforced polymer (GFRP), and carbon fiber reinforced polymer (CFRP). Carbon steel and aluminum are modeled using the piecewise linear plasticity, while GFRP and CFRP are modeled using the material of enhanced composite damage.

A.

Carbon steel and Aluminum Material Definition

Carbon steel material was defined by material properties obtained from a study by Wang et al. [11], while aluminum material was defined using Al 6061–T6 properties from ASM Material Data (basic properties) [21], Garcia’s paper (true stress-strain curve) [22], and Abotula’s paper (strain rate sensitivity parameters) [23]. The material data are detailed in Table 4.

Table 4. Material properties for non-composite materials (carbon steel and aluminum).

Non-Composite Material Properties		Value		Unit
	Type	Carbon Steel	Aluminium (Al6061-T6)	-
Basic Mechanical Property	Density (ρ)	7850.0	2700	kg/m3
	Young Mod (E)	210.0	68.9	GPa
	Yield Strength ($\sigma$)	350.0	276	MPa
	Poisson’s Ratio (ν)	0.3	0.33	-
Strain-rate sensitivity	C	-	25,000
	P	-	0.95

The curve of true plastic strain versus effective stress for both materials are also indicated in Figure 14.

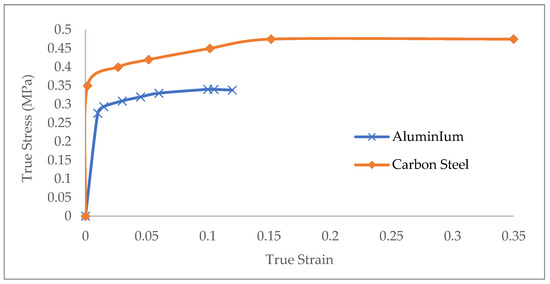
Figure 14. True stress-strain curve of carbon steel and aluminum Al6061-T6.

• B. Composite Material Definition (GFRP and CFRP)

In this study, GFRP material was defined by material properties obtained by research by Dong [18] and Tanapornraweekit [19]. As for CFRP material, the definition used properties from a study by Mutalib [20]. The properties are shown in Table 5.

Table 5. Composite material properties.

Composite Material Properties	Value		Unit
Type	GFRP	CFRP	-
Density (ρ)	1600.0	2700	kg/m3
Longitudinal Young Mod. (E1)	75.6	68.9	GPa
Lateral Young Mod. (E2)	17.7	68.9	GPa
In-plane shear mod. (G12)	2.8	5.24	GPa
Out-of-plane shear mod. (G23)	-	2.24
In-plane shear strength (S12)	0.07	0.071	GPa
Longtd. Tensile strength (XT)	1.33	2.28	GPa
Transv. Tensile str. (YT)	0.069	0.057	GPa
Longtd. Compressive str. (XC)	0.547	1.44	GPa
Tranvs. Compressive str. (YC)	0.262	0.228	GPa
In-plane Poisson Ratio (PR12)	0.3	0.021	-
Out-of-plane Poisson Rat. (PR13)	-	0.021	-
${\epsilon }_T$ max	-	1.38%	-
${\epsilon }_C$ max	-	1.175%	-

3.1.3. Sampling Process

To build an accurate and representative model, a wide and diverse range of samples should be chosen but must also be limited to restrict the required computational time. Therefore, the sample number was set to 100, divided into 80 samples for the training data set and 20 samples for the validation data set. The division was based on an 80–20 ratio for the training-validation data set, which is machine learning optimization’s rule of thumb to ensure accuracy and not overfit the model [27]. The predicted SEA value from the machine learning algorithm was compared with the result of numerical simulation; hence, the error can be calculated.

The sampling was performed using two method(s): discrete variable values were chosen with Uniform Probability Distribution, and continuous variable values were chosen with Latin Hypercube Sampling (LHS). LHS is a statistical method for generating a near-random sample of parameter values from a multidimensional distribution [28]. LHS generates samples by considering the previously created sample points. Therefore, it can ensure that the set of random numbers is representative of the real variability.

In this case, 100 samples and three continuous variables were distributed randomly using LHS to determine the representative sample points to build an accurate model. The generated sample variables’ distributions are indicated in Figure 15 (continuous variable), Figure 16 (categorical variable), and Figure 17 (numerical sampling space distribution).

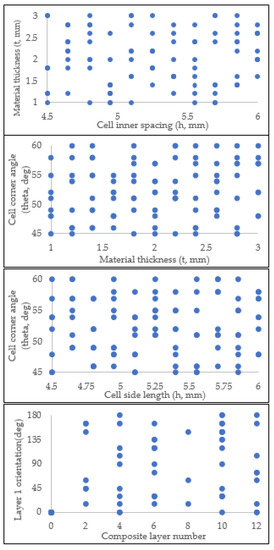
Figure 15. Generated sample space of continuous variables, which are cell thickness (t), corner angle ($\theta$), inner spacing (h), and composite layer orientation.

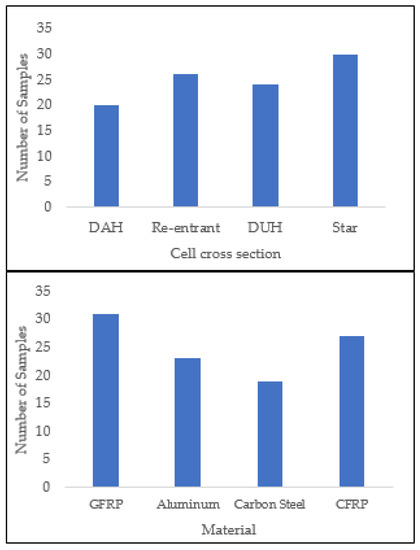
Figure 16. Generated sample space of categorical variables, which are cell cross section and material type.

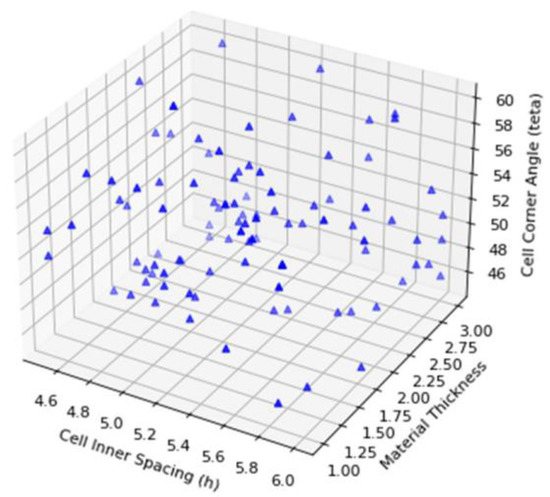
Figure 17. Generated sample space of continuous variables in a three-dimensional space, which are cell inner spacing (h), material thickness, and cell corner angle. One node indicates one variable combination.

These sampled data were then used as input for numerical simulation to obtain the value of the SEA output variable. The keyword configuration was set according to previous validation modeling. After the value was obtained, the data set was complete. The parameters for simulation are indicated in Figure 18.

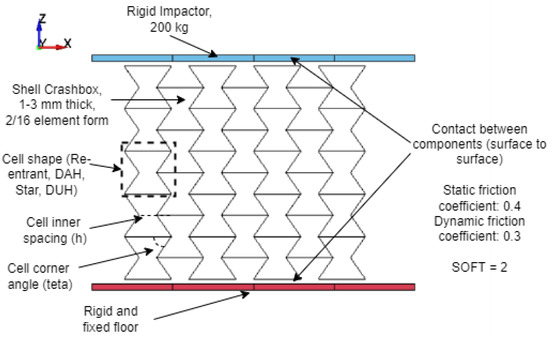
Figure 18. Numerical simulation configuration to obtain the specific energy absorption in each sample, consisting of the cell structure, impactor, and floor.

3.1.4. Numerical Simulation of Samples

The generated samples were then modeled for the numerical simulation to compute their crush resistance performance, as shown in Figure 19, Figure 20, Figure 21 and Figure 22. The elements were meshed using meshes 2 mm in size.

Figure 19. Numerical simulation configuration of Re-entrant cells.

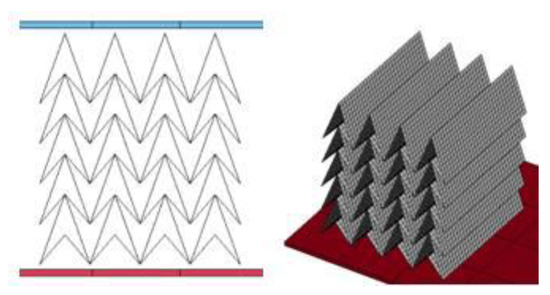
Figure 20. Numerical simulation configuration of DAH cells.

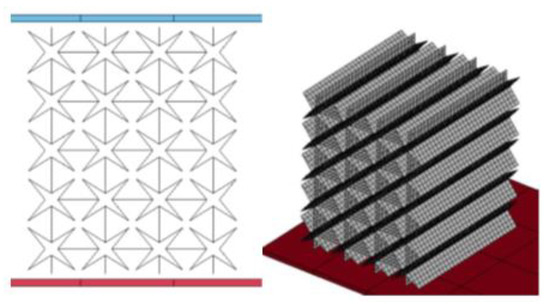
Figure 21. Numerical simulation configuration of Star-shaped cells.

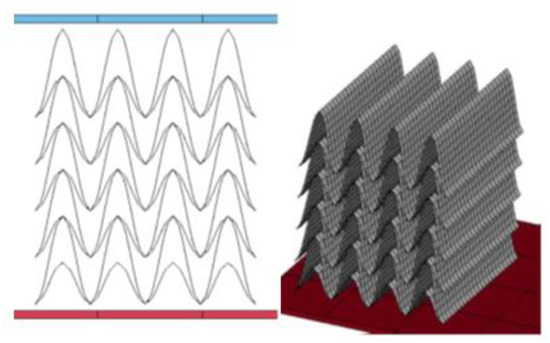
Figure 22. Numerical simulation configuration of DUH cells.

3.1.5. Output

The parameter output is the Specific Energy Absorption (SEA), which indicates the amount of absorbed energy per unit mass of the structure affected during the impact. The objective is the maximum SEA amount since it yields the most efficient energy absorption. Therefore, SEA was evaluated as the optimization output. The energy absorbed was calculated using the following formula:

$$EA={{\displaystyle \int }}_{t_i}^{t_f}F\left(x\right) d\delta$$

(11)

where F(x) = crushing force during impact (kN). F(x) was obtained from a force curve generated by the numerical simulation.

dδ = infinitesimal displacement during impact (mm)

The total mass was computed from the model. After both variables are computed, the SEA (Specific Energy Absorption) can be calculated:

$$SEA=\frac{EA}{mass}, objective=maximum SEA$$

(12)

3.2. Data Preprocessing

The generated sample data were pre-processed before they could be used as an input for the ANN model. Categorical data (in this case, the shape of the cross-section) should be converted into a proper form in numerical quantification. The process was completed in two steps: (1) changing categorical variables into a unique index number, namely 1, 2, 3, and 4; and (2) building an artificial variable to address these variables independently. The transformed data are presented in Table 6.

Table 6. Categorical variables transformation to dummy variables. This pre-processing was performed using the OneHotEncoder algorithm, which encodes categorical features as a one-hot numeric array. In addition, dummy variable “1” was removed from each categorical variable to prevent a “dummy trap” (multi-collinearity between two variables) [29].

Categorical Variable		Variable Index	Dummy Variable
			1	2	3	4
Cross-section shape	Re-entrant	1	1	0	0	0
	DAH	2	0	1	0	0
	Star	3	0	0	1	0
	DUH	4	0	0	0	1
Material type	GFRP	1	1	0	0	0
	CFRP	2	0	1	0	0
	Carbon Steel	3	0	0	1	0
	Aluminium	4	0	0	0	1

The transformed categorical variable was then combined with other previously sampled inputs, i.e., cross-section dimension (inner cell spacing and corner angle), thickness, number of composite layers, and composite orientations. Since the composite layers are also varied, the unused layers will have a null orientation angle, and the null value should be defined properly to differentiate that with 0° angles. Meanwhile, a composite with 0° orientation means that it has a direction aligned with the longitudinal axis of the structure. Therefore, the composite layer orientations need to be transformed into the following equation set:

$$i-th layer orientation=\{\begin{array}{l}2-cos\left({\beta }_i\right), if layer-i exist\\ 0, if layer-i not exist\end{array}$$

(13)

where $\beta$ = ply orientation, and $0°\le \beta <180°$ (if $\beta =180°$, then change it to $0°$ first).

3.3. Model Architecture of Artificial Neural Network (ANN)

The Artificial Neural Network (ANN) model was used as a regressor model for the optimization equations. The model configuration had five hidden layers, with a uniform 10 neuron units each. These numbers number of hidden layers and units were chosen based on an iterative process to minimize the value of error or loss function. In this research, ANN was modeled using the Keras package (Python) from Tensorflow [30].

There were 16 units in the input layer (to connect the pre-processed variables) and one unit in the output layer, which illustrated in Figure 23. These layers were the frontmost and rearmost layers of the ANN model, respectively, which were connected through several hidden layers. The parameters of each hidden layer are described in Table 7. The input variables, which are fed into input layer, are also defined in Table 8

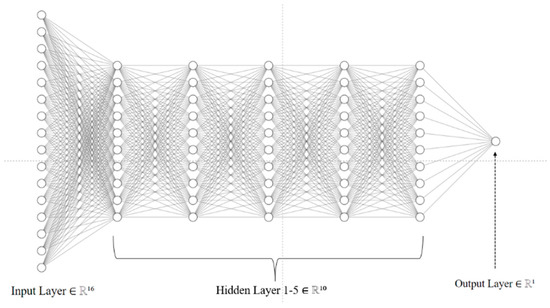
Figure 23. ANN model architecture (input, hidden, and output layers configuration), which consisted of neurons (nodes) and its connecting line.

Table 7. Neuron units, weights, biases, and activation function in each ANN layer.

Layer	Number of Neuron Units	Number of Weight	Number of Bias	Activation Function
Dense_1 (Input to Hidden Layer 1)	16	160	10	Linear
Dense_2 (Hidden Layer 1 to 2)	10	100	10	Relu
Dense_3 (Hidden Layer 2 to 3)	10	100	10	Sigmoid
Dense_4 (Hidden Layer 3 to 4)	10	100	10	Relu
Dense_5 (Hidden Layer 4 to 5)	10	100	10	Sigmoid
Dense_6 (Hidden Layer 5 to 6)	10	100	10	Relu
Dense_7 (Output)	1	10	1	Sigmoid

Table 8. Input variables for the design optimization.

Input Number	Variable	Data Type
1	Dummy 2 Cell Shape (DAH)	Boolean (0/1)
2	Dummy 3 Cell Shape (Star)	Boolean (0/1)
3	Dummy 4 Cell Shape (DUH)	Boolean (0/1)
4	Dummy 2 Material (CFRP)	Boolean (0/1)
5	Dummy 3 Material (Carbon Steel)	Boolean (0/1)
6	Dummy 4 Material (Aluminium)	Boolean (0/1)
7	Inner spacing (h)	Float (4.5–6)
8	Thickness	Float (1–3)
9	Corner angle	Float (45–60)
10	Number of layers	Integer (2, 4, 6, 8, 10, 12)
11	Layer 1 & 12 Orientation	Float (0–3)
12	Layer 2 & 11 Orientation	Float (0–3)
13	Layer 3 & 10 Orientation	Float (0–3)
14	Layer 4 & 9 Orientation	Float (0–3)
15	Layer 5 & 8 Orientation	Float (0–3)
16	Layer 6 & 7 Orientation	Float (0–3)

The output variable, SEA, had a Float data type. The ANN optimization model was built using the Sequential() function contained under TensorFlow Keras package [31], of which the parameters were defined as shown in Table 9.

Table 9. Parameters for Sequential() function as predictor algorithm.

Parameter	Value
Learning Batch	5
Validation Data Split	20%
Epoch (number of iterations)	4000
Epoch Step	300
Initialization	Normal Distribution
Activation Function	Linear, ReLU (Rectified Linear Unit), and Sigmoid
ANN Optimizer	Adam
Error Parameter	Mean Squared Error (MSE)

3.4. Model Output of Artificial Neural Network

Based on the iteration performed by the ANN model, that the results showed that the created ANN architecture yielded relatively small errors. The obtained model loss for training and validation data set was described as MSE and MAE, as shown in Table 10.

$$MAE=\frac{1}{N}{\displaystyle \sum }_{i=1}^N\left|y_i-\widehat{y_i}\right|, MSE=\frac{1}{N}{\displaystyle \sum }_{i=1}^N{\left(y_i-\widehat{y_i}\right)}^2$$

(14)

where $MAE$ = Mean Absolute Error

Table 10. ANN model metrics (MSE and MAE) at Epoch 4000.

Parameter	Training Set	Validation Set
Mean Squared Error (MSE)	2.64 × 10−7	0.0274
Mean Absolute Error (MAE)	2.49 × 10−4	0.1245

• $MSE$ = Mean Squared Error
• $N$ = number of samples
• $i$ = index of sample data point
• $y_i$ = i-th predicted data value from ANN
• $\widehat{y_i}$= true value of i-th sample

Based on these results, it can be seen that the model had a relatively low absolute error of 0.1245 (12.45%). The ANN model also obtained the weight and bias for each layer. The total obtained weight amounted to the number of layers multiplied by the number of branches of each layer, while the total obtained bias was 1 for each unit.

Since the activation function used was ReLU and sigmoid, a linear equation could not be directly derived from the generated weight and bias. Instead, the ANN model was imported directly to the NSGA-II optimization algorithm.

3.5. Single Variable Optimization Using NSGA-II

The ANN model was then used as input for the NSGA-II algorithm to determine the set of design parameters for the maximum SEA. This algorithm used the trained ANN model and iterated the variables’ values based on the defined constraint and objectives. The objective for NSGA-II optimization was limited to achieve the maximum possible SEA, while the constraint was the geometrical and material definition range.

The NSGA-II algorithm iterated the design variables, including h (inner cell spacing), θ (cell corner angle), t (material thickness), and composite layer orientations. The iteration was set to 1000 times, which resulted in design point candidates which satisfied the maximum SEA requirement.

3.6. Decision on Optimized Model

The NSGA-II algorithm generated the largest predicted SEA of 37,346.37 J/kg. The largest SEA was achieved with design variables shown in Table 11.

Table 11. Obtained optimum design variables.

Design Details	Value	Unit
Cross-section	Star	-
Material	Aluminium	-
Cell inner spacing ($h$)	5.557	mm
Material thickness ($t$)	2.95	mm
Cell corner angle ($\theta$)	56.82	degrees
Number of the composite layer	0
Predicted SEA	37,346.37	J/kg

The obtained design variables were then modeled (as shown in Figure 24) and tested using LS-DYNA to ensure the accuracy of ANN prediction and NSGA-II optimization. The design configuration was similar to the design sampling configuration.

Figure 24. Numerical simulation configuration of the optimized (left) and baseline model (right).

The amount of force, energy absorption, mass, and SEA can be obtained from numerical simulations. The comparison of design variables and output values is indicated in Table 12.

Table 12. Design input and output variables. The optimized model had 1220.6% higher SEA than the baseline model, and the SEA approximation error of ANN-NSGA method was equal to 6.7% compared with the FEM.

	Baseline Model		Optimized Model
Design Input Variables	Value	Unit	Value	Unit
Cross-section	Re-entrant	-	Star	-
Material	Carbon Steel	-	Aluminium	-
Cell inner spacing (h)	4.6	mm	5.6	mm
Material thickness (t)	1.0	mm	2.9	mm
Cell corner angle ($\theta$)	55.4	degrees	56.8	degrees
# of composite layer	0	-	0	-
Output Variables	Value	Unit	Value	Unit
Mass	0.6	kg	0.7	kg
Energy Absorbed	1676.2	J	28,579.6	J
Calculated SEA from FEM	3031.0	J/kg	40,027.4	J/kg
Predicted SEA from ANN-NSGA	-	-	37,346.4	J/kg
Error between ANN-NSGA and FEM			6.7%
Comparison of Optimized SEA with Baseline SEA			1220.6%

The optimized model had 1220% higher SEA than the baseline model. On the other hand, its predicted SEA differed by only 6.70% from the actual SEA from numerical simulation. The results imply that the generated ANN-NSGA II model can accurately predict SEA. Therefore, this optimized model was chosen and tested with full system simulation using the optimized auxetic structures, battery, and enclosing plates. The force versus displacement curves of the optimized and baseline model are shown in Figure 25. Note that the force amount of the baseline model is shown using the secondary axis on the right side since the force difference was relatively huge.

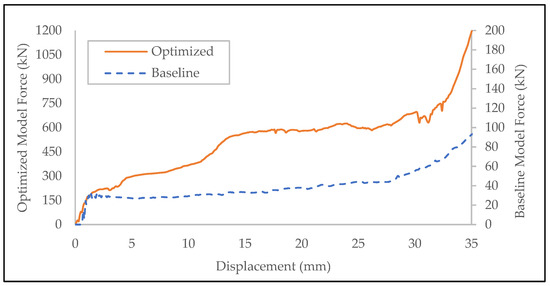
Figure 25. Comparison of the force vs. displacement curve between the optimized and baseline model. It can be seen that the optimized model had a higher force amount compared with the baseline model.

From the force versus displacement plot, the crushing force of the optimized model had a significantly larger magnitude than that of the baseline model, which led to much higher energy absorption. The total energy plot during computation is shown in Figure 26.

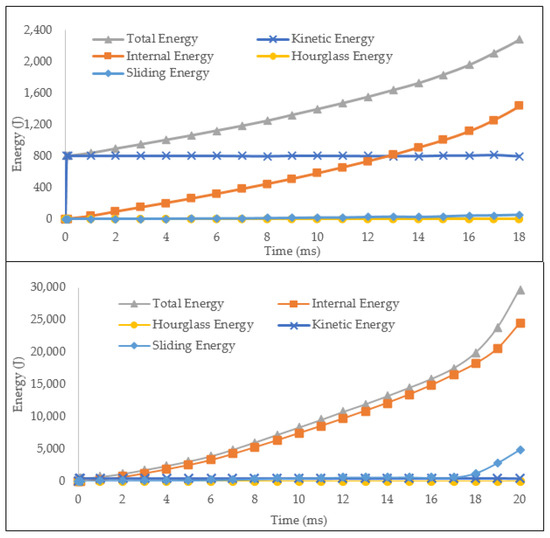
Figure 26. Energy plot for the baseline (upper) and optimized (lower) model during the impact.

Note that the impactor moved in quasi-static mode with constant velocity, so the kinetic energy value was constant. Both energy curves indicate that no negative energy occurred and the internal energy continuously increased. Therefore, both the baseline and optimized model showed high fidelity in the numerical computation.

4. Numerical Analysis of Battery System with Optimized Protection Structure Design

4.1. Numerical Modeling

This final simulation, which modeled as shown in Figure 27, demonstrates how effective the optimized structure can be applied during a real ground impact case to a battery placed underneath an electric vehicle. The configuration was based on the ground impact model of Lightweight Structures Laboratory ITB with some modifications, cited from the battery protection system model by Biharta [10]. The material properties, keywords, and dimensions of the battery system were set according to the cited model.

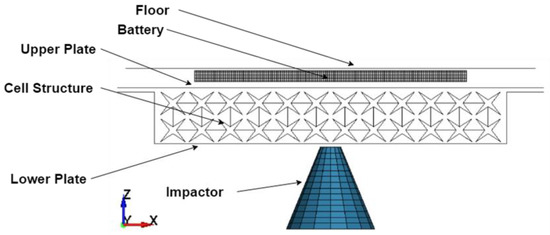
Figure 27. Battery system configuration with the cell.

The battery system consisted of a pouch battery, floor, plate enclosure for the auxetic structure, and impactor. The floor represents the vehicle’s structure base, and the complete system of plate and auxetic structure formed a sandwich structure. The impactor was modeled as a cone to represent a foreign object that may interfere with the battery system.

This simulation ensures that the optimized structure can prevent excessive pouch battery deformation through its energy absorption mechanism. According to a study by Sahraei et al. [13], the maximum displacement for pouch batteries before a thermal runaway is 2.9 mm. If the structure can absorb impact energy and prevent the excessive deformation, it can be concluded that the structure is crashworthy and eligible for battery protection.

4.2. Simulation Results

The numerical simulation result was performed with a time range of 2 ms. The result of impact simulation can be seen in Figure 28, with a time range of 2.00 ms.

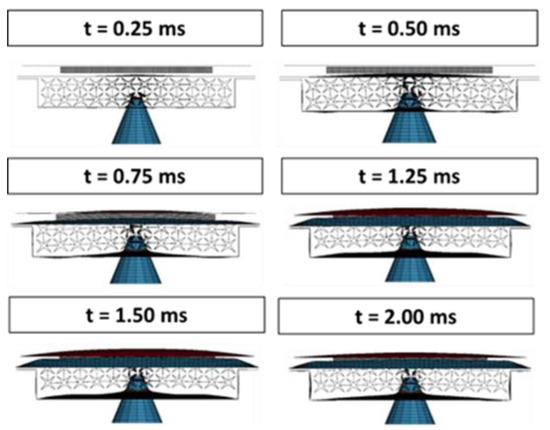
Figure 28. Numerical impact simulation result.

The battery system and cell structure energy values were also plotted to check the ability of the structure to absorb impact energy. It can be seen from Figure 29 and Figure 30 that the system’s internal energy increased as the impactor’s kinetic energy decreased; therefore, the crash energy was absorbed.

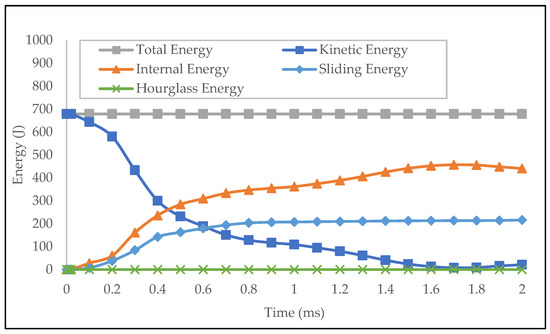
Figure 29. Impact energy plot of the complete battery system (battery and protection structure).

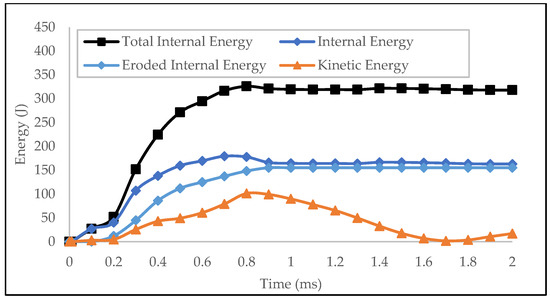
Figure 30. Impact energy curve of the protection structure only.

The displacement of nodes along the battery was calculated to check whether the cell structure could limit battery deformation. Battery deformation was examined in five different points within the battery planar (as indicated in Figure 31), which was expected to have the most significant deformation. At each point, the distance between the uppermost and lowermost nodes, the local thickness, was calculated throughout the simulation time range to see the deformation as a time function, which can be defined by the following equation:

$${\delta }_i\left(t\right)=h_i-h_0=\left(z_{i, upper}-z_{i, lower}\right)-5.35 \mathrm{mm}$$

(15)

where ${\delta }_i\left(t\right)$ = deformation/change of local thickness as a function of time

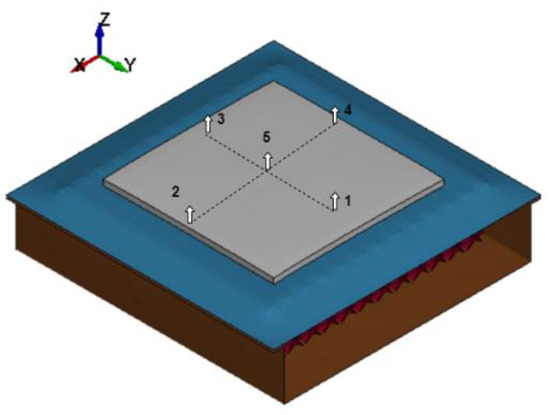
Figure 31. Measurement positions to check the battery deformation.

• $i$ = index of analyzed point within the battery
• $h_i$ = final local thickness after deformation (equals to the difference of z-coordinate of upper and lower points, or $z_{i,upper}-z_{i,lower}$)
• $h_0$ = local thickness before deformation (which is uniform at 5.35 mm)

For points 1, 2, 3, and 4, the maximum deformation occurred at the closest points to the vehicle base floor edges (located right over the battery). The floor’s sides were constrained, which caused the battery to be more compressed, and therefore, they experienced larger compression than other points. On the other hand, point 5 had the largest displacement due to the impact but did not have the largest compression since the vehicle base floor adjusted its shape. From the Measure tool in LS-DYNA, the change in local battery thickness during the impact can be obtained, as shown in Figure 32 and Table 13. The largest deformation was experienced by point 1, which was equal to 1.338 mm.

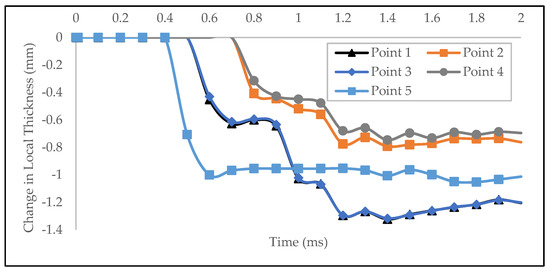
Figure 32. Change in the local battery thickness throughout the simulation. Note that points 1 and 3 experienced almost similar deformation; therefore, the curve overlaps each other.

Table 13. Deformation value at each measured point.

Deformation (in mm)	Point 1	Point 2	Point 3	Point 4	Point 5
Maximum	−1.338	−0.799	−1.336	−0.746	−1.058
Minimum	−9.54 × 10−7	−5.09 × 10−3	−1.00 × 10−6	−6.38 × 10−3	0.000

Since the maximum battery deformation was less than 2.9 mm, the optimized structure design can prevent battery failure.

5. Discussion and Conclusions

The optimal auxetic structure design with maximum SEA was determined using a machine learning method with the Artificial Neural Network (ANN) and Nondominated Sorting Genetic Algorithm II (NSGA II), as shown in Table 10. The design parameters included the cross-section shape, dimensions, and material. It was found that a Star-shaped auxetic made by aluminum Al 6061 T6, with 2.95 mm of thickness, 5.557 mm of inner spacing, and 56.82° of corner angle, resulted in the maximum SEA within the specified variable range. This SEA prediction method had the accuracy of 12.45% based on validation of the mean absolute error (Table 9).

This optimized model has a 12-times higher SEA than the baseline model and a Re-entrant auxetic structure made by carbon steel with a thickness of 1 mm. This implies that the structure can absorb more impact energy with a much lighter mass. The ANN-NSGA method predicted that the optimized model had 37.35 kJ/kg of SEA, while the baseline model had 3.03 kJ/kg of SEA. FEM simulation was performed to validate the optimized model and obtained that the SEA was 40.03 kJ/kg. Therefore, the error between the ANN-NSGA prediction and FEM simulation was 6.7%, indicating that the optimized model is valid.

The obtained design was numerically tested within a complete battery system model to check whether the design could protect the battery from impact or not. The model used was a pouch battery type, and it was set to experience ground impact, modeled with an impactor moving from the bottom. It was obtained that the design could absorb crash energy and prevent the battery from failure, in which the maximum battery deformation was 1.338 mm, while the allowable deformation was 2.9 mm.

Further research works in the future are encouraged to develop this research by expanding the data training, exploring more machine learning algorithms, and considering heat dissipation for optimization. First, the data training can be expanded to more auxetic shape options and dimension variations. Second, more machine learning algorithms can be explored, such as Pareto-dominance-based, decomposition-based, and indicator-based algorithms [32]. Lastly, heat dissipation simulation and optimization can also be performed to verify that the structure can optimally dissipate battery heat to prevent thermal runaway, along with protecting the battery from external impact.