Optimal Sizing, Control, and Management Strategies for Hybrid Renewable Energy Systems: A Comprehensive Review

Abstract

To meet the expanding energy demand, all available energy sources must be utilized. Renewable energies are both eternal and natural, but their major downside is their inconsistency. Due to the rising costs of fossil fuels and the CO₂ they emit, hybrid renewable energy (HRE) sources have gained popularity as an alternative in remote and rural areas. To address this issue, a hybrid renewable energy system (HRES) can be developed by combining several energy sources. In order to build modern electrical grids that have advantages for the economy, environment, and society, the hybrid system is preferable. A summary of various optimization methods (modeling techniques) of an HRES is presented in this paper. This study offers an in-depth analysis of the best sizing, control methodologies, and energy management strategies, along with the incorporation of various renewable energy sources to form a hybrid system. Modern hybrid renewable energy system utilities rely more on an optimal design to reduce the cost function. Reviews of several mathematical models put out by various academicians are presented in this work. These models were created based on reliability analyses incorporating design factors, objective functions, and economics. The reader will get familiar with numerous system modelling optimization strategies after reading this study, and they will be able to compare different models based on their cost functions. Numerous modeling approaches and software simulation tools have been created to aid stakeholders in the planning, research, and development of HRES. The optimal use of renewable energy potential and the meticulous creation of applicable designs are closely tied to the full analysis of these undoubtedly complicated systems. In this field, as well, several optimization restrictions and objectives have been applied. Overall, the optimization, sizing, and control of HRES are covered in this paper with the energy management strategies.

1. Introduction

Solar energy is the most cost-effective way for India to meet its future energy needs. Solar energy is becoming more affordable in India, attracting buyers interested in environmentally friendly energy sources [1]. Until 2015, the majority of Indian cities had no solar power plants. As a result, improved hybrid PV facilities will be required to meet future energy demand. This research may be used to aid in the selection of the optimal hybrid PV system for a smart city, taking into account the specialized displays as well as environmental and economic concerns [2]. HRES are one of the most viable and dependable alternatives to the main power grid for electrifying rural consumers, as they help to reduce fossil fuel consumption while mitigating climate change [3]. An HRES has the advantages such as high reliability, less energy storage capacity needed, increased efficiency, modularity, and minimized LCOE over single-energy-source-based systems [4,5].

To meet the global energy demand, industry will continue to devour all available resources in the near future. Due to the coronavirus epidemic and total shutdown, global energy consumption fell 5.9% in 2020 compared to 2019 [6]. New wind and solar projects built in recent years have increased productivity. Renewables usually obtain grid preference, so they do not have to adjust their production to match demand [7]. According to Exxon Mobil’s most current energy prediction [8], green and nuclear energy will contribute to around 25% of global power in 2040.

Poorly structured and disorganized HRES project development can lead to higher-than-expected investment costs. As a result, various modeling and methodologies and simulation software have been used to assist HRES stakeholders in their research, planning, and development efforts [9]. In reality, HRES simulation includes calculating numerical formulas that outline the mathematical models for the function of the relevant HRES components. As a result, the system’s behavior can be illustrated, and the decision-making process for the project can be aided [10]. It is worth noting that the simulation algorithms generate non-identical combinations of renewable energy systems based on the user’s input parameters (for example, meteorological data and size parameter range) [11,12]. The non-identical combinations of the various simulation approaches can be attributed to their inherent diverse dispatch strategies [13]. Given the system components, the terrain of the area, and the meteorological data, the HRES performance optimization must be performed with a method that is proven to work [14].

Figure 1 depicts the parameters that comprise a relevant HRES optimization process. Regardless of its complexity, an efficient understanding, analysis, design, and planning of an HRES project necessitates conducting a thorough theoretical prefeasibility analysis and thoroughly examining the validity of its results using specialized simulation software and relevant scenarios used as case studies [4,11]. As a result, a comprehensive HRES study is directly related to effective RES utilization and precise project design [15]. The “Holy Grail” for HRES optimization in this area is to use a well-designed and efficient sizing method that works [16]. One ideal size methodology is needed to properly and cost-effectively utilize renewable energy supplies. By fully using the PV, WT, and battery bank, the best size approach may assist in securing the lowest investment, allowing the hybrid system to function at its most cost-effective and dependable levels. When you set cost goals and look at the system’s performance over time, you can obtain the best balance of dependability and cost [17]. An HRES is a type of electrical system that combines one renewable energy source with several others. The system may be used on or off the grid, and it can employ traditional, sustainable, or hybrid energy sources [18]. Many commercial software programs, including HOMER, iHOGA, PVSyst, PVSOL, TRNSYS, RETScreen, INSEL, and others, have been found to be useful in sizing and optimizing HRES [19].

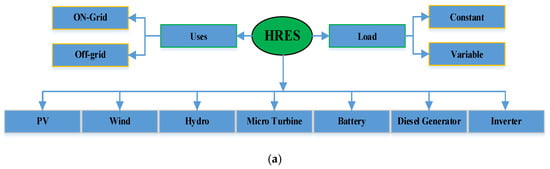
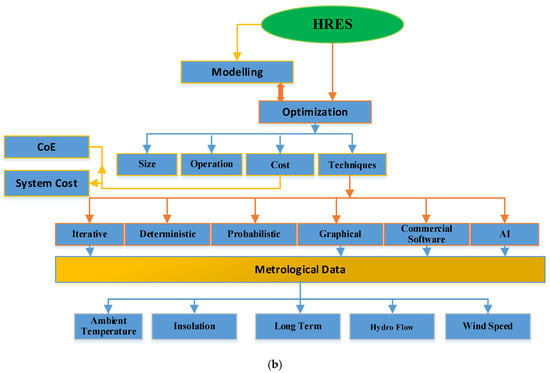
Figure 1. (a,b) An HRES optimization methodology.

R. Siddaiah et al., focuses on most current methodologies published for sizing a PV/wind hybrid system, as well as a quick assessment of advancements in optimization methods, cost analysis tools, and storage system strategies [20]. S. Dawoud et al., focus on unique approaches offered in hybrid energy practice based on physical modelling with diverse hybrid network optimization processes [21]. Vivas et al., reviewed the most recent research on off-grid renewable energy systems using hydrogen storage technology [22]. Tezer et al. [23] looked at how multi-objective optimization strategies for system cost and durability have progressed over the previous two decades. In a feasibility study, Khare et al. looked at optimal size, modelling, control components, and reliability issues. Furthermore, this review [24] discusses the use of development technologies and game theory in the construction of HRES. Energy management measures must be employed to ensure the appropriate functioning of HRES, as well as to sustain demand and improve performance. A well-thought-out energy management strategy allows the system to meet demand while simultaneously prolonging the life of system components, minimizing operational costs and enhancing the use of RES. It also allows the system to conserve energy, prevent elements from being damaged by overload, and improve the power system’s reliability, all of which lead to improved system performance [6]. Energy needs and RE provisioning approaches, energy frameworks, HRES deployment, and energy readiness management were all examined by Y. Liu et al., SPV, WT, DGs, and battery solutions that are more efficient have all been proved [25]. Figure 2 depicts the number of publications for HRES (1992 to 2022) based on various configurations.

Figure 2. Number of Publications for HRES (1992 to 2022) depending on various configurations.

The majority of renewable energy installations are used to power off-grid locations or to fulfill global network demand (buildings, industry, and the residential sector). This section will concentrate on the most commonly used HRES energy consumption profile. Isolated area: This type of load can be an island, a small settlement in the Sahara, a mountain, or a small number of houses off the grid; dwelling sector: This sort of load varies depending on the location of the resident (poor or wealthy country) and the amount of appliances installed; industry: due to technical and economic constraints, such as the need for a vast space, the continuity of energy production, the quality of energy, and the need for a substantial investment fund, this type is rarely explored by researchers in their investigations; buildings: this sort of building can be a market, a university, a laboratory, an administration, an education facility, etc., and it is defined by low consumption (few kilowatts) and grid connectivity, transportation, etc.) [26].

This study gives a thorough review of the most recent HRES research along four important axes: sizing (using commercial software or a traditional and new generation approach), optimization (conventional, novel generation, and hybrid methods), planning and controlling (centralized, distributed, hybrid, and new generation methods), and energy management (technical goal-oriented strategy, economic goal-oriented strategy, and techno-economic goal-oriented strategy). This research also focuses on the most recent hybrid system approaches that have been published and established, as well as the generators used in these systems. At the end of the section, there is a detailed comparison of algorithm applications, as well as their benefits and drawbacks.

The following is a summary of the current study’s novelty:

• According to a study framework on energy consumption profiles, when HRES is adjusted technically and economically using sophisticated optimization techniques or commercial software, it may successfully meet energy demand in remote places.
• HRES is frequently optimized using advanced optimization techniques such as fuzzy logic, ANNs, and evolutionary algorithms. The most prevalent commercial scaling software is HOMER PRO and RET Screen.
• The most frequently used control technology for providing stability, protection, and power balancing is MPPT (based on PSO, neural networks, and fuzzy logic).
• In order to choose the finest one, the current literature study exposes advanced optimization approaches and software.
• This paper discusses the objective function, figures of merit, limitations, conclusions, challenges, and future research.

This paper is divided into six sections: The Section 1 is an introduction; the Section 2 dealt with HRES optimization methods (modeling techniques) in depth; and the Section 3 discusses the method for sizing an HRES. The Section 4 is about the HRES control mechanism and management strategy. In the Section 5, challenges and further studies of an HRES are discussed. Finally, Section 6 is made of this study in the sixth section.

2. HRES Optimization Methods (Modeling Techniques)

In a hybrid system, there are numerous objectives that need to be optimized, such as size, modeling, control, and management [27]. In this section, a list of the most often utilized optimization methods in recent years is compiled. Subramanian et al., categorized energy systems modeling methodologies into two groups based on modeling approach and application area requirements [10]. Ghofrani and Hosseini [28] used a different approach and divided the major optimization algorithms into three categories: classical algorithms, metaheuristics algorithms, and hybrids energy system modelling strategies were classified as analytical, simulation, or MCS (Monte Carlo simulations) methods by Tina et al. [29] and Khatod et al. [30]. The last category included three modeling sub-approaches depending on input variable management techniques. Simple time series, probabilistic approaches, and average daily (or even monthly) energy balance values were also considered. The numerous optimization strategies discussed can be grouped into two main groups, according to another approach [10,17,31]: traditional optimization techniques and next generation optimization approach techniques. The modelling approaches reported in this study are grouped into three categories according to the structure employed by most scientists in the HRES “enterprise,” as illustrated in Table 1 as:

Table 1. Modeling techniques overview.

Techniques		Reference
Conventional Optimization Techniques	Iterative techniques:  ✓ Linear Programming  ✓ Dynamic Programming  ✓ Multi-objective optimization Probabilistic techniques Deterministic techniques Graphical construction techniques	[32,33] [34,35] [36,37,38] [10,29,39,40] [41,42,43] [10,44,45]
New generation Optimization Techniques	GA AI techniques ANN FL PSO SA ACO ABC TLBO techniques	[10] [17,31] [17,46] [47] [47,48,49,50,51] [52,53,54] [54,55,56,57] [47,49] [58]
Hybrid Techniques	Probabilistic and Deterministic technique SA-PSO ANN-GA Downhill Simplex technique	[30] [54] [59] [60]

2.1. Conventional Optimization Techniques

The iterative technique uses a series of mathematical simulations to arrive at a set of roughly approximated outcomes that may be used to address the problem at hand. The simulations are run on a computer until all of the conditions are fulfilled [10]. To be more specific, iterative approaches are used to perform the linear adjustment of the values supplied to HRES decision variables, resulting in a scan of all potential generating unit configurations. In this light, the computation of how dependable the system’s power may be by evaluating each design, as well as the ideal configuration, is discovered. The evolutionary algorithm (sometimes known as a heuristic approach) is a development of the well-known iterative technique. Despite the faults that result in a localized rather than a global optimum solution, the number of choice variables has minimal impact on the evolutionary process; its growth is proportional to an exponential increase in simulation time [61]. Linear programming techniques [32,33], dynamic programming techniques [34,35], and multi-objective optimization approaches [36,37,38] are examples of iterative techniques. Probabilistic approaches are defined as a statistical explanation of the design of each variable, awarding random values based on the data imported. Hourly or daily simulations are carried out [10,29,39,40]. On the other side, deterministic approaches look at load demand and resources as predictable quantities with known time-series variation [41,42,43]. Graphical construction procedures are created when the optimization functions and the outlines are drawn in the same graph. These strategies can solve the optimization problem [10,44,45] by focusing on the region of implementation. Table 2 outlines several common optimization strategies.

Table 2. Conventional optimization techniques used in HRES.

Techniques	Methods	System Components	Description	Objectives	Objective Function	References
Conventional Optimization Techniques	Iterative approach	PV/Wind/Battery	A recursive approach to find the best solution This strategy is easy to understand and can detect hazards early	Minimizing the cost of system	$$\begin{gathered} \mathrm{Minimize}: \mathrm{TLCC} ({\mathrm{A}}_{\mathrm{PV}}, {\mathrm{A}}_{\mathrm{WT}}, {\mathrm{N}}_{\mathrm{BAT}})=\min \\ {{\displaystyle \sum }}_{m=PV,WT,BAT,Inv}{\mathit{LCC}}_{\mathrm{m}} \end{gathered}$$	[62]
	Probabilistic approach	Wind/FC/Electrolyzer/Battery	Variable randomness affects a system’s performance It cannot depict the hybrid system’s changing nature	Loss of power probability Lowering TNPC while meeting demand	$$\begin{gathered} \mathrm{Minimize}: \mathrm{TNPC}=[{\mathrm{NPC}}_{\mathrm{WT}}+{\mathrm{NPN}}_{\mathrm{FC}}+{\mathrm{NPC}}_{\mathrm{Elect}}+ \\ {\mathrm{NPC}}_{\mathrm{Tank}}+{\mathrm{NPC}}_{\mathrm{CON}}+{\mathrm{NPC}}_{\mathrm{Comp}}+{\mathrm{NPC}}_{\mathrm{Ref}\&\mathrm{Reac}}] \\ \mathrm{Minimize}: \mathrm{LSSP}=\frac{{{\displaystyle \sum }}_{t=1}^{8760}LPS\left(t\right)}{{{\displaystyle \sum }}_{m=1}^{8760}{P}_L\left(t\right)} \end{gathered}$$	[29,63]
	Linear programming	PV/Wind/Biomass	Best solution for complex problems due to liner relationship Unreasonable assumptions between input and output	Minimizing the outsourced electricity supply Maintaining a healthy energy storage capacity	$$\begin{gathered} mi{n}_{x_{1\in {\Omega }_1}}OES={\displaystyle \sum }_{j\in J}{\displaystyle \sum }_{t\in T}{P}_{jt}^{as}\mathsf{\Delta }t \\ mi{n}_{x_{2\in {\Omega }_2}}ESC={\displaystyle \sum }_{s\in S}{q}_s^{cap} \end{gathered}$$	[64]
	Graphical construction	PV/Wind/Battery	Graphical representation of the optimization constraint’s solution Unpractical to incorporate PV and Wind turbine system parameters	Minimizing the cost of system	${\mathrm{C}}_{\mathrm{CS}}={{\displaystyle \sum }}_{k=PV,WT,}N$K (CCK + CMK + CIK) + CBatt,N $\mathrm{LPSP}=\frac{{{\displaystyle \sum }}_{t=0}^{T}LP{S}_t}{{{\displaystyle \sum }}_{t=0}^T{P}_{L\left(t\right)}}$	[44,45]
	Method of trade-off	Solar/Wind	It is based on the principle of gain at the expense of loss Not utilized in the research of hybrid systems commonly	Assign alternative possibilities Necessary to limit risk	$\mathrm{C} = [{{\displaystyle \sum }}_{\mathrm{K}=\mathrm{PV},\mathrm{WT},\mathrm{GI},\mathrm{BAT}}(I_{\mathrm{K}}{\mathrm{S}}_{\mathrm{PK}} + {\mathrm{OM}}_{\mathrm{PK}})] + \frac{1}{E_{y\ast N}}$	[65]

2.2. New Generation Optimization Techniques

Metaheuristics optimization approaches can be used to describe the techniques in this area: GA approaches are global search heuristics, which are subsets of evolutionary algorithms [10]. They are elitist search techniques with a simulation in which the greatest individual in a generation is passed on to the next generation without degeneration [29]. GA employs Darwin’s theory to describe the survival of species in a population, which consists of three fundamental processes (selection, crossover, and mutation) and three critical regulatory parameters (population size, crossover, and mutation rates) [58,59]. Following a random selection of people from the initial population (“the parents”), the three major processes are used to create the “children” for the following generation. After that, the technique continues with consecutive generations of individual solution adjustments until the required optimal population evolution is achieved [66]. By using broad crossover and mutation procedures that produce new populations at every stage of the process, GA avoids jeopardizing adherence to the local optimum. Nonetheless, in order to solve the optimization problem, GA requires a huge number of control decision variables as input. It’s crucial to figure out what the best controlling coefficients are, because changing them can change the algorithm’s performance [58]. M. Paulitschke et al., employed a GA to build and optimize a hybrid system for feeding remote locations in Senegal that included a solar generator, WT, DG, and storage system (battery). This research has two goals: one is economic, and the other is environmental. The first aim is to lower the level cost of the system, and the second is to reduce CO₂ emissions. The data reveals an inverse relationship between levelized cost and CO₂ emissions, with CO₂ emissions declining from 762.08 to 11.89 per year when leveled cost rises from 1.22 to 2.05 €/kWh [67].

ANNs are computational (or mathematical) models based on biological neural networks [17]. They use a connectionist approach to simulation to depict the assessed system’s intermediate solutions and analyze the incoming data. They’re made up of linked artificial neuron clusters [68,69]. Amirtharaj et al. AGONN’s approach [70] is a hybrid of ANN and AGOA that leverages ANN to determine optimal utilization and reduce switching loss in a system. In terms of current, voltage, and power signal, the results reveal that the proposed methodology outperforms the GOA, CMBSNN, and WOANN.

PID controllers use FL to calculate the error as well as the change in error between the actual outputs and the reference (or control) inputs. The scaled values are accepted by the “main controller” at the controller’s operational level (fuzzification (or input) stage) depending on the decision-making mechanism (fuzzy inference (or processing) stage). The defuzzification (or output) step generates the output values, which are then fed into the fuzzification stage. It’s vital to continue the technique until you have an ideal result (error convergence to zero) [47]. Derrouazin et al. employed FL multi inlet/outlet to regulate the energy flux of a hybrid system that included SPV, WT, and batteries. The results show that the electronic switches’ signals accurately and quickly track the hybrid power system’s imposed input power states [71].

PSO [72] is a technique for population-based evolutionary simulation. Its prominence is expanding due to its quick convergence and ease of usage in single-peak and multisensory activities. Swarm optimization [48] is a method inspired by nature that optimizes non-linear functions by imitating bird flocking and fish schooling. Its accuracy [50] is related to its popularity as the most widely used metaheuristic algorithm [49]. To achieve the global optimum, each iteration stage computes the position and velocity of each particle in the swarm individually. In order to achieve the required outcome, each particle records two possible values: pbest (the best solution discovered thus far) and swarm best (the best solution found by the entire swarm) [54]. According to Kennedy and Eberhart [48], the tracking of the aforementioned data is conceptually similar to the GA crossover procedure. When Bilal et al. blended this methodology with a GA to enhance a hybrid model based on SPV and CSP with battery, the results demonstrated an improvement in both financial (leveled expense of 16.33€/kWh) and technological (static effectiveness of 10.92% and 305,940 MWh energy output) parameters when compared to other approaches and processes [73].

SA [52,53,54] is a strategy used to tackle discrete search space optimization issues. TLBO [58] is a population-based approach that uses two phases for simulation, similar to GA and ABC. It is based on the conventional classroom technique (teaching–learning). The learner/student and the instructor (who is receiving instruction from the teacher) are the two phases (during the final phase, each person strives to develop by engaging with other students). The population to achieve the global solution in this nature-inspired method is a group of students. The numerous optimization problems control variables produce the various subjects proportionally allotted to the learners. Each learner is assigned a value grade for each subject that corresponds to a possible alternative, and the quality of the proposed answer is reflected in the overall mean grade. The greatest response for the entire population is represented by the instructor [57].

The ACO is a straightforward and trustworthy heuristic search strategy that mimics ant behavior physiologically. It is used for highly non-linear situations [54,55,56,57] when there is no utility in adopting standard procedures. A recently created metaheuristic approach is inspired by the well-structured work division and organization that includes employed bees, observer bees, and scout bees. Honeybees’ natural waggle-dancing behavior for foraging reasons [49] inspired ABC. Scout bees are in charge of exploration, whereas spectator bees are in charge of exploitation [47]. The ABC approach achieves the global optima while avoiding the local optima by ignoring Hessian and gradient matrix data while using population-based stochastic principles. The ABC techniques include two steps: initialization and repetition, with the latter separated into three categories: engaged bee step, bystander bee step, and Scout bee step [49]. Some new generation optimization techniques in Table 3.

Table 3. A list of the new generation optimization techniques.

Techniques	Methods	System Components	Description and Objectives		Objective function	Reference
New Generation Optimization	ANN	PV/WT/hydrogen	The ANN is a modelling technique derived from human sensory organs It allows for learning by instance using representative sample that portrays a tangible event or a subsequent decision	Lowering TLCC	$$\begin{gathered} \mathrm{Minimize}: \mathrm{TLCC} ({\mathrm{A}}_{\mathrm{PV}}, {\mathrm{A}}_{\mathrm{WT}}, \mathrm{N}{\mathrm{H}}_2)=\mathrm{Min} \\ {{\displaystyle \sum }}_{k=PV,WT,FC,Ele,H2,Inv}{\mathit{LCC}}_K \end{gathered}$$	[74]
	FL	PV/WT/Battery	Fuzzy logic, which is based on basic if-then principles, is one of the artificial intelligence fields that mimics human reasoning in terms of linguistic variables Fuzzy logic may also be used to forecast chaotic behavior	Lowering ACS	ACS = (ICPV + ICWT + ICBAT + ICINV) + (MCPV + MCWT) + (DCPV + DCWT) min ACS (APV, rWT, SOCmax)	[75]
	COA (or CSA)	PV/WT/Battery	For continuous non-linear optimization, the cuckoo optimization algorithm (COA) is utilized COA is based on the lifestyle of the cuckoo family of birds The construction of this optimization technique is based on the living style, egg laying characteristics, and breeding of these birds	Lowering TSC	$\mathrm{Minimize}: {\mathrm{C}}_{\mathrm{TOTAL}}=\mathrm{Min} \sum n_i$$\{ {\mathrm{R}}_{\mathrm{i}}{\mathrm{A}}_{\mathrm{i}}=\mathrm{Min} \sum n_i$$\{ {\mathrm{R}}_{\mathrm{i}}{\mathrm{A}}_{\mathrm{i}}\frac{r_0{\left(1+r_0\right)}^m}{{\left(1+r_0\right)}^m-1}$ + o&m RiAi} + CostRelaibility (PV, WTG, BAT, INV)	[76]
	BFO	PV/WT	It obtains its inspiration from bacteria’s ageing processes	Examination of dependability	${\mathrm{EIR}}_{\mathrm{Y}}=1-\frac{{{\displaystyle \sum }}_{m=1}^{12}EEN{S}_m}{{{\displaystyle \sum }}_{m=1}^{12}{L}_m}$	[29]
	PSO and GA	PV/Battery/FC	It is a technique that follows the spontaneous selection approach It solves optimization issues using spontaneous progression processes including heredity, mutation choice, and cross-over Problems with several solutions are easy to resolve	Lowering LCC	$$\begin{gathered} {\mathrm{T}}_{\mathrm{PV}}={\mathrm{T}}_{\mathrm{PV}, \mathrm{kal}} \\ {\mathrm{T}}_{\mathrm{batt}}=\max (\frac{Z_{batt}}{Z_{batt,max}},T_{batt,kal}) \\ {\mathrm{T}}_{\mathrm{FC}/\mathrm{Elect}}=\max (\frac{S_{FC/Elect}}{S_{FC/Elect,,max}},\frac{T_{Oh,FC/Elect}}{T_{Oh,FC/Elect,,max}},T_{FC/Elect,cal}) \end{gathered}$$	[67,72]
	PSO	PV/wind/DG/battery	It is inspired by fish and bird behavior PSO’s calculations are simple and quick, and they may be finished quickly PSO is unable to solve issues that are not in a coordinate system	Lowering ACE, LCOE, and the CO2 emissions	$\mathrm{Minimize}: \mathrm{ACE}=\frac{LCOE\left(x\right)}{E_{annual}}$ Minimize: LCOE (x) = CCAP(x) + CMAINT(x) + CREPL(x)	[73,77]
	SA	PV/wind/battery	It imitates the annealing process of a material. It uses a technique known as trajectory random inquiry to do global optimization The capacity to avoid local minima is its primary benefit It can handle with noisy data but very non-linear processes	load demand with the minimal TAC	$$\begin{gathered} \mathrm{Minimize}: \mathrm{TAC}=\mathrm{Capital}+\mathrm{Maintenance} \\ \mathrm{CRF}=\frac{r_0{\left(1+r_0\right)}^m}{{\left(1+r_0\right)}^m-1} \end{gathered}$$ Capital = CRF [NWTCWT + NPVCPV + NBatteryCBattery + NConv/InvCConv/Inv] Maintenance = NPVCPV,M + NWTCWT,M	[78]
	ACA	Water/wind/solar/Hydrogen	This method, which is based on a pheromone strategy, is supported by the ageing nature of ants This approach showed how ants look for the quickest path between their colonies and their food supply This algorithm includes both global and local searches	reliability of the system, Lowering TAC	FTotal(x) = a1 TAC(x) + a2 LPSP(x) min[TAC(x)] = min[Capital(x) + Maintenance(x)] x = [NPV, NWT, PHydro, PFC, PELECT]	[79]
	MOCSA	PV/DG/FC	The multi-objective crow search algorithm (MOCSA) uses the max-min technique to define the fitness function from a set of weight vectors	optimal design of system components, Lowering TNPC and LPSP	$$\begin{gathered} \mathrm{Minimize} \mathrm{TNPC}({\mathrm{N}}_{\mathrm{PV}}, {\mathrm{N}}_{\mathrm{DG}}, {\mathrm{N}}_{\mathrm{FC}}, {\mathrm{N}}_{\mathrm{Elect}}, {\mathrm{N}}_{\mathrm{HT}})= \\ [{\mathrm{NPC}}_{\mathrm{PV}}+{\mathrm{NPC}}_{\mathrm{DG}}+{\mathrm{NPC}}_{\mathrm{FC}}+{\mathrm{NPC}}_{\mathrm{Elect}}+{\mathrm{NPC}}_{\mathrm{HT}}+{\mathrm{P}}_{\mathrm{C}}] \\ \mathrm{Minimize} \mathrm{LSSP} ({\mathrm{N}}_{\mathrm{PV}}, {\mathrm{N}}_{\mathrm{DG}}, {\mathrm{N}}_{\mathrm{FC}}, {\mathrm{N}}_{\mathrm{Elect}}, {\mathrm{N}}_{\mathrm{HT}})=\frac{{{\displaystyle \sum }}_{t=1}^{8760}LPS\left(t\right)}{{{\displaystyle \sum }}_{m=1}^{8760}{P}_L\left(t\right)} \end{gathered}$$	[80]
	ABSO MESCA PPA	PV/WT/FC	This optimization approach was proposed by Karaboga and Basturk This algorithm is based on the honey bee’s sophisticated foraging behavior	Lowering TCS, LCE, and LSSP	$$\begin{gathered} \mathrm{C}{\mathrm{TCS}}_{ }={\displaystyle \sum }_{\mathrm{k}=\mathrm{PV}, \mathrm{WT}}(N_{\mathrm{K}} ({\mathrm{C}}_{\mathrm{CK}}+{\mathrm{C}}_{\mathrm{MK}}+{\mathrm{C}}_{\mathrm{IK}}))+{\mathrm{C}}_{\mathrm{BOS}}+{\mathrm{C}}_{\mathrm{Batt}},\mathrm{N} \\ {\mathrm{C}}_{\mathrm{TACS}}=\min ({\mathrm{C}}_{\mathrm{TCS}} \mathrm{CRF}) \\ \mathrm{CRF}=\mathrm{CRF}=\frac{r_0{\left(1+r_0\right)}^m}{{\left(1+r_0\right)}^m-1} \\ \mathrm{LCE}=\frac{C_{TACS}}{{{\displaystyle \sum }}_{t=0}^T{E}_L\left(t\right)} \\ \mathrm{LPSP}=\frac{{{\displaystyle \sum }}_{t=0}^T{E}_D\left(t\right)}{{{\displaystyle \sum }}_{t=0}^T{E}_L\left(t\right)} \end{gathered}$$	[81]
	FGA	WT/PV/micro turbine/Battery	It is a GA that is based on FL By altering the system parameters, the purpose of this blending is to maximize the performance of the GAs	Lowering the ACS, capturing the maximum amount of energy from the wind turbine/solar array	$$\begin{gathered} \mathrm{Minimize}: \mathrm{ACS}={{\displaystyle \sum }}_{m=PV,WT,BAT,,Inv,Cont}{C}_{\begin{array}{c}ACAP\\ \end{array}}\left(m\right) \\ +{{\displaystyle \sum }}_{m=BAT}{C}_{\begin{array}{c}BAT\\ \end{array}}\left(m\right)+{{\displaystyle \sum }}_{m=PV,WT,BAT,,Inv,Cont}{C}_{\begin{array}{c}O\wedge M\\ \end{array}}\left(m\right) \\ +{{\displaystyle \sum }}_{m=MT}{C}_{\begin{array}{c}FUEL\\ \end{array}}\left(m\right) \end{gathered}$$	[82]
	FHBO	PV/WT/Battery	The fuzzy honey bee’s method imitates honey bee foraging behavior to find the optimal solution to an optimization issue	Cover the load, maintain dependability, and reduce LCC	$$\begin{gathered} \mathrm{Minimize}: \mathrm{TLCC} ({\mathrm{A}}_{\mathrm{PV}},{\mathrm{A}}_{\mathrm{WT}}, {\mathrm{N}}_{\mathrm{BAT}})=\min \\ {{\displaystyle \sum }}_{m=PV,WT,BAT,ROD,Inv}LC{C}_{\mathrm{m}} \\ \mathrm{Minimize}: \mathrm{LPSP}=\frac{{{\displaystyle \sum }}_{t=1}^{T}LPS\left(t\right)}{{{\displaystyle \sum }}_{t=1}^T{E}_{Load}\left(t\right)} \end{gathered}$$	[83]
	F-QBPSO	PV/FC/Battery	The quantum behaved PSO algorithm incorporates quantum computing into the PSO algorithm To begin, assume that every particle in space has a quantum nature	Improve the hybrid system’s performance	-	[84]

2.3. Hybrid Techniques

A hybrid technique is any approach that combines two or more algorithms in order to take use of the benefits of each algorithm while overcoming the shortcomings of the single algorithm [27]. SA-CS [85], CSHSSA, IHSCSA [74], and HSSA [86] are only a few of the hybrid approaches for optimizing hybrid systems that have been developed in recent years. There are other hybrid approaches [87], GAPSO [88], MOCSA [80], GMDHMNN- MFFOA [89], and others, which integrate Monte Carlo simulation with numerous energy-balance/financial equations [90]. Table 4 highlights several hybrid optimization strategies as:

Table 4. A list of hybrid optimization techniques.

Techniques	Methods	System Components	Objectives	Objective Function	Reference
Hybrid Techniques	SA-CS	PV/WT/Battery	Lowering TLCC	$$\begin{gathered} \mathrm{Minimize}: \mathrm{TLCC} ({\mathrm{A}}_{\mathrm{PV}},{\mathrm{A}}_{\mathrm{WT}}, {\mathrm{N}}_{\mathrm{BAT}})=\min \\ {{\displaystyle \sum }}_{m=PV,WT,FC,Elect,BAT,,Inv}LC{C}_{\mathrm{m}} \\ \mathrm{Minimize}: \mathrm{LPSP}=\frac{{{\displaystyle \sum }}_{t=1}^{T}LPS\left(t\right)}{{{\displaystyle \sum }}_{t=1}^T{E}_{Load}\left(t\right)} \end{gathered}$$	[85]
	CSHSSA	PV/WT/hydrogen	Lowering TLCC and improved system dependability	$$\begin{gathered} \mathrm{Minimize}: \mathrm{TLCC} ({\mathrm{A}}_{\mathrm{PV}},{\mathrm{A}}_{\mathrm{WT}}, \mathrm{N}{\mathrm{H}}_2)=\min \\ {{\displaystyle \sum }}_{m=PV,WT,FC,H2,Electr,,Inv}LC{C}_{\mathrm{m}} \\ \mathrm{Minimize}: \mathrm{LPSP}=\frac{{{\displaystyle \sum }}_{t=1}^{T}LPS\left(t\right)}{{{\displaystyle \sum }}_{t=1}^T{E}_{Load}\left(t\right)} \end{gathered}$$	[74]
	HSSA	PV/WT/hydrogen/Battery	Lowering TLCC	$$\begin{gathered} \mathrm{Minimize}: \mathrm{TLCC} ({\mathrm{A}}_{\mathrm{PV}}, {\mathrm{A}}_{\mathrm{WT}}, {\mathrm{N}}_{\mathrm{BAT}}, {\mathrm{N}}_{\mathrm{H}2})=\min \\ {{\displaystyle \sum }}_{m=PV,WT,BAT,Elect,H2,Inv}LC{C}_{\mathrm{m}} \\ \mathrm{Minimize}: \mathrm{LPSP}=\frac{{{\displaystyle \sum }}_{t=1}^{T}LPS\left(t\right)}{{{\displaystyle \sum }}_{t=1}^T{E}_{Load}\left(t\right)} \end{gathered}$$	[86]
	GA-PSO	PV/WT/Battery	Lowering TPC while meeting load demand includes original costs, operation and maintenance costs, and replacement costs	$$\begin{gathered} \mathrm{Minimize}: \mathrm{TPC}=\mathrm{IC}+\mathrm{MC}\&\mathrm{OC}+\mathrm{RC}= \\ ({\mathrm{N}}_{\mathrm{PV}}{\mathrm{IC}}_{\mathrm{PV}}+{\mathrm{N}}_{\mathrm{WT}}{\mathrm{IC}}_{\mathrm{WT}}+{\mathrm{N}}_{\mathrm{BAT}}{\mathrm{IC}}_{\mathrm{BAT}}+{\mathrm{N}}_{\mathrm{INV}}{\mathrm{IC}}_{\mathrm{IN}})+ \\ ({\mathrm{N}}_{\mathrm{PV}}{\mathrm{C}}_{\mathrm{O}\&\mathrm{M},\mathrm{PV}}+{\mathrm{N}}_{\mathrm{WT}}{\mathrm{C}}_{\mathrm{O}\&\mathrm{M},\mathrm{WT}}+{\mathrm{N}}_{\mathrm{BAT}}{\mathrm{C}}_{\mathrm{O}\&\mathrm{M},\mathrm{BAT}}) \\ {{\displaystyle \sum }}_{t=1}^T{\left(\frac{1+infR}{1+\int R}\right)}^t+({\mathrm{N}}_{\mathrm{BAT}}{\mathrm{C}}_{\mathrm{REP},\mathrm{BAT}}+{\mathrm{N}}_{\mathrm{INV}}{\mathrm{C}}_{\mathrm{REP},\mathrm{INV}})\ast {{\displaystyle \sum }}_{t=1}^T{\left(\frac{1+infR}{1+\int R}\right)}^t \\ \mathrm{LPS}={\displaystyle \sum }_{t=1}^{8760}[P_{Load}\left(t\right)-(P_{PV}\left(t\right)\left(t\right)+P_{WT}\left(t\right)+P_{BAT}\left(t\right))] \end{gathered}$$ Minimize: $\mathrm{LPSP}=\frac{{{\displaystyle \sum }}_{t=1}^{8760}LPS\left(t\right)}{{{\displaystyle \sum }}_{t=1}^{8760}{P}_{Load}\left(t\right)}$	[88]
	GMDHNN-MFFOA	PV/WT	Estimate sun irradiance, wind speed, and energy usage	Maximize: f1 = PICP (w, b) Minimize: f2 = PINAW (w, b)	[89]
	MCS and multi energy balance/financial equations	Solar PV/Thermal	Lowering LCOE, NPV, and payback period	$$\begin{gathered} \mathrm{Minimize} \mathrm{Overall} \mathrm{Cos}\mathrm{t}={\mathrm{C}}_{\mathrm{I}}+{\mathrm{C}}_{\mathrm{O}\&\mathrm{M}} \ast {\mathrm{D}}_{\mathrm{F}}+{\mathrm{C}}_{\mathrm{R}}-{\mathrm{C}}_{\mathrm{S}} \\ =[{\mathrm{N}}_{\mathrm{PV}}{\mathrm{C}}_{\mathrm{PV}}+{\mathrm{N}}_{\mathrm{WT}}{\mathrm{C}}_{\mathrm{WT}}+{\mathrm{N}}_{\mathrm{BAT}}{\mathrm{C}}_{\mathrm{BAT}}+{\mathrm{P}}_{\mathrm{CON}}{\mathrm{C}}_{\mathrm{CON}}] + \\ ([{\mathrm{N}}_{\mathrm{PV}}{\mathrm{C}}_{\mathrm{PV}}+{\mathrm{N}}_{\mathrm{WT}}{\mathrm{C}}_{\mathrm{WT}}+{\mathrm{N}}_{\mathrm{BAT}}{\mathrm{C}}_{\mathrm{BAT}}+{\mathrm{P}}_{\mathrm{CON}}{\mathrm{C}}_{\mathrm{CON}}](\frac{1}{{(1+\frac{R-f}{1+f})}^{L_t}}))+ \\ [{\mathrm{N}}_{\mathrm{PV}}{\mathrm{C}}_{\mathrm{R},\mathrm{PV}}+{\mathrm{N}}_{\mathrm{WT}}{\mathrm{C}}_{\mathrm{R},\mathrm{WT}}+{\mathrm{N}}_{\mathrm{BAT}}{\mathrm{C}}_{\mathrm{R},\mathrm{BAT}}+{\mathrm{P}}_{\mathrm{CON}}{\mathrm{C}}_{\mathrm{R},\mathrm{CON}}]- \\ [{\mathrm{C}}_{\mathrm{R}}-\frac{L_{C }-\left(L_t-L_C\ast round\left(\frac{L_C}{L_t}\right)\right)}{L_{C }}] \\ \mathrm{LPSP}=\frac{{{\displaystyle \sum }}_{t=1}^T[P_{Load}\left(t\right)-\left(P_{PV}\left(t\right)\left(t\right)+P_{WT}\left(t\right)+P_{BAT}\left(t\right)\right]}{{{\displaystyle \sum }}_{t=1}^T{P}_{Load }\left(t\right)} \end{gathered}$$	[90]

2.4. Evaluation of Various Optimization Techniques

Optimization techniques are distinguished by their high performance, capacity to tackle difficult problems, and ability to apply many objective functions. The most common disadvantage of all optimization approaches, however, is that they take too long and are difficult. Traditional techniques to economic optimization are the most successful, but they have a limited number of optimization parameters. Due to the sophisticated procedure and codes utilized, the new generation optimization approach requires high hardware performance to function. The efficacy and speed of this strategy, as well as its precision, are its primary advantages. Integrating classical and new generation optimization approaches reveals a methodology with great speed and resilience, but it also necessitates advanced design and difficult code generation. The Table 5 highlights the benefits and downsides of each optimization method:

Table 5. Benefits and downsides of each optimization techniques [19,20,26,91].

Techniques	Advantages	Drawbacks
Conventional Optimization Techniques	Beneficial in making investment decisions Make it possible to solve a multi-objective problem It took less time	Relationship between variables is linear Optimizing limited space Discrete and continuous probability are required for this method
New generation Optimization Techniques	Accurate calculations Maximum degree of efficiency Very fast convergence	Complicated problem-solving procedure Long-term memory storage is required There are a number of modifications that must be made
Hybrid Techniques	Less time is needed Highest efficiency The highest level of durability Rapid convergence	The system’s design is complicated Solutions that are more extensive Difficulty in obtaining code

3. Methods for Sizing an HRES

The hybrid system’s size is a crucial factor in determining the generators’ capabilities. The system may be undersized or enormous if it is not properly sized. The most difficult part is calculating true load and step time so that oscillations can be adequately accounted for. Most studies, on the other hand, use data samples of a few hours, days, or months [91]. There are two sorts of sizing methods: software-based and conventional approaches as shown in Figure 3 as:

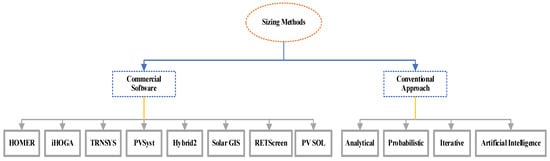
Figure 3. Methods of sizing.

3.1. Software for an HRES Sizing

There are several commercial apps for scaling hybrid systems, and the bulk of them, such as RET Screen, iHOGA, INSEL, HOMER, ReOpt, SAM, and WISDEM, operate on Windows and utilize the programming language Visual C++ [92]. Baneshi et al. size a hybrid system in Shiraz, Iran, that comprises a DG, SPV, and WT, as well as a storage system (battery), using the HOMER software tool. The goal of this article is to develop a hybrid model that is both financially feasible and low in CO₂. According to [93], the best economic outcome is a total leveling cost of 9.3 to 12.6 cents per kWh, with 43.9 percent coming from global production and renewable fuels. Fadaeenejad et al. used the iHOGA tool to make a hybrid model that involves two RES (SPV and WT) and two typical units (DG and batteries) for a tiny Malaysian community [94]. The RERL at the University of Massachusetts designed the Hybrid2 tools with an NREL grant. Mills et al. in Chicago use this tool to size a combined PV/wind/FC plant. The modelling for the fuel cell alternative [95] reveals that there is enough RE to cover the peak load.

“RET Screen”, a tool for projecting and evaluating energy infrastructure, analyses systems from a variety of perspectives, including technological, financial, ecological, and power efficiency [96]. P. Kumar et. al. used a Canadian modelling tool to analyze systems from a variety of perspectives, including technological, financial, ecological, and power efficiency, simulate model SPV, WT, DG, and a blended battery bank. The results reveal a 99% decrease in CO₂ emissions [97], owing to the hybrid system’s reliance on renewable energy. Table 6 summarized the inlet and outlet attributes of each scaling tool as:

Table 6. Sizing tool’s input and output [19,20,23,26,92,93,94,95,96,97].

Input	HOMER	PV SOL	RETScreen	TRNSYS	PVSyst	Solar GIS	iHOGA	Hybrid2
Load demand	√							√
Resources data	√	√	√	√	√	√	√	√
Component data	√	√				√	√	√
Constraints	√	√			√		√
Controlling a system	√		√
Data on emissions	√		√				√
Data on the economy	√				√		√
Financial information	√	√						√
Databases for projects			√		√
Database of products			√
Models taken from own collection	√			√
Output	HOMER	PV SOL	RETScreen	TRNSYS	PVSyst	Solar GIS	iHOGA	Hybrid2
Optimizing the size	√		√		√		√	√
technical evaluation	√		√	√			√	√
financial assessment	√	√	√		√	√	√	√
Environmental analysis	√		√			√
Optimization with many objectives	√						√
Emissions from a life cycle	√		√				√
Analytical probability	√		√				√
Risk assessment and sensitivity analysis	√		√	√		√
Thermoelectric and thermal energy system dynamic modeling behavior	√			√	√

The tool “TRNSYS” is largely used to model thermal systems [96]. Kumar et al., use this tool to make and model PV and thermic hybrid systems; the analysis reveals that hybrid solutions outperform SPV systems both economically and technologically [97].

The comparison of tools reveals various qualities and limits for each one, as shown in Table 7. The most significant points are picking the finest software depending on system usage and degree of size optimization, which means that RET Screen and HOMER can size any system using a simple optimization formula, with a 10 kW restriction, iHOGA may size any system, Solar GIS has less technical parameters and requires internet, and PV SOL has not supported an advanced sizing algorithm, TRNSYS & PV Syst cannot size all generators without optimization since Hybrid2 has certain inherent issues. RET Screen and HOMER are the best software package for sizing HRES, as per the outcomes of this evaluation.

Table 7. Evolution of different scaling approaches (professional tools) used in hybrid system [1,19,26,92,93,94,95,96,97,98].

Commercial Software	Advantages	Limitations
HOMER	Create an efficiency graph with the results Simple to comprehend	Employs first-order linear equations Time series data cannot be imported It’s going to take a lot of information to get started The user is unable to pick relevant system components intuitively
PV SOL	In a short period of time, develop and estimate a PV power system Graphics are quite precise	A complex computation isn’t possible Sometime a circuit schematic is presented incorrectly
RETScreen	The most comprehensive meteorological database Excel-based software	Input of data is reduced Data from time series cannot be imported
TRNSYS	Simulator adaptability Graphics are quite accurate	Some generators, such as hydropower, are unable to be simulated There is no option for optimization
PVSyst	Fast design and estimate of a PV power system Simulator flexibility	Simulation takes a long time There is no single-line diagram There isn’t a way to optimize it
Solar GIS	Simulations that are easy to use and quick to complete Extensive meteorological database, including a map	Because there are fewer technical factors, a feasibility study is not possible To perform the simulation, you’ll need access to the internet
iHOGA	Simulation step time is short Genetic algorithms are used to carry out the task, which can be mono or multi-objective	Lack of sensitivity analysis and probability analysis Daily load limitation (10 kWh) Only one configuration should be simulated at a time
Hybrid2	A wide range of electrical load possibilities Dispatching options that are more detailed In terms of optimization variables, it is comprehensive, and it necessitates a higher degree of system configuration expertise	Simulations should take a long time Despite the fact that the project was completed successfully, certain simulation flaws were discovered Only one configuration should be simulated at a time

3.2. Traditional Approaches for Scaling HRES

Traditional sizing procedures are divided into four categories, such as: (1) analytical techniques, (2) iterative techniques, (3) probabilistic techniques, and (4) AI techniques, as explained below.

3.2.1. Analytical Techniques

The scale of the hybrid model is characterized by feasibility [99], which is depicted by a mathematical formula. In 2015, Madhlopa et al. published a study in South Africa that employed an analytical approach to build a hybrid model that included wind and solar generator elements. The purpose is to take steps to improve the hybrid system’s water efficiency. A hybrid core delivers 100 GWh/year, 0.97 €/kWh, and 75 km³/year, according to Figures [100].

3.2.2. Iterative Techniques

This approach is a recursive algorithm program that ends when the optimal system design is achieved [19,96]. Camargo et al. adopted this methodology to size a standalone hybrid model driven by SPV, WT, and batteries for supply to a Brazilian rural hamlet. The aim of this exercise is to establish a system which is both inexpensive and trustworthy. According to models, the optimum hybrid model architecture is 500 W of SPV, three WTs (600 W each), and five batteries (1200 Wh each). With a leveled cost of 1.044 R$/Wh [101], the total cost of this system is 25.6720 kR$.

3.2.3. Probabilistic Techniques

In probabilistic techniques to integrate system size [96], the impact of meteorological conditions, isolation, and oscillations on the proposed system is taken into account. Although this is one of the most widely used size approaches, the results show that it may not be the best option for obtaining the best result [19]. The P-PoPA method was used by Wen Hui Liu et al. to size SPV, WT, biomass, and batteries. The outcome suggests that strong storage capacity and power rating are increased while offshore electricity demand is lowered [102].

3.2.4. AI Techniques

In his review paper “A Study on Configurable, Control, and Scaling Approaches of HRES”, Upadhyay [103] stated, “AI is a phrase that in its widest meaning would represent the abilities of a tool or object to accomplish identical types of functions that describe human cognition”. The GA [104], MOSaDE [105], NSGA-II [106], MBA [107], PSO [108], MLUCA [101], ABSA [109], IFFA [110], A-Strong [111], BFA [112], ANN [74], FL [75], BBO [113], CS [76], DHS [114], SA-CS [85], ACO [115], and so on have all been used to discover the appropriate size for hybrid systems. Table 8 outlines the different size methodologies [17], together with their components of the system and target functions:

Table 8. Recent studies on optimum sizing.

Sizing Methods		System Component	Objective	Reference
Analytical Method		Wind/PV	LCOE	[100]
		Wind/PV/BAT	Load demand, reduce initial cost, and operation cost.	[116]
Iterative Method		Wind/PV/BAT	Lowering LPSP	[101]
Probabilistic Method		Wind/PV/Biomass/BAT	Lowering STC, ACS, LCOE, and Maximizing NPV	[102]
AI Method	GA and BMNLIP	Wind/PV/FC/Battery	reduction of investment cost and operation cost	[98]
	GA	PV/CSP	Optimize capacity factor while lowering LCOE and total initial investment	[104]
	MOSaDE	Wind/PV/DG/BAT	Minimize COE and LPSP	[105]
	SACS	Wind/PV/BAT	Minimize TLCC	[108]
	IFFA	Wind/PV/DG/BAT	Lowering costs and emissions	[110]
	ANN	Wind/PV/H2	Lowering TLCC	[74]
	Fuzzy logic	Wind/PV/BAT	Lowering ACS	[75]
	BBO	Wind/PV/DG/BAT	Lowering TC	[113]
	ACO	Wind/PV/DG/BAT	Lowering TAC	[115]
	GOA	Wind/PV/BAT/DG	Lowering LOCE	[117]
	MBOA	Wind/PV/FC/BAT	Lowering the overall ACS	[107]
	PSO and a novel energy filter algorithm improved grey wolf optimizer (IGWO)	Wind/PV/BAT Wind/PV/DG/BAT	Lowering the TSC and increasing reliability Lowering cost of energy (COE) and the loss of power supply probability	[118] [119]

3.3. Evaluation of Various Sizing Techniques

Traditional methods are characterized by their ease of use and speed, yet these advantages restrict their performance and analysis. Because artificial intelligence uses multi-objective functions to tackle complicated problems, this flaw can be overlooked. This problem can be resolved through an iterative algorithm if the approach is based on a fundamental algorithm that engages in a cyclical process to build the best-sized configuration. Based on a basic numerical model, an analytical technique may quickly size up a hybrid system with limited functionality. However, this approach has the drawback of ignoring some important elements. For all difficult procedures, as compared to earlier approaches (analytical and iterative), AI is the best solution as it is endless and generates outstanding results. The complexity codes that are employed in this approach are the most difficult parts of the challenge. Table 9 compares the various hybrid system sizing methods.

Table 9. Comparison of various scaling approaches (conventional approach) employed in hybrid systems [1,19,26,27,30].

Methods	Advantages/Features	Limitations/Drawbacks
Analytical method	Quick and simple to use Time-series data is no longer required	The degree of flexibility is extremely limited The optimization procedure can only involve two parameters
Iterative method	Easy to operate Eliminate the need of time-series data	Some critical parameters of higher wind turbines and solar photovoltaic slope angle were overlooked Typically, this leads to higher computing effort and poorer results
Probabilistic Method	Easy to operate Time-series data is no longer required	No way to show the hybrid system’s dynamic performance
AI Method	Solve a multi-objective and complex problem Find the global best system configuration with the least amount of compute Capable of balancing at least two conflicting goals at the same time	High complexity

4. HRES Control Mechanisms and Management Strategy

4.1. HRES Control Mechanisms

The following parameters should be monitored in any blended system: [120,121,122,123]:

• System stability refers to the system’s voltage and frequency.
• Protection entails keeping an eye on the power flow.
• Power balance refers to the allocation of loads in the most efficient way.

A variety of control systems for wind turbines have been proposed in the literature, including MPPT based on PSO [124], allocation of voltage vectors on the grid side converter relying on DPC [125], and pitch control employing a resilient sliding mode technique [126]. Several control strategies have been used to enhance solar panel effectiveness [127,128], including MPPT based on GRNN [129], deep learning neural network for solar photovoltaic prediction [130], and using MPPT in partially shadowed scenarios [131]. Voltage control [132], frequency control [133], and reactive power [134] have all been key research fields for DGs. Controlling hybrid renewable power systems may be achieved in a variety of ways, including centralized control [135], distributed control [136], and hybrid control [137], as well as RBC [138] and P-I control [139]. Classical techniques include neural network algorithms [140], FL controllers [141], multi-objective PSO [142], and ANFIS [143].

Because distributed or hybrid control is efficient in decentralizing control, minimizing system failure, and allowing the use of several forms of control in a single hybrid system, it is used in the majority of hybrid systems. The intricacy of the connection and processing codes is the only drawback to this sort of control. When used in a small size HRES, this type of control demonstrates high efficacy, better performance, and ease of building. Furthermore, as compared to dispersed or hybrid control, the cost of centralized control is lower. Until then, there is a good chance that the system will be entirely shut down if there is an issue with the generators or that maintenance will be scheduled. Table 10 highlights the key categories of control, as well as their benefits and drawbacks.

Table 10. A comparison of the various control techniques [19,26,96,97].

Method of control	Advantages	Drawbacks
Centralize Control	Energy expenses are kept to a minimum Able to achieve global optimization	Utilize only single-point systems of control
Distributed Control	There’s a low chance of a system failure. Achieve low and medium levels of utilization	Internal system connections are difficult to understand Most of the solutions are not optimal
Intelligence Control (Classical Control)	Power expenses are kept to a minimum Optimize the entire system	Controlling the system is very difficult It’s incredibly difficult to design an algorithm
Hybrid Control	Centralized control allows for local optimization Local controllers are rarely used	Controlling the system is very complex The system’s connections pose a number of difficult problems.

4.2. An HRES Management Strategy

Hybrid system management enables year-round system supply [22], a rise in element longevity, a reduction in economic parameters (global cost, leveling cost, etc.), and, as a consequence, system performance optimization (Figure 4). HRES management strategies are classified into three groups as shown in Figure 5 as:

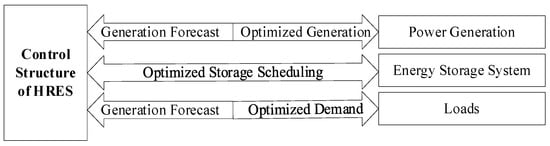
Figure 4. Intelligent energy flow structure.

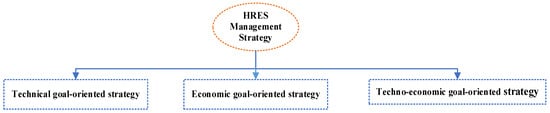
Figure 5. HRES management strategies.

4.2.1. Technological Goal-Oriented Strategy

The main objective of this approach is to take into account the technical parameters of hybrid systems in order to cover energy demands [144,145,146], enhance device lifespans [147], boost performance [148], boost stability of the system [149], boost storage network lifespans (BAT, FC, super capacity, etc.) [98], and many other parameters that characterize hybrid system power sources (Table 11). PMC [150], PSO [151], real-time optimization [152], ANN [153], and HOMER PRO [154] are some of the systems employed to regulate these parameters.

Table 11. Management methods and its characteristics of hybrid system [99,155,156].

Management Methods	Design Constraints	Main Features	Advantages	Drawbacks
Technical goal-oriented strategy	Power balance Battery SOC Storage system degradation	Algorithm to control power balance Battery short time Flow chart algorithm	Less complex Increase lifetime Increase performance	Operation and maintenance cost are not optimized
Economic goal-oriented strategy	Power balance Battery SOC Cost function	Algorithm to minimize cost Power reference and priority	Minimize the system cost	Complex algorithm Increase operation and maintenance cost Lifetime are not optimized
Techno-economic goal-oriented strategy	Power balance Battery SOC Cost function Storage system degradation	Algorithm to optimized multi-objective function Power reference determination using optimization algorithm	High performance	Complex algorithm Increase operation and maintenance cost

4.2.2. Economic Goal-Oriented Strategy

Any strategy that considers particular variables that impact the system’s economic situation, independent of its technological position (stability, system performance, and so on), is an economic objective strategy (Table 11) [99]. The model predictive control [154], GA [157], differential evolution algorithm [158], MILP [159], FL [160], interior search algorithm [161], commercial software such as HOMER [162], and so on are employed in significant published economic approach studies to achieve two fundamental objectives: coverage of demand and cost-cutting of the system.

4.2.3. Technological-Economic Goal-Oriented Strategy

This method for solving multi-objective functions is based on nonlinear optimization, and takes into account both technological and economic variables. This strategy has the benefit of improving technical characteristics such as component performance and lifespan while decreasing economic factors such as global cost (Table 11) [156]. Two of the most widely used approaches in this strategy are FL [163] and PSO [164]. This concept employs a variety of approaches, including a flow chart [165], an artificial electric field algorithm [166], evolutionary computational intelligence [167,168,169], and HOMER software [72]. Table 12 lists all of the management techniques.

Table 12. Management methods review.

Techniques	Algorithm Used/Commercial Software	System Components	Objectives	Reference
Technical	SOCP	PV/DG	Maintain system security while minimizing losses	[144,145]
	PMC	Wind/PV/FC/BAT	Increase system dependability while ensuring demand	[150]
	PSO	PV/Wind/FC/BAT	Lowering LPSP and increasing SF	[151]
	ANN	PV/Wind/BAT/utility grid	Reducing PLPSP and ensuring that electricity and water demand are met	[153]
	HOMER	PV/WT/DG/Battery	Increase RES and meet electricity demand	[154]
Economical	Predictive Model Control	Wind/PV/FC/BAT	Operating and investment expenses are reduced	[155]
	GA	Wind/PV/utility grid	Reducing operational expenses	[157]
	Differential evolution algorithm	PV/Thermal	Reducing the total cost of ownership	[158]
	FL	Wind/PV/FC/BAT	Ensure that demand is met	[160]
	Interior Search Algorithm	Wind/PV/FC	Lowering costs and ensuring demand	[161]
	HOMER	Wind/PV/DG/BAT/hydropower	Lowering levelized cost	[162]
	MILP	PV/BAT	Lowering NPV	[170]
	Linear programming and simulation tools	PV/Wind/Battery	Lowering TSC	[101]
	Numerical approach and MATLAB	PV/Battery	Lowering TAC	[171]
	MILP	PV/Wind	Lowering TOC	[172,173]
	MILP and solved by GAMS software	PV	Lowering TOC	[174]
	GOA and MAT Lab	PV/Wind/Battery/Diesel Generator	Lowering LCOE	[175]
Techno-Economical	FL	Wind/PV	Improve line reliability by reducing line loss	[163]
	PSO	Wind/PV/FC/BAT	Ensure demand, save costs, and improve longevity and performance	[164]
	Artificial Electric Field Algorithm	Wind/PV/DG/BAT	Ensure demand, cost reduction, andincrease lifetime	[166]
	HOMER	PV/DG/BAT	Ensures a stable power supply, extends battery life, and lowering COE and NPC.	[72]
	RAMP-RATE CONTROL SCHEME	PV/BAT/ultra-capacitors	Increasing the NPV	[176]
	MOGA(NGAS-II)	Wind/PV	Cost reduction andensure demand	[177]
	PVSyst and RET Screen Lyapunov technique and SPSA approach	PV PV/WT/BAT	To lowering per-unit costs and greenhouse gas emissions. Improved system reliability and stability	[178] [179,180,181]

5. Challenges and Further Studies

Hybrid systems have long been seen as a viable grid-supply alternative. After it has been proven that oversizing increases system costs and inadequate power supply undersizing increases system costs, dimensioning, and optimization algorithms must successfully seek an acceptable mix of critically assessing elements such as system cost and efficiency.

• The authors used two basic methodologies are: Commercial software and conventional approaches, according to a recent study on HRES scaling. When the two approaches are compared, it becomes clear that commercial software is easier to use, more versatile in simulation, and faster, but it is limited by the use of unsophisticated optimization formulae. Conventional approaches can optimize the sizing field better than commercial tools, produce faster results, and address multi-objective problems, but they are difficult to use and complex to implement.
• Authors have been focusing on the three approaches: Traditional, next generation optimization, and hybrid methods, according to a survey of the literature. Conventional approaches in techno-economic analysis are characterized by speed and efficiency, with the disadvantage that the optimization area is limited. Because of its superior efficiency, accuracy, and faster convergence, new generation optimization methods are the most widely used in optimization; nevertheless, the downside of this strategy is that it necessitates the employment of specialized processing software.
• Hybrid approaches use the benefits of each approach to improve performance and minimize optimization processing time by combining the efficiency and speed of traditional methods with the accuracy and speed of next-generation optimization methods. Despite all of these benefits, the most significant disadvantages of hybrid approaches are the complexity of design and the difficulty of providing code.
• HRES control might be centralized, distributed, classical, or hybrid in nature. With distributed and hybrid control being the most popular due to their efficiency in controlling each generator individually, decreased system failure risk, increased system lifetime, and the ability to apply the most up-to-date control methods for each component individually. The most uncomfortable aspect of this control is the intricacy of connectivity inside the system or in program processing.

6. Conclusions

The research goals have an impact on how energy is managed in hybrid systems. Most researchers, for example, concentrate on techno-economic objectives because this type of analysis ensures both a technical (enhance life span, cover utilization, and boost performance) and an economical (mitigate the system cost and improve power cost) of HRES in order to achieve the best configuration. Many approaches are used to supervise HRES parts, including FL, PSO, ANN, and commercial software such as HOMER.

The importance of HRES for electrifying distant areas, feeding the main grid, conserving energy, reducing emissions, and lowering leveled energy costs was investigated in this research. Furthermore, the benefits and limitations of each strategy were reviewed, as well as the primary strategies for each axis (optimization, sizing, control, and management strategies). Following are the major conclusions:

• HRES may successfully fulfill energy demand in remote locations when optimized technically and economically (minimize investment cost or leveled cost) utilizing modern generation optimization techniques or commercial software.
• Traditional techniques to economic optimization are the most successful, but they have a limited number of optimization parameters. Due to the sophisticated procedure and codes utilized, the new generation optimization approach requires high hardware performance to function. The efficacy and speed of this strategy, as well as its precision, are its primary advantages. Integrating classical and new generation optimization approaches reveals a methodology with great speed and resilience, but it also necessitates advanced design and difficult code generation.
• The comparison of commercial software reveals various qualities and limits for each one, as shown in Table 7. The most significant points are picking the finest software depending on system usage and degree of size optimization. RET Screen and HOMER are the best software package for sizing HRES, as per the outcomes of this evaluation.
• Because distributed or hybrid control is efficient in decentralizing control, minimizing system failure, and allowing the use of several forms of control in a single hybrid system, it is used in the majority of hybrid systems. The intricacy of the connection and processing codes is the only drawback to this sort of control. When used in a small size HRES, this type of control demonstrates high efficacy, better performance, and ease of building. Furthermore, as compared to dispersed or hybrid control, the cost of centralized control is lower.
• To manage the HRES, techniques such as technological, economical, and techno-economical are used to reduce the entire system’s cost with the help of commercial software and other optimization techniques are reviewed.
• In order to obtain the best results in optimization, sizing, control, and management of an HRES, each research must employ a variety of approaches. On comparing numerous approaches, it ensures that the system performs well, and the objectives are fulfilled.

This review study will be helpful in navigating the difficulties and complexity involved in the investigation of HRES size, optimization, control, and management strategy. The detailed evaluation and comparative study, in this work will benefit industry, professionals, practicing engineers, and researchers for the understanding of an HRES.