Constant Power Factor Model of DFIG-Based Wind Turbine for Steady State Load Flow Studies

Abstract

DFIG (Doubly Fed Induction Generator)-based WPP (Wind Power Plant) is the most popular type of wind-driven electric power generation configuration. The main reason for its popularity is that the DFIG system can capture wind energy more optimally than other WPP configurations. Due to the increasing penetration of WPP in power systems, the need to study its impact on power system performance is becoming increasingly important. To enable such a study to be conducted properly, the first and probably the most crucial step is to model all system components (including the WPP). This paper proposes a new steady state model of DFIG-based WPP for load flow analysis. The proposed model is derived based on DFIG power formulas (i.e., DFIG stator and rotor power formulas). The model in the present work is simple and can easily be incorporated into load flow analysis. Representation of the DFIG in both sub-synchronous and super-synchronous conditions can be carried out by using a single mathematical model. Furthermore, since DFIG can be operated at a constant power factor (i.e., unity, leading, or lagging power factor), this important feature is also considered in the proposed model development.

1. Introduction

It has been acknowledged that the most popular types of generators used in variable speed WPP structures are induction and synchronous generators. However, due to its lower price and simpler design, the induction generator is currently more popular than the synchronous generator. Induction generators are also used in fixed speed WPP schemes. In fixed speed WPP, the frequency of the power system or grid will determine the rotational speed of the WPP generator. Therefore, the generator speed of this WPP type is only allowed to vary within a very narrow interval (around 1–2% above the synchronous speed). Since the allowed speed variation is very limited, the wind energy captured by fixed speed WPP is also not optimal. The basic structure of a fixed speed WPP usually consists of SCIG (Squirrel Cage Induction Generator) that is directly connected to the power grid via a step-up transformer [1,2,3].

Due to the disadvantage of fixed speed WPP, the application of variable speed WPP has significantly increased in recent years. The variable speed operation of a WPP can be obtained through the application of DFIG or PMSG (Permanent Magnet Synchronous Generator). However, since the cost of PMSG is relatively higher, the application of DFIG is currently more popular. Compared with fixed speed WPP, DFIG-based WPP operates at a much wider speed range. In its operation, the speed of DFIG is allowed to vary between 40% below synchronous speed and 30% above synchronous speed. This is the reason why the DFIG-based WPP can capture more wind energy than fixed speed WPP [3,4].

Since the penetration of WPP in power systems has been increasing, the need to study its impact on power system performance is becoming increasingly important. To enable such a study to be conducted properly, the first and probably the most crucial step is to model all system components (including the WPP). Regarding the WPP steady state load flow modeling, several techniques have been introduced and reported in [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. In [5,6,7,8,9,10,11,12,13], the methods to incorporate fixed speed WPP into load flow analysis have been investigated. On the other hand, in [14,15,16,17,18,19,20,21,22], steady state models of DFIG-based variable speed WPP for load flow analysis have also been proposed. It is to be noted that most of the methods discussed in [14,15,16,17,18,19,20] assume that the DFIG was operated at the unity power factor.

Moreover, in [15,16,17,18], the DFIG has been represented by two different models. One model was used to describe the DFIG in sub-synchronous conditions, and another was used in super-synchronous conditions [15,16,17,18]. In [21,22], steady state load flow models of DFIG-based WPP have also been proposed. The models presented in [21,22] were applicable for DFIG operating in voltage control mode, where during the WPP operation, its voltage magnitude can be kept constant at a specified value. However, the DFIG power factor cannot be regulated in these control modes of operations.

The present work proposes a simple steady state model of variable speed (i.e., DFIG-based) WPP for load flow analysis. The model is obtained using formulas that calculate the DFIG stator and rotor powers. The important contribution of the method in the present work can be described as follows:

(i)

In contrast to the methods discussed in [14,15,16,17,18,19,20] where the DFIG power factor was assumed to be constant at unity, he proposed model allows the DFIG power factor to be controlled. In addition, it can be applied not only to the unity power factor but also to lagging and leading power factor operation modes. This contribution is particularly important since DFIG-based WPP in power factor control operation mode is also often adopted in practice.

(ii)

Another important feature of the present paper is that representation of the DFIG in both sub-synchronous and super-synchronous conditions can be carried out by using a single mathematical model. It is to be noted that in the previously published methods [15,16,17,18], two models have to be used to represent the conditions.

An extensive case study based on a representative test system (i.e., IEEE 14-bus power system) is also carried out and presented in this paper to validate the method proposed. The rest of the paper is structured as follows. Section 2 presents the turbine mechanical power formula as a wind speed function. Section 3 discusses the derivation of DFIG stator and rotor power formulas. The proposed model of DFIG-based WPP and its incorporation into load flow analysis is also discussed in this section. In Section 4, an investigation of the proposed method’s capability in solving load flow analysis of power systems containing DFIG-based WPP is carried out. Finally, in Section 5, some important conclusions of the present work are given.

2. Wind Turbine Power

The amount of energy or mechanical power captured by the turbine from the wind depends highly on the wind speed, as represented in the following equation [1,2,19]:

$$P_m=0.5\rho \pi R^2{V}_w^3{C}_p$$

(1)

where:

Pm	:	turbine mechanical power (Watt)
ρ	:	air density (kg/m3)
R	:	turbine blade length (m)
Vw	:	wind speed (m/s)
Cp	:	turbine performance coefficient

The turbine performance coefficient (C_p) in (1) is usually expressed as a function of tip speed ratio (λ) and pitch angle (θ) as follows [2,19]:

$$C_P=c_1\left(\frac{c_2}{{\lambda }_i}-c{}_3\theta -c{}_3\theta {}^{c_4}-c_6\right)e^{-c_7/{\lambda }_i}$$

(2)

where:

$${\lambda }_i=\frac{1}{\frac{1}{\lambda +c_8\theta }-\frac{c_9}{{\theta }^3+1}}$$

(3)

The tip speed ratio in (3) can be determined using the following relationship:

$$\lambda =\frac{a_g{\omega }_S(1-s)R}{p{V}_w}$$

(4)

where:

ag	:	turbine gear ratio
ωs	:	synchronous speed (rad/s)
s	:	induction generator slip
p	:	number of pole pairs of induction generator

In practice, the values of turbine performance coefficients are usually in the range 0.4 to 0.5, and those of tip speed ratios have typical values of 6 to 8 [1,19].

3. DFIG Structure and Power Calculations

3.1. DFIG Structure and Equivalent Circuit

Figure 1 shows the basic structure of a DFIG-based WPP [19,20,21,22,23,24,25,26]. It is currently the most popular and widely used type of WPP. In DFIG-based WPP, the main component for electric power generation is WRIG (Wound Rotor Induction Generator). It can be seen from Figure 1 that WRIG stator winding is directly connected to the power system or grid. On the other hand, its rotor winding is connected to the grid through a PEC (Power Electronic Converter) via slip rings. This PEC consists of RSC (Rotor Side Converter), DC link, and GSC (Grid Side Converter). Since the rotor circuit is controlled by a PEC, DFIG has the ability to import or export reactive power.

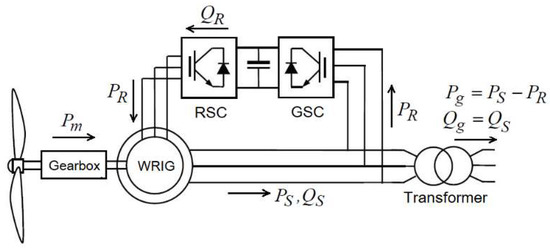
Figure 1. The basic structure of DFIG-based WPP.

In Figure 1, P_m is turbine mechanical power, P_S and Q_S are active and reactive powers in WRIG stator, P_g and Q_g are active and reactive power outputs of DFIG. It is to be noted that the direction of the reactive power output (Q_g) depends on the DFIG operation mode as follows: (i) in leading power factor operation mode, DFIG will export reactive power (Q_g is positive), (ii) in lagging power factor operation mode, DFIG will import reactive power (Q_g is negative), and (iii) in unity power factor operation mode, no reactive power will be imported or exported by the DFIG (Q_g is zero). In addition, in Figure 1, P_R is rotor active power (power injected to WRIG rotor). In super-synchronous conditions, P_R will be negative (power is delivered by the rotor). However, in sub-synchronous conditions, P_R will be positive (power is absorbed by the rotor). Q_R in Figure 1 is the reactive power produced by WRIG rotor. This reactive power is used to compensate for the reactive power consumed by WRIG and to support the reactive power needed during the leading power factor operation mode.

Steady state equivalent circuit of DFIG is given in Figure 2 [19,20,21,22,23,24]. In the figure, V_S and I_S are WRIG stator circuit voltage and current, V_R and I_R are WRIG rotor circuit voltage and current. Subscripts S, R, and M are used to identify the electrical quantities in the stator, rotor, and magnetic core circuits, respectively. In addition, the formulations for Z_S, Z_R, and Z_M in Figure 2 will have the following forms:

$$Z_S=R_S+j{X}_S$$

(5a)

$$Z_R=\frac{R_R}{s}+j{X}_R$$

(5b)

$$Z_M=j{R}_c{X}_m/(R_c+j{X}_m)$$

(5c)

where:

RS, XS	:	resistance, reactance of stator circuit
RR, XR	:	resistance, reactance of rotor circuit
Rc, Xm	:	resistance, reactance of core magnetic circuit

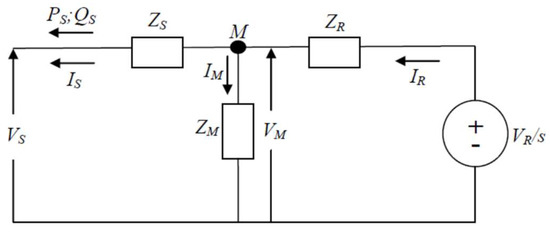
Figure 2. Equivalent circuit of DFIG.

Figure 3 also shows an equivalent circuit of DFIG. In Figure 3, modification to the circuit in Figure 2 has been made to represent the turbine mechanical power and rotor power in the equivalent circuit. A more detailed explanation of DFIG power formulas will be given in the next section. It is to be noted that Z_RR in Figure 3 is determined using:

$$Z_{RR}=Z_R-R_R\frac{1-s}{s}=\left(\frac{R_R}{s}+j{X}_R\right)-\left(\frac{R_R}{s}-R_R\right)=R_R+j{X}_R$$

(6)

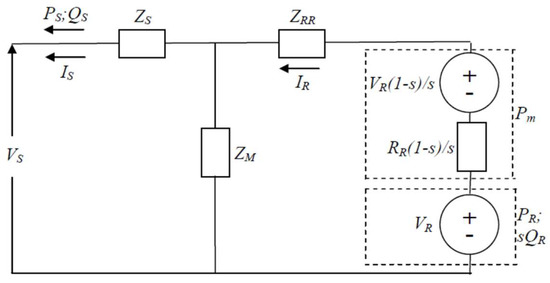
Figure 3. Modified equivalent circuit of DFIG.

3.2. Steady State Model of DFIG-Based WPP

By referring to Figure 1, the active and reactive powers in DFIG stator are:

$$P_S=P_g+P_R$$

(7a)

$$Q_S=Q_g=P_{g}tan\phi$$

(7b)

where $\phi$ is power factor angle of the DFIG.

In addition, by looking at Figure 2 and Figure 3, the stator, rotor, and mechanical powers can be formulated as follows:

$$P_S+j{Q}_S=V_S{I}_S^{\ast }$$

(8a)

$$P_R+js{Q}_R=V_R{I}_R^{\ast }$$

(8b)

$$P_m=\left[P_R-R_R{\left|I_R\right|}^2\right]\frac{1-s}{s}$$

(8c)

where superscript ‘*’ denotes the complex conjugate.

On using (7) in (8a), the following equation that relates DFIG powers, power factor, and stator voltage/current can be obtained as:

$$P_g\left(1+jtan\phi \right)+P_R=V_S{I}_S^{\ast }$$

(9)

Based on (8b) and (9), the steady state model of DFIG in power factor control mode for load flow analysis is proposed as follows:

$$P_R+js{Q}_R-V_R{I}_R^{\ast }=0$$

(10a)

$$P_g\left(1+jtan\phi \right)+P_R-V_S{I}_S^{\ast }=0$$

(10b)

The mathematical model (10) is then integrated into the power system load flow problem formulation without WPP as follows [27,28]:

$$S_{Gi}-S_{Li}-V_i{\displaystyle \sum _{j=1}^n{Y}_{ij}^{\ast }{V}_j^{\ast }}=0$$

(11)

where:

i = 1, 2, …, n	:	bus number
n	:	total number of buses
SGi = PGi + jQGi	:	power generation at bus i
SLi = PLi + jQLi	:	power load at bus i
Vi = |Vi|ejδi	:	voltage at bus i
Yij = |Yij|ejθij	:	element ij of admittance matrix

The two sets of Equations (10) and (11) are then simultaneously solved for the unknown electrical quantities. Details of the equations to be solved and electrical quantities to be computed are presented in Table 1. Since V_S is also the voltage at the WPP terminal or bus (V_i), then for every WPP bus, |V_i| and δ_i are included as the unknown quantities. Moreover, power generations at the WPP bus are P_G = P_g and Q_G = P_gtan$\phi$. It can also be shown that the rotor voltage and current in (10a) can be related to the stator voltage and current using:

$$V_R=E{V}_S+F{I}_S$$

(12a)

$$I_R=G{V}_S+H{I}_S$$

(12b)

where:

$$E=\frac{s(Z_R+Z_M)}{Z_M}$$

(13a)

$$F=\frac{s(Z_S{Z}_M+Z_R{Z}_M+Z_S{Z}_R)}{Z_M}$$

(13b)

$$G=\frac{1}{Z_M}$$

(13c)

$$H=\left(1+\frac{Z_S}{Z_M}\right)$$

(13d)

Table 1. Type of buses, equation and quantities.

Bus Type	Equation(s)	Known Variables	Unknown Variables
Slack	(11)	|V| and δ = 0o	PG and QG
PV	(11)	PG and |V|	δ and QG
PQ	(11)	PG = QG = 0	|V| and δ
WPP	(10) and (11)	$\phi$, s, and Pm	|V|, δ, PG = Pg, QR, Re(IS) and Im(IS)

On using (12b) in (8c), the rotor active power in (10) can also be related to stator voltage and current as follows:

$$P_R=\frac{s}{1-s}{P}_m+R_R{\left|G{V}_S+H{I}_S\right|}^2$$

(14)

4. Case Study

4.1. Test System

The case study is based on the IEEE 14-bus power system adopted from [29] (see Figure 4). The system has a total three-phase load of 897 MW and 243.9 MVAR. Data for the test system are presented in Table 2 and Table 3. The system is then modified by adding WPP at bus 14 via a step-up transformer with an impedance of j0.05 pu. The WPP consists of 100 identical wind turbine generator (WTG) units. Data for the WTG unit are given in Table 4. A base value of 100 MVA has been used for all data in pu.

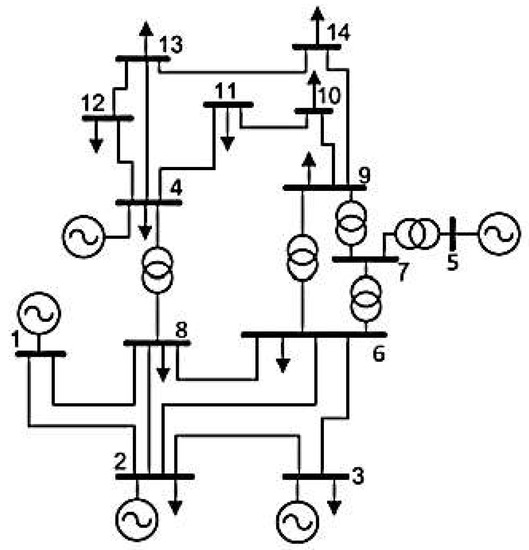
Figure 4. Test system.

Table 2. Test system line data (in pu).

Line	Sending Bus	Receiving Bus	Series Impedance
1	1	2	0.01938 + j0.05917
2	2	3	0.04699 + j0.19797
3	2	6	0.05811 + j0.17632
4	1	8	0.05403 + j0.22304
5	2	8	0.05695 + j0.17388
6	3	6	0.06701 + j0.17103
7	6	8	0.01335 + j0.04211
8	4	8	j0.25202
9	6	7	j0.20912
10	5	7	j0.17615
11	6	9	j0.55618
12	7	9	j0.11001
13	9	10	0.03181 + j0.08450
14	4	11	0.09498 + j0.19890
15	4	12	0.12291 + j0.25581
16	4	13	0.06615 + j0.13027
17	9	14	0.12711 + j0.27038
18	10	11	0.08205 + j0.19207
19	12	13	0.22092 + j0.19988
20	13	14	0.17093 + j0.34802

Table 3. Test system bus data (in pu).

Bus	|V|	δ	Generation	Load	Note
1	1.060	0	-	0	Slack
2	1.045	-	0.4 + j-	0.217 + j0.127	PV
3	1.010	-	j-	0.942 + j0.190	PV
4	1.070	-	j-	0.112 + j0.075	PV
5	1.090	-	j-	0	PV
6	-	-	0	0.478 + j0.039	PQ
7	-	-	0	0	PQ
8	-	-	0	0.176 + j0.016	PQ
9	-	-	0	0.295 + j0.166	PQ
10	-	-	0	0.190 + j0.058	PQ
11	-	-	0	0.135 + j0.018	PQ
12	-	-	0	0.161 + j0.016	PQ
13	-	-	0	0.135 + j0.058	PQ
14	-	-	0	0.149 + j0.050	PQ

Note: notation ‘-’ denotes quantities to be calculated.

Table 4. WTG unit data.

Turbine	Blade length: 40 m Rated power: 3.0 MW Speed: Cut-in: 3 m/s; Rated: 14 m/s; Cut-out: 23 m/s
Gearbox	Ratio: 1/90
Generator	Type: DFIG Rated power: 3.0 MW Pole pairs: 2 Voltage: 690 Volt Resistances/Reactances (in pu): RS = 1; XS = 10; RR = 1; XR = 10; Rc = 5000; Xm = 500
Pad-Mount Transformer	Impedance (in pu): j5

4.2. WRIG Slip and Turbine Power Calculations

In the present work, the tip speed ratio and turbine performance coefficient have been assumed to be 7.95 and 0.41, respectively [19]. Thus, according to (1), the turbine mechanical power as a function of wind speed is:

$$P_m=0.5\times 1.225\times \pi {40}^2{V}_w^3\times 0.41$$

(15)

In (15), the air density is considered to be normal (or ρ = 1.225 kg/m³). In addition, on using (4), the generator slip as a function of wind speed is:

$$s=1-\frac{2\times 7.95\times V_w}{100\pi (1/90)40}$$

(16)

Table 5 shows the values of machine slip and turbine mechanical power for various wind speeds ranging from 5 to 12 m/s. It has been assumed in the calculations that all wind generator units in the WPP receive the same wind speed (uniform wind speed).

Table 5. Generator slip and turbine power.

Vw (meter/s)	s	Pm (MW)	ΣPm (MW)
5	0.4306	0.15780	15.78
6	0.3167	0.27270	27.27
7	0.2029	0.43300	43.30
8	0.0809	0.64630	64.63
9	−0.0249	0.92020	92.02
10	−0.1388	1.26230	126.23
11	−0.2526	1.68010	168.01
12	−0.3665	2.18120	218.12

4.3. Aggregation of Wind Turbine Generator Units

In the present work, the group of WTG units is aggregated into a single machine equivalent to simplify the load flow analysis (note: aggregation technique as proposed in [7,23] has been used in the process). In the WPP single machine representation, parameters of the WRIG and pad mount transformer equivalent are presented in Table 6.

Table 6. Parameter of WPP single machine representation.

WRIG	RS,eq = 0.01; XS,eq = 0.10; RR,eq = 0.01; XR,eq = 0.10; Rc,eq = 50; Xm,eq = 5
Pad-Mount Transformer	ZT,eq = 0.05

The WPP parameter values in Table 6 are then used in the Formulation (10) to obtain the WPP steady state model to be used in load flow analysis.

4.4. Load Flow Results and Discussion

Results of the load flow analysis are presented in Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14 and Table 15. Three power factor operation modes of DFIG, namely: unity, leading, and lagging power factors, are considered in the case study. The results are also given in graphical forms (see Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14). In Table 8, Table 11 and Table 14, P_LOSS is the WRIG active power loss, and Q_LOSS is the WRIG reactive power loss. These WRIG power losses are calculated using the following formula:

$$S_{loss}=I_S{I}_S^{\ast }\left(Z_S+Z_M\right)+I_R{I}_R^{\ast }\left(Z_{RR}+Z_M\right)-\left(I_R{I}_S^{\ast }+I_S{I}_R^{\ast }\right)Z_M$$

(17)

Table 7. DFIG power flow (PF = 1.0).

ΣPm (MW)	Pg (MW)	Qg = QS (MVAR)	PS (MW)	PR (MW)
15.78	9.4127	0	21.4955	12.0828
27.27	20.8045	0	32.8212	12.0167
43.30	36.6883	0	47.9329	11.2446
64.63	57.8139	0	64.4185	6.6046
92.02	84.9318	0	83.0831	−1.8487
126.23	118.7934	0	103.9265	−14.8669
168.01	160.1414	0	126.9522	−33.1892
218.12	209.7292	0	152.1444	−57.5848

Table 8. DFIG reactive power and losses (PF = 1.0).

ΣPm (MW)	QR (MVAR)	PLOSS (MW)	QLOSS (MVAR)
15.78	63.6728	6.3673	63.6728
27.27	64.6551	6.4655	64.6551
43.30	66.1171	6.6117	66.1171
64.63	68.1608	6.8161	68.1608
92.02	70.8821	7.0882	70.8821
126.23	74.3658	7.4366	74.3658
168.01	78.6861	7.8686	78.6861
218.12	83.9077	8.3908	83.9077

Table 9. WPP voltages, G1 to G5 power outputs and line losses (PF = 1.0).

ΣPm (pu)	Voltage (pu)	G1 to G5 Outputs		Line Losses
		MW	MVAR	MW	MVAR
15.78	1.0160	941.7797	479.5449	54.1924	235.6449
27.27	1.0196	928.6547	470.9905	52.4592	227.0905
43.30	1.0243	910.5415	459.8925	50.2298	215.9925
64.63	1.0301	886.7778	446.5797	47.5917	202.6797
92.02	1.0368	856.8002	431.8180	44.7320	187.9180
126.23	1.0440	820.1648	416.8994	41.9582	172.9994
168.01	1.0512	776.5829	403.7411	39.7243	159.8411
218.12	1.0575	725.9341	395.0049	38.6634	151.1049

Table 10. DFIG power flow (PF = 0.95 leading).

ΣPm (MW)	Pg (MW)	Qg = QS (MVAR)	PS (MW)	PR (MW)
15.78	9.3484	3.0727	21.4447	12.0962
27.27	20.6617	6.7912	32.5085	11.8469
43.30	36.4350	11.9756	47.7337	11.2987
64.63	57.4122	18.8705	64.1035	6.6913
92.02	84.3374	27.7203	82.6185	−1.7189
126.23	117.9556	38.7701	103.2733	−14.6823
168.01	159.0028	52.2617	126.0661	−32.9368
218.12	208.2259	68.4405	150.9748	−57.2511

Table 11. DFIG reactive power and losses (PF = 0.95 leading).

ΣPm (MW)	QR (MVAR)	PLOSS (MW)	QLOSS (MVAR)
15.78	67.3883	6.4316	64.3156
27.27	72.8742	6.6083	66.0830
43.30	80.6255	6.8650	68.6499
64.63	91.0488	7.2178	72.1783
92.02	104.5468	7.6826	76.8265
126.23	121.5143	8.2744	82.7441
168.01	142.3333	9.0072	90.0716
218.12	167.3817	9.8941	98.9412

Table 12. WPP voltages, G1 to G5 power outputs and line losses (PF = 0.95 leading).

ΣPm (pu)	Voltage (pu)	G1 to G5 Outputs		Line Losses
		MW	MVAR	MW	MVAR
15.78	1.0192	941.7856	476.2581	54.1341	235.4308
27.27	1.0265	928.6796	463.7667	52.3413	226.6579
43.30	1.0364	910.6097	447.2361	50.0447	215.3117
64.63	1.0489	886.9239	426.7644	47.3361	201.7349
92.02	1.0641	857.0613	402.8550	44.3987	186.6753
126.23	1.0818	820.5608	376.4609	41.5164	171.3310
168.01	1.1016	777.0774	349.0208	39.0802	157.3825
218.12	1.1232	726.3667	322.4684	37.5925	147.0090

Table 13. DFIG power flow (PF = 0.95 lagging).

ΣPm (MW)	Pg (MW)	Qg = QS (MVAR)	PS (MW)	PR (MW)
15.78	9.4768	−3.1149	21.5466	12.0698
27.27	20.9437	−6.8838	33.7330	12.7893
43.30	36.9277	−12.1376	48.1273	11.1996
64.63	58.1782	−19.1222	64.7191	6.5409
92.02	85.4413	−28.0832	83.5136	−1.9278
126.23	119.4594	−39.2644	104.5087	−14.9507
168.01	160.9575	−52.9042	127.7034	−33.2541
218.12	210.6572	−69.2397	153.0724	−57.5848

Table 14. DFIG reactive power and losses (PF = 0.95 lagging).

ΣPm (MW)	QR (MVAR)	PLOSS (MW)	QLOSS (MVAR)
15.78	59.9176	6.3032	63.0324
27.27	56.3795	6.3263	63.2634
43.30	51.5852	6.3723	63.7228
64.63	45.3961	6.4518	64.5183
92.02	37.7034	6.5787	65.7866
126.23	28.4412	6.7706	67.7056
168.01	17.6207	7.0525	70.5249
218.12	5.3885	7.4628	74.6282

Table 15. WPP voltages, G1 to G5 power outputs and line losses (PF = 0.95 lagging).

ΣPm (pu)	Voltage (pu)	G1 to G5 Outputs		Line Losses
		MW	MVAR	MW	MVAR
15.78	1.0128	941.7820	482.9034	54.2587	235.8885
27.27	1.0125	928.6695	478.4409	52.6131	227.6571
43.30	1.0118	910.5955	473.1122	50.5232	217.0747
64.63	1.0103	886.9325	467.6194	48.1106	204.5972
92.02	1.0074	857.1856	463.2116	45.6270	191.2284
126.23	1.0025	821.0420	461.8678	43.5014	178.7034
168.01	0.9940	778.4596	466.5709	42.4171	169.7667
218.12	0.9801	729.7969	479.8147	41.4541	168.6751

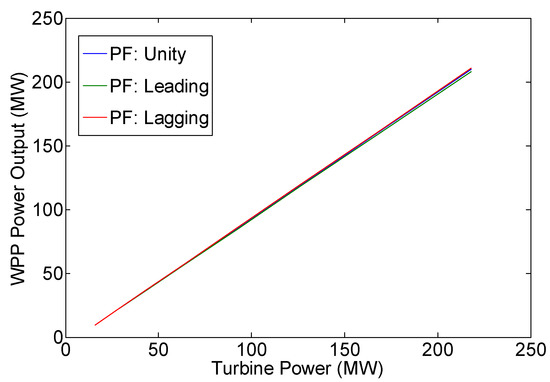
Figure 5. Variation of WPP active power output (P_g).

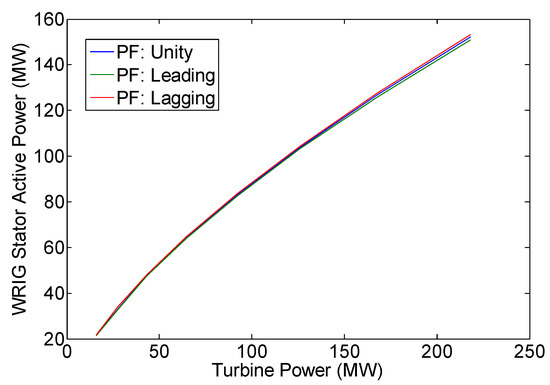
Figure 6. Variation of WRIG stator power (P_S).

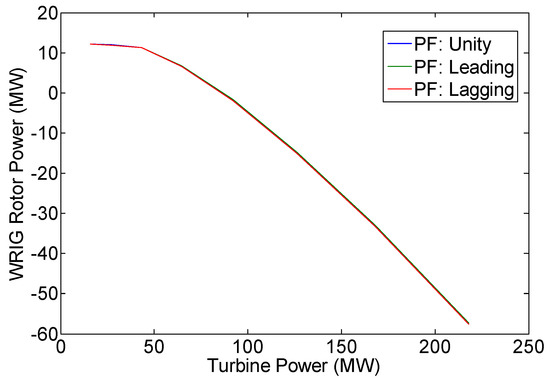
Figure 7. Variation of WRIG rotor power (P_R).

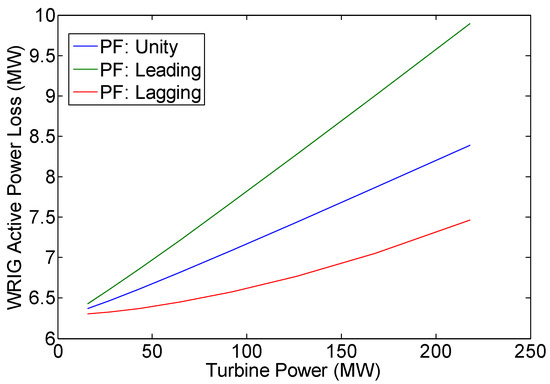
Figure 8. Variation of WRIG active power loss (P_LOSS).

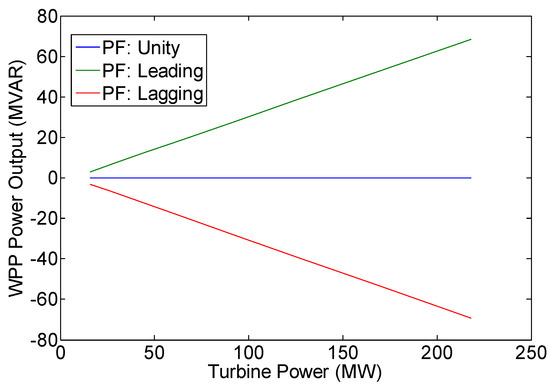
Figure 9. Variation of WPP reactive power output (Q_g).

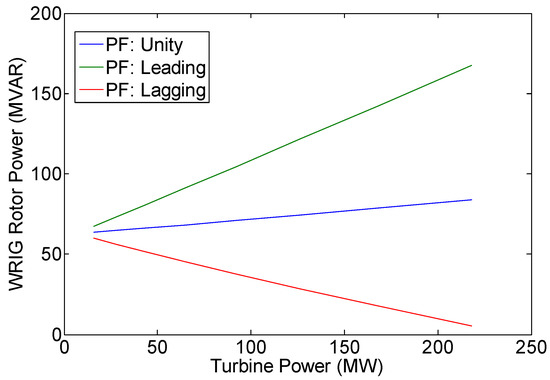
Figure 10. Variation of WRIG rotor power (Q_R).

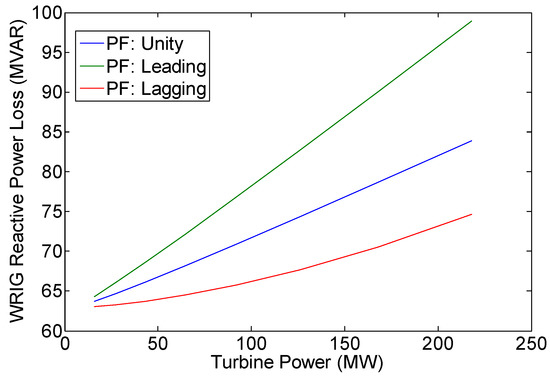
Figure 11. Variation of WRIG reactive power loss (Q_LOSS).

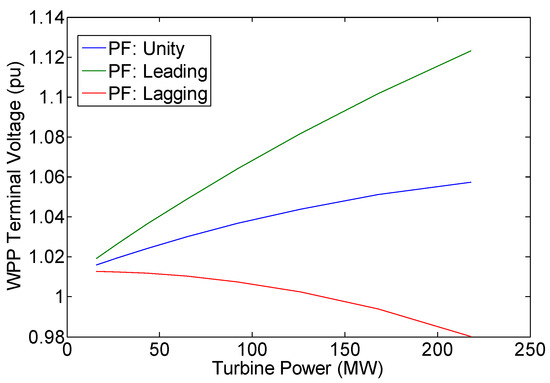
Figure 12. Variation of WPP terminal voltage.

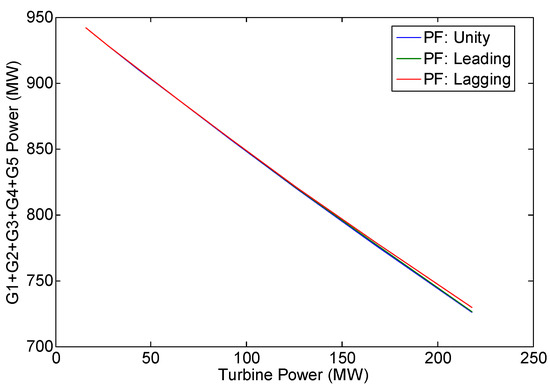
Figure 13. Variation of G1 + G2 + G3 + G4 + G5 active power output.

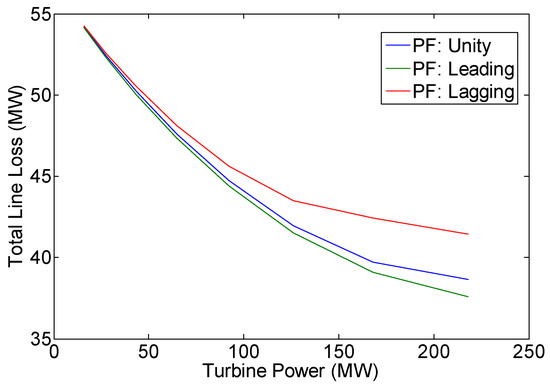
Figure 14. Variation of total line loss.

Figure 5 shows that in all operation modes (i.e., unity, leading, and lagging power factor operations), DFIG always delivers active power to the grid (see column 2 of Table 7, Table 10 and Table 13). This active power output equals the turbine mechanical power minus the WRIG active power loss. This active power output is also the difference between WRIG stator active power and rotor active power (see Figure 6, Figure 7 and Figure 8). It is to be noted that in sub-synchronous operation, rotor active power is positive, or the WRIG rotor absorbs power in the amount of P_R. On the other hand, in super-synchronous operation, rotor active power is negative, or power in the amount of P_R is delivered by the WRIG rotor (see also column 5 of Table 7, Table 10 and Table 13).

Figure 9 indicates that in unity power factor operation, there is no reactive power exchange between DFIG and power grid, or Q_g is zero. However, in leading power factor operation, the DFIG system delivers reactive power to the grid, or Q_g is positive. On the other hand, in lagging power factor operation, the DFIG system absorbs reactive power from the grid, or Q_g is negative (see also column 3 of Table 7, Table 10 and Table 13). The amount of the DFIG reactive power output is equal to the reactive power produced by WRIG rotor minus the WRIG reactive power loss or the reactive power consumed by the WRIG for core circuit magnetization (see Figure 10 and Figure 11). The load flow results also show that with the increase in turbine power (i.e., WPP power output), the WPP power losses will also increase (see Figure 8 and Figure 11). The rise in WPP power losses is due to the DFIG current increase as the amount of WPP power output increases.

The best system voltage profile is obtained during DFIG leading power factor operation (see Figure 12 and column 2 of Table 9, Table 12 and Table 15). This result is expected since, in this mode of operation, DFIG always delivers reactive power to the power system (grid) and, therefore, can support the system voltage profile. It is also to be noted that the increase in turbine mechanical power will decrease the total active power generation of G1 to G5 (see Figure 13 and column 3 of Table 9, Table 12 and Table 15). These results are also expected as the increase in turbine mechanical power will increase the WPP active power output, and the total active power generation of G1 to G5 will decrease since the WPP supplies some loads.

The decrease in G1 to G5 power generation is one of the advantages of WPP installation since G1 to G5 generators usually consist of conventional generators that use non-renewable energy sources. Another advantage is that the total line losses can be reduced with the increase in WPP power output (see Figure 14 and column 5 of Table 8, Table 11 and Table 14). Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13 and Table 14 confirm the validity of the model proposed. This validity can also be verified by examining the results where G1 to G5 power output plus WPP power output (P_g + jQ_g) is always equal to total system load plus total line loss where the line loss has been computed based on the line impedances and currents.

5. Conclusions

The present work proposes a steady state model of variable speed (i.e., DFIG-based) WPP for load flow analysis. The model is obtained using formulas that calculate the DFIG stator and rotor powers. Modeling of DFIG power electronic converter is not required in the model derivation. Another important feature of the present paper is that representation of the DFIG in both sub-synchronous and super-synchronous conditions can be carried out by using a single mathematical model. Moreover, the power factor of the DFIG (often assumed to be unity) is also considered in the proposed model development. The method proposed in the present work can accommodate all three power factor operation modes (i.e., unity, leading, and lagging power factors). Results of the case study have also been presented in this paper. The proposed method’s application in a representative power system has been investigated in the case study. For all the power factor operation modes considered in the case study, the results confirm the capability of the proposed method in solving load flow analysis of power systems containing DFIG-based WPP.