Rotor Fault Detection in Induction Motors Based on Time-Frequency Analysis Using the Bispectrum and the Autocovariance of Stray Flux Signals

Abstract

The aim of this work is to find out, through the analysis of the time and frequency domains, significant differences that lead us to obtain one or several variables that may result in an indicator that allows diagnosing the condition of the rotor in an induction motor from the processing of the stray flux signals. For this, the calculation of two indicators is proposed: the first is based on the frequency domain and it relies on the calculation of the sum of the mean value of the bispectrum of the flux signal. The use of high order spectral analysis is justified in that with the one-dimensional analysis resulting from the Fourier Transform, there may not always be solid differences at the spectral level that enable us to distinguish between healthy and faulty conditions. Also, based on the high-order spectral analysis, differences may arise that, with the classical analysis with the Fourier Transform, are not evident, since the high order spectra from the Bispectrum are immune to Gaussian noise, but not the results that can be obtained using the one-dimensional Fourier transform. On the other hand, a second indicator based on the temporal domain that is based on the calculation of the square value of the median of the autocovariance function of the signal is evaluated. The obtained results are satisfactory and let us conclude the affirmative hypothesis of using flux signals for determining the condition of the rotor of an induction motor.

1. Introduction

In the electric motor condition monitoring area, there is a continuous search for new techniques that are able to enhance the performance and to avoid the drawbacks of the currently existing ones. In this context, the analysis of alternative machine quantities is being explored, as a way to complement the information provided by the well-known methods that are widespread in the industry (currents and vibrations). This is especially important, taking into consideration that no single quantity has been proved to be reliable enough to diagnose the condition of the whole machine, and that the best option seems to be to combine the information obtained from different sources [1,2,3].

Induction motor fault detection (FD) methods, such as stray flux data analysis [4,5,6,7,8], have specific advantages that make them especially attractive for certain applications. Fault diagnosis and processing techniques based on stray flux signals are completely non-invasive and their set up is relatively simple, although the application of this approach requires a specific sensor and a priori knowledge of the distribution of the magnetic field around the electrical machine, which depends, in general, on the manufacturing characteristics of the induction motor [1].

In reference [6], fault detection from the analysis of stray flux signals is based on the variation of the amplitude versus the load of a specific harmonic for two different positions of the flux sensor. The advantage of this method is that it does not require information about the machine behavior in a healthy state. In reference [4], the use of an analytical model that allows us to determine the magnetic flux approximation under conditions of healthy and faulty states for the case of a short circuit between the stator turns and the broken bars is explained. We also refer to [7] for another method for short circuitdetection using stray flux signals.

Fault diagnosis using stray flux signals is based on spectral analysis, through statistical methods, of the harmonics signals obtained from the flux sensor at different relative positions. Compared with classical methods based on analysis of currents such as MCSA (Monte Carlo Statistical Analysis), a disadvantage is that the results may depend on the position of the sensor, and it is not possible to theoretically establish a general rule to obtain the optimum position in the measurement. Moreover, there are no defined thresholds to determine the severity of the fault based on the analysis of these quantities.

In spite of the drawbacks of stray flux data analysis, the progressive cost decrement of necessary flux sensors together with the aforementioned advantages of this technique have led to a renewed dynamism in the research devoted to the study of this technique. Recent works have even extrapolated its application to transient analysis, showing especial advantages in comparison with other methods [9]. Stray flux analysis is adequate to avoid occasional false indications appearing when other techniques are applied to rotor fault detection [10]. Moreover, the suitability of stray flux analysis for non-adjacent bar breakage detection has been explored in [11,12]. Regarding statistical analysis using stray flux signals, an algorithm has been proposed in [13] that relies on the use of the mean value and the standard deviation of the spectral components. Its performance has been tested with three levels of faults, see also [14,15].

In the present work, an algorithm to determine the rotor condition of induction motors from the analysis of stray flux signals is proposed. The detection of the healthy and faulty state conditions is based on a time-frequency analysis of the bispectrum and of the autocovariance function. The results are satisfactory and show the potential of this approach, which provides valuable information to detect the state of the rotor or, at least, to supplement the information provided by other quantities, improving the performance of classical techniques.

2. Materials and Methods

2.1. Data Acquisition

The experimental test bench was based on a 1.1 kW induction motor that was driving a direct current generator. Stray flux measurements were obtained by registering the electromotive force waveforms induced in an external coil sensor that was attached tovarious positions of the motor frame. The flux sensor was a coil with 1000 turns with an external diameter of 80 mm and an internal diameter of 39 mm.

Different operating conditions of the motor were considered. To differentiate the results by working regimes, our samples were taken during the motor startup (the motor was fed at 60% of the rated voltage) and at steady state (in this case the motor was fed 100% of the nominal voltage). We have obtained eight samples of flux signals of a healthy motor and sixteen samples of flux signals of a motor with adamaged rotor (one broken bar). All the measurements in the experiments were taken under similar characteristics in both cases, in order to facilitate subsequent comparisons. In both experiments, the sampling frequency was 5 kHz.

We show in Table 1 and Table 2 the different conditions of the experiments for capturing the flux signals of the healthy and faulty motors during start-up (60% of the supply voltage), as well as the corresponding sensor positions (see Figure 1). In these tables, NL stands for ‘No load’ whereas FL means ‘Full Load’.

Table 1. Characteristics of the experiment for the healthy motor during start-up.

Sample	Position	Load	Speed (r/min)	Torque (Nm)	Supply Voltage (%)	Time (s)
0	DMA	NL	988	0.49	60	1
2	DM	NL	988	0.49	60	1
4	E	NL	987	0.51	60	1
6	L	NL	986	0.54	60	1

Table 2. Characteristics of the experiment for the damaged motor with a broken bar during start-up.

Sample	Position	Load	Speed (r/min)	Torque (Nm)	Supply Voltage (%)	Time (s)
0	DMA	NL	985	0.49	60	1
2	DM	NL	988	0.49	60	1
4	E	NL	987	0.49	60	1
6	L	NL	985	0.49	60	1
8	DMA	FL	755	5.1	60	1
10	DM	FL	750	5	60	1
12	E	FL	760	5	60	1
14	L	FL	765	5	60	1

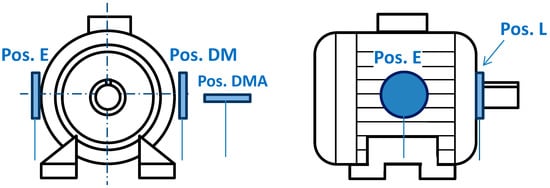
Figure 1. Different positions considering the flux sensor.

Similar experiments were carried out with the motor under permanent regime (100% of the supply voltage). We summarize in Table 3 and Table 4 the experimental conditions of the motor operation at steady state.

Table 3. Characteristics of the experiments for the healthy motor at steady state.

Sample	Position	Load	Speed (r/min)	Torque (Nm)	Supply Voltage (%)	Time (s)
1	DMA	NL	994	0.49	100	8
3	DM	NL	994	0.48	100	8
5	E	NL	995	0.51	100	8
7	L	NL	995	0.5	100	8

Table 4. Characteristics of the experiment for the damaged motor with a broken bar at steady state.

Sample	Position	Load	Speed (r/min)	Torque (Nm)	Supply Voltage (%)	Time (s)
1	DMA	NL	994	0.52	100	8
3	DM	NL	994	0.53	100	8
5	E	NL	994	0.55	100	8
7	L	NL	997	0.58	100	8
9	DMA	FL	940	6.2	100	8
11	DM	FL	940	6.13	100	8
13	E	FL	940	6.1	100	8
15	L	FL	940	6.09	100	8

2.2. Analysis in the Frequency Domain: Theoretical Foundation

Let $\left\{x\left(n\right)\right\}, n=0,\pm 1,\pm 2,\dots$ be a stationary random vector. Let us consider the high-order moments, see [13,14],

$$m_k^x\left({\tau }_1,{\tau }_2,\dots ,{\tau }_{k-1}\right)=E\left\{x\left(n\right)x\left(n+{\tau }_1\right)\dots x\left(n+{\tau }_{k-1}\right)\right\}$$

(1)

that represents the moment of order $k$ of the vector, which depends only on the different time intervals ${\tau }_1,{\tau }_2,\dots {\tau }_{k-1},{\tau }_i=0,\pm 1,\dots$ for all $i$. Since, in practice cumulants are functions dependent on the expected value, they have to be estimated, since we have a finite amount of data to process ${\left\{x\left(n\right)\right\}}_{n=0}^{N-1}$.

These estimators are of a stationary nature and are characterized by first- and second-order statistical functions such as the mean value and variance. Then, let $\left\{x\left(n\right)\right\}, n=0,\pm 1,\pm 2,\dots$ be a stationary process of zero mean value. The third ordercumulant is given by:

$$C_{3x}\left({\tau }_1,{\tau }_2\right)=\frac{1}{N}{\displaystyle \sum }_{n=N_1}^{N_2}x\left(n\right)·x\left(n+{\tau }_1\right)·x\left(n+{\tau }_2\right)$$

(2)

where $N_1$ and $N_2$ are chosen in such a way that the summation involves only x(n) with $n\in \left[0,N-1\right]$, $N$ being the number of samples to be evaluated in the cumulant region, see [15]. Likewise, the bispectrum is defined by the Fourier Transform of the third order cumulant, which is given by:

$$\begin{array}{c}{B}_x^N\left(f_1,f_2\right)={\displaystyle {\displaystyle \sum }_{{\tau }_1=-N-1}^{N-1}}{\displaystyle {\displaystyle \sum }_{{\tau }_2=-N-1}^{N-1}}{C}_{3x}\left({\tau }_1,{\tau }_2\right)·e^{-2\pi f_1{\tau }_1}·e^{-2\pi f_2{\tau }_2}\\ =\frac{1}{N^2}X\left(f_1,f_2\right)·X\left(f_1\right)·X\left(f_2\right)\end{array}$$

(3)

where $X\left(f\right)$ is the Fourier Transform of the sequence ${\left\{x\left(n\right)\right\}}_{n=0}^{N-1}$, see [15].

For the detection of the healthy and the damaged state conditions of an induction motor, an algorithm based on the sum of the mean value of the bispectrum absolute values $(B_{x-mean}^N\left(f\right))$ of the flux signal is proposed. From (3), we can obtain its formal description, shown as follows:

$$(B_{x-mean}^N\left(f\right))=\frac{1}{N}{\displaystyle \sum }_{i=1}^N{\left|B_x^N\left(f_1,f_2\right)\right|}_i$$

(4)

where $N$ is the number of rows of the $N\times N$ square matrix obtained from the bispectrum. The obtained result in (4) is a $1\times N$ vectorthat contains the average frequency values of the amplitude bispectrum matrix of the flux signal. From the obtained result in (4), we define an indicator variable in the frequency domain by the following expression, as the summation of every average frequency values of the amplitude bispectrum:

$$\mathrm{Ind}\left(\mathrm{f}\right)={\displaystyle \sum }_{i=1}^N{B}_{x-mean}^N{\left(f\right)}_{\left(i\right)}$$

(5)

that will be used for the detection of the healthy and faulty condition of the induction motor.

2.3. Temporal Domain Analysis

First, we process the flux signals in the time domain, using the initial data of the experiment, see Table 1, Table 2, Table 3 and Table 4. During the start-up, it is shown that the indicator variable in the frequency domainleads to good results and a palpable difference is observed, which enables us to discriminate between healthy and damaged state conditions of arotor. However, when the motor works at steady state, at 100% of the rated voltage, the method based on the analysis in the frequency domain is not completely effective.

Therefore, to solve the aforementioned issues and to obtain a reliable indicator to be applied in both situations, enabling the discrimination between healthy and damaged rotors, an algorithm based on the autocovariance function of the stray flux signals is proposed. This algorithm is based on the square value of the median of the autocovariance matrix of the flux signal. The theoretical foundations of the proposed are described below:

The autocovariance function of a random stationary process ${\left\{x\left(n\right)\right\}}_{n=0}^{N-1}$ is a measure of its dispersion around its mean value and is defined as a function dependent on the first- and second-order moments as follows [16]:

$$C_2^x\left(\tau \right)=m_2^x\left(\tau \right)-{\left(m_1^x\right)}^2$$

(6)

where $m_2^x\left(\tau \right)$ is the autocorrelation function and ${\left(m_1^x\right)}^2$ is the first order moment. From (6), it can be noted that if the process is of zero mean value, the autocovariance coincides with the autocorrelation function. Then, replacing in (6) $m_2^x\left(\tau \right)$ and applying second order statistics we have:

$$C_2^x\left(\tau \right)=\frac{1}{N}{\displaystyle \sum }_{t=0}^{N-1-\tau }x\left(t\right)·x\left(t+\tau \right)$$

(7)

Then, after obtaining the autocovariance function, we proceed to calculate the square value of the median, for each sample used in the experiment, which is as follows [16,17]:

Let be $x_1,x_2,x_3,\dots ,x_n$ the data of an ordered sample in increasing order and designating the median as $M_e$, if $n$ is odd, the median is the value that the position occupies: $M_{e\left(c_2^x\right)}=\frac{c_2^x{\left(\mathsf{\tau }\right)}_{\left(n+1\right)}}{2}$, then if $n$ is pair, the median is the arithmetic mean of the two central values. Then, $M_{e\left(c_2^x\right)}$ would be:

$$M_{e\left(c_2^x\right)}=\frac{c_2^x{\left(\tau \right)}_{\left(\frac{n}{2}\right)}+c_2^x{\left(\tau \right)}_{\left(\frac{n}{2}+1\right)}}{2}$$

(8)

Substituting to find out the temporary indicator:

$$In{d}_t={\left(M_{e\left(c_2^x\right)}\right)}^2$$

(9)

The obtained result in (9) will be taken as the variable of indication in the time domain for the detection of the healthy and faulty conditions in the induction motor.

3. Results

3.1. Results in the Frequency Domain

Using the data obtained in the experiments, we have applied the algorithm described in the Section 2.2 in order to obtain the indication variable in the frequency domain, based on the bispectrum of the flux signal. This enabled us to discriminate between the healthy and faulty conditions of an induction motor. The bispectrum has been calculated in a window of 1024 samples, which results in a square matrix, where the number of rows and columns coincides with the data window to be processed, i.e., 1024 × 1024.

We have used the algorithm based on the bispectruminstead of the analysis based on the one-dimensional Fourier transform. The reason is the following: when applying the proposed method using the sum of the mean of the frequency spectrum absolute value, no relative differences were observed between the healthy and the damagedstates if the one-dimensional Fourier transform is used, as mentioned above.

This statement has been checked using sample 0 (position DMA of Table 1) corresponding to the samples of flux signals of the healthy motor and comparing the results with sample 0 (position DMA of Table 2) corresponding to the samples of flux signals of the motor with one broken rotor bar. The obtained results are shown in Figure 2 and Table 5, respectively.

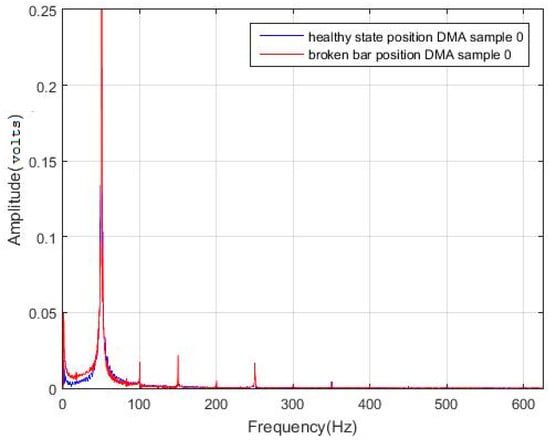
Figure 2. Comparison of the frequency spectra of the flux signals for the healthy state (blue) and for the faulty state with one broken bar (red). Sample 0, DMA position.

Table 5. Obtained results by applying the one-dimensional Fourier Transform and calculating the indicator (Equations (4) and (5)).

Sample	Obtained Indicator in Frequency Domain
0, DMA position, healthy state	9.1160·10−4
0, DMA position, damage state (one broken bar)	8.8375·10−4

In Table 5, the difference that exists between both values of the indicator is 2.7857·10⁻⁵, which is not significant to reliably discriminate between healthy and faulty conditions. Likewise, in Figure 2, no relevant differences are clearly observed in the spectra of both samplesfor the same position (DMA).

Taking into consideration the previous results, we decided to use the bispectrum of the flux signals. The algorithm based on Equations (4) and (5) was applied to obtain an indication variable that was able to detect differences between the healthy and damaged conditions. Figure 3 shows the bispectrum of the flux signal in the healthy state (sample 0, position DMA) and faulty state (sample 0, position DMA).

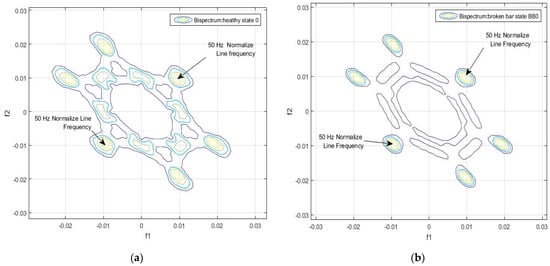
Figure 3. (a) Contour of bispectrum of the motor flux signal in healthy condition (sample 0, DMA position) (b) Contour of bispectrum of the motor flux signal in faulty condition (sample 0, DMA position).

As can be seen in Figure 3, the bispectrum has two circles corresponding to fundamental frequency values of the form $\left(f_1, f_2\right),$ in this case (0.01,0.01), which corresponds to the frequency of 50 Hz (normalized to 1), depicted in Figure 2, corresponding to the frequency spectrum using the one-dimensional Fourier transform.

Similarly, around these two points there are other four circles which correspond to the frequency values, multiples of the fundamental frequency of 50 Hz. As shown in Figure 3, there are differences between the bispectrum of the flux signal of the healthy motor and of the damaged motor.

These six circles visualized in the contour of the bispectrum appear in all the analyzed samples, both in the healthy and in the faulty state conditions. This can be observed in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9.

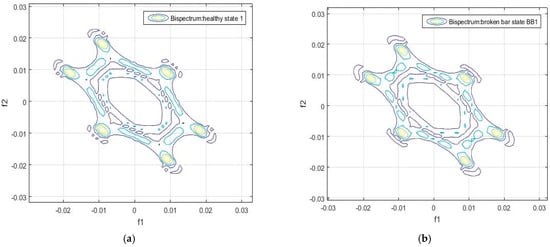
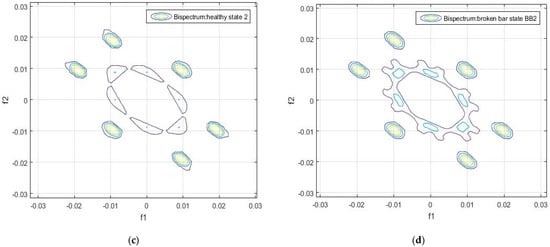
Figure 4. Contour of the bispectrum of the motor flux signal: (a) Sample 1 of the healthy motor, (b) Sample 1 of the damaged motor, (c) Sample 2 of the healthy motor, (d) Sample 2 of the damaged motor.

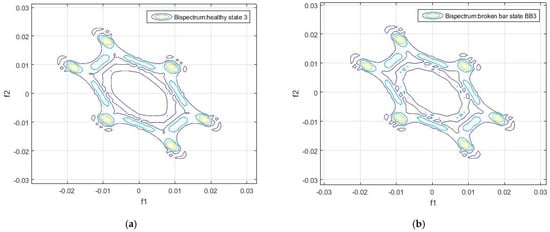
Figure 5. Contour of the bispectrum of the motor flux signal: (a) Sample 3 of the healthy motor and (b) Sample 3 of the damaged motor.

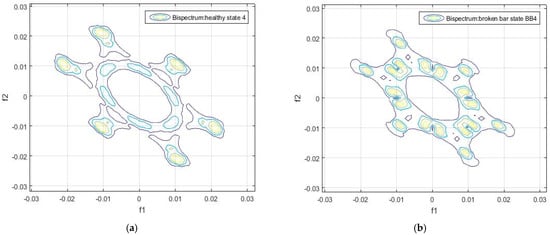
Figure 6. Contour of the bispectrum of the motor flux signal: (a) Sample 4 of the healthy motor, (b) Sample 4 of the damaged motor.

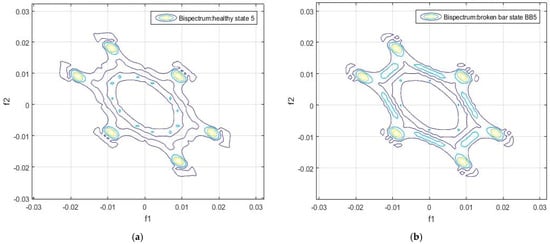
Figure 7. Contour of the bispectrum of the motor flux signal: (a) Sample 5 of the healthy motor and (b) Sample 5 of the damaged motor.

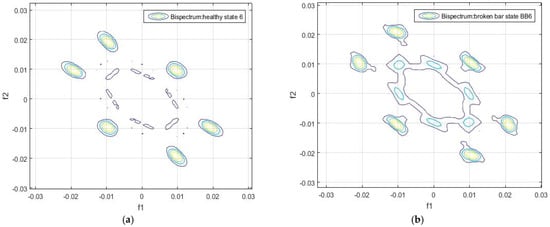
Figure 8. Contour of the bispectrum of the motor flux signal: (a) Sample 6 of healthy the motor, (b) Sample 6 of the damaged motor.

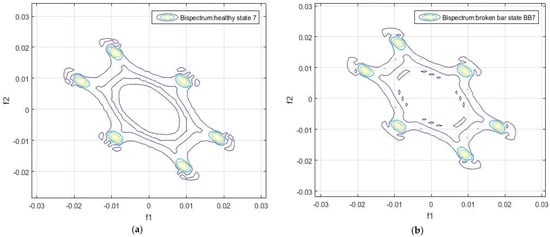
Figure 9. Contour of the bispectrum of the motor flux signal: (a) Sample 7 of the healthy motor, and (b) Sample 7 of the damaged motor

In Figure 3, Figure 4, Figure 5 and Figure 6 we show the differences in the bispectrum between the healthy and the damaged motors, for the different positions at which the measurements of the flux signals were taken. Note that in some graphs there are more substantial differences, such as in Figure 3 as well as in Figure 4c,d. The differences depend on the position in which the measurement was taken, as well as on the load, and on the supply, and will also depend on obtaining a more or less significant difference in relation to the value of the indicator in the frequency domain (Equation (5)).

The calculation of the indicator in the frequency domain based on Equations (4) and (5) was performed for the data in Table 1, Table 2, Table 3 and Table 4, which correspond to the motor under healthy and faulty conditions. The obtained results are shown in Table 5 and Table 6.

Table 6. Results of the indicator in the frequency domain based on Equations (4) and (5) for the data of the experiment with the healthy motor during start-up.

Sample	Position	Load	Speed (r/min)	Torque (Nm)	Supply Voltage (%)	Time (s)	Indicator
0	DMA	NL	988	0.49	60	1	30.38804
2	DM	NL	988	0.49	60	1	27.28881
4	E	NL	987	0.51	60	1	28.56996
6	L	NL	986	0.54	60	1	26.75429

From the results shown in Table 6 and Table 7, it can be seen that for similar operating conditions, the indicator in the frequency domain depends on the position of the sensor, as can be seen for samples 0, 4, 8 and 14. In these cases, the relative differencesare appreciable and it is possible to discern between one state and the other. On the other hand, the difference in the values of the indicator for the other positions, such as with samples 2 and 6, is not significant. In any case, the values of the indicator for the faulty condition are always greater than those of the equivalent healthy one.

Table 7. Results of the indicator in the frequency domain based on Equations (4) and (5) for the data of the experiment with the faulty motor with a broken bar, during start-up.

Sample	Position	Load	Speed (r/min)	Torque (Nm)	Supply Voltage (%)	Time (s)	Indicator
0	DMA	NL	985	0.49	60	1	38.15795
2	DM	NL	988	0.49	60	1	28.76003
4	E	NL	987	0.49	60	1	38.77947
6	L	NL	985	0.49	60	1	28.88013
8	DMA	FL	755	5.1	60	1	32.06025
10	DM	FL	750	5	60	1	25.04451
12	E	FL	760	5	60	1	23.42840
14	L	FL	765	5	60	1	41.01978

On the other hand, we show in Table 8 and Table 9 show the values of the indicator when the motor works at steady-state (100% of the nominal voltage).

Table 8. Results of the indicatorin the frequency domain based on Equations (4) and (5) for the data of the experiments with the healthy motor at steady state.

Sample	Position	Load	Speed (r/min)	Torque (Nm)	Supply Voltage (%)	Time (s)	Indicator
1	DMA	NL	994	0.49	100	8	1.152108
3	DM	NL	994	0.48	100	8	1.192266
5	E	NL	995	0.51	100	8	0.597756
7	L	NL	995	0.5	100	8	0.726403

Table 9. Results of the indicator in the frequency domain based on Equations (4) and (5) for the data of the experiments with the faulty motor with a broken bar at steady state.

Sample	Position	Load	Speed (r/min)	Torque (Nm)	Supply Voltage (%)	Time (s)	Indicator
1	DMA	NL	994	0.52	100	8	0.842987
3	DM	NL	994	0.53	100	8	0.854711
5	E	NL	994	0.55	100	8	0.975386
7	L	NL	997	0.58	100	8	0.709328
9	DMA	FL	940	6.2	100	8	3.707399
11	DM	FL	940	6.13	100	8	3.254082
13	E	FL	940	6.1	100	8	3.979508
15	L	FL	940	6.09	100	8	2.998851

From the results shown in Table 8 and Table 9, it is noted that the differences between the values of the indicator in the frequency domain for healthy and faulty conditionsare not significant when the motor works at steady state. This may be due to the fact that, during startup, certain harmonics vary in frequency and amplitude [9]. This does not happen under the steady state regime, during which the harmonics maintain well-defined frequencies and amplitudes, as long as the load level does not change.

From the results shown in the above tables, it can be deduced that, under the healthy condition, the indicator in the frequency domainreachesa maximum value of 30.38804, and the minimum value is 0.597756. On the other hand, the indicator for the faulty condition (motor with a broken bar) ranges between 0.709328 and 41.0198. The value of the indicator for the healthy condition never exceeds the value of 31 for all measurements.

All the comparisons related to the values of the indicator have been carried out between measurements that were obtained under similar operating conditions. This leads to the conclusion that the position of the sensor plays a crucial role and that significant differences are not obtained in every position.

3.2. Results in the Time Domain

Taking into consideration the previous results obtained in the frequency domain, a new algorithm based on the square value of the median of the autocovariance matrix of the flux signal was proposed, as described in Equation (8). This gives a fault detection indicator in the time domain. The results obtained after applying this last algorithmare shown in Figure 10, and they are summarized in Table 10, Table 11, Table 12 and Table 13.

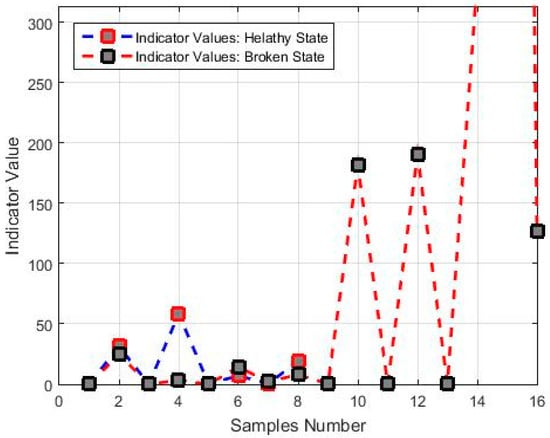
Figure 10. Values of the indicator in the time domain for all the samples used in the experiments.

Table 10. Results of the indicatorin the time domain, based on Equations (6)–(8), for the data of the experiments with the healthy motor during startup.

Sample	Position	Load	Speed (r/min)	Torque (Nm)	Supply Voltage (%)	Time (s)	Indicator
0	DMA	NL	988	0.49	60	1	0.071959
2	DM	NL	988	0.49	60	1	0.027691
4	E	NL	987	0.51	60	1	0.435514
6	L	NL	986	0.54	60	1	0.537173

Table 11. Results of the indicator in the time domain, based on Equations (6)–(8), for the data of the experiments with the motor with one broken bar during startup.

Sample	Position	Load	Speed (r/min)	Torque (Nm)	Supply Voltage (%)	Time (s)	Indicator
0	DMA	NL	985	0.49	60	1	0.003537
2	DM	NL	988	0.49	60	1	0.009451
4	E	NL	987	0.49	60	1	0.009606
6	L	NL	985	0.49	60	1	2.046191
8	DMA	FL	755	5.1	60	1	0.370122
10	DM	FL	750	5	60	1	0.033363
12	E	FL	760	5	60	1	0.005345
14	L	FL	765	5	60	1	2227.965

Table 12. Results of the indicator, based on Equations (6)–(8), for the data of the healthy motor experiments under the steady state regime.

Sample	Position	Load	Speed (r/min)	Torque (Nm)	Supply Voltage (%)	Time (s)	Indicator
1	DMA	NL	994	0.49	100	8	31.38462
3	DM	NL	994	0.48	100	8	58.30218
5	E	NL	995	0.51	100	8	6.948441
7	L	NL	995	0.5	100	8	19.03505

Table 13. Results of the indicator, based on Equations (6)–(8), for the data of the faulty motor experiments under the steady state regime.

Sample	Position	Load	Speed (r/min)	Torque (Nm)	Supply Voltage (%)	Time (s)	Indicator
1	DMA	NL	994	0.52	100	8	24.67371
3	DM	NL	994	0.53	100	8	3.342042
5	E	NL	994	0.55	100	8	14.26557
7	L	NL	997	0.58	100	8	7.897072
9	DMA	FL	940	6.2	100	8	181.7043
11	DM	FL	940	6.13	100	8	190.5501
13	E	FL	940	6.1	100	8	334.8858
15	L	FL	940	6.09	100	8	126.3791

The previous results show that there is a notable difference between the values of the indicator when the motor works at steady-state (100% of the rated supply), but not during the start-up, when it works at 60% of the rated supply.

4. Discussion

We group the previous results with respect to the flux sensor location in order to compare the indicator values obtained in the frequency and time domains, for different fault conditions and operating regimes, see Table 14 and Table 15.

Table 14. Results of the time and frequency indicators for the DMA position.

Sample	Position	Load	Speed (r/min)	Torque (Nm)	Supply Voltage (%)	Time (s)	Frequency Indicator	Time Indicator	State
0	DMA	NL	988	0.49	60	1	30.38804	0.071959	Healthy
	DMA	NL	994	0.49			38.15795	0.003537	Faulty
1	DMA	NL	994	0.49	100	8	1.152108	31.38462	Healthy
	DMA	NL	994	0.52			0.842987	24.67371	Faulty

Table 15. Results of the time and frequency indicators for the DM position.

Sample	Position	Load	Speed (r/min)	Torque (Nm)	Supply Voltage (%)	Time (s)	Frequency Indicator	Time Indicator	State
2	DM	NL	988	0.49	60	1	27.28881	0.027691	Healthy
	DM	NL	988	0.49			28.76003	0.009451	Faulty
3	DM	NL	994	0.48	100	8	1.192266	58.30218	Healthy
	DM	NL	994	0.53			0.854711	3.342042	Faulty

For the sample corresponding to the DMA position, the difference of the indicators values is noticeable at the startup, when working in the frequency domain. The difference in the temporal indicator between the healthy and faulty condition is preceded by a multiplication factor of 20. When the motor works at steady-state (with 100% of the rated supply), the difference in the values of the time indicator is appreciable. At startup, the indicator in the frequency domain is always greater for the faulty state; the opposite occurs with the temporary indicator at steady-state.

For the sample corresponding to the DM position, the difference of the indicators values at startup is not as noticeable compared to the values obtained at the DMA position, when working in the frequency domain. The difference in the time indicator between the healthy and damaged state is preceded by a multiplication factor of 3. When the motor works at steady-state, the difference of the time indicator is as significant as for the DMA position. At startup, the indicator in the frequency domain is always greater for the faulty condition; the opposite occurs with the temporal indicator at steady-state.

For the sample corresponding to the E position, there is a significant difference between the values of the indicator in the frequency domain at the startup, as with the DMA position. The difference in the temporal indicator between the healthy and the faulty condition is preceded by a multiplication factor of 45. At steady-state, with 100% of the rated voltage, the differences of the temporal indicatorsare significant. At startup, the indicator in the frequency domain is always greater for the faulty state; the same occurs in this case for the time indicator at steady-state, contrary to what happens in positions DM and DMA.

For the sample corresponding to the L position, the difference of the indicator at start-up is not clearly noticeable when working in the frequency domain as with the DMA and E sensor positions. The difference in the temporal indicator between the healthy and the faulty conditions is preceded by a multiplication factor of 4. When working at steady-state, the difference of the temporal indicator is significant. The indicator in the frequency domain is higher for the faulty state during start-up; the opposite occurs with the temporal indicator at steady-state.

From the results obtained in Table 14, Table 15, Table 16 and Table 17, for the four sensor positions analyzed (DMA, DM, E, L), the following can be concluded:

Table 16. Results of the time and frequency indicators for the E position.

Sample	Position	Load	Speed (r/min)	Torque (Nm)	Supply Voltage (%)	Time (s)	Frequency Indicator	Time Indicator	State
4	E	NL	987	0.51	60	1	28.56996	0.435514	Healthy
	E	NL	987	0.49			38.77947	0.009606	Faulty
5	E	NL	995	0.51	100	8	0.597756	6.948441	Healthy
	E	NL	994	0.55			0.975386	14.26557	Faulty

Table 17. Results of the time and frequency indicators for the L position.

Sample	Position	Load	Speed (r/min)	Torque (Nm)	Supply Voltage (%)	Time (s)	Frequency Indicator	Time Indicator	State
6	L	NL	986	0.54	60	1	26.75429	0.537173	Healthy
	L	NL	985	0.49			28.88013	2.046191	Faulty
7	L	NL	995	0.5	100	8	0.726403	19.03505	Healthy
	L	NL	997	0.58			0.709328	7.897072	Faulty

• The indicator in the frequency domain for the healthy condition varies in a range of $26\le In{d}_f\le 30$, and for the faulty condition it varies from $28\le In{d}_f\le 38$ during start-up. In this regime, the values of the indicator in the frequency domain for the healthy state are always lower than the corresponding values for the faulty state.
• When the motor operates at steady state, the indicator in the time domain ranges from $6\le In{d}_t\le 58$ for the healthy condition, and between $3\le In{d}_t\le 24$ for the faulty one.
• The best results are obtained when the measurement is carried out in the DMA position, since the values of both indicators are within the limits of obtained values.
• In order to discern between the healthy and faulty conditions, the signal obtained from the flux sensor must first be evaluated during the start-up, for which the indicator is calculated based on the analysis in the frequency domain. At steady-state, the signal should be better evaluated using the time indicator.
• A diagnostic decision based on the limit values for both indicators should be finally adopted. In order to obtain a more reliable conclusion of the rotor condition, the two indicators must be evaluated.

The accuracy of the proposed method as a classification of the condition of the damaged-healthy state of the induction motor depends, to a large extent, on the relative position where the measurement is made. Although regardless of the obtained results and the relative positions of each measurement, it can be noted that the average of the indication values obtained for the indicator in the frequency domain never exceeds the value of 28.250275 for the healthy state and 33.644395 for the damaged case. Similarly, if the analysis is performed for the indicator in the time domain, we have an average value of 28.91757275 for the healthy state, and of 12.5445985 for the faulty one. That is, in an a priori analysis, a result of the indication variable greater than these values, both for the frequency and time domains, can be concluded as an affirmative diagnosis of failure, as shown for the cases of the DMA and E positions.

5. Conclusions

The spectral analysis based on the bispectrum of the flux signals captured at external positions of an induction motor was proposed in order to provide a criterion to discriminate between healthy and faulty rotor conditions in induction motors.

To this end, an algorithm based on the sum of the mean value of the bispectrum module of the induction motor flux signal was theoretically described and implemented.

To demonstrate the results experimentally, several real samples of flux signals were registered, both for healthy and faulty conditions of the rotor cage, and for different operating conditions.

The proposed algorithms are based on the sum of the mean value of the bispectrum module of the flux signal and on the square value of the median of the autocovariance function. The results have shown they can be considered as indicators that enable us to provide a criterion for the discrimination between healthy and faulty conditions of the motor.

We can also conclude that the position where the measurement of the flux signal is carried out is an important factor, as well as the operating regime of the motor.

In conclusion, the study carried out in this paper implies that, with the analysis of stray flux signals, it is possible to obtain indicator variables that discriminate between faulty and healthy motors, which is an improvement and a complementtoexisting results obtained by using classical techniques for the diagnosis of failures in electrical machines and, in the future, may be a contribution to the development of portable industrial diagnostic devices.

As future work, it is proposed to carry out an estimation analysis of the accuracy of the proposed method and to obtain an algorithm for the optimization of the relative position of the flux sensor at the time of the measurement.