Study on Multi-DOF Actuator for Improving Power Density

Abstract

This study focuses on improving the power density of a spherical multi-degree-of-freedom (multi-DOF) actuator. A spherical multi-DOF actuator that can operate in three DOFs is designed. The actuator features a double air gap to reduce eddy current loss. However, a multi-DOF actuator driven by a single actuator exhibits low power density. Therefore, a Halbach magnet array is applied to improve the power density of a spherical multi-DOF actuator, and its output characteristics are compared with those of an existing spherical multi-DOF actuator via finite element analysis. Additionally, the output characteristics are analyzed based on changes in the coil pitch angle and magneto-motive force of the rotating winding. Furthermore, it is necessary for a spherical multi-DOF actuator to move to the command position. Hence, a stability analysis is performed to ensure that the spherical multi-DOF actuator is stably driven based on the command position.

1. Introduction

Recently, a significant amount of interest has been directed toward the robot industry owing to the advent of the fourth industrial revolution. Currently, one-degree-of-freedom (DOF) systems require one actuator, whereas three-DOF systems require three actuators. For systems with two or more DOFs, an additional structure is required to connect the actuators [1,2,3]. Most applications that implement such multi-DOF systems by connecting multiple actuators include robotic joints [4,5] and drone gimbal systems [6,7]. However, the volume of the systems is high, and this constitutes a problem. Therefore, several studies have focused on developing actuators capable of being driven in multiple axes [8,9,10,11,12,13].

Based on extant studies, two types of multi-DOF actuators and motors are known to be driven in multiple axes, namely the permanent-magnet-type [14,15,16,17] and induction-type multi-DOF actuators [18]. Permanent-magnet-type multi-DOF actuators exhibit the advantage of large magnetic flux density. Additionally, most of these actuators are designed with tooth-concentrated windings to improve power density. However, for induction-type multi-DOF actuators, distributed windings are required to decrease the effects of harmonics such as crawling phenomena. Thus, most studies tend to focus on the structure of a permanent-magnet-type multi-DOF actuator.

Furthermore, multi-DOF actuators are divided into core-type actuators [19,20] and slotless-type actuators [12,18]. A core-type multi-DOF actuator exhibits the advantage of low-leakage magnetic flux because magnetic flux mainly flows through the iron core, which has high permeability. Conversely, a slotless-type multi-DOF actuator suffers from the disadvantage of a high leakage of magnetic flux due to the absence of an iron core within the winding. However, the slotless multi-DOF actuator is advantageous in terms of position control given the absence of a reluctance difference between the stator and rotor. Multi-DOF motors also exist in the form of ultrasonic motors [21,22,23] and bearingless motors [16].

Several studies have focused on multi-DOF actuators. However, most multi-DOF actuators exhibit low power density. Moreover, multi-DOF actuators are multi-axis driven, in contrast to conventional actuators or motors; thus, losses due to changes in magnetic flux in multi-DOF actuators are high.

In this study, a dual-airgap slotless-type spherical multi-DOF actuator was developed, as shown in Figure 1, with the aim to decrease eddy current loss by simultaneously moving internal and external rotors. In Section 2, the theory of dual-airgap slotless-type spherical multi-DOF actuator is discussed. As explained in Section 3, a Halbach magnet array was applied to the actuator to improve output characteristics.

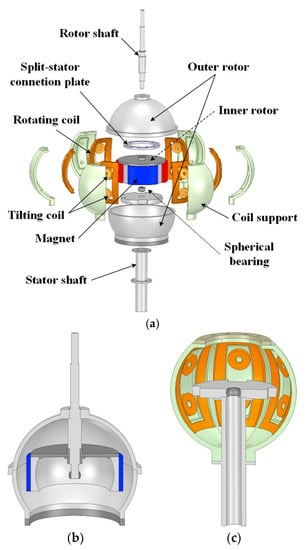
Figure 1. Structure of the dual-airgap slotless- type spherical multi-degree-of-freedom (multi-DOF) actuator: (a) Full model; (b) Rotor part; (c) Stator part.

2. Theory of Dual-Airgap Slotless-Type Spherical Multi-DOF Actuator

2.1. Operation of the Spherical Multi-DOF Actuator

The structure of the dual-airgap slotless-type spherical multi-DOF actuator is shown in Figure 1. Figure 1a shows the structure of the full model. Figure 1b,c show the structure of the rotor and stator parts. As shown in Figure 1a,b, the actuator consists of two rotors to decrease eddy current losses. Additionally, the material used for the inner rotor’s back yoke and outer rotor was steel 1001. The inner rotor features a surface permanent magnet to form the main magnetic flux. The outer rotor is utilized to decrease the leakage of the magnetic flux by creating paths for the magnetic flux. It is connected to the inner rotor by the rotor shaft and both rotors move simultaneously. If the back yoke is applied to the stator as opposed to the outer rotor, then the magnetic flux leakage is low and a magnetic flux path is formed; however, the eddy current loss due to the back yoke of the stator increases. Therefore, the outer rotor replaces the back yoke of the stator, and the resulting structure is capable of decreasing eddy current loss. The rotor and stator shafts are separated using a spherical bearing for three-axis operation. The stator windings are composed of rotating coils and tilting coils for rotation and tilting, respectively. Additionally, a plastic-material coil support is used to wind the coil to the desired position.

Figure 2 shows the movement of the dual-airgap slotless-type spherical multi-DOF actuator during tilting operation. Therein, the dual air gap can be identified. Here, α is a moving angle from the z-axis, β is a moving angle from the x-axis, and δ is an angle from the moving axis to the xy-plane. The actuator moves simultaneously based on α and β command angles because the internal and external rotors are connected to the same rotor shaft. The stator is connected to the stator shaft, but it does not move based on command angles such as α and β.

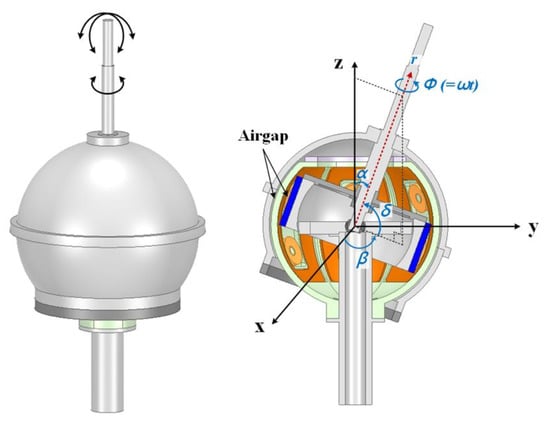
Figure 2. Operation of the dual-airgap slotless-type spherical multi-DOF actuator.

The basic model specifications of dual-airgap slotless-type spherical multi-DOF actuator are listed in Table 1. The basic model consists of three phases and exhibits low torque and efficiency.

Table 1. Specifications of the basic model of the dual-airgap slotless-type spherical multi-degree-of-freedom (multi-DOF) actuator.

Contents	Value	Unit
Number of phases	3	−
Number of poles	4	−
Number of rotating coils & tilting coils	6/6	−
Number of rotating turns & tilting turns	170/250	turns
Input current	0.5	Amax
Pole pitch angle	130	°E
Average rotating torque (α = 0°, β = 0°)	410	mNm
Power density (α = 0°, β = 0°)	7744.3	W/m3
Efficiency at 300 rpm (α = 0°, β = 0°)	77.97	%

Rotating and tilting currents flow through the rotating and tilting coils during the operation of the actuator. The rotating currents are equated as follows:

$$i_{r,a}=I_r\cos \left\{p\left({\omega }_{m}t+\beta \right)\right\}=i_{r,d}$$

(1)

$$i_{r,b}=I_r\cos \left\{p\left({\omega }_{m}t+\beta \right)-\frac{2}{3}\pi \right\}=i_{r,e}$$

(2)

$$i_{r,c}=I_r\cos \left\{p\left({\omega }_{m}t+\beta \right)-\frac{4}{3}\pi \right\}=i_{r,f}$$

(3)

where i_r,a, i_r,b, i_r,c, i_r,d, i_r,e, and i_r,f are the rotating current flowing in the phases from a to f, respectively, and I_r is the maximum value of the rotating current, p is the number of pole pairs, and ω_m is the mechanical angular velocity.

The tilting currents are as follows:

$$i_{tu,a}=I_t{l}_p\cos \left\{\frac{\pi }{4}\left(1-l_p\frac{\alpha }{{\theta }_c}\cos \beta \right)\right\}=-i_{td,a}$$

(4)

$$i_{tu,b}=I_t{l}_p\cos \left[\frac{\pi }{4}\left\{1-l_p\frac{\alpha }{{\theta }_c}\cos \left(\beta -\frac{2\pi }{3p}\right)\right\}\right]=-i_{td,b}$$

(5)

$$i_{tu,c}=I_t{l}_p\cos \left[\frac{\pi }{4}\left\{1-l_p\frac{\alpha }{{\theta }_c}\cos \left(\beta -\frac{4\pi }{3p}\right)\right\}\right]=-i_{td,c}$$

(6)

$$i_{tu,d}=I_t{l}_p\cos \left[\frac{\pi }{4}\left\{1-l_p\frac{\alpha }{{\theta }_c}\cos \left(\beta -\frac{2\pi }{p}\right)\right\}\right]=-i_{td,d}$$

(7)

$$i_{tu,e}=I_t{l}_p\cos \left[\frac{\pi }{4}\left\{1-l_p\frac{\alpha }{{\theta }_c}\cos \left(\beta -\frac{8\pi }{3p}\right)\right\}\right]=-i_{td,e}$$

(8)

$$\begin{array}{c}{i}_{tu,f}=I_t{l}_p\cos \left[\frac{\pi }{4}\left\{1-l_p\frac{\alpha }{{\theta }_c}\cos \left(\beta -\frac{10\pi }{3p}\right)\right\}\right]=-i_{td,f},\\ ※\{\begin{array}{l}{l}_p=1(\alpha >0^{\circ })\\ l_p=-1(\alpha <0^{\circ })\end{array}\end{array}$$

(9)

where α and β are the position angles of the rotor, i_tu,a, i_tu,b, i_tu,c, i_tu,d, i_tu,e, and i_tu,f are the tilting currents of the upper coils, i_td,a, i_td,b, i_td,c, i_td,d, i_td,e, and i_td,f are the tilting currents of the lower coils, I_t,m is the maximum value of the tilting current, and θ_c is the angle of the coil from the xy reference plane.

A common three-phase current flows through the rotating coil to generate a rotating field. The tilting coils are composed of a pair of upper and lower parts. The direction of the current flowing through the upper coil is opposite to that flowing through the lower coil. Additionally, the tilting current is a function of α and β, which are the position angles. Hence, the values of the six pairs of tilting currents change according to the values of α and β.

2.2. Spherical Multi-DOF Actuator Using Halbach Magnet Array Structure

Conventional multi-DOF actuators have low power density. To solve the problem, a Halbach magnet array was added to the existing magnet structure located in the internal rotor, as shown in Figure 3. The Halbach magnet array concentrates magnetic flux and reduces leakage flux.

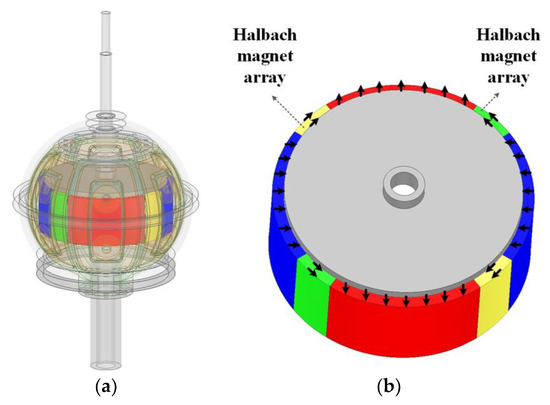
Figure 3. Spherical multi-DOF actuator using Halbach magnet array: (a) Structure of spherical multi-DOF actuator with the Halbach magnet array; (b) Internal rotor and magnetization direction.

The magnetic flux density of spherical multi-DOF actuator with a Halbach magnet array is equated as follows [23]:

$$\{\begin{array}{ll}{B}_1={\mu }_0{H}_1& \mathrm{Region}1\text{\hspace{0.17em}:\hspace{0.17em}}\mathrm{air}-\mathrm{gap}\\ B_2={\mu }_0{\mu }_r{H}_2+{\mu }_0{M}_r& \mathrm{Region}2\text{\hspace{0.17em}:\hspace{0.17em}}\mathrm{permanet}\mathrm{magnet}\\ B_3={\mu }_0{\mu }_m{H}_3& \mathrm{Region}3\text{\hspace{0.17em}:\hspace{0.17em}}\mathrm{inner}\mathrm{rotor}\end{array}$$

(10)

where H is the magnetic field intensity, μ₀ is the permeability of free space, μ_r is the relative permeability of the permanent magnet, M_r is the residual magnetization vector, and μ_m is the relative permeability of the inner rotor.

The residual magnetization vector of the jth permanent magnet cab be written as follows:

$$\begin{array}{l}{M}_r=\left[\begin{array}{c}{M}_{rr}\\ M_{r\alpha }\\ M_{r\beta }\end{array}\right]=\left|M_r\right|\left[\begin{array}{c}\cos \left(\beta -\frac{\left(1-p\right)\left(j-1\right)\pi }{pl}\right)\sin \alpha \\ \cos \left(\beta -\frac{\left(1-p\right)\left(j-1\right)\pi }{pl}\right)\cos \alpha \\ -\sin \left(\beta -\frac{\left(1-p\right)\left(j-1\right)\pi }{pl}\right)\end{array}\right]\\ ※\frac{\pi }{2}-\frac{L_{mag}}{2}\le \alpha <\frac{\pi }{2}+\frac{L_{mag}}{2},j=1,2,\cdots ,2pl\\ -\frac{\pi }{2pl}+\frac{\pi \left(j-1\right)}{pl}\le \beta <\frac{\pi }{2pl}+\frac{\pi \left(j-1\right)}{pl}\\ \end{array}$$

(11)

where L_mag is the axial length of permanent magnet and l is the number of segments per pole. This is l = 2.

Based on Equations (10) and (11), the residual magnetization vector and scalar potentials are expressed as follows:

$$\nabla ·M_r=\nabla ·\left(\frac{B_r}{{\mu }_r}\right)=0$$

(12)

$${\nabla }^2{\Phi }_k=0,k=1,2,3$$

(13)

Additionally, the scalar potential Φ_k is obtained as follows [24]:

$$\begin{array}{l}{\Phi }_k={\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{m=-n}^n\left(A_n^m{r}^n+B_n^m{r}^{-\left(n+1\right)}\right)Y_n^m\left(\alpha ,\beta \right)}}\\ ※Y_n^m\left(\alpha ,\beta \right)=\frac{1}{2^{n}n!}\sqrt{\frac{2n+1}{4\pi }\frac{\left(n-\left|m\right|\right)!}{\left(n+\left|m\right|\right)!}}{\left(1-x^2\right)}^{\raisebox{1ex}{$\left|m\right|$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\frac{d^{\left|m\right|+n}}{d{x}^{\left|m\right|+n}}{\left(x^2-1\right)}^n\left(\cos \alpha \right)e^{im\beta },x=\cos \alpha \\ =P_n^{\left|m\right|}\left(x\right)\sqrt{\frac{2n+1}{4\pi }\frac{\left(n-\left|m\right|\right)!}{\left(n+\left|m\right|\right)!}}\left(\cos \alpha \right)e^{im\beta },(m=0,\pm 1,\pm 2,\cdots ,\pm n)\end{array}$$

(14)

where A_n^m, B_n^m, m, and n are determined by boundary conditions, Y_n^m (α, β) is the spherical harmonic function, and P_n^|m| (x) is a function represented by Legendre polynomial.

The distribution of the magnetic field is determined by a spherical harmonic function of M_rr (α, β). M_rr (α, β) as follows:

$$\begin{array}{c}{M}_{rr}\left(\alpha ,\beta \right)=\sum _{n=0}^{\infty }\sum _{m=-n}^n\left|{\mathbf{M}}_{\mathbf{r}}\right|c_{mn}\left(a_m\pm b_{m}i\right)Y_n^m\left(\alpha ,\beta \right)\hfill \\ ※ c_{mn}={\int }_{\left(\pi -L_{mag}\right)/2}^{\left(\pi +L_{mag}\right)/2}\frac{1}{2^{n}n!}\sqrt{\frac{2n+1}{4\pi }\frac{\left(n-\left|m\right|\right)!}{\left(n+\left|m\right|\right)!}}{\left(1-x^2\right)}^{{}^{\left|m\right|}/{}_2}\frac{d^{\left|m\right|+n}}{d{x}^{\left|m\right|+n}}{\left(x^2-1\right)}^n\left(cos\alpha \right){sin}^2\alpha d\alpha \hfill \\ a_m\pm b_{m}i=\sum _{j=1}^{2pl}{\int }_{\pi \left(2j-3\right)/2pl}^{\pi \left(2j-1\right)/2pl}cos\left(\beta -\frac{\left(1-p\right)\left(j-1\right)\pi }{pl}\right)e^{-im\beta }d\beta \hfill \end{array}$$

(15)

Therefore, the air-gap magnetic flux density of the spherical multi-DOF actuator with the Halbach magnet array is obtained as follows [23]:

$$B_1=\left[\begin{array}{c}{B}_r\\ B_{\alpha }\\ B_{\beta }\end{array}\right]=\left[\begin{array}{c}{\displaystyle \sum _{n=2,4,\cdots }^{\infty }{\displaystyle \sum _{m=-n}^n\left(\left(n+1\right){\mu }_r{B}_n^{-m}{r}^{-\left(n+2\right)}\right)Y_n^m\left(\alpha ,\beta \right)}}\\ {\displaystyle \sum _{n=2,4,\cdots }^{\infty }{\displaystyle \sum _{m=-n}^n\left(-{\mu }_r{B}_n^m{r}^{-\left(n+2\right)}\right)\frac{\partial Y_n^m\left(\alpha ,\beta \right)}{\partial \alpha }}}\\ {\displaystyle \sum _{n=2,4,\cdots }^{\infty }{\displaystyle \sum _{m=-n}^n\left(-{\mu }_r{B}_n^m{r}^{-\left(n+2\right)}\right){\sin }^{-1}\theta \frac{\partial Y_n^m\left(\alpha ,\beta \right)}{\partial \beta }}}\end{array}\right]$$

(16)

where B_r, B_α, and B_β are the air-gap magnetic flux densities in the r, α, and β directions of the spherical coordinate system, respectively, m and n are determined by boundary conditions, B_n^m is the magnetic flux density obtained by the boundary condition, r is the distance from the center of the spherical coordinate system, and Y_n^m (α, β) is the spherical harmonic function.

3. Power Density Improvement

3.1. Output Characteristics Based on Magnet Array Structure

The dual-airgap slotless-type spherical multi-DOF actuator exhibits different output characteristics based on the magnet array structure. Figure 4 shows the magnetic flux density vector of the internal rotors of the basic model and that of the Halbach magnet array model under a no-load condition for the same pole pitch angle. Additionally, Table 2 summarizes the fundamental wave components of the air-gap magnetic flux density (B_g1) of the basic and Halbach magnet array models. The fundamental wave component of the Halbach magnet array model is larger than that of the basic model because the magnetic flux density is concentrated in a wider area. Furthermore, the fundamental wave of the air-gap magnetic flux density is large in the model with the Halbach magnet array; thus, the output characteristics of the spherical multi-DOF actuator with the Halbach magnet array are excellent. The output characteristics of the basic model and Halbach magnet array model are summarized in Table 3.

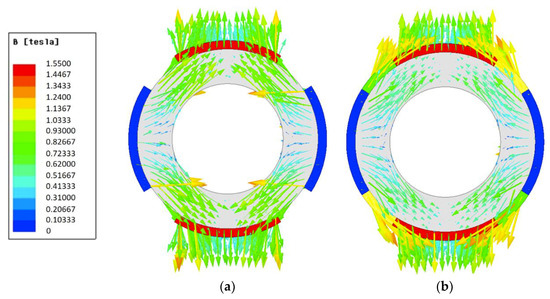
Figure 4. Magnetic flux density vector of the inner rotor: (a) Basic model; (b) Halbach magnet array model.

Table 2. Fundamental wave components of air-gap magnetic flux density of the basic model and Halbach magnet array model.

Contents	Basic Model	Halbach Magnet Array Model	Unit
Air-gap magnetic flux density (Bg1)	0.39	0.41	T

Table 3. Comparison between the output characteristics of the basic model and Halbach magnet array model.

Contents	Basic Model	Halbach Magnet Array Model	Unit
Speed	300		rpm
Pole pitch angle	130		°E
Average torque	482.4	523.3	mNm
Torque ripple rate	24.4	10.2	%
Power	15.2	16.4	W
Power density	8749.8	9119.5	W/m3
Efficiency	80.7	81.9	%

3.2. Detailed Design of Spherical Multi-DOF Actuator Using Halbach Magnet Array

The rotating coils of the existing spherical multi-DOF actuators exhibit a low fill factor rate. Therefore, the fill factor rate increases based on the arrangement space of the rotating coils in order to improve the power density. Thus, the number of rotating windings increases as shown in Table 4. Furthermore, the output torque increases when the electric load increases.

Table 4. Comparison of output characteristics with increased the number of rotating windings.

Contents	Halbach Magnet Array Model	New Halbach Magnet Array Model	Unit
Speed	300		rpm
Pole pitch angle	130		°E
Number of rotating turns	170	370	turns
Average torque	523.3	811.9	mNm
Power	16.4	25.5	W
Power density	9119.5	13,601.3	W/m3

The Halbach magnet array structure concentrates the magnetic flux passing in the direction of the air gap. However, the width of the Halbach magnet is inversely proportional to the width of the dipole magnet magnetized in the radial direction. Therefore, it is important to determine the appropriate pole pitch angle. The magnetic flux is concentrated if the width of the magnet magnetized in the radial direction is smaller than the width of the Halbach magnet. However, the outgoing magnetic flux in the radial direction decreases and the output characteristic is poor.

Figure 5 and Figure 6 show the output characteristics based on pole pitch angle and command position, respectively, of the spherical multi-DOF actuator with Halbach magnet array using the model with improved fill factor rate. As the command angles α and β change, the values of the tilting current and the rotating current change. The average torque and torque ripple rate exhibit excellent characteristics in the pole pitch angle ranges of 140–170 °E and 140–150 °E (°E is the electrical degree), respectively. Additionally, Figure 7 shows the torque waveform according to the pole pitch angle when the command angles are α = 10° and β = 30°. Thus, the model with excellent output characteristics for most command positions and a pole pitch angle of 150 °E are selected for the final model. Table 5 shows the specifications of the final model.

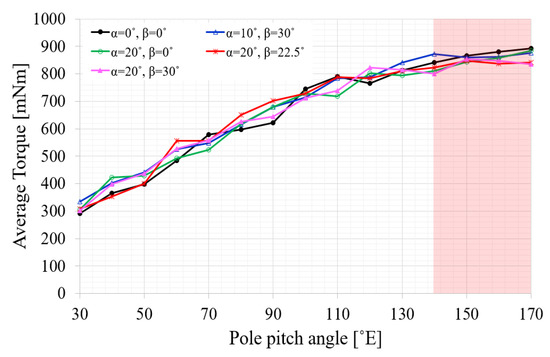
Figure 5. Average torque of the spherical multi-DOF actuator with Halbach magnet array based on pole pitch angle and command position.

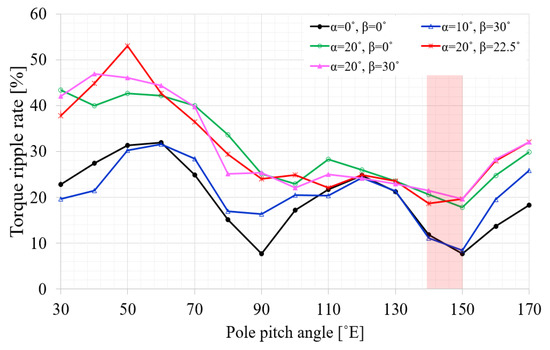
Figure 6. Torque ripple rate of the spherical multi-DOF actuator with Halbach magnet array based on pole pitch angle and command position.

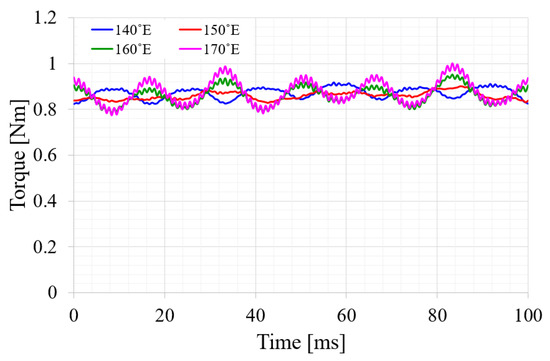
Figure 7. Torque waveform according to the pole pitch angle at α = 10° and β = 30°.

Table 5. Specifications of final model of the dual-airgap slotless-type spherical multi-DOF actuator.

Contents	Value	Unit
Diameter of the outer rotor	147	mm
Diameter of the inner rotor	113.7	mm
Thickness of the outer rotor	137	mm
Thickness of the inner part’s airgap (min/max)	1.5/5.15	mm
Thickness of the outer part’s airgap	1.5	mm
Thickness of the magnet	5	mm
Pole pitch angle	150	°E
Residual magnetic flux density of the magnet	1.25	T
Total mass	4.99	kg

3.3. Stability Characteristics

To position the rotor of the spherical multi-DOF actuator with Halbach magnet array at the command position, the positioning torque at the command position must be zero. Figure 8 describes a positioning torque (also termed as magnetic arrangement torque).

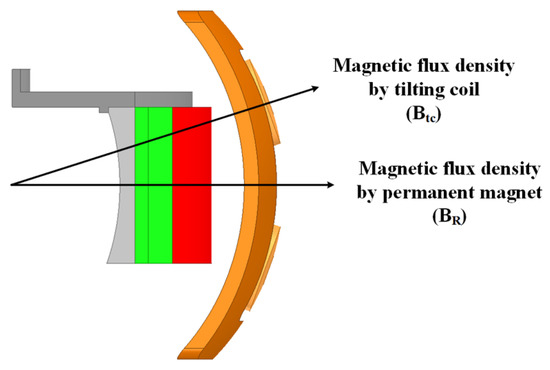
Figure 8. Principle of generating positioning torque.

The positioning torque is given as follows:

$${\mathsf{\tau }}_p=k{B}_R\times B_{tc}$$

(17)

where τ_p is the positioning torque, k is the coefficient based on the radius of the coil, length of the coil, and permeability, B_R is the magnetic flux density of the permanent magnet located in the rotor, and B_tc is the magnetic flux density of the tilting coil located in the stator.

The rotor of the spherical multi-DOF actuator with Halbach magnet array is subjected to a force such that the magnetic flux directions of the permanent magnet and coil coincide. The positioning torque is zero and reaches the command position when the two magnetic fluxes coincide. In addition, the positioning torque is zero when the two magnetic flux vectors coincide with each other in a vector in the opposite direction. However, the positioning torque deviates from the command position if an external disturbance is applied.

Figure 9 shows two models to determine the stability of the positioning torque when a coil is placed at one pole (Figure 9a) and when two coils are placed at a pole (Figure 9b).

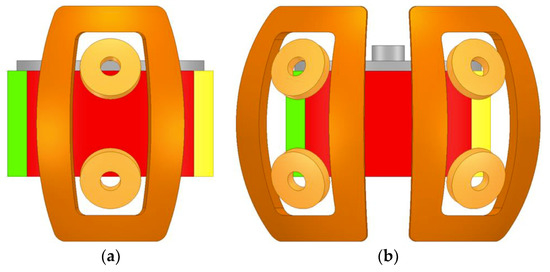
Figure 9. Two models to determine the stability of the positioning torque: (a) One coil located at a pole; (b) Two coils located at a pole.

The positioning torque characteristics of the selected model are shown in Figure 10 for command angles α = 0°, β = 0° (Figure 10a) and α = 0°, β = 30° (Figure 10b). At the point where α = 0°, the positioning torque exhibits a value of zero and negative slope. Hence, a negative torque is generated if an external disturbance causes a displacement in the positive direction in the vicinity of α = 0°. Additionally, a positive torque is generated if the displacement occurs in the negative direction. Therefore, the spherical multi-DOF actuator with Halbach magnet array can be stably driven based on the command.

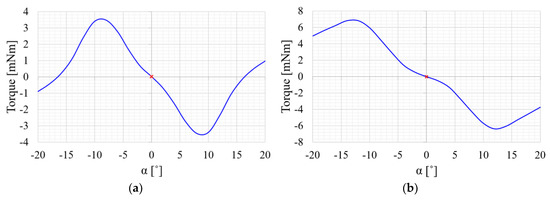
Figure 10. Positioning torque characteristic when pole pitch angle is 150 °E: (a) α = 0°, β = 0°; (b) α = 0°, β = 30°.

3.4. Control Method

Position control of the multiple DOF actuators is achieved via two non-contact image sensors. As shown in Figure 11a, the two image sensors are arranged with a spatial difference of 90°. Figure 11b shows the values when Sensor 1 is sensing the rotating surface. The two image sensors are spatially 90° apart; thus, the displacements Δy₁ and Δy₂ are as follows [25]:

$$\Delta y_1=y_{\max }\left(\alpha \right)\sin \beta$$

(18)

$$\Delta y_2=y_{\max }\left(\alpha \right)\cos \beta$$

(19)

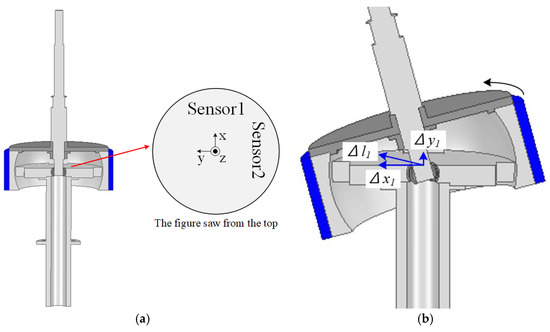
Figure 11. Image sensor for position control: (a) Position of image sensor; (b) Measured value of Sensor 1.

As shown in Figure 11b, the rotation angle ϕ is as follows:

$$\varphi =\frac{\sqrt{{\left(\Delta x_1\right)}^2+{\left(\Delta y_1\right)}^2}}{r}=\frac{\Delta l_1}{r}$$

(20)

where r is the distance from the center of the rotor to the measurement surface, and Δl₁ is the movement distance about the rotational trajectory measured by Sensor 1.

For achieving position control of the multi-DOF actuator, α and β should be obtained. First, using Equations (12) and (13), β is determined as follows:

$$\tan \beta =\frac{\Delta y_1}{\Delta y_2}=\frac{y_{\max }\left(\alpha \right)\sin \beta }{y_{\max }\left(\alpha \right)\cos \beta }$$

(21)

$$\beta =\arctan 2\left(\Delta y_1,\Delta y_2\right)$$

(22)

Figure 12 shows a state where β = 90°. Additionally, α represents the angle between Δl₁ and Δx₁. Using Figure 12 and Equation (12), α is derived as follows:

$$y_{\max }\left(\alpha \right)=\frac{\Delta y_{1,\beta ={90}^{\circ }}}{\sin {\beta }_{\left(={90}^{\circ }\right)}}=\Delta y_{1,\beta ={90}^{\circ }}$$

(23)

$$\sin \left(\alpha \right)=\frac{\Delta y_{1,\beta ={90}^{\circ }}}{\Delta l_{1,\beta ={90}^{\circ }}}$$

(24)

$$\alpha =\arcsin \left(\frac{\Delta y_{1,\beta ={90}^{\circ }}}{\Delta l_{1,\beta ={90}^{\circ }}}\right)$$

(25)

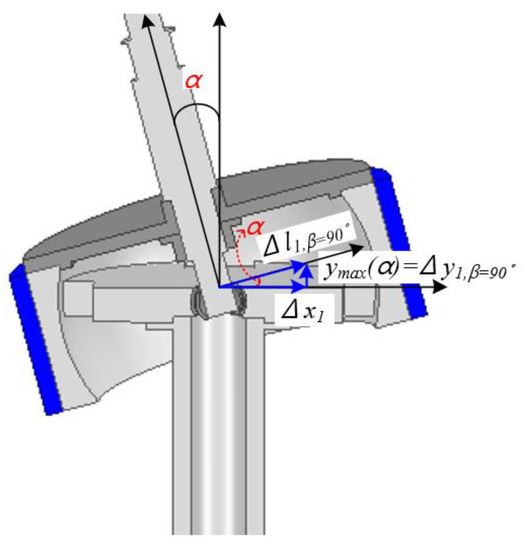
Figure 12. State of the multi-DOF actuator when β = 90°.

Therefore, position control is achieved by obtaining ϕ, α, and β via the image sensor.

4. Conclusions

In this study, we propose a structure for a dual-airgap slotless-type spherical multi-DOF actuator and examine its power density improvement over a multi-DOF actuator. To improve the output power density of the multi-DOF actuator, a dual-airgap and slotless-type spherical structure was selected to decrease eddy current loss via simultaneous movements of the internal and external rotors. Additionally, a three-phase structure with an induced voltage with a large fundamental wave size and a small harmonic size was selected. Furthermore, a Halbach magnet array was added to existing magnets to increase magnetic flux density of the permanent magnets. We used a detailed design of the winding and rotor magnet structure to finally select a model with high output power density and low torque ripple. Additionally, it is necessary for the multi-DOF actuator to move to the position of the entered command. Therefore, stability analysis is essential to determine whether the actuator moves to the command position. For the actuator to run stably, the torque at the command position must be zero and should exhibit a torque curve with negative slope. If the torque at command position is zero but the torque curve has a positive slope, the actuator deviates from the command position when a slight disturbance is applied. Therefore, stability analysis was performed to confirm whether the spherical multi-DOF actuator with Halbach magnet array was positioned based on the command. Additionally, two image sensors were used for the position control of the multi-DOF actuator. Herein is designed a spherical multi-DOF actuator that improves power density and is located at the desired command position.