Multi-Agent Optimization for Residential Demand Response under Real-Time Pricing

Abstract

Demand response (DR) programs encourage consumers to adapt the time of using electricity based on certain factors, such as cost of electricity, renewable energy availability, and ancillary request. It is one of the most economical methods to improve power system stability and energy efficiency. Residential electricity consumption occupies approximately one-third of global electricity usage and has great potential in DR applications. In this study, we propose a multi-agent optimization approach to incorporate residential DR flexibility into the power system and electricity market. The agents collectively optimize their own interests; meanwhile, the global optimal solution is achieved. The agent perceives its environment, predicts electricity consumption, and forecasts electricity price, based on which it takes intelligent actions to minimize electrical energy cost and time delay of using household appliances. The decision-making action is formulated into a convex program (CP) model. A distributed heuristic algorithm is developed to solve the proposed multi-agent optimization model. Case studies and numerical analysis show promising results with low variation of the aggregated load profile and reduction of electrical energy cost. The proposed approaches can be utilized to investigate various emerging technologies and DR strategies.

1. Introduction

Demand response (DR) is designed to change electricity consumption patterns, which includes shifting electricity load from on-peak to off-peak periods, shifting electricity consumption to when renewable energy is abundant, reducing demand when the system reliability is jeopardized, or responding to dynamic price signals. DR can be applied to (1) reduce greenhouse gas (GHG) emissions by integrating renewable energy [1,2], (2) provide ancillary services such as frequency control and operating reserves [3,4], and (3) balance power generation and demand in an electricity market [2,5,6]. DR is considered as the most economical approach to these applications and has gained increasing attention from both academics and industry. To support DR applications, the U.S. Department of Energy lists three types of price-based DR options: time of use (TOU), real-time pricing (RTP), and critical peak pricing (CPP) [7]. Other mechanisms include inclining block rate (IBR), direct load control (DLC), demand bidding, and capacity programs in the electricity market. A more recent review of state-of-the-art approaches to implement DR programs in a smart grid environment can be found in [8].

Compared to DR implementation in the commercial/industry sector, residential DR implementation is more challenging because: (1) individual residential load is small in scale; (2) residential electricity consumption is random in nature; and (3) consumers’ acceptance of inconvenience from shifting loads and/or privacy issues must be considered.

Multi-agent systems (MAS), optimization models, and game theories are useful and suitable tools to tackle these challenges. In general, a MAS is defined as a group of autonomous agents that interact, cooperate, and negotiate with each other to reach both the design objectives of individual agents as well as the global objectives [9,10,11]. The IEEE Power Engineering Society’s Multi-Agent Systems Working Group has identified two novel approaches of using MAS in power engineering applications, namely: (1) building flexible and extensible systems; (2) simulation and modeling [12].

A number of examples of agent-based modeling and simulation for residential DR can be found in the literature. The automated DR problem under RTP was studied in a MAS, and a novel control mechanism was proposed to cope with disconnected communication among agents [13]. A MAS-based multistep and multilevel optimization algorithm was developed to incorporate DR in a community energy management system (EMS) [14]. However, the benefits of DR for householders were not evaluated in [13,14]. For example, the work in [14] focuses on reducing system operational cost. The work in [15] develops an agent-based multi-layered hierarchical control scheme for residential DR under RTP. Optimal stopping rule theory was applied to tackle price uncertainty. An hour-ahead DR algorithm for a home EMS was developed, in which the artificial neural network (ANN) technique was used to predict the electricity prices and multi-agent reinforcement learning was adopted to control household loads [16]. Potential benefits from individual appliances were evaluated. However, DR benefits at a utility level were not studied in [15,16]. A load forecasting algorithm based on ANN was developed and further incorporated into a MAS model for virtual power plants in [17]. Agent-based simulation platforms have been developed. The work in [18] presents a smart grid co-simulation software platform—SimApi. It is an open source smart grid software infrastructure that provides a benchmark for building control algorithms. A Multi-Agent Smart Grid Simulation Platform (MASGriP) is presented in [19].

A microgrid consisting of 1000 residential homes and various generators was simulated in a MAS [20]. The flexible loads were electric heating appliances. The impact on GHG emissions and generation dispatch requirements were studied by incorporating wind power through DR. Energy management strategies to effectively reveal vehicle-to-grid (V2G) potential in grid-connected microgrids were proposed and evaluated in [21]. This work focuses on managing electric vehicle (EV) charging/discharging and different strategies were suggested based on the accuracy of electricity price forecasts. A hierarchical MAS was developed to incorporate air conditioning (AC) loads to the day-ahead electricity market under DR [22]. However, the studies in [20,21,22] only consider one particular type of appliance as the controllable load. In our proposed MAS, we have modelled a variety of household loads, and an optimal control model under DR is incorporated in the MAS. We evaluated the DR benefits for both homes and utilities.

Various deterministic and stochastic optimization models can be seen in the literature. A mixed-integer linear programming (MILP) model was developed to study V2G technology and energy storage systems (ESS) responding to the combination of a RTP with a peak power limiting-based strategy, and a 65% reduction in the cost of electrical energy was reported [23]. A bi-level optimization model was developed in a MAS framework in response to dynamic prices to flatten the load profile [24]. A DLC strategy was evaluated in [25]. An incentive-based strategy was investigated to find the trade-off between rewards and comfort levels [26]. A decentralized DR framework was proposed for DR programs considering generation cost, the consumers’ discomfort cost, and transmission constraints [27]. A transactive DR model was proposed with high EV penetration levels [28].

An important aspect of residential loads is human intervention in load control. Additionally, renewable energy availability is stochastic in nature. Use of stochastic optimization approaches such as stochastic programming, robust optimization, and stochastic game theory have become a new trend to investigate influences of this unpredictability on residential DR applications. The impacts from human behaviors on DR have been investigated in [29]. Two-stage stochastic and three-stage programming models were developed for applications in the electricity market [2,5,6,30]. A distributed random access framework was developed to mitigate bus congestion and voltage drops [31]. Since individual residential load is small/trivial in DR applications, a load aggregator was introduced between utility operators and end-users in [32]. Multi-layer optimization models were developed and solved through the intermediation by the aggregator. An incentive-based residential DR program was proposed in [33] to aggregate the loads to meet a pre-defined load profile. A load aggregator was also introduced in a day-head market for various objectives [34,35]. Game theories were applied in demand response applications [36,37,38]. A stochastic game approach was proposed to study the interactions among service providers, EV charging stations, and EV owners, and a Nash equilibrium provides a RTP scheme [39].

In this study, we develop a MAS framework. We also develop a household load forecast model, an electricity price forecast model, and an optimization model. The optimization model incorporates the human impact on electricity consumption. These models are further incorporated into the proposed MAS. The software agents collectively optimize their own profits; meanwhile, the global optimal solution is achieved. This study is based on our earlier work [40] but with significant enhancement. The difference and improvements are listed as follows.

• We developed a co-operative MAS, in which the home agents (HAs) collectively optimize their objectives. The global optimal solution is achieved through integration among the HAs.
• The HAs optimize the objective based on global information through the interaction among HAs.
• Game theory is used to prove the existing and uniqueness of the optimal solution.
• The impact of EV penetration levels and charging strategies are evaluated.

The main contributions of this paper are summarized as follows.

• A MAS with incorporated load and price forecast models and an optimization model is developed. The proposed system is linearly scalable and can be implemented in parallel into large-scale applications.
• The prediction model forecasts household load including EV charging as a benchmark for heterogeneous homes. Each home has a unique load profile. The benefits of DR applications and the effectiveness of the proposed approaches are clearly demonstrated.
• The individual privacy load information is not exposed for any homes because the exchanged load profile is the sum of all the other homes.
• The proposed multi-agent optimization approach can significantly reduce electricity payment/cost and improve the energy efficiency.

The rest of this paper is organized as follows. In Section 2, we describe the multi-agent system. Section 3 discusses the mathematical formulations and models. Case studies are shown in Section 4. A discussion of this work is presented in Section 5 followed by conclusions and future work.

2. Multi-Agent System

We assume a group of residential customers participate in a DR program in a wholesale electricity market. The group of homes are modeled by software agents, namely home agents (HA): $\mathrm{HA}=\left\{1,\cdots ,n\right\}$ where $n$ is the number of HAs. Each home has a set of appliances $\mathcal{A}\mathcal{P}$, which is further divided into a set of un-schedulable appliances $\mathcal{U}\mathcal{A}\mathcal{P}$ and schedulable appliances $\mathcal{S}\mathcal{A}\mathcal{P}$. Figure 1 shows the basic optimization procedure.

Figure 1. Operation process and information flow of the agents.

We now define the environment, optimization model, actions, and information exchange model for a HA.

2.1. Environment

The HA resides and perceives its environment, which has electricity price $P$, household load $L$, consumption constraints $ct$, and human factor $\Lambda$.

$${ℰ}_{HA}=\left\{P, L,ct,\Lambda \right\}$$

(1)

$$\Lambda =\left\{{\lambda }^{ap}\right\} \forall ap\in \mathcal{S}\mathcal{A}\mathcal{P}$$

(2)

where P and L is defined as a column vector of the electricity price and the household load at different discrete times. $ct$ is a set of operational constraints. $\Lambda$ is a vector of unwillingness factors to reschedule the set of schedulable appliances. $ap$ is a household appliance. ${\lambda }^{ap}$ is a non-negative number representing customers’ unwillingness to reschedule the electricity usage of $ap$.

2.2. Optimization Models

The HAs collectively minimize the electrical energy cost with consideration of the unwillingness of rescheduling the electricity load.

$$\mathrm{minimize} {\displaystyle \sum }_{i=1}^n\left(P_i{L}_i+{\Lambda }_i{\mathsf{Փ}}_i\right) \mathrm{subject} \mathrm{to}: ct$$

(3)

where $P_i{L}_i$ is the electrical energy cost for agent $i$. ${\Lambda }_i$ is a vector of unwillingness factors to reschedule the set of schedulable appliances for agent $i$. ${\mathsf{Փ}}_i$ is a vector of efforts to reschedule the set of schedulable appliances for agent $i$. Note that ${\Lambda }_i$ and ${\mathsf{Փ}}_i$ can be different for various agents.

2.3. Actions

HAs can take three types of actions.

$$\mathcal{A}{\mathcal{C}}_{HA}=\left\{forecast load,forcast price, reschedule load \right\}$$

(4)

The HA can forecast the electricity consumption of the household load as well as the electricity price. Based upon the load and price information, the HA plans the electricity usage of schedulable loads to minimize the electrical energy cost. The rescheduled load action is to obtain maximum benefits for homeowners based on the optimization model discussed in Section 2.2.

2.4. Information Exchange Rules

A HA forecasts electricity price based on local information and exchanged information from its neighbors and then takes actions to reschedule electricity usage by applying the proposed optimization model. We define the rules for information exchange as follows.

• Broadcast load profile if and only if the load profile is changed compared with the load profile in the earlier reschedule.
• Assign equal weights to the local load profile and received load profile.
• Assign zero weight to HAs from whom the agent does not receive information.
• Assume HA has connectivity to all the rest agents but form the network only for HAs who have changed load profiles.

3. Mathematical Formulation

In this section, we illustrate the mathematical models, namely, the load forecast model, the real-time pricing model, and the optimization model. The load forecast model and the real-time pricing model have been developed in our earlier work [40]. However, for the notion purpose, they are concisely introduced. We then focus on describing the optimization model.

3.1. Load Forecast Model

The load forecast model is defined as follows.

$$l_t^{ap}=q_{rated}^{ap}, \forall ap\in \mathcal{A}\mathcal{P}, t\in \left[t_0^{ap}, t_0^{ap}+\Delta t^{ap}\right]$$

(5)

$$l_t^{ap}=0, \forall ap\in \mathcal{A}\mathcal{P}, t\in \mathcal{T}\backslash \left[t_0^{ap}, t_0^{ap}+\Delta t^{ap}\right]$$

(6)

where $l_t^{ap}$ represents the electricity load of an appliance $ap$ at a time $t$. $q_{rated}^{ap}$ is defined as the rated power. $t_0^{ap}$ is the initial operating time and $\Delta t^{ap}$ is the operating period. The standby power is assumed to be zero. Detailed mechanisms of how to obtain the parameters of $q_{rated}^{ap}$, $t_0^{ap}$, and $\Delta t^{ap}$ can be found in our earlier publication [40].

The predicted load and energy consumption are defined as follows.

$$\widehat{L}=⟨\widehat{l_1^{ap}},\cdots , \widehat{l_T^{ap}}⟩$$

(7)

$$\widehat{E_{\mathcal{U}}^{ap}}={\displaystyle \sum }_t\widehat{l_t^{ap}}, \forall ap\in \mathcal{U}\mathcal{A}\mathcal{P}, t\in \left[t_0^{ap}, t_0^{ap}+\Delta t^{ap}\right]$$

(8)

$$\widehat{E_{\mathcal{S}}^{ap}}={\displaystyle \sum }_t\widehat{l_t^{ap}}, \forall ap\in \mathcal{S}\mathcal{A}\mathcal{P}, t\in \left[t_0^{ap}, t_0^{ap}+\Delta t^{ap}\right]$$

(9)

where $\widehat{L}$ is the column vector of the predicted load profile. $\widehat{E_u^{ap}}$ and $\widehat{E_s^{ap}}$ is the predicted electrical energy of un-schedulable appliances and schedulable appliances. Note that $\widehat{E_u^{ap}}$ and $\widehat{E_s^{ap}}$ are column vectors (e.g., $\widehat{E_u^{ap}}= ⟨\widehat{E_{u,1}^{ap}},\cdots ,\widehat{E_{u,T}^{ap}}⟩$).

3.2. Real-Time Pricing Model

Multiple types of power generators, such as thermal, hydro, natural gas generators, etc., are required to meet the demand. These generators are economically dispatched based on their marginal generation cost, i.e., the generation cost increases with demand since cheapest generations must be used first followed by more expensive ones. In this study, we define the electricity price as piecewise linear functions of power (kW) as indicated as follows.

$$p\left(l_t\right)=\{\begin{array}{c}{\alpha }_1{l}_t+{\beta }_1, \forall l_t\le l_{TH}, t\in T\\ {\alpha }_2{l}_t+{\beta }_2, \forall l_t>l_{TH}, t\in T\end{array}$$

(10)

where ${\alpha }_1$, ${\alpha }_2$, ${\beta }_1$ and ${\beta }_2$ are constant parameters. The increase of electricity price based on load is accelerated once it exceeds the threshold $l_{TH}$. This is indicated by $0<{\alpha }_1<{\alpha }_2$. The parameters are determined by linear regression using the data from PJM [41].

In our study, we focus on a microgrid of 100 homes and assume the existence of a local electricity market. It is noted that the electricity price or locational marginal price (LMP) relatively depends on the load profile, rather than being based on the absolute magnitude of the power consumption. As can be seen from PJM data, the load consumption in the American Electric Power (AEP) zone is about ten times more than the Duquesne Lighting Company (DUQ) zone, but the LMP in two zones are similar [41].

3.3. Optimization Model

HAs reschedule the load based on the proposed optimization model to minimize electrical energy cost as well as discomfort from rescheduling the load. We define this optimization problem as a convex program (CP) model.

Minimize

$${\displaystyle \sum }_{t\in \mathcal{T}}p\left({\displaystyle \sum }_{ap\in \mathcal{A}\mathcal{P}}{l}_t^{ap}+{\displaystyle \sum }_{H{A}_{-i}}{\displaystyle \sum }_{ap\in \mathcal{A}\mathcal{P}}{l}_t^{ap} \right)\left({\displaystyle \sum }_{ap\in \mathcal{A}\mathcal{P}}{l}_t^{ap}\right)+{\displaystyle \sum }_{t\in \mathcal{T}}{\displaystyle \sum }_{ap\in \mathcal{S}\mathcal{A}\mathcal{P}}{\lambda }^{ap} w^{ap}{l}_t^{ap}$$

(11)

Subject to:

$$0\le l_t^{ap}\le q_{rated}^{ap}, \forall ap\in \mathcal{S}\mathcal{A}\mathcal{P}, t\in \left[t_0^{ap},t_1^{ap}\right]$$

(12)

$$l_t^{ap}=0, \forall ap\in \mathcal{S}\mathcal{A}\mathcal{P}, t\in \mathcal{T}\backslash \left[t_0^{ap},t_1^{ap}\right]$$

(13)

$${\displaystyle \sum }_{ap}{\displaystyle \sum }_t{l}_t^{ap}=\widehat{E_{\mathcal{S}}^{ap}}, \forall ap\in \mathcal{S}\mathcal{A}\mathcal{P}, t\in \left[t_0^{ap},t_1^{ap}\right]$$

(14)

$${\displaystyle \sum }_{ap\in \mathcal{S}\mathcal{A}\mathcal{P}}{l}_t^{ap}+{\displaystyle \sum }_{ap\in \mathcal{U}\mathcal{A}\mathcal{P}}\widehat{l_t^{ap}} \le Q_{HA}^{max}, \forall t\in \mathcal{T}$$

(15)

The optimization model has a combined two objectives. The first objective is to minimize the electrical energy cost shown by the first term in Equation (11). ${\displaystyle \sum }_{ap\in \mathcal{A}\mathcal{P}}{l}_t^{ap}$ is the load of the HA and ${\displaystyle \sum }_{H{A}_{-i}}{\displaystyle \sum }_{ap\in \mathcal{A}\mathcal{P}}{l}_t^{ap}$ is the aggregated load profile of the other HAs denoted as $H{A}_{-i}$. The aggregated load profile is obtained through information exchange. The electricity price $p(·)$ is defined in Equation (10). The HA predicts the electricity price based on the global load information. The second objective shown by the second term in Equation (11) is the consideration of discomfort of the rescheduling of the load. ${\lambda }^{ap}$ is a scaler to reflect the magnitude of discomfort to reschedule load $ap$. $w^{ap}$ is delayed time due to the load reschedule defined in Equation (16). $l_t^{ap}$ represents the amount of rescheduled load. The second term ${\displaystyle \sum }_{t\in \mathcal{T}}{\displaystyle \sum }_{ap\in \mathcal{S}\mathcal{A}\mathcal{P}}{\lambda }^{ap} w^{ap}{l}_t^{ap}$ performs as a penalty function to balance the two objectives.

$$w^{ap}=t-t_0^{ap}$$

(16)

Equations (12)–(15) show the constraints of the model. Equations (12) and (13) show that the appliance should operate in the period of $\left[t_0^{ap},t_1^{ap}\right]$. $t_1^{ap}$ is the deadline for the operation to be completed. In this period, the appliance may run at any power between 0 kW and the rated power $q_{rated}^{ap}$. However, since $w^{ap}$ in the objective function is a monotonically increasing function, the optimal solution will lead to a sparse vector. In other words, the decision variables will be either 0 or $q_{rated}^{ap}$. Equation (14) shows that the energy consumption will not change after the rescheduling of usage. Equation (15) is an operational constraint.

The HAs solve the optimization model locally but with exchanged information in order to achieve a global optimal solution. We have developed a heuristic algorithm (shown in Algorithm 1) to accomplish this task. The HAs schedule their load by solving the optimization model in a random order. Note that in the first round, the first HA only has local information. However, the HAs get more and more information from other HAs. They have the opportunity to reschedule the electricity consumption. This progress will continue till no HA reschedules its loads.

Algorithm 1. The algorithm for the multi-agent optimization model.

Round repeat

for $HA$ in a random order

1: Input: The forecasted local load profile and the exchanged information

2: Solving the proposed optimization model

3: Determine the electrical energy cost

if this is the first round

Store the electrical energy cost for the HA

else

if the cost < earlier cost

Update the load profile for the HA

Broadcast the load profile

else

Keep the load profile from the last round

4: Output: Optimal solution

Next round till no HA is willing to reschedule the schedulable loads

Furthermore, it is now shown that the solution is unique for any particular order of HAs in the scheduling process.

Proof. 

The proposed model be formulated as a finite game as follows.

Players: The $\mathrm{HA}\in \mathcal{H}\mathcal{A}$, where $\mathcal{H}\mathcal{A}$ represents a set of HAs.

Strategies: Each $\mathrm{HA}\in \mathcal{H}\mathcal{A}$ minimizes the objective function in the proposed optimization model. In other words, each HA determines its load profile ${\displaystyle \sum }_{ap\in \mathcal{A}\mathcal{P}}{l}_t^{ap}$ to maximize its payoff.

Payoffs: The payoffs can be seen as the maximum utility denoted as negative of the objective function:

$$payoff=-\left[{\displaystyle \sum }_{t\in \mathcal{T}}p\left({\displaystyle \sum }_{ap\in \mathcal{A}\mathcal{P}}{l}_t^{ap}+{\displaystyle \sum }_{H{A}_{-i}}{\displaystyle \sum }_{ap\in \mathcal{A}\mathcal{P}}{l}_t^{ap}\right)\left({\displaystyle \sum }_{ap\in \mathcal{A}\mathcal{P}}{l}_t^{ap}\right)+{\displaystyle \sum }_{t\in \mathcal{T}}{\displaystyle \sum }_{ap\in \mathcal{S}\mathcal{A}\mathcal{P}}{\lambda }^{ap} w^{ap}{l}_t^{ap}\right]$$

Existence: Theorem (Nash, 1951). Every game with a finite number of players and strategy profiles has at least one Nash equilibrium [42] (p. 71). In this case, no players/HAs are willing to reschedule their schedulable loads.

Unique: Since the objective function is strictly convex, the $payoff$ is strictly concave. Therefore, the Nash equilibrium is unique [43].  □

Therefore, the proposed algorithm can be converged, and the solution is unique for any particular order of HAs in the scheduling process.

4. Case Study and Numerical Analysis

This section presents simulation results for three cases:

• The reference case in which no load is scheduled. The results are solely based on the load forecast and the HA takes no actions to schedule the load. A flat electricity price is applied.
• Using the proposed mechanism. The multi-agent optimization model is applied and the RTP is used.
• Evaluation of EV numbers and different charging strategies.

CVX [44,45] is used to solve the CP model. We used TRLabs Execution Environment for Mobile Agents (TEEMA) as the agent execution environment (AEE) to develop the system because of its familiarity to the authors [40,46,47]. TEEMA provides standard libraries to support various types of operations for agents such as addressing, naming, messaging, mobility, security, and logging [48].

4.1. Simulation Setup

In all the cases, we consider a group of 100 homes. We assume 20 homes have EVs and each home has only one EV, i.e., there are 20 EVs in the system. The maximum power of one home is $Q_{HA}^{max}=24 \mathrm{kW}$. The simulation period is 24 h and the time interval is 1 h. The linear regression method is used to determine the parameters in the price forecast model, as shown in Table 1.

Table 1. Coefficients of the price prediction model [40].

Coefficient	${\mathit{\alpha }}_1$	${\mathit{\beta }}_1$	${\mathit{\alpha }}_2$	${\mathit{\beta }}_2$
Single home load	0.282	2.025	0.459	1.317
Aggregated load from 100 homes	0.015	1.776	0.025	0.911

4.2. Case 1: Reference Case

No schedule load actions were taken, and a flat electricity rate was applied in this case. Figure 2 shows the simulation results. The load profile was simulated by the residential load forecast model. The red dash line shows the generation cost with load and the blue dash-dot line shows the equivalent flat electricity rate assuming a budget-balanced market. The consumed electrical energy was 1716.9 kWh, and the electrical energy cost in the day was calculated as $62.77 based on the generation cost. To keep the budget balanced, the equivalent flat rate is calculated as follows: $62.77/1716.9 kWh = 3.66 ¢/kWh.

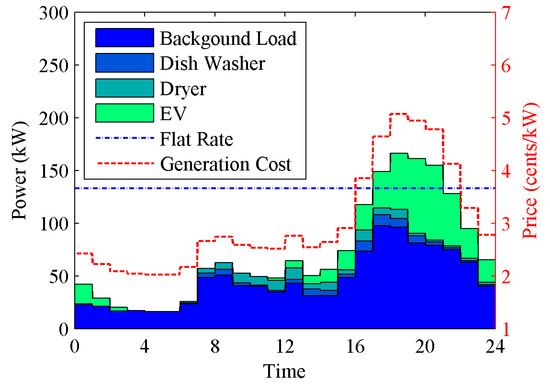
Figure 2. Aggregated load profile, electricity price, and the generation cost in the reference case [40]. EV: electric vehicle.

Figure 3 shows the electrical energy cost by blue circles for each HA. For EV owners, the electrical energy cost averaged at $1.27. The maximum electrical energy cost was $1.66 while the minimum cost was $0.97. For non-EV owners, the average cost was $0.47. The maximum cost was $0.96 and the minimum was $0.21. The statistical information is as follows. The standard deviation of the load profile was 47.7 kW. The same predicted energy consumption was used for all other cases in this study in order to make them comparable and reproducible.

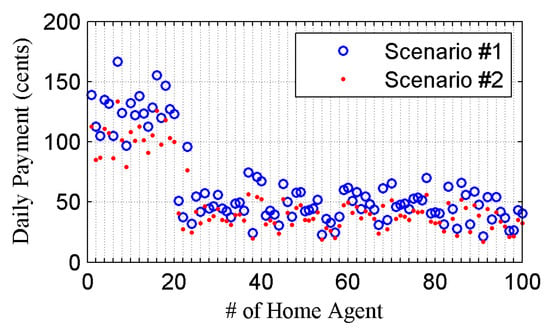
Figure 3. Electrical energy cost of 100 homes.

4.3. Case 2: Using the Proposed Mechanism

This case evaluates the proposed mechanism with 20% EV penetration. The HAs schedule the loads using the proposed multi-agent optimization approach. The factor ${\lambda }^{ap}$ has two roles in the model: (1) reflect the discomfort to change the consumption patterns; (2) average the weight of the two objectives in the objective function. Therefore, it should not be too small because of the first role while it could not be too large due to the second role. We have conducted a quantitative study on the impact of ${\lambda }^{ap}$ [40]. Based on the study, we set ${\lambda }^{ap}=0.1$ in this case.

Figure 4 shows the simulation results. The generation cost or electricity price is shown by the red dashed line, which is used to calculate the electrical energy cost for HAs. The standard deviation of the load profile was decreased to 13.03 kW and the electrical energy cost was dropped to $50.46. Electrical energy cost from individual homes is shown in Figure 3. The average daily electrical energy cost for EV owners was reduced by 18.8% to $1.03. The maximum cost of EV owners was $1.33, which is a 24.5% reduction. The minimum cost was $0.79 representing a 17.5% reduction. For non-EV owners, the percentage of cost reduction was also significant. The maximum reduction was 26.1% and the cost was $0.77. The minimum cost was $0.17 and it was 16.6% of the reduction. The average electrical energy cost was $0.37, which is a 20.2% reduction.

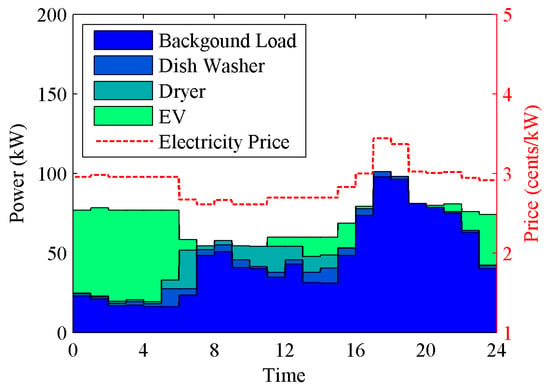
Figure 4. Aggregated load profile and electricity price in case #2.

The algorithm to realize the proposed approach is round-based and the process quickly converges. More particularly, 45 HAs scheduled the loads in the first round. Four HAs did it in the second round and there were no HAs rescheduling the load in the third round.

4.4. Case 3: Evaluation of EV Numbers and Different Charging Strategies

4.4.1. The Impact of EV Numbers

The number of EVs has a significant impact on the power system. It affects not only the magnitude of electricity usage but also the strategies to mitigate the negative impacts. In this section, we study the impacts on the electricity load profile. The standard deviation of the load profile is normalized to make the results comparable under different EV numbers.

Table 2 shows the normalized standard deviation and the energy consumption with different EV numbers. The energy consumption with 20 EVs was 1.72 × 10³ kWh while with 50 EVs, it was 2.36 × 10³ kWh. Figure 5 shows a plot of statistic information of the load profile with EV numbers of 20, 30, 40, and 50. The peak-to-average power ratio (PAPR) shows a promising result with increasing the EV numbers while the normalized standard deviation fluctuated. The lowest of normalized standard deviations is achieved at the scenario of 30 EVs. If there are more EVs, normalized standard deviation will increase, which has a negative impact on the power system. The reason is because EV charging was restricted in the period when the EV was home. Therefore, the EV charging period should be made more flexible. This can be accomplished by incorporating charging EVs elsewhere, e.g., the work place and supermarket. However, in this study, we focus on residential EV charging. We assume a battery system is available at some homes and therefore the EVs can have an extended charging time. This is studied in the next subsection.

Table 2. Statistic information of the load profile and the energy consumption with EV numbers of 20, 30, 40, and 50.

EV numbers	20	30	40	50
Normalized Standard Deviation	0.0366	0.0309	0.0451	0.0492
Energy Consumption (×103 kWh)	1.72	1.93	2.15	2.36

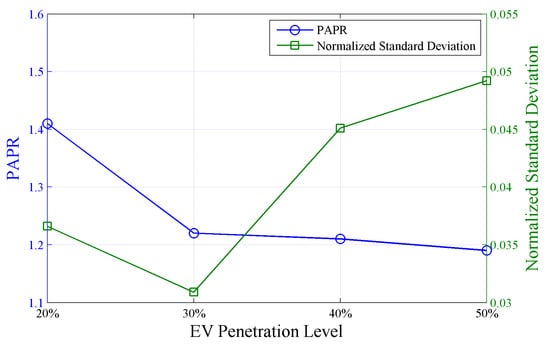
Figure 5. Statistic information of the load profile with EV number of 20, 30, 40, and 50. PAPR: peak-to-average power ratio.

4.4.2. The Impact of EVs with an Extended Charging Period

We assume that 50 among 100 homes have an EV and evaluate the impact from the number of EVs with an extended charging period. Table 3 and Figure 6 illustrate the statistic information of the load profile. The number of EVs with an extended charging period increased from 5 to 25. It can be seen that the normalized standard deviation monotonically decreases from 0.0364 to 0.0017. Figure 7 shows the simulation result in which 15 EVs have an extended charging period, in which the load profile is most leveled.

Table 3. The PAPR and the normalized standard deviation of the load profile.

Number of EVs with Extended Charging Period	5	10	15	20	25
PAPR	1.16	1.11	1.03	1.06	1.04
Normalized Standard Deviation	0.0364	0.0185	0.0043	0.0034	0.0017

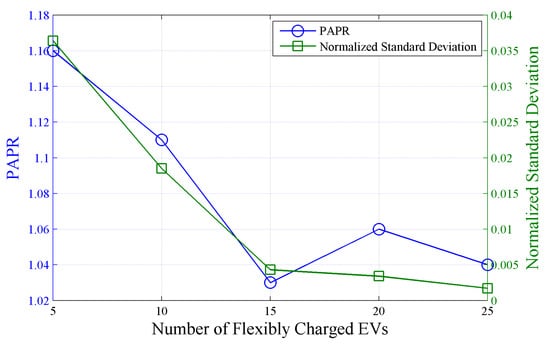
Figure 6. The PAPR and the normalized standard deviation of the load profile with a different number of flexibly charged EVs at a 50% EV penetration level.

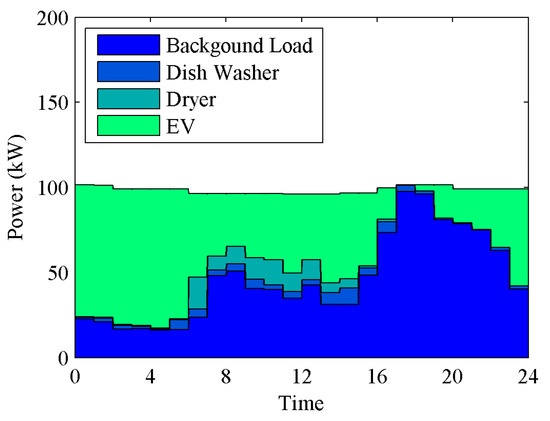
Figure 7. Aggregated load profile (15 EVs have extended charging time).

5. Discussions

The power system prefers a load profile with low variations, i.e., low values for PAPR and standard deviation. In Table 4, it can be seen that lower values for PAPR, standard deviation, and electrical energy cost are achieved using the proposed approach. Table 5 shows the electrical energy cost for the homes individually. Because EV charging requires significant energy, the homes with an EV have much higher cost than those without EVs. However, all the homes enjoy a significant drop of the electrical energy cost by using the proposed approach. Specifically, the homes in the EV group have an average cost reduction of 18.8%. The cost reduction for the homes with no EVs was even more pronounced, with an average reduction of 20.2%. The maximum cost reduction is 24.5%. This clearly demonstrates the effectiveness of the proposed mechanism.

Table 4. Summary of case #1 and #2.

Observations	PAPR	Standard Deviation (kW)	Cost ($)
Case #1	2.32	47.74	62.77
Case #2	1.41	13.03	50.46

Table 5. The summary of the individual electrical energy cost.

	Own EV	Electrical Energy Cost ($)			Cost Reduction (%)
		Average	Max	Min	Average	Max	Min
Case #1	Yes	1.27	1.66	0.97	-	-	-
	No	0.47	0.96	0.21	-	-	-
Case #2	Yes	1.03	1.33	0.79	18.8	24.5	17.5
	No	0.37	0.77	0.17	20.2	26.1	16.6

In this study, we focus on demand-side management in terms of improving power system stability and energy efficiency. However, this work can be readily incorporated into renewable energy sources (RES), e.g., solar and wind power. We could develop a roof-top solar power prediction model and consider it as a household appliance with negative load consumption. The utility level of RES will change the landscape of smart grids, which could be captured by a RES agent and included into the MAS. New objectives, e.g., to minimize CO₂ emission can be incorporated in the CP model.

6. Conclusions and Future Work

Instead of solely relying on the power generation control, DR provides a highly economical mechanism to improve power system stability and energy efficiency. Since the residential electricity consumption is significant and contributes the most to the peak demand, it has great potential in DR applications. However, it faces many challenges, such as the small magnitude of individual household electricity usage, privacy issues, and lack of effective mechanisms. In this work, we have developed a multi-agent optimization approach to incorporate residential electricity flexibility to the power system and electricity market through a DR application. A multi-agent system was developed to collectively minimize the electrical energy cost and time delay of appliances’ usage. The EV penetration level to the power system was also studied. A hypothesis of extended charging strategies was developed and investigated. Case studies and analysis show promising results using the proposed models and strategies. From a comparison with the benchmark scenario, the electrical energy cost for the utility was dropped by 19.6% and the maximum electrical energy cost saving for home owners was 24.5%. This clearly demonstrates the effectiveness of the proposed mechanism. Case study #3 shows that high EV penetration levels to the residential sector can have negative impacts on power systems even with the optimal load management. Therefore, the EV charging should be compensated by commercial and industry sectors e.g., the work place and supermarket. The multi-agent system and distributed control algorithm can be embedded in a home energy management system for DR programs. The proposed models can be used by a load aggregator and/or a utility to predict residential load profile and plan optimal DR applications to reduce electrical energy cost and improve the energy efficiency.

The future work includes: (1) Real-time load control mechanism can be designed using the optimal load profiles as references. (2) V2G applications will be included. (3) RES and ESS should be incorporated. (4) DR applications in local communities or smart grids can be studied.