Abstract
We provide a comprehensive framework for forecasting five minute load using Gaussian processes with a positive definite kernel specifically designed for load forecasts. Gaussian processes are probabilistic, enabling us to draw samples from a posterior distribution and provide rigorous uncertainty estimates to complement the point forecast, an important benefit for forecast consumers. As part of the modeling process, we discuss various methods for dimension reduction and explore their use in effectively incorporating weather data to the load forecast. We provide guidance for every step of the modeling process, from model construction through optimization and model combination. We provide results on data from the largest deregulated wholesale U.S. electricity market for various periods in 2018. The process is transparent, mathematically motivated, and reproducible. The resulting model provides a probability density of five minute forecasts for 24 h.
1. Introduction
Intraday load forecasts are essential tools for decision makers in modern electric power markets. Forecasts of between one and thirty minutes, referred to in the literature and electric utility industry as very-short-term load forecasts, are used for generation dispatch, renewable integration, and frequency control. Because electricity storage is currently prohibitively expensive, grid operators must balance generation and demand at all times. Accurate short term load forecasts can help minimize generation costs by providing efficient dispatch instructions to utilities. Understanding short-term demand minimizes over- and under-generation, allowing frequency to be kept near its nominal value. Additionally, forecasts of up to 24 h, known in the literature as short-term load forecasts, are used by financial traders in power markets to predict the future price of power. An accurate load forecast helps traders ascertain which generators will be required to meet the load and at what cost.
In this paper, we introduce a procedure for creating an intraday electric load forecast using probabilistic non-parametric models known as Gaussian processes. Our method produces accurate predictions as well as uncertainty estimates. We detail a methodology for customizing the Gaussian process by identifying an appropriate covariance structure for short term load forecasting. We then identify techniques from the machine learning and optimization literature to estimate the parameters of the model. Finally, we implement a model combination procedure to create forecasts which are more accurate and have better estimates of uncertainty. We report forecast results for PJM (The acronym PJM represents the initial three member states, Pennsylvania, New Jersey, Maryland. It has since expanded to cover all or part of 13 states and the District of Columbia), the largest deregulated wholesale electricity market in the United States.
Modelers can choose which framework best suits the needs of the forecast consumers. In [1], the authors compared multiple frameworks and suggested that “It is very important for researchers and practitioners to understand that a universally best technique simply does not exist”. Nevertheless, it is possible to whittle down the desiderata so that the choice of framework becomes clear for particular forecast applications. Multiple researchers have suggested that traditional point forecasts provided by frequentist statistics cannot meet the increasingly sophisticated needs of forecast consumers [1,2,3,4,5].
Several authors have proposed methods for incorporating uncertainty into the modeling process. In [4], the authors used a model combination technique known as quantile regression and use the empirical distribution of the residuals to estimate a prediction interval. We use a less ad hoc method for estimating the uncertainty by adopting a Bayesian approach, using Gaussian processes, as in [3]. In [3], the authors used an off-the-shelf positive definite kernel to specify the covariance structure of their Gaussian process. We extended the approach of Mori and Ohmi [3] by designing a custom kernel specific to load forecasting, allowing for a richer class of models by specifying known parameters and using the data to inform the remaining parameters. As our manuscript demonstrates, this change allows incorporating domain expertise into the modeling process, a substantial benefit of using kernel methods that is overlooked in [3].
Market Background
Accurate intraday load forecasting ensures that electricity is provided reliably at the lowest possible cost. Each percentage point reduction in the mean absolute percentage error (MAPE) is estimated to reduce the cost of supplying electricity by $1.6 million annually for a 10 GW utility [6]. The expansion of deregulated electricity markets [7,8], renewable generation [9,10] and demand response programs [11] have increased the importance of accurate intraday load forecasts. Load forecasts are particularly useful as an input to energy price forecasting and as a means for identifying which days may have similar price structure [12].
We focus on forecasting load for PJM, a region covering all or part of 13 states stretching from the Mid-Atlantic through Illinois. PJM is served by a regional transmission organization (RTO) that coordinates the generation and distribution of electricity. Figure 1 provides a map of the PJM region. Intraday load forecasts for PJM are particularly useful for electricity market traders. Western Hub, comprised of around 100 electricity buses in western PJM, is the most liquid electricity trading hub in the United States. Market participants (generators, load serving entities and financial traders) can buy and sell financial contracts tied to electricity prices to hedge their exposure to financial and physical transactions. The Commodity Futures Trading Commission (CFTC) has found that trading at Western Hub provides a valuable price discovery mechanism for electricity buyers and sellers. This claim is based on the following 2010 CFTC notice: Orders Finding That the PJM WH Real Time Peak Contract and PJM WH Real Time Off-Peak Contract Offered for Trading on the IntercontinentalExchange, Inc., Perform a Significant Price Discovery Function. Intercontinental Exchange (ICE) reports over 250,000 MW of daily volume in the balance of day (BalDay) Western Hub product which trades live during market operations.
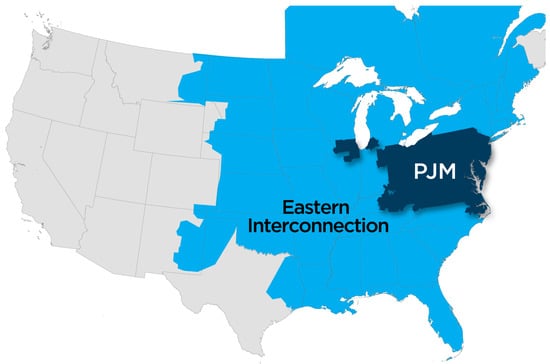
Figure 1.
PJM service area. The dark blue area is the region. The light blue area is the Eastern Interconnection, which is electrically connected to PJM. The Regional Transmission Organization (RTO) is charged with balancing supply and demand over this region as well as managing imports and exports of electricity. source: https://www.pjm.com/.
PJM publishes five-minute load forecasts up to seven days out. These load forecasts are updated every five minutes as new realizations of actual load arrive. Changes in the intraday forecast have significant impact on the price of electricity at Western Hub and thus the value of the ICE contract. Accurate intraday load forecasts give market participants an advantage in determining the right price to pay to hedge their electricity market risk.
Relatively few intraday demand forecasts provide intuitive expressions of uncertainty, a notable exception being [7] wherein The authors incorporated load uncertainty in developing an energy price forecast. The importance of decision making under uncertainty has been recognized in the mathematics and computer science communities [13], and in finance [14] but has not yet found prominence in energy price forecasting despite the uncertainty of many of the input variables for pricing models.) We contribute to the literature by proposing a method that produces a straightforward measure of uncertainty by allowing for draws from the posterior process. Understanding forecast uncertainty is particularly important for market participants who use load forecasts to schedule generation [15] or trade in financial markets. Different hours may have the same forecasted load levels but very different variances. High variance forecasts might encourage grid operators to prepare extra flexible generating capacity to come online if needed. Analogously, traders need measures of forecast uncertainty to understand the risk that their positions face. Measures of portfolio risk, e.g., value at risk (VaR), require some measure of uncertainty. Load forecast uncertainty can also be a key input into electricity price forecasts which are widely used in the industry.
2. Methodology
2.1. Posterior Predictive Process
Gaussian processes give rise to a class of Bayesian nonparametric models which have garnered tremendous attention in the machine learning community. The recent attention belies the fact that Gaussian processes, and more broadly kernel methods, have been used in scientific computing and numerical analysis for over 70 years. These methods draw on a rich theoretical and practical background. The popularity of Gaussian processes is due to the flexibility of modeling in infinite-dimensional space, the efficiency with which the data are used, the ease of implementation, and the natural handling of uncertainty. These properties make Gaussian processes ideal to forecast load for energy trading where accurate point estimates are required and uncertainty (i.e., risk) quantification is desirable.
Consider a matrix of input data such that , and are column vectors. For this paper, the input data consist of temperatures , dew points , and a time component , such that for ,
Output data, load, are also observed, such that . The goal is to predict the load, , at future times given future inputs . For Gaussian processes, the posterior distribution of the predictive process relies on the particular positive definite kernel chosen for the task; the properties of various kernels are discussed in Section 2.3. For shorthand, it is a common abuse of notation to pass the kernel matrix-valued arguments; the corresponding output is a kernel matrix (often referred to as the Gram matrix), as discussed in Appendix A. The posterior process is derived in [16], and the result is that , when conditioned on the observed data is Gaussian distributed. This is denoted as follows:
where is the posterior mean,
and is the posterior variance,
The mean term is also referred to as the maximum a posteriori (MAP) estimate. In our context, it is a point forecast of the load. Sample realizations can be drawn from the predictive distribution, providing a mathematically rigorous and computationally efficient estimate of uncertainty. As a density estimate for future load, the posterior distribution can be used downstream in electricity price forecasting and modeling the risk associated with generation or trading decisions.
2.2. Data Processing
2.2.1. Temperature
Including weather data in the intraday load forecast raises a number of issues. How many and which weather station locations should be used? The issue is discussed in [17], we abstract from it in this paper. What weather variables should be included? How does the use of too few or too many locations affect the quality of prediction? The final question is extremely pressing in the domain of prediction. A common approach in the machine learning community is to over-parameterize models and allow the information contained in the data to dictate which facets come to the forefront. Such an approach is data-inefficient. For example, if there are not enough weather stations to provide broad coverage, then out-of-sample forecast accuracy is likely to be poor. Such phenomena are explored in the statistical learning theory literature [18].
An important restriction in intraday load forecasting is that the algorithms must train quickly enough to be used in real-time planning. This means the amount of data employed in the model must be limited and over-parameterization should be avoided. On the other hand, excluding temperature information or hand-picking a small number of stations leads to an under-parameterized model in a geographically large market such as PJM. A well-tuned time series model is often adequate for prediction, but on the days where a dramatic change in temperature causes loads to spike beyond what recent temporal trends would suggest, weather must be included. Those days or hours coincide with the most active periods in the market so including information to capture those events is crucial.
We begin with 32 weather stations located across the PJM region. By using geographically diverse stations from across the entire ISO, we reduce the sampling bias that comes from choosing a small number of representative stations. To avoid over-parameterization that comes from including so many input dimensions and the known challenges of using distance metrics in high-dimensional spaces [19], we explore several different techniques for dimension reduction, as outlined in Section 2.6.
Before modeling, we must also ensure the time resolution of the different datasets is consistent. The temperature data used for this paper are hourly, while the load data are reported in five-minute increments. We deal with this by interpolating hourly data to five-minute data using a piecewise cubic Hermite interpolating polynomials, as described in [20]. The results of this interpolation for temperature data over a ten day period are provided in Figure 2. We use the Hermite spline for several reasons: an efficient implementation is available in most scientific programming languages; it is a true interpolating polynomial in that its output agrees with the observations, and it enforces first order smoothness and monotonicity between observations. These last two properties are realistic in that temperatures do not typically have discontinuities in their derivative and observations are sampled frequently enough that temperature can be assumed not to oscillate between consecutive observations.
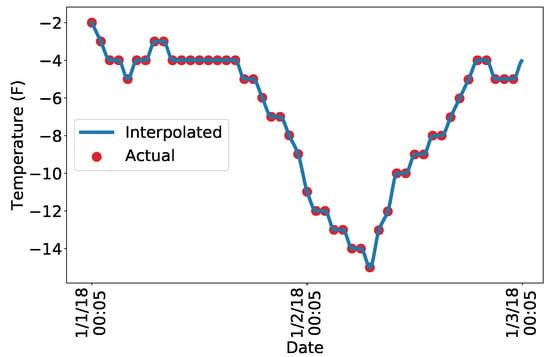
Figure 2.
Representative interpolation for approximately ten days of temperature data in Philadelphia, Pennsylvania using piecewise cubic Hermite interpolating polynomials.
2.2.2. Dew Point
In [21], it is shown that incorporating dew points leads to substantial forecast accuracy improvements over dry-bulb temperatures alone. We collect hourly dew points from the same weather stations as the temperature data. To remain consistent with temperature data, we apply the same dimension reduction techniques used for the temperatures.
2.2.3. Load
We gather one year of five-minute market-wide load data for PJMISO. Over the course of the year, 83 ticks, or approximately seven hours of data were not reported by the ISO. As with the weather, and with similar rationale, we interpolate this missing data using a piecewise cubic Hermite interpolating polynomial. Furthermore, Gaussian processes are sensitive to scale, thus we normalize the load:
Here, and , respectively, represent the mean and standard deviation of the observed data. The mean and standard deviation are stored in memory to be applied to “undo” the scaling on the forecast.
2.2.4. Data Sampling
A known issue with Gaussian processes is that the computation time generally scales cubically with the number of observations. In the context of load forecasting, training on one month of 5-min ticks results in 8928 observations, which is about the limit of computational feasibility for a modern desktop computer. Substantial efforts have been made in the machine learning community to address the scalability problem [22,23,24,25], but discussion and implementation of the proposed algorithms are beyond the scope of this paper. A simpler approach, common in the numerical analysis community, is to sample at appropriate intervals. Empirical and theoretical research has shown that, for interpolation, errors tend to increase near the boundary of the domain and that the location of observations can have a dramatic effect on this error ([26] Section 14.3). We are extrapolating beyond the boundary of the domain so the theoretical results from approximation theory may not apply; nevertheless, it seems intuitive that a sampling scheme which works well on the boundary may be more effective than sampling observations uniformly at random. Thus, in accordance with wisdom from numerical analysis [26], we sample our training data more densely near the boundary of prediction, similar to the placement of Chebyshev nodes. The seminal paper by Hoel and Levine [27] shows that, for extrapolation based on polynomials, Chebyshev nodes provide the optimal spacing. Although our predictions are made with Gaussian processes rather than polynomials, the result of Hoel and Levine [27] along with the intuition that points near the boundary provide more relevant information suggest that Chebyshev nodes are an appropriate choice. Figure 3 provides a visualization of three different methods for sampling: the uniform random method samples observations from the training set uniformly at random, Chebyshev samples more observations near the prediction boundary, and mesh spacing samples observations on a coarse evenly spaced grid (e.g., every three observations).

Figure 3.
Three different observation sampling methods for 30 of 100 hypothetical observations. The vertical axis is only meant to separate the different spacing methods.
2.3. Properties of Positive Definite Kernels
Equations (1) and (3) make clear that the problem of modeling in a Gaussian process framework revolves around the positive definite kernel K, and its kernel matrix . A brief mathematical background on positive definite kernels is provided in the Appendix. Gaussian processes are nonparametric models due to the fact that parameters do not appear in the model (see, for instance, Equation (1)). This nomenclature is somewhat confusing as the kernel itself is typically parameterized. The parameterization of the kernel is important to the modeling process; it allows the analyst to impose structure on the covariance (to specify, for instance, periodicity), and allows for intuitive interpretations of the model. In the statistics literature, a positive definite kernel is referred to as a covariance kernel, emphasizing that is a covariance function. Evaluating this function at particular arguments, , provides the covariance between two points and ; performing this operation for and yields the kernel matrix . The goal is to identify the correct covariance structure of the data by selecting an appropriate kernel and parameterizing it correctly. Since the choice of kernel and its parameterization determine the properties of the model, making an appropriate selection is crucial. In this section, we provide examples of the kernels used in our model, explain the rationale behind their use, and discuss mathematical properties needed to construct the model from these kernels.
The most obvious structure of the data is the cyclic nature over the course of the day, week, and year. A discussion of the 7- and 365-day seasonality can be found in [28], where the authors showed load data in the frequency domain to identify the cyclic behavior. Their analysis has intuitive appeal as it confirms the seasonal structure of power demand one might expect before observing any data. The periodic kernel, first described in [29], can be used to model seasonality:
where are the amplitude, the period, and the length-scale, respectively. Figure 4 provides examples of periodic kernels of different length-scales, as well as realizations of Gaussian processes drawn using the kernels as covariance functions.
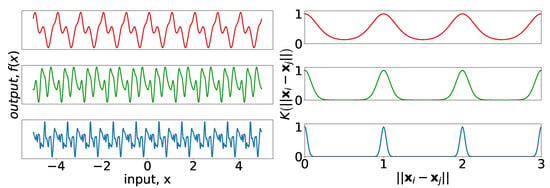
Figure 4.
(left) Random simulations from Gaussian processes with covariances defined by three different periodic kernels. In all cases, the amplitude is 1 and the period is 1. The length-scales are 2, 1, 0.5 for top, middle, and bottom, respectively. (right) Covariance kernels corresponding to the cases on the left.
The Gaussian (also known as squared-exponential) kernel is commonly used in the machine learning literature. It has the form
where in this context are the amplitude and length-scale parameters, respectively. Figure 5 provides insight into the effect of the length-scale parameter for the Gaussian kernel. Notice that the samples in all cases are smooth even for short length-scales, which is characteristic of the Gaussian kernel.
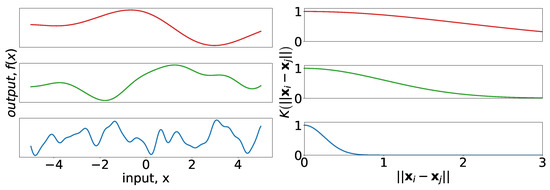
Figure 5.
(left) Random draws from Gaussian processes with covariances defined by three different Gaussian kernels. In all cases, the amplitude is 1. The length-scales are 2, 1, 0.5 for top, middle, and bottom, respectively. (right) Covariance kernels corresponding to the cases on the left.
The Matérn 5/2 kernel, commonly used in the spatial statistics literature, has the form
Here, are the amplitude and length-scale parameters, respectively, which are analogous to their counterparts in the Gaussian and periodic kernels. The general Matérn kernel can be viewed as a generalization of the covariance function of the Ornstein–Uhlenbeck (OU) process to higher dimensions ([16] Section 4.2). The OU process has been used before to forecast load (see, e.g., [30]), although in a different context then we use the Matérn here. Figure 6 provides insight into the effect of the length-scale parameter for the Matérn 5/2 kernel. Although Figure 6 (right) appears almost indistinguishable from the corresponding frame of Figure 5, it is apparent in Figure 6 (left) that draws from Gaussian processes with the Matérn kernel are not smooth (though they are twice-differentiable).
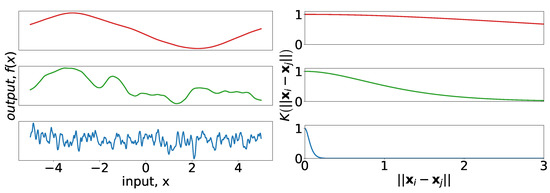
Figure 6.
(left) Random draws from Gaussian processes with covariances defined by three different Matérn 5/2 kernels. In all cases, the amplitude is 1. The length-scales are 2, 1, 0.25 for top, middle, and bottom, respectively. (right) Covariance kernels corresponding to the cases on the left.
At this point, we have introduced several kernels, but the posterior predictive distribution outlined in Section 2.1 only identifies a single kernel. The following properties of positive definite kernels allow for their combination:
Remark 1.
Let be two positive definite kernels taking arguments from a vector space . Then, for all :
- is a positive definite kernel.
- is a positive definite kernel.
Furthermore, if takes arguments from (for instance, time), takes arguments from (for instance, space). Then, for all in and all in :
- is a positive definite kernel.
- is a positive definite kernel.
Proofs of the statements in the above remark are straightforward and can be found in ([31] Section 13.1). This remark allows for the combination of all the kernels that have been discussed in a way that is intuitive and easy to code. For example, we use the periodic kernel with a Matérn decay on time:
The kernel can be interpreted as follows: the Matérn portion allows for a decay away from strict periodicity. This allows the periodic structure to change with time. A small length-scale for corresponds to rapid changes in the periodic structure, whereas a long length-scale would suggest that the periodicity remains constant over long periods of time. We combine the amplitude parameters of each kernel into a single parameter, . Figure 7 demonstrates the effect that varying of Equation (7) has on the kernel, and on realizations of a process using that kernel. Consider that the structure of the top realization in Figure 7 (left) has clear similarities between successive periods, but after four or five periods the differences become more pronounced; this is in contrast to the bottom realization for which the similarities after two periods are already difficult to identify.
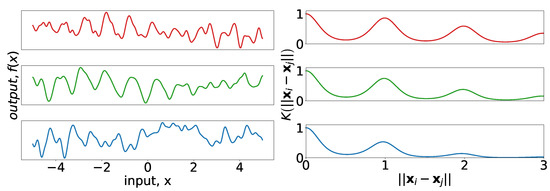
Figure 7.
(left) Random draws from Gaussian processes with covariances defined by three different decaying periodic kernels. In all cases, the amplitude is 1, the period is 1, and the length-scale of the periodic kernel is 1. The length-scales of the Matérn kernel are 2, 1, 0.5 for top, middle, and bottom, respectively. (right) Covariance kernels corresponding to the cases on the left.
2.4. Creating a Composite Kernel for Load Forecasts
To showcase the properties of this method, and to give insight into how one might go about creating a composite kernel using domain expertise, we step through the construction of one such kernel in this section. At each step, we discuss the desired phenomena that we would like to capture with the structure of the latest model. We also provide figures to help interpret the effect the changes have on the resulting predictions. The purpose of this section is to demonstrate how practitioners and researchers can create kernels which incorporate their own understanding of the ways load can vary with the forecast inputs. For illustrative purposes, we use the same training/test data for every step in this process.
We train each model on PJMISO data beginning on 17 September 2018 and ending on 26 October 2018. We then predict load for 27 October 2018. The point estimate prediction is the posterior mean of the Gaussian process. We also draw 1000 samples from the posterior distribution to illustrate the uncertainty of the model. Parameters that are not set manually are estimated via maximum likelihood, as described in Section 2.5. The parameter is not associated with any kernel, but reflects the magnitude of the noise, and is required for regularizing the kernel, as shown in Equations (1) and (3).
We begin with two kernels meant to capture the periodicity. As discussed in Section 2.3, there is known daily and weekly seasonality to the data, thus we fixed the parameters that control the period. The kernel is thus,
where is the amplitude of the composite kernel. The parameters are provided in Table 1.

Table 1.
The parameters of the composite kernel described by Equation (8).
Figure 8 shows that the daily and weekly periodicity capture a substantial portion of the variation in load. As expected, a purely periodic structure is not sufficient to accurately predict future load. Nevertheless, capturing the weekly and daily periodicity is an important first step for creating an accurate model. The estimated uncertainty is too low, likely because the model is not flexible enough to capture all the variation in load. We next develop a kernel that specifies a more realistic model to address this problem.
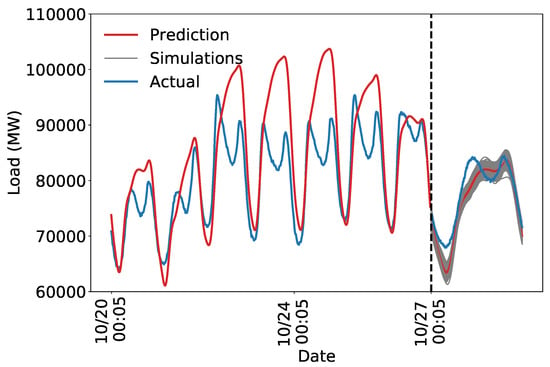
Figure 8.
Backcasted and forecasted load using a composite kernel with daily and weekly periodicity. Dashed vertical line indicates the transition from training data to test data.
Studying the structure of the forecasted and actual data in Figure 8 suggests that a decay away from exact periodicity is desirable. One way to achieve this is via the kernel described in Equation (7). In particular, we want to allow consecutive days to co-vary more strongly than nonconsecutive days, and similarly for weeks. This structure is described in Equation (9) and Table 2

Table 2.
The parameters of the composite kernel described by Equation (9).
Relaxing the strict periodic structure gives the model the flexibility required to capture the shape of the load curve. The noise term regularizes as needed to avoid overfitting. The training set is nearly perfectly predicted, but the model seems to generalize adequately, suggesting the regularization is working. Figure 9 shows that the decaying periodic model better captures the structure of the load, and the uncertainty is more realistic. The predicted uncertainty is too high which we address by adding more structure to the model.
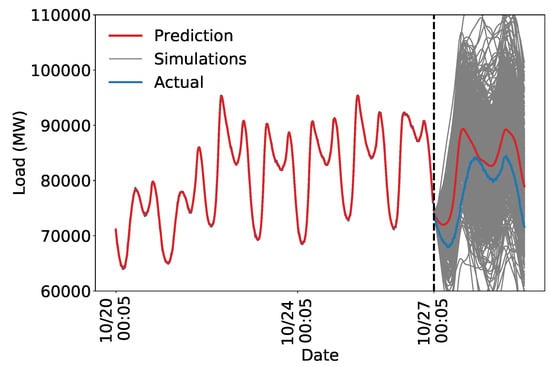
Figure 9.
Backcasted and forecasted load using a composite kernel with a decay away from strict daily and weekly periodicity. Dashed vertical line signifies the transition from training data to test data.
The model appears to explain the temporal trends in the training data. For example, note the distinct dip and rise in the test predictions around the morning peak, characteristic of an autumn load curve. The discrepancy between the forecast and actual values on the test set may be due to the inability of a strictly time series model to capture all of the intricacies of power demand on the electric grid.
A reasonable next step is to incorporate temperature information. We do this with a tensor product over time to allow for a decay of the relevance of information as time passes. The resulting kernel is described by Equation (10) with the parameters outlined in Table 3. The temperature data are modeled with a single Gaussian kernel, which gives changes in temperature at every location equal weight. More sophisticated methods for handling the high-dimensional temperature data are discussed in Section 2.6. Figure 10 shows the results of using the kernel to predict only on the test set. The simulations shown in Figure 10 are more accurate than those shown in Figure 9. The errors are smaller and the uncertainty appears more reasonable. Clearly, some phenomena are not picked up by the model. There remains a persistent error of approximately 5000 MW throughout the day. A more rigorous evaluation of the performance and a more thorough analysis of the forecast error and uncertainty for more complex models is provided in Section 3.

Table 3.
The parameters of the composite kernel described by Equation (10).
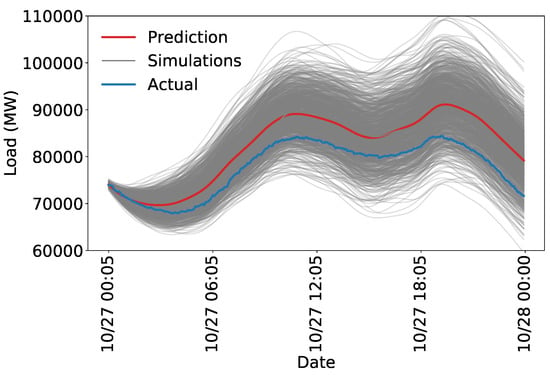
Figure 10.
Forecasted load using a composite kernel with a decay away from strict daily and weekly periodicity, as well as a temperature component.
The model used in Section 3 is the result of creating a composite kernel using the procedure described in this section. The final kernel includes additional structure meant to capture phenomena not discussed in this section. In contrast to many modern machine learning techniques, we develop this structure consistent with domain specific knowledge as described above. The ability to incorporate this type of knowledge makes Gaussian processes among the most powerful tools available to researchers with subject expertise. The benefits of Gaussian processes are likely smaller for situations where the modeler has little domain specific knowledge.
2.5. Parameter Estimation
Once the kernel has been specified, the values of the parameters of the model must be determined. We use maximum likelihood estimation, a popular and mathematically sound method for parameter estimation. The log marginal likelihood of a Gaussian process is
where the parameter vector is implicit in the kernel and det is the determinant of the matrix. The observed data are fixed, thus the goal is to choose the parameters which are most likely to have resulted in the observed data. Equation (11) has a convenient interpretation that helps explain why Gaussian processes are useful for modeling complex phenomena: the first term is the data-fit, encapsulating how well the kernel evaluated at the inputs represents the outputs. The second term is a penalty on the complexity of the model, depending only on the covariance function and the inputs. The third term is a normalization constant. Maximum likelihood estimation of the Gaussian process occurs over the hyperparameters and the complexity penalty inherently regularizes the solution.
Likelihood maximization is an optimization problem that can be tackled in a variety of ways. Due to the high-dimensionality of the problem, a grid search is too time consuming. For the forecasts in Section 3, we use a generalization of gradient descent called stochastic subspace descent, as described in [32] and defined in Algorithms 1 and 2.
| Algorithm 1 Generate a scaled Haar distributed matrix (based on [33]). |
|
Algorithm 2 is called by passing a random initialization of the parameters as well as a step-size, and a parameter ℓ which dictates the rank of the subspace that is used for the descent. The generic function that Algorithm 2 minimizes is specified by Equation (11).
| Algorithm 2 Stochastic subspace descent. |
|
This particular optimization routine is designed for high-dimensional problems with expensive function evaluations and gradients that are difficult or impossible to evaluate. Stochastic subspace descent uses finite differences to compute directional derivatives of low-dimensional random projections of the gradient in order to reduce the computational burden of calculating the gradient. The subroutine in Algorithm 1 defines a random matrix that is used to determine which directional derivatives to compute. Automatic differentiation software such as autograd for Python [34] can speed up the implementation by removing the need for finite differences, or, for simpler kernels, the gradients can be calculated by hand. For complex kernels, this may not be feasible so for generality and programming ease we use a zeroth-order method.
An important attribute of stochastic subspace descent is that the routine avoids getting caught in saddle points which is a typical problem in high-dimensional, non-convex optimization as discussed in [35]. Despite the fact that this algorithm avoids saddle points, there is no guarantee that the likelihood surface is convex for any particular set of data and associated parameterization. Non-convexity implies that there may be local maxima with suboptimal likelihood that are far from the global maximum in parameter space. To address this concern, we perform multiple restarts of the optimization routine with the parameters initialized randomly over the domain.
2.6. Dimension Reduction
Using a separate kernel to model the weather effects of every location for both temperature and dew point is inefficient as it causes the parameter space to be higher dimensional (and thus, more difficult to optimize over) than necessary. There are several existing methods for reducing the dimension of the parameter space while retaining information. In this section, we introduce four such techniques, each with its own merits. Because there is no preferred dimension reduction technique for forecasting, we assess the performance of these methods discussed using the data described in Section 2.4.
2.6.1. Random Sampling
This method is the most naïve, but perhaps the most common, and certainly the easiest to implement. From the available weather stations a random subset is chosen according to some probability distribution, typically the discrete uniform distribution. An obvious downside to using the uniform distribution is that weather readings from the largest cities are given no preference in the selection. This fails to incorporate the fact that populous cities contribute more to demand than rural areas, and that the impact of weather in large cities has a more pronounced effect on demand. Furthermore, sampling uniformly may lead to drastically different results from one trial to the next. A simple, albeit tedious fix which we do not pursue in this paper is to select locations for inclusion in proportion to their population. Additionally, choosing representative subsamples is an active area of research in graph theory (see, e.g., [36]); recent research extending the results of Leskovec and Faloutsos [36] to address compromised data can be found in [37] but for the remainder of this paper we assume that the weather data are high-fidelity. In Section 3, we use a discrete uniform probability distribution to select three random locations to be used.
2.6.2. Truncated Singular Value Decomposition
Another approach that is not specific to Gaussian processes is to use a truncated singular value decomposition (tSVD). This approach is possible due to the inherent spatial structure of temperature data, and is motivated by the following theorem due to Carl Eckart and Gale Young which can be found with proof in [38].
Theorem 1
(Eckart–Young). Let the SVD of be . Let and
denote the rank r truncated SVD of where represent the ith column of , and respectively, and is the ith diagonal element of Σ. Then,
Theorem 1 says that the optimal (in the sense of distance) low rank approximation of the original data is exactly the truncated singular value decomposition, and the approximation error is exactly the first omitted singular value (which are ordered from largest to smallest). The implication of Theorem 1 for reducing the dimensionality of temperature data is striking: since there is strong spatial structure for a particular region it is possible to collapse the dimension while retaining much of the information. Just as importantly, we know exactly how much information is lost by such an approximation. In this way, we are able to incorporate the important temperature information while maintaining a reasonable model size and avoiding overfitting. Table 4 shows the percentage of variance retained by several low rank approximations for various durations. A single dimension of the data contains up to 90% of the information. In our tests, we use a rank 3 approximation. Since we began with 32 weather stations, this represents a reduction in parameter space of over 90% with almost complete fidelity to the variation in the original data.

Table 4.
Each cell denotes the percentage of variation captured by the corresponding low rank approximation and training set. These results are specific to the times and the weather stations used and provide general guidance on the trade off between dimension reduction and information loss.
A potential problem with using a truncated SVD is that the actual load plays no role in the determination of the resulting low rank subspace. If extraneous locations are included in the dataset, information from them will be used in the dimension reduced model. An important practical consequence is that weather information from across the country can be provided to the model, allowing for flexibility with regard to which market is being predicted. This can provide substantial savings in development time as forecasts for different markets can quickly be provided by changing the load data that is passed in, without any other changes to the code.
2.6.3. Automatic Relevance Determination Kernel
The automatic relevance determination (ARD) kernel introduced in [39,40] is a popular tool for dimension reduction in Gaussian processes as the dimension reduction takes place as part of the modeling phase. Any radial kernel, that is, any kernel for which the values rely solely on distance but not direction, can be made into an ARD kernel. We show the Gaussian ARD kernel here. Recall are vectors of temperatures at locations. For simplicity, we demonstrate using only temperatures, although in the models we use both temperature and dew point. Thus,
where is a diagonal matrix and with each entry corresponding to the length-scale along the associated dimension. Since these parameters are learned during the likelihood maximization phase, no pre- or post-processing is required as part of the dimension reduction step. If irrelevant features are included in the model, the length-scale corresponding to those features will become very large indicating that the covariance is independent of those features, effectively removing them from the prediction.
There are d parameters to this kernel, thus, if there are hundreds or thousands of locations being used, it may not be a feasible option. As d grows, the likelihood function is more likely to become non-convex. Even the 32 dimensions of weather in our model required multiple restarts to ensure a global solution.
2.6.4. Rich Covariance Dimension Reduction
A potential shortcoming of the ARD kernel is that the matrix is diagonal, enforcing axis-alignment of the kernel. Temperatures have a correlation structure that could be exploited with a richer covariance structure to . This structure, introduced in [41] can be loosely considered as a hybrid between the ARD kernel and a truncated SVD approach. Consider the kernel
where and is the desired rank of the kernel. Consider that is rank r, and writing it as such we recover a form similar to the ARD kernel. As in the ARD kernel, the entries of are learned during the optimization phase so that the only parameter that must be specified by the user is r, the desired rank. Similar to the truncated SVD the result is a low rank subspace of the original input data, but this method considers the relationship between load and the temperature at each individual location. Though this is the most flexible option described, its primary weakness is that parameters must be learned, requiring a tremendous amount of data.
We evaluated different dimension reduction techniques on a subset of the data to choose which to pursue for the remainder of the analysis. We used the same training and test set for each trial in this section. The data used to determine the parameters of the model are Chebyshev samples of 1/12 of the possible observations beginning 17 September 2018 and ending 26 October 2018, with three random initializations used to ensure that optimization does not terminate at spurious local minima. We tested the learned model on data from 27 October 2018 to 4 November 2018 with an updated forecast every 15 min. Table 5 shows the results.

Table 5.
Results for the four methods described in Section 2.6, averaged over 576 forecasts (new forecasts every 15 min for six days). The credible interval coverage is a Monte Carlo approximation to the true coverage. It represents the percentage of data points in the test period that fall below the corresponding credible interval using 1000 samples from the posterior distribution. The kernels used for the models in Table 5 are described in Appendix C.
The random subsets model appears to predict well, but its performance is deceptive. The weather stations provided are all within the geographic region of PJM; in a more general setting where load forecasts are meant to be generated for multiple markets with little oversight, the model would not perform well. Furthermore, the performance of random subset models may vary drastically from one run to the next as different locations are selected. Thus, despite its promising performance in Table 5, we do not explore random subset methods further in this paper. The rich covariance structure appears to have overfit the data set and fits the test data poorly. This is likely due to the relatively high ratio of parameters to training observations. Using more observations would likely mitigate the apparent overfitting. The rich covariance structure dramatically underestimates the uncertainty. The performance of the tSVD model is surprising given its nice theoretical properties. Further testing would be required to determine if its relative under-performance is standard. In the remainder of this document we use the ARD model for dimension reduction.
2.7. Model Combination
Ensemble methods, which combine multiple models to create a single more expressive model, have been common in the machine learning community for many years, see [42] for an early review in the context of classification. Recently, such methods have been applied successfully to load forecasting; in a paper analyzing the prestigious M4 load forecasting competition [43], model combination is touted as one of the most important tools available to practitioners. Done correctly, models can be created and combined without substantial additional computational overhead. This is due to the parallel nature of many ensembles and is true of our proposed method. Several strategies exist for combining models, particularly in the Bayesian framework which allows for a natural weighting of different models by the model evidence ([44] Section 3.4), which in our case is expressed by (11). Extensive research has been conducted into the combination of Gaussian process models, a comparison of various methods is provided in [24]. In this paper, we propose using the Generalized Product of Experts (GPoE) method originally described in [45].
The standard product of experts (PoE) framework [46] can take advantage of the Gaussian nature of the posterior process. We recall the posterior density from Equation (1) with an additional subscript to denote the model index
The product of Gaussian densities remains Gaussian, up to a constant:
where M is the number of models to be combined. The density of the PoE model is
Although Equation (12) may look complicated, it has a simple interpretation. We can re-write the mean as , where is a weight matrix for the jth model, corresponding to the inverse of the uncertainty of that model. That is, models for which the uncertainty is high are down-weighted compared to those with low uncertainty. The variance can readily be seen as the inverse of the sum of the constituent precision matrices .
It is apparent that models with low uncertainty will dominate , and cause the variance of the PoE model to be relatively small. This is because if is small, then will be large, dominating the variance of the other models in the sum. The GPoE framework is designed to ameliorate this by allocating additional weight to those models for which the data are most informative to the model. The details of the algorithm, including how we measure the informativeness of data to a model, are available in Appendix B. See [45] for a more detailed discussion.
There is a trade-off to model combination. On the one hand, it is straightforward to implement, provides empirically and provably better estimates (see, e.g., [42] for a straightforward explanation in the context of classification), and has enormous practical value as demonstrated in the M4 competition. The cost of these benefits is that there is no longer a single kernel to provide interpretability. Since the method for combining the models is to take a product of the densities, the kernels of the individual models get lost in the mix, turning the GPoE model into a black box. Depending on the application, interpretability may or may not be a relevant consideration. The ability to combine models in this way provides the data analyst the opportunity to make a decision based on the requirements placed on the forecast.
3. Results
We found that combining models via the GPoE method described in Section 2.7 creates more accurate predictions. We trained the models on the 40 days leading up to test time, sampling of the possible observations using Chebyshev sampling. We performed six random initializations for the parameters of each model and then trained two different models: one with an emphasis on the effect of weather, and the other with an emphasis on the periodic structure. The kernels for each model are defined in Appendix D. In total, we obtained 12 model/parameter combinations and combined the resulting predictive distributions using the GPoE framework. We created a 24-h prediction from the GPoE distribution. We used the same parameters, step forward fifteen minutes, re-train the model with the additional fifteen minutes of data, and again forecast forward 24 h. This process of creating a new prediction every fifteen minutes was repeated for six days (representing seven total days of forecasts) for a total of (6 days × 24 h/day × 4 forecasts/h) = 576 forecasts. Parameter estimation was by far the most time-consuming portion of this exercise, thus the parameters were only learned once at the beginning of the six-day forecasting period. In Figure 12 we observe minimal degradation in the forecast from the beginning to the end of the period; nevertheless, we recommend re-parameterizing the model at least every week. For comparisons sake, we provide results for the GPoE model as well as the single best model, without any combination. Here, best is the one model, out of the twelve created, most informed by the data at the time of prediction, as described in Appendix B. Table 6 provides a breakdown of the results for test data from two weeks in 2018.

Table 6.
Results for the GPoE and uncombined models. The first two data columns correspond to the error GPoE model, and the second two correspond to the single best model for each forecast. The credible interval coverage is a Monte Carlo approximation to the true coverage. It represents the percentage of data points in the test period that fall below the corresponding credible interval using 1000 samples from the posterior distribution.
The forecast themselves provide more insight than can be captured by the table. In Figure 11, we provide each of the forecasts from the autumn test set. Although it may appear as though there is high uncertainty in the models, recall that there were 1000 simulations, thus the top and bottom gray lines are approximately 0.1% credible intervals.
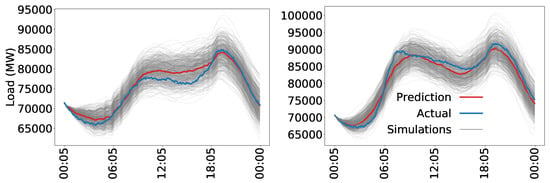
Figure 11.
Load forecast examples: (left) 28 October 2018; and (right) 29 October 2018.
A time series view of the error can assist in diagnosing whether the parameters ought to be updated. A noticeable increase in errors between forecasts may signal that a new parameterization is required. Figure 12 displays the evolution of the errors in successive forecasts for each of the models and test sets. For visual clarity, we only display the 30-min and 12-h error.
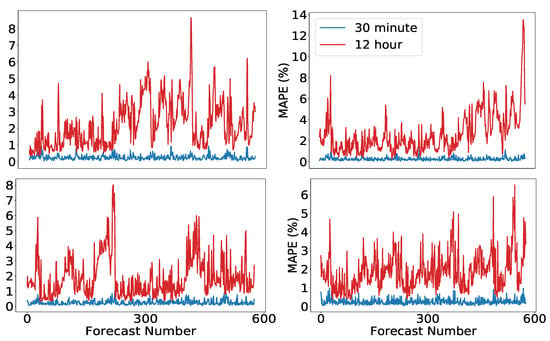
Figure 12.
MAPE for models: (Top) 28 February–7 March test set; (Bottom) 27 October–4 November test set; (Left) best model; and (Right) GPoE.
The model combination approach does not appear to be uniformly better than using the single best model. It does appear to improve results on the higher-load difficult spring period, but this could be an artifact of the small sample. Our tentative recommendation is to use the best single model if interpretability is important, otherwise use the model combination. Interpretation of the model can be conducted either by looking at the individual parameters, or by examining a slice of the Gram matrix as in Figure 13.
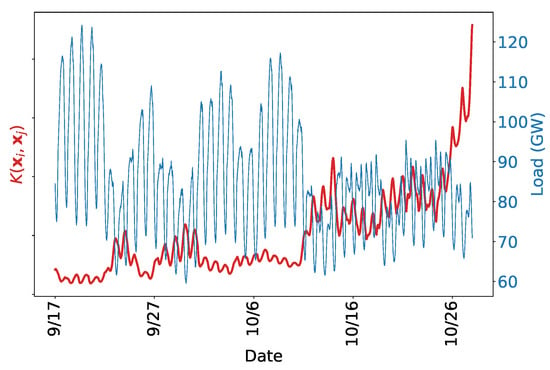
Figure 13.
Values for the first row of .
Figure 13 can be analyzed in the same way as Figure 5. Only the relative magnitude of the kernel values is important, so ticks on the left vertical axis are omitted. As expected, the test data co-varies most strongly with recently observed training data. The daily periodic structure is easy to identify, although the weekly periodicity is more difficult to pick out. There are jumps in the covariance around 25 September, 29 September, and 14 October; this is due to weather similarity between the test set and those days. The kernel used on the temperature component of this model is the ARD kernel described in Section 2.6. Recall that it has the ability to determine the relevance of its arguments. The implication is that the weather on 25 September, 29 September, and 14 October is similar to the weather on 27 October (the test set) in ways that are relevant to the load. We notice that days with higher covariance appear to be low-load days, indicating that 27 October is expected to also be low load. The kernel can also be viewed in terms of its constituents, as in Figure 14.
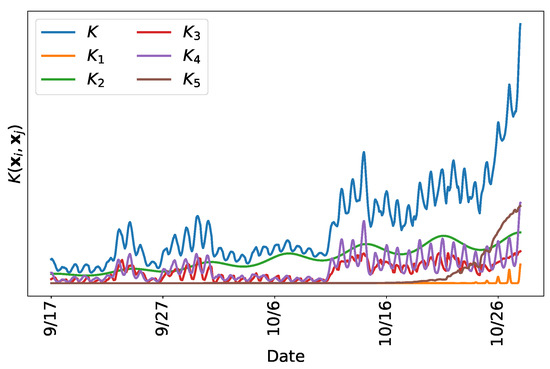
Figure 14.
Values for the first row of , and for all of its constituent kernels.
Figure 14 can be interpreted as follows: K is the sum of the individual kernels. Although K may be difficult to interpret, each of its pieces is designed specifically for a purpose, as discussed in Section 2.4, and is readily interpretable. In particular, is the daily periodicity with a decay term; is the weekly periodicity with a decay term; is the periodic effect of temperature; is the periodic effect of dew point; and is the recent effect of temperature and dew point. This particular kernel is used in the model which puts an emphasis on weather, and is defined rigorously in Appendix D. We see, for instance, that temperature and dew point play a similar role, although dew point is slightly more influential. The daily periodicity contributes very little, likely due to the fact that it is captured by the periodic nature of the weather. Recency has a large effect that appears to collapse after about five days, but the weekly periodic structure appears to be important and decays very slowly as we look back on the training set.
4. Discussion
We describe a Gaussian process approach to modeling short term load using a positive definite kernel designed explicitly for such a purpose. We applied this model to data from PJMISO to forecast between 5 min and 24 h from the last observed datum. We discuss the use of weather information, and propose several mechanisms for dimension reduction to keep the models from growing too large. We describe methods that can be easily interpreted, as well as black-box models that result from combining the result of several Gaussian processes. To test the robustness of the model to changes in the system, we provide results for different times of the year. The density predictions provided by our proposed methodology allow users to accurately assess uncertainty which is important for load forecasts where prediction errors can be particularly costly.
There are several interesting directions for future work. Below, we lay them out in order from what we believe to be the most obvious to the most speculative. Most directly, in [47], the authors showed that correctly accounting for holidays has a drastic positive impact both on holiday forecasts and on non-holiday periods. It would be straightforward to extend this model to include an indicator for holidays because Gaussian processes allow for indicators. More robust ways of incorporating holidays into the forecast are an important extension to this work.
For this model, we performed six random restarts on two different models but the predictions could be made more accurate by including additional models. Additional models were too computationally expensive, but the model combination technique we develop here scales without additional computational time provided enough cores are available to parallelize the computations. In [24], for example, up to 32,768 models are combined. Adding additional models would likely improve the forecast’s accuracy.
While the work presented here is on short-term load forecasts with high frequency, it is likely that similar techniques would work on a coarser mesh; that is, medium-term load forecasts of one day to two weeks with hourly or daily observations. Such a forecast would find use in both financial markets and power plant and line maintenance scheduling decisions. These forecasts are likely to have wider use among market participants and power grid dispatchers than the very short run forecasts presented here.
A major shortcoming of this work, and indeed of naïve implementations of Gaussian processes in general, is that Equation (1) requires the inversion of a dense matrix, an operation. Because of this, a typical desktop computer at the time of writing would have difficulty training the model we propose on datasets with more than about 10,000 observations, roughly one month of data at five-minute frequency. This problem of scalability has been thoroughly discussed in the literature, and many solutions have been proposed (see, e.g., [22,23,24,25]).
In ([48] Section 4.2), the authors discussed the value of density forecasts for electricity price modeling and lamented the scarcity of such models. It would be interesting to couple the uncertainty provided by this load forecast with a probabilistic LMP forecast which makes use of that uncertainty, similar to the premise of [7]. This could be useful in real-time generator scheduling, as discussed in [15].
In Section 3, we present several choices and interpretations for the kernel. The kernels were chosen based on an intuitive understanding of the phenomena we wanted to represent, but they are not the only options available. More work could be done to fine tune the kernel for this problem, either by incorporating more domain knowledge or with a purely data-driven approach, as in [49]. Exploring ways to reliably automate model turning is an important direction of future work in this area.
Finally, the kernels discussed in this paper all rely solely upon the distance between the arguments without regard to their actual value. They are called stationary kernels and have advantageous properties such as computational efficiency and Bochner’s theorem to prove positive definiteness [26]. However, they also yield models which are second-order stationary, a property which is not ideal in load forecasting. There are kernels which are designed specifically to address this shortcoming. One such example is the kernel discussed in [50], which is non-stationary and anisotropic, created explicitly to model temporal processes for which predictions begin after the last observation and the covariance between equidistant points may vary with time. The practical consequence of incorporating such structure is that the uncertainty can increase with the distance between the forecasted time and the last observation.
Author Contributions
Conceptualization, D.K.; Methodology, D.K.; Resources, S.H.; Writing—original draft, D.K., S.H. and G.E.F.; and Writing—review and editing, G.E.F.
Funding
Funding for open access to this research was provided by University of Tennessee’s Open Publishing Support Fund.
Acknowledgments
DK would like to thank Tao Hong for introducing him to principled load forecasting. We express our gratitude to Luis Tenorio for extensive discussions regarding the Bayesian approach to modeling. Funding for open access to this research was provided by University of Tennessee’s Open Publishing Support Fund.
Conflicts of Interest
Holladay has an active grant from the Sloan Foundation which funds research related to environmental economics and policy. Holladay is a co-founder of Yes Energy, a company that sells software to energy market participants, including utilities and traders in wholesale electricity markets. These companies and foundation have no specific interest in the results of this research.
Appendix A. Kernels
Definition A1
(Gram matrix). Let be a non-empty set. Given a function , and data , the matrix with elements
is said to be the Gram matrix of K with respect to .
Before discussing positive definite functions, we must define positive definiteness in a linear algebraic sense.
Definition A2.
A matrix is said to be positive definite if for all
The Gram matrix is merely a particular instantiation of the function K. The next definition suggests that, if all such matrices of the function are positive definite, then K is a positive definite kernel.
Definition A3.
Let be a non-empty set. A function which for all and all gives rise to a positive definite Gram matrix is called a positive definite kernel.
The properties given by Remark 1 follow directly from these definitions. In particular, see ([31] Section 13.1) for proofs.
Appendix B. Generalized Product Of Experts
As discussed in Section 2.7, Equation (12) has a tendency to underestimate the variance. We address this issue by allocating more weight to models which are strongly influenced by the data, and less to those for which the prior and posterior distributions are similar. In this framework, Equation (12) becomes
where is the change in entropy between the prior and the posterior variance for the jth model. That is,
where we recall that the prior variance is merely the kernel function of the jth model evaluated at the test points. The are normalized to sum to one. Strong priors have a tendency to induce low prior variance, artificially lowering the overall variance of the final model in the PoE framework. The weights express a preference for those models for which the data is the determining factor in the posterior variance, rather than the prior. In Section 3, we use as the best model by setting the model with the highest value of to have weight one, and the remaining models to have weight 0.
Appendix C. Kernels for Dimension Reduction
Although the form of this kernel is identical to , in this case the and correspond to the first, second, and third eigenvectors provided by the truncated SVD rather than randomly selected locations. Due to this change, a different parameterization is learned.
It is important to note that temperature and dew point share the same ARD kernel: . This is to reflect the fact that a location relevant for temperature should also be relevant for dew point, effectively halving the number of parameters required to model temperature effects.
Once again, temperature and dew point share the same kernel. In this instance, it is particularly important, as each rank-3 RC kernel at 32 locations requires learning 96 parameters.
Appendix D. Kernels for Final Models
Two different kernels are used to create the models that are combined by the GPoE framework of Section 2.7. One kernel places a heavy emphasis on the weather:
The other kernel places a heavy emphasis on the periodic structure of load:
In both kernels, and have a fixed period of one day, while and have a fixed period of one week. Additionally, in the kernel which relies more heavily on the periodic structure, has a fixed length-scale of one day. The remainder of the parameters are estimated by maximum likelihood, as described in Section 2.5.
References
- Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Fan, S. Density forecasting for long-term peak electricity demand. IEEE Trans. Power Syst. 2010, 25, 1142–1153. [Google Scholar] [CrossRef]
- Mori, H.; Ohmi, M. Probabilistic short-term load forecasting with Gaussian processes. In Proceedings of the 13th International Conference on Intelligent Systems Application to Power Systems, Arlington, VA, USA, 6–10 November 2005. [Google Scholar]
- Liu, B.; Nowotarski, J.; Hong, T.; Weron, R. Probabilistic load forecasting via quantile regression averaging on sister forecasts. IEEE Trans. Smart Grid 2017, 8, 730–737. [Google Scholar] [CrossRef]
- Nowotarski, J.; Weron, R. Recent advances in electricity price forecasting: A review of probabilistic forecasting. Renew. Sustain. Energy Rev. 2018, 81, 1548–1568. [Google Scholar] [CrossRef]
- Hobbs, B.F.; Jitprapaikulsarn, S.; Konda, S.; Chankong, V.; Loparo, K.A.; Maratukulam, D.J. Analysis of the value for unit commitment of improved load forecasts. IEEE Trans. Power Syst. 1999, 14, 1342–1348. [Google Scholar] [CrossRef]
- Bo, R.; Li, F. Probabilistic LMP forecasting considering load uncertainty. IEEE Trans. Power Syst. 2009, 24, 1279–1289. [Google Scholar]
- Geng, X.; Xie, L. Learning the LMP-Load Coupling From Data: A Support Vector Machine Based Approach. IEEE Trans. Power Syst. 2017, 32, 1127–1138. [Google Scholar]
- Orwig, K.D.; Ahlstrom, M.L.; Banunarayanan, V.; Sharp, J.; Wilczak, J.M.; Freedman, J.; Haupt, S.E.; Cline, J.; Bartholomy, O.; Hamann, H.F.; et al. Recent Trends in Variable Generation Forecasting and Its Value to the Power System. IEEE Trans. Sustain. Energy 2015, 6, 924–933. [Google Scholar] [CrossRef]
- Matos, M.; Bessa, R.; Botterud, A.; Zhou, Z. Forecasting and setting power system operating reserves. In Renewable Energy Forecasting; Kariniotakis, G., Ed.; Woodhead Publishing Series in Energy; Woodhead Publishing: Cambridge, UK, 2017; pp. 279–308. [Google Scholar]
- Quilumba, F.L.; Lee, W.J.; Huang, H.; Wang, D.Y.; Szabados, R.L. Using smart meter data to improve the accuracy of intraday load forecasting considering customer behavior similarities. IEEE Trans. Smart Grid 2015, 6, 911–918. [Google Scholar] [CrossRef]
- Kath, C.; Ziel, F. The value of forecasts: Quantifying the economic gains of accurate quarter-hourly electricity price forecasts. Energy Economics 2018, 76, 411–423. [Google Scholar] [CrossRef]
- Kochenderfer, M.J. Decision Making under Uncertainty: Theory and Application; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Biswas, T. Decision-Making under Uncertainty; Macmillan International Higher Education: London, UK, 1997. [Google Scholar]
- Donti, P.; Amos, B.; Kolter, J.Z. Task-based End-to-end Model Learning in Stochastic Optimization. In Advances in Neural Information Processing Systems 30; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2017; pp. 5484–5494. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Hong, T.; Wang, P.; White, L. Weather station selection for electric load forecasting. Int. J. Forecast. 2015, 31, 286–295. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Aggarwal, C.C.; Hinneburg, A.; Keim, D.A. On the surprising behavior of distance metrics in high dimensional space. In International Conference on Database Theory; Springer: Berlin/Heidelberg, Germany, 2001; pp. 420–434. [Google Scholar]
- Fritsch, F.N.; Carlson, R.E. Monotone piecewise cubic interpolation. SIAM J. Numer. Anal. 1980, 17, 238–246. [Google Scholar] [CrossRef]
- Raza, M.Q.; Baharudin, Z.; Islam, B.; Zakariya, M.; Khir, M. Neural network based STLF model to study the seasonal impact of weather and exogenous variables. Res. J. Appl. Sci. Eng. Technol. 2013, 6, 3729–3735. [Google Scholar] [CrossRef]
- Williams, C.K.I.; Seeger, M. Using the Nyström Method to Speed Up Kernel Machines. In Advances in Neural Information Processing Systems 13; Leen, T.K., Dietterich, T.G., Tresp, V., Eds.; MIT Press: Cambridge, MA, USA, 2001; pp. 682–688. [Google Scholar]
- Snelson, E.; Ghahramani, Z. Sparse Gaussian Processes using Pseudo-inputs. In Advances in Neural Information Processing Systems 18; Weiss, Y., Schölkopf, B., Platt, J.C., Eds.; MIT Press: Cambridge, MA, USA, 2006; pp. 1257–1264. [Google Scholar]
- Deisenroth, M.; Ng, J.W. Distributed Gaussian Processes. In Proceedings of the 32nd International Conference on Machine, Lille, France, 6–11 July 2015; pp. 1481–1490. [Google Scholar]
- Titsias, M. Variational Learning of Inducing Variables in Sparse Gaussian Processes. In Machine Learning Research, Proceedings of the Twelth International Conference on Artificial Intelligence and Statistics, Clearwater, FL, USA, 16–19 April 2009; van Dyk, D., Welling, M., Eds.; PMLR, Hilton Clearwater Beach Resort: Clearwater Beach, FL, USA, 2009; Volume 5, pp. 567–574. [Google Scholar]
- Fasshauer, G. Meshfree Approximation Methods with MATLAB; Interdisciplinary Mathematical Sciences, World Scientific Publishing Company: Singapore, 2007. [Google Scholar]
- Hoel, P.; Levine, A. Optimal spacing and weighting in polynomial prediction. Ann. Math. Stat. 1964, 35, 1553–1560. [Google Scholar] [CrossRef]
- Nowicka-Zagrajek, J.; Weron, R. Modeling electricity loads in California: ARMA models with hyperbolic noise. Signal Process. 2002, 82, 1903–1915. [Google Scholar] [CrossRef]
- MacKay, D.J. Introduction to Gaussian processes. NATO ASI Ser. F Comput. Syst. Sci. 1998, 168, 133–166. [Google Scholar]
- Weron, R.; Kozłowska, B.; Nowicka-Zagrajek, J. Modeling electricity loads in California: A continuous-time approach. Phys. A Stat. Mech. Its Appl. 2001, 299, 344–350. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond (Adaptive Computation and Machine Learning); The MIT press: Cambridge, MA, USA, 2002. [Google Scholar]
- Kozak, D.; Becker, S.; Doostan, A.; Tenorio, L. Stochastic Subspace Descent. arXiv 2019, arXiv:1904.01145. [Google Scholar]
- Mezzadri, F. How to Generate Random Matrices from the Classical Compact Groups; Notices of the American Mathematical Society; American Mathematical Society: Providence, RI, USA, 2006; Volume 54. [Google Scholar]
- Maclaurin, D.; Duvenaud, D.; Adams, R.P. Autograd: Effortless Gradients in Numpy; ICML 2015 AutoML Workshop: Lille, France, 2015. [Google Scholar]
- Dauphin, Y.N.; Pascanu, R.; Gulcehre, C.; Cho, K.; Ganguli, S.; Bengio, Y. Identifying and attacking the saddle point problem in high-dimensional non-convex optimization. In Advances in Neural Information Processing Systems 27; Ghahramani, Z., Welling, M., Cortes, C., Lawrence, N.D., Weinberger, K.Q., Eds.; Curran Associates, Inc.: New York, NY, USA, 2014; pp. 2933–2941. [Google Scholar]
- Leskovec, J.; Faloutsos, C. Sampling from large graphs. In Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Philadelphia, PA, USA, 20–23 August 2006; pp. 631–636. [Google Scholar]
- Shang, Y. Subgraph Robustness of Complex Networks Under Attacks. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 821–832. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations; JHU Press: Baltimore, MD, USA, 2012; Volume 3. [Google Scholar]
- MacKay, D.J. Bayesian methods for backpropagation networks. In Models of Neural Networks III; Springer: New York, NY, USA, 1996; pp. 211–254. [Google Scholar]
- Neal, R.M. Bayesian Learning for Neural Networks. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 1995. AAINN02676. [Google Scholar]
- Snelson, E.; Ghahramani, Z. Variable noise and dimensionality reduction for sparse Gaussian processes. CoRR 2006, arXiv:1206.6873. [Google Scholar]
- Dietterich, T.G. Ensemble methods in machine learning. In International Workshop on Multiple Classifier Systems; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–15. [Google Scholar]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. The M4 Competition: Results, findings, conclusion and way forward. Int. J. Forecast. 2018, 34, 802–808. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning (Information Science and Statistics); Springer-Verlag: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Cao, Y.; Fleet, D.J. Generalized product of experts for automatic and principled fusion of Gaussian process predictions. CoRR 2014, arXiv:1410.7827. [Google Scholar]
- Hinton, G.E. Training products of experts by minimizing contrastive divergence. Neural Comput. 2002, 14, 1771–1800. [Google Scholar] [CrossRef]
- Ziel, F. Modeling public holidays in load forecasting: A German case study. J. Mod. Power Syst. Clean Energy 2018, 6, 191–207. [Google Scholar] [CrossRef]
- Weron, R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef]
- Duvenaud, D.; Lloyd, J.R.; Grosse, R.; Tenenbaum, J.B.; Ghahramani, Z. Structure discovery in nonparametric regression through compositional kernel search. arXiv 2013, arXiv:1302.4922. [Google Scholar]
- McCourt, M.; Fasshauer, G.; Kozak, D. A nonstationary designer space-time kernel. arXiv 2018, arXiv:1812.00173. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).