Abstract
It is of great significance for wind power plant to construct an accurate multi-step wind speed prediction model, especially considering its operations and grid integration. By integrating with a data pre-processing measure, a parameter optimization algorithm and error correction strategy, a novel forecasting method for multi-step wind speed in short period is put forward in this article. In the suggested measure, the EEMD (Ensemble Empirical Mode Decomposition) is applied to extract a series of IMFs (intrinsic mode functions) from the initial wind data sequence; the LSTM (Long Short Term Memory) measure is executed as the major forecasting method for each IMF; the GRNN (general regression neural network) is executed as the secondary forecasting method to forecast error sequences for each IMF; and the BSO (Brain Storm Optimization) is employed to optimize the parameter for GRNN during the training process. To verify the validity of the suggested EEMD-LSTM-GRNN-BSO model, eight models were applied on three different wind speed sequences. The calculation outcomes reveal that: (1) the EEMD is able to boost the wind speed prediction capacity and robustness of the LSTM approach effectively; (2) the BSO based parameter optimization method is effective in finding the optimal parameter for GRNN and improving the forecasting performance for the EEMD-LSTM-GRNN model; (3) the error correction method based on the optimized GRNN promotes the forecasting accuracy of the EEMD-LSTM model significantly; and (4) compared with all models involved, the proposed EEMD-LSTM-GRNN-BSO model is proved to have the best performance in predicting the short-term wind speed sequence.
1. Introduction
As the awareness of environmental protection increases, the application and promotion of renewable energy has attracted worldwide attention. As one type of promising renewable energy, wind power is experiencing a rapid development [1]. Nevertheless, owning to the instability and stochastic property of wind power generation, the instability of power system is caused easily when considering wind power [2]. Therefore, it is imperative to propose an accurate prediction method for wind speed to reduce the instability risk of the power system and the economic losses for wind power enterprises.
In recent years, many scholars have done extensive research on predicting the wind speed sequence. The traditional prediction measures are universally recognized as four kinds: (1) physical method; (2) statistical method; (3) intelligent approach; and (4) hybrid model [3]. The physical method commonly takes advantage of physical data, for example temperature, air density, topographic information and so on [4], which is mainly obtained through numerical weather prediction [5], to get the prediction results. However, the physical methods are not good at forecasting wind speed in short period and the methods also require plenty of time to compute and additional resources [6]. The statistical measures, such as the autoregressive integrated moving average (ARIMA) measure, are built with easy procedures of pattern recognition, parameter estimation and model checking [7]. However, this kind of methods cannot afford to deal with the non-linear problems [8]. Owning to the ability to recognize the non-linear characters, the intelligent approaches, for instance artificial neural networks (ANNs) [9,10,11], support vector machine (SVM) [12], the genetic algorithm [13] and the general regression neural network (GRNN) [14], have been utilized to forecast wind speed effectively. Due to the superior ability to recognize the non-linear structure, intelligent approach is better at forecasting the wind speed of short period than traditional time series based methods. Nevertheless, the single intelligent approaches also suffer form certain problems. For example, genetic algorithm measure has the problem of premature convergence, which limits its searching ability to obtain the optimal value. Furthermore, with the function to recognize deep characteristics in the data, the deep learning approaches, for example the deep convolutional neural network [15] and LSTM [16], have been investigated in the process of prediction for wind speed in recent studies.
However, due to the unstable property of wind speed, a single intelligent model may occasionally fall into local extremum and result in poor forecasting performance. Hence, to fix this problem, hybrid models to predict wind speed are put forward. There are four types of hybrid forecasting models [17].
(1) The hybrid methods involving weighting approaches give a weighing parameter to each single approach based on their forecasting performance and then add the weighted forecasting results together. For example, Shi et al. [18] put forward a weighting based hybrid approach involving grey relational analysis as well as the distribution characteristics of wind velocity, which integrates the LSSVM (least square support vector machine) and the RBFNN (Radial Basis Function Neural Networks). The weighting parameters in the approach can be calculated based on data sequences in each month. The results reveal that the suggested combination measure effectively promotes the performance in forecasting the wind speed in very short term. Xiao et al. [10] utilized the nonnegative constraint theory and hybrid smart approaches to obtain the wind speed prediction, in which the importance degrees of the latter combined approaches are decided utilizing the chaos particle optimization algorithm as well as the genetic algorithm. The afore-mentioned hybrid approaches take advantage of the strength of single forecasting methods, thus the forecasting accuracy is significantly improved.
(2) The signal pre-processing measure is executed to obtain a collection of sub-sequences, which are stationary and regular, from the initial non-linear time series. Different decomposition approaches have been utilized in latest hybrid prediction approaches extensively. For instance, in [19], the raw data series is preprocessed by wavelet transform (WT) before being brought into the forecasting procedure of SVM. The final outcomes indicate that the suggested approach consisting of WT and SVM is superior to the single SVM approach in prediction accuracy. Fan [20] used a combination measure integrating the empirical mode decomposition (EMD) and SVM, in which the initial wind speed data are processed with EMD for the purpose of fluctuation deduction. However, the EMD method cannot afford to dispose the problem of mode mixing. Therefore, to compensate for the disadvantage of EMD, the ensemble empirical mode decomposition (EEMD) measure is utilized in [21]. Cheng [22] utilized a hybrid model integrated with the EEMD approach to construct the forecasting process for wind speed, where the EEMD is applied for information extraction from the raw wind speed series. The final outcomes reveal that the suggested approach with EEMD shows a better prediction performance than the EMD or LSSVM method.
(3) Hybrid models integrating parameter optimization, which applies the optimization methods to find optimal setting for the prediction models in the training procedure, are investigated recently. Chitsaz et al. [23] presented a novel prediction measure which has the structure of the Wavelet Neural Network (WNN) as well as multi-dimensional Morlet wavelet. The modified Clonal selection method is used for finding the optimal parameters in WNN with the training criterion of Maximum Correntropy Criterion. The final outcomes demonstrate the validity of the suggested method. In [24], a novel hybrid wind speed prediction measure in short period consisting of mutual information, wavelet transform, evolutionary particle swarm optimization (EPSO) and the adaptive neuro-fuzzy inference system (ANFIS) is developed, in which the EPSO is utilized to search the optimal parameter for ANFIS. The final results reveal that the suggested measure has advantages in forecasting accuracy over the other comparison models. Yuan et al. [25] presented the gravitational search algorithm (GSA) for searching the best parameter for LSSVM model. The experiment outcomes show that the suggested LSSVM-GSA combination measure have the highest forecasting accuracy, compared with other models. The Brain Storm Optimization (BSO) approach, which is enlightened from the process of brainstorming for people, is put forward in [26]. Modeling BSO algorithm requires simulating the form of gathering various experts together to propose potential solutions for the current problem [27]. Each individual is grouped into different teams for collaborative investigation. Various teams are able to locate different answer space areas to promote the possibility to find the best solution, which possesses an excellent global exploration ability [28]. The significance of BSO has been validated by numerous scholars [29,30].
(4) Unlike the aforementioned hybrid methods, the hybrid models based on the data post-processing technique emphasize using the error correction method to reduce the adverse effect brought by the forecasting error. For instance, Liang et al. [31] put forward a novel hybrid model, in which the forecasting step for the raw data sequence of wind power is conducted with the SVM, and then the prediction error for the SVM is forecasted utilizing the SVM together with the ELM. The numerical outcomes demonstrate that the proposed combination measure with error correction can promote the wind power prediction performance effectively. Jiang et al. [32] put forward a combined structure, in which the EEMD is executed to pre-process the wind speed sequences with mean zero, and the chosen sub-layers are forecasted using LSSVM. Then, the LSSVM and the Generalized Auto-Regressive Conditionally Heteroscedastic (GARCH) measure are applied for forecasting the error sequences. The outcomes demonstrate that the error correction method contributes to the forecasting accuracy improvement. Moreover, in [33], the prediction errors of the wind speed series in short period, which are acquired by the measure of grey forecasting, are forecasted utilizing the Markov method for wind speed forecasting error correction before it is turned into wind power forecasting, and the results show the superiorities of the proposed approach in forecasting accuracy improvement.
All four types of hybrid forecasting model mentioned above can contribute to the improvement of forecasting performance. In this paper, the signal pre-processing technique, the parameter optimization algorithm and the error correction method are considered. The suggested combination model involving the signal decomposition technique, the parameter optimization algorithm and the error correction method is built as follow: (1) The EEMD is applied to extract a collection of IMFs from the raw wind speed sequence. (2) The LSTM network is used to forecast each IMF. (3) The GRNN is conducted to predict the error sequence for each IMF (intrinsic mode function). (4) The BSO is executed to optimize the parameter for GRNN. (5) The ultimate prediction result is obtained through merging all the predictions of IMFs.
The major contribution in the article is proposing a novel multi-step wind speed prediction structure combining the data pre-processing technique, the parameter optimization algorithm and the error correction method to achieve a satisfactory forecasting performance, and to analyze the influences of every element of the proposed hybrid model in forecasting accuracy contribution. As far as we know, the potential performance of the suggested structure, which integrates three kinds of improvements in one hybrid model, has not been studied in the prediction for short-term wind speed. Thus, aiming at investigating the effectiveness of each component, the overall prediction performance and the generalization of the suggested combination measure, eight diverse approaches were applied to forecast two different 5-min wind speed sequences and one 30-min wind speed sequence. Finally, the prediction accuracy of all the approaches involved in this paper were estimated utilizing different evaluating indicators.
The structure for this article is described as below. Section 2 describes the application process of the suggested hybrid measure and the single models required. Section 3 introduces the evaluation criteria for prediction capacity. Section 4 presents two 5-min wind speed forecasting case studies to prove the forecasting capacity of the suggested hybrid measure. Section 5 presents an additional 30-min case to further validate the generalization of the suggested measure. Finally, the conclusions are drawn in Section 6.
2. Methodology
2.1. The Overall Structure of the Suggested Combination Measure
The structure of the suggested EEMD-LSTM-GRNN-BSO approach is shown in Figure 1. The specific processes are described below:
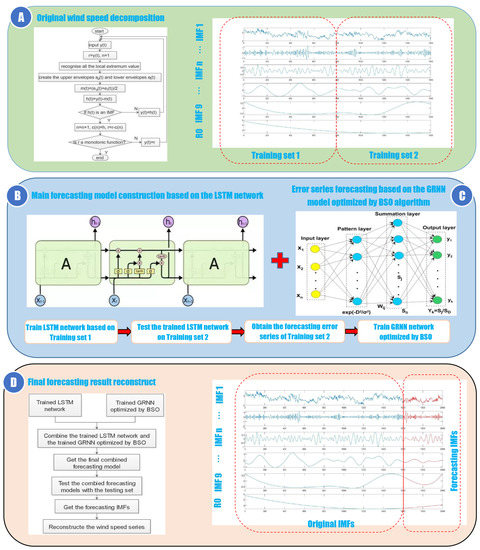
Figure 1.
The whole process of the EEMD-LSTM-GRNN-BSO.
- (1)
- The EEMD method is executed to extract a collection of IMFs from the wind speed observations. The ratio of the standard deviation of the added noise takes 0.01 and the ensemble number for the EEMD takes 100. Finally, 11 IMFs are obtained utilizing EEMD. The process of the EEMD measure are shown in Section 2.2.
- (2)
- The IMFs are classified into two training sets. The input matrixes and output matrixes are formed with data in each set based on the procedures described in Figure 2 to train the forecasting models.
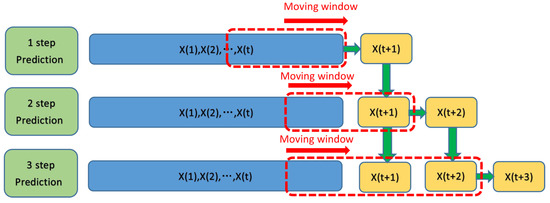 Figure 2. The structure of the multi-step forecasting strategy.
Figure 2. The structure of the multi-step forecasting strategy. - (3)
- The LSTM network is trained with the data in Training Set 1 to predict each IMF; the trained LSTM networks are tested with data in Training Set 2; the forecasting error series are obtained by finding the difference between the observations and predictions of Training Set 2. The procedures of the LSTM models are described in Section 2.3.
- (4)
- The GRNN approach is trained with the error sequence of the Training Set 2 to model the prediction errors for the LSTM network. The BSO algorithm is executed to search the optimal smooth factor for further prediction accuracy improvement, in which the smooth factor is treated as the variable to be optimized and the mean absolute error (MAE) calculated with the predictions and observations is considered as the fitness function of BSO. Each value of smooth factor in the searching space is brought in to the GRNN to obtain the predictions and the corresponding fitness, until the optimal value is found. Section 2.4 and Section 2.5 describe the details of GRNN and BSO, respectively.
- (5)
- The LSTM network and the GRNN model optimized by BSO are combined to construct the proposed hybrid forecasting measure. The suggested combination measure is validated using the test set for getting each IMF predictions and the error predictions. The overall prediction for each IMF can be obtained with the equation below:where i is the number of IMF determined by the EEMD method. stands for the corrected prediction for each IMF. represents the original predictions for each IMF forecasted by BSO. stands for the error prediction for each IMF forecasted by optimized GRNN. The final predicted wind speed sequences are gained by means of merging all the corrected predictions of IMF together.
- (6)
- To test and verify the wind speed prediction performance of the suggested combination EEMD-LSTM-GRNN-BSO approach, seven other prediction methods were used as comparisons. The comparison models involved in this study are the ARIMA measure, the BP network, the GRNN measure, the LSTM measure, the LSTM-GRNN-BSO measure, the EEMD-LSTM measure, and the EEMD-LSTM-GRNN measure. Comparisons between models were also utilized to reveal the effectiveness of each component in forecasting accuracy improvement.
2.2. Ensemble Empirical Mode Decomposition
Being a valid data series disposing measure, empirical mode decomposition (EMD) can draw the feature information from the raw data series [34]. Utilizing the EMD approach, a collection of intrinsic mode functions (IMFs) are acquired. Following the EMD measure, the ensemble empirical mode decomposition (EEMD) was studied to handle the mode mixing issue, which cannot be solved by the EMD approach. The main process for the EEMD measure [22] is described as follows:
- (1)
- Create a novel data series by adding white noise into the raw data series .
- (2)
- Recognize all the local extremum values for the data series .
- (3)
- Construct the upper envelopes and lower envelopes for
- (4)
- Generate the average value with the upper envelope and the lower envelope.
- (5)
- Calculate the distinction between the raw data series and as the first part :
- (6)
- Iterated the sifting procedure several times. The iterative process continues for k times until is an IMF. After that the first IMF part is shown as follow:
- (7)
- The residue is considered as a new series, and Steps (2)–(6) are repeated to get all and a residue . Finally, by adding up all the IMFs and the residue obtained, the following is acquired:
EEMD is regarded as an approach to help analyze data with noise by means of mixing white noise into the raw series, and it is useful to mitigate the problem caused by mode mixing.
2.3. Long Short Term Memory Measure
Improved from Recurrent Neural Network (RNN), the LSTM measure was put forward by Hochreiter and Schmidhuber [35] in 1997. The important parts of the LSTM network are its memory cells, which make it different from the traditional RNN. Graves and Schmidhuber [36] explained that three types of multiplicative units exist in the structure of LSTM model: the input gate, the output gate and the forget gate in the memory cells. These gates change the state of the memory cells following the steps below [37]: (a) by activating the input gate, as the latest data enters, the input message is able to be accumulated to the cell; (b) by activating the forget gate, the former cell states are to be abandoned during the procedure; and (3) the output gate is responsible for deciding if the latest cell output is propagated to the final state.
In terms of short wind speed forecasting, is the historical wind speed series and is the forecasting value. The prediction of the wind speed sequence is computed as below [38]:
where represents the input gate, represents the forget gate, represents the activation vector for every cell, stands for the output gate, stands for the activation vectors for every memory block, W represents the weigh matrices, b represents the bias vectors and the mathematical symbol “·” stands for the scalar product.
stands for the standard logistic function:
stands for the centered logistic function:
stands for the centered logistic function:
2.4. General Regression Neural Network
Specht put forward the GRNN method in 1991 [39]. The GRNN has many advantages such as strong non-linear mapping abilities, flexible network framework and satisfactory robustness, which makes it a perfect choice to deal with non-linear problems. Although the GRNN has a similar structure to the RBFNN, its approaching ability and learning speed is better. The structure of GRNN includes the input layer, the pattern layer, the summation layer and the output layer. The framework of GRNN is described in Figure 1C. The input for GRNN is and the output is . The following descriptions explains the detailed process of GRNN:
- (1)
- Input layer: The amount of neurons and the dimension of the input data of the training set should be kept consistent. Every neuron denotes an easy distribution unit that delivers the input information straightly to the pattern layer.
- (2)
- Pattern layer: The number of neurons equals the number of training data. Every neuron denotes a diverse sample. The calculation for the neuron transfer function of the pattern layer is shown below:where X stands for the input variables for the model and stands for the training data of neuron i. The width parameter of the Gaussian function is controlled by smoothing factor .
- (3)
- Summation layer: The procedure of summation is calculated with two kinds of neurons. One way is to merge the output of each neuron in pattern layer with the formula of to obtain the summation for the summation layer. The combination weighting parameter connecting the pattern layer and each neuron is equal to one, and the transfer formula is shown below:The other way is to conduct the summation of all the neurons in the pattern layer with different weights, whose formula is represented by . The jth component of ith output sample defines the weighting parameter connecting the ith neuron in the pattern layer and the jth molecule in the summation layer. The corresponding transfer formula is as follow.
- (4)
- Output layer: The amount of neurons and the dimension of the output vector in the sample should be kept consistent. The output of neuron j is equal to the jth component of the calculated outcome , which is calculated as:
As the parameter takes a great value, is closer to the average value of all the sample based variables. Conversely, as the value of parameter is closer to zero, is similar to the training set. Under the situation that the predicted point are part of the training set, the prediction for the dependent variable is rather similar to the corresponding dependent variable of the training set. When this happens, the corresponding sample cannot be considered, which may lead to unsatisfactory forecasting performance and generalization. When the smooth factor takes a proper value, the calculation of includes the dependent variable of all training data, and the distance between the dependent variable and the corresponding forecasting point is assigned with a larger weight. Thus, based on the significant influence of smooth factor on the forecasting performance of GRNN, the BSO is utilized to search the optima value for GRNN during the training process.
2.5. Brain Storm Optimization
The BSO [40,41] is an algorithm based on population aiming at mimicking brainstorming meetings conducted by people. In the process of BSO, each population can be considered as a set of ideas. Each idea stands for a solution for the issue. In every iteration, a population of ideas (solutions) is renewed. At first, ideas are allocated to search space randomly. Every single idea is renewed by the following steps.
- Firstly, k-means clustering can be utilized to identify similar solutions and the optimal idea of each cluster is marked as the cluster center.
- Secondly, BSO creates a novel idea by making it equal to one of options mentioned below.
- -
- A probabilistically chosen cluster center
- -
- A randomly chosen idea from a probabilistically selected cluster
- -
- The stochastic integration of two probabilistically chosen cluster centers
- -
- The stochastic integration of two randomly chosen ideas from two probabilistically chosen clusters
One of the options is randomly chosen according to several parameters, , , and . Besides, a cluster is probabilistically chosen based on its scale, which reflects the amount of ideas in the cluster. - Thirdly, the created is perturbed utilizing a step-size parameter and Gaussian distribution.
- Finally, substitutes the current if its fitness is better. If not, it is abandoned.
The main steps of BSO algorithm [42] is described in Figure 3, where n represents the population scale, m represents the amount of clusters, and stands for a normal distribution in which the average value is 0 and the standard deviation is 1. represents a dynamically updated step-size and k is for altering the slope of the function. As the special evolution of BSO, making diverse groups to explore wide solution space area helps BSO to avoid local extremum trap and increase the probability to find the optimal value, thus making BSO a good choice to optimize the smooth factor for GRNN.
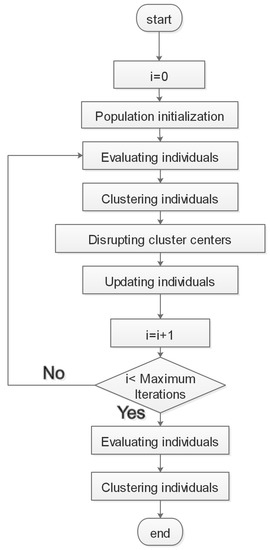
Figure 3.
The main procedure of BSO.
3. Evaluation Criteria for Prediction Capacity
Aiming to investigate the forecasting capacity of the suggested combination forecasting model, three widely used evaluation indexes were applied to compare the prediction capacity: mean absolute error (MAE), root mean square error (RMSE), and mean absolute percent error (MAPE). The indicators are described as below:
where represents the actual observation data of the moment t and represents the value of prediction for the corresponding moment. T is the number of predicted points. Moreover, aiming at analyzing the forecasting capacity increase of the suggested measure, the percentage improvements of MAE, MAPE and RMSE, which are represented by , , , respectively, were also used in this study. These evaluation indexes can be defined as follows:
4. Case Study
4.1. Datasets
Figure 4 and Figure 5 demonstrate two different datasets with a time interval of 5 min collected from 1 January 2018 to 7 January 2018 and from 1 May 2018 to 7 May 2018 at different wind power plants in Zhang Jiakou, Hebei, China. Training Set 1, including samples from 1 to 800 of each sequence, were applied to train the LSTM network; and Training Set 2, including samples from 801 to 1600 of each sequence, were applied to create the error series and train the GRNN model, which was optimized by BSO. Samples 1601–2000 of each sequence were executed to test and estimate the prediction capacity of the models mentioned in this study.
Figure 4.
The observations for Wind Speed Sequence I.
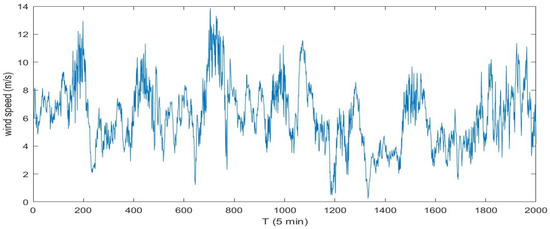
Figure 5.
The observations for Wind Speed Sequence II.
4.2. Experiments
Aiming at validating the prediction capacity of the EEMD-LSTM-GRNN-BSO method, the suggested combination approach together with seven comparison methods were conducted on the two different datasets of wind speed. The comparison approaches were the ARIMA method, the BP method, the GRNN method, the LSTM method, the LSTM-GRNN-BSO measure, the EEMD-LSTM measure, and the EEMD-LSTM-GRNN measure. The actual wind speed sequence and the forecasting values of all involved approaches are presented in Figure 6 and Figure 7. The calculation outcomes of evaluation indicators for the involved wind speed forecasting approaches are demonstrated in Table 1 and Table 2.
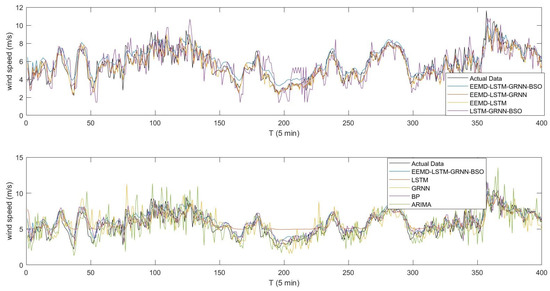
Figure 6.
The comparisons between the observations and the predictions for Wind Speed Sequence I.
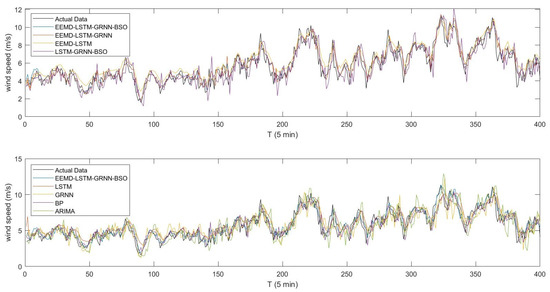
Figure 7.
The comparisons between the observations and the predictions for Wind Speed Sequence II.

Table 1.
The multi-step calculation results for evaluation indicators of involved approaches on Wind Speed Sequence I.

Table 2.
The multi-step calculation results for evaluation indicators of involved approaches on Wind Speed Sequence II.
4.3. Comparison and Analysis
As shown in the above two tables, the calculation outcomes for evaluation indicators of the two wind speed sequences forecasting cases demonstrate the same trend. Table 3 and Table 4 provide the percentage improvements for the three evaluation indicators of the suggested combination EEMD-LSTM-GRNN-BSO approach on the two different datasets in comparison with the other measures mentioned.

Table 3.
The multi-step percentage improvements of the suggested EEMD-LSTM-GRNN-BSO approach in comparison with the other measures on Wind Speed Sequence I.

Table 4.
The multi-step percentage improvements of the suggested EEMD-LSTM-GRNN-BSO approach in comparison with the other measures on Wind Speed Sequence II.
From the results in Table 1, Table 2, Table 3 and Table 4 and Figure 6 and Figure 7, some analyses could be obtained. Take Wind Speed Sequence I as an example.
- (a)
- The forecasting capacity of the EEMD-LSTM-GRNN-BSO approach was obviously superior to that of the ARIMA method. For example, in Case 1, the percentage improvement of MAE for the EEMD-LSTM-GRNN-BSO model, compared with the ARIMA approach, in 1–5-step predictions were 45.87%, 61.96%, 70.35%, 72.07% and 72.85%, respectively; the percentage improvement of MAPE for the EEMD-LSTM-GRNN-BSO model, compared with the ARIMA approach, in 1–5-step predictions were 53.56%, 62.24%, 70.45%, 71.59% and 71.65%, respectively; and the percentage improvement of RMSE for the EEMD-LSTM-GRNN-BSO model, compared with the ARIMA approach, in 1–5-step predictions were 47.31%, 60.29%, 69.84%, 72.25% and 72.91%, respectively.
- (b)
- The forecasting capacity of the EEMD-LSTM-GRNN-BSO approach was obviously superior to that of the BP method. For example, in Case 1, the percentage improvement of MAE for the EEMD-LSTM-GRNN-BSO model, compared with the BP approach, in 1–5-step predictions were 25.37%, 31.51%, 35.90%, 52.77% and 43.01%, respectively; the percentage improvement of MAPE for the EEMD-LSTM-GRNN-BSO model, compared with the BP approach, in 1–5-step predictions were 41.89%, 37.41%, 40.83%, 60.80% and 51.41%, respectively; and the percentage improvement of RMSE for the EEMD-LSTM-GRNN-BSO model, compared with the BP approach, in 1–5-step predictions were 23.12%, 25.29%, 32.08%, 49.83%, and 37.87%, respectively.
- (c)
- The forecasting capacity of the EEMD-LSTM-GRNN-BSO approach was obviously superior to that of the GRNN method. For example, in Case 1, the percentage improvement of MAE for the EEMD-LSTM-GRNN-BSO model, compared with the GRNN approach, in 1–5-step predictions were 42.30%, 48.43%, 54.24%, 55.63% and 49.75%, respectively; the percentage improvement of MAPE for the EEMD-LSTM-GRNN-BSO model, compared with the GRNN approach, in 1–5-step predictions were 53.49%, 51.33%, 56.36%, 60.77% and 55.10%, respectively; and the percentage improvement of RMSE for the EEMD-LSTM-GRNN-BSO model, compared with the GRNN approach, in 1–5-step predictions were 39.01%, 42.02%, 50.14%, 54.11% and 47.03%, respectively.
- (d)
- The forecasting capacity of the EEMD-LSTM-GRNN-BSO approach was obviously superior to that of the LSTM method. For example, in Case 1, the percentage improvement of MAE for the EEMD-LSTM-GRNN-BSO model, compared with the LSTM approach, in 1–5-step predictions were 33.77%, 32.90%, 31.06%, 29.79% and 20.65%, respectively; the percentage improvement of MAPE for the EEMD-LSTM-GRNN-BSO model, compared with the LSTM approach, in 1–5-step predictions were 52.42%, 43.18%, 36.59%, 38.81% and 28.11%, respectively; and the percentage improvement of RMSE for the EEMD-LSTM-GRNN-BSO model, compared with the LSTM approach, in 1–5-step predictions were 30.21%, 24.50%, 27.08%, 26.66% and 14.44%, respectively.
- (e)
- The forecasting capacity of the EEMD-LSTM-GRNN-BSO approach was obviously superior to that of the LSTM-GRNN-BSO method. For example, in Case 1, the percentage improvement of MAE for the EEMD-LSTM-GRNN-BSO model, compared with the LSTM-GRNN-BSO approach, in 1–5-step predictions were 42.05%, 38.69%, 38.80%, 27.07% and 10.75%, respectively; the percentage improvement of MAPE for the EEMD-LSTM-GRNN-BSO model, compared with the LSTM-GRNN-BSO approach, in 1–5-step predictions were 54.26%, 42.93%, 42.04%, 31.14% and 14.86%, respectively; and the percentage improvement of RMSE for the EEMD-LSTM-GRNN-BSO model, compared with the LSTM-GRNN-BSO approach, in 1–5-step predictions were 38.97%, 31.86%, 34.61%, 25.20% and 6.31%, respectively.
- (f)
- The forecasting capacity of the EEMD-LSTM-GRNN-BSO approach was obviously superior to that of the EEMD-LSTM method. For example, in Case 1, the percentage improvement of MAE for the EEMD-LSTM-GRNN-BSO model, compared with the EEMD-LSTM approach, in 1–3-step predictions were 32.44%, 21.44% and 20.60%, respectively; the percentage improvement of MAPE for the EEMD-LSTM-GRNN-BSO model, compared with the EEMD-LSTM approach, in 1–3-step predictions were 33.08%, 22.92% and 21.97%, respectively; and the percentage improvement of RMSE for the EEMD-LSTM-GRNN-BSO model, compared with the EEMD-LSTM approach, in 1–3-step predictions were 23.45%, 22.49% and 13.23%, respectively.
- (g)
- The forecasting capacity of the EEMD-LSTM-GRNN-BSO approach was obviously superior to that of the EEMD-LSTM-GRNN method. For example, in Case 1, the percentage improvement of MAE for the EEMD-LSTM-GRNN-BSO model, compared with the EEMD-LSTM-GRNN approach, in 1–5-step predictions were 12.89%, 7.50%, 56.08%, 50.34% and 65.46%, respectively; the percentage improvement of MAPE for the EEMD-LSTM-GRNN-BSO model, compared with the EEMD-LSTM-GRNN approach, in 1–5-step predictions were 12.09%, 16.51%, 54.48%, 53.52% and 66.37%, respectively; and the percentage improvement of RMSE for the EEMD-LSTM-GRNN-BSO model, compared with the EEMD-LSTM-GRNN approach, in 1–5-step predictions were 4.52%, 5.89%, 54.88%, 50.95% and 62.90%, respectively.
- (h)
- Among all the wind speed forecasting models involved in 1–5-step predictions, the proposed EEMD-LSTM-GRNN-BSO hybrid model showed the highest forecasting accuracy. For example, the error statistical estimation for one-step forecast of Wind Speed Sequence I are shown in Figure 8, which shows that most errors of the proposed method were less than 10%. The reasons for the satisfactory forecasting accuracy improvement were as follows: (1) In terms of the data pre-processing method, EEMD method could recognize the non-linear features of the dataset well and effectively decompose the original wind speed series effectively to provide abundant information to the forecasting model, which contributed to the forecasting accuracy improvements. (2) In terms of the parameter optimization algorithm, the BSO approach could effectively optimize the parameter of GRNN in the training process, which improved the performance of GRNN on error series forecasting. However, the forecasting performance might become worse if the parameter in GRNN were not set properly. (3) Combined with the error correction of the GRNN optimized by BSO, the forecasting accuracy of EEMD-LSTM was significantly improved. The accuracy improvements of data preprocess, error correction and parameter optimization in 1–5-step wind speed predictions for case one are shown in Table 5.
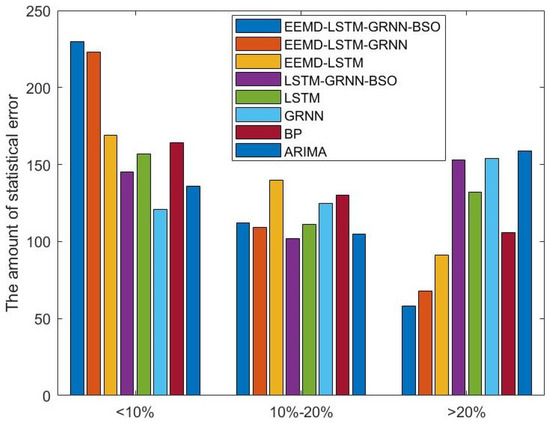 Figure 8. The error statistical estimation for one step forecast of Wind Speed Sequence I.
Figure 8. The error statistical estimation for one step forecast of Wind Speed Sequence I. Table 5. The accuracy improvements of data preprocess, error correction and parameter optimization in 1–5-step prediction for Wind Speed Sequence I.
Table 5. The accuracy improvements of data preprocess, error correction and parameter optimization in 1–5-step prediction for Wind Speed Sequence I.
5. Additional Prediction Case
Aiming at further studying the generalization capacity of the suggested hybrid measure, the proposed EEMD-LSTM-GRNN-BSO hybrid model was conducted on am additional case with 30-min interval: Wind Speed Sequence III. The actual data of Wind Speed Sequence III, taken from 1 October 2018 to 10 November 2018, are shown in Figure 9. The additional experiment was conducted with the same procedure of the aforementioned three experiments, and the forecasting results are shown in Figure 10. Table 6 demonstrates the multi-step calculation outcomes for evaluation indicators of all the models involved. Table 6 illustrates the multi-step percentage improvements of the three evaluation indices for the suggested EEMD-LSTM-GRNN-BSO approach compared with other comparison models on wind speed series III. It is observed in Table 6 and Table 7 that the calculation outcomes of the evaluation indicators on the additional prediction case showed the same basic behavior as the the two aforementioned forecasting cases in Section 4. Again, the suggested combination EEMD-LSTM-GRNN-BSO approach demonstrated the highest forecasting accuracy compared with all the other models mentioned. This additional case witnessed the generalization and validity of the suggested combination model on wind speed series with longer time interval.
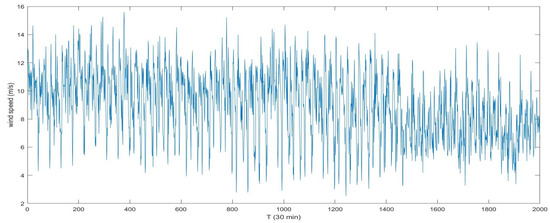
Figure 9.
The observation values of Wind Speed Sequence III.
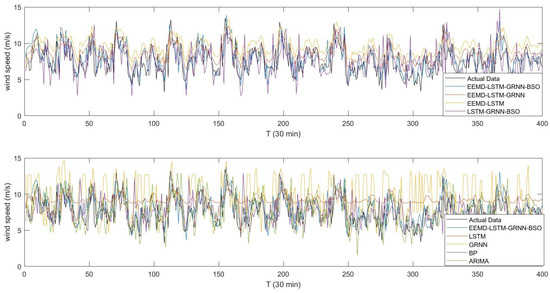
Figure 10.
The comparisons between the observations and the predictions for Wind Speed Sequence III.

Table 6.
The multi-step calculation results for evaluation indicators of involved approaches on Wind Speed Sequence II.

Table 7.
The multi-step percentage improvements of the suggested EEMD-LSTM-GRNN-BSO approach in comparison with the other measures on Wind Speed Sequence III.
6. Conclusions
A new combination approach integrated with signal pre-processing, parameter optimization and the error correction strategy is proposed in this article. The combination approach consists of the EEMD measure, the LSTM algorithm, the GRNN measure and the BSO measure. The EEMD is executed to decomposed the original dataset into a collection of IMFs. The LSTM algorithm is applied as the major forecasting method of each IMF. The GRNN model is used as the secondary forecasting method to forecast error sequences for each IMF. The BSO algorithm is executed to optimize the parameter of GRNN during the training procedure. Aiming at validating the effectiveness and generalization of the suggested combination EEMD-LSTM-GRNN-BSO approach, seven other forecasting methods were conducted on three different datasets as comparisons: the ARIMA measure, the BP measure, the GRNN measure, the LSTM measure, the LSTM-GRNN-BSO measure, the EEMD-LSTM measure, and the EEMD-LSTM-GRNN measure. According to the calculation outcomes, the following conclusions are drawn: (1) the EEMD can contribute to the promotion of the wind speed prediction capacity and robustness of the LSTM approach effectively; (2) the BSO based parameter optimization method is effective in finding the optimal parameter for GRNN and improving the forecasting performance for the EEMD-LSTM-GRNN model; (3) the error correction based on the optimized GRNN promotes the prediction ability of the EEMD-LSTM method obviously; and (4) in comparison with all other measures involved, the suggested EEMD-LSTM-GRNN-BSO measure is certified to demonstrate the best prediction ability on wind speed forecasting in short period.
Author Contributions
L.Y. designed this study and wrote the original manuscript; S.L. offered review and editing advice; and Y.H. and G.W. offered modification suggestions.
Funding
This research received no external funding.
Conflicts of Interest
No conflict of interest are declared by the authors.
References
- Ouyang, T.; Zha, X.; Liang, Q. A combined multivariate model for wind power prediction. Energy Convers. Manag. 2017, 144, 361–373. [Google Scholar] [CrossRef]
- Jung, J.; Broadwater, R.P. Current status and future advances for wind speed and power forecasting. Renew. Sustain. Energy Rev. 2014, 31, 762–777. [Google Scholar] [CrossRef]
- Li, H.; Wang, J.; Lu, H.; Guo, Z. Research and application of a combined model based on variable weight for short term wind speed forecasting. Renew. Energy 2018, 116, 669–684. [Google Scholar] [CrossRef]
- Zhao, J.; Guo, Z.H.; Su, Z.Y.; Zhao, Z.Y.; Xiao, X.; Liu, F. An improved multi-step forecasting model based on WRF ensembles and creative fuzzy systems for wind speed. Appl. Energy 2016, 162, 808–826. [Google Scholar] [CrossRef]
- Landberg, L.; Watson, S.J. Short-term prediction of local wind conditions. J. Wind. Eng. Ind. Aerodyn. 1994, 89, 235–245. [Google Scholar] [CrossRef]
- Zhao, W.; Wei, Y.M.; Su, Z. One day ahead wind speed forecasting: A resampling-based approach. Appl. Energy 2016, 178, 886–901. [Google Scholar] [CrossRef]
- Lei, M.; Luan, S.; Jiang, C.; Liu, H.; Yan, Z. A review on the forecasting of wind speed and generated power. Renew. Sustain. Energy Rev. 2009, 13, 915–920. [Google Scholar] [CrossRef]
- Qin, M.; Li, Z.; Du, Z. Red tide time series forecasting by combining ARIMA and deep belief network. Knowl.-Based Syst. 2017, 125, 39–52. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, J.; Wang, K.; Wang, Z. Wind Power Prediction Considering Nonlinear Atmospheric Disturbances. Energies 2015, 8, 475–489. [Google Scholar] [CrossRef]
- Xiao, L.; Wang, J.; Dong, Y.; Wu, J. Combined forecasting models for wind energy forecasting: A case study in China. Renew. Sustain. Energy Rev. 2015, 44, 271–288. [Google Scholar] [CrossRef]
- Yan, Y.; Li, J.; Gao, D.W. Condition Parameter Modeling for Anomaly Detection in Wind Turbines. Energies 2014, 7, 3104–3120. [Google Scholar] [CrossRef]
- Hu, J.; Wang, J.; Zeng, G. A hybrid forecasting approach applied to wind speed time series. Renew. Energy 2013, 60, 185–194. [Google Scholar] [CrossRef]
- Zhong, J.; Dong, G.; Sun, Y.; Zhang, Z.; Wu, Y. Application of the nonlinear time series prediction method of genetic algorithm for forecasting surface wind of point station in the South China Sea with scatterometer observations. Chin. Phys. B 2016, 25, 167–173. [Google Scholar] [CrossRef]
- Da, L.; Wang, J.; Hui, W. Short-term wind speed forecasting based on spectral clustering and optimised echo state networks. Renew. Energy 2015, 78, 599–608. [Google Scholar]
- Wang, H.Z.; Li, G.Q.; Wang, G.B.; Peng, J.C.; Hui, J.; Liu, Y.T. Deep learning based ensemble approach for probabilistic wind power forecasting. Appl. Energy 2017, 188, 56–70. [Google Scholar] [CrossRef]
- Hui, L.; Mi, X.; Li, Y. Smart multi-step deep learning model for wind speed forecasting based on variational mode decomposition, singular spectrum analysis, LSTM network and ELM. Energy Convers. Manag. 2018, 159, 54–64. [Google Scholar]
- Tascikaraoglu, A.; Uzunoglu, M. A review of combined approaches for prediction of short-term wind speed and power. Renew. Sustain. Energy Rev. 2014, 34, 243–254. [Google Scholar] [CrossRef]
- Jie, S.; Ding, Z.; Lee, W.J.; Yang, Y.; Liu, Y.; Zhang, M. Hybrid Forecasting Model for Very-Short Term Wind Power Forecasting Based on Grey Relational Analysis and Wind Speed Distribution Features. IEEE Trans. Smart Grid 2014, 5, 521–526. [Google Scholar]
- Liu, D.; Niu, D.; Wang, H.; Fan, L. Short-term wind speed forecasting using wavelet transform and support vector machines optimized by genetic algorithm. Renew. Energy 2014, 62, 592–597. [Google Scholar] [CrossRef]
- Fan, G.F.; Peng, L.L.; Zhao, X.; Hong, W.C. Applications of hybrid EMD with PSO and GA for an SVR-based load forecasting model. Energies 2017, 10, 1713. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2011, 1. [Google Scholar] [CrossRef]
- Cheng, Q.; Chen, L.; Cheng, Y.; Zhang, Q.; Gao, J. Short-term wind power forecasting method based on EEMD and LS-SVM model. Electr. Power Autom. Equip. 2018. [Google Scholar] [CrossRef]
- Chitsaz, H.; Amjady, N.; Zareipour, H.; Chitsaz, H.; Amjady, N.; Zareipour, H. Wind power forecast using wavelet neural network trained by improved Clonal selection algorithm. Energy Convers. Manag. 2015, 89, 588–598. [Google Scholar] [CrossRef]
- Osório, G.J.; Matias, J.C.O.; Catalão, J.P.S. Short-term wind power forecasting using adaptive neuro-fuzzy inference system combined with evolutionary particle swarm optimization, wavelet transform and mutual information. Renew. Energy 2015, 75, 301–307. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, C.; Yuan, Y.; Huang, Y.; Tan, Q. Short-term wind power prediction based on LSSVM–GSA model. Energy Convers. Manag. 2015, 101, 393–401. [Google Scholar] [CrossRef]
- Cheng, S.; Qin, Q.; Chen, J.; Shi, Y. Brain storm optimization algorithm: A review. Artif. Intell. Rev. 2015, 6728, 1–14. [Google Scholar] [CrossRef]
- Jordehi, A.R. Brainstorm optimisation algorithm (BSOA): An efficient algorithm for finding optimal location and setting of FACTS devices in electric power systems. Int. J. Electr. Power Energy Syst. 2015, 69, 48–57. [Google Scholar] [CrossRef]
- El-Abd, M. Global-best brain storm optimization algorithm. Swarm Evol. Comput. 2017, 37, 27–44. [Google Scholar] [CrossRef]
- Jadhav, H.; Sharma, U.; Patel, J.; Roy, R. Brain storm optimization algorithm based economic dispatch considering wind power. In Proceedings of the 2012 IEEE International Conference on Power and Energy (PECon), Kota Kinabalu, Malaysia, 2–5 December 2012; pp. 588–593. [Google Scholar]
- Jia, Z.; Duan, H.; Shi, Y. Hybrid brain storm optimisation and simulated annealing algorithm for continuous optimisation problems. Int. J. Bio-Inspired Comput. 2016, 8, 109–121. [Google Scholar] [CrossRef]
- Liang, Z.; Liang, J.; Wang, C.; Dong, X.; Miao, X. Short-term wind power combined forecasting based on error forecast correction. Energy Convers. Manag. 2016, 119, 215–226. [Google Scholar] [CrossRef]
- Yan, J.; Huang, G. Short-term wind speed prediction: Hybrid of ensemble empirical mode decomposition, feature selection and error correction. Energy Convers. Manag. 2017, 144, 340–350. [Google Scholar]
- Chen, S.; Lin, Y.; Zhang, G.; Zeng, C.; Dong, S.; Dai, C. Short-term wind power prediction based on combined grey-Markov model. In Proceedings of the International Conference on Advanced Power System Automation & Protection, Beijing, China, 16–20 Octorber 2011. [Google Scholar]
- Lei, Y.; He, Z.; Zi, Y. Application of the EEMD method to rotor fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2009, 23, 1327–1338. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Graves, A.; Schmidhuber, J. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Netw. 2005, 18, 602–610. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Hao, W.; Woo, W.C.; Woo, W.C.; Woo, W.C. Convolutional LSTM Network: A machine learning approach for precipitation nowcasting. In Proceedings of the International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Liu, H.; Tian, H.Q.; Liang, X.F.; Li, Y.F. Wind speed forecasting approach using secondary decomposition algorithm and Elman neural networks. Appl. Energy 2015, 157, 183–194. [Google Scholar] [CrossRef]
- Specht, D.F. A general regression neural network. IEEE Trans. Neural Netw. 1991, 2, 568–576. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y. Brain Storm Optimization Algorithm. IEEE Congr. Evol. Comput. 2011, 6728, 1–14. [Google Scholar]
- Shi, Y. An Optimization Algorithm Based on Brainstorming Process. In Proceedings of the International Symposium on Intelligence Computation & Applications, Budapest, Hungary, 21–22 November 2011; pp. 35–62. [Google Scholar]
- Maa, X.; Jin, Y.; Dong, Q. A Generalized Dynamic Fuzzy Neural Network Based on Singular Spectrum Analysis Optimized by Brain Storm Optimization for Short-Term Wind Speed Forecasting; Elsevier Science Publishers B. V.: Amsterdam, The Netherlands, 2017; pp. 296–312. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).