Abstract
The accurate monitoring of state of charge (SOC) and state of health (SOH) is critical for the reliable management of lithium-ion battery (LIB) systems. In this paper, online model identification is scrutinized to realize high modeling accuracy and robustness, and a model-based joint estimator is further proposed to estimate the SOC and SOH of an LIB concurrently. Specifically, an adaptive forgetting recursive least squares (AF-RLS) method is exploited to optimize the estimation’s alertness and numerical stability so as to achieve an accurate online adaption of model parameters. Leveraging the online adapted battery model, a joint estimator is proposed by combining an open-circuit voltage (OCV) observer with a low-order state observer to co-estimate the SOC and capacity of an LIB. Simulation and experimental studies are performed to verify the feasibility of the proposed data–model fusion method. The proposed method is shown to effectively track the variation of model parameters by using the onboard measured current and voltage data. The SOC and capacity can be further estimated in real time with fast convergence, high stability, and high accuracy.
1. Introduction
Lithium-ion batteries (LIBs) are one of the leading energy storage technologies and have been applied widely in various fields, such as modern electric grids, portable electronics, and transportation electrification [1,2,3,4]. To date, lots of efforts have been made for the improvement of cell chemistry, materials, and components [5,6,7,8]. However, LIBs are typically complicated from an electrochemical perspective and their performance is easily degraded in long-term operation [9]. To this end, a high-fidelity battery management system (BMS) that accurately monitors the key battery states is critical for the safety, efficiency, and life expectancy of LIB systems [10].
The state of charge (SOC) is an important variable that should be monitored in a BMS. The accurate monitoring of SOC contributes to preventing unsuitable over-charge or over-discharge, which causes irreversible damage to an LIB. The coulomb counting (CC) method is most widely applied in commercial BMS products due to its low computing cost. However, the CC method is vulnerable to current measurement error and depends on an accurate knowledge about the initial SOC, which problematizes its application. The open-circuit voltage (OCV) measurement method is straightforward but needs a long relaxation time to obtain an accurate OCV, which is unrealistic under continuous and dynamic load conditions.
The model-based observers enjoy the merits of high accuracy and robustness; thus, they have been widely studied for online SOC estimation [11,12]. An accurate battery serves as the prerequisite for this category of methods. In terms of an LIB, the existing models include the electrochemical model [13,14,15], the black-box model [16], and the equivalent circuit model (ECM) [17,18,19]. Amongst others, the ECMs have a better trade-off between accuracy and complexity and thus are favorable candidates for application in micro-controller units. Generally, ECMs are used to simulate the dynamics of an LIB, while the states of interest are estimated in real time with various observers, such as the Luenberger observer [20], the extended Kalman filter (EKF) [21,22,23], the square root cubature Kalman filter [24], the unscented Kalman filter (UKF) [25], the sliding mode observer (SMO) [26], the particle filter (PF) [27], and the nonlinear observer [28]. For these methods, the ECMs are calibrated offline and the model parameters are assumed to be fixed during operation. Nevertheless, the model parameters of ECMs are typically affected by multiple factors, such as SOC, C-rate, temperature, and ageing status [29]. The model’s robustness and estimation accuracy may decline largely by the absence of an online model update as LIB systems are commonly operated under highly dynamic working conditions in real applications. Integrated model identification and state estimation have therefore been investigated to improve the overall robustness in recent years.
The existing co-estimation methods can be broadly categorized into three groups. The first group is called joint estimation, which lumps the OCV and model parameters in one state vector for joint estimation with advanced filters, such as recursive least squares (RLS) [30] and KF-based methods [31]. The SOC is then inferred from the pre-calibrated SOC-OCV look-up table. The joint estimation methods manifest themselves with one filter to extract all the variables of interest, but stability is a major challenge if model uncertainties are significant. The second group is called dual estimation, which uses two parallel filters to observe the model parameters and battery states concurrently [32]. For example, Xiong et al. [33] proposed a multi-scale dual extended Kalman filter (DEKF) to track the slow-varying model parameters and the fast dynamics of the SOC accurately. Recently, a dual estimation method with different filtering techniques, i.e., EKF-based model identification and PF-based state estimation, was proposed for LIB management [34]. The third group is the data–model fusion method, which online identifies the model parameters with data-driven methods such as RLS while simultaneously estimating the SOC with advanced filters [22,35,36,37]. In recent years, some modified methods, such as the vector-type RLS [38], have been proposed to improve the performance of model parameters identification. This method is theoretically computationally efficient compared to the dual and joint estimation methods due to the low computing cost of RLS. For all the three groups of methods, the model robustness and estimation accuracy can be well-improved, but careful tuning is required to guarantee algorithmic convergence and numerical stability. Also, the computing complexity may potentially be a barrier to their application in low-cost micro-controllers, especially if using high-order models or observing multiple battery states. To this end, necessary modification will be of value to further improve the performance of estimation. Moreover, instantaneous capacity is generally included in the state-space formula of the model-based observers; thus, the online update of it is critical to ensure sufficient SOC accuracy over long-term operation [39].
The capacity is a direct indicator describing the state of health (SOH) of an LIB. In the literature, the DEKF [40] and the dual nonlinear predictive filter (DNPF) [41] were used to co-estimate the SOC and capacity. However, the model parameters are not fully adapted; thus, the robustness to dynamic working conditions and ageing can be further improved. Alternatively, the capacity was lumped with the parameter vector, and afterwards the model parameters and SOC were estimated simultaneously with the DEKF [32,33] to guarantee high robustness. However, the dual and high-order EKF framework may suffer from instability issues and a high computing cost, which should be carefully addressed in real applications [42]. In Reference [42], the model parameters were updated by an offline fourth-order EKF in the macro timescale, while the SOC was estimated by a second-order EKF in the micro timescale. In Reference [43], multiple proportional-integral estimators are formulated based on an electrochemical model to realize the concurrent estimation of impedance, SOC, and capacity.
Although lots of efforts have been made towards the online estimation of SOC and SOH, major challenges still exist to improve the robustness and stability while lowering the computing cost. In this paper, a new data–model fusion method is proposed to observe the SOC and SOH of an LIB simultaneously based on an online adaptive battery model. A first-order resistor–capacitor (RC) model is adopted with the model parameters online identified with an adaptive forgetting recursive least squares (AF-RLS) method to enhance the tracking ability and numerical stability. Leveraging the online parameterized model, a joint estimator based on OCV pre-estimation and a low-order state observer is proposed to co-estimate the SOC and capacity, with the expectation that it will guarantee the stability and reduce the filtering dimension. Simulation and experiments are further performed to verify the feasibility of the proposed method.
The rest of paper is organized as follows. Section 2 presents the battery modeling and AF-RLS-based model identification. Section 3 describes the co-estimation method of SOC and capacity with a simple OCV observer. Section 4 and Section 5 present the simulation and experimental results to verify the proposed method, while Section 6 draws the main conclusions.
2. Battery Modeling and Identification
2.1. Battery Modeling
An ECM with a higher order can better reproduce LIB dynamics with multiple time constants, but the higher computing complexity is not favorable for online embedded systems. Hu et al. [17] systematically studied the ECMs used for LIBs and found that the first-order RC model kept a good trade-off between model precision and computing complexity. The first-order RC model as shown in Figure 1 is thereby adopted in this paper to simulate the dynamics of the LIB in use. The voltage source is used to simulate the OCV, which is SOC-dependent. Rs is the ohmic resistance. The polarization resistance (Rp) and capacitance (Cp) construct an RC network to simulate the transient dynamics of an LIB.
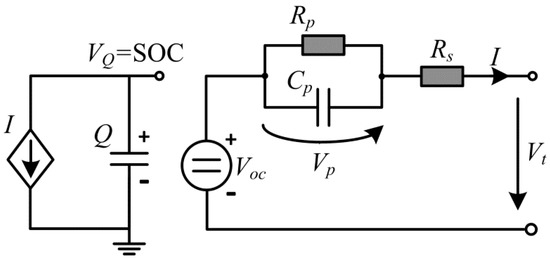
Figure 1.
Circuit diagram of the first-order RC model.
The following governing equations can be written to describe the electrical characteristics of the used circuit model:
where I is the load current that is defined as positive for discharge process throughout this paper and Vt and Vp are the terminal and polarization voltage, respectively.
The OCV is a nonlinear function with respect to SOC. An SOC-OCV test was performed on a LiNiMnCoO2 (NMC) cell (ICR18650-26F, Samsung, Seoul, Korea), which has a nominal capacity of 2.2 Ah, to determine the correlation between SOC and OCV. The cell was first fully charged with the constant-current-constant-voltage (CCCV) method until the upper cut-off voltage of 4.2 V was reached, where the SOC was defined as 100%. Afterwards, the cell was discharged with a series of current pulses until the lower cut-off voltage of 3 V was reached, where the SOC was defined as 0%. The cell was left in an open-circuit condition for 5 h for depolarization at the end of each pulse current discharge, then the terminal voltages were measured and treated as discharge OCVs. At the same time, the corresponding SOCs were calibrated with coulombic counting. The same procedures were executed for the charging process to obtain charge OCVs. The real OCVs were averaged from the discharge and charge OCVs. As a long depolarization time is applied, the hysteresis voltage is found to be very small based on the calibration result. The hysteresis effect is therefore not considered in the modeling for the purpose of simplification. In this paper, the SOC-OCV function is determined by polynomial fitting to the offline tested SOC-OCV correction as:
where z is the battery SOC, np is the order of polynomial fitting (np = 5 here), and ci is the polynomial coefficient obtained using least-squares-based curve fitting. The experimentally determined and curve-fitted SOC-OCV relations are shown in Figure 2.
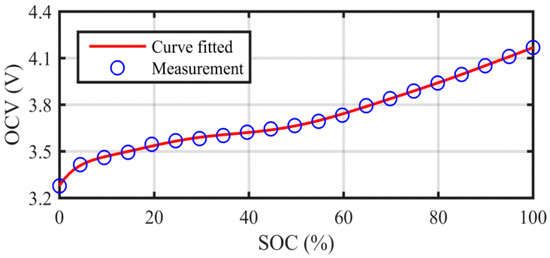
Figure 2.
Measured and calibrated correlation between the SOC and OCV.
2.2. Online Identification of Model Parameters
This paper identifies the model parameters by formulating a regression problem. A new variable is defined as y = Vt − Voc. Then, the transfer function of Equation (1) can be expressed as:
By adopting the bilinear transform s = 2 (q − 1)/ts/(q + 1), Equation (4) can be re-written as:
where
where ts is the onboard sampling interval. From Equation (5), the following discrete-time expression can be written as:
where θk = [a1,k b0,k b1,k]T, φk = [−yk−1 Ik Ik−1]T. Then, the model identification problem boils down to solving the regression model represented by Equation (7).
2.3. Adaptive Forgetting Recursive Least Squares
A classical method to solve Equation (7) is the RLS method. The estimation law of RLS is given by:
Parameter vector update law:
Gain update law:
Covariance matrix update:
The basic RLS assumes that λ = 1, which makes the covariance matrix decay gradually. Thus, the algorithm cannot retain the necessary alertness or adaptivity to track time-varying parameters.
One simple method to ensure estimation alertness is to use a forgetting factor of λ < 1, which means heavier weights are given to the more recent data. However, the selection of a forgetting factor is an interesting trade-off that should be addressed carefully. Specifically, a small λ leads to a large P and L; thus, the estimates tend to be uncertain. In contrast, a large λ potentially causes a loss of tracking capability for fast-varying parameters. This can be explained by analyzing Equation (10): under sufficient excitation, the term on the right-hand side inside the square brackets decays faster than it is inflated by the multiplier 1/λ, resulting in the gradual decay of the covariance matrix.
Moreover, exponential forgetting potentially leads to the covariance wind-up problem under alow excitation condition. This is because the term Pk−1φk in this case is close to zero; thus, Equation (10) becomes Pk = Pk/λ, indicating that the covariance matrix grows exponentially. When the excitation recovers, the covariance matrix and gain have been very large and cause large fluctuations in the estimation.
In seeking to overcome the aforementioned drawbacks of basic RLS and RLS with exponential forgetting, the use of an adaptive forgetting factor is suggested by modifying Equations (9) and (10) according to [44]:
where I represents the unit matrix, and ε is the estimation residual calculated by:
To impose an upper bound on the covariance matrix, P is updated as [45]:
The above update laws comprise the AF-RLS, which will be used in this paper for the online identification of model parameters. It is clear that the forgetting factor is online adaptive, with λ automatically set close to 1 when the estimation residual is small while it is set to a small value when the estimation residual is large. It should be noted that two more tuning parameters have been introduced by the adaption of the forgetting factor, i.e., the gain (σ) controlling the sensitivity of the forgetting factor to the output mismatch and the upper bound to the trace of the covariance matrix (C).
3. Co-Estimation of SOC and SOH
Based on the online adaptive model, this section further seeks to propose a low-order estimator to estimate the SOC and SOH jointly. The capacity is used as the indicator for SOH in this paper.
3.1. H-Infinity Filter (HIF)
Compared with the well-known Kalman filtering (KF)-based methods, the HIF can better withstand modeling uncertainty and the estimation accuracy is not dependent on knowledge of the noise statistics. It is thereby expected that the estimation will have a better robustness to model uncertainty and noise statistics [46]. A general nonlinear discrete-time state-space equation is expressed as:
where xk, uk, and yk are the system state, input, and measurement, respectively; wk and vk are, respectively, the process and measurement noises with covariance matrices Q and R; δk is a linear combination of different system states, and hk is a user-defined matrix. The state-space model represented by Equation (16) aims to obtain the optimized estimate of δk. It is needed to set hk = I if xk is estimated directly.
The HIF aims to provide a uniformly small estimation error for any x0, wk, and vk. The measure of performance is then given by the following cost function:
where , is an a priori estimate of x0, and Sk and P0 are user-defined symmetric positive matrices. The following operation regarding an arbitrary matrix M and vector n is defined as follows to clarify Equation (17):
According to the worse-case performance measure, the optimal estimation of δk among all possible estimates should satisfy:
where “sup” denotes the supremum and τ is a pre-defined performance bound. The discrete HIF boils down to a minimax problem where the estimate of δk plays against the exogenous inputs, i.e., x0, wk, and vk. Then, the optimization criterion of HIF can be expressed as:
Different from the typical minimum variance filters, such as KF, the HIF addresses the deterministic disturbances and no prior knowledge on noise statistics is needed. As the system measurement is known, vk can be obtained by using Equation (16) if the optimal estimates of x0 and wk are determined. Therefore, Equation (20) can be alternatively rewritten as:
where
Afterwards, the complete solution of HIF under the criterion of Equation (21) with respect to the system characterized by Equation (16) can be summarized in Table 1. The relative theorem and specific proof are not elaborated here but can be found in the existing literature [47].

Table 1.
Algorithmic procedures of the H-Infinity Filter (HIF).
3.2. OCV Observation
With the HIF discussed in Section 3.1, the real-time observation of SOC and capacity can be realized by using the procedures summarized in Table 1.
The existing state observers typically lump multiple system states, including the polarization voltages and the LIB states of interest, into one vector for observation. A potential problem is that high-order filtering is prone to a high computing cost and low stability due to the high-dimension matrix operation and the cross interferences among multiple system states. In light of this, order reduction is always plausible for accurate state estimation. This paper thus also seeks to propose a low-order state observer for SOC and SOH joint estimation. To realize this, a simple OCV observer is first proposed. It is clear that Equation (7) can be rewritten in the following discrete-time form:
Adopting transposition to Equation (23) yields:
where and Δk are the OCV estimate and the estimation residual, respectively, which can be expressed as:
It is shown that the estimation residual is close to zero if the OCV changes slowly during two adjacent sampling times. The can thereby be viewed as the OCV estimate with small disturbances. The deduction in this subsection is a general framework and, thus, can be easily extended to fit higher-order RC models.
3.3. Joint Estimaiton of SOC and Capacity
The capacity is used to infer the SOH of an LIB. A closed-loop observer is formulated here by using the online adapted ECM to online estimate the SOC and capacity concurrently. The state-space model in the form of Equation (16) should be formulated firstly to allow for the use of HIF in Table 1.
As a major difference from the existing joint estimators, in this paper, the in Equation (24) is viewed as a noisy system measurement. In this regard, the polarization voltage (Vp) can be ruled out from the state vector as it has no correlation with the OCV. Therefore, the system input and measurement are defined as I and , respectively, while the state vector is defined as x = [z, 1/Q]T. The following state-space formula can then be formulated:
where G(xk, uk) is the function of OCV with regard to the system state and input, which can be determined by the calibrated SOC-OCV function expressed by Equation (3); η is the coulombic efficiency describing the ratio of the total charge extractable from the battery to the total charge that can be injected into the battery over a full cycle. It is calibrated to be 99.2% in this paper.
Referring to the state-space formula expressed by Equation (26), the reference matrices ( and ) in Table 1 can be expressed as:
The HIF can then be used to keep track of both the SOC and capacity while leveraging the described definitions and algorithmic procedures. As the polarization voltage has been ruled out from the state vector, the dimension of filtering is effectively reduced. It has to be pointed out that the dimension compression will be more significant based on the proposed method if models with higher orders are in use.
4. Simulation Study
This section aims to verify the proposed method on both online model identification and state joint estimation with simulations. An ideal battery model is used to eliminate the modeling uncertainties so that the method can be well-evaluated from a purely theoretical perspective.
4.1. Data Acquisition
The first-order ECM as shown in Figure 1 was built in the Matlab/Simulink Environment (R2015b, MathWorks, Inc., Nattick, MA, USA). The OCV was defined with the calibrated SOC-OCV function of the cell in use. The ohmic resistance and polarization resistance were defined to be time-variant, while the polarization capacitance was assumed to be constant at a user-defined value. A user-defined hybrid pulse test (HPT) and the Federal Urban Dynamic Schedule (FUDS) were used in this section to evaluate the proposed method. The current was loaded to the ECM in Simulink and the corresponding terminal voltage and SOC were obtained accordingly as shown in Figure 3.
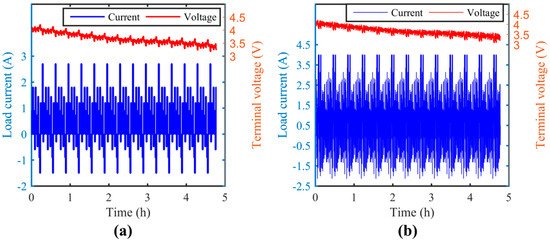
Figure 3.
Load current and terminal voltage of the simulation study: (a) hybrid pulse test (HPT); (b) Federal Urban Dynamic Schedule (FUDS).
4.2. Simulation Results
The simulated current and voltage data are used to verify the proposed method. As no prior knowledge can be obtained on the model parameters and system states, the algorithm is randomly initialized as follows throughout this paper if not otherwise defined: Rs = Rp = 10 mΩ, Cp = 1 kF, SOC0 = 60%, Q0 = 1.8 Ah.
The results of the online model identification under the HPT condition are shown in Figure 4. It is shown that the change of parameters can be tracked effectively by the proposed method. The identification experiences a short transition time with a certain overshooting for the correction of the erroneous initialization at the initial stage, and afterwards the model parameters have been identified with reasonable accuracy. The online model adaption facilitates the maintenance of high modeling accuracy and good robustness for state estimation.
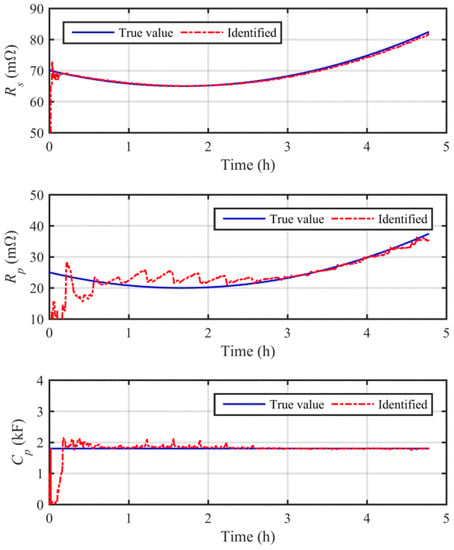
Figure 4.
Results of online model parameters identification under the HPT simulation study.
The results of SOC and capacity joint estimation under the HPT are shown in Figure 5. As shown, the proposed method keeps track of the reference SOC accurately with rapid convergence from the large initialization error of 35%. The estimation error has been well-confined to the 1% error bound for the entire simulation. The capacity estimation is also shown to converge to the expected value. However, the convergence is much slower compared to the estimation of SOC. This is because the capacity changes very slowly in real applications, so that a very small process noise covariance component is assigned to the capacity-relevant state to stabilize the estimation. It can be observed that the estimated capacity matches closely with the reference value once the algorithm converges.
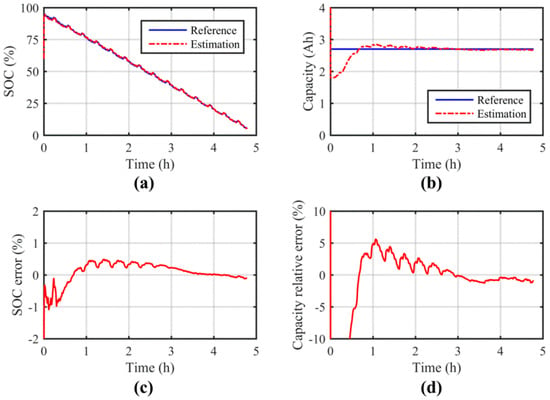
Figure 5.
Results of SOC and capacity joint estimation under the HPT simulation study: (a) estimation of SOC; (b) estimation of capacity; (c) error of SOC estimation; (d) relative error of capacity estimation.
Results of online model identification and state joint estimation under the FUDS condition are shown in Figure 6 and Figure 7, respectively. Similar to the case under the HPT condition, the proposed method shows easy convergence and high accuracy on model identification and SOC and capacity estimation.
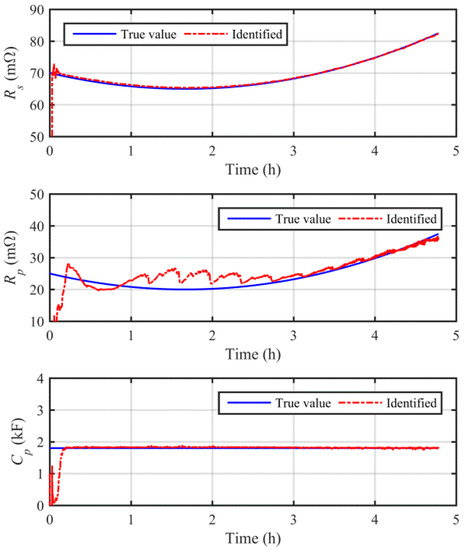
Figure 6.
Results of online model parameters identification under the FUDS simulation study.
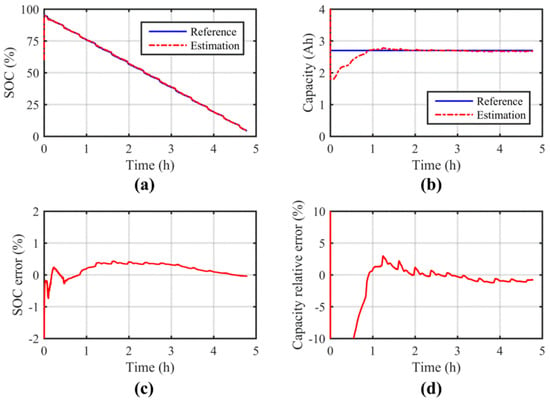
Figure 7.
Estimation results of SOC and capacity under the FUDS simulation study: (a) estimation of SOC; (b) estimation of capacity; (c) error of SOC estimation; (d) relative error of capacity estimation.
To give a quantitative evaluation for the algorithmic performance, the mean absolute error (MAE) and root mean square error (RMSE) of SOC estimation as important performance measures are summarized in Table 2, while the mean relative error (MRE) and RMSE of capacity estimation are summarized in Table 3. All the performance measures are calculated after the estimation converges to the 10% error bound in seeking to rule out the uncertain impact of the convergence process. Results suggest that the estimation is of high fidelity in terms of online estimation; thus, the theoretical feasibility of the proposed method has been confirmed.

Table 2.
Algorithmic performance on SOC estimation for the simulation study.

Table 3.
Algorithmic performance on capacity estimation for the simulation study.
5. Experimental Study
The simulation study in Section 4 is based on an ideal ECM to evaluate the proposed method from the theoretical prospective. It should be noted that the model uncertainties caused by unmodeled battery dynamics and the SOC-OCV fitting error will decrease the accuracy of both model identification and state estimation. Therefore, the proposed method is further evaluated with real experiments in this section.
5.1. Experimental Setup
Experiments are performed on a Samsung 18,650 lithium-ion battery, which has a nominal capacity of 2200 mAh. The hybrid pulse current as shown in Figure 3a is inputted to the LIB with a cell-level battery testing system, while the terminal voltage is collected accordingly. The current and voltage sensors have measurement ranges of 10 A and 5 V, respectively, while the error limits of sensing are both within 0.05%. The ambient temperature is controlled at 22 °C for all experiments. The data of interest are sampled at 1 Hz by using a data acquisition system and stored in a host computer.
5.2. Reference Data Extraction
A reference SOC profile is required to verify the result of SOC estimation. The CC method can obtain the reference SOC accurately provided that the cell can be preset to a known SOC. Therefore, the cell in use is first fully charged under the CCCV criterion. Afterwards, a constant current is applied to discharge the cell to a known initial SOC by CC. The reference SOC can then be obtained during the real experiments.
The verification of the proposed method on model identification results requires the reference values of model parameters. For this purpose, several time points are selected at a defined time interval during the HPT. A set of current and voltage signals are sampled around each time point, and then the reference model parameters can be extracted offline. In detail, Rs is calibrated by the instantaneous voltage jump following a step change of current, i.e., Rs = ΔVt/ΔI. The time constant, Rp, and Cp can be calibrated by observing both the percentile and absolute change of voltage in terms of time. However, this method is performed offline based on a certain hybrid pulse characterization. The calibrated parameters are optimal for the offline testing condition, but may deviate from real values in real experiments, as the experimental condition, especially for the current pattern, can be substantially different from the testing environment. Alternatively, in this paper, these values are determined from the pure modeling perspective by minimizing the prediction error. As OCVs can be known from reference SOCs, Rp and Cp are determined by fitting the voltage responses to real measurements. In this way, the model parameters are obtained from real experiments instead of offline testing; thus, the problem of load pattern mismatch can be avoided. The selection of the calibration method will be made on a case-by-case basis depending on the real application.
5.3. Experimental Results
Figure 8 shows the experimental results of online model identification. From the offline calibration results, it is shown that all the model parameters exhibit time-variant features, which further confirms the necessity of online model adaption to maintain sufficient modeling accuracy. To this end, the existing observing techniques with fixed battery models are theoretically less accurate due to the lack of adaptability to the variation of working conditions. By using the proposed method, it is observed that the identification converges from the initialization error and tracks the varying model parameters with reasonable accuracy. The error-prone and time-consuming model calibration can thereby be avoided with the mechanism of online model adaption.
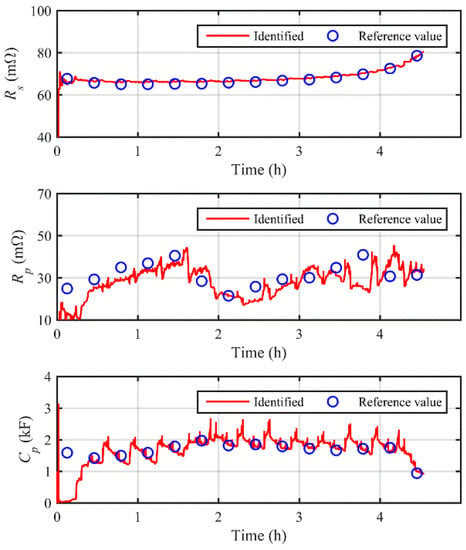
Figure 8.
Results of online model parameters identification for the experimental study.
Leveraging model update in real time, the SOC and capacity are estimated jointly and shown in Figure 9. It is shown that the estimated SOC converges very fast from the large initialization offset; afterwards, the trajectory of the reference SOC has been projected accurately with the error confined to a 1% error boundary throughout the experiment. By comparison, the estimated capacity also converges stably to the reference value, but the convergence is slower than the SOC estimation. Once the estimation converges, the capacity estimation error is well-constrained within 5%. The performance measures, including MAE and RMSE, are summarized in Table 4 to give a quantitative evaluation. Compared to the simulation results in Table 2 and Table 3, the accuracy is slightly lower but is still quite favorable in terms of online estimation. Is spite of the existence of model uncertainties in real experiments, the estimation proves to be highly accurate for both SOC and capacity.
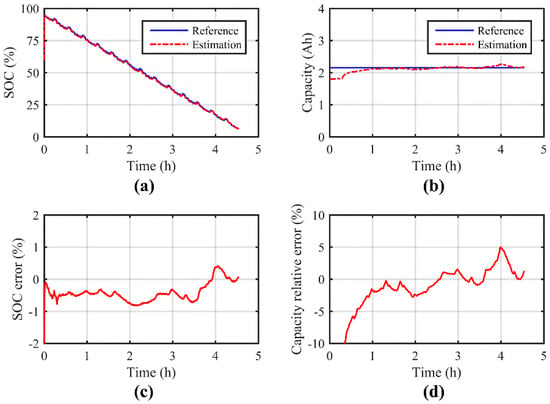
Figure 9.
Estimation results of SOC and capacity for the experimental study: (a) estimation of SOC; (b) estimation of capacity; (c) error of SOC estimation; (d) relative error of capacity estimation.

Table 4.
Algorithmic performance on SOC and capacity estimation for the experimental study.
6. Conclusions
This paper proposes a new data–model fusion method for SOC and SOH co-estimation based on an online adaptive battery model. The model parameters are online identified with the AF-RLS method to maintain high modeling accuracy and robustness. Based on the online adaptive model, a joint estimator based on OCV observation and a low-order state observer is proposed to achieve the co-estimation of SOC and capacity. Simulation and experimental results suggest that the proposed method can keep track of the model parameters effectively. The SOC and capacity estimation have also been verified to have fast convergence, high accuracy, and high stability. As a data-driven method, the proposed method online requires the onboard measured current and voltage data; thus, it has good prospects for real application in BMSs.
Author Contributions
Methodology, Z.W.; Resources, F.L. and Z.H.; Validation, Z.W., W.Z. and K.L.; Writing (original draft), Z.W.; Writing (review and editing), F.L., Z.H., W.Z. and K.L.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Torres-Moreno, J.L.; Gimenez-Fernandez, A.; Perez-Garcia, M.; Rodriguez, F. Energy Management Strategy for Micro-Grids with PV-Battery Systems and Electric Vehicles. Energies 2018, 11, 522. [Google Scholar] [CrossRef]
- Vidhi, R.; Shrivastava, P. A Review of Electric Vehicle Lifecycle Emissions and Policy Recommendations to Increase EV Penetration in India. Energies 2018, 11, 483. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, L.; Jiang, J.; Wei, S.; Liu, S.; Zhang, W. A Data-Driven Learning-Based Continuous-Time Estimation and Simulation Method for Energy Efficiency and Coulombic Efficiency of Lithium Ion Batteries. Energies 2017, 10, 597. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, D.; Mu, B.; Wang, L.Y.; Bao, Y.; Jiang, J.; Morais, H. Decentralized electric vehicle charging strategies for reduced load variation and guaranteed charge completion in regional distribution grids. Energies 2017, 10, 147. [Google Scholar] [CrossRef]
- Chen, H.; Ruckenstein, E. Nanomembrane Containing a Nanopore in an Electrolyte Solution: A Molecular Dynamics Approach. J. Phys. Chem. Lett. 2014, 5, 2979–2982. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Luo, L.; Kunal, P.; Bonifacio, C.S.; Duan, Z.; Yang, J.; Humphrey, S.M.; Crooks, R.M.; Henkelman, G. Oxygen Reduction Reaction on Classically Immiscible Bimetallics: A Case Study of RhAu. J. Phys. Chem. C 2018, 122, 2712–2716. [Google Scholar] [CrossRef]
- Wang, S.; Yang, B.; Chen, H.; Ruckenstein, E. Popgraphene: A new 2D planar carbon allotrope composed of 5–8–5 carbon rings for high-performance lithium-ion battery anodes from bottom-up programming. J. Mater. Chem. A 2018, 6, 6815–6821. [Google Scholar] [CrossRef]
- Li, H.; Henkelman, G. Dehydrogenation Selectivity of Ethanol on Close-Packed Transition Metal Surfaces: A Computational Study of Monometallic, Pd/Au, and Rh/Au Catalysts. J. Phys. Chem. C 2017, 121, 27504–27510. [Google Scholar] [CrossRef]
- Hu, X.; Zou, C.; Zhang, C.; Li, Y. Technological developments in batteries: A survey of principal roles, types, and management needs. IEEE Power Energy Mag. 2017, 15, 20–31. [Google Scholar] [CrossRef]
- Zou, C.; Klintberg, A.; Wei, Z.; Fridholm, B.; Wik, T.; Egardt, B. Power capability prediction for lithium-ion batteries using economic nonlinear model predictive control. J. Power Sources 2018, 396, 580–589. [Google Scholar] [CrossRef]
- Tang, X.; Liu, B.; Gao, F.; Lv, Z. State-of-charge estimation for li-ion power batteries based on a tuning free observer. Energies 2016, 9, 675. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Zhang, L.; Liu, S.; Wang, L.; Loh, P.C. A generalized SOC-OCV model for lithium-ion batteries and the SOC estimation for LNMCO battery. Energies 2016, 9, 900. [Google Scholar] [CrossRef]
- Zheng, L.; Zhu, J.; Wang, G.; Lu, D.D.C.; He, T. Lithium-ion battery instantaneous available power prediction using surface lithium concentration of solid particles in a simplified electrochemical model. IEEE Trans Power Electron. 2018. [Google Scholar] [CrossRef]
- Zou, C.; Manzie, C.; Nešić, D.; Kallapur, A.G. Multi-time-scale observer design for state-of-charge and state-of-health of a lithium-ion battery. J. Power Sources 2016, 335, 121–130. [Google Scholar] [CrossRef]
- Yang, X.; Chen, L.; Xu, X.; Wang, W.; Xu, Q.; Lin, Y.; Zhou, Z. Parameter Identification of Electrochemical Model for Vehicular Lithium-Ion Battery Based on Particle Swarm Optimization. Energies 2017, 10, 1811. [Google Scholar] [CrossRef]
- Tang, X.; Yao, K.; Liu, B.; Hu, W.; Gao, F. Long-Term Battery Voltage, Power, and Surface Temperature Prediction Using a Model-Based Extreme Learning Machine. Energies 2018, 11, 86. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Wei, Z.; Zou, C.; Leng, F.; Soong, B.H.; Tseng, K.-J. Online model identification and state-of-charge estimate for lithium-ion battery with a recursive total least squares-based observer. IEEE Trans. Ind. Electron. 2018, 65, 1336–1346. [Google Scholar] [CrossRef]
- Yang, S.; Deng, C.; Zhang, Y.; He, Y. State of Charge Estimation for Lithium-Ion Battery with a Temperature-Compensated Model. Energies 2017, 10, 1560. [Google Scholar] [CrossRef]
- Wei, Z.; Meng, S.; Xiong, B.; Ji, D.; Tseng, K.J. Enhanced online model identification and state of charge estimation for lithium-ion battery with a FBCRLS based observer. Appl. Energy 2016, 181, 332–341. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Liu, C.; Pan, R.; Chen, Z. Multi-timescale power and energy assessment of lithium-ion battery and supercapacitor hybrid system using extended Kalman filter. J. Power Sources 2018, 389, 93–105. [Google Scholar] [CrossRef]
- Wei, Z.; Bhattarai, A.; Zou, C.; Meng, S.; Lim, T.M.; Skyllas-Kazacos, M. Real-time monitoring of capacity loss for vanadium redox flow battery. J. Power Sources 2018, 390, 261–269. [Google Scholar] [CrossRef]
- Cui, X.; Jing, Z.; Luo, M.; Guo, Y.; Qiao, H. A New Method for State of Charge Estimation of Lithium-Ion Batteries Using Square Root Cubature Kalman Filter. Energies 2018, 11, 209. [Google Scholar] [CrossRef]
- Dong, G.; Wei, J.; Chen, Z.; Sun, H.; Yu, X. Remaining dischargeable time prediction for lithium-ion batteries using unscented Kalman filter. J. Power Sources 2017, 364, 316–327. [Google Scholar] [CrossRef]
- Huangfu, Y.; Xu, J.; Zhao, D.; Liu, Y.; Gao, F. A Novel Battery State of Charge Estimation Method Based on a Super-Twisting Sliding Mode Observer. Energies 2018, 11, 1211. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, C.; Chen, Z. A method for state-of-charge estimation of LiFePO4 batteries at dynamic currents and temperatures using particle filter. J. Power Sources 2015, 279, 306–311. [Google Scholar] [CrossRef]
- Zhao, L.; Ji, G.; Liu, Z. Design and Experiment of Nonlinear Observer with Adaptive Gains for Battery State of Charge Estimation. Energies 2017, 10, 2046. [Google Scholar] [CrossRef]
- Waag, W.; Fleischer, C.; Sauer, D.U. Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles. J. Power Sources 2014, 258, 321–339. [Google Scholar] [CrossRef]
- Duong, V.-H.; Bastawrous, H.A.; Lim, K.; See, K.W.; Zhang, P.; Dou, S.X. Online state of charge and model parameters estimation of the LiFePO4 battery in electric vehicles using multiple adaptive forgetting factors recursive least-squares. J. Power Sources 2015, 296, 215–224. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.; Sun, F.; Zhao, K. Evaluation on state of charge estimation of batteries with adaptive extended Kalman filter by experiment approach. IEEE Trans. Veh. Technol. 2013, 62, 108–117. [Google Scholar] [CrossRef]
- Hu, C.; Youn, B.D.; Chung, J. A multiscale framework with extended Kalman filter for lithium-ion battery SOC and capacity estimation. Appl. Energy 2012, 92, 694–704. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.; Chen, Z.; He, H. A data-driven multi-scale extended Kalman filtering based parameter and state estimation approach of lithium-ion olymer battery in electric vehicles. Appl. Energy 2014, 113, 463–476. [Google Scholar] [CrossRef]
- Dong, G.; Chen, Z.; Wei, J.; Zhang, C.; Wang, P. An online model-based method for state of energy estimation of lithium-ion batteries using dual filters. J. Power Sources 2016, 301, 277–286. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, F.; Gong, X.; Gao, C. A data-driven based adaptive state of charge estimator of lithium-ion polymer battery used in electric vehicles. Appl. Energy 2014, 113, 1421–1433. [Google Scholar] [CrossRef]
- Wei, J.; Dong, G.; Chen, Z. On-board adaptive model for state of charge estimation of lithium-ion batteries based on Kalman filter with proportional integral-based error adjustment. J. Power Sources 2017, 365, 308–319. [Google Scholar] [CrossRef]
- Xia, B.; Lao, Z.; Zhang, R.; Tian, Y.; Chen, G.; Sun, Z.; Wang, W.; Sun, W.; Lai, Y.; Wang, M. Online parameter identification and state of charge estimation of lithium-ion batteries based on forgetting factor recursive least squares and nonlinear Kalman filter. Energies 2017, 11, 3. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, J.; Ji, D.; Tseng, K.J. A multi-timescale estimator for battery state of charge and capacity dual estimation based on an online identified model. Appl. Energy 2017, 204, 1264–1274. [Google Scholar] [CrossRef]
- Wei, Z.; Tseng, K.J.; Wai, N.; Lim, T.M.; Skyllas-Kazacos, M. Adaptive estimation of state of charge and capacity with online identified battery model for vanadium redox flow battery. J. Power Sources 2016, 332, 389–398. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J.; Lee, J.; Cho, B.H. State-of-charge and capacity estimation of lithium-ion battery using a new open-circuit voltage versus state-of-charge. J. Power Sources 2008, 185, 1367–1373. [Google Scholar] [CrossRef]
- Hua, Y.; Cordoba-Arenas, A.; Warner, N.; Rizzoni, G. A multi time-scale state-of-charge and state-of-health estimation framework using nonlinear predictive filter for lithium-ion battery pack with passive balance control. J. Power Sources 2015, 280, 293–312. [Google Scholar] [CrossRef]
- Zou, Y.; Hu, X.; Ma, H.; Li, S.E. Combined state of charge and state of health estimation over lithium-ion battery cell cycle lifespan for electric vehicles. J. Power Sources 2015, 273, 793–803. [Google Scholar] [CrossRef]
- Zheng, L.; Zhang, L.; Zhu, J.; Wang, G.; Jiang, J. Co-estimation of state-of-charge, capacity and resistance for lithium-ion batteries based on a high-fidelity electrochemical model. Appl. Energy 2016, 180, 424–434. [Google Scholar] [CrossRef]
- Fortescue, T.; Kershenbaum, L.S.; Ydstie, B.E. Implementation of self-tuning regulators with variable forgetting factors. Automatica 1981, 17, 831–835. [Google Scholar] [CrossRef]
- Cordero, A.O.; Mayne, D. Deterministic convergence of a self-tuning regulator with variable forgetting factor. In IEE Proceedings D-Control Theory and Applications; IET: London, UK, 1981; pp. 19–23. [Google Scholar]
- Xia, B.; Zhang, Z.; Lao, Z.; Wang, W.; Sun, W.; Lai, Y.; Wang, M. Strong Tracking of a H-Infinity Filter in Lithium-Ion Battery State of Charge Estimation. Energies 2018, 11, 1481. [Google Scholar] [CrossRef]
- Shen, X.-M.; Deng, L. Game theory approach to discrete H/sub/spl infin//filter design. IEEE Trans. Signal Process. 1997, 45, 1092–1095. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).