Abstract
In view of the advancement of zero emission transportation and current discussions on the reliability of nominal passenger car fuel economy, this article considers the procedure for assessing the potential for reducing the fuel consumption of passenger cars by using electric power to operate them. The analysis compares internal combustion engines, hybrid and fully electric concepts utilizing batteries and fuel cells. The starting point for the newly developed, simulation-based fuel consumption analysis is a longitudinal vehicle model. Mechanical power requirements on the drive side incorporate a large variety of standardized drive cycles to simulate typical patterns of car usage. The power requirements of electric heating and air conditioning are also included in the simulation, as these are especially relevant to electric powertrains. Moreover, on-board grid-load profiles are considered in the assessment. Fuel consumption is optimized by applying concept-specific operating strategies. The results show that the combination of low average driving speed and elevated onboard power requirements have severe impacts on the fuel efficiency of all powertrain configurations analyzed. In particular, the operational range of battery-electric vehicles is strongly affected by this due to the limited storage capacity of today’s batteries. The analysis confirms the significance of considering different load patterns of vehicle usage related to driving profiles and onboard electrical and thermal loads.
1. Introduction
Climate change and the corresponding imperative to reduce carbon dioxide (CO2) emissions, locally active pollutants, dependence on imported raw energy materials, as well as economic and technological competitiveness, are seen as global driving forces of the sought-after change in energy technology. Worldwide, around 17% of all greenhouse gas emissions are caused by road traffic, with some 61% of these being attributable to passenger cars [1]. Moreover, this is underpinned by strong dependence on imported crude oil, with more than 90% of fuels for road traffic being produced from this. In the mid to long term, the electricity surplus from renewable energy sources could be made usable for road traffic. Hydrogen produced via electrolysis could be stored on an industrial scale and used as a fuel for electric powertrains with highly efficient fuel cells. Significant advantages over advanced internal combustion engines (ICEs) using gasoline and diesel can already be discerned today.
Passenger cars with fuel cells (fuel cell-electric vehicles, FCVs) will, in future, compete with advanced ICVs (internal combustion engine vehicles), hybrid electric vehicles (HEVs) based on ICE, as well as battery-electric vehicles (BEV). Overall, a multitude of powertrain variants are conceivable, which can be distinguished by the way in which they use electrical energy. In the following, four drive concepts are selected and assessed via dynamic simulations based on various combinations of the load spectra of the powertrain and on-board power system.
1.1. Simulation-Based Fuel Consumption Analysis
Numerous studies pertain to fuel consumption analyses or optimizations regarding individual, sometimes technically-realized, passenger car concepts, or that conduct comparative assessments of different concepts. Table 1 displays a selection of these. Typically, comparative assessments of passenger car powertrains take the approach of simulation-supported tank-to-wheel (TTW) analyses as part of a well-to-wheels (WTW) assessment framework. Relevant analyses have been performed on FCVs by Brown et al. [2] and Kisacikoglu et al. [3], on FCVs and BEVs by Campanari et al. and on HEVs by Li et al. [4], Mansour et al. [5] and Varnhagen et al. In a broader context, Gupta et al. [6] and Kromer et al. [7] conducted comparative assessments of different conventional and alternative powertrains. One of the most comprehensive studies, however, is the well-to-wheels assessment in JEC [8], which provides a very large spectrum of vehicle and fuel combinations.

Table 1.
Simulation-based fuel consumption analysis—literature overview. Simulation platform: Matlab/Simulink® (release R2013a, The Mathworks, Inc., Natick, MA, USA) (unless otherwise stated); ANL: Argonne National Laboratory (USA); APU: auxiliary power unit; EPRI: Electric Power Research Institute (USA); FCV: fuel cell vehicle, including hybrids (considered here only in direct hydrogen operation mode); FTP: Federal Test Procedure; HEV: hybrid electric passenger car as a parallel (PAH), series (SEH) or power-split hybrid (PSH); HWFET: Highway Fuel Economy Test; ICV: passenger car with internal combustion engine; NREL: National Renewable Energy Laboratory (USA); PHEV: plug-in HEV.
A simulation package that has frequently been used for tank-to-wheel fuel economy analysis is the Advanced Vehicle Simulator ADVISOR (National Renewable Energy Laboratory, Golden, CO, USA) [9], although this is no longer available. Examples of its application can be found in JEC [8], Kisacikoglu et al., Kromer et al. [7] and Li et al. [4].
From the literature overview outlined in Table 1, it can be concluded that the comparability of results from fuel economy assessments is not optimal, as the studies are, in some cases, based on different vehicle classes and drive cycles. Moreover, on-board power loads are generally considered constant. In reality, however, they vary over time as engine-independent consumers are affected by factors such as the actual driving situation and are expected to increase for more electrified powertrains. For this reason, the task of this assessment was to develop an analytical tool with standardized parameter definitions and simulation, as well as optimization approaches. The target was to provide an improved possibility of comparatively assessing passenger car drive concepts that use varying levels of electric power for the powertrain and on-board power system. Standardized definitions and procedures are particularly applicable to:
- Passenger car characteristics: external parameters specific to vehicle classes;
- Consumers of the on-board power system and their time-dependent load profiles;
- Approaches to scaling drive components;
- Fuel consumption-optimized operating strategies.
Special attention is given to the use of varying driving cycles, which are classified into urban, rural and highway driving, as well as detailed observations of on-board power demand. The calculations are performed for passenger cars within parameters typical of the A- and C-segments. The applied operating strategies follow a standardized approach, despite the varying degrees of freedom due to the different drive concepts. Scaling “routines” are developed in order to scale the powertrain components, including the determination of vehicle mass. A full-scale analysis can be found in Grube [22]. It should be noted that the operational strategies developed here need to be applicable to a variety of powertrain concepts, and therefore cannot consider more specific optimization constraints that are the subject of real-world developments for specific vehicles, such as detailed component characteristics, robustness with regard to the full scale of environmental and road conditions or even degradation effects. Such aspects are the subject of highly-specific research efforts with advanced development and implementation methods.
1.2. Use of Electrical Power in Passenger Car Drive Concepts
In this article, four drive concepts for passenger cars are considered that differ in their manner of generating and using electricity. As a comparative concept, a conventional powertrain utilizing an internal combustion engine (ICV) is included in the analysis. Table 2 shows the drive topologies of the concepts analyzed.

Table 2.
Passenger car concepts and drive topologies. The pictograms of the drive topologies include only the main energy flows of the drive; auxiliary consumers are disregarded in this representation. Symbols are adapted from Isermann [23].
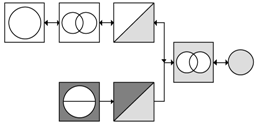
Using the example of a parallel hybrid-electric vehicle (PAH), the energy flows considered are outlined in Figure 1. Mechanical power is provided by an internal combustion engine (ICE) and electric machine (EM), assuming a single-shaft hybrid. Both devices exert power on the gearbox input shaft, but the ICE can be uncoupled from the drivetrain.

Figure 1.
Simplified schematic of the parallel hybrid drive PAH. Line losses (which were taken into consideration in the simulation) are not depicted here; DP: drive power, AC: air conditioning, AT: axle drive, BT: battery, CP: cooling power, DC: DC converter, EM: electric machine, FT: fuel tank, GB: gearbox, HP: heat power, HT: heating element, ICE: internal combustion engine, OG: 14 V on-board power system.
With the aim of optimizing fuel consumption, the operating strategy (also taking into consideration the on-board power demand) determines the mode of operation and respective torques of the ICE and EM. Typical consumers using 14 V on-board power systems and vehicle air conditioning devices powered by high-voltage, on-board systems are included as auxiliary consumers. A list of auxiliary consumers considered in this study is provided in Table 3. Depending on the operating state of the ICE, thermal energy can be used to heat the vehicle interior. Torque losses in the gearbox and DC converter are taken into account as transmission losses. Here, the ICE and EM are depicted as characteristic curve diagram models.

Table 3.
Electric power requirement of auxiliary consumers. Values in ; Sources: [24,25,26,27,28,29] C: continuous operation; D: demand-driven operation; f/r: front/rear; N.A.: not applicable; PTC: Positive temperature coefficient.
2. Methodology
The following section describes the methodology utilized for determining the fuel consumption of the powertrain alternatives considered in this study. As well as the definitions of parameters relating to the vehicle body that are relevant to the powertrain component scaling, details on how component simulation models and optimizing strategies are implemented are outlined.
2.1. Energy Balance and Scaling the Drive Components
The drive torque is established by applying a longitudinal vehicle model based on determining the resisting forces that characterize each state of motion. For a dynamic simulation, the tractive power equation is used in the integral form so that the vehicle’s velocity can be given as a function of the time-dependent wheel torque, MR. Rolling resistance is included in the calculation as a function of velocity. In order to take into consideration the rotating masses to be accelerated, additional rotating mass factors are also calculated. Additional vehicle parameters for passenger cars of the A- and C-segments are listed in Table 4. Due to the smaller masses and reference areas of A-segment cars, the wheel torques—and therefore drive power—necessary to achieve the same driving performance are also smaller.

Table 4.
Parameters of the A- and C-segment passenger cars investigated. These values are based on the mean values of current A- and C-segment production cars equipped with standard engines (author’s own research). The mass of the basic vehicles does not include the drive or fuel tank [31,32,33].
Specially developed scaling routines are used for the automated scaling of powertrain components, permitting the iterative determination of the engine’s necessary power output and mass by shifting the engines’ torque curve of ICEs and EMs. In order to determine the masses, the values of the engines’ specific power outputs are applied. Drawing on information presented in JEC [8] and Li et al. [4], 0.58 kW kg−1 approximates direct fuel injection gasoline engines, 0.51 kW kg−1 direct fuel injection diesel engines and 1.0 kW kg−1 for electric machines. The storage capacity of BEVs is determined in accordance with their range and that of PAHs as a function of regenerative braking energy. Using the specific energy—assumed here to be 100 Wh kg−1—the battery mass can be determined. The drive performance requirements to be fulfilled are listed in Table 5. The determination of ranges for BEVs and FCVs is based on the European standard driving cycle MVEG.

Table 5.
Driving performance requirements for A- and C-segment passenger cars for the scaling of drives. corresponds to a maximum slope of 50%; the values in brackets are applied to BEVs.
Driving cycles used to determine fuel consumption can be classified into urban, rural and highway driving. Standardized cycles usually include sub-cycles that encompass relevant usage patterns. For the simulations in this study, a total of 25 driving cycles are presented, with an excerpt to be found in Table 6 (the full list is available in Table A2 in the Appendix A). This table lists the mean velocities and positive and negative mechanical energy consumption values for the HYZEM driving cycle and its sub-cycles. The values are based on a C-segment passenger car with specifications as listed in Table 4 and a vehicle mass of 1373 kg. The values show that for these driving cycles, the positive mechanical energy consumption increases with rising mean velocity while, in contrast, the energy potentially available for regenerative braking decreases. A full list is available in the appendix.

Table 6.
Characterization of driving cycles used. The mechanical energy consumption is given for positive and negative tractive forces. A total of 25 drive cycles were used for the analysis.
2.2. Dynamic Simulation
The dynamic simulation models used here were developed in the software environment Matlab/Simulink® using theoretical, as well as curve-diagram-based and curve-based model components. The driver and powertrain form a control loop, in which the driver represents the controller.
The parameterization of the models is affected across three stages by specifying:
- Globally-applicable constants;
- Vehicle class-specific parameters; and
- Characteristic values of the model components.
Based on the parameters defined in this way, concept-specific calculations, for instance to determine the gear ratios or the vehicle’s mass, are performed. Additionally, full-load simulations are applied for the automated, program code-based scaling of the powertrain components. Acceleration performance and maximum velocity are determined and correlated with the requirements given in Table 5, using an iteration method. Shifting the torque curve permits the powertrain’s performance to be adapted.
The operational strategies are implemented as deterministic online strategies that identify and select points of component operation for minimum fuel consumption. As a constraint, a battery’s state of charge must be kept in a range of 55–65%. Adaptive or predictive elements were not included in the operational strategies.
For the powertrain, curve diagrams describing the performance of ICE (adapted from Rhode-Brandenburger [34] and Gossen [35]) and EM (adapted from Rodatz [36]) are used, in addition to the physical wheel-road model. Engine warm-up and its effect on fuel consumption and efficiency, respectively, was not considered.
In PAHs and BEVs, the electric machine also generates electricity: in BEVs only during regenerative braking, in PAHs also as part of temporary load point elevations controlled by the operating strategy. In ICVs, electricity is generated by a three-phase generator (alternator) that is also represented by a curve diagram in the model. For the ICV and PAH cases, the drive engines exert their power on the drive axle via a six-speed gearbox. Selecting the gear is part of the operating strategy.
Electrical power for the powertrain is provided by batteries in BEVs and PAHs and fuel cells and batteries in FCVs. The representation of batteries is based on an equivalent circuit diagram consisting of ideal electrical components (see Figure 2). The parameters of the state-of-charge-dependent resistances and capacitances of individual cells are adapted from Chen [37]. Scaling is undertaken through the serial and parallel connection of battery cells.

Figure 2.
Battery model for the simulation. Equivalent circuit diagram to visualize the dynamic operation behavior of a li-ion battery (adapted from Chen et al. [37]). One serial resistor in the series to one RC element with long time constants (minutes range “L”) and one RC element with short time constants (seconds range “S”) according to Chen et al. [37].
The model component for a fuel cell system is shown as a schematic in Figure 3. The current-voltage characteristics of the fuel cell stack are represented by characteristic curves (Kromer et al. [7]) Mass and heat balances are taken into consideration in order to determine the compression and expansion work on the air side, on the one hand, and the available heat, on the other. If required, the latter decreases the thermal power needed to heat the vehicle interior (see below).

Figure 3.
Electricity generation system with low-temperature fuel cells (PEFCs). Hum.: humidifier; Cds.: condensation trap; Cab.: vehicle interior heating; Pump: coolant pump; Comp.: compressor; Cooler: air cooler; PEFC: polymer electrolyte fuel cell; Turb.: turbine.
In order to determine on-board power requirements, auxiliary consumers are factored in a time-constant manner and operated in defined cycles. The electric power requirements of the air-conditioning for the vehicle interior are determined as a dynamic load by a simplified thermal model whose input parameters include vehicle velocity and environmental conditions such as the position of the sun. The thermal flows analyzed are shown in Figure 4. Parameterization and velocity-dependent heat transfer coefficients in particular draw on the work in Großmann [38] and Konz et al. [39]. For the simulated C-segment passenger car, this model allows for a maximum heating capacity of 4.3 kW and cooling capacity of 2.2 kW to be specified. These values are determined for a vehicle velocity of 18 km h−1 and −15 °C when heating and 36 °C when cooling, and—with 0.2 kW and 0.1 kW—only differ slightly from those specified in Jung et al. [40].

Figure 4.
Simplified thermal model of the vehicle interior and designation of the heat flows considered. Source: author’s own illustration, adapted from Konz [39].
In this study, three cases are defined that consider different ambient conditions relevant to interior heating and cooling. Table 7 gives the corresponding definitions. Here, it is assumed that the cabin is occupied by a single person. The cabin temperature is calculated as the average temperature of the inlet and outlet air. Mass flow and the temperature of the air inlet are also affected, controlling the cabin temperature.

Table 7.
Cases analyzed regarding interior heating and cooling. The ambient temperature of the cases SUD (summer day) and FRD (frost day) is defined in accordance with climatologic reference days from Germany’s national meteorological service, Deutscher Wetterdienst [41]. Further parameters are: ambient pressure: pamb = 1.013 bar, solar azimuth angle: ψsol = 45° (related to driving direction) and solar zenith angle: φsol = 60°.
2.3. Optimizing Operating Strategies
Depending on the vehicle concept, there are various possibilities for influencing engine operating points to optimize the entire system. In the case of ICVs, the choice of gear permits a shift of engine operating points (operating point shift, OPS) in conjunction with the power hyperbola.
For PAHs, the ICE operating point cannot only be elevated or reduced by varying the gears, but also by changing the torque of the electric machine. In this way, the hybrid functions of the operating point shift (OPS) and load point elevation (LPE) and load point reduction (LPR) can be realized. By adding an EM torque at maximum ICE load, the overall torque of the drive is increased (boost function). During braking phases, PAHs, BEVs and FCVs use braking energy to charge the battery or provide on-board power (regenerative braking). A summary of all functions available for each concept examined is presented in Table 8.

Table 8.
Functionalities of vehicle concepts analyzed. Pure internal combustion engine (ICE) driving, battery-electric (BE) driving, load point elevation (LPE), load point reduction (LPR) and operating point shift (OPS) are chosen in this work as the names of functions and are adapted from Hofmann [42].
The functions are controlled on the basis of operating strategies developed for the concepts studied here, whose aim is to optimize fuel consumption. Additional aspects, such as the drivability of the car and acoustics were not considered due to the objective of the analysis (potential analysis). The optimization methods are based on immediately available system parameters. The approach here can be defined as instant-analytic. Supplementary heuristic rules are applied to control the battery’s state of charge in PAHs and FCVs, which constrain the operating strategy’s range of optimization.
The optimization procedure is based on resolving the degrees of freedom into option vectors whose elements are assessed at each time interval with regard to adhering to the operating range of the powertrain components and are evaluated in terms of energy use. The term option vector refers to the value range of a parameter defined as a degree of freedom. Examples include the gear vector with five elements and the torque vector of the electric machine with n elements, for which the following applies: MEM,min ≤ MEM,n ≤ MEM,max.
The vector element leading to the lowest fuel consumption is used to derive control parameters for the powertrain components. Since hybrid concepts temporarily store energy from the LPE, but the operating states of powertrain components at the time of use of this energy are not known a priori, some of the respective efficiencies must be estimated.
Approaches to operating strategies that are documented in the literature often consider a specific prototype car or powertrain topology. A selection of relevant developments is summarized in Table 9. The typical goal of the developments is to reduce fuel consumption, which is partly supplemented by criteria relating to tail gas emissions [43] or drivability [44]. The practical implementation of evaluation functions could also aim to minimize power losses [43,44,45] or specific cost functions [46]. Altenthan [44] derives a heuristic operational strategy from an analytical online evaluation function. This operational strategy is then applied to a two-mode hybrid SUV (sports utility vehicle).

Table 9.
Overview of studies related to the development of operational strategies.
Böckl [48] developed adaptive predictive energy management strategies based on past electrical power data. These are used to predict power demands in the near future, yielding a defined set of points for load variation in the engine. In order to control the battery state of charge, hybrid functions are set in such a way that the SOC is kept within a specified range. In the predictive mode of the operational strategy, the SOC is dynamically adjusted, e.g., the SOC is decreased before the car reaches a descending section of road. Kleimaier [43] and Jörg [45] take the sum of power losses as the function to minimize. Both studies consider a parallel hybrid car with a continuously variable transmission. Kleimaier [43] uses a weighing factor for controlling the battery SOC via the load point variation of the engine. This factor affects the evaluation function and, thereby, the engine’s set point. Examples of heuristic, Fuzzy Logic Controller (FLC)-based operating strategies can be found in Li et al. [4] and Schouten et al. [17], where they are applied to parallel hybrids. Moreover, Kisacikoglu et al. [3] and Eren et al. [49] employ FLC-based approaches for FCVs that are hybridized with ultra-capacitors.
This study aims at a consistent approach to all concepts under consideration that is easily applicable and robust with regard to adjustments made to component scaling. Heuristic strategies appear not to be practical for this purpose, because the required rules entail substantial efforts for readjustment when powertrain parameters are changed. For this reason, analytical optimization strategies are used. Simplified heuristic rules are only used for controlling the SOC. The optimization function considers fuel efficiency, which is to be maximized. The general equation for this is:
The manipulated variables are engine torque, gear selection and the selected mode of operation. Priority is given to the fulfillment of the driver’s demands with respect to the vehicle’s state of motion. Depending on velocity, the battery’s target state of charge (SOC) is varied between 0.55 and 0.65 in order to control how much energy from regenerative braking can be utilized. The operating range of optimized fuel consumption is set to ±5% points of the target SOC. Within this range, hybrid functions are not limited. If the limits of this operating range are reached, a linear function is used to increasingly prioritize charging (when the SOC is low) or discharging (when the SOC is high) of the battery.
The simplified program plan illustrated in Figure 5 shows the structure of the simulation models and highlights the fact that the dynamic model of the powertrain is supplemented by further dynamic and quasistatic models.
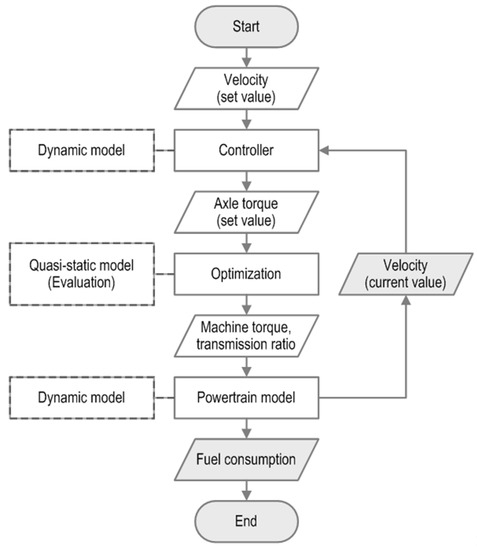
Figure 5.
Structure of the simulation models, represented as a simplified program plan.
The optimization algorithm utilized in this study builds on discretized parameters of powertrain operation, e.g., torque at the gearbox input shaft—a similar approach was followed in Back [47]. For this purpose, parameters are selected that offer variability with respect to fuel economy optimization while maintaining driving performance:
- Transmission ratio (gear) for all concepts;
- EM and ICE torque for PAH;
- Fuel cell system power for FCV.
The discretized parameters are then tested regarding compliance with the component-specific operational limits. The subset of valid elements is, consequently, used for identifying ICE, EM or fuel cell system set-points for optimized fuel economy.
The simplest case exists for ICVs and BEVs, where the optimization strategy chooses one out of z transmission ratios (gears). In this study, z is six for the ICV and PAH and two for the electric powertrains in the BEV and FCV. Selecting the highest gear possible results in better fuel economy in most driving scenarios.
For PAHs, the situation is more complex, because in addition to the transmission ratio, the continuous parameters of engine torque, as well as the torque of the electric machine (EM), can vary. Within the operational limits, the engine torque could be elevated (LPE) or reduced (LPR) for optimized fuel economy. EM torque is then adjusted so that the required gearbox input torque is realized. In hybridized FCV powertrains, the fuel cell system’s power can be varied with the battery SOC as a constraint in order to optimize overall fuel economy.
In the PAH and FCV cases, appropriate discretization methods must be identified. The following vectorized parameters are defined in this work:
(i) Vector of optional gearbox input torques for all concepts:
where : vector of options; : at gearbox input shaft, : gear (; ); : number of gears.
This vector contains torque values that are derived from the actual driving torque according to the driving situation: accelerating, constant velocity or decelerating. At this stage, the engine limits are disregarded.
(ii) Vector of optional rotational speeds at gearbox input for all concepts:
where : vector of options; : at gearbox input shaft, : gear (; ); : number of gears.
The elements of this vector are strictly bound to the actual velocity via the transmission ratios.
(iii) PAH-specific, the vector of optional EM torques:
where : electric machine; : minimum value; : maximum value; vector resolution.
This vector covers the full EM range of torque, disregarding the machine’s operational limits. The resolution of this vector is set at .
(iv) PAH-specific, the vector of optional ICE torques:
Based on the vector definitions specified in Equations (2) and (4), this vector holds optional torque values of the ICE, again disregarding the engine’s operational limits.
(v) FCV-specific, the vector of optional fuel cell system power levels:
where : fuel cell system; : lower and upper limits of the operational range.
Covering the full range of the fuel cell system’s power, this vector provides values that are evaluated in the optimization strategy. The step size of this vector of options is set at 1 kWe.
In addition to every vector of options, an additional vector of the same dimension is defined for logical statements with Boolean-type elements. If such an element carries the value of 0, the corresponding element in the vector of options is not a valid option, e.g., it is outside the component’s operational range. These vectors are defined as:
The value range of the option vectors, in accordance with Equations (2)–(6), is initially tested within the component’s operational limits. The subset of valid vector elements is then delivered to the energy balancing and the optimal control parameters are derived. With respect to concept-specific degrees of freedom, one-dimensional (ICV, BEV and FCV) and two-dimensional (PAH) problems must be resolved. Examples of the option vectors are given in Figure 6 for the PAH case. The upper diagram shows the optional torques at the gearbox’s input shaft. These depend on the specific transmission ratios of the six gears. The lower diagram in Figure 6 represents the optional torques of the EM during the first 70 s of the EUDC driving profile. The values in the negative range refer to the generator mode and comply with the hybrid functionality of load point elevation (LPE). Positive values denote EM motor operation. The bold line represents the torque in pure EV mode while the IC engine is shut off. This mode is not possible in the time range of 57 s to 62 s, because the required torque is then outside the operational limits of the EM.

Figure 6.
Left: EUDC-related optional torques at gearbox input for all gears (before testing against operational limits). Right: optional EM torques of the first gear (first 70 s of EUDC only). Calculations using C-segment PAH with SI engine.
Making use of the option vectors, the energy input requirement of the powertrain components can be determined. Also considering onboard electric consumers and heat requirements, the energy balances are set up according to Equations (8)–(13), returning the fuel efficiency for each time step and for each gear. While ICVs and BEVs only require z (number of gears) calculations, for PAH options must be evaluated, with comprising the number of elements of the option vector :
where e, electrical; m, mechanical; th, thermal; ch, chemical; aux, auxiliary; batt, battery; cab, cabin (passenger compartment); dch, discharge; del, delayed use; dir, direct use; EM, electric machine; GB, gear box input; ICE, internal combustion engine; pgen, power generation; pt, powertrain.
Based on these calculations, gear selection can be optimized (all concepts), as well as the set points for EM, IC engine (PAH) and the fuel cell system (FCV). Additionally, PAHs and FCVs require the analysis of the charge-discharge cycle of the battery for cases where electricity is taken from the battery or delivered to it for later use.
In order to control the brake energy recovery, the gearbox input torque and speed are used to evaluate the available electric power for each gear. Ideally, the gear with the maximum electric power available is selected. As this would lead to high engine speeds, the evaluation function is again biased, prioritizing gears with input speeds close to the medium speed range.
2.4. Fuel Economy Assessment
Bringing together the two vehicle segments and 25 drive cycles considered in this study, as well as a total of four load cases, as shown in Table 10 (three cases according to Table 7 plus the “base-load only case”, BSL) integrating electrical and thermal loads, an assessment matrix was defined according to Table 11. Included here are the additional load cases, BSL (“base load only”), that exclusively considers the auxiliary consumers required for operating the vehicle and NHC (“no heating or cooling”) that considers additional 14 V consumers for comfort and safety, but with no heating or cooling. The load case SUD (summer day) is not considered for the ICV, because the cabin temperature cannot be controlled in the same way as for PAHs, BEVs and FCVs. Moreover, the assessment matrix is applied for the two scenarios “Standard” and “Advanced” aimed at considering development progress related to improved component performance and reduced driving resistances. Details are shown in Table 12.


Table 11.
Matrix of fuel economy assessments of passenger car concepts considered. Definition of BSL (“Baseload only”), NHC (“No heating and cooling”), FRD (“Frost day”) and SUD (“Summer day”) cases see Table 10; ICV: internal combustion engine vehicle; PAH: Parallel hybrid; BEV: Battery electric vehicle; FCV: Fuel cell electric vehicle; G: Gasoline; D: Diesel; For a specification of car segments, see Table 4.

Table 12.
Assumptions related to the calculation scenarios “Standard” and “Advanced”.
For every car concept, a total of 25 fuel economy calculations per load case is required, resulting in 300 calculations for ICV, 400 for PAH and 200 for the BEV and FCV, respectively. Simulation runs are repeated so as to achieve a balanced battery SOC at the end of the drive cycle.
In preparation for the fuel economy calculations, component scaling is carried out in semi-automated procedures, ensuring that the performance targets defined in Table 5 are complied with. This yields concept-, segment- and scenario-specific vehicle masses that are shown in the Appendix A, Table A3. Moreover, the power class of the ICEs and EMs is given in the table. Due to the additional weight of storage and fuel cell systems, FCVs have the highest mass. However, the reduced operational range and maximum speed of the BEV must be taken into account.
The results of fuel economy calculations will be presented here as MJ km−1 for the full range of results and, specifically, for the drive cycles MVEG and WLTC, including their sub-cycles. More detailed values for all driving cycles can be found in Grube [22].
3. Results and Discussion
Figure 7 summarizes the calculation results for all cases, related to the scenario “Advanced” as box plots. Values for the “Standard” scenario are displayed in the Appendix A, Figure A1. A figure with all values from the present analysis can be found in the Appendix A, Figure A2, as well as concrete values of the MVEG und WLTP drive cycles, also including their sub-cycles, Table A4, Table A5, Table A6 and Table A7. The largest spread of results can typically be seen for the urban drive cycles. Here, the largest consumption figures are doubled or even tripled compared to the lowest values. The highest fuel consumption corresponds to the drive cycles with the lowest average speed, “Artemis urban” and “MODEM slow-urban” for those load cases with high auxiliary loads (“Frost day”, FRD and “Summer day”, SUD). For drive cycles with higher average speed, fuel consumption is, as expected, less sensitive to auxiliary load. For the two concepts, BEV and FCV, it should be noted that even though the absolute consumption values are lowest, the deviation from nominal consumption (comparable here to the load case, “Base load only”, BSL) is more severe than for the other concepts. As energy storage is limited on the basis of storage mass, volume and cost—increased fuel consumption considerably limits the operational range. An extreme example is the electric energy demand of 125 MJ (100 km)−1 (35 kWh (100 km)−1) for the C-segment BEV in the “Standard” scenario and the load case FRD for the “MODEM slow-urban” drive cycle. With a battery capacity of 48 kWh, the operational range decreases to less than half of the design value.

Figure 7.
Results of the fuel economy analysis according to all concepts and onboard load cases related to the “advanced” scenario, for (a) A-segment and (b) C-segment cars. Values are displayed as box plots related to the cycle groups of urban, extra-urban, freeway and combined with (from below): minimum, third quartile, median, first quartile and maximum. A similar figure with values related to the “standard” scenario is available in the Appendix A, Figure A1.
A validation of the results from fuel economy calculations was not possible within the parameters of this study. In order to provide a better orientation, selected values from the literature, drawing on Kromer et al. [7] and JEC [8], both on the basis of the simulation tool ADVISOR (see Table 1), are used for comparison.
Figure 8 depicts the range of results from the fuel economy calculations conducted in this study and also data from the literature. Due to differences in the vehicle parameters, component characteristics, drive cycles and time horizon, the results are not fully comparable. Values drawn from Kromer et al. have been calculated on the basis of the Combined Adjusted drive cycle, which is comprised of the two driving patterns, US FTP and HWFET, have been used separately in the present study. Moreover, Kromer et al. did not specify auxiliary consumers of the onboard grid. According to JEC [8], the fuel economy results apply to the MVEG drive cycle and a constant auxiliary load of 300 We, which is lower than in this study. Values derived from Kromer et al. show the highest degree of comparability with the MVEG-based results in the scenario “advanced” for the load case BSL, which are on display as hatched circles in Figure 8. In comparison to Kromer et al., the fuel economy figures for ICV are slightly elevated in the case of the gasoline engine and slightly lower in the case of the diesel engine. For BEVs, reduced driving resistances, particularly related to the low vehicle mass of 1193 kg, compared to the 1620 kg reported by Kromer et al., resulted in lower electric energy consumption in this study. The respective values listed in JEC are somewhat lower than those in the present study, with the exception of the parallel hybrid with a diesel engine. As JEC reports, the FCV shows considerably lower fuel consumption. This is primarily due to the higher fuel cell system efficiency, peaking at slightly above 60%. In the present study, the maximum fuel cell system efficiency is 55%. The results of the present study are, however, in accordance with those of Kromer et al. A more detailed comparison is, however, not possible because detailed simulation results are currently lacking. Consequently, Figure 8 shows that fuel consumption figures for MVEG—which is typical for drive cycles integrating urban and extra-urban driving—are in the mid to lower range of the overall range of results. Higher fuel consumption occurs during city driving and, in particular, in cases with high onboard electric power demand.

Figure 8.
Comparison of results with data from the literature. The range of values accord to the fuel economy calculations for the scenario, “advanced”. Selected values apply for the MVEG drive cycle considering the cases, “Frost day” (FRD), “No heating & cooling” (NHC) and “Base load only” (BSL). For definitions, see Table 10. Values from the literature correspond to JEC [8] in the configuration “2010+” and Kromer et al. [7] for the timeframe 2030.
4. Conclusions
This article describes a procedure for assessing the potential to reduce the fuel consumption of passenger cars operated by electric power. This procedure is based on a simulation-supported fuel consumption analysis. The analysis is carried out for four selected passenger car concepts that differ from each other in their manner of generating and using electricity. The influences of passenger car use patterns and time-dependent, on-board power requirements are given special emphasis. In powertrains that are more dependent on electricity, the latter play an increasing role in the fuel consumption assessment due to changed technical conditions concerning vehicle interior heating and cooling, as well as an overall rise in on-board power requirements. Different usage patterns of passenger cars can be taken into consideration, particularly by using a number of drive cycles, classified as urban, rural and highway driving. The calculation results clearly show that auxiliary power demand shows a severe impact on fuel economy, particularly when driving at low average speeds, i.e., in urban contexts. The lowest overall consumption is seen in BEVs and FCVs. BEVs, however, are the most sensitive to an increase in auxiliary energy demand, as special constraints exist with respect to the mass and volume of the battery.
The contribution of this analysis is to confirm the significance of considering different load patterns of vehicle usage related to driving profiles and onboard electrical and thermal loads. However, a validation of the simulation models results was not possible, as the required data from real-world tests are not available. Additionally, the operational strategies implemented are directed to fuel consumption optimization. In reality, criteria such as drivability and noise emissions must also be considered, which was not possible within the analysis presented here. The results of our analysis are, however, comparable to the literature values provided, while assumptions for vehicle class and powertrain configuration were chosen in a similar way. In relation to overall vehicle fuel consumption, it must be noted that the energy demand of powertrain and cabin heating are affected by cold-start operation, particularly at low ambient temperatures. This aspect was not included in our analysis and should be considered in future work. Moreover, the analysis should be extended to plug-in powertrain concepts with internal combustion engines or fuel cells, which are increasingly in the focus of vehicle development.
Author Contributions
Thomas Grube and Detlef Stolten jointly developed and validated the idea of this research topic and conceived the assessment. Thomas Grube developed the model, collected the relevant information from the literature, conducted the analysis and evaluated the results. He also wrote the paper. Detlef Stolten gave valuable advice during the preparation and revised the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Acronyms.
Table A1.
Acronyms.
| Acronym | Description | Acronym | Description |
|---|---|---|---|
| AC | Air conditioning | HYZEM | Drive cycle |
| AD | Axle drive | ICE | Internal combustione engine |
| APU | Auxiliary power unit | ICV | Internal combustione engine vehicle |
| ASG | Automated gearbox | LPE | Load point elevation |
| BE | Battery electric | LPR | Load point reduction |
| BEV | Battery electric vehicle | MODEM | Drive cycle |
| BSL | Base load only (load case) | MVEG | European standard driving cycle |
| BT | Battery | NHC | No heating or cooling (load case) |
| CP | Cooling power | OG | 14 V on-board power system |
| CVT | Continuously variable transmission | OPS | Operating point shift |
| DC | DC (direct current) converter | PAH | Parallel hybrid |
| EM | Electric machine | PEFC | Polymer electrolyte fuel cell |
| EUDC | MVEG sub-cycle for extra urban driving | PHEV | Plug-in hybrid |
| EV | Electric vehicle | PSH | Power-split hybrid |
| FCV | Fuel cell vehicle | RC | Resistor capacitor element |
| FLC | Fuzzy logic controller | SEH | Series hybrid |
| FRD | Frost day | SI | Spark ignition |
| FT | Fuel tank | SOC | State of charge |
| FTP | Federal Test Procedure | SUD | Summer day |
| GB | Gear box | SUV | Sports utility vehicle |
| HEV | Hybrid electric vehicle | TTW | Tank-to-wheel |
| HP | Heating power | WLTC | Worldwide harmonized light vehicles test cycles |
| HT | Heating element | WTW | Well-to-wheel |
| HWFET | Highway Fuel Economy Test |

Table A2.
Characterization of drive cycles used in this study. Box plots consider positive power values only. The mechanical energy displayed relates to positive and negative tractive forces. ARTEMIS Motorway is chosen with a maximum velocity of . All values for ICV-G in the scenario “Standard” with a car mass of , cross-sectional area of and air drag coefficient of .
Table A2.
Characterization of drive cycles used in this study. Box plots consider positive power values only. The mechanical energy displayed relates to positive and negative tractive forces. ARTEMIS Motorway is chosen with a maximum velocity of . All values for ICV-G in the scenario “Standard” with a car mass of , cross-sectional area of and air drag coefficient of .
| Drive Cycle Name | Average Velocity | Mechanical Energy at the Wheels | Box Plot of Passenger Car Drive Power (Histogram) |
|---|---|---|---|
| Cycle group “urban” | |||
| ARTEMIS urban | ; |  | |
| ECE |  | ||
| US FTP 72 |  | ||
| HYZEM urban |  | ||
| Japan 08 |  | ||
| MODEM free flow urban |  | ||
| MODEM slow urban |  | ||
| SFTP-SC03 |  | ||
| WLTC, ver. 4.0 low |  | ||
| WLTC, ver. 4.0 middle |  | ||
| Cycle group “Extra urban” | |||
| ARTEMIS road |  | ||
| EUDC |  | ||
| HYZEM rural |  | ||
| MODEM road |  | ||
| SFTP-US06 |  | ||
| WLTC, ver. 4.0 high |  | ||
| Cycle group “Motorway” | |||
| ARTEMIS motorway (130) |  | ||
| US Highway |  | ||
| HYZEM highway |  | ||
| MODEM motorway |  | ||
| WLTC, ver. 4.0 very high |  | ||
| Cycle group “Combined“ | |||
| HYZEM |  | ||
| MODEM |  | ||
| MVEG | ; |  | |
| WLTC, ver. 4.0 | ; |  | |
Example histogram (MVEG) | |||

Table A3.
Vehicle mass (kg) and power of an IC engine and electric machine (kW) of all concepts examined.
Table A3.
Vehicle mass (kg) and power of an IC engine and electric machine (kW) of all concepts examined.
| Concept | A-Segment | C-Segment | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| “Standard” | “Advanced” | “Standard” | “Advanced” | ||||||||||
| ICV-G | n.a. | n.a. | n.a. | n.a. | |||||||||
| ICV-D | n.a. | n.a. | n.a. | n.a. | |||||||||
| PAH-G | |||||||||||||
| PAH-D | |||||||||||||
| BEV | n.a. | n.a. | n.a. | n.a. | |||||||||
| FCV | n.a. | n.a. | n.a. | n.a. | |||||||||
BEV: Battery-electric vehicle; D: Diesel; FCV: Fuel cell-electric vehicle; G: Gasoline; ICV: Internal combustion engine vehicle; n.a.: not applicable; PAH: Parallel hybrid. Indices: EM: electric machine; ICE: Internal combustion engine; m: mechanical; V: vehicle.
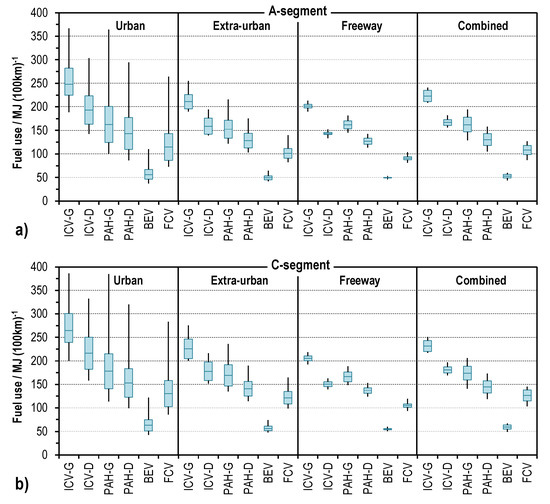
Figure A1.
Results of fuel economy analysis for all concepts and onboard load cases related to the “standard” scenario, for (a) A-segment and (b) C-segment cars. Values are displayed as box plots related to the cycle groups of urban, extra-urban, freeway and combined with (from below): minimum, third quartile, median, first quartile and maximum.
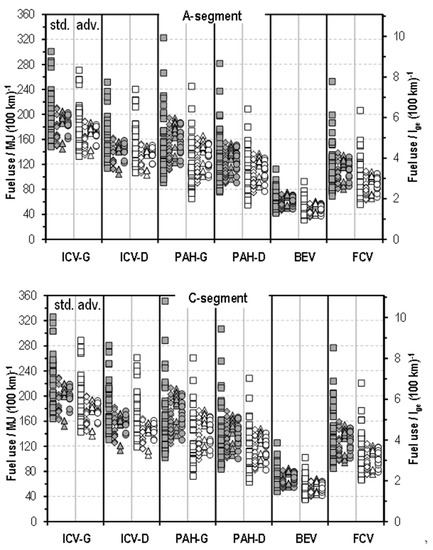
Figure A2.
Results of fuel economy analysis for all scenarios, car segments and load cases considered. The filled symbols for Scenario “standard” (std.), open symbols for scenario “advanced” (adv.); the squares relate to urban, diamonds to extra-urban, triangles to freeways and circles to combined drive cycles; lge: liters of gasoline equivalent.

Table A4.
Fuel economy figures of an ICV considering different load cases and drive cycles. First line: Range of results for all 25 drive cycles. Second line: Values for ECE|EUDC|MVEG; Third line: Values for WLTC-Low|WLTC-Middle|WLTC-High|WLTC-Very high. Values for cars with internal combustion engine vehicles based on spark ignition (ICV-G) and diesel engines (ICV-D).
Table A4.
Fuel economy figures of an ICV considering different load cases and drive cycles. First line: Range of results for all 25 drive cycles. Second line: Values for ECE|EUDC|MVEG; Third line: Values for WLTC-Low|WLTC-Middle|WLTC-High|WLTC-Very high. Values for cars with internal combustion engine vehicles based on spark ignition (ICV-G) and diesel engines (ICV-D).
| A-Segment | C-Segment | |||
|---|---|---|---|---|
| Concept | “Standard” | “Advanced” | “Standard” | “Advanced” |
| ICV-G “Base load only” (BSL) | 144–224 | 132–203 | 152–255 | 136–227 |
| 171|154|161 | 159|142|149 | 187|165|174 | 170|147|156 | |
| 167|148|151|165 | 148|132|138|149 | 185|164|162|179 | 162|143|144|157 | |
| ICV-G “Frost day” (FRD) | 154–300 | 143–270 | 161–325 | 144–288 |
| 225|167|189 | 203|154|172 | 243|178|202 | 216|159|180 | |
| 233|171|166|186 | 211|153|152|169 | 250|186|177|199 | 222|162|157|176 | |
| ICV-G “No heating & cooling” (NHC) | 153–282 | 142–255 | 160–303 | 144–270 |
| 210|165|182 | 192|152|167 | 226|176|195 | 203|157|174 | |
| 224|167|164|183 | 202|150|150|166 | 238|181|175|196 | 211|158|155|173 | |
| ICV-D “Baseload only” (BSL) | 104–183 | 103–176 | 113–215 | 106–202 |
| 136|113|122 | 137|110|120 | 156|126|138 | 154|117|131 | |
| 134|113|112|125 | 130|106|109|120 | 154|130|125|141 | 145|119|116|129 | |
| ICV-D “Frost day” (FRD) | 112–251 | 110–240 | 121–280 | 113–261 |
| 184|125|147 | 176|120|141 | 206|138|163 | 195|127|152 | |
| 190|133|126|143 | 184|125|121|137 | 211|151|139|159 | 197|137|128|146 | |
| ICV-D “No heating & cooling” (NHC) | 112–228 | 110–222 | 121–252 | 112–239 |
| 168|123|140 | 164|118|136 | 187|136|155 | 181|125|146 | |
| 176|128|123|139 | 174|121|119|134 | 194|144|136|154 | 185|132|125|142 | |

Table A5.
Fuel economy figures of PAH considering different load cases and drive cycles. First line: Range of results for all 25 drive cycles. Second line: Values for ECE|EUDC|MVEG; Third line: Values for WLTC-Low|WLTC-Middle|WLTC-High|WLTC-Very high Values for parallel hybrids based on spark ignition (PAH-G) and diesel engines (PAH-D).
Table A5.
Fuel economy figures of PAH considering different load cases and drive cycles. First line: Range of results for all 25 drive cycles. Second line: Values for ECE|EUDC|MVEG; Third line: Values for WLTC-Low|WLTC-Middle|WLTC-High|WLTC-Very high Values for parallel hybrids based on spark ignition (PAH-G) and diesel engines (PAH-D).
| A-Segment | C-Segment | |||
|---|---|---|---|---|
| Concept | “Standard” | “Advanced” | “Standard” | “Advanced” |
| PAH-G “Baseload only” (BSL) | 90–177 | 65–152 | 102–195 | 72–165 |
| 105|129|119 | 83|108|99 | 114|139|130 | 90|115|106 | |
| 90|96|116|125 | 65|73|94|103 | 102|107|129|140 | 72|84|105|113 | |
| PAH-G “Frost day” (FRD) | 145–322 | 116–245 | 158–351 | 124–260 |
| 229|157|185 | 186|131|152 | 251|169|200 | 198|138|161 | |
| 226|147|151|171 | 173|116|124|140 | 244|161|163|185 | 186|124|131|150 | |
| PAH-G “No heating & cooling” (NHC) | 110–183 | 89–158 | 122–201 | 98–170 |
| 145|139|138 | 111|117|115 | 153|147|151 | 119|124|125 | |
| 134|110|126|140 | 109|89|107|118 | 149|122|140|155 | 118|98|116|127 | |
| PAH-G “Summer day” (SUD) | 120–214 | 91–159 | 133–222 | 98–171 |
| 174|145|152 | 116|118|118 | 188|154|169 | 122|123|125 | |
| 155|120|130|147 | 115|91|108|119 | 169|133|147|163 | 119|98|116|128 | |
| PAH-D “Baseload only” (BSL) | 75–139 | 55–126 | 83–154 | 63–136 |
| 78|97|90 | 59|87|76 | 87|108|100 | 65|91|82 | |
| 75|77|93|100 | 55|62|79|86 | 83|91|104|112 | 63|69|86|93 | |
| PAH-D “Frost day” (FRD) | 116–281 | 99–208 | 125–306 | 107–228 |
| 197|122|148 | 158|108|127 | 216|135|164 | 168|116|134 | |
| 199|120|120|138 | 152|101|102|119 | 213|133|133|151 | 167|108|111|128 | |
| PAH-D “No heating & cooling” (NHC) | 92–153 | 77–131 | 103–163 | 82–141 |
| 119|106|111 | 99|95|97 | 126|117|121 | 112|100|103 | |
| 116|92|102|113 | 96|77|88|100 | 123|103|114|125 | 104|82|95|106 | |
| PAH-D “Summer day” (SUD) | 99–176 | 79–137 | 112–190 | 83–143 |
| 137|111|121 | 103|96|99 | 148|122|132 | 101|100|104 | |
| 131|99|106|120 | 101|79|90|101 | 142|112|119|133 | 105|83|95|107 | |

Table A6.
Fuel economy figures of BEVs considering different load cases and drive cycles. First line: Range of results for all 25 drive cycles. Second line: Values for ECE|EUDC|MVEG; Third line: Values for WLTC-Low|WLTC-Middle|WLTC-High|WLTC-Very high.
Table A6.
Fuel economy figures of BEVs considering different load cases and drive cycles. First line: Range of results for all 25 drive cycles. Second line: Values for ECE|EUDC|MVEG; Third line: Values for WLTC-Low|WLTC-Middle|WLTC-High|WLTC-Very high.
| A-Segment | C-Segment | |||
|---|---|---|---|---|
| Concept | “Standard” | “Advanced” | “Standard” | “Advanced” |
| “Baseload only” (BSL) | 41–74 | 31–58 | 47–81 | 35–65 |
| 44|51|48 | 32|39|37 | 50|57|54 | 37|44|41 | |
| 43|41|48|53 | 31|31|37|41 | 50|47|55|60 | 36|35|42|47 | |
| “Frost day” (FRD) | 54–112 | 43–92 | 61–125 | 48–102 |
| 87|59|69 | 71|47|56 | 96|66|77 | 77|52|62 | |
| 87|57|57|66 | 70|45|45|53 | 97|64|64|74 | 78|50|51|59 | |
| “No heating & cooling” (NHC) | 49–75 | 38–62 | 55–84 | 42–68 |
| 59|55|56 | 48|44|45 | 66|61|63 | 52|48|50 | |
| 60|49|53|59 | 49|38|42|47 | 67|55|59|66 | 54|42|47|53 | |
| “Summer day” (SUD) | 52–84 | 39–64 | 59–95 | 42–68 |
| 67|57|60 | 50|44|46 | 75|63|68 | 53|48|50 | |
| 68|52|56|62 | 51|39|43|48 | 76|59|62|70 | 54|42|47|53 | |

Table A7.
Fuel economy figures of an FCV considering different load cases and drive cycles. First line: Range of results for all 25 drive cycles. Second line: Values for ECE|EUDC|MVEG; Third line: Values for WLTC-Low|WLTC-Middle|WLTC-High|WLTC-Very high.
Table A7.
Fuel economy figures of an FCV considering different load cases and drive cycles. First line: Range of results for all 25 drive cycles. Second line: Values for ECE|EUDC|MVEG; Third line: Values for WLTC-Low|WLTC-Middle|WLTC-High|WLTC-Very high.
| A-Segment | C-Segment | |||
|---|---|---|---|---|
| Concept | “Standard” | “Advanced” | “Standard” | “Advanced” |
| “Base load only” (BSL) | 69–124 | 55–101 | 84–147 | 66–115 |
| 79|88|85 | 63|70|67 | 93|106|101 | 71|83|79 | |
| 77|69|81|90 | 59|55|64|73 | 89|84|99|106 | 66|66|75|83 | |
| “Frost day” (FRD) | 88–252 | 72–206 | 101–276 | 82–220 |
| 187|102|132 | 149|80|105 | 205|118|149 | 162|93|118 | |
| 186|101|98|118 | 151|82|83|96 | 204|114|117|135 | 161|88|90|107 | |
| “No heating & cooling” (NHC) | 83–135 | 68–112 | 96–152 | 76–124 |
| 106|95|99 | 88|76|81 | 120|112|113 | 97|89|90 | |
| 105|83|89|101 | 88|68|73|82 | 118|96|106|117 | 96|76|84|93 | |
| “Summer day” (SUD) | 92–170 | 71–133 | 106–192 | 83–141 |
| 132|100|113 | 102|78|88 | 151|120|131 | 109|93|99 | |
| 133|96|100|112 | 102|75|78|88 | 148|110|116|128 | 108|83|87|99 | |
References
- DeCicco, J.M. Factoring the car-climate challenge: Insights and implications. Energy Policy 2013, 59, 382–392. [Google Scholar] [CrossRef]
- Brown, D.; Alexander, M.; Brunner, D.; Advani, S.G.; Prasad, A.K. Drive-train simulator for a fuel cell hybrid vehicle. J. Power Sources 2008, 183, 275–281. [Google Scholar] [CrossRef]
- Kisacikoglu, M.C.; Uzunoglu, M.; Alam, M.S. Load sharing using fuzzy logic control in a fuel cell/ultracapacitor hybrid vehicle. Int. J. Hydrogen Energy 2009, 34, 1497–1507. [Google Scholar] [CrossRef]
- Li, X.; Williamson, S.S. Efficiency Analysis of Hybrid Electric Vehicle (HEV) Traction Motor-inverter Drive for Varied Driving Load Demands. In Proceedings of the Applied Power Electronics Conference and Exposition, Austin, TX, USA, 24–28 February 2008; pp. 280–285. [Google Scholar]
- Mansour, C.; Zgheib, E.; Saba, S. Evaluating impact of electrified vehicles on fuel consumption and CO2 emissions reduction in Lebanese driving conditions using onboard GPS survey. Energy Procedia 2011, 6, 261–276. [Google Scholar] [CrossRef]
- Gupta, S.; Patil, V.; Himabindu, M.; Ravikrishna, R.V. Life-cycle analysis of energy and greenhouse gas emissions of automotive fuels in India: Part 1—Tank-to-Wheel analysis. Energy 2016, 96, 684–698. [Google Scholar] [CrossRef]
- Kromer, M.A.; Heywood, J.B. A Comparative Assessment of Electric Propulsion Systems in the 2030 US Light-Duty Vehicle Fleet. In Proceedings of the SAE 2008 World Congress, Detroit, MI, USA, 14–17 April 2008. [Google Scholar]
- Jardine Engineering Corporation (JEC). Joint Research Centre-EUCAR-CONCAWE Collaboration: Well-to-Wheels Analysis of Future Automotive Fuels and Powertrains in the European Context; Tank-to-Wheels Report; European Commission, Joint Research Centre: Ispra, Italy, 2011. [Google Scholar]
- Wipke, K.B.; Cuddy, M.R.; Burch, S.D. ADVISOR 2.1: A User-Friendly Advanced Powertrain Simulator Using a Combined Backward/Forward Approach. IEEE Trans. Veh. Technol. 1999, 48, 1751–1761. [Google Scholar] [CrossRef]
- Williamson, S.S.; Emadi, A. Comparative Assessment of Hybrid Electric and Fuel Cell Vehicles Based on Comprehensive Well-to-Wheels Efficiency Analysis. IEEE Trans. Veh. Technol. 2005, 54, 856–862. [Google Scholar] [CrossRef]
- Moore, R.M.; Hauer, K.H.; Friedman, D.; Cunningham, J.; Badrinarayanan, P.; Ramaswamy, S.; Eggert, A. A dynamic simulation tool for hydrogen fuel cell vehicles. J. Power Sources 2005, 141, 272–285. [Google Scholar] [CrossRef]
- Delorme, A.; Rousseau, A.; Sharer, P.; Pagerit, S.; Wallner, T. Evolution of Hydrogen Fueled Vehicles Compared to Conventional Vehicles from 2010 to 2045. In Proceedings of the SAE World Congress, Detroit, MI, USA, 20–23 April 2009. [Google Scholar]
- Rousseau, A.; Shidore, N.; Carlson, R.; Freyermuth, V. Research on PHEV Battery Requirements and Evaluation of Early Prototypes. In Proceedings of the Advanced Automotive Battery Conferences (AABC), Long Beach, CA, USA, 16–18 May 2007. [Google Scholar]
- Nelson, P.; Amine, K.; Rousseau, A.; Yomoto, H. Advanced lithium-ion batteries for plug-in hybrid-electric vehicles. In Proceedings of the 23rd International Electric Vehicle Symposium (EVS23), Anaheim, CA, USA, 2–5 December 2007. [Google Scholar]
- Cao, Q.; Pagerit, S.; Carlson, R.; Rousseau, A. PHEV hymotion Prius model validation and control improvements. In Proceedings of the 23rd International Electric Vehicle Symposium (EVS23), Anaheim, CA, USA, 2–5 December 2007. [Google Scholar]
- Kim, N.; Rousseau, A. Assessment by Simulation of Benefits of New HEV Powertrain Configurations. In Proceedings of the International Scientific Conference on Hybrid an Electric Vehicles, Rueil-Malmaison, France, 6–7 December 2011. [Google Scholar]
- Schouten, N.J.; Salman, M.A.; Kheir, N.A. Fuzzy Logic Control for Parallel Hybrid Vehicles. IEEE Trans. Control Syst. Technol. 2002, 10, 460–468. [Google Scholar] [CrossRef]
- Biedermann, P.; Grube, T.; Höhlein, B. (Eds.) Methanol as an Energy Carrier; Forschungszentrum, Zentralbibliothek: Jülich, Germany, 2006. [Google Scholar]
- Grube, T.; Stolten, D. Bewertung von Fahrzeugkonzepten mit Brennstoffzellen und Batterien; Innovative Fahrzeugantriebe: Dresden, Germany, 2010. [Google Scholar]
- Grube, T.; Höhlein, B.; Menzer, R. Assessment of the Application of Fuel Cell APUs and Starter-Generators to Reduce Automobile Fuel Consumption. Fuel Cells 2007, 7, 128–134. [Google Scholar] [CrossRef]
- Campanari, S.; Manzolini, G.; Garcia de la Iglesia, F. Energy analysis of electric vehicles using batteries or fuel cells through well-to-wheel driving cycle simulations. J. Power Sources 2009, 186, 464–477. [Google Scholar] [CrossRef]
- Grube, T. Potentiale des Strommanagements zur Reduzierung des Spezifischen Energiebedarfs von PKW; Technische Universität Berlin: Jülich, Germany, 2014. [Google Scholar]
- Isermann, R. Mechatronische Systeme: Grundlagen; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Büchner, S. Energiemanagement-Strategien für Elektrische Energiebordnetze in Kraftfahrzeugen; Technische Universität Dresden: Dresden, Germany, 2008. [Google Scholar]
- Reif, K.; Noreikat, K.E.; Borgeest, K. Kraftfahrzeug-Hybridantriebe—Grundlagen, Komponenten, Systeme, Anwendungen; Vieweg + Teubner Verlag: Wiesbaden, Germany, 2012. [Google Scholar]
- Braess, H.-H.; Seiffert, U. (Eds.) Vieweg-Handbuch Kraftfahrzeugtechnik; Vieweg + Teubner Verlag: Wiesbaden, Germany, 2011. [Google Scholar]
- Lubischer, F.; Pickenhahn, J.; Gessat, J.; Gilles, L. Kraftstoffsparpotenzial durch Lenkung und Bremse. Automob. Z. 2008, 110, 996–1005. [Google Scholar] [CrossRef]
- Reif, K.; Dietsche, K.H. Kraftfahrtechnisches Taschenbuch, 25th ed.; Vieweg: Wiesbaden, Germany, 2003. [Google Scholar]
- Körner, C. Wirkungsgradoptimiertes Offline-Und Online-Energiemanagement bei Einem Seriellen Hybridantrieb; Universität Ulm: Göttingen, Germany, 2002. [Google Scholar]
- Sparen Beim Fahren—Stromerzeugung Kostet Sprit. Available online: http://www.adac.de/ (accessed on 19 September 2013).
- Fahrzeug Konfigurator (Adam Opel AG). Available online: www.opel.de (accessed on 30 June 2011).
- BMW Konfigurator. Available online: www.bmw.de (accessed on 30 June 2011).
- Mercedes-Benz Konfigurator. Available online: www.mercedes-benz.de (accessed on 30 June 2011).
- Rhode-Brandenburger, K. Verfahren zur Einfachen und Sicheren Abschätzung von Kraftstoffverbrauchspotentialen; Haus der Technik Essen: Essen, Germany, 1996. [Google Scholar]
- Gossen, F. Brennstoffzellenfahrzeuge im Vergleich zu Weiterentwickelten Konventionell Angetriebenen Fahrzeugen; RWTH Aachen: Aachen, Germany, 2000. [Google Scholar]
- Rodatz, P. Gemessenes Wirkungsgradkennfeld Einer Asynchron-Elektromaschine; Springer: Zürich, Switzerland, 2001. [Google Scholar]
- Chen, M.; Gabriel, A.R.-M. Accurate Electrical Battery Model Capable of Predicting Runtime and I–V Performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Großmann, H. Pkw-Klimatisierung—Physikalische Grundlagen und Technische Umsetzung; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Konz, M.; Lemke, N.; Försterling, S.; Eghtessad, M. Spezifische Anforderungen an das Heiz-Klimasystem Elektromotorisch Angetriebener Fahrzeuge; Forschungsvereinigung Automobiltechnik e.V. (FAT): Berlin, Germany, 2011. [Google Scholar]
- Jung, M.; Kemle, A.; Strauss, T.; Wawzyniak, M. Innenraumheizung von Hybrid- und Elektrofahrzeugen. Automob. Z. 2011, 113, 396–401. [Google Scholar] [CrossRef]
- Wetterlexikon—Klimatologische Kenntage. Available online: www.dwd.de (accessed on 26 March 2012).
- Hofmann, P. Hybridfahrzeuge—Ein Alternatives Antriebskonzept für die Zukunft; Springer: Wien, Austria, 2010. [Google Scholar]
- Kleimaier, A. Optimale Betriebsführung von Hybridfahrzeugen; Technische Universität München: München, Germany, 2003. [Google Scholar]
- Altenthan Weiyherhaus, J.V.G. Ableitung Einer Heuristischen Betriebsstrategie für ein Hybridfahrzeug aus Einer Online-Optimierung; Technische Universität München: München, Germany, 2010. [Google Scholar]
- Jörg, A. Optimale Auslegung und Betriebsführung von Hybridfahrzeugen; Technische Universität München: München, Germany, 2009. [Google Scholar]
- Stiegeler, M. Entwurf einer Vorausschauenden Betriebsstrategie für Parallele Hybride Antriebsstränge; Universität Ulm: Ulm, Germany, 2008. [Google Scholar]
- Back, M. Prädiktive Antriebsregelung zum Energieoptimalen Betrieb von Hybridfahrzeugen; Universität Karlsruhe: Karlsruhe, Germany, 2006. [Google Scholar]
- Böckl, M. Adaptives und Prädiktives Energiemanagement zur Verbesserung der Effizienz von Hybridfahrzeugen; Technische Universität Wien: Wien, Austria, 2008. [Google Scholar]
- Eren, Y.; Erdinc, O.; Gorgun, H.; Uzunoglu, M.; Vural, B. A fuzzy logic based supervisory controller for an FC/UC hybrid vehicular power system. Int. J. Hydrogen Energy 2009, 34, 8681–8694. [Google Scholar] [CrossRef]
- Die Studie Golf BlueMotion—Die Ersten Fakten. Available online: www.volkswagen.de (accessed on 14 August 2013).
- Schinke, H.; Kreckel, U.; Orschel, B.; Ott, M. Ergonomie und Ökonomie in schnittiger Verpackung. Automob. Z. 2012, 17, 20–23. [Google Scholar] [CrossRef]
- Department of Energy. Multi-Year Research, Development and Demonstration Plan, Hydrogen, Fuel Cells & Infrastructure Technologies Program; Department of Energy: Washington, DC, USA, 2012.
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).