Abstract
Open communication is an exigent need for future power systems, where time delay is unavoidable. In order to secure the stability of the grid, the frequency must remain within its limited range which is achieved through the load frequency control. Load frequency control signals are transmitted through communication networks which induce time delays that could destabilize power systems. So, in order to guarantee stability, the delay margin should be computed. In this paper, we present a new method for calculating the delay margin in load frequency control systems. The transcendental time delay characteristics equation is transformed into a frequency dependent equation. The spectral radius was used to find the frequencies at which the root crosses the imaginary axis. The crossing frequencies were determined through the sweeping test and the binary iteration algorithm. A one-area load frequency control system was chosen as a case study. The effectiveness of the proposed method was proven through comparison with the most recent published methods. The method shows its merit with less conservativeness and less computations. The impact of the proportional integral (PI) controller gains on the delay margin was investigated. It was found that increasing the PI controller gains reduces the delay margin.
1. Introduction
For a stable power system operation, loads and the demands must be matched in real time. This task is achieved through a load frequency control (LFC) system. Load frequency control is one of the classical power system control problems where the imbalance between the generation and the load is sensed through measuring the frequency. The LFC system must perform three main tasks: (1) to maintain uniform frequency; (2) to share the load between the generators; and (3) to control the tie-line interchange schedule [1]. In order to achieve these tasks the automatic generation control (AGC) signals are sent through dedicated communication links, and if this link fails, voice communication through telephone lines is used [2]. To guarantee uniform frequency in multi-area power systems, the area control error (ACE) and the generator control error (GCE) signals are distributed between the different areas [3]. Since the control signals are exchanged over communication networks, the time delay is inevitable, especially if the open communications are adopted in the power system [4]. Time delays could arise in power systems for different reasons and their magnitudes depend on the type of the communication link. The communication links used are telephone lines, fiber-optics, power lines, and satellites [5].
The presence of the time delay could lead to poor system performance or at worst results in system instability. Extensive research has been carried out in the last decades to tackle the problems associated with the delay in the LFC system. The published research either focuses on stabilization of the LFC system with the presence of the time delay or computing the delay margin required for system stability. The latter is the focus of this paper. The stabilization of the LFC system while considering the time delay has been studied by many researchers, the reader can refer to References [6,7,8,9,10,11,12,13,14,15] and the references there in.
The delay margin is defined at the maximum time delay that the system can withstand without losing stability. In the published research work two approaches are used to determine the delay margin; the first one is based on Lyapunov–Krasovskii theorem and the second approach is based on tracking the eigenvalues in the s-domain. The s-domain methods prove to give less conservative delay margins; however, they can only be applied to constant time delay. The simulation is used in Reference [2] to investigate the impact of the time delay on the stability of the LFC system. Two types of the time delays are studied; the constant and the random. It was found that the large number of packet losses or long-time delays could lead to LFC system instability; however, the authors do not consider computing the delay margin or stabilization of the LFC system with the presence of the delay and data loss. In Referene [16], the delay margin for single-area and multi-area LFC systems is computed through solving a set of linear matrix inequalities (LMIs). The LMIs are derived through solving Lyapunov–Krasovskii functionals, replacing the time delay terms with a Newton–Leibnitz formula, and introducing free weighting matrices (FWMs) [17]. The introduction of the variable FWMs reduces the conservativeness of the delay margin values. The effect of the proportional integral (PI) controllers, KP and KI, on the delay margin was also investigated. In Reference [18], an improved and less conservative criterion for computing the delay margin was introduced. The Lyapunov–Krasovskii functional was used to reduce the conservativeness of the method, the Wirtinger inequality and Jenson integral inequality were applied to bound the derivative of the Lyapunov function. It was reported in References [10,19] that the number of decision variables were reduced compared to the number of decision variables in Reference [16], and this will lead to less conservative results for the delay margin.
Yu and Tomsovic [7] applied a simple LMI stability criterion for computing the delay margin of an LFC system; however, the results were very conservative. In Reference [20] an improved delay-dependent stability method of load frequency control system was presented. The Lyapunov–Krasovskii functional was used where the time derivative was bounded using truncated second-order Bessel–Legendre (B-L) inequality. Then, the resulting LMIs were solved using the binary iteration algorithm. This results were less conservative results. A hybrid method has been proposed by Xiong et al. in Reference [21], where a constant time delay margin criterion was used for delay margin computation. Then a robust LMI method was applied to derive robust PI controller. In Reference [22], the Lyapunov–Krasovskii functional along with the Jesen inequality and the extended reciprocally convex matrix inequality were used to derive stability criterion for load frequency control systems with two time delays.
The energy storage units could improve the load frequency system performance in the power system [23]. The LFC multi-area power system with plug-in electric vehicles and communication delay was investigated in Reference [24]. The particle swarm optimization and the linear matrix inequalities techniques are was used to derive a robust PID controller. The robust control theory was also applied in Reference [25] to handle both the inertia uncertainty and the time varying communication delay where the LFC system with the Electric Vehicles (EVs) and the communication delay was modeled as an uncertain time delay system. The time delay margin of load frequency control system was computed in Reference [26] for a power system with electric vehicles using the Lyapunov–Krasovskii functional with the Wirtinger-based improved integral inequality. The literature presented in this paper covers only the issue of the delay margin computation for a load frequency control system. The stability and stabilization of the load frequency control system is a very broad research area; for a comprehensive review the reader can refer to References [27,28,29] and the references therein.
In Reference [30], the direct method for computing the delay margin is presented. Rekasius substitution was used to eliminate the transcendency in the characteristic equation and to convert it to a polynomial. The imaginary roots for positive delays were tracked and then Routh–Hurwitz criterion was used to determine the time delay margin. However, the results of the delay margin reported in Reference [30] were less conservative than the results of the method reported in Reference [16]; the drawback of the method in Reference [30] is the increased complexity in the case of multiple time delay systems. In Reference [31], the set of the PI controller parameters of the single-area LFC system that satisfies the stability with a given time delay was determined. In Reference [32], an exact method for computing the delay margin was introduced. The transcendental equation was transformed to normal polynomial in jω. The analysis was carried out in the frequency domain without any approximations which reduces the conservativeness of the results. The exponential terms were eliminated and the transcendental equation was converted to a frequency dependent equation where the number of frequencies that cross the imaginary access are finite.
Determining the delay margin is crucial for an LFC system operation. In the event of communication failure, the fault counter counts for a specified period before the LFC mechanism is suspended [16]. This period is usually selected to be very conservative which is determined from experience. The delay margin is also very important in determining the upper bound for the sampling time and aiding the control designer in the tuning [3,8]. In this paper, we present an accurate method for computing the delay margin for LFC systems. Many of the published methods are derived with advanced mathematics, which is based on the Lyapunov-Krasovskii theorem. For the method to have wide application in practice, it should be with less complexity while giving accurate results. Relative to the methods reported in the literature, the proposed method has a simple structure and easy to follow procedures while giving accurate values of the delay margin which is very important. The spectral radius was used to track movement of the system roots from which the crossing frequencies could be determined with high accuracy. In the next sections, the dynamic model of a single-area LFC system was briefly described. Then the stability analysis of the LFC system was analyzed in the frequency domain. The sweeping test and the binary iteration were used to compute the delay margin. A single-area LFC system was chosen as a case study. The results of the delay margin using the proposed method were compared with the results of the most recent published research.
2. Dynamic Model of One-Area LFC System with Time Delay
The one-area LFC system is shown in Figure 1. When an imbalance between the generation occurs, the frequency will deviate. In order to reset the frequency deviation to zero an integral control is required, as shown in Figure 1. The main assumption is that all the generators are equipped with non-reheat turbines. The state-space linear model of a one-area LFC system is expressed as [16]:
where; ; .
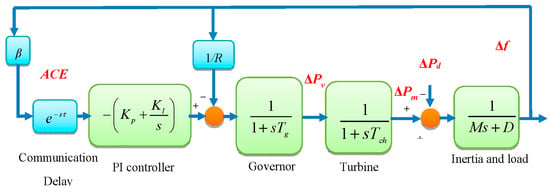
Figure 1.
Dynamic model of a one-area load frequency control (LFC) scheme.
The parameters are defined as: ΔPd is the load deviation, ΔPm is the generator mechanical output deviation, ΔPv is the valve position deviation, Δf is the frequency deviation. M (=2H) is the inertia constant, D is the load damping coefficient [33,34], Tg is the time constant of the governor, Tch is the time constant of the turbine, R is the speed drop, and β is the frequency bias factor. For a one-area LFC system, the area control error ACE is given as [16]:
The AGC has two components: the first is updated every 5 min and the second is updated in the order of 1–5 s. The latter signal delay is the one considered in the paper. Stabilizing the system with a conventional PI controller is given as:
where KP is the proportional gain, KI is the integral gain, and ∫ ACE is the integration of the area control error. With the PI controller, the closed-loop system is expressed as follows:
where; .
The time delay τ is composed of a transducer delay, analog-to-digital conversion delay, processing delay, multiplexing delay, and the delay in the communication link [5]. This time delay can be constant in dedicated communication links and time varying if open communication is used [16]. Setting ΔPd to zero, the single-area LFC system becomes a linear time delay system, then Equation (4) becomes:
To find the maximum delay margin, , we transform Equation (5) using Laplace transform and the characteristics equation becomes:
The system is asymptotically stable for a given delay if all the roots of Equation (6) lie on the left half plane. The free delay system is assumed to be stable and all the roots are on the left half plane. For some values of the delay one or more roots will cross the imaginary excess. One of the approaches is to replace s with jω and perform the analysis in the frequency domain.
3. Delay Margin Computation Using the Sweeping Test
Time delay systems can be either delay-independent or delay-dependent. The delay-dependent system is asymptotically stable for , marginally stable for , and unstable for . The delay independent system is asymptotically stable for any positive value of the time delay. For the single-area LFC system represented by Equation (5) to be asymptotically stable independent of delay, we must have:
where is the open right half plane. If Equation (7) is satisfied, then there are no positive roots for any value of the time delay. The delay-dependent stability implies that for time delays less than the delay margin the system is asymptotically stable and all the roots are on the closed left half plane, and when the time delay exceeds the delay margin the system becomes unstable and some roots will be on the right half plane. In this manner, the roots will cross the imaginary axis when . We are interested in determining both the delay-independent and delay-dependent conditions of the system. To simplify the analysis, we replace s with . Now, we turn our attention to find the delay that produce frequencies on the imaginary axis. Then system (5) is said to be asymptotically stable independent of delay if [35]:
If Equation (8) is not satisfied for some values of , then the system is delay-dependent stable. Now the problem is to find the crossing frequency, , where the roots crosses the imaginary axis. To find the crossing frequencies we use the spectral radius in the following definition.
Definition 1
([36]).The spectral radius of two matrices pair is defined as:
whereis the ith eigenvalue of the matrix A andis the generalized eigenvalue of matrix pair A, and Ad.
The computation of the delay margin is carried out in the domain. To compute the maximum delay margin we adopt the sweeping test [37]. The sweeping test is very valuable tool especially with the advances in the computing capabilities of the today’s computers. The seeping test is better for its simplicity with less computation and accurate results. To find the delay margin of the LFC system we use the following theorem.
Theorem 1
([36]).For the system (5) stable at τd = 0, i.e., A + Ad is stable and rank(Ad) = q, we define
Then, and the system in (5) is stable for alland becomes unstable at.
Proof
([35,36,37,38]). The system (5) is stable independent of the time delay if the following condition is satisfied:
Condition (10) implies that the system is stable with , that is, . Now we assume that the system becomes unstable for some value of . This means . Now, we assume that:
This can be true for , and consequently at this condition:
For any , we must have:
When there is a pair that satisfies , and consequently:
□
Corollary 1
([36]).The system (5) is stable independent of delay if and only if:
- (i)
- A is stable,
- (ii)
- A + Ad is stable, and
- (iii)
The three conditions in Corollary 1 represents the delay independent stability, where (i) states that the system is stable at , (ii) the system is stable at , and (iii) the system is stable for every in the range .
Theorem 1 determines both the delay independent and the delay dependent stability. First, we can verify the delay independent stability by checking the following condition:
If the above condition is satisfied, then the system is stable independent of time delay and if it is not satisfied for some values of ω that makes then we calculate the crossing frequencies using the algorithm in Figure 2. Finally, we compute the exact delay margin. The algorithm can be summarized as follows:
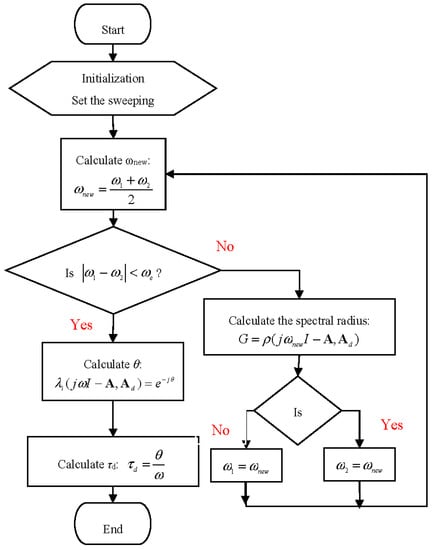
Figure 2.
The delay margin calculation algorithm.
Step 1: With the given system parameters, compute A and Ad. Using the sweeping test, check if the system is stable independent of delay or not, that is for . If for some values of , , then proceed to step 2, otherwise the system is stable independent of the time delay.
Step 2: Define a range . At the spectral radius and at the spectral radius . Now the crossing frequency, , lies in the range from to , in other words .
Step 3: Use the binary iteration to find the crossing frequency, , with a given error tolerance [39,40]. We set , if then and if then . Now the search range is reduced every iteration until the desired accuracy is reached.
Step 4: When the desired accuracy is reached, we calculate , the crossing angles, through solving . Finally, is the desired delay margin.
4. Case Study: One-Area LFC System
To compare the results of our proposed method with the published ones we use the same parameters in References [16,18,32]. The parameters of the LFC system shown in Figure 1 are given as: Tch = 0.3, Tg = 0.1, R = 0.05, D = 1.0, β = 21.0, and M = 10. Under an open communication network, the remote terminal unit (RTU) sends the signals to the central controller through the shared network, and then the controller sends the commands back. In most of the studies these two delays are aggregated into a single delay and this assumption is made in this paper. The ACE signals are updated every 2–4 s [10]. In power systems the data collection is in the order of 1−5 s [4]. The results of the delay margin with different values of the controller gains, KP and KI, are shown in Table 1 along with the results of the methods in References [16,18,32]. It should be noted that the method in Reference [32] gives the most accurate reported delay margins. Table 1 shows clearly that the proposed method gives almost exactly as the results of the method reported in Reference [32]; however, the proposed method is simpler with less computations.

Table 1.
The delay margin for different values of KP and KI.
The delay margin as a function of the integral gain for various values of the proportional gain with the proposed method and the method reported in Reference [32] are shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. As can be seen, the proposed method accurately determines the delay margin for the single-area LFC system. The relative error between the proposed method and the method published in Reference [32] is very small. The average relative percentage error is 0.023867% which shows that the delay margin values are nearly exactly as the same reported in Reference [32].
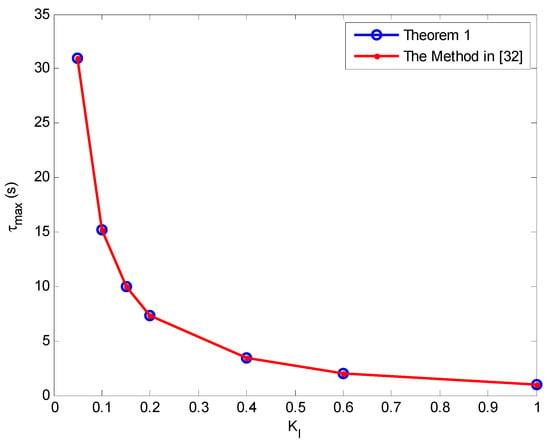
Figure 3.
The delay margin as function of the integral gain, KI with KP = 0.
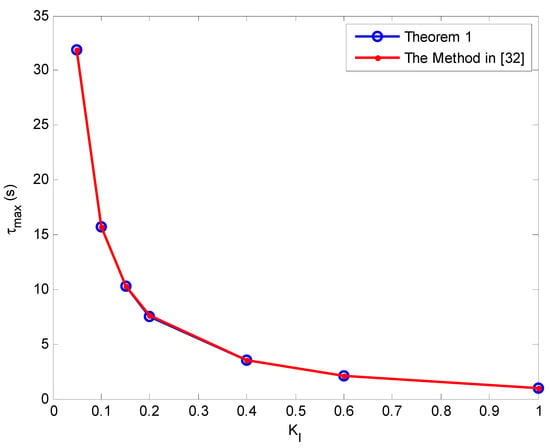
Figure 4.
The delay margin as function of the integral gain, KI with KP = 0.05.
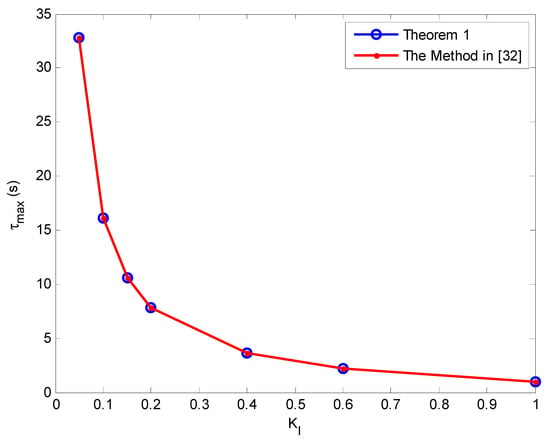
Figure 5.
The delay margin as function of the integral gain, KI with KP = 0.1.
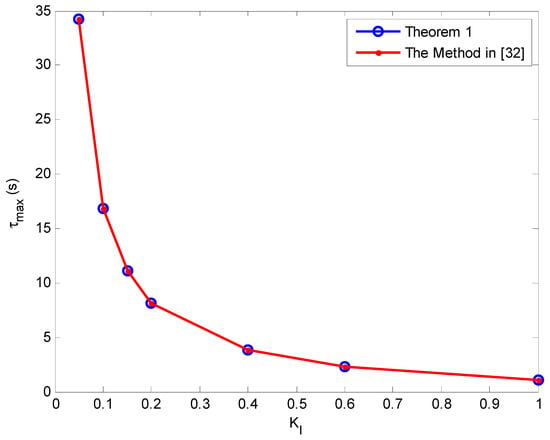
Figure 6.
The delay margin as function of the integral gain, KI with KP = 0.2.
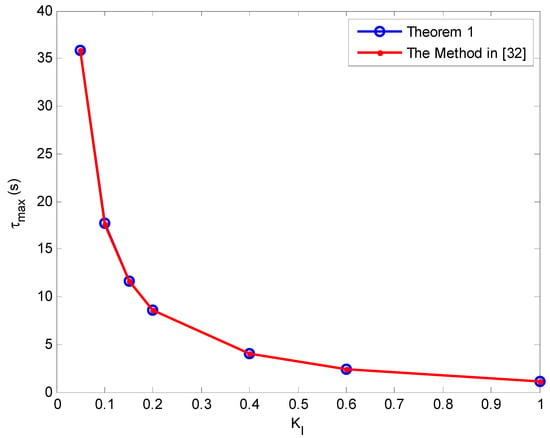
Figure 7.
The delay margin as function of the integral gain, KI with KP = 0.4.
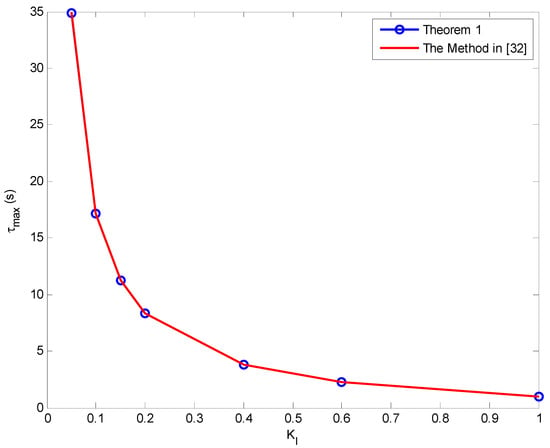
Figure 8.
The delay margin as function of the integral gain, KI with KP = 0.6.
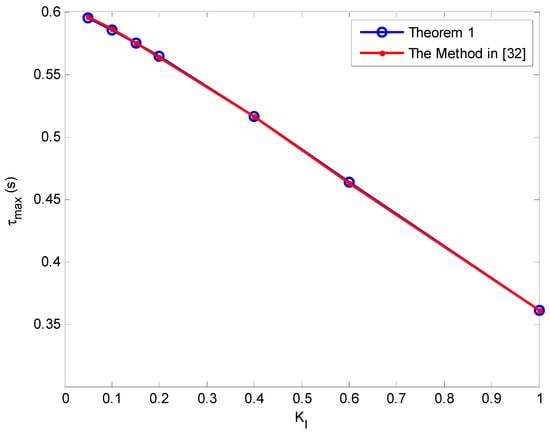
Figure 9.
The delay margin as function of the integral gain, KI with KP = 1.0.
Case I (KP = 0 and KI = 0.4): In Reference [32], it is reported that the delay margin with KP = 0 and KI = 0.4 is 3.382 s, with the proposed method it was 3.382 s. The proposed method gives accurate values of the delay margin as the method reported in Reference [32]. The proposed method gives less conservative results than the LMI methods reported in Reference [16,18]. To validate the results, simulations with Matlab/Simulink were carried out. The frequency response of the LFC system with KP = 0 and KI = 0.4 for different values of the time delay is shown in Figure 10. A 0.1 p.u change in the load occurs at 10 s. Figure 10 shows the frequency response with 3.3 s, 3.382 s, and 3.4 s, and it is clear that the system is stable with 3.3 s and unstable with 3.4 s. From the simulation the system was marginally stable with 3.384 s. The percentage error with the simulation-based delay margin was 0.071%. For this system, we have only one generalized eigenvalue. The spectral radius as a function of ω is shown in Figure 11. From Figure 11 the crossing frequency was 0.4025 rad/s, solving Equation (14), we have θ = 1.3678 rad which makes the delay margin equal 3.382 s. From Figure 10 the oscillating frequency was 0.4025 rad/s which proves the validity of the results.
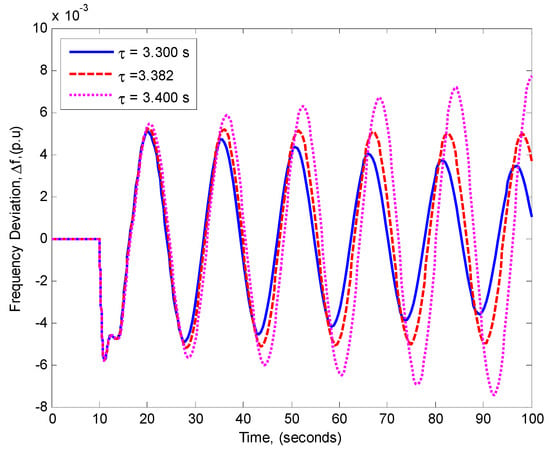
Figure 10.
The frequency response for different values of the time delay with KP = 0 and KI = 0.4.
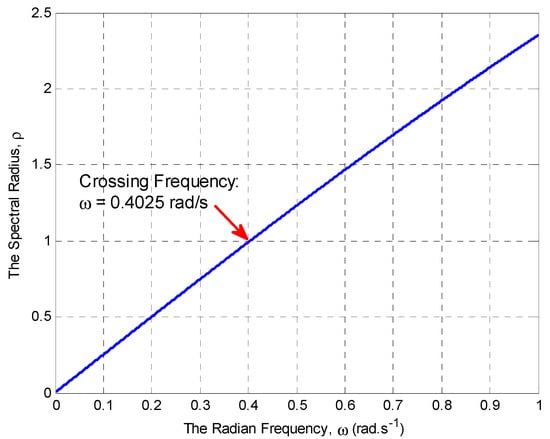
Figure 11.
The spectral radius as function of ω for KP = 0 and KI = 0.4.
Case II (KP = 0.6 and KI = 0.6): In Reference [32] it is reported with KP = 0.6 and KI = 0.6 that the delay margin is 2.281 s, while with our method it was 2.281 s. The frequency response with different delays is shown in Figure 12. The system is stable with 2.1 s; however, it becomes unstable with 2.4 s which is larger than the delay margin. The simulation-based delay margin was 2.282 s. The crossing frequency was 0.8015 rad/s, solving Equation (14) for θ, then; θ = 1.8283 rad. Figure 13 shows the spectral radius as a function of ω for KP = 0.6 and KI = 0.6.
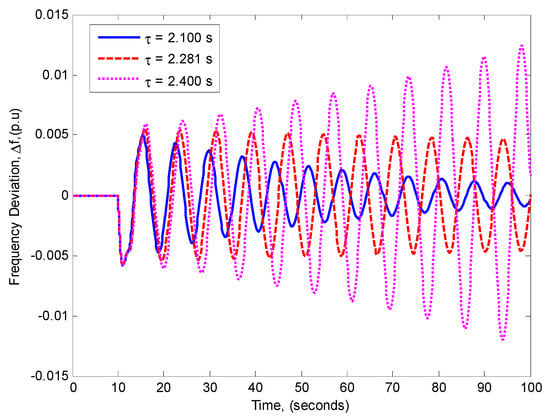
Figure 12.
The frequency response for different values of the time delay with KP = 0.6 and KI = 0.6.
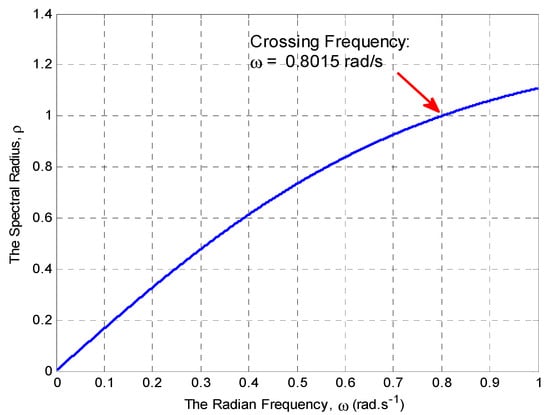
Figure 13.
The spectral radius as function of ω for KP = 0.6 and KI = 0.6.
Case III (KP = 0.05 and KI = 0.05): In Reference [32] it is reported with KP = 0.05, KI = 0.05 that the delay margin is 31.875 s, while with our method it was 31.8509 s. The frequency response with different delays is shown in Figure 14. The system is stable with 31.8509 s; however, it becomes unstable with 33 s which is larger than the delay margin. The simulation-based delay margin was 31.88 s. The relative percentage error was 0.0438%. The crossing frequency was 0.0502 rad/s, solving Equation (14) for θ then θ = 1.596 rad. Figure 15 shows the spectral radius as a function of ω for KP = 0.05 and KI = 0.05.
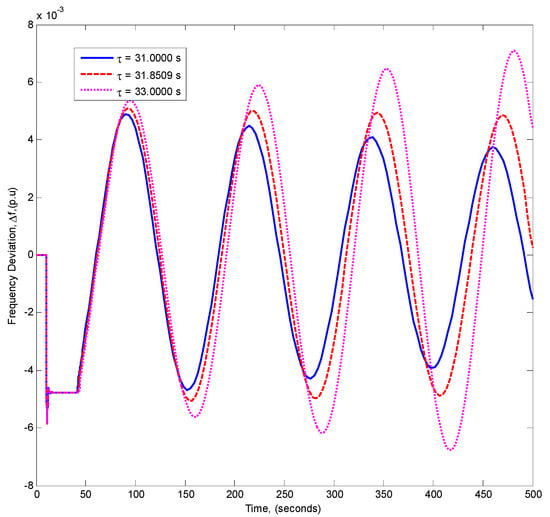
Figure 14.
The frequency response for different values of the time delay with KP = 0.05 and KI = 0.05.
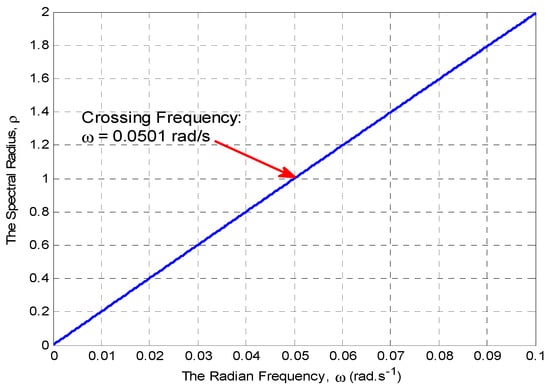
Figure 15.
The spectral radius as function of ω for KP = 0.05 and KI = 0.05.
The delay margin for different values of the PI controller gains is shown in Figure 16. The delay margin dependence on KI, and KP shows similar behavior as observed in References [16,18,32]. The crossing frequencies and the crossing angles are shown in Table 2 and Table 3 respectively. The variations of the crossing angle and the crossing frequency give more details on the dependence of the delay margin on KP and KI. From Figure 16, the delay margin decreases with increasing KI if KP is kept constant. The delay margin increases as KP increase in the range KP < 0.4, then the delay margin decreases as KP becomes larger than 0.4. This is the same behavior observed in References [16,18,32]. The delay margin becomes large for small values of KP and KI.
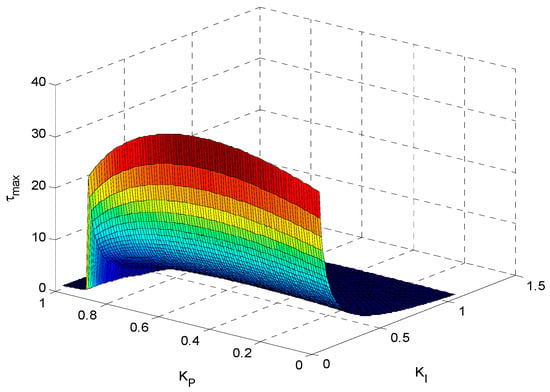
Figure 16.
The delay margin with different values of KP and KI.

Table 2.
The crossing angle with different values of KP and KI.

Table 3.
The crossing frequency with different values of KP and KI.
From Table 3, the LFC system oscillate with lower frequencies for small values of KP and KI. The LFC system tends to oscillate with higher frequency with large values of KP and KI.
The delay margins, crossing angles and the crossing frequencies with different values of KI when KP = 0 are shown in Table 4. It is interesting to observe that the crossing frequency with KP = 0 numerically equals KI. As KP is made larger than 0.2, the crossing frequency increases with increasing KP.

Table 4.
The delay margin for various values of KI and KP = 0.
The proposed method has been compared with four different published methods. The delay margin results are less conservative than the results of the LMI method reported in References [16,18]; however, the LMI method has the advantage of dealing with time varying delays. The results of the delay margin are equal to the delay margins obtained by the frequency domain methods reported in References [30,32]; however, the proposed method is simpler for implementation.
5. Conclusions
In this paper, we propose a method for analyzing the stability of load frequency control systems with a communication delay. The method is a frequency domain method without any approximation to the resultant delay system. The delay margins are computed through the binary iteration and the sweeping test. A single-area load frequency control system has been chosen as a case study and the delay margin values have been compared with values reported in the literature. The method gives accurate delay margins which is proved by time delay simulation and comparison with the published methods. The main two advantages of the proposed method are its accuracy and its simplicity compared with the other methods. Additionally, the method can determine accurately the oscillating frequency of the load frequency control system when the time delay equals the delay margin. The proposed method in this paper is applied to a single-delay load frequency system. The method will be extended to deal with multiple time delays which is the case for multi-area load frequency control systems.
Author Contributions
A.K. derived the mathematical model and applied the stability criterion. A.S.P. made the simulations. A.K. and A.S.P. wrote and edited the paper.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Saadat, H. Power System Analysis; McGraw-Hill Companies: New York, NY, USA, 1999. [Google Scholar]
- Bhowmik, S.; Tomsovic, K.; Bose, A. Communication Models for Third Party Load Frequency Control. IEEE Trans. Power Syst. 2004, 19, 543–548. [Google Scholar] [CrossRef]
- Khalil, A.; Wang, J.; Mohammed, O. Robust stabilization of load frequency control system under networked environment. Int. J. Autom. Comput. 2017, 14, 93–105. [Google Scholar] [CrossRef]
- Mak, K.H.; Holland, B.L. Migrating electrical power network SCADA systems to TCP/IP and Ethernet networking. Power Eng. J. 2002, 16, 305–311. [Google Scholar]
- Naduvathuparambil, B.; Valenti, M.C.; Feliachi, A. Communication delays in wide area measurement systems. In Proceedings of the Thirty-Fourth Southeastern Symposium on System Theory, Huntsville, Alabama, 18–19 March 2002; pp. 118–122. [Google Scholar]
- Bevrani, H.; Hiyama, T. A control strategy for LFC design with communication delays. In Proceedings of the 2005 International Power Engineering Conference, Singapore, 29 November–2 December 2005; pp. 1087–1092. [Google Scholar]
- Xiaofeng, Y.; Tomsovic, K. Application of linear matrix inequalities for load frequency control with communication delays. IEEE Trans. Power Syst. 2004, 19, 1508–1515. [Google Scholar]
- Zhang, C.K.; Jiang, L.; Wu, Q.H.; He, Y.; Wu, M. Delay-Dependent Robust Load Frequency Control for Time Delay Power Systems. IEEE Trans. Power Syst. 2013, 28, 2192–2201. [Google Scholar] [CrossRef]
- Peng, C.; Zhang, J. Delay-Distribution-Dependent Load Frequency Control of Power Systems with Probabilistic Interval Delays. IEEE Trans. Power Syst. 2016, 31, 3309–3317. [Google Scholar] [CrossRef]
- Zhang, C.K.; Jiang, L.; Wu, Q.H.; He, Y.; Wu, M. Further Results on Delay-Dependent Stability of Multi-Area Load Frequency Control. IEEE Trans. Power Syst. 2013, 28, 4465–4474. [Google Scholar] [CrossRef]
- Dey, R.; Ghosh, S.; Ray, G.; Rakshit, A. H1 load frequency control of interconnected power systems with communication delays. Electr. Power Energy Syst. 2012, 42, 672–684. [Google Scholar] [CrossRef]
- Ojaghi, P.; Rahmani, M. LMI-Based Robust Predictive Load Frequency Control for Power Systems with Communication Delays. IEEE Trans. Power Syst. 2017, 32, 4091–4100. [Google Scholar] [CrossRef]
- Singh, V.P.; Kishor, N.; Samuel, P. Load Frequency Control with Communication Topology Changes in Smart Grid. IEEE Trans. Ind. Inform. 2016, 12, 1943–1952. [Google Scholar] [CrossRef]
- Bevrani, H.; Hiyama, T. On Load Frequency Regulation with Time Delays: Design and Real-Time Implementation. IEEE Trans. Energy Convers. 2009, 24, 292–300. [Google Scholar] [CrossRef]
- Khalil, A.; Wang, J. Stabilization of load frequency control system under networked environment. In Proceedings of the 2015 21st International Conference on Automation and Computing (ICAC), Glasgow, UK, 11–12 September 2015; pp. 1–6. [Google Scholar]
- Jiang, L.; Yao, W.; Wu, Q.H.; Wen, J.Y.; Cheng, S.J. Delay-Dependent Stability for Load Frequency Control with Constant and Time-Varying Delays. IEEE Trans. Power Syst. 2012, 27, 932–941. [Google Scholar] [CrossRef]
- He, Y.; She, J.-H.; Wu, M. Stability Analysis and Robust Control of Time-Delay Systems; Springer: Berlin, Germany, 2010. [Google Scholar]
- Ramakrishnan, K. Delay-dependent stability criterion for delayed load frequency control systems. In Proceedings of the IEEE Annual India Conference (INDICON), Bangalore, India, 16–18 December 2016; pp. 1–6. [Google Scholar]
- Ramakrishnan, K.; Ray, G. Improved results on delay dependent stability of LFC systems with multiple time delays. J. Control Autom. Electr. Syst. 2015, 26, 235–240. [Google Scholar] [CrossRef]
- Yang, F.; He, J.; Pan, Q. Further Improvement on Delay-Dependent Load Frequency Control of Power Systems via Truncated B–L Inequality. IEEE Trans. Power Syst. 2018, 33, 5062–5071. [Google Scholar] [CrossRef]
- Xiong, L.; Li, H.; Wang, J. LMI based robust load frequency control for time delayed power system via delay margin estimation. Electr. Power Energy Syst. 2018, 100, 91–103. [Google Scholar] [CrossRef]
- Liu, P.; Huang, Z.; Liu, Y.; Wang, Z. Delay-dependent stability analysis for load frequency control systems with two delay components. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 6476–6481. [Google Scholar]
- Popli, N.; Ilić, M.D. Storage devices for automated frequency regulation and stabilization. In Proceedings of the 2014 IEEE PES General Meeting|Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar]
- Fan, H.; Jiang, L.; Zhang, C.-K.; Mao, C. Frequency regulation of multi-area power systems with plug-in electric vehicles considering communication delays. IET Gener. Transm. Distrib. 2016, 10, 3481–3491. [Google Scholar] [CrossRef]
- Jia, H.; Li, X.; Mu, Y.; Xu, C.; Jiang, Y.; Yu, X.; Wu, J.; Dong, C. Coordinated control for EV aggregators and power plants in frequency regulation considering time-varying delays. Appl. Energy 2018, 210, 1363–1376. [Google Scholar] [CrossRef]
- Ko, K.S.; Sung, D.K. The Effect of EV Aggregators with Time-Varying Delays on the Stability of a Load Frequency Control System. IEEE Trans. Power Syst. 2018, 33, 669–680. [Google Scholar] [CrossRef]
- Shankar, R.; Pradhan, S.R.; Chatterjee, K.; Mandal, R. A comprehensive state of the art literature survey on LFC mechanism for power system. Renew. Sustain. Energy Rev. 2017, 76, 1185–1207. [Google Scholar] [CrossRef]
- Alhelou, H.H.; Hamedani-Golshan, M.; Zamani, R.; Heydarian-Forushani, E.; Siano, P. Challenges and Opportunities of Load Frequency Control in Conventional, Modern and Future Smart Power Systems: A Comprehensive Review. Energies 2018, 11, 2497. [Google Scholar] [CrossRef]
- Pandey, S.K.; Mohanty, S.R.; Kishor, N. A literature survey on load–frequency control for conventional and distribution generation power systems. Renew. Sustain. Energy Rev. 2013, 25, 318–334. [Google Scholar] [CrossRef]
- Sönmez, Ş.; Ayasun, S.; Eminoğlu, U. Computation of time delay margins for stability of a single-area load frequency control system with communication delays. Wseas Trans. Power Syst. 2014, 9, 67–76. [Google Scholar]
- Sonmez, S.; Ayasun, S. Stability Region in the Parameter Space of PI Controller for a Single-Area Load Frequency Control System with Time Delay. IEEE Trans. Power Syst. 2016, 31, 829–830. [Google Scholar] [CrossRef]
- Sonmez, S.; Ayasun, S.; Nwankpa, C.O. An Exact Method for Computing Delay Margin for Stability of Load Frequency Control Systems with Constant Communication Delays. IEEE Trans. Power Syst. 2016, 31, 370–377. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw Hill: New York, NY, USA, 1994. [Google Scholar]
- Eremia, M.; Shahidehpour, M. Handbook of Electrical Power System Dynamics: Modeling, Stability, and Control; Wiley-IEEE Press: New York, NY, USA, 2013. [Google Scholar]
- Chen, J. On Computing the Maximal Delay Intervals for Stability of Linear Delay Systems. IEEE Trans. Autom. Control 1995, 40, 1087–1093. [Google Scholar] [CrossRef]
- Gu, K.; Kharitonov, V.L.; Chen, J. Stability of Time-Delay Systems; Springer: Berlin, Germany, 2003. [Google Scholar]
- Chen, J.; Latchman, H.A. Frequency Sweeping Tests for Stability Independent of Delay. IEEE Trans. Autom. Control 1995, 40, 1640–1645. [Google Scholar] [CrossRef]
- Chen, J.; Gu, G.; Nett, C.N. A New Method for Computing Delay Margins for Stability of Linear Delay Systems. In Proceedings of the IEEE 33rd Conference on Decision and Control, Lake Buena Vista, FL, USA, 14–16 December 1994; pp. 433–437. [Google Scholar]
- Elkawafi, S.; Khalil, A.; Elgaiyar, A.I.; Wang, J. Delay-dependent stability of LFC in Microgrid with varying time delays. In Proceedings of the 2016 22nd International Conference on Automation and Computing (ICAC), Colchester, UK, 7–8 September 2016; pp. 354–359. [Google Scholar]
- Khalil, A.; Elkawafi, S.; Elgaiyar, A.I.; Wang, J. Delay-dependent stability of DC Microgrid with time-varying delay. In Proceedings of the 2016 22nd International Conference on Automation and Computing (ICAC), Colchester, UK, 7–8 September 2016; pp. 360–365. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).