Abstract
In recent years, distributed generation (DG) has developed rapidly. Renewable energy, represented by wind energy and solar energy, has been widely studied and utilized. At present, most distributed generators follow the principle of “installation is forgetting” after they are connected to a distribution network. This principle limits the popularization and benefit of distributed generation to a great extent. In order to solve these problems, this paper presents a two-tier model for optimal allocation of distributed power sources in active distribution networks (ADN). The objective of upper level planning is to minimize the annual comprehensive cost of distribution networks, and the objective of lower level planning is to minimize the active power cut-off of distributed generation through active management mode. Taking into account the time series characteristics of load and distributed power output, the improved K-means clustering method is used to cluster wind power and the photovoltaic output in different scenarios to get the daily curves in typical scenarios, and a bilevel programming model of distributed generation based on multiscenario analysis is established under active management mode. The upper level programming model is solved by Quantum genetic algorithm (QGA), and the lower level programming model is solved by the primal dual interior point method (PDIPM). The rationality of the model and the effectiveness of the algorithm are verified by simulation and analysis of a 33-bus distribution network.
1. Introduction
With the increasing demand for electricity, the deepening of the traditional energy shortage situation, and increasingly prominent environmental problems, the development of distributed generation (DG), especially renewable energy generation technology, has been widely supported. DG has the advantages of high energy efficiency, clean environmental protection, flexible installation position, and so on [1,2,3]. It can effectively solve many potential problems, such as high cost, difficult operation, and so on. It is an inevitable trend for Distributed Renewable Energy with high permeability to be connected to a distribution network, but it puts forward new requirements for a distribution network planning method with a large number of DG connections [4,5,6].
In most of the existing studies, distributed power generation is planned from two aspects of economy and technology [7,8,9,10,11]. In the DG planning process, most of them assume that the output of DG is constant [7,8], but there is a gap between this assumption and the actual situation. Especially for intermittent DG, such as wind power generation, photovoltaic power generation, the size of its processing, depends on its geographical location and climate environment. DG is planned by considering the load level, but only some specific load levels are considered, without considering the time series characteristics of DG output and load [9,10]. DG with different capacities is distinguished. Small capacity DG is considered a constant negative load, whereas large capacity DG behaves as a voltage dependent current source [11]. The planning results without considering the time series characteristics will lead to the following deviations: The maximum load and the maximum output of DG often do not occur at the same time, so the obtained DG capacity allocation results are not reasonable; the technical indicators calculated based on a certain value or several load levels are quite different from the actual situation, resulting in the planning. The technical index of the grid in the model is inaccurate, and the complementarity of wind power generation and photovoltaic power generation is not considered, resulting in the waste of energy and investment.
When uncertainties are considered in active distribution networks (AND), a large number of uncertainties in the planning process are described and simulated with corresponding random variables, using chance constrained programming [12,13,14]. Another way is to use the multiscene technology planning method [15,16,17]. Multiscenario technology transforms uncertain factors into deterministic factors, and then models are solved. However, when there are too many uncertainties, it is important and difficult to analyze large-scale scenes and improve computational efficiency. Therefore, it is very important and meaningful to reduce the large-scale scene in the planning process on the premise of ensuring the accuracy of the model.
There are two kinds of DG programming methods considering uncertainty in ADN: One is the DG single-level programming method, and the other is the DG bi-level programming method based on Bi-level theory. Generally, the DG single-level programming method is used, and the multiperiod optimal power flow method based on the interior point method is used to solve this kind of model. The other is the DG bilevel programming method, based on bilevel programming theory, which belongs to a very complex mixed integer nonlinear bilevel programming model [18,19,20,21]. Considering the demand response, a two-level solution model is established [18]. A stochastic programming bilevel model is established through stochastic programming [19]. A bilevel optimization model is presented for the risk assessment of transmission systems [20]. Generally, an intelligent algorithm or intelligent algorithm is used to solve the problem. This kind of algorithm is better in small-scale systems, but when the scale of the problem increases, and its computational efficiency and convergence are affected.
Active management measures, including active fault level management, active voltage control, and active power flow management, are the main manifestations of active distribution network initiative [22,23]. Most DGs still follow the so-called “installation is forgetting” principle when they are connected to a distribution network, which is still a passive power grid management mode [24,25]. The existing research methods have little research on the optimal allocation of distributed generation under active management mode. In order to give full play to the role of active distribution networks, the influence of active management mode must be considered in the planning process.
This paper discusses the possible impact of the assumption of the DG output model in the process of distributed generation planning. In view of the possible errors caused by the assumption of constant power output, Weibull distribution with two parameters is widely used for wind speed uncertainty. For light intensity, beta distribution is used to express its uncertainty. On the basis of considering uncertainty, this paper considers that the distributed generation planning method based on multiscenario technology can reasonably transform the uncertain model into the deterministic programming model, which can effectively reduce the difficulty of modeling and solving, and can fully consider its time on the basis of uncertain modeling of distributed generation. The difficulty of multiscene technology has been pointed out. The improved K-means clustering method can effectively solve this problem. Compared to the Monte Carlo/Latin hypercube sampling method, the scene tree method, and the non-parametric probability prediction method, this method causes less damage to data characteristics and can accurately describe the data changes of the original scene. The results are not conservative, and can be effectively reduced. A hybrid algorithm of the quantum genetic algorithm (QGA) and the dual interior point method is proposed to solve the bilayer model. Compared to the single intelligent algorithm and its improved algorithm, the hybrid algorithm can effectively reduce power system coordination and optimization. It also has low iteration times, and can improve computing efficiency. Compared to other planning methods, this paper focuses on the active characteristics of the active distribution network, and through a large number of comparative analyses shows that active management mode may affect distributed power planning.
Based on the above analysis, the uncertainties of wind power and photovoltaic system are firstly established considering the characteristics of distributed generation and load timing. A typical daily output curve is obtained through the annual output curve of wind power and PV. Combined with active management mode, a bilevel programming model of intermittent distributed generation based on multiscenario analysis is established. The upper-level programming model aims to minimize the annual comprehensive cost of distribution networks, and the lower-level model aims to minimize the amount of DG active power cut-off. The planning model fully influences active management mode. The quantum evolutionary algorithm and primal dual interior point method are used to solve the upper and lower layers of the proposed model. It is verified by the Institute of Electrical and Electronics Engineers (IEEE) 33-bus distribution network system. The results show that the two-layer model is reasonable and the algorithm is effective.
2. Uncertainty Modeling of Distributed Generation and Load
2.1. Probabilistic Model of Wind Power
Wind power output is mainly affected by wind speed. Wind speed is uncertain, so wind power output is uncertain. The uncertainty of wind speed can be expressed by its probability model [26,27,28,29,30,31]. In this paper, the two-parameter Weibull model is used to model wind speed uncertainty. Its probability density function is:
where v is the wind speed at the hub of a wind turbine impeller. k and c are the shape parameters and scale parameters of Weibull distribution, respectively.
where and are standard deviation and average value of v, respectively, is power generation, and Γ is Gamma function.
The piecewise function of active power of wind turbines can be expressed as:
where as cutting wind speed, is the cutting speed, is rated wind speed, is the rated output power of wind turbines.
Distributed wind turbines in distribution networks generally use asynchronous generators, which need to absorb reactive power from the system during operation. Assuming that wind turbines are controlled by constant power factor, the reactive power output of wind turbines is:
where is the power factor of wind turbine generators.
2.2. Probabilistic Model of Photovoltaic Generator
Photovoltaic power output is affected by many factors, which are mainly divided into two aspects: Lighting conditions and PV modules. Light intensity has the greatest impact on PV output [5]. The intensity of illumination is also uncertain. Its uncertainty can also be expressed by the probability model [5,15,32,33,34]. In this paper, the most widely used Beta distribution is used to model the uncertainty of illumination intensity. Its probability density function is:
where S is light intensity, is the maximum value of light intensity. and are two shape parameters of Beta distribution, which are calculated by the expected and variance of illumination intensity in a certain period of time.
The function of active power of photovoltaic generator is expressed as:
where is Photovoltaic generator rated output power and is rated light intensity.
3. Seasonal Scene Reduction
The output of wind and photovoltaic power generation is uncertain and random, and most of the time the output cannot reach the rated value [35]. Without considering the timing characteristics of wind and photovoltaic power, the output characteristics of different distributed generators cannot be fully reflected, and there is no difference between different distributed generators. Therefore, when the distribution network is connected to both wind and photovoltaic power, the timing characteristics of distributed generation output must be considered. There are significant differences in wind speed in different seasons. According to the meteorological data, the wind speed time series curves of different regions in the region to be planned can be obtained, and the time series characteristic curves of wind power output can be calculated. Light intensity is affected by weather and season at the same time, so the photovoltaic output time series characteristic curve, on the basis of seasonal division, can be calculated at the same time, according to weather conditions for each season division.
If the time interval between the sample data of wind speed, illumination intensity, and load is one hour, there are 8760 data samples a year, or 8760 scenes. In the process of model solving, scenario data need to be calculated for each scenario. The scene selection methods mainly include the full cycle time series scenario [11] and the periodic reduction scenario method [36]. Continuous multitime scenarios can cause “Curse of dimensionality”. Therefore, it is very necessary to reduce the uncertainty scene. In this paper, the improved K-means clustering algorithm is used to cluster the scenes with similar features before the hybrid algorithm is used to solve the model. After scene clustering, the original data are simplified, and the computation amount and time are reduced. After clustering, the output of wind turbine generators (WTG) and photovoltaic generators (PVG) in each scene can be calculated according to the method of Section 2.1 and Section 2.2.
3.1. Improved K-Means Clustering Algorithm
The K-means clustering algorithm [37] assigns the data objects to the nearest class according to the minimum distance principle of the pre-selected K initial clustering centers, and divides the datasets into different classes through the iterative process, so that the algorithm using the criterion Fu to evaluate the clustering performance is optimal. However, the traditional clustering algorithm cannot give the optimal number of clusters. This paper improves the traditional K-means clustering algorithm by selecting the appropriate clustering validity index [38]. In the range of clustering numbers, the clustering results are analyzed to determine the optimal number of clusters.
3.1.1. Selection of Calinski–Harabasz Validity Index and Optimal Cluster Number
The search range is integer number in [2, ] [39]. N is the total number of samples in the dataset. Searching clustering space can output a series of clustering results with different numbers of clusters. The clustering validity index is used to evaluate the quality of clustering results and the optimal number of clusters corresponding to the optimal clustering results is taken as the optimal number of clusters. In this paper, the index suitable for K-means clustering is selected as an effective index. The definition of a index is:
and are the sum of squares of classes and intra class deviations at k, respectively. and respectively reflect inter class separability and intra class compactness. With the increase of k value, tends to decrease, and tends to increase, while the index value may reach the maximum value at a certain k, which corresponds to the optimal number of clusters. Finding the best clustering number k is equivalent to finding the largest number. We should selcect the clustering results with large index and small class number.
3.1.2. The Steps of the Improved K-Means Clustering Algorithm
The steps of the improved K-means clustering algorithm are as follow:
- The search scope for setting the cluster number is [2, ];
- The initial clustering center is selected according to the principle of maximum and minimum distance in the search range. The K-means clustering algorithm is used to update the clustering center until the convergence of the distance criterion function. The index is calculated according to the clustering results. Turn to 2;
- Comparing the index under different k values, the corresponding k value is the best cluster number when the index reaches the maximum value;
- Output best clustering results.
3.2. Seasonal Scene Reduction
The annual wind power output curve of a region is shown in the Figure 1.
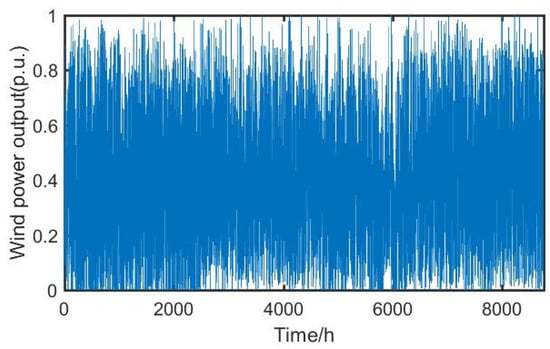
Figure 1.
Annual fluctuation of wind power output.
From the annual output curve of wind power, it can be observed that the sustained output time characteristics of the wind power generator are directly related to wind resources, and the variation of wind speed in different seasons is quite different. Wind power output at all times of the year is uncertain, which can be described by the probability distribution of wind power output, and is approximately subordinate to Weibull distribution. Wind power is a kind of intermittent energy. Wind speed has a strong intermittent, and for any period of time from the measuring point of wind, speed change does not have continuity. The intermittent performance of wind power is larger or smaller wind speed when its output is zero, as in Figure 1, where there is part of the wind power output which is zero. Affected by the fluctuation of wind speed, the output of wind power fluctuates obviously in a short time. In a short time, the output curve of wind power rises and falls sharply, and the data of adjacent time becomes larger, even appears larger jump.
According to the Section 3.1, the wind power output fluctuation curve after the seasonal scene is reduced is shown in Figure 2.
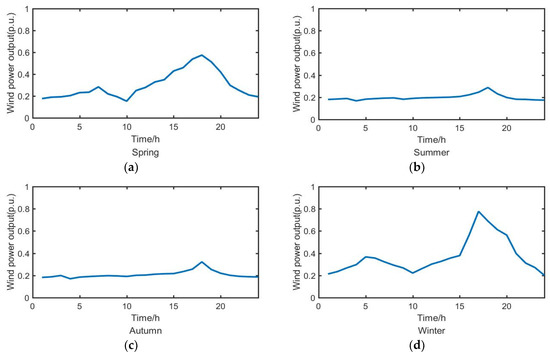
Figure 2.
Wind power output fluctuation curve: (a) Wind power fluctuation curve in spring; (b) Wind power fluctuation curve in summer; (c) Wind power fluctuation curve in autumn; (d) Wind power fluctuation curve in winter.
The wind power output in Figure 2a,c,d fluctuates greatly, which shows a certain inverse peak characteristic. The wind power output in Figure 2b is small and stable. The wind power output curve after clustering can better reflect the change characteristics of the original scene and is representative. The variation characteristics, stochastic characteristics, and inverse peak shaving characteristics of wind power output in different seasons are reflected in the power fluctuation curves in different scenarios.
The PV output curve of a region in all seasons is shown in Figure 3.
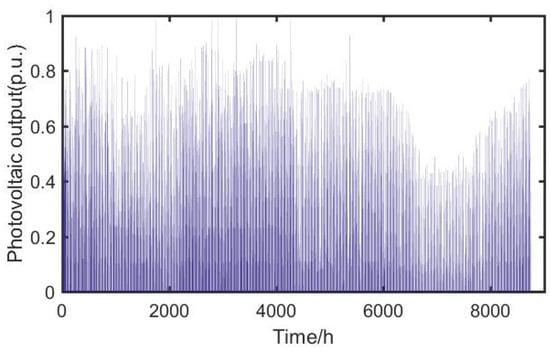
Figure 3.
Annual fluctuation of Photovoltaic output.
The diurnal fluctuation curve of PV output on typical sunny, cloudy, and rainy days after seasonal scenario reduction using the same method is shown in Figure 4.
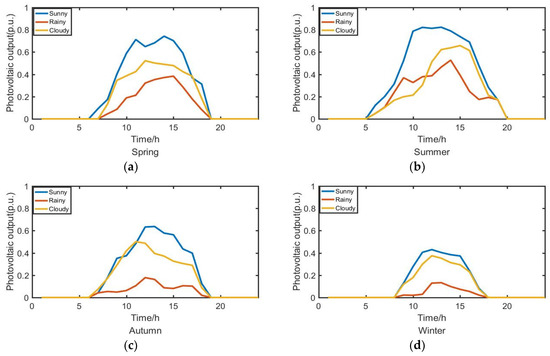
Figure 4.
PV fluctuation curve: (a) PV fluctuation curve in spring; (b) PV fluctuation curve in summer; (c) PV fluctuation curve in autumn; (d) PV fluctuation curve in winter.
The photovoltaic output characteristics of the reduced seasonal typical weather are obvious, and the variation of light intensity and sunlight is consistent. The photovoltaic output is largest near noon. The influence of weather is obvious, and the maximum output of PV is on sunny days. The photovoltaic output curve after clustering can better reflect the variation characteristics of the original scene. The variation characteristics and volatility of photovoltaic output in different seasons and different weather conditions are reflected in the output fluctuation curve.
According to the law of large numbers, when the sample size is large enough, the occurrence frequency of the event is almost close to its occurrence probability [40]. The typical weather probability of the seasonal reduction is shown in Table 1.

Table 1.
The probability of typical temperatures throughout one year.
At present, in the power planning and power industry statistics, power load is often divided into four types of typical load, such as industrial, agricultural, commercial, municipal life. The load is obviously affected by the season. According to the specific circumstances of the planning area, the load is divided into two categories: The civil load and the commercial load. The time series characteristic curves of these two loads are shown in Figure 5 and Figure 6.
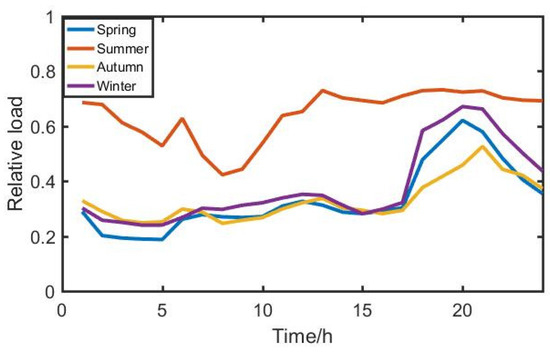
Figure 5.
Civil load time series characteristic curve.
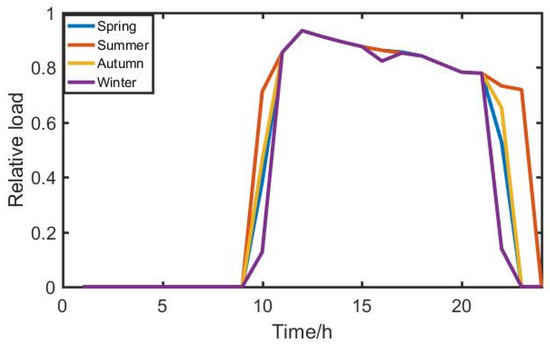
Figure 6.
Commercial load time series characteristic curve.
Figure 5 shows the time-dependent persistence curve of residential users during the four typical days of spring, summer, autumn, and winter. In terms of electricity consumption, the residential load in summer, with the use of air conditioning, or other refrigeration equipment, the load required is the highest. The maximum load will be around 8 p.m. and a small peak will appear around 12 p.m. and the minimum load will be around 3 a.m. Figure 6 shows the temporal persistence characteristics of commercial users over time over the four typical days of spring, summer, autumn, and winter. The four typical power consumption patterns of commercial users in spring, summer, autumn, and winter are relatively small, and the time series characteristics tend to be consistent. The power consumption periods are relatively concentrated between 12 p.m. and 11 p.m.
4. Bilevel Programming Model of Distributed Generation Based on Multiscenario Analysis under Active Management Mode
As an important part of ADN, active management can effectively overcome the drawbacks of passive management mode, and actively play the positive role of DG in improving distribution network operation mode, energy saving, and emission reduction. Active management is to achieve optimal control of DG and distribution equipment on the basis of effective measurement of distribution network operation parameters [41]. Active management mode can effectively solve this problem and give DG friendly access to distribution networks. It is unable to give full play to the positive role of DG in improving branch power flow, network loss, and node voltage. This paper adopts the following three kinds of active management measures [42].
- Distributed generator output control;
- Switching of reactive power compensation;
- Adjustment of on load transformer.
4.1. Upper Planning Mathematical Model
The objective function of the upper planning objective function is the minimum annual comprehensive cost of the distribution network. The objective function can be expressed as:
- Annual equivalent investment cost of distributed generation:where is the number of nodes in the distribution network, r is the discount rate, y is the life span of DG for 20 years, and are fixed investment costs of unit capacity of wind power and PV installed at the i node, respectively, and are the rated capacity of wind power and PV installed at the i node, respectively.
- Operation and maintenance fee:where is the scenario probability of the n scenario, and are the operation and maintenance costs of the wind power and the photovoltaic unit electricity received by the i node, and and are the wind power received by the i node and the photovoltaic unit electricity generated during the t period of the n typical day, respectively.Distributed generator output control
- Operators purchasing electricity from higher authorities:where is the t time of n typical days to buy electricity from a higher power grid. is the unit cost of operators purchasing electricity from a higher power grid.
- Environmental subsidy:where and are environmental subsidies for unit capacity of wind power generation and environmental subsidies for unit power consumption of photovoltaic units. and are, respectively, the output of wind power and photovoltaic in the i period of the n typical day.
- Loss of net loss:where is the net loss of the n typical day t period, is the unit network loss cost.
The constraints are:
- DG installation capacity constraint:where and are the wind capacity and PV capacity node i, respectively. and correspond to the maximum access capacity of DG, respectively.
- DG total installed capacity constraint:where is the maximum installed capacity.
4.2. Lower Level Programming Mathematical Model
The lower level planning model aims at minimizing the amount of DG active output. The expression is:
where is the amount of excision amount of active output in the t period of the n scenario
The constraints are:
- Node power balance constraint:where and are the active output of the t time of the n scenario, respectively. and are the active power of residential and commercial loads at the first time of t in the first n scenario, respectively. and are the reactive power of DG at the t time of the n scenario, respectively. and are the reactive power of resident load reactive power and commercial load at the t time of the n scenario, respectively. is reactive power supplied by reactive power compensation device. and are the voltage amplitude of node i and the voltage amplitude of node j at the t time node of the n scenario, respectively. is the phase difference between node i and node j of t in the n scenario, respectively.
- Node voltage constraint:where is node voltage. and are the minimum voltage values and maximum voltage values allowed by node i, respectively.
- Branch flow constraint:where is the apparent power of branch L. is the limit of branch transmission capacity.
- Distributed generator output control constraint:where and are the minimum active power output of node i and the maximum active power output of distributed generation, respectively.
- Reactive power compensation device constraint:where and are the minimum value of reactive power compensation device of node I and the maximum value of reactive power compensation device.
- Transformer tap constraint:where is the tap position of transformer i. and are the tap values of transformer i and the maximum tap value of i, respectively.
5. Solving Algorithm
5.1. Quantum Evolutionary Algorithm
The genetic algorithm (GA) [43] is a kind of method to deal with complex optimization problems by simulating the rules of survival of the fittest and the mechanism of chromosome information exchange within the population. The quantum genetic algorithm (QGA) [44,45,46,47] is based on the state vector representation of quantum. It refers the probability amplitude representation of quantum bits to the coding of chromosomes, so that a chromosome can express the superposition of multiple states, and uses quantum revolving gate and quantum non-gate to realize the finer operation of chromosomes, thus achieving the optimal solution of the goal.
5.1.1. Qubit Representation
In QGA, chromosomes are represented not by deterministic values (such as binary numbers, floating-point numbers, symbols, etc.) but by quantum bits, or by random probabilities. A qubit represents not only a state of 0 or 1, but also any intermediate state between the two states. Subbits can represent states simultaneously, so the population size of QGA is much smaller than that of traditional GA for the same optimization problem.
In QGA, a qubit may be in the intermediate state between and , that is, different superposition states of and , so the state of a qubit can be expressed as:
and can be plural, which indicates the probability amplitude of the corresponding state and satisfies the following normalization conditions:
where indicates the probability of , and indicates the probability of .
5.1.2. Quantum Genetic Manipulation
In QGA, the state of chromosome is superimposed or entangled, so the genetic operation of QGA cannot adopt the traditional GA selection, crossover, and mutation, but the way of quantum gate acting on each superimposed state or entangled state, respectively. The probability amplitude of an individual and its state is determined by the probability amplitude of the individual. The genetic operation is mainly to act as the constructed quantum gate on the ground state of a quantum superposition state or an entangled state to interfere with each other and change the phase, thus changing the probability amplitude of each ground state. Quantum gate construction is a major problem in quantum genetic manipulation. In QGA, the quantum revolving door is used mainly.
where is the rotation angle.
5.1.3. QGA Algorithm
Based on the representation of qubit and the superposition principle of quantum mechanics, the concrete algorithm of QGA is as follows:
- Initialization. The population containing N individuals is where is the individual of the T generation in the population, and there are:where m is the quantum dot number, that is, the length of the quantum chromosome. At the beginning, all , took ;
- According to the value of probability amplitude in , R(t) is constructed. , is a binary string of m length;
- Each individual in R(t) is evaluated by fitness evaluation function, and the optimal individual in this generation is retained. If a satisfactory solution is obtained, the algorithm terminates; otherwise, it is transferred to (4) to continue;
- Update P(t) with appropriate quantum gate U(t);
- Genetic algebra , algorithm to (2) continue.
5.2. Two-Level Model Solving Algorithm
In the bilevel programming model, the upper level programming model determines the planning scheme of the distributed generation, including the installation type, location, and capacity of the distributed generation. The scheme determined by the upper-level programming model is transferred to the lower-level programming model, and the original dual interior point method is used to determine the optimal operation mode of the active distribution network in different scenarios, and the optimal value is fed back to the upper-level programming model. The process of the bilevel optimal allocation model is shown in Figure 7.
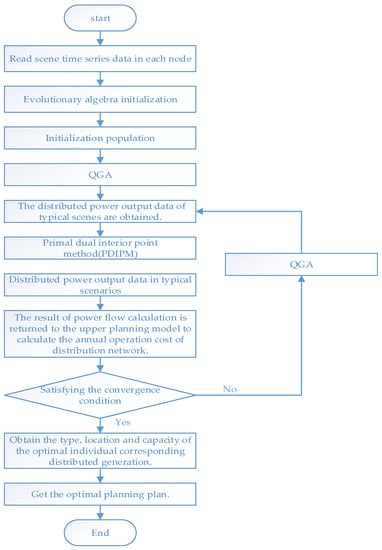
Figure 7.
Process of the bilevel optimal allocation model. QGA: quantum genetic algorithm.
6. Examples and Analysis of Planning Results
6.1. Examples
In this paper, the IEEE-33 node distribution network [48] is taken as an example, as shown in the Figure 8.
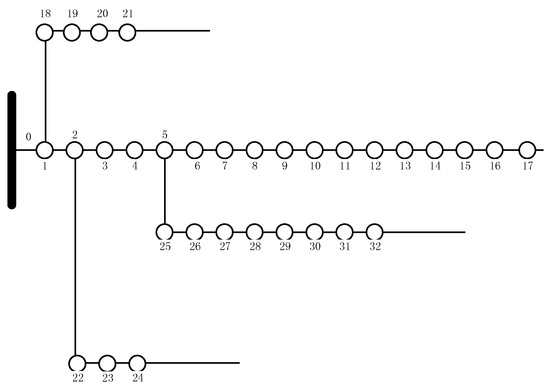
Figure 8.
Institute of Electrical and Electronics Engineers (IEEE)33-bus distribution network system.
The system voltage is 12.66 kV, the total active load is 3.715 MW, the total reactive load is 2.300 MW, and the system parameters are listed in Appendix A, Table A1. The parameters of Weibull distribution are k = 2.30, c = 8.92, the wind power access cost is 6500 yuan/kW, the operation and maintenance cost is 0.3 yuan/kWh, the environmental protection subsidy is 0.1 yuan/kWh, the rated illumination intensity of the photovoltaic generator is 1 kW/m2, the shape parameter of beta distribution is 0.85, b = 0.85, the photovoltaic access cost is 10,000 yuan/kW, the operation and maintenance cost is 0.2 yuan/kWh, and the environmental protection subsidy is 0.36/kWh. The rated capacity of a single distributed power supply is 125 kW. The economic life of equipment is 20 years, and the discount rate is 0.1. Business load nodes are 1, 3, 4, 7, 11, 12, 20, 22, 24, 25, 32, 33. Residential load nodes are 2, 5, 6, 8, 9, 13, 14, 15, 16, 17, 18, 19, 21, 23, 26, 27, 30, 31, 32, 33. The installed node for wind power installation is 5, 7, 11, 12. The installed node for wind power installation is 20, 23.The optimal configuration schemes of distributed generation considering active management mode and not considering active management mode are compared.
6.2. Result Analysis
Under the above conditions, the distributed power supply is optimized. The installation types, capacities, and costs of distributed generators under active and non-active management modes are shown in Table 2. The active power cut-off amount under active and non-active management modes is shown in Table 3. The node voltage expectation curve is shown in Figure 9.

Table 2.
Optimal allocation schemes with and without active management. WG: Wind generator

Table 3.
The excision amount of active output (MW h).
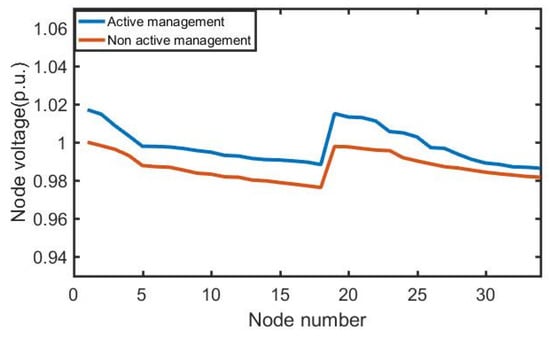
Figure 9.
Nodal voltage curve.
When active management mode is considered, the optimal configuration scheme can utilize 1375 kW, which is 250 kW higher than 1125 kW when active management mode is not considered. At the same time, the application of active management mode in an active distribution network can reduce the operation and maintenance cost of a power grid and the purchase cost from the superior power grid. It can be seen that active management mode can give full play to the ability of an active distribution network to utilize distributed power and reduce the annual operation cost of a power grid. As for the installation capacity of distributed generation, the installed capacity of wind turbines under active management mode accounts for 76.9% of the total connected capacity of distributed generation. From the output curve obtained after scene reduction, it can be seen that the output timing characteristics of wind turbines can be well matched with the load timing characteristics curve, so the installed capacity of wind turbines is far greater than PV installed capacity. At this stage, the investment and operation and maintenance costs of DG are higher, and even after subsidization, the price of electricity is still higher than that of purchasing electricity from a superior power grid. However, the proper use of distributed generation can significantly reduce the probability of voltage overrun, improve the power flow, and reduce the overall operation and maintenance costs and purchase costs of power grid, so as to achieve the purpose of reducing the annual operating costs of distribution network.
From the node voltage curve Figure 9, it can be seen that the voltage rise effect of distributed generation access point 5, 7, 11, 12, 20, 23, under active management mode, or 5, 7, 11, 20, 23, under non-active management mode, is obvious. Relevant optimal allocation cases have shown that the maximum and maximum voltage of nodes in distribution networks are all over-the-limit constraints [49]. Comparing the two management modes, it can be found that the voltage unit value of a distribution network is 0.017 higher than that of non-active management mode because of the introduction of active management mode, and the overall voltage of the network is 0.017 higher than that of non-active management mode. This is closer to the reference voltage, effectively preventing the occurrence of voltage limits.
Considering the installation location, under the assumption of the access point in this paper, most of the distributed generators are installed in the nodes 11, 12, 23, which are closer to the end of the network under active management mode, and most of the distributed generators are installed in the nodes 11, 23, which are closer to the end of the network under non-active management mode. DG can improve the distribution of network power flow and reduce active power and power of feeder, but the closer the access point is to the end of the network, the more obvious the voltage rise will be, which may lead to the voltage of distributed generation exceeding the upper limit constraint. To prevent this from happening, we can see that, in Table 2, the total amount of distributed generation access decreases under non-active management mode, and the node 12 closer to the end of the network is no longer connected to the distributed generation.
The distribution network with distributed photovoltaic power is one of the main factors limiting the capacity and permeability of distributed photovoltaic power. The problem of overvoltage in a distribution network is usually caused by the higher output power of distributed generators. At this time, the grid-connected active power is larger. Because the line impedance ratio X/R is larger, the load power factor is higher, the reactive power required to suppress overvoltage is also larger, and the current carrying capacity of distribution network line is limited, while the capacity of inverter is larger. Power factor limits may also lead to failure of control scheme. Especially in the case of high permeability of distributed power supply in this paper, according to the above analysis, it is easier for it to lead to voltage overrun. Table 3 shows that in spring and winter, when load demand is less, the removal of active power under non-active management mode is 42.70 MWh and 45.20 MWh, respectively. The removal of large-scale distributed generation reduces the utilization of distributed generation, and cannot give full play to the role of distributed generation, while “wind abandonment” and “light abandonment” will lead to an increase in annual operation and maintenance costs. Under active management mode, in summer and autumn, when the electricity load is the largest, the active power output is only 1.78 MWh and 7.19 MWh, respectively, which basically makes full use of the electric energy. In spring and autumn, the removal of active power decreases by 72.4% and 70.5%, respectively, compared to that without active management. Thus, the “active” measures in an active distribution network play an obvious role in a high permeability distribution network.
7. Conclusions
The main work of this paper was to optimize the configuration of the active distribution network intermittence distributed generators under active management mode. Active management mode is the most important feature of an active distribution network, and it must be considered when planning a distributed power supply. Based on the uncertainty modeling and multiscenario reduction of distributed generation, a bilevel programming model of distributed generation based on multiscenario analysis under active management mode is proposed in this paper.
Through this model, the types, quantity, and cost of distributed generation installation under active management mode and non-active management mode are compared. The case results show that the capacity of distributed power supply in active mode is increased from 1125 kW to 1375 kW by 22%, the operation and maintenance cost is reduced from 1,126,400 to 609,200 by 45.9%, and the comprehensive cost is reduced from 5,037,600 to 469,000. High permeability access of distributed generation to a power grid is the current development trend, and the reduction of annual comprehensive costs reduces the access threshold of distributed generation.
Compared to economic indicators, it is more important to optimize the technical indicators of a distribution network. The benchmark voltage of a distribution network is increased from 1 to 1.017, and the whole voltage value is closer to the benchmark voltage. The active power cut-off amount in each season is also reduced significantly, and it is close to full utilization in the summer with a heavy load. Most of the existing articles focus on the economic indicators of optimal allocation of distributed energy. However, distributed generation is not only a kind of clean energy, but at this stage it plays an important role in improving power flow distribution, enhancing the voltage level of each node and reducing the network, and comprehensively improving the power quality of the grid. Therefore, it is very necessary to consider active management mode in the process of optimal allocation of distributed power.
It is difficult to solve the bi-level model under multiscene technology. The intelligent algorithm and its improved algorithm are generally used in existing papers. However, when system planning increases, the computation time of the algorithm will increase significantly, and the convergence speed is slow and the precision is low. In order to reduce the computation load, this paper reduces the multiscene and uses hybrid algorithm to solve the problem. The example proves that the solution is effective. The algorithm is effective.
Although uncertain load modeling is carried out in this paper, the correlation between uncertain loads is not taken into account. Establishing a mathematical model considering uncertainties is a subject that needs further study. At the same time, when the size of the system increases and the constraint conditions increase, more efficient algorithms are needed to solve them.
Author Contributions
All authors contributed to the research in the paper. Z.W., N.T. and X.J. conceived and designed the model. X.Y. provided the data. Z.S. analyzed the data. Y.J. wrote the paper.
Funding
This work is supported by the National Natural Science Foundation of China (Grant Nos.51477099); Key Laboratory of Control of Power Transmission and Conversion (SJTU), Ministry of Education (Grant Nos. 2016AB14).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Parameters of 33-bus distribution network.
Table A1.
Parameters of 33-bus distribution network.
| Line Data | |||
|---|---|---|---|
| Access Rd | Branch Impedance/Ω | ||
| First Spot Number | End Point Number | Resistance | Reactance |
| 1 | 2 | 0.922 | 0.047 |
| 2 | 3 | 0.493 | 0.2511 |
| 3 | 4 | 0.366 | 0.1864 |
| 4 | 5 | 0.3811 | 0.1941 |
| 5 | 6 | 0.819 | 0.707 |
| 6 | 7 | 0.1872 | 0.6188 |
| 7 | 8 | 0.7114 | 0.2351 |
| 8 | 9 | 1.03 | 0.74 |
| 9 | 10 | 1.044 | 0.74 |
| 10 | 11 | 0.1966 | 0.065 |
| 11 | 12 | 0.3744 | 0.1238 |
| 12 | 13 | 1.468 | 1.155 |
| 13 | 14 | 0.5416 | 0.7129 |
| 14 | 15 | 0.591 | 0.526 |
| 15 | 16 | 0.7463 | 0.545 |
| 16 | 17 | 1.289 | 1.721 |
| 17 | 18 | 0.732 | 0.574 |
| 2 | 19 | 0.164 | 0.1565 |
| 19 | 20 | 1.5042 | 1.3554 |
| 20 | 21 | 0.4095 | 0.4784 |
| 21 | 22 | 0.7089 | 0.9373 |
| 3 | 23 | 0.4512 | 0.3083 |
| 23 | 24 | 0.898 | 0.7091 |
| 24 | 25 | 0.896 | 0.7011 |
| 6 | 26 | 0.203 | 0.1034 |
| 26 | 27 | 0.2842 | 0.1447 |
| 27 | 28 | 1.059 | 0.9337 |
| 28 | 29 | 0.8042 | 0.7006 |
| 29 | 30 | 0.5075 | 0.2585 |
| 30 | 31 | 0.9744 | 0.963 |
| 31 | 32 | 0.3105 | 0.3619 |
| 32 | 33 | 0.341 | 0.5302 |
References
- Anaya, K.L.; Pollitt, M.G. Going smarter in the connection of distributed generation. Energy Policy 2017, 105, 608–617. [Google Scholar] [CrossRef]
- Mehigan, L.; Deane, J.P.; Gallachoir, B.P.O.; Bertsch, V. A review of the role of distributed generation (DG) in future electricity systems. Energy 2018, 163, 822–836. [Google Scholar] [CrossRef]
- Allan, G.; Eromenko, I.; Gilmartin, M.; Kockar, M.; Mcgregor, P. The economics of distributed energy generation: A literature review. Renew. Sustain. Energy Rev. 2015, 42, 543–556. [Google Scholar] [CrossRef]
- Li, R.; Wang, W.; Xia, M.C. Cooperative planning of active distribution system with renewable energy sources and energy storge systems. IEEE Access 2017, 6, 5916–5926. [Google Scholar] [CrossRef]
- Heidari, S.; Fotuhi-Firuzabad, M.; Kazami, S. Power distribution network expansion planning considering distribution automation. IEEE Trans. Power Syst. 2015, 30, 1261–1269. [Google Scholar] [CrossRef]
- Montoya-Bueno, S.; Mnoza-Hernandez, J.I.; Contreras, J. Uncertainty management of renewable distributed generation. J. Clean. Prod. 2016, 138, 103–118. [Google Scholar] [CrossRef]
- Abbasi, F.; Hosseini, S.M. Optimal DG allocation and sizing in presence of storge systems considering network configuration effects in distribution systems. IET. Gener. Transm. Dis. 2016, 10, 617–624. [Google Scholar] [CrossRef]
- Blanco, R.F.; Dvorkin, Y.; Xu, F.; Wang, Y.; Kirschen, D. Optimal energy storge siting and sizing: A WECC case study. IEEE Trans. Sustain. Energy 2017, 8, 733–743. [Google Scholar] [CrossRef]
- Ziari, I.; Ledwich, G.; Ghosh, A. Optimal allocation and sizing of DGs in distribution network. In Proceedings of the IEEE Power and Energy Society General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–8. [Google Scholar]
- El-Sayed, M.A.; Alsaffar, M.A. Two stage methodology for optimal siting and sizing of distributed generation in medium voltage network. In Proceedings of the 2016 IEEE Green Technologies Conference, Kansas City, MO, USA, 6–8 April 2016. [Google Scholar]
- Othman, M.M.; El-Khattam, W.; Hegazy, Y.G.; Abdelaziz, A.Y. Optimal placement and sizing of distributed generators in unbalanced distribution systems using supervised big bang-big crunch method. IEEE Trans. Power Syst. 2015, 30, 911–919. [Google Scholar] [CrossRef]
- Hadian, A.; Haghifam, M.R.; Zohrevand, J.; Akhavan-Rezai, E. Probabilistic approach for renewable DG placement in distribution systems with uncertain and time varying loads. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009. [Google Scholar]
- Zeng, B.; Zhang, J.H.; Yang, X.; Wang, J.H.; Dong, J.; Zhang, Y.Y. Intergrated planning for transition to low-carbon distribution systems with renewable energy generation and demand response. IEEE Trans. Power Syst. 2014, 29, 1153–1165. [Google Scholar] [CrossRef]
- Thrampoulidis, C.; Bose, S.; Hassibi, B. Optimal placement of distributed energy storge in power networks. IEEE Trans. Autom. Control 2016, 61, 416–429. [Google Scholar] [CrossRef]
- Kaloudas, C.G.; Ochoa, L.F.; Marshall, B.; Majithia, S.; Fletcher, I. Assessing the feature trends of reactive power demand of distribution networks. IEEE Trans. Power Syst. 2017, 32, 4278–4288. [Google Scholar] [CrossRef]
- Zou, K.; Agalgaonkar, A.P.; Muttaqi, K.M. Distribution system planning with incorplorating DG reactive capability and system uncertainties. IEEE Trans. Sustain. Energy 2012, 3, 112–123. [Google Scholar] [CrossRef]
- Shen, X.W.; Shahidehpour, M.; Zhu, S.Z.; Han, Y.D.; Zheng, J.H. Multi-stage planning of active distribution networks considering the co-optimization of operation strategies. IEEE Trans. Smart Grid 2018, 9, 1425–1433. [Google Scholar] [CrossRef]
- Asensio, M.; Munoz-Delgado, G.; Contreras, J. Bi-level approach to distribution network and renewable energy expansion planning considering demand response. IEEE Trans. Power Syst. 2017, 32, 4298–4309. [Google Scholar] [CrossRef]
- Cai, Y.; Lin, J.; Wan, C.; Song, Y.H. Stochastic bi-level trading model for an active distribution company with DGs and interruptible loads. IET Renew. Power Gen. 2017, 11, 278–288. [Google Scholar] [CrossRef]
- Ding, T.; Li, C.; Yan, C.; Li, F.X.; Bie, Z.H. A bilevel optimization model for risk assement and contingency ranking in transmission system reliability evaluation. IEEE Trans. Power Syst. 2017, 32, 3803–3813. [Google Scholar] [CrossRef]
- Zhang, J.T.; Fan, H.; Tang, W. Planning for distributed wind generation under active management mode. Int. J. Electr. Power 2013, 47, 140–146. [Google Scholar] [CrossRef]
- Koutsoukis, N.C.; Georgilakis, P.S.; Hatziargyriou, N.D. Multistage coordinated planning of active distribution networks. IEEE Trans. Power Syst. 2018, 33, 32–34. [Google Scholar] [CrossRef]
- Turitsyn, K.; Sulc, P.; Backhaus, S.; Chertkov, M. Options for control of reactive power by distributed photovoltaic generators. Proc. IEEE 2011, 99, 1063–1073. [Google Scholar] [CrossRef]
- Kane, L.; Ault, G.W. Evaluation of wind power curtailment in active network management schemes. IEEE Trans. Power Syst. 2015, 30, 672–679. [Google Scholar] [CrossRef]
- Anikumar, R.; Devriese, G.; Srivastava, A.K. Voltage and reactive power control to maximize the energy saving in power distribution system with wind energy. IEEE Trans. Ind. Appl. 2018, 54, 656–664. [Google Scholar] [CrossRef]
- Du, E.S.; Zhang, N.; Kang, C.Q.; Kroposki, B.; Huang, H.; Miao, M.; Xia, Q. Managing wind power uncertainty through strategic reserve purchasing. IEEE Trans. Power Syst. 2017, 32, 2547–2559. [Google Scholar] [CrossRef]
- Zhang, S.X.; Cheng, H.Z.; Zhang, L.B. Probabilistic evaluation of available load supply capability for distribution system. IEEE Trans. Power Syst. 2013, 28, 3215–3225. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, Z.; Botterud, A.; Zhang, K.F. Optimal wind power uncertainty intervals for electricity market operation. IEEE Trans. Sustain. Energy 2018, 9, 199–210. [Google Scholar] [CrossRef]
- Shi, J.; Ding, Z.H.; Lee, W.J.; Yang, Y.P.; Liu, Y.Q.; Zhang, M.M. Hybrid forecasting model for very-short term wind power forecasting based on grey relational analysis and wind speed distribution features. IEEE Trans. Smart Grid 2014, 5, 521–526. [Google Scholar] [CrossRef]
- Soroudi, A.; Afrasiab, M. Binary PSO-based dynamic multi-objective model for distributed generation planning under uncertainty. IET Renew. Power Gen. 2012, 6, 67–78. [Google Scholar] [CrossRef]
- Li, Z.G.; Wu, W.C.; Shahidehpour, M.; Zhang, B. Adaptive Robust Tie-line scheduling considering wind power uncertainty for interconnected power systems. IEEE Trans. Power Syst. 2016, 31, 2701–2713. [Google Scholar] [CrossRef]
- Xu, L.; Ruan, X.; Mao, C. An improved optimal sizing method for wind-solar-battery hybrid power system. IEEE Trans. Sustain. Energy 2013, 4, 774–785. [Google Scholar]
- Wan, C.; Lin, J.; Song, Y.H.; Xu, Z.; Yang, G.Y. Probabilistic forecasting of photovoltaic generation: An efficient statistical approach. IEEE Trans. Power Syst. 2017, 32, 2471–2472. [Google Scholar] [CrossRef]
- Tabone, M.D.; Callaway, D.S. Modeling variability and uncertainty of photovoltaic generation: A hidden state spatial statistical approach. IEEE Trans. Power Syst. 2015, 30, 2965–2973. [Google Scholar] [CrossRef]
- Dvorkin, Y.; Lubin, M.; Backhas, S.; Chertkov, M. Uncertainty set for wind power generation. IEEE Trans. Power Syst. 2016, 31, 3326–3327. [Google Scholar] [CrossRef]
- Xu, X.; Chen, K.; Long, Y. Optimal site selection and capacity determination of multi-types of distributed generation in microgrid considering environment cost and timing characteristics. Power Syst. Technol. 2013, 37, 914–921. [Google Scholar]
- Jia, L.; Li, M.; Zhang, P.; Wu, Y.; Zhu, H.H. SAR image change detection based on multiple kernel K-means clustering with local-neighborhood information. IEEE Geosci. Remote Sens. Lett. 2016, 13, 856–860. [Google Scholar] [CrossRef]
- Ding, M.; XIE, J.L.; Liu, X.Y.; Shi, W.H. The Generation Method and Application of Wind Resources/Load Typical Scenario of Wind Power Grid Integration. Available online: http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CJFQ&dbname=CJFDLAST2016&filename=ZGDC201615006&uid=WEEvREcwSlJHSldRa1FhdXNXa0hFbGhTTER1WVFtbkhRV3I2V2RwWkppcz0=$9A4hF_YAuvQ5obgVAqNKPCYcEjKensW4IQMovwHtwkF4VYPoHbKxJw!!&v=MTcyMzk4ZVgxTHV4WVM3RGgxVDNxVHJXTTFGckNVUkxLZmJ1Um1GeUhsVWJyUFB5clBiYkc0SDlmTnFvOUZZb1I= (accessed on 15 July 2018).
- Stegmayer, G.; Milone, D.H.; Kamenetzky, L.; Lopez, M.G.; Carrari, F. A Biologically inspired validity measure for comparison of clustering methods over metabolic data sets. IEEE ACM Trans. Comput. Biol. Bioinform. 2012, 9, 706–716. [Google Scholar] [CrossRef] [PubMed]
- Yao, K.; Gao, J.W. Law of large numbers for uncertain random variables. IEEE Trans. Fuzzy Syst. 2016, 24, 615–621. [Google Scholar] [CrossRef]
- Koutsoukis, N.C.; Siagkas, D.O.; Georigilakis, P.S.; Hatziargyriou, N.D. Online Reconfiguration of Active Distribution Networks for Maximum Integration of Distributed Generation. IEEE Trans. Autom. Sci. Eng. 2016, 14, 437–448. [Google Scholar] [CrossRef]
- Zhang, J.T.; Cheng, H.Z.; Wang, C. Technical and economic impacts of active management on distribution network. Int. J. Electr. Power 2009, 31, 130–138. [Google Scholar] [CrossRef]
- Cheng, Y.F.; Shao, W.; Zhang, S.J.; Li, Y.P. An improved multi-objective genetic algorithm for large planar array thinning. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Zhu, X.T.; Xiong, J.B.; Liang, Q. Fault Diagnoise of rotation machinery based on support vector machine optimized by Quantum genetic algotithm. IEEE Access 2018, 6, 33583–33588. [Google Scholar] [CrossRef]
- Jin, Z.F.F.; Hou, Z.Q.; Yu, W.S.; Wang, X. Target tracking approach via quantum genetic algorithm. IET Comput. Vis. 2018, 12, 241–251. [Google Scholar] [CrossRef]
- Zhang, L.B.; Lv, H.P.; Tan, D.P.; Xu, F.; Chen, J.L.; Bao, G.J.; Cai, S.B. Adaptive quantum genetic algorithm for task sequence planning of complex assembly systems. Electron. Lett. 2018, 54, 870–872. [Google Scholar] [CrossRef]
- Liu, J.Y.; Wang, H.X.; Sun, Y.Y. Real-coded quantum-inspired gentic algotithm-based BP neural network algorithm. Math. Probl. Eng. 2015, 2015, 1–10. [Google Scholar]
- Paul, T.G.; Hossain, S.J.; Ghosh, S.; Mandal, P.; Kamalasadan, S. A quadratic programming based optimal power and battery dispatch for grid connected microgrid. IEEE Trans. Ind. Appl. 2018, 54, 1793–1805. [Google Scholar] [CrossRef]
- Zhang, S.X.; Chen, K.; Long, Y.; Cheng, H.Z.; Li, K. Distributed wind generator planning based on shuffled frog leaping algorithm. Autom. Electr. Power Syst. 2013, 37, 76–82. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).