Bayesian Meta-Analysis for Binary Data and Prior Distribution on Models
Abstract
1. Introduction
2. The Bayesian Binomial Model
2.1. The Linking Distribution
2.2. Clusters
2.3. The Likelihood of for a Particular Partition
2.4. The Likelihood of the Prior Distribution over the Partitions
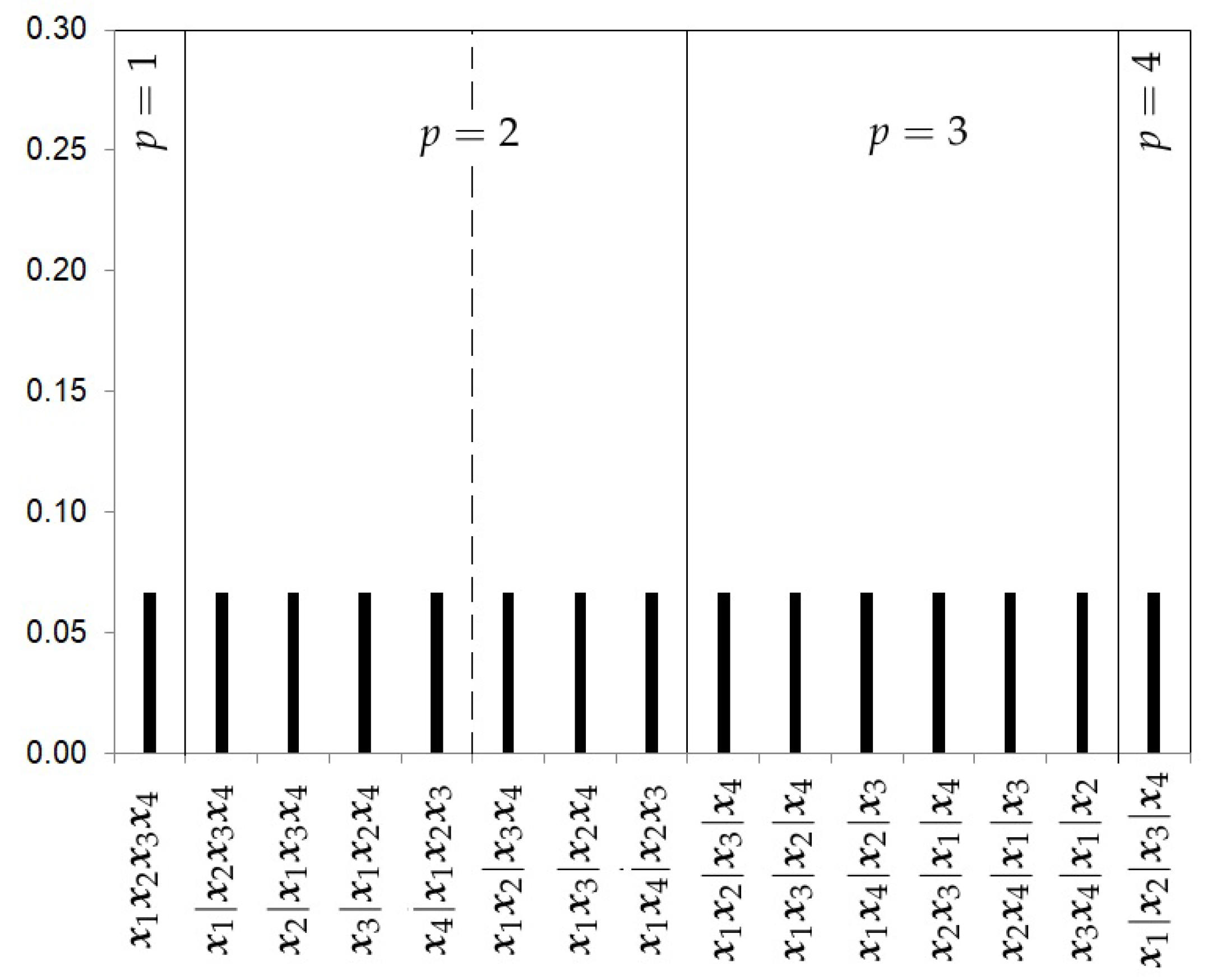
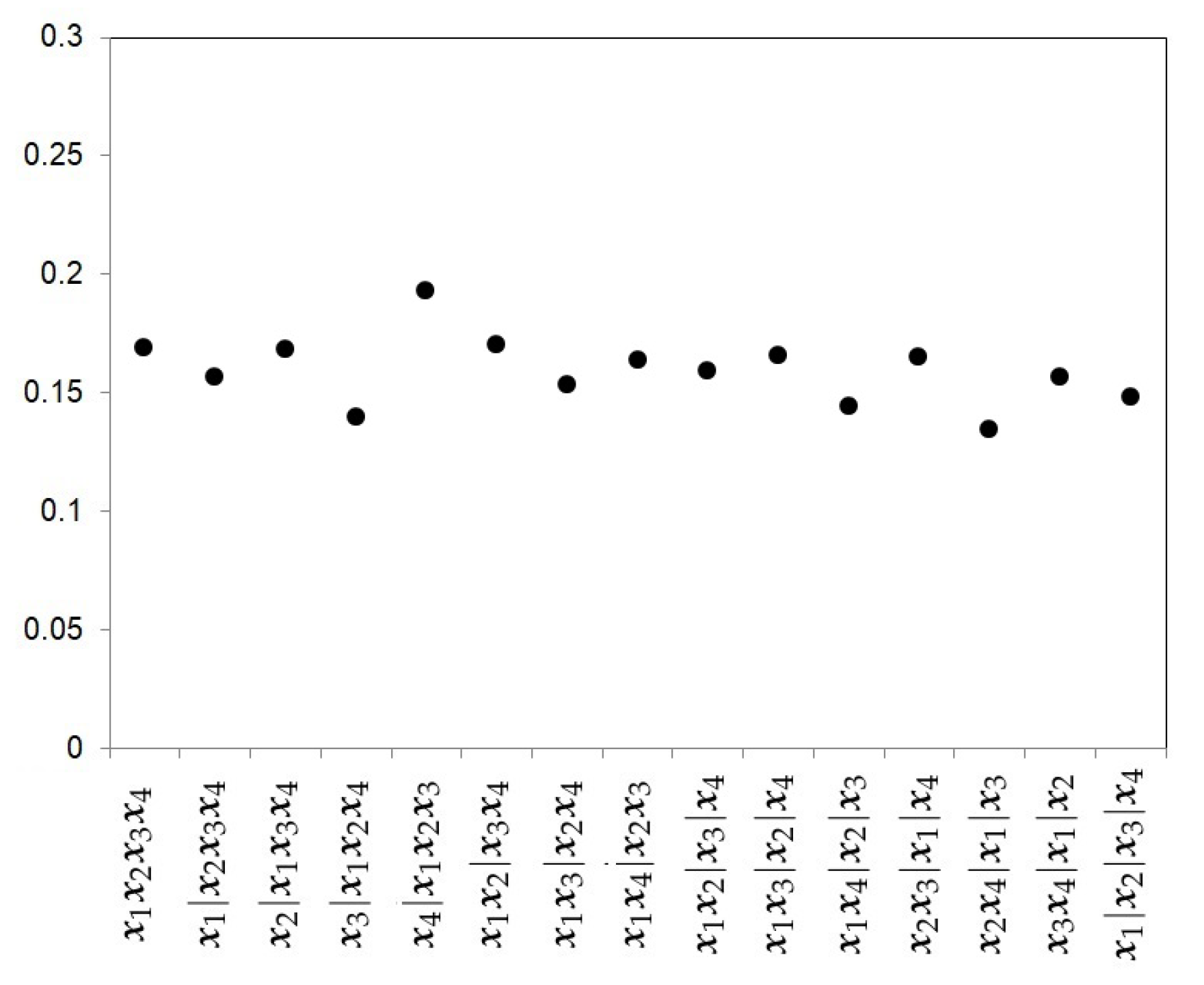
- The Uniform prior.The first prior proposed is the uniform prior (U), which gives the same probability to every model, that is,where , the Bell number, is the number of subsets a set of size k can be partitioned into. Figure 2 shows the prior probabilities for each partition when four studies are considered. In this example, the Bell number is 15. This choice does not take into account the level of complexity of each partition.
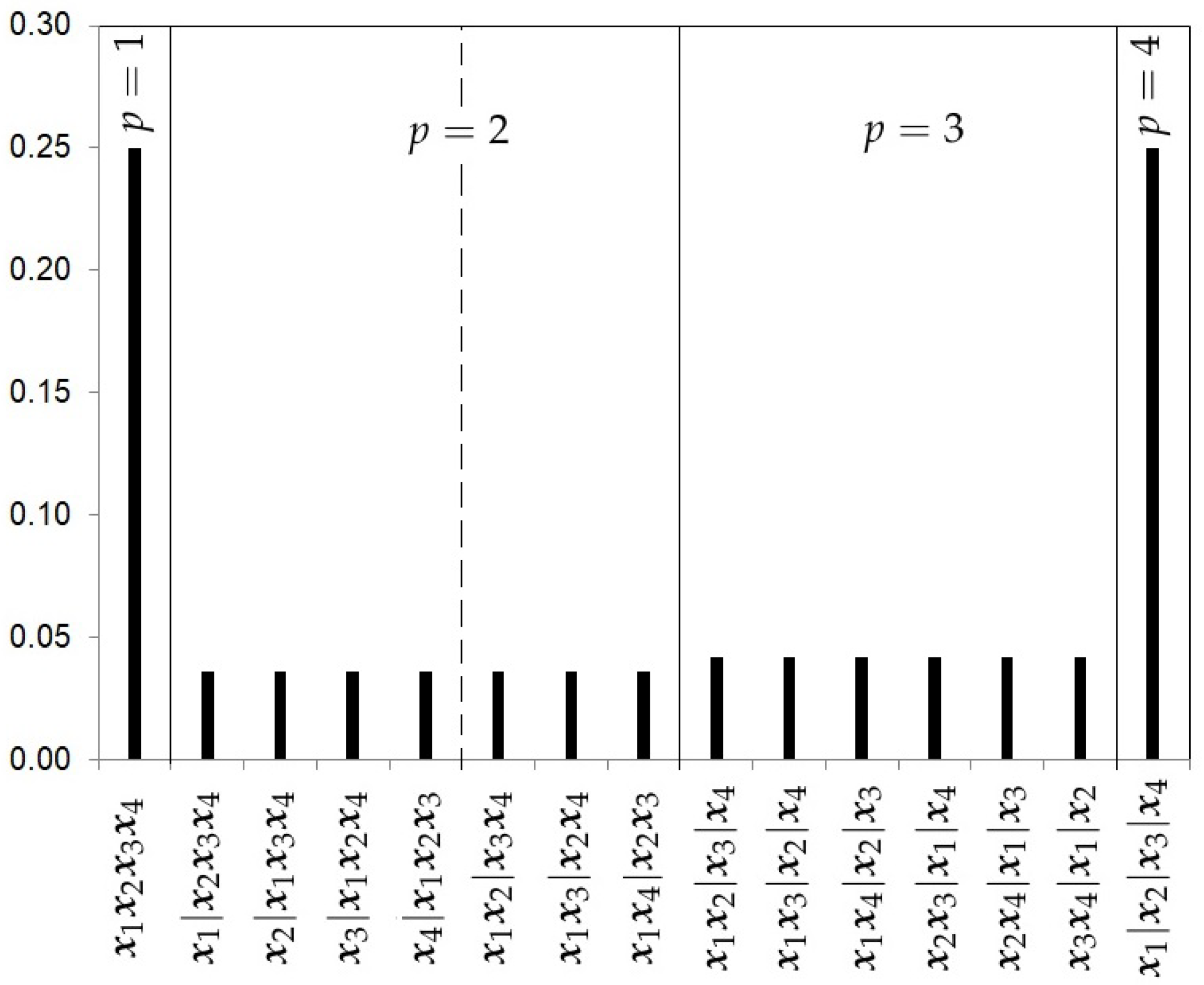
- The Hierarchical Uniform Prior with 2 levels (HU2).As recommended by Casella et al. [13], a hierarchical uniform prior can be appropriate to take into account the different levels of complexity of the partitions. This prior distribution distinguishes two levels of complexity in the partitions. The first level is given by the number of clusters p in which the k samples are grouped. The second level will be given by the number of possible partitions of the k samples into p clusters. Let represent this set of partitions into p clusters, which we call the cluster class. The number of partitions in is given by the Stirling number of the second kind and can be written aswhere is the multinomial coefficient and corrects the count by considering the redundant strings corresponding to the vector . For instance, to calculate the Stirling number , there are two possible vectors , the vector , and the vector , and the Stirling number would bewhich is the number of possible partitions for and .The hierarchical uniform distribution for 2 levels will be given by the decompositionFigure 3 shows the prior probabilities for each partition using the hierarchical uniform prior with 2 levels with 4 studies. Note that this hierarchical distribution assigns a higher prior probability to cases of homogeneity and heterogeneity.
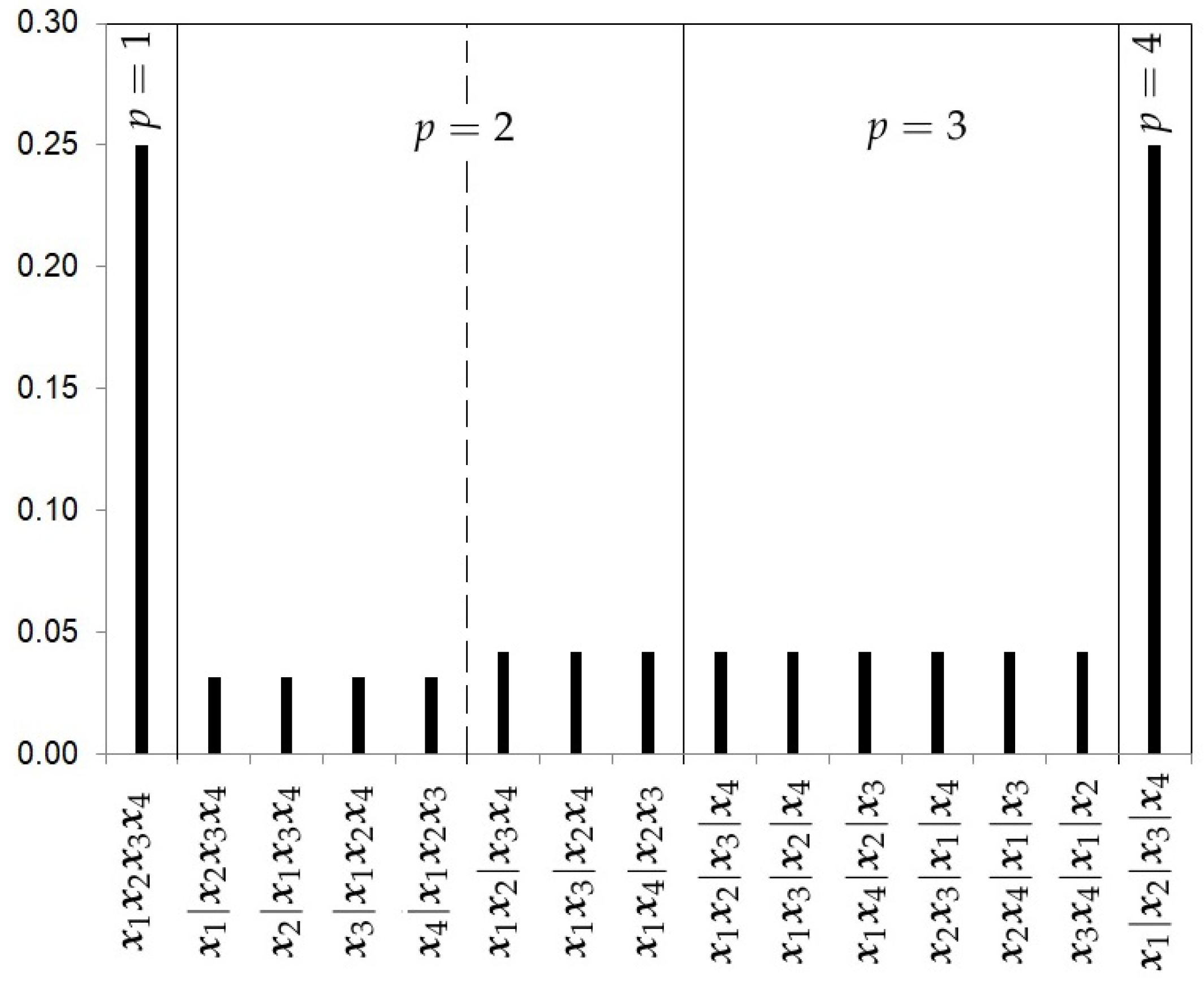
- The Hierarchical Uniform Prior with 3 levels (HU3).Following Casella et al. [13] and Moreno et al. [10], the prior specification for can be decomposed in three levels:Unlike the previous prior distribution, the hierarchical uniform prior with 3 levels considers the number of ways the integer k can be partitioned into p clusters. We will call it the number of configuration classes within each and it will be denoted by . In our illustrative example with , this value is equal to 1 for (, and only for the cluster class there are two configuration classes, corresponding to the configurations and , so .The hierarchical uniform prior with 3 levels is given by the expressionFigure 4 shows the prior probabilities for each partition using the hierarchical uniform prior with 3 levels and 4 studies.
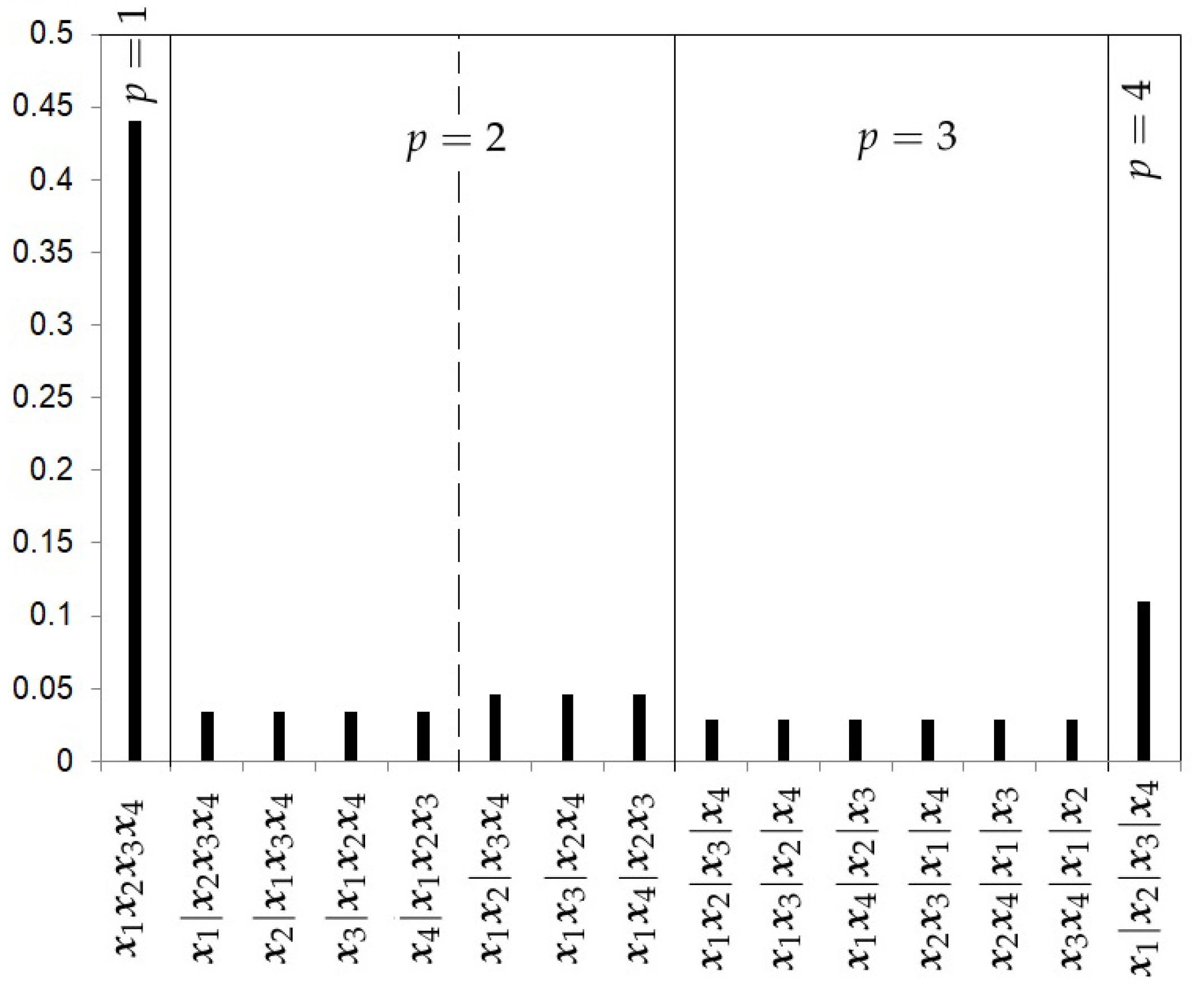
- The Hierarchical Poisson Prior with 3 levels (HP3).Casella et al. [13] argue that when analyzing a cluster problem of a sample size k, the extreme case of having k clusters should be given a priori a smaller probability than that given to any other case. Extending this argument for any k, it might be reasonable that the prior distribution on the number of clusters might be a truncated Poisson distribution , where is an unknown parameter. We can assume an intrinsic prior for , constructed by testing the Poisson null hypothesis versus [17],where denotes the confluent hypergeometric function. The reason for taking is that the one cluster model is the reference model throughout the analysis. The resulting marginal intrinsic distribution for p isWe cannot assume a Poisson distribution for the other two levels of the hierarchical structure because there is no a clear order in relation to complexity. For this reason, a uniform distribution is assumed for the other two levels. The hierarchical Poisson prior will be given byFigure 5 shows the prior probabilities for each partition using the hierarchical Poisson prior with 4 studies. The prior probability for the homogeneity cluster is more than four times higher than the prior probability of the heterogeneity case.
2.5. Bayesian Model Averaging in the Meta-Analysis
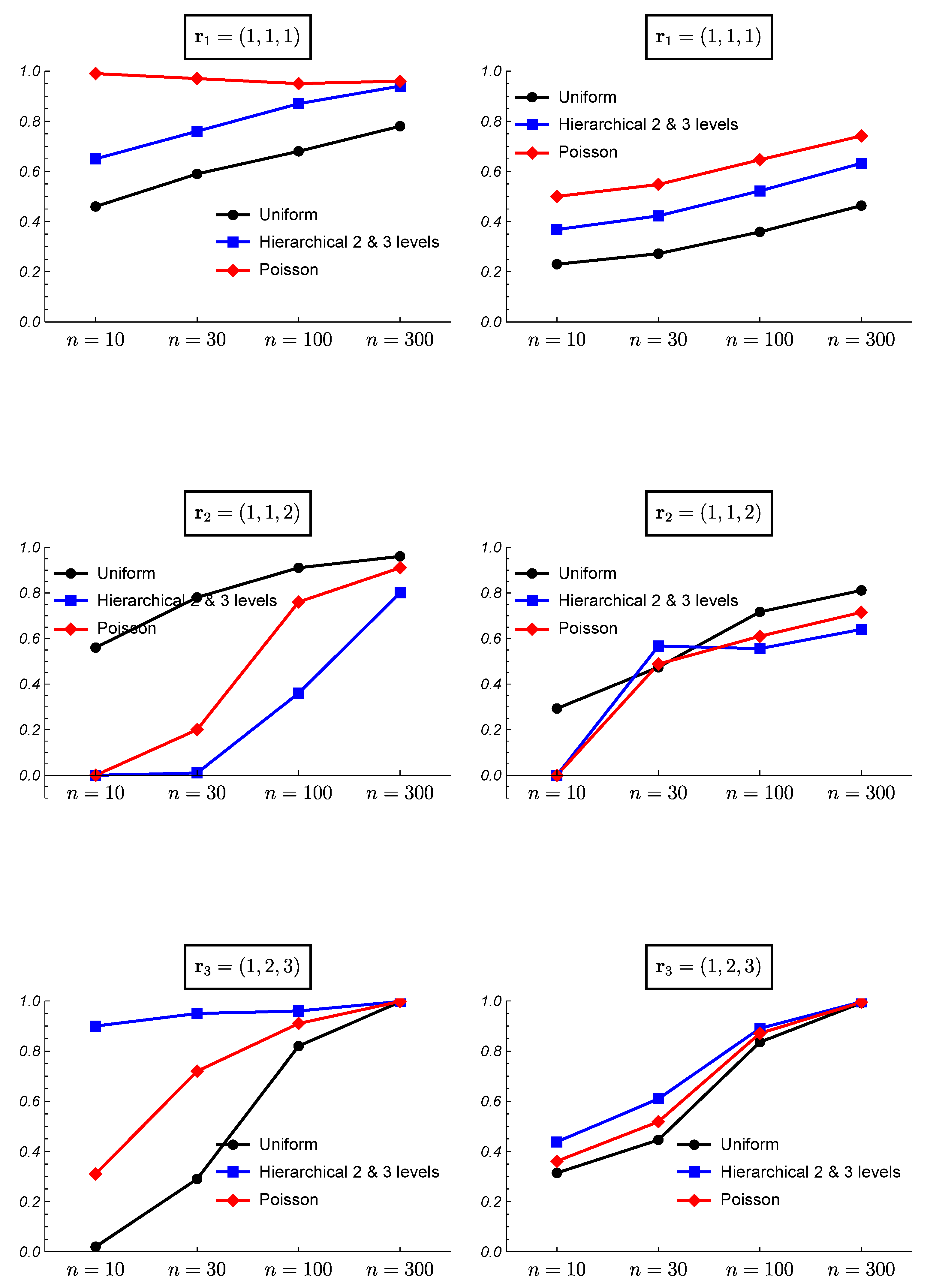
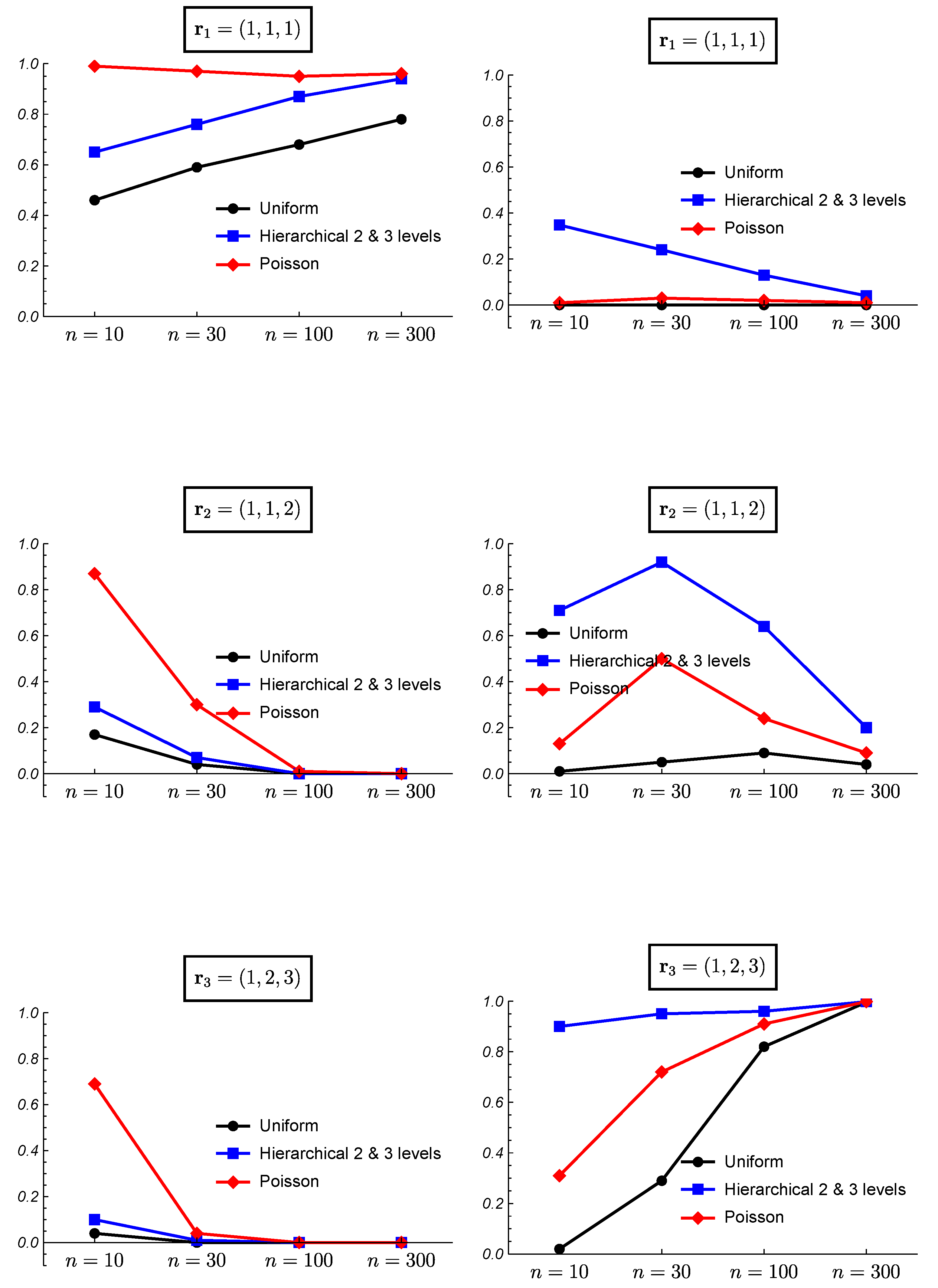
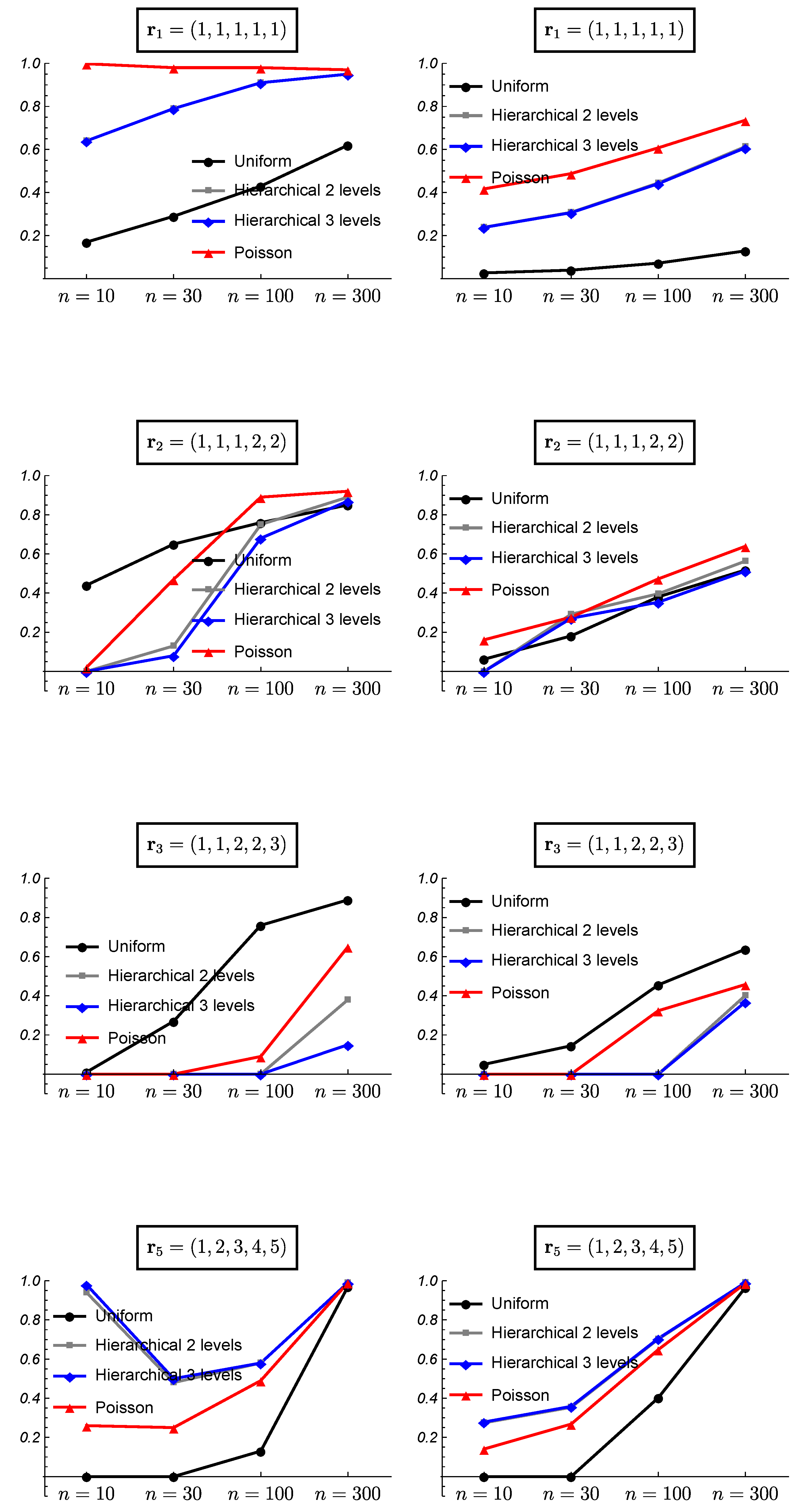
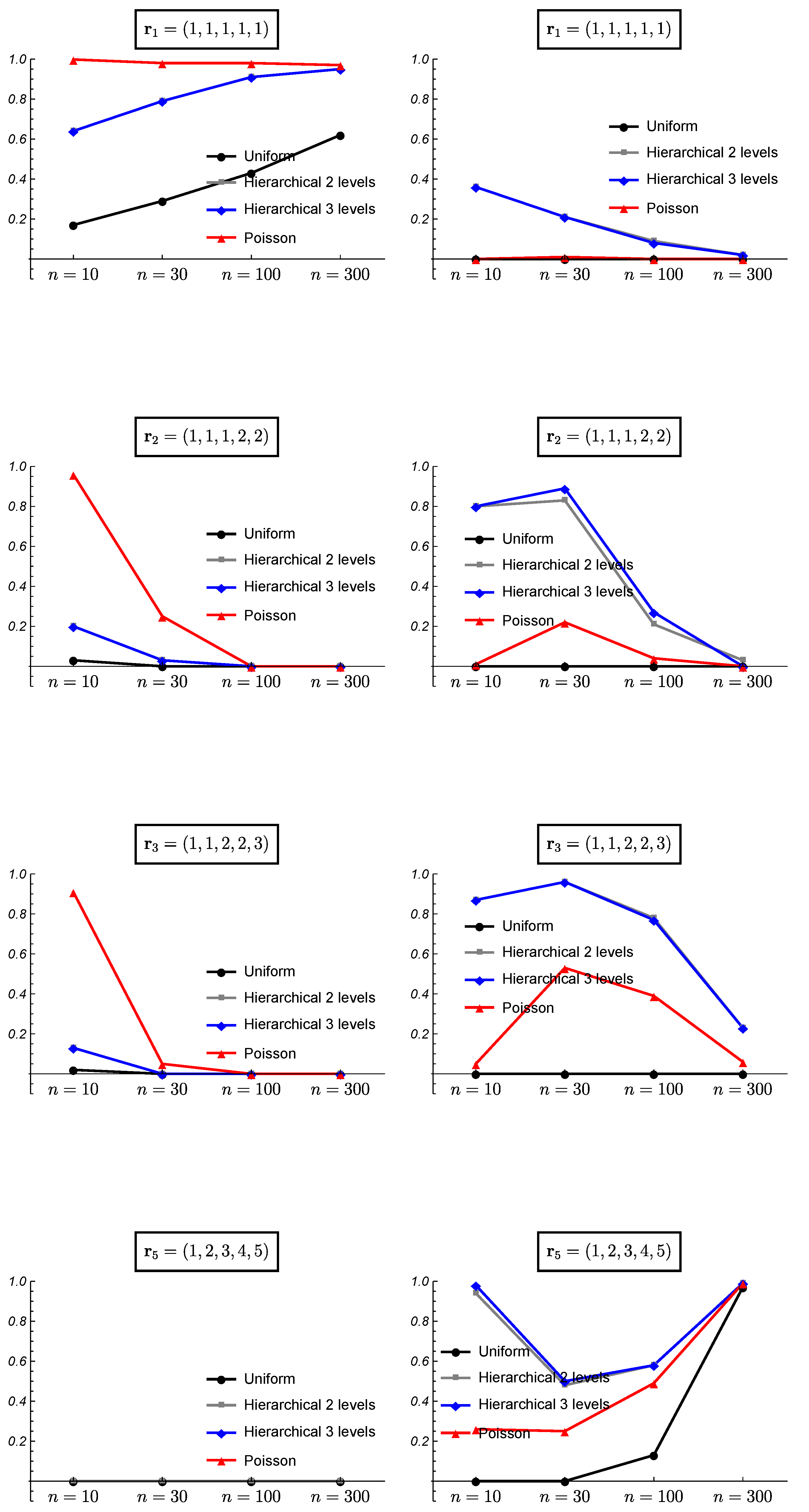
3. Simulated Data and Frequentist Validation
3.1. Simulated Data
3.2. Frequentist Evaluation
4. An Illustrative Example with Real Data
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thomas, D.; Radji, S.; Benedetti, A. Systematic review of methods for individual patient data meta- analysis with binary outcomes. BMC Med. Res. Methodol. 2014, 14, 79. [Google Scholar] [CrossRef]
- Charles, P.; Giraudeau, B.; Dechartres, A.; Baron, G.; Ravaud, P. Reporting of sample size calculation in randomised controlled trials: Review. BMJ 2009, 338, b1732. [Google Scholar] [CrossRef]
- Sutton, A.J.; Abrams, K.R. Bayesian methods in meta–analysis and evidence synthesis. Stat. Methods Med. Res. 2001, 10, 277–303. [Google Scholar] [CrossRef]
- Morris, C.N.; Norm, S.L. Hierarchical models for combining information and for meta–analyses. In Bayesian Statistics 4; Bernardo, J.M., Berger, J.O., Dawid, A.P., Smith, A.F.M., Eds.; Clarendon Press: Oxford, UK, 1992; pp. 321–344. [Google Scholar]
- Carlin, J.B. Meta–analysis for 2x2 tables: A Bayesian approach. Stat. Med. 1992, 11, 141–159. [Google Scholar] [CrossRef]
- Sutton, A.J.; Abrams, K.R.; Jones, D.R.; Sheldon, T.A.; Song, F. Methods for Meta–Analysis in Medical Research; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Bhaumik, D.K.; Amatya, A.; Norm, S.L.T.; Greenhouse, J.; Kaizar, E.; Neelon, B.; Gibbons, R.D. Meta–Analysis of rare binary adverse event. J. Am. Stat. Assoc. 2012, 107, 555–567. [Google Scholar] [CrossRef]
- Sweeting, M.J.; Sutton, A.J.; Lambert, P.C. What to add to nothing? Use and avoidance of continuity corrections in meta–analysis of sparse data. Stat. Med. 2004, 23, 1351–1375. [Google Scholar] [CrossRef]
- Moreno, E.; Vázquez–Polo, F.J.; Negrín, M.A. Objective Bayesian meta–analysis for sparse discrete data. Stat. Med. 2014, 33, 3676–3692. [Google Scholar] [CrossRef]
- Moreno, E.; Vázquez–Polo, F.J.; Negrín, M.A. Bayesian meta–analysis: The role of the between–sample heterogeneity. Stat. Methods Med. Res. 2018, 27, 3643–3657. [Google Scholar] [CrossRef]
- Hartigan, J. Partition models. Commun. Stat. Theory Met. 1990, 19, 2745–2756. [Google Scholar] [CrossRef]
- Barry, D.; Hartigan, J.A. Product partition models for change point problems. Ann. Stat. 1992, 20, 260–279. [Google Scholar] [CrossRef]
- Casella, G.; Moreno, E.; Girón, F.J. Cluster analysis, model selection, and prior distributions on models. Bayesian Anal. 2014, 9, 613–658. [Google Scholar] [CrossRef]
- Tuyl, F.; Gerlach, R.; Mengersen, K. A comparison of Bayes–Laplace, Jeffreys, and other priors: The case of zero events. Am. Stat. 2008, 62, 40–44. [Google Scholar] [CrossRef]
- Tuyl, F.; Gerlach, R.; Mengersen, K. Posterior predictive arguments in favor of the Bayes–Laplace prior as the consensus prior for binomial and multinomial parameters. Bayesian Anal. 2009, 4, 151–158. [Google Scholar] [CrossRef]
- Berger, J.O.; Pericchi, L.R. The intrinsic Bayes factor for model selection and prediction. J. Am. Stat. Assoc. 1996, 91, 109–122. [Google Scholar] [CrossRef]
- Moreno, E. Objective Bayesian methods for one–sided testing. Test 2005, 14, 181–198. [Google Scholar] [CrossRef]
- Davey, J.; Turner, R.M.; Clarke, M.J.; Higgins, J.P. Characteristics of meta–analyses and their component studies in the Cochrane Database of Systematic Reviews: A cross–sectional, descriptive analysis. BMC Med. Res. Methodol. 2011, 11, 160. [Google Scholar] [CrossRef]
- Stanworth, S.; Massey, E.; Hyde, C.; Brunskill, S.J.; Navaretter, C.; Lucas, G.; Marks, D.; Paulus, U. Granulocyte transfusions for treating infections in patients with neutropenia or neutrophill dysfunction (Review). Cochrane Libr. 2010, 8, 1–32. [Google Scholar]
- Friede, T.; Röver, C.; Wandel, S.; Neuenschwander, B. Meta–analysis of few small studies in orphan diseases. Res. Syn. Methods 2017, 8, 79–91. [Google Scholar] [CrossRef]
- Pateras, K.; Nikolakopoulos, S.; Mavridis, D.; Roes, K.C.B. Interval estimation of the overall treatment effect in a meta–analysis of a few small studies with zero events. Contemp. Clin. Trials Comm. 2018, 9, 98–107. [Google Scholar] [CrossRef]
- Berger, J. The case for objective Bayesian analysis. Bayesian Anal. 2006, 1, 385–402. [Google Scholar] [CrossRef]
- Crowley, E.M. Product partition models for normal means. J. Am. Stat. Assoc. 1997, 92, 192–198. [Google Scholar] [CrossRef]
- Quintana, F.A.; Iglesias, P.L. Bayesian clustering and product partition models. J. R. Stat. Soc. Ser. B Stat. Methodol. 2003, 65, 557–574. [Google Scholar] [CrossRef]
- McCullagh, P.; Yang, J. Stochastic classification models. In Proceedings of the International Congress of Mathematicians; Springer: Berlin/Heidelberg, Germany, 2006; pp. 669–686. [Google Scholar]
- Jensen, S.T.; Liu, J.S. Bayesian Clustering of Transcription Factor Binding Motifs. J. Am. Stat. Assoc. 2008, 103, 188–200. [Google Scholar] [CrossRef]
- Negrín, M.A.; Vázquez–Polo, F.J. Incorporating model uncertainty in cost–effectiveness analysis: A Bayesian model averaging approach. J. Health Econ. 2008, 27, 1250–1259. [Google Scholar] [CrossRef]

| True Model () | Parameters (’s) | Sample Sizes () |
|---|---|---|
| Study | Treatment | |
|---|---|---|
| Events | Total | |
| Herzig 1977 () | 1 | 16 |
| Higby 1975 () | 2 | 17 |
| Scali 1978 () | 0 | 13 |
| Vogler 1977 () | 7 | 17 |
| Prior # 1: Uniform | Prior # 2: HU with 2 levels | Prior # 3: HU with 3 Levels | Prior # 4: HP with 3 Levels | ||||
|---|---|---|---|---|---|---|---|
| Cluster Model | Post. Prob. | Cluster Model | Post. Prob. | Cluster Model | Post. Prob. | Cluster Model | Post. Prob. |
| 0.19 | 0.37 | 0.37 | 0.21 | ||||
| 0.14 | 0.11 | 0.10 | 0.18 | ||||
| 0.11 | 0.09 | 0.09 | 0.14 | ||||
| 0.11 | 0.08 | 0.08 | 0.8 | ||||
| 0.09 | 0.08 | 0.08 | 0.08 | ||||
| the rest | <0.09 | the rest | <0.07 | the rest | <0.07 | the rest | <0.07 |
| BMA estimates of the meta-parameter | |||||||
| Posterior mean: 0.164 | Posterior mean: 0.159 | Posterior mean: 0.159 | Posterior mean: 0.163 | ||||
| HDI: 0.050–0.317 | HDI: 0.049–0.312 | HDI: 0.049–0.311 | HDI: 0.048–0.327 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Negrín-Hernández, M.-A.; Martel-Escobar, M.; Vázquez-Polo, F.-J. Bayesian Meta-Analysis for Binary Data and Prior Distribution on Models. Int. J. Environ. Res. Public Health 2021, 18, 809. https://doi.org/10.3390/ijerph18020809
Negrín-Hernández M-A, Martel-Escobar M, Vázquez-Polo F-J. Bayesian Meta-Analysis for Binary Data and Prior Distribution on Models. International Journal of Environmental Research and Public Health. 2021; 18(2):809. https://doi.org/10.3390/ijerph18020809
Chicago/Turabian StyleNegrín-Hernández, Miguel-Angel, María Martel-Escobar, and Francisco-José Vázquez-Polo. 2021. "Bayesian Meta-Analysis for Binary Data and Prior Distribution on Models" International Journal of Environmental Research and Public Health 18, no. 2: 809. https://doi.org/10.3390/ijerph18020809
APA StyleNegrín-Hernández, M.-A., Martel-Escobar, M., & Vázquez-Polo, F.-J. (2021). Bayesian Meta-Analysis for Binary Data and Prior Distribution on Models. International Journal of Environmental Research and Public Health, 18(2), 809. https://doi.org/10.3390/ijerph18020809







