Abstract
Energy-saving and low-carbon technologies play important roles in reducing environmental risk and developing green tourism. An energy-saving and low-carbon technology scheme selection may often involve multiple criteria and sub-criteria as well as multiple stakeholders or decision makers, and thus can be structured as a hierarchical multi-criteria group decision making problem. This paper proposes a framework to solve group consensus decision making problems, where decision makers’ preferences between the alternatives considered with respective to each criterion are elicited by the paired comparison method, and expressed as triangular fuzzy preference relations (TFPRs). The paper first simplifies the existing computation formulas used to determine triangular fuzzy weights of TFPRs. A consistency index is then devised to measure the inconsistency degree of a TFPR and is used to check acceptable consistency of TFPRs. By introducing a possibility degree formula of comparing any two triangular fuzzy weights, an index is defined to measure the consensus level between an individual ranking order and the group ranking order for all alternatives. A consensus model is developed in detail for solving group decision making problems with TFPRs. A case study of selecting energy-saving and low-carbon technology schemes in star hotels is provided to illustrate how to apply the proposed group decision making consensus model in practice.
1. Introduction
The tourism industry has become one of the advantageous industries for developing the economy in China. However, this industry usually links a mass of energy consumption and carbon emissions [1,2], and has caused an increasing stress on the environment [3]. To save energy and reduce carbon emissions, the Chinese government has strongly promoted the development of the green economy. Green tourism has been considered an effective solution for energy-saving and environmental protection [4,5]. Constructing an energy-saving and low-carbon system in a star hotel is the fundamental way to respond in green tourism development [6,7]. On the other hand, there often exist different technologies used in constructing energy-saving and low-carbon systems in star hotels. Therefore, it is necessary to select the best one from multiple energy-saving and low-carbon technology schemes when a star hotel wishes to associate with green tourism.
Selection of energy-saving and low-carbon technology schemes in star hotels is frequently based on multiple assessment criteria and involves multiple experts or decision makers. This implies that such a selection can be viewed as a multi-criteria decision making (MCDM) problem with a group of experts.
The paired comparison method is a popular approach to eliciting decision makers’ preferences or judgments for solving MCDM problems. The judgments in typical paired comparison matrices are characterized by exact ratios. In order to treat with fuzziness of linguistic term-based preferences, Van Laarhoven and Pedrycz [8] proposed the concept of triangular fuzzy numbers and introduced triangular fuzzy preference relations (TFPRs) to model decision makers’ fuzzy judgments. Because decision input information often involves ambiguity, the TFPR based analytic hierarchy process (AHP) (also called fuzzy AHP) has become a common MCDM method, and has triggered a large number of applications in solving real-world decision problems [9].
In group MCDM with paired comparisons, a crucial issue is to check the quality of judgments provided by decision makers, where consistency and acceptable consistency play key roles. For typical paired comparison matrices, Saaty [10] proposed a consistency index (CI) to measure inconsistency degrees and introduced a consistency ratio (CR) to check acceptable consistency. Crawford & Williams [11] put forward another row-geometric-mean-based CI, which was formulated as a geometric consistency index (GCI) in [12]. For TFPRs, different consistency models have been developed in the literature [13,14,15,16]. Recently, Wang [16] used basic triangular fuzzy weights to define consistent TFPRs, and presented computation formulas used to determine triangular fuzzy weights of TFPRs. Some researchers [13,15,16] have pointed out that it is a challenge to develop an appropriate consistency index for measuring inconsistency of TFPRs and checking acceptable consistency of TFPRs.
Group consensus decision making with paired comparisons involves three different processes. The first process is to check acceptable consistency of individual judgments. The second process called a consensus reaching process is to seek a solution that is sufficiently supported by all decision makers. The last process is to derive a ranking order of all alternatives considered, or to select the best alternative(s). In solving group consensus decision making problems, it is important to develop a consensus model due to the fact that there often exists a large difference among initial judgments provided by decision makers, and thus different ranking orders may be obtained from individual judgments. On the other hand, it is hard to implement a unanimous consensus in solving an actual group decision making problem. A practice method is to use soft consensus measurement [17]. Different soft consensus models have been devised under fuzzy environments [18]. Chiclana et al. [19] gave a comparative study on similarity-based soft consensus models. For hesitant linguistic group decision making, Dong et al. [20] developed a minimum adjustment soft consensus model. Xu et al. [21] proposed a soft consensus model of group decision making with hesitant fuzzy preference relations, and applied it in water allocation management. Soft consensus models of group decision making with intuitionistic fuzzy preference relations can be found in [22,23]. Tan et al. [24] put forward a soft consensus model of group decision making with interval fuzzy preference relations, and used it to solve cooking method selection problems for decreasing organic pollutants in food of animal origin. However, there are two main limitations in the aforementioned soft consensus models: (i) acceptable consistency of individual fuzzy judgments is not enough considered; and (ii) they are based on similarity between individual judgments and aggregated group preferences, implying that the similarity between individual and group decision results is not sufficiently taken into account.
In this paper, we simplify the triangular fuzzy weight computation formulas given in [16]. Based on the simplified expressions, a consistency index is presented to measure the inconsistency degree of a TFPR, and used to check acceptable consistency of TFPRs. We put forward a possibility degree formula for comparing and ranking triangular fuzzy weights. A likelihood degree matrix based index is defined to measure the consensus level between individual and group decision results. Based on the proposed consistency index and consensus index, the paper develops a consensus model for solving group decision making problems with TFPRs.
The remainder of the paper is organized as follows. Section 2 provides the theoretical background, including triangular fuzzy numbers, consistency and triangular fuzzy weights of TFPRs. In Section 3, we simplify the triangular fuzzy weight computation formulas and develop a consistency index for TFPRs. A likelihood degree matrix-based consensus index is defined and a consensus model of group decision making with TFPRs is proposed in Section 4. Section 5 offers a case study of selecting energy-saving and low-carbon technology schemes in star hotels to examine the developed fuzzy group consensus decision making model. Finally, Section 6 draws concluding remarks.
2. Theoretical Background
2.1. Triangular Fuzzy Numbers and Triangular Fuzzy Preference Relations
The fuzzy set theory introduced by Zadeh [25] uses membership functions to represent possibility distributions of imprecise data. A triangular fuzzy number is a fuzzy subset of the real line with the following membership function:
where is the modal value of , and and are the lower and upper bounds of the support interval of , respectively.
Obviously, is a triangular and piecewise linear function. Thus, the triangular fuzzy number can be characterized by a triplet . If , then is called a positive triangular fuzzy number. In addition, the reciprocal of is often denoted by , that is, .
Triangular fuzzy numbers are an effective tool for modelling semantic values of linguistic terms. In constructing fuzzy-based decision support systems, we need to assign a set of fuzzy numbers corresponding to a linguistic term set [26,27]. Different triangular fuzzy assignment models (also called triangular fuzzy scales) have been proposed in the literature [28,29,30,31]. Recently, Centobelli et al. [32,33] used trapezoidal fuzzy numbers to assign two linguistic term sets respectively characterizing formalization and sharing degrees of knowledge management tools and knowledge management practices.
In fuzzy MCDM with pairwise comparison matrices, the linguistic term set used must be bipolar, and must have a neutral linguistic term, such as “Indifference” or “Equal importance”. This implies that the set of the codified triangular fuzzy numbers has reciprocity. In other words, for any triangular fuzzy number in the set, its reciprocal is also an element of the set.
Once linguistic term-based triangular fuzzy scales have been established, decision makers can use them to elicit paired comparison results, and TFPRs can be employed to describe the decision makers’ fuzzy judgments.
Let be a set of considered alternatives. A pairwise comparison matrix is said a TFPR on if
where is a positive triangular fuzzy number, and indicates a ratio-based fuzzy preference of alternative over .
Because of efficiency and effectiveness of expressing paired comparison results with vagueness, TFPRs have been widely used in practice, and promoted the theoretical development of fuzzy MCDM [9]. Numerous applications of fuzzy MCDM can be found in the current literature. For instance, Yücenur et al. [34], Lima Junio et al. [35] and Yu et al. [36] used triangular fuzzy MCDM to solve supplier selection problems in green supply chains of industrial industry. Azadeh and Zadeh [37] used a MCDM combined fuzzy analytic hierarchy process to examine maintenance policy selection problems in green manufacturing (also called environmentally conscious manufacturing). Çelikbilek and Tüysüz [38] employed an integrated grey based MCDM method to evaluate renewable energy sources. Grujic et al. [39] applied MCDM in selecting the optimal heat demand in a centralized supply system. Tong and Wang [40] put forward an intuitionistic fuzzy MCDM method for solving low-carbon supplier selection problems. An evaluation indicator system was constructed in Cho et al. [41] by using a fuzzy pairwise comparison-based analytic hierarchy process. Mardani et al. [42] adopted fuzzy MCDM to evaluate energy-saving technologies in five star hotels.
2.2. Consistency and Fuzzy Weights of Triangular Fuzzy Preference Relations
For a triangular fuzzy weight vector with (), let
where
It is easy to confirm that satisfies (2) and thus, is a TFPR.
A triangular fuzzy weight vector is said to be modal-value normalized [16] if the following equation holds true.
A fuzzy weight vector is called a basic triangular fuzzy weight vector [16] if the following equation is satisfied.
Wang [16] showed that basic triangular fuzzy weight vectors and modal-value normalized triangular fuzzy weight vectors can be equivalently converted into each other, and thus used the basic triangular fuzzy weight vectors to define consistent TFPRs as follows.
Definition 1.
[16] A TFPRis said to be consistent if there exists a basic triangular fuzzy weight vector such that.
In [16], some goal programming models were developed to obtain triangular fuzzy weights denoted by three computation formulas from TFPRs. For any TFPR (), let
Then, its triangular fuzzy weight vector with () is determined as follows.
where
It has been shown in [16] that if , then () defined by (12)–(14) are optimized triangular fuzzy weights derived from . Moreover, the following important result can be used to judge whether a TFPR is consistent under Definition 1.
Lemma 1.
[16] A TFPR () is consistent if and only if , where is defined by (3) and (4).
3. Inconsistency Measurement for Triangular Fuzzy Preference Relations
This section first simplifies the three computation Formulas (12)–(14). A consistency index of TFPRs is then introduced to measure the inconsistency degree of a TFPR.
Let
Obviously, for all . Then we have following result.
Theorem 1.
Let() be a TFPR, then
Proof.
If , it follows from (18) that . As per (9) and (10), one can obtain and . Thus,
Similarly, (19) and (20) hold true because if . Thus, the proof of Theorem 1 is completed. □
Based on Theorem 1, (11) can be equivalently expressed as
Let
Then, we have the following theorem.
Theorem 2.
Let() be a TFPR, then() defined by (12)–(14) can be equivalently expressed as
where,,andare defined by (7), (15), (22) and (23), respectively.
Proof.
It is obvious that the second formula in (24) is the same as (13). Next, we prove that (12) and (14) can be respectively rewritten as the first formula in (24) and the last formula in (24) by considering the following three cases.
Case 1: . In this case, . As per (16) and (17), we have . It follows from (9), (10), (12) and (14) that
where the third equality in (25) is derived from (19), and the third equality in (26) is obtained from (20) in Theorem 1.
Case 2: . In this case, it directly follows from (22), (23) and that and . Thus, we have .
According to Theorem 1, one gets
As per (16) and (17), we obtain and . By (9), (10), (12) and (14), one has
where the last equality in (28) is confirmed by , and the third equality in (28) is obtained from (20).
Case 3: . In this case, as per (22), (23) and , we have and . Therefore, one has
According to (19) and (20), we obtain
According to (16) and (17), one gets and . It follows from (9), (10), (12) and (14) that
where the last equality in (29) is obtained from , and the third equality in (29) is derived from (19) in Theorem 1.
Therefore, we complete the proof of Theorem 2. □
According to (5), it is easy to confirm that if , then the triangular fuzzy weight vector with () defined by (24) is modal-value normalized. If for all , then is a basic triangular fuzzy weight vector. If and , then is a normalized basic triangular fuzzy weight vector.
Motivated by the geometric inconsistency measurement model for pairwise comparison matrices presented by Crawford and Williams [11], we define the following consistency index to measure the inconsistency degree of a TFPR.
Definition 2.
Given a TFPR, andthetriangular fuzzy weights() obtained by (24), a consistency index (CI) is defined as
Obviously, . The first part is the squared distance between the log of the lower bound of the support interval of the fuzzy judgment and the log of the value . The second part in (31) is squared distance between the log of the modal value of the fuzzy judgment and the log of the ratio . The last part is the squared distance between the log of the upper bound of the support interval of the fuzzy judgment and the log of the value . This implies that gives a distance between the two TFPRs and , where and is defined by (3) and (4). As per Lemma 1, if is consistent. The bigger the value , the stronger the inconsistency level of the fuzzy judgments in .
According to (24) and the reciprocity of , can be equivalently expressed as
Definition 3.
Given a TFPR, and an acceptable consistency threshold(), thenis acceptable if.
If a FFPR becomes an original comparison matrix [10], that is, for all , then by (7), (22) and (23), we have , and for each . In this case, , which is the same as the geometric inconsistency index reformulated by Aguaron and Moreno-Jimenez [12]. This shows that the approximated thresholds given in [12] can be used to check acceptable consistency of TFPRs. These thresholds are shown in Table 1.

Table 1.
Geometric inconsistency approximated thresholds.
4. A Group Decision Making Consensus Model Based on Triangular Fuzzy Preference Relations
This section introduces a possibility degree formula to compare any two positive triangular fuzzy weights. An index is defined to measure the consensus levels of individual TFPRs, and a consensus model is developed to solve group MCDM problems with TFPRs.
For a group decision making problem with a set of decision makers , each decision maker () carries out pairwise comparisons on , and provides a TFPR to describe his/her fuzzy judgments. As per (3.7), one can obtain a triangular fuzzy weight vector denoted by with () for each of ().
Assume that the importance weight of the decision maker is , where and , then a group TFPR is obtained by using the following aggregation method.
According to (24), a group triangular fuzzy weight vector is derived and denoted by with ().
In order to compare and rank triangular fuzzy weights obtained from TFPRs by using the computation Formula (24), a possibility degree formula is introduced as follows.
Definition 4.
Given any twotriangular fuzzy weightsand, the likelihood degree ofbeingno less thanis defined as
As and , one has , and .
Based on (34) and the obtained triangular fuzzy weights (), a likelihood degree matrix can be established as
for each .
Similarly, based on the group triangular fuzzy weights (), a group likelihood degree matrix is established as
Based on (35) and (36), an index is introduced to measure the consensus of individual judgments with respect to and the group result.
Definition 5.
Let() be the likelihood degree matrix defined by (35), andbe the group likelihood degree matrix defined by (36), the consensus index of the individual judgments inwith respective to the group result is defined as
Obviously, for each . If , then , implying that the likelihood of the ranking order of any two alternatives based on is the same as that based on , and the ranking orders of all alternatives obtained from and are fully identical. The bigger the value of , the stronger the consensus between the individual ranking order with likelihoods and the group result.
Let () be an acceptable consensus threshold, if for all , then there is a consensus result among the m decision makers. If (), then there does not exist a consensus among the m decision makers. In this case, the fuzzy judgments in should be returned to the decision maker for a re-statement.
Based on the aforesaid analysis, we devise an acceptable consistency and acceptable consensus-based group decision making procedure as follows.
Step 1: Employ the computation Formula (32) to compute the inconsistency index for each of the individual TFPRs ().
Step 2: Check acceptable consistency of () according to Definition 3. If all individual TFPRs () are of acceptable consistency, then go to the next step; otherwise, return the unacceptable TFPR () to the decision maker for a revision and go to step 10.
Step 3: Aggregate individual TFPRs () into a group TFPR as per (33).
Step 4: Utilize the computation Formula (24) to obtain triangular fuzzy weights () from each of the individual TFPRs (), and to derive the group fuzzy weights () from .
Step 5: Use the Formula (34) to calculate likelihood degrees () and ().
Step 6: Establish likelihood degree matrices () and as per (35) and (36).
Step 7: Use (37) to determine the consensus index of the individual judgments in for each . If for all , then go to the next step; otherwise, return the TFPR having () to the decision maker for a modification and go to step 10.
Step 8: Sum values in the ith row of the group likelihood degree matrix , and obtain ranking scores ().
Step 9: Rank the alternatives in according to the decreasing order of the scores ().
Step 10: End.
5. A Case Study of Selecting Energy-Saving and Low-Carbon Technology Schemes in Star Hotels
In this section, the proposed group decision making consensus model is applied to examine an energy-saving and low-carbon technology scheme selection problem for star hotels.
With the development of green tourism, numerous star hotels in China have faced the construction of a sustainable energy-saving and low-carbon system. An important stage in constructing such a system is to select the best one from multiple energy-saving and low-carbon technology schemes. According to the experts’ viewpoints and literature on energy-saving and low-carbon technologies, key criteria are identified and categorized into three groups as follows:
- (1)
- : Energy efficiency. Efficiencies of the considered energy equipment and the overall technical system are two important factors in selecting energy-saving and low-carbon technology schemes for star hotels. Energy efficiency has been widely acknowledged as a promising approach for tackling environmental issues, and thus improving energy efficiency in star hotels is becoming increasingly significant. Energy efficiency programs offer a development prospect of renewable energy requirements. The energy efficient equipment in star hotels includes energy saving light bulbs, boilers and cooling equipment with high efficiency, recovery systems, and so on.
- (2)
- : Capacity of energy-saving and carbon emission reduction. This capacity indicates the suitable performance of a technology scheme. The stronger the capacity, the better the technology scheme. Moreover, this criterion could be divided to two sub-criteria below.
- (i)
- : Energy-saving capacity. This sub-criterion reflects the energy-saving performance and indicates how much energy is saved from the technology scheme.
- (ii)
- : Low-carbon capacity. This sub-criterion reflects the low-carbon performance and shows how much carbon emission is reduced by the technology scheme.
- (3)
- : Economic effectiveness. To rank energy-saving and low-carbon technology schemes, the investment cost plays an important role. The main goal of this criterion is lower investment cost with better performance. Therefore, this criterion is often measured and reflected by investment payback periods of per unit energy-saving and per unit carbon emission reduction.
After preliminary screening, four technology schemes () are determined by a star hotel as the evaluated alternatives. Hence, this MCDM problem can be structured as a hierarchy shown in Figure 1.
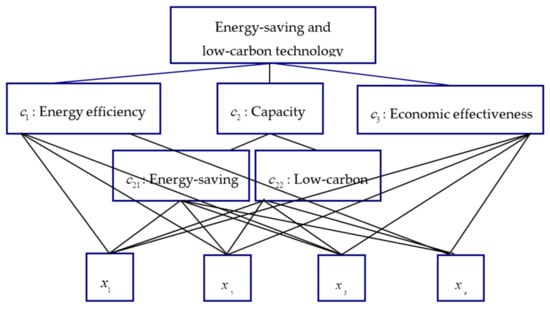
Figure 1.
Decision Hierarchical structure.
Assume that three experts , and are asked to evaluate the four technology schemes based on the above criteria and sub-criteria, and their importance weights are 04, 0.3 and 0.3, respectively. Each expert () employs the paired comparison method to elicit his/her fuzzy judgments for the four technology schemes with respect to each of the four criteria or sub-criteria and , and structured these fuzzy judgments as TFPRs listed in Table , where .
According to the computation Formula (32), inconsistency indices of the individual TFPRs given in Table 2, Table 3 and Table 4 are determined and shown in the second column in Table 5.

Table 2.
Triangular fuzzy judgments provided by the expert .

Table 3.
Triangular fuzzy judgments provided by the expert .

Table 4.
Triangular fuzzy judgments provided by the expert .

Table 5.
Inconsistency and consensus indices as well as triangular fuzzy weights.
Assume that an acceptable consistency threshold is set to be 0.3562, which is a geometric inconsistency approximated threshold value corresponding to pairwise comparison matrices and listed in Table 1. Thus, as per Definition 3, all individual TFPRs given in Table 2, Table 3 and Table 4 are of acceptable consistency. According to (33), group TFPRs are obtained and shown in Table 6.

Table 6.
The obtained group triangular fuzzy judgments.
By using the computation Formula (24), triangular fuzzy weights () are determined and respectively listed in the last four columns in Table 5 for each individual TFPR. Similarly, group triangular fuzzy weights are derived from each group TFPR given in Table 6, and are shown in Table 7.

Table 7.
Triangular fuzzy weights of group TFPRs.
As per (34) and (35), twelve likelihood degree matrices are obtained from triangular fuzzy weights given in Table 5 for the individual TFPRs. By using (34) and (36), we can establish four likelihood degree matrices from the group triangular fuzzy weights shown in Table 7. According to (37), consensus indices of the individual judgments listed in Table 2, Table 3 and Table 4 are determined and shown in the third column in Table 5.
Assume that acceptable consensus thresholds are respectively set to be 0.8, 0.7, 0.65 and 0.75 for group decision making problems on the key criteria or sub-criteria and . Then, it follows from the consensus indices given in Table 5 that each consensus index is more than or equal to its acceptable threshold. This implies that the three experts reach a consensus ranking order listed in the last column in Table 7.
In order to obtain a final ranking order of the four technology schemes, we need to aggregate triangular fuzzy weights in Table 7 into overall fuzzy weights of (). Assume that importance weights of criteria or sub-criteria and are 0.35, 0.2, 0.15 and 0.3. Using triangular fuzzy geometric weighting method yields overall fuzzy weights as
According to (34), a likelihood degree matrix is established as
By summing values in the ith row of the above matrix , we obtain ranking scores and . As , the four technology schemes are ranked as , and thus is the best technology scheme.
6. Conclusions
This paper has developed a triangular fuzzy group consensus decision making model. This model takes both acceptable consistency of individual judgments and acceptable consensus of individual and group decision results into consideration. A consistency index has been proposed to measure inconsistency of TFPRs. A possibility degree-based index has been devised to measure consensus of individual and group ranking orders of all alternatives. A case study of selecting energy-saving and low-carbon technology schemes in star hotels has been offered to examine the application of the group consensus decision making model developed.
Some significant issues could be addressed in the future. For instance, sometimes, a decision maker may provide extremely fuzzy judgments in a TFPR while this TFPR may be judged to be acceptable under the proposed acceptable consistency model. In addition, some judgments in an original TFPR may be missing. It is worth examining how the simplified computation formulas and the proposed consistency index are adapted and extended to handle these cases.
Author Contributions
P.L. was responsible for developing the consensus model and the case study, and drafted the initial manuscript. X.Y. was responsible for deriving the consistency index model and participated in the case study. Z.-J.W. offered the relevant literature review and the major idea of the developed models, and finalized the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 71671160), the Zhejiang Provincial Natural Science Foundation of China (Grant No. Y19G010018), the Open Foundation of Medical Data Mining and Application Engineering Research Center of Fujian Province of China (Grant No. MDM2018001), the Education Scientific Project of Young Teacher of Fujian Province of China (Grant No. JAS160381), and the Social Science Program of Zhejiang Province of China (Grant No. 16NDJC148YB).
Acknowledgments
The authors would like to thank the Editor and anonymous reviewers whose comments and suggestions improved the quality of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cheng, Q.; Su, B.; Tan, J. Developing an evaluation index system for low-carbon tourist attractions in China—A case study examining the Xixi wetland. Tour. Manag. 2013, 36, 314–320. [Google Scholar] [CrossRef]
- Liu, X.; Liu, J. Measurement of low carbon economy efficiency with a three-stage data envelopment analysis: A comparison of the largest twenty CO2 emitting countries. Int. J. Environ. Res. Public Health 2016, 13, 1116. [Google Scholar] [CrossRef] [PubMed]
- Bailey, I.; Caprotti, F. The Green Economy: Functional Domains and Theoretical Directions of Enquiry. Environ. Plan. A 2014, 46, 1797–1813. [Google Scholar] [CrossRef]
- Dagoumas, A.S.; Barker, T.S. Pathways to a low-carbon economy for the UK with the macro-econometric E3MG model. Energy Policy 2010, 38, 3067–3077. [Google Scholar] [CrossRef]
- Pan, S.Y.; Gao, M.; Kim, H.; Shah, K.J.; Pei, S.L.; Chiang, P.C. Advances and challenges in sustainable tourism toward a green economy. Sci. Total Environ. 2018, 635, 452–469. [Google Scholar] [CrossRef] [PubMed]
- Tölkes, C. Sustainability communication in tourism—A literature review. Tour. Manag. Perspect. 2018, 27, 10–21. [Google Scholar] [CrossRef]
- Azam, M.; Alam, M.M.; Hafeez, M.H. Effect of tourism on environmental pollution: Further evidence from Malaysia, Singapore and Thailand. J. Clean. Prod. 2018, 190, 330–338. [Google Scholar] [CrossRef]
- Van Laarhoven, P.J.M.; Pedrycz, W. A fuzzy extension of Saaty’s priority theory. Fuzzy Sets Syst. 1983, 11, 229–241. [Google Scholar] [CrossRef]
- Zyoud, S.H.; Fuchs-Hanusch, D. A bibliometric-based survey on AHP and TOPSIS techniques. Expert Syst. Appl. 2017, 78, 158–181. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Crawford, G.; Williams, C. A note on the analysis of subjective judgment matrices. J. Math. Psychol. 1985, 29, 387–405. [Google Scholar] [CrossRef]
- Aguaron, J.; Moreno-Jimenez, J.M. The geometric consistency index: Approximated thresholds. Eur. J. Oper. Res. 2003, 147, 137–145. [Google Scholar] [CrossRef]
- Liu, F.; Pedrycz, W.; Wang, Z.X.; Zhang, W.G. An axiomatic approach to approximation-consistency of triangular fuzzy reciprocal preference relations. Fuzzy Sets Syst. 2017, 322, 1–18. [Google Scholar] [CrossRef]
- Wang, Z.J.; Lin, J. Acceptability measurement and priority weight elicitation of triangular fuzzy multiplicative preference relations based on geometric consistency and uncertainty indices. Inf. Sci. 2017, 402, 105–123. [Google Scholar] [CrossRef]
- Krejčí, J. On multiplicative consistency of interval and fuzzy reciprocal preference relations. Comput. Ind. Eng. 2017, 111, 67–78. [Google Scholar] [CrossRef]
- Wang, Z.J. A goal-programming-based heuristic approach to deriving fuzzy weights in analytic form from triangular fuzzy preference relations. IEEE Trans. Fuzzy Syst. 2018. [Google Scholar] [CrossRef]
- Cabrerizo, F.J.; Moreno, J.M.; Pérez, I.J.; Herrera-Viedma, E. Analyzing consensus approaches in fuzzy group decision making: Advantages and drawbacks. Soft Comput. 2010, 14, 451–463. [Google Scholar] [CrossRef]
- Herrera-Viedma, E.; Cabrerizo, F.J.; Kacprzyk, J.; Pedrycz, W. A review of soft consensus models in a fuzzy environment. Inf. Fusion 2014, 17, 4–13. [Google Scholar] [CrossRef]
- Chiclana, F.; Tapia-Garcia, J.M.; del Moral, M.J.; Herrera-Viedma, E. A statistical comparative study of different similarity measures of consensus in group decision making. Inf. Sci. 2013, 221, 110–123. [Google Scholar] [CrossRef]
- Dong, Y.C.; Chen, X.; Herrera, F. Minimizing adjusted simple terms in the consensus reaching process with hesitant linguistic assessments in group decision making. Inf. Sci. 2015, 297, 95–117. [Google Scholar] [CrossRef]
- Xu, Y.; Cabrerizo, F.J.; Herrera-Viedma, E. A consensus model for hesitant fuzzy preference relations and its application in water allocation management. Appl. Soft Comput. 2017, 58, 265–284. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z.; Zeng, X.J.; Xu, D.L. An enhanced consensus reaching process in group decision making with intuitionistic fuzzy preference relations. Inf. Sci. 2016, 329, 274–286. [Google Scholar] [CrossRef]
- Liao, H.; Li, Z.; Zeng, X.J.; Liu, W. A comparison of distinct consensus measures for group decision making with intuitionistic fuzzy preference relations. Int. J. Comput. Intell. Syst. 2017, 10, 456–469. [Google Scholar] [CrossRef]
- Tan, X.; Gong, Z.; Huang, M.; Wang, Z.J. Selecting cooking methods to decrease persistent organic pollutant concentrations in food of animal origin using a consensus decision-making model. Int. J. Environ. Res. Public Health 2017, 14, 187. [Google Scholar] [CrossRef] [PubMed]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Watanabe, N. Statistical methods for estimating membership functions. Jpn. J. Fuzzy Theory Syst. 1979, 5, 17–25. [Google Scholar]
- Dubois, D. The role of fuzzy sets in decision sciences: Old techniques and new directions. Fuzzy Sets Syst. 2011, 184, 3–28. [Google Scholar] [CrossRef]
- Herrera, F.; Martínez, L. A 2-Tuple fuzzy linguistic representation model for computing with words. IEEE Trans. Fuzzy Syst. 2000, 8, 746–752. [Google Scholar]
- Martínez, L.; Herrera, F. An overview on the 2-tuple linguistic models for computing with words in decision making: Extensions, applications and challenges. Inf. Sci. 2012, 207, 1–18. [Google Scholar] [CrossRef]
- Wang, T.C.; Chen, Y.H. Applying fuzzy linguistic preference relations to the improvement of consistency of fuzzy AHP. Inf. Sci. 2008, 178, 3755–3765. [Google Scholar] [CrossRef]
- Lin, H.; Wang, Z.J. Linguistic multi-attribute group decision making with risk preferences and its use in low-carbon tourism destination selection. Int. J. Environ. Res. Public Health 2017, 14, 1078. [Google Scholar] [CrossRef] [PubMed]
- Centobelli, P.; Cerchione, R.; Esposito, E. Aligning enterprise knowledge and knowledge management systems to improve efficiency and effectiveness performance: A three-dimensional Fuzzy-based decision support system. Expert Syst. Appl. 2018, 91, 107–126. [Google Scholar] [CrossRef]
- Centobelli, P.; Cerchione, R.; Esposito, E. How to deal with knowledge management misalignment: A taxonomy based on a 3D fuzzy methodology. J. Knowl. Manag. 2018, 22, 538–566. [Google Scholar] [CrossRef]
- Yücenur, G.N.; Vayvay, O.; Demirel, N.Ç. Supplier selection problem in global supply chains by AHP and ANP approaches under fuzzy environment. Int. J. Adv. Manuf. Technol. 2011, 56, 823–833. [Google Scholar] [CrossRef]
- Lima Junior, F.R.; Osiro, L.; Carpinetti, L.C.R. A comparison between fuzzy AHP and fuzzy TOPSIS methods to supplier selection. Appl. Soft Comput. 2014, 21, 194–209. [Google Scholar] [CrossRef]
- Yu, M.C.; Keng, I.; Chen, H.X. Measuring service quality via a fuzzy analytical approach. Int. J. Fuzzy Syst. 2015, 17, 292–302. [Google Scholar] [CrossRef]
- Azadeh, A.; Zadeh, S.A. An integrated fuzzy analytic hierarchy process and fuzzy multiple-criteria decision-making simulation approach for maintenance policy selection. Simulation 2016, 92, 3–18. [Google Scholar] [CrossRef]
- Çelikbilek, Y.; Tüysüz, F. An integrated grey based multi-criteria decision making approach for the evaluation of renewable energy sources. Energy 2016, 115, 1246–1258. [Google Scholar] [CrossRef]
- Gruji, M.; Ivezi, D.; Zivkovi, M. Application of multi-criteria decision-making model for choice of the optimal solution for meeting heat demand in the centralized supply system in Belgrade. Energy 2014, 67, 341–350. [Google Scholar] [CrossRef]
- Tong, X.; Wang, Z.J. A group decision framework with intuitionistic preference relations and its application to low carbon supplier selection. Int. J. Environ. Res. Public Health 2016, 13, 923. [Google Scholar] [CrossRef] [PubMed]
- Cho, Y.J.; Wang, Y.; Hsu, L.L.I. Constructing Taiwan’s low-carbon tourism development suitability evaluation indicators. Asia Pac. J. Tour. Res. 2016, 21, 658–677. [Google Scholar] [CrossRef]
- Mardani, A.; Zavadskas, E.K.; Streimikiene, D.; Jusoh, A.; Nor, K.M.D.; Khoshnoudi, M. Using fuzzy multiple criteria decision making approaches for evaluating energy saving technologies and solutions in five star hotels: A new hierarchical framework. Energy 2016, 117, 131–148. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).