Impact of Link Unreliability and Asymmetry on the Quality of Connectivity in Large-scale Sensor Networks

1. Introduction and Motivation

2. Related Work

2.1. Overview of Wireless Radio Link Models

A lot of existing works are based on the Boolean disk model, as illustrated in Figure 1(a). Two nodes are either connected or disconnected depending on the transmitter-receiver distance and the disk radius. Recent works [2, 13] argue that the real characteristics of low-power wireless links differ greatly from the ideal model especially in their unreliability and asymmetry. Some studies have improved the disk model and consider the shadowing effect. The radiation pattern is squeezed and stretched as shown in Figure 1(b). It is proved in [14] that irregular radio patterns can achieve connectivity more easily if they can maintain an average number of functioning connections. The two models above are basically deterministic either with assured transmission or assured probability of transmission within the communication range. However, several studies [2, 13, 15-19] have pointed out that the communication range of a wireless node cannot be specified and they propose to use probabilistic link model, as shown in Figure 1(c) (the sickness of the line represents the probability of connection), instead of deterministic model. It is found that the successful transmission probability at a given distance s, namely P(s), is a non-monotonically decreasing function to s. P relies not only on the distance s between two nodes but various parameters such as the channel parameters like the path loss exponent, the shadowing variance and the degree of irregularity (DOI) [16], the radio parameters including modulation, encoding, output power, receiver noise and frame size.

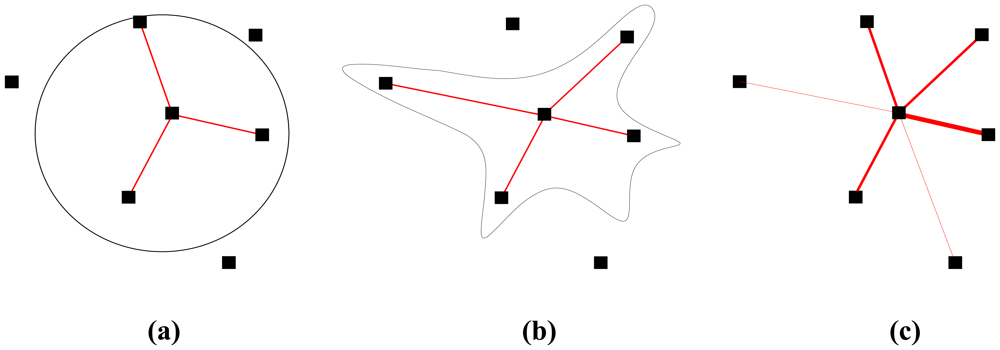
Figure 1. Different kinds link models. (a) Boolean disk model. (b) Shadowing model. (c) Probabilistic model.

The third link model discussed above is supported by many experimental studies and significantly affects networks behavior. Woo et al. have identified in [2] the existence of three distinct reception regions in wireless links: connected, transitional and disconnected. The transitional region is relatively large in size and is characterized by high variance in reception rates and asymmetric connectivity. In a typical sensor networks, a large number of links (even higher than 50%) can be unreliable because of the transitional region. Ganesan et al. [17] provide a wealth of empirical data from studies of large scale, dense wireless network, which demonstrate that even a simple flooding algorithm entails complex behavior under unreliable links. Zhou et al. [16] find that radio irregularity has a significant impact on the routing protocols in wireless sensor networks, especially location-based routing, such as geographic forwarding. All these research results lead us to stress the need for realistic link models for wireless sensor networks.

Several recent studies have proposed communication models based on empirical data and analyzed related phenomena for more accurate evaluation of upper-layer protocols. Woo et al. [2] present a simple synthetic link model to generate data under specific radio and environment based on an assumption of Gaussian distribution of the packet reception rate for given transmitter-receiver distance. These synthetic traces are used for simulation of passive link estimators that snoop traffic over the channel and estimate link qualities. Cerpa et al. [15] study the relationships between location and communication properties using non-parametric statistical techniques. They provide a probability density function that completely characterizes the relationship and develop a series wireless network models that produce networks of arbitrary size with empirical observed properties. The accuracy of their models is evaluated through a set of communication tasks like connectivity maintenance and routing. Lal et al. [18] propose link inefficiency as a cost metric based on detailed observations of link quality variation and explore how link inefficiency can be measured in energy efficient way. They find that only a few measurements of the channel are sufficient to obtain a good estimate of the cost metric. Leskovec et al. [19] concentrate on estimating the link quality between pairs of sensors. Received signal strength is chosen as the link quality indicator. They use dimensionality reduction technique such as SVM to understand the topology of the network and identify potential bottleneck of the network. Zhou et al. [16] establish a radio model called the Radio Irregular Model (RIM) with empirical data obtained from the Mica2 platform. RIM takes into account both the non-isotropic properties of the propagation media and the heterogeneous properties of devices. With this model, they find solutions to improve the communication performance in the presence of radio irregularity.

Most important to our work is the analysis of transitional region in [13]. Different from empirical models which require specific radio and environment conditions, the analytical model in [13] has a general methodology and can be used for a number of different configurations and hardware designs. The incorporation of different parameters in the link model greatly facilitates our analysis of network connectivity in presence of unreliable and asymmetric links. Detailed description of the link model we use can be found in Section 3.3.

3. Network Connectivity Analysis

3.3. Link Probability Analysis

Depending on different radio link model, the link probability P(L|s) is of different values. For Boolean model, either disk or irregular shape as shown in Figure 1(a) and Figure 1(b), P(L|s) is a logical function, equal to either 0 or 1 depending on the communication range. Hence,

$$\xi =\pi r^2\rho$$

(12)

where r is the real communication radius or equivalent radius for Boolean disk model and Boolean shadowing model. For probabilistic model as shown in Figure 1(c), P(L|s) is not deterministic 0 or 1, but defined as the packet reception rate (PRR) ψ over a period of time τ. In practice, ψ can be estimated over a moving time window. However, we can use it in simulation as a stationary variable to indicate the probability of instant link success or failure.

Empirical studies have shown that the lognormal shadowing model provides more accurate multipath channel models than other models like Nakagami and Rayleigh models [13]. According to this model, the received power P_r in dB is given by:

$$P_r(s)=P_t-\mathit{\text{PL}}(s_0)-10\eta {log}_{10}(\frac{s}{s_0})+\mathcal{N}(0,\sigma )$$

(13)

where P_t is the output power, η is the path loss exponent, N(0,σ) is a Gaussian random variable with mean 0 and variance σ², and PL(s₀) is the power decay for the reference distance s₀. σ can be high in the case of severe signal fluctuations due to irregularities in the surrounding of the receiver and transmitter's antennas.

(13) does not include anisotropic properties of the radio. To incorporate it, we add a coefficient K_i to represent the difference in path loss in different directions. (13) can be modified as :

$$\begin{array}{l}{P}_r(s)=P_t-\left(\mathit{\text{PL}}(s_0)+10\eta {log}_{10}(\frac{s}{s_0})\right)\times K_i+\mathcal{N}(0,\sigma )\hfill \\ K_i=\{\begin{array}{cc}1\hfill & \text{if}i=0\hfill \\ K_{i-1}\pm \mathit{\text{rand}}\cdot \mathit{\text{DOI}}& \text{if}0<i<360\text{and}i\in N\end{array}\hfill \\ \mathit{\text{DOI}}=0.01821\hfill \end{array}$$

(14)

DOI represents the degree of irregularity. The reference value is suggested by [16] to be 0.01821, which is measured using Mica2 mote. We can generate 360 values for 360 different directions. However, to make the simplicity, we just adopt 4 directions in the simulation.

For a modulation method M and encoding method E, the PRR ψ is defined as a function of bit-error rate β_M, while β_M is a function of SNR γ. Takeing Manchester encoding for example:

$$\phi (\gamma )={(1-{\beta }_M(\gamma ))}^{8(2f-h)}$$

(15)

where f is the frame size (preamble, payload and CRC), h is the preamble (both in bytes). The value of β_M depends on modulation, and more generally on transmitting and receiving techniques (diversity, equalization, etc.). Here we take non-coherent FSK for example, which is the default modulation scheme in Mica2 Mote. Expressions for β_M is:

$${\beta }_M=\frac{1}{2}{e}^{-\frac{\gamma }{2}},\gamma ={10}^{{\gamma }_{dB}/10}$$

(16)

Plugging (16) into (15), we have:

$$\mathrm{\Psi }(\gamma )={(1-\frac{1}{2}{e}^{-\frac{\gamma }{2}})}^{8(2f-h)}$$

(17)

The SNR γ can be obtained from (14) and is given by:

$${\gamma }_{dB}(s)=P_r(s)-P_n$$

(18)

where P_n is the noise floor which depends on both the radio and the environment. Considering an ambient temperature of 27°C and no interference signals, the noise floor is −115 dB [13]. Note that γ in (18) can also be regarded as a Gaussian random variable N(μ(s),σ) with mean μ(s) and variance σ², where μ(s) is given by:

$$\mu (s)=P_t-(\mathit{\text{PL}}(s_0)+10\eta {log}_{10}(\frac{s}{s_0}))\cdot K_i-P_n$$

(19)

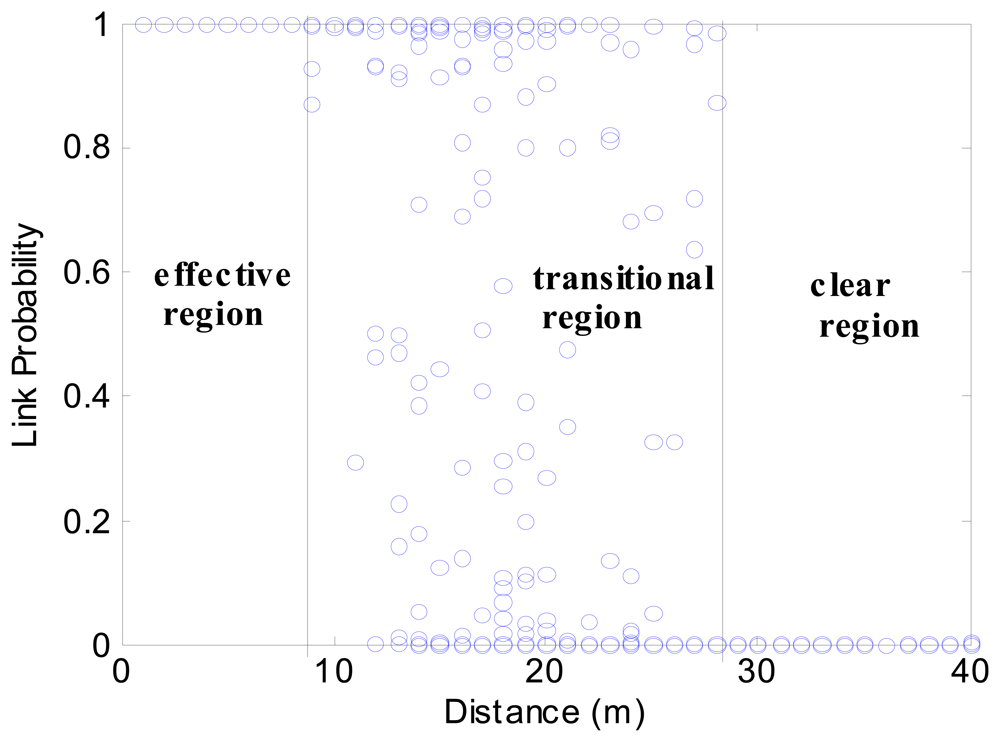
According to (19) and (17), given the distance and some related parameters, the PRR can be calculated. Figure 2 shows the analytical model of PRR to distance in one direction. It is clear that there is a large transitional region, in which the PRR is unstable. With the following definitions, we can further outline the transitional region.

Figure 2. Analytical PRR to distance, obtained from (19) and (17), P_t=-5 dB, η=3, σ=3.3, f=50 Byte, h=2 Byte.

Definition 3

If the link between two nodes has a high probability (>p_h) of having high PRR (>ξ_h), then the two nodes are strongly connected. The upper bound of the connected range is s_l.

Definition 4

If the link between two nodes has a high probability (>p_h) of having low PRR (<ξ_l), then the two nodes are almost disconnected. The lower bound of the disconnected range is s_h.

According to definition 3 and definition 4, the region between s_l and s_h is the transitional region, as illustrated in Figure 2. This agrees with empirical observations in [2, 28]. The existence of this region has been explained in [13], which is the joint effect of non-perfect-threshold receiver, noisy environment and multi-path effects.

With consideration of different pass loss and shadow fading along different direction, we draw contour plot of the reception rate for a node located at the center of the region. Figure 3 shows the difference of the communication area of a Boolean disk model and a shadowing fading model. Figure 3(b) captures the real characteristic of wireless link and shows spatial irregularity as the empirical results in [14].

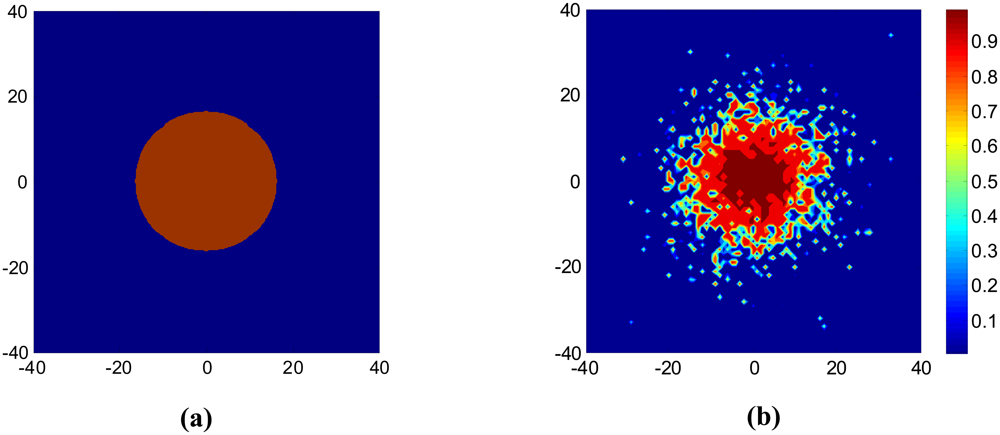
Figure 3. Contour plot for different link models. (a) Boolean disk model. (b) Log-normal shadowing based probabilistic model.

To calculate P(Ī), the value of ξ is crucial. As depicted in Figure 2, it is difficult to derive a continuous function for P(L|s). Instead, we calculate the expected value of P, denoted as E(P). Thus, ξ can be written as:

$$\xi ={\int }_0^{\infty }P\left(L\mid s\right)\mathit{\text{sds}}\approx {\int }_0^{\infty }{\int }_{-\infty }^{\infty }\Psi \left(\gamma \right)f\left(\gamma \mid s\right)\cdot sd\gamma ds$$

(20)

where f(γ|s) represents the probability density function of SNR. According to (17), we draw the PRR as a function of γ. As the power-law relationship entails a sharp threshold, linear approximation turns available. Ψ(γ) can be approximated as the following piecewise linear functions:

$$\begin{array}{c}\Psi \left(\gamma \right)=\{\begin{array}{ll}0\hfill & \gamma \le {\gamma }_0\hfill \\ k_{\phi }\gamma +b_{\phi }\hfill & {\gamma }_0<\gamma <{\gamma }_1\hfill \\ 1\hfill & \gamma \ge {\gamma }_1\hfill \end{array}\\ \begin{array}{cc}{k}_{\phi }=\frac{0.9-0.1}{{\gamma }_1-{\gamma }_0},& b_{\phi }=\frac{0.1{\gamma }_1-0.9{\gamma }_0}{{\gamma }_1-{\gamma }_0}\end{array}\\ \begin{array}{cc}{\gamma }_0={\Psi }^{-1}\left(0.1\right),& {\gamma }_1={\Psi }^{-1}\left(0.9\right)\end{array}\end{array}$$

(21)

where γ₀ and γ₁ represent the receiver's range of threshold.

Similarly, f(γ|s) can also be evaluated by linear approximation since the interval [γ₀, γ₁] is relatively narrow compared with [μ-4σ, μ+4σ].

$$\begin{array}{l}f(\gamma \mid s)=k_f(s)\gamma +b_f(s),\gamma \in [{\gamma }_0,{\gamma }_1]\hfill \\ k_f(s)=\frac{f({\gamma }_1\mid s)-f({\gamma }_0\mid s)}{{\gamma }_1-{\gamma }_0},b_f(s)=\frac{f({\gamma }_0\mid s){\gamma }_1-f({\gamma }_1\mid s){\gamma }_0}{{\gamma }_1-{\gamma }_0}\hfill \end{array}$$

(22)

Figure 4 shows the approximation procedure for Ψ(σ) and f(y|s). Finally, ξ can be approximated by:

$$\begin{array}{ll}\xi \hfill & ={\int }_0^{\infty }{\int }_{-\infty }^{\infty }\Psi \left(\gamma \right)f\left(\gamma \mid s\right)\cdot sd\gamma ds\hfill \\ & \approx {\int }_0^{\infty }{\int }_{{\gamma }_0}^{\infty }\Psi \left(\gamma \right)f\left(\gamma \mid s\right)\cdot sd\gamma ds\hfill \\ & \approx {\int }_0^{\infty }({\int }_{{\gamma }_0}^{{\gamma }_1}(k_{\phi }\gamma +b_{\phi })(k_f(s)\gamma +b_f(s))d\gamma +(1-\mathrm{\Phi }(\frac{{\gamma }_1-\mu (s)}{\sigma })))\mathit{\text{sds}}\hfill \\ & \approx {\int }_0^{d_h}{\int }_{{\gamma }_0}^{{\gamma }_1}(k_{\phi }\gamma +b_{\phi })(k_f(s)\gamma +b_f(s))\cdot sd\gamma ds+{\int }_0^{d_h}(1-\mathrm{\Phi }(\frac{{\gamma }_1-\mu (s)}{\sigma })))\mathit{\text{sds}}\hfill \end{array}$$

(23)

where Φ(·) is the cdf of SNR and μ is given by (19). In fact, the upper bound of the integration can be any value lager than s_h. The approximation deviation by lowering the integration upper bound from ∞ to s_h can be tolerated.

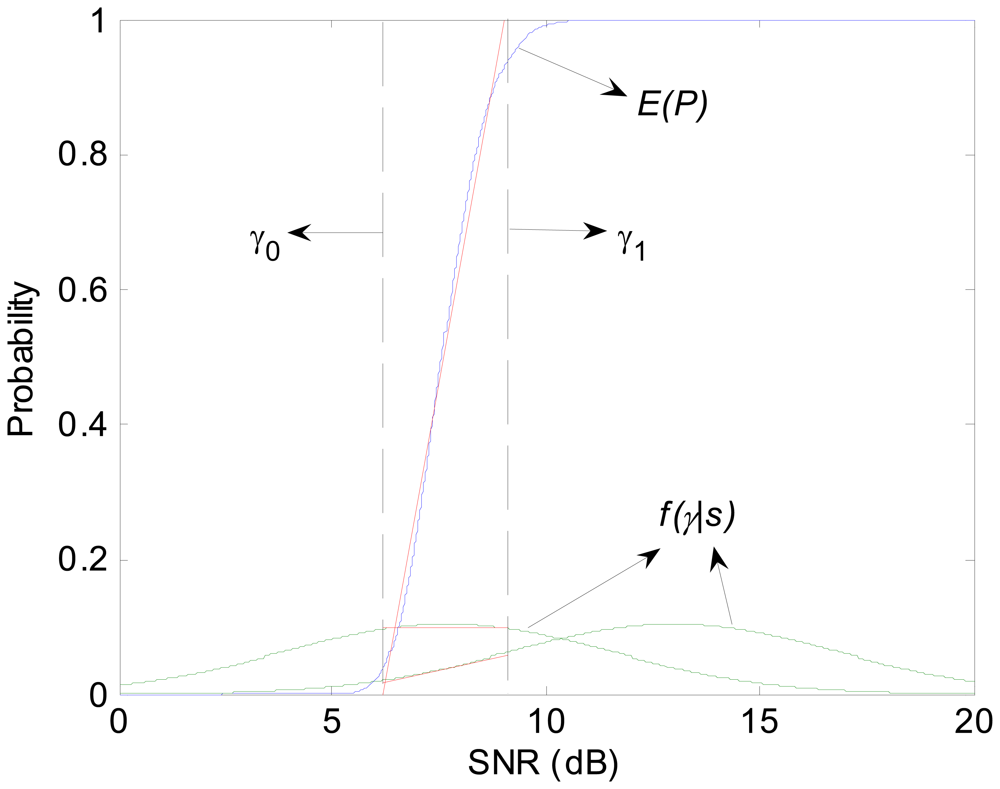
Figure 4. The procedure of linear approximation for Ψ(γ) and f(γ|s).

In the following, we will use simulations to verify the theoretical analysis.

4. Simulation Results and Discussion

Theorem 1

If the graph G has C connected components, then L(G) has exactly C zero eigenvalues (other eigenvalues are positive). Based on Theorem 1, the graph is one-connected if L(G) possesses only one zero eigenvalue. The probability for one-connectivity is estimated from a representative sample of ad hoc sensor networks' connectivity graph as the ratio between one-connected graph and all sample graphs.

Figure 5 shows the simulated results. Each subplot corresponds to a different configuration. Figure 5(a) serves as a benchmark for comparison. The critical node densities in different scenarios are reported in Table 1. Through comparing and analyzing the 7 groups of simulated data, we draw the following conclusions and give the explanations.

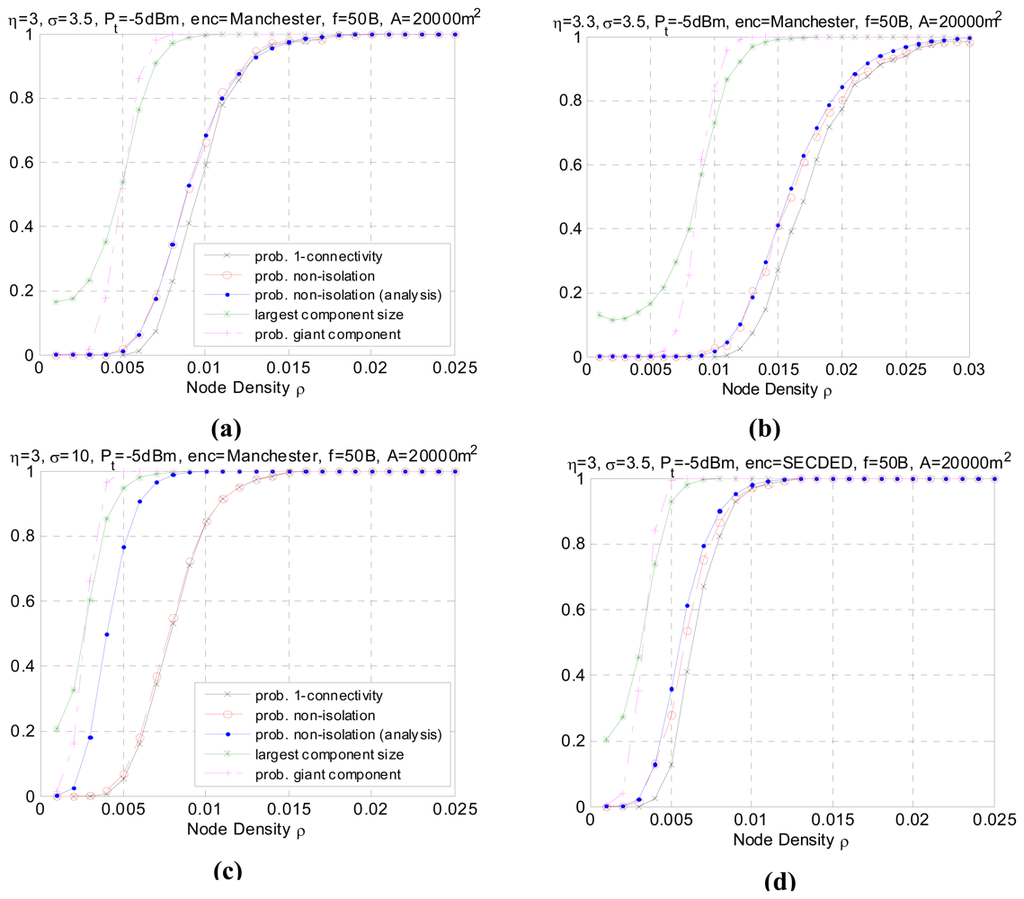
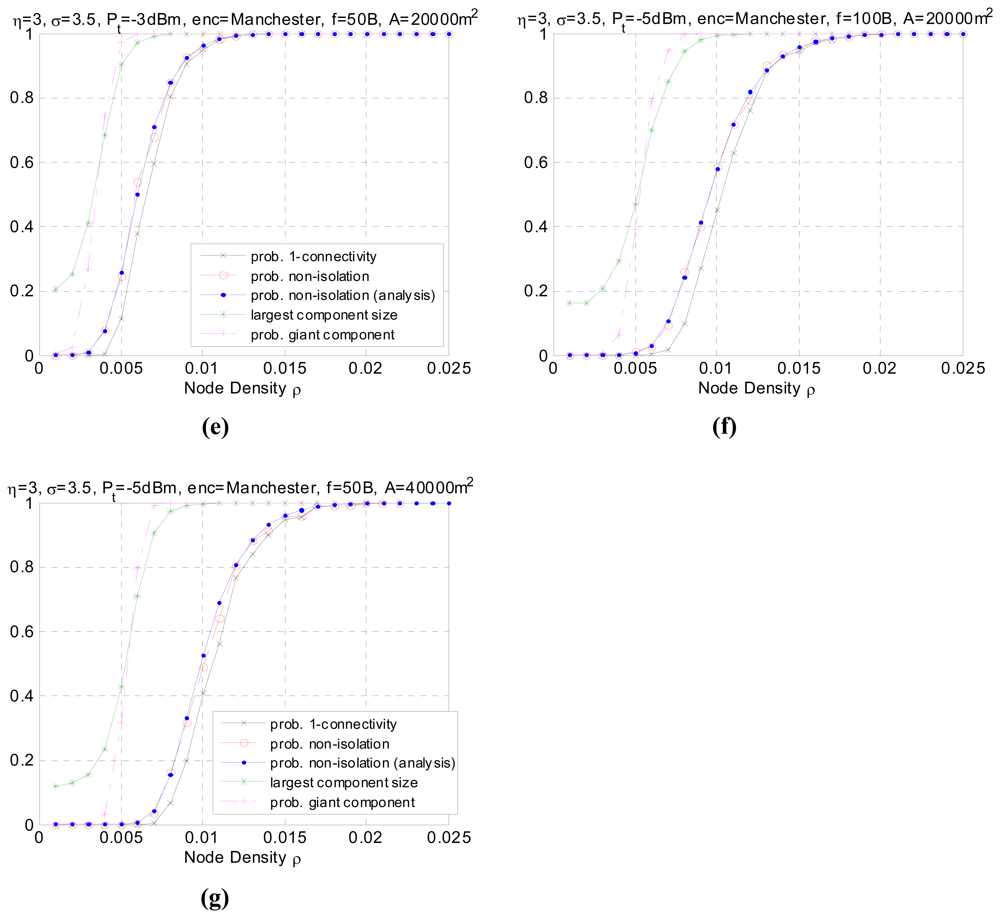
Figure 5. Simulated results for different settings. (a) Benchmark. (b) Change path loss exponent η. (c) Changing shadowing variance σ. (d) Change encoding method E. (e) Change transmission power P_t. (f) Change frame size f. (g) Changing area size ‖A‖.

Table 1. Critical density for giant component, one-connectivity and non-isolation under different settings, comparison of analytical and simulation results.

• In all simulation cases, as the node density increases, the network graph becomes denser and the transition from low connectivity to nearly full connected or appearance of giant component is quite sharp over a small range of ρ. The phenomenon consists with the results in [22] which uses the theory of continuum percolation. No matter what kind of radio link model adopted, either Boolean disk model or more realistic model with fading and shadowing, the phenomenon of phase transition exists, which gives us a tool for analyzing and determining resource efficient regime of operation for wireless sensor networks. For example, following the settings in Figure 5(a), it tells us that for the nodes with identical transmission power, distributed in an area of 20000 m² according to homogeneous Poisson process, the node density must be higher than 0.007 to form giant component and higher than 0.0125 to reach one-connectivity. The density threshold is an energy- efficient point of operation, in that to the left of this threshold the network is disconnected with high probability, and to the right of this threshold, additional energy expenditure results in a negligible increase in the high probability of connectivity.
• In all simulation cases, the non-isolation probability serves as the upper bound for probability of one-connectivity. Generally, the difference between the two probabilities is non-negligible. However as node density increases, the two probabilities converge to 1. This result agrees with inequality (3). With respect to critical node density, this means that

  $$\rho \left(P\left(C\right)=p\right)=\rho \left(P\left(\overline{I}\right)=p\right)+\delta ,\delta >0.\text{As}p\to 1,\delta \to 0.$$

  (24)

  For p=90%, the critical node densities for each setting are listed in Table 1. It is observed that when the shadowing effect σ is of a large value (σ=10), the difference δ becomes very small over the whole node density range. This can be explained by the fact that as σ increases, the increase in long links and the decrease in short links have reduced the correlation between links. As a result, the geometric random graph behavior approaches generic random graph behavior and the probability of one-connectivity approaches the probability of non-isolation.
• It should be noted that, the analytical performance of non-isolation probability closely matches the real non-isolation probability in different settings except when σ is large (σ=10), as shown in Figure 5(c). This is also reflected in Table 1 with minor difference between the simulating and analytical critical density for P(Ī) except when σ=10. In some related papers [10-11], it is argued that a large value of σ helps the network to be connected because the number of added long links is larger than the number of removed short links. However, it should be note that the network also suffers severe link asymmetry as the shadowing variance increases. The analytical approach has underestimated the asymmetry problem, which leads to an overestimate of network connectivity. In practical, the analytical values have to be calibrated with certain asymmetry coefficient to match the simulated data. Besides, in practice, some realistic issue like antenna diversity, battery power difference etc. will also cause link asymmetry and is more complicated to simulate. We will leave it as future work.
• Comparing Figure 5(b) with Figure 5(a), we can see that the path loss decreases the connectivity of the network. The reason is obvious since the higher η, the faster the decay of the signal strength, resulting in a shortened transmission range. The simulated result agrees with the analytical one. Similar is Figure 5(e) and 5(g) compared with Figure 5(a). As the transmission power increases, the average transmission range also increases accordingly, thus a lower node density is sufficient to make the network connected with the same high probability, as shown in Table 1. The giant component probability shows consistent tendency.
• Figure 5(d) shows the impact of a different encoding scheme. The connectivity is better using SECDED encoding than Manchester encoding. This result is due to the error correction capabilities of SECDED, which comes at a cost of energy efficiency (encoding ratio 1:3) while Manchester does not provide error correction and the encoding ratio is 1:2. Simulated results for different encoding schemes agree with the expected analytical behavior.
• Figure 5(f) shows the connectivity performance as the packet size is doubled. It can be observed that the performance merges to 1 at a slightly higher node density. The impact of packet size on the global connectivity is not obvious compared to other parameters.
• The impact of area size ‖A‖ on the connectivity is straightforward. As the sub-area size gets larger, to reach the global connectivity requires higher node density. The quantity can be estimated via Equation (10). However, to form a giant component, the probability has not been affected by the area size ‖A‖.

In summary, a higher transmission power, larger shadowing variance and more complicated encoding method can improve the network connectivity. However, it is energy inefficient to sacrifice the transmission power for better QoC unconditionally; higher shadowing variance σ² can increase the chance of link asymmetry and typically comes with a higher path loss exponent η; complicated encoding method consumes more system resource (energy, memory space etc.) and takes more time. With reference to the improvement space of each parameter, one should better balance the connectivity performance and the sacrifices of resource and energy. Other techniques such as collaborative radio [31] and multiple antennas [10], although effective in theory to improve global connectivity, need more detailed infrastructure design and proof of their effectiveness in practice. In all simulation cases, we find that the giant component probability converges to 1 much faster than one-connectivity. In some applications, a few isolated nodes or small clusters outside the giant component do not change the overall performance. In that case, a lower node density is sufficient for operation. Besides, the largest component size is also an alternative of connectivity measurement. It not only provides information about the network is one-connected or not, but also the fraction of the connected part. Thus a random size of largest component can be designated satisfying different requirement of QoC.

5. Conclusions and Future Work

References

1. Gupta, P.; Kumar, P.R. The capacity of wireless networks. IEEE Tran. Inf. Theo. 2000, 46, 388–404. [Google Scholar]
2. Woo, A.; Tong, T.; Culler, D. Taming the underlying challenges of reliable multihop routing in sensor networks. Proceedings of the ACM Conference on Embedded Networked Sensor Systems(SenSys), Los Angeles, California, USA; 2003; pp. 14–27. [Google Scholar]
3. Li, Y.; Chen, C.S.; Song, Y.Q.; Wang, Z.; Sun, Y. A two-hop based real-time routing protocol for wireless sensor networks. Proceedings of the IEEE International Workshop on Factory Communication Systems (WFCS), Dresden, Germany; 2008; pp. 1–10. [Google Scholar]
4. Chen, C.S.; Li, Y.; Song, Y.Q. Exploring geographic routing in using k-hop information for wireless sensor networks. Proceedings of the International Conference on Communications and Networking in China (CHINACOM), Hangzhou, China; 2008; pp. 1–6. [Google Scholar]
5. Gupta, P.; Kumar, P.R. Critical power for asymptotic connectivity in wireless networks. In Stochastic Analysis, Control, Optimization and Applications: A Volume in Honor of W.H. Fleming.; McEneaney, William M., Yin, G. George, Zhang, Qing., Eds.; Birkhäuser: Boston, 1998; pp. 547–566. [Google Scholar]
6. Dousse, O.; Thiran, P.; Hasler, M. Connectivity in ad-hoc and hybrid networks. Proceedings of the IEEE Computer Communications (INFOCOM), Miami, USA; 2005; pp. 1079–1088. [Google Scholar]
7. Bettstetter, C. On the connectivity of ad hoc networks. Comput. J. 2004, 47, 432–447. [Google Scholar]
8. Xue, F.; Kumar, PR. The number of neighbors needed for connectivity of wireless networks. Wirel. Netw. 2004, 10, 169–181. [Google Scholar]
9. Bettstetter, C.; Hartmann, C. Connectivity of wireless multihop networks in a shadow fading environment. Wirel. Netw. 2005, 11, 571–579. [Google Scholar]
10. Hekmat, R.; Mieghem, V.P. Connectivity in wireless ad-hoc networks with a lognormal radio model. Mob. Netw. Appl. 2006, 11, 351–360. [Google Scholar]
11. Miorandi, D.; Altman, E. Coverage and connectivity of ad hoc networks presence of channel randomness. Proceedings of the IEEE INFOCOM, Miami, USA; 2005; pp. 491–502. [Google Scholar]
12. Mica2 datasheet. http://www.crossbow.com.
13. Zuniga, M.; Krishnamachari, B. Analyzing the transitional region in low-power wireless links. the Proceedings of the IEEE Sensor and Ad Hoc Communications and Networks (SECON), Santa Clara, California, USA; 2004; pp. 517–526. [Google Scholar]
14. Franceschetti, M.; Booth, L.; Bruck, J.; Cook, M.; Meester, R. Percolation in multi-hop wireless networks.; Technical Report UCB/ERL M03/18; EECS Department University of California: Berkeley, 2003. [Google Scholar]
15. Cerpa, A.; Wong, JL.; Kuang, L.; Potkojak, M.; Estrin, D. Statistical Model of lossy links in wireless sensor networks. Proeedings of the IEEE /ACM Symposium on Information Processing in Sensor Networks (IPSN), Los Angeles, California, USA; 2005; pp. 81–88. [Google Scholar]
16. Zhou, G.; He, T.; Krishnamurthy, S.; Stankovic, JA. Models and solutions for radio irregularity in wireless sensor networks. ACM Trans. Sens. Netw. 2003, 2, 221–262. [Google Scholar]
17. Ganesan, D.; Krishnamachari, B.; Woo, A.; Culler, D.; Estrin, D.; Wicker, S. Complex behavior at scale: An experimental study of low-power wireless sensor networks. In Technical Report CSD- TR 02-0013; UCLA: Los Angeles, California, February 2002. [Google Scholar]
18. Lal, D.; Manjeshwar, A.; Herrmann, F.; Uysal-Biyikoglu, E.; Keshavarzian, A. Measurement and characterization of link quality metrics in energy constrained wireless sensor networks. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM), San Francisco, USA; 2003; pp. 446–452. [Google Scholar]
19. Leskovec, J.; Sarkar, P.; Guestrin, C. Modeling link qualities in a sensor network. Proceedings of the SIKDD at multi-conference IS, Ljubljana, Slovenia; 2005. [Google Scholar]
20. Cheng, Y.C.; Robertazzi, T.G. Critical connectivity phenomena in multihop radio models. IEEE Trans. Commun. 1989, 37, 770–777. [Google Scholar]
21. Ingmar, G.; Wolfram, K.; Rudolf, S.; Martin, G. Continuum percolation of wireless ad hoc communication networks. Stat. Mech. Appl. 2003, 325, 577–600. [Google Scholar]
22. Krishnamachari, B.; Wicker, SB.; Béjar, R. Phase transition phenomena in wireless ad-hoc networks. Proceedings of IEEE GLOBECOM, San Antonio, Texas, USA; 2001; pp. 2921–2925. [Google Scholar]
23. Dousse, O.; Baccelli, F.; Thiran, P. Impact of interferences on the connectivity in ad hoc networks. IEEE/ACM Trans. Netw. 2005, 13, 425–436. [Google Scholar]
24. Miorandi, D.; Altman, E. Connectivity in one-dimensional ad hoc networks: a queueing theoretical approach. Wirel. Netw. 2006, 12, 573–587. [Google Scholar]
25. Cavalcanti, D.; Agrawal, D.; Kelner, J.; Sadok, D. Exploiting the small-world effect to increase connectivity in wireless ad hoc networks. Proceedings of the International Conference on Telecommunications (ICT), Fortaleza, Brazil; 2004; pp. 388–393. [Google Scholar]
26. Bollobás, B. Random graphs, 2nd Edition ed; Cambridge University Press: Cambridge, 2001. [Google Scholar]
27. Gorce, J-M.; Zhang, R.; Parvery, H. Impact of radio links unreliability on the connectivity of wireless sensor networks. EURASIP J. Wirel. Commun. Netw. 2007. [Google Scholar] [CrossRef]
28. Xia, F.; Tian, Y.-C.; Li, Y.; Sun, Y. Wireless sensor/actuator network design for mobile control applications. Sensors 2007, 7, 2157–2173. [Google Scholar]
29. Dousse, O.; Tavoularis, C.; Tiran, P. Delay of intrusion detection in wireless sensor networks. Proceedings of the ACM Symposium on Mobile Ad hoc Networking and Computing (MobiHoc), Florence, Italy; 2006; pp. 155–165. [Google Scholar]
30. Wang, X.; Wang, S.; Bi, D.; Ma, J. Distributed peer-to-peer target tracking in wireless sensor networks. Sensors 2007, 7, 1001–1027. [Google Scholar]
31. Song, S.; Goeckel, D.; Towsley, D. Collaboration improves the connectivity of wireless networks. Proceedings of the IEEE INFOCOM, Barcelona, Spain; 2006; pp. 1–11. [Google Scholar]
32. Bettstetter, C.; Gyarmati, M.; Schilcher, U. An inhomogeneous spatial node distribution and its stochastic properties. Proceedings of the ACM International Symposium on Modeling, Analysis and Simulation of Wireless and Mobile Systems (MSWiM), Chania, Greece; 2007; pp. 400–404. [Google Scholar]
33. Lili, Z.; Boon-Hee, S. k-Connectivity in shadowing wireless multi-hop networks. Proceedings of the IEEE GLOBECOM, San Francisco, USA; 2006; pp. 1–4. [Google Scholar]