A Novel Digital Twin Architecture with Similarity-Based Hybrid Modeling for Supporting Dependable Disaster Management Systems
Abstract
1. Introduction
2. Related Works
2.1. Digital Twin Software Architecture
2.2. Modeling Scheme for the Disaster Digital Twin
3. The Proposed Digital Twin
3.1. The Proposed Digital Twin Architecture
3.2. Digital Twin Behavior for the Disaster Digital Twin
3.2.1. Monitoring Behavior
| Algorithm 1 Data preprocessing functional element |
| Input: Attr1 … AttrN, Shape |
| Output: Results |
| 1: Results ← list() |
| 2: for i ← 1 to N do |
| 3: if isFiltered(Attri) is True then |
| 4: cleansing(Attri) |
| 5: resizing(Attri) |
| 6: formatting(Attri) |
| 7: Results.append(Attri) |
| 8: else |
| 9: continue |
| 10: end if |
| 11: end for |
3.2.2. Identifying Behavior
3.2.3. Adapting Behavior
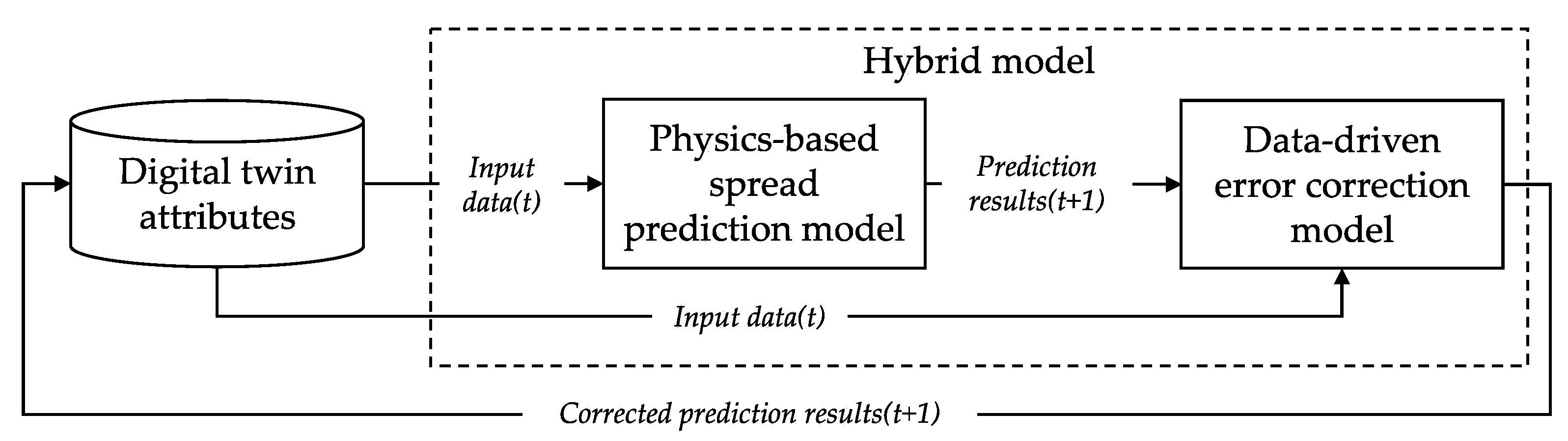
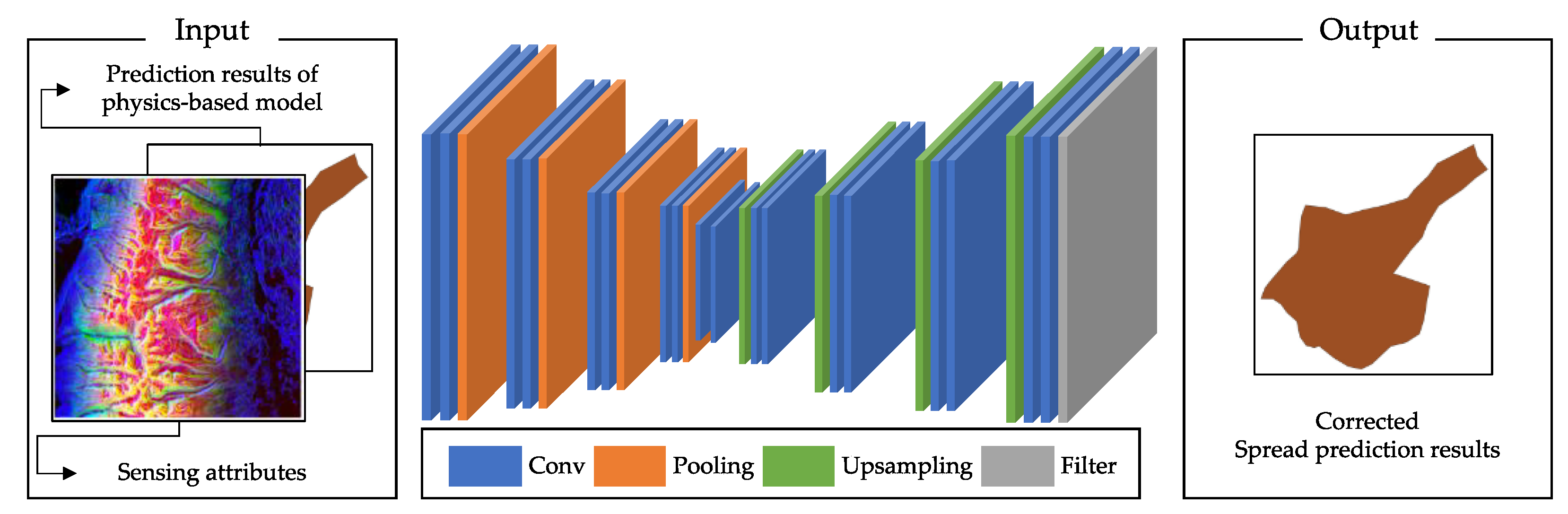
3.2.4. Predictive Behavior
3.3. Digital Twin Manager
3.3.1. Digital Twin LC Control Module
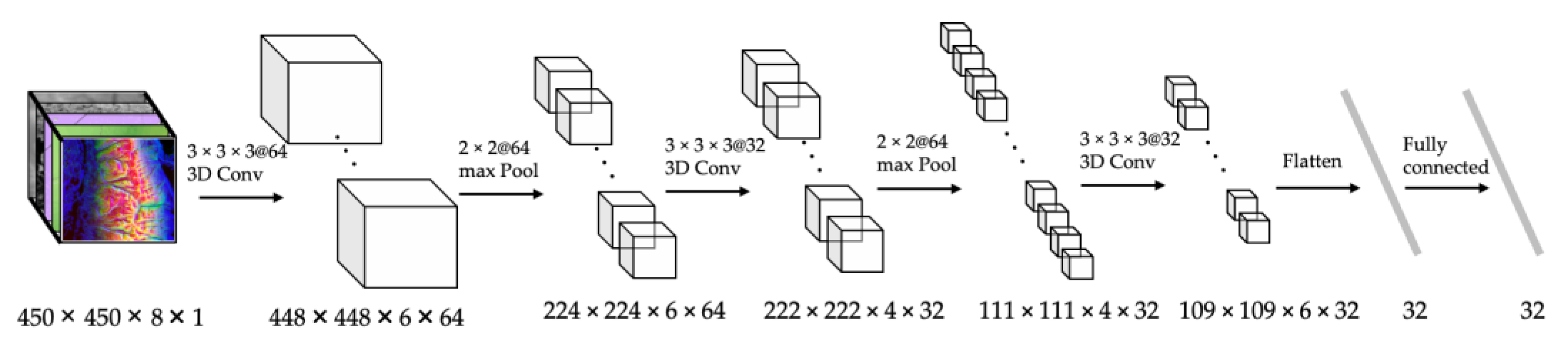
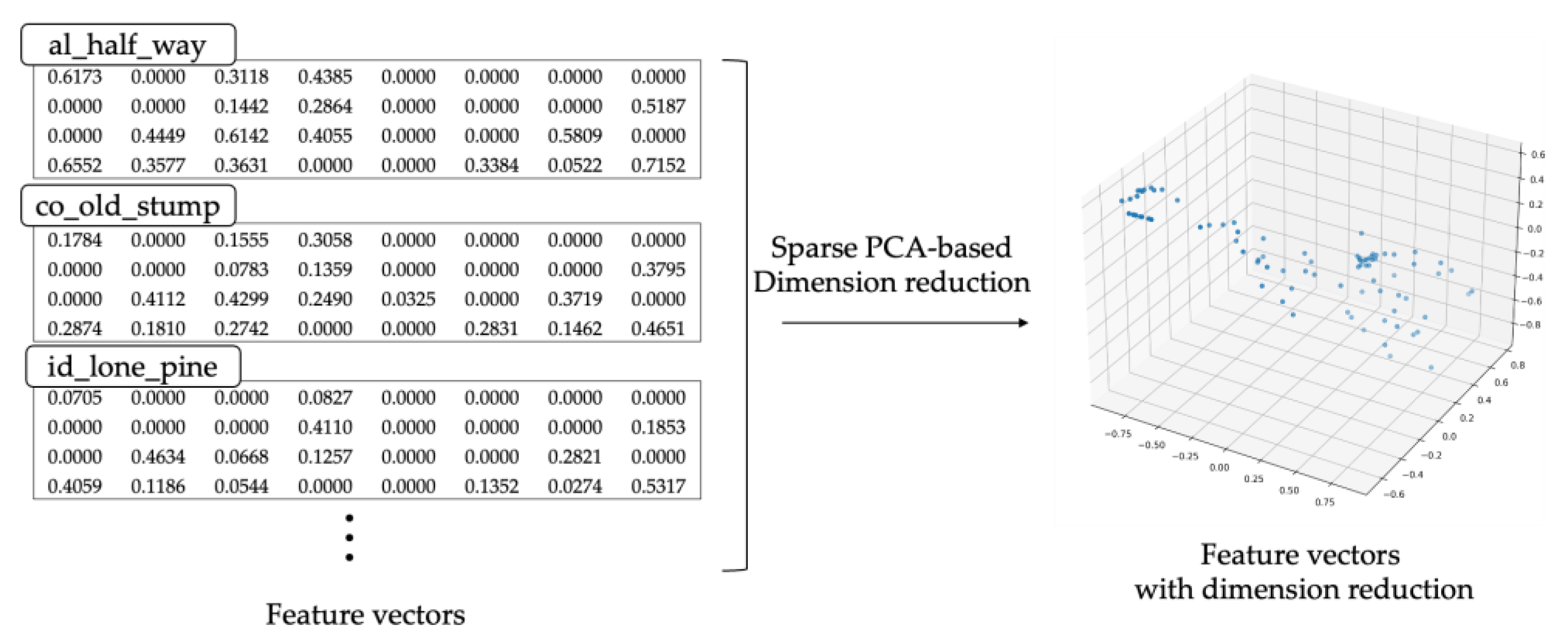
3.3.2. Feature Extraction Module
3.3.3. Similarity-Based Hybrid Modeling Module
| Algorithm 2 Similarity-based hybrid modeling |
| Input: Ftarget, F1 … FN, N1… NN, S |
| Output: Mdd |
| 1: Dictdistance ← dict() |
| 2: Ftarget ← dimReduction(Ftarget) |
| 3: for i ← 1 to N do |
| 4: Fi ← dimReduction(Fi) |
| 5: Dictdistance[Ni] ← calcVectorDistance(Ftarget, Fi) |
| 6: end for |
| 7: sortByValue(Dictdistance) |
| 8: Datatraining←list() |
| 9: keyList ←getKeys(Dictdistance) |
| 10: for i ← 1 to S do |
| 11: appendList(Datatraining), getAttributes(keyList[i]) |
| 12: end for |
| 13: Mdd ← loadEmptyModel() |
| 14: trainModel(Mdd, Datatraining) |
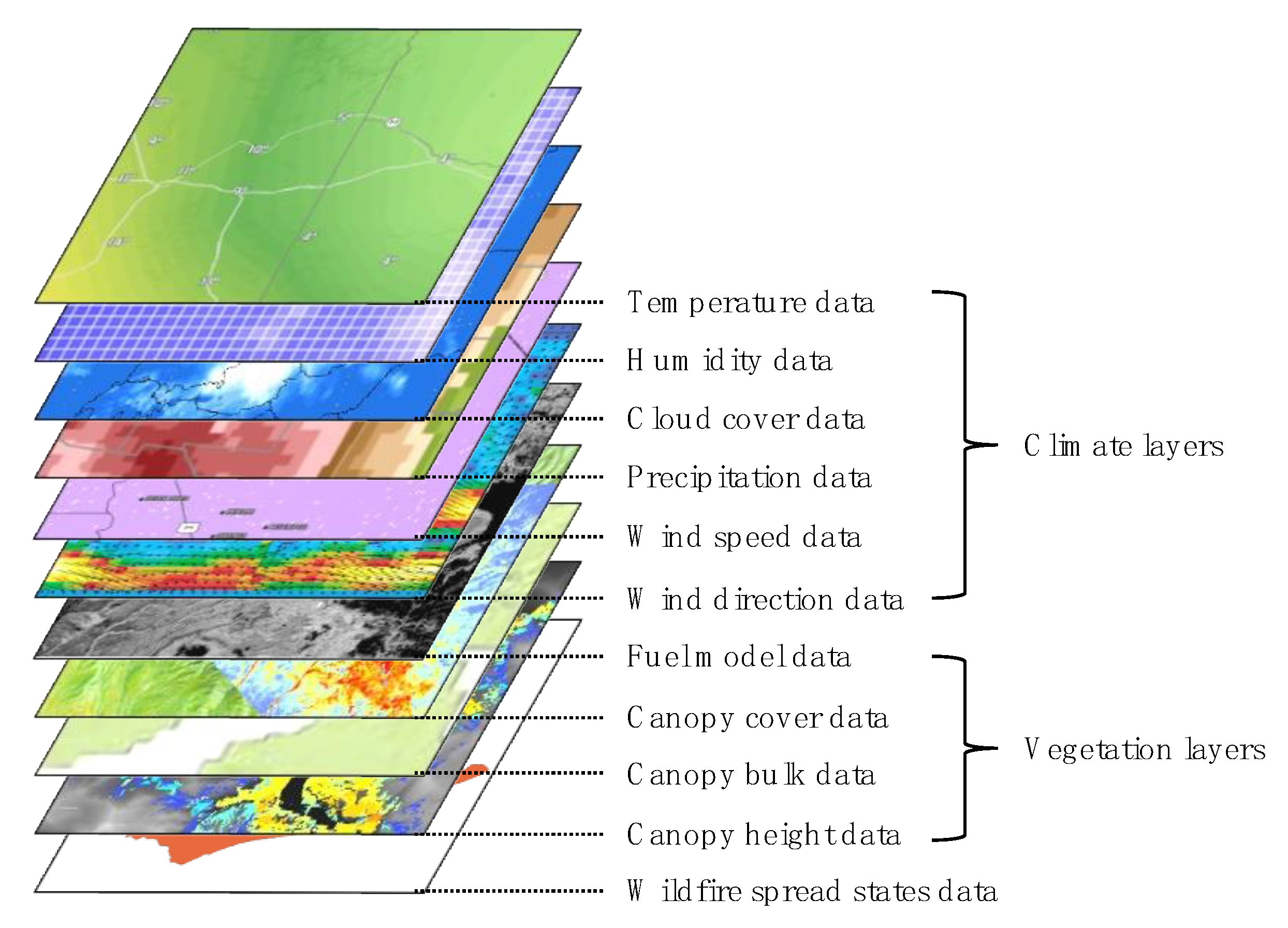
4. Case Study
4.1. Simulation Setups
4.2. Simulation Scenarios
4.3. Simulation Results
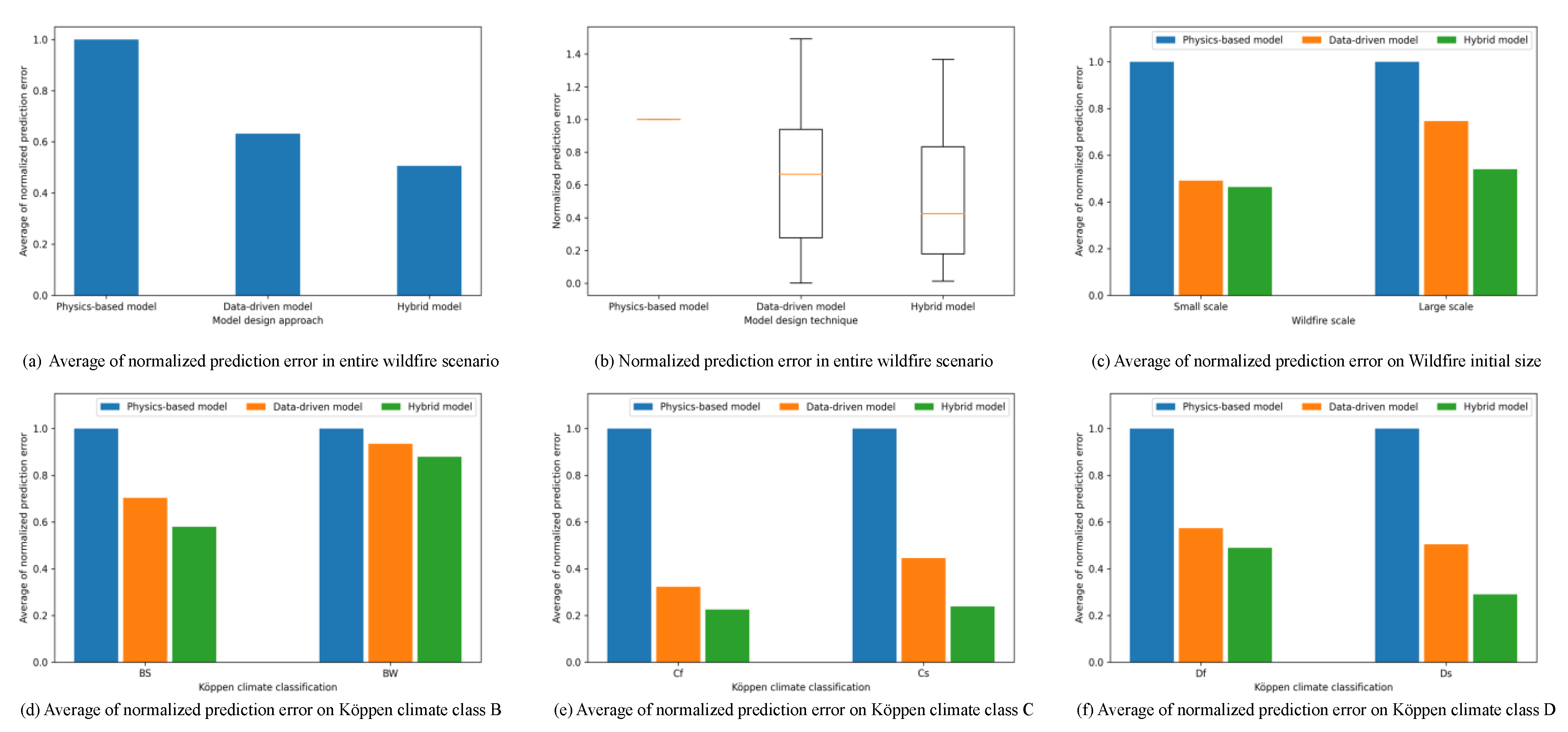
4.3.1. Simulation Results on the Accuracy of the Hybrid Model
4.3.2. Simulation Results on the Data Independency of the Hybrid Model
4.3.3. Simulation Results on the Proposed Hybrid Modeling Schemes
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zandalinas, S.I.; Fritschi, F.B.; Mittler, R. Global warming, climate change, and environmental pollution: Recipe for a multifactorial stress combination disaster. Trends Plant Sci. 2021, 26, 588–599. [Google Scholar] [CrossRef]
- Guindon, L.; Gauthier, S.; Manka, F.; Parisien, M.A.; Whitman, E.; Bernier, P.; Beaudoin, A.; Villemaire, P.; Skakun, R. Trends in wildfire burn severity across Canada, 1985 to 2015. Can. J. For. Res. 2021, 51, 1230–1244. [Google Scholar] [CrossRef]
- Rolland, E.; Patterson, R.A.; Ward, K.; Dodin, B. Decision support for disaster management. Oper. Manag. Res. 2010, 3, 68–79. [Google Scholar] [CrossRef]
- Boschert, S.; Rosen, R. Digital twin—The simulation aspect. In Mechatronic Futures; Springer: Cham, Denmark, 2016; pp. 59–74. [Google Scholar]
- Yu, D.; He, Z. Digital twin-driven intelligence disaster prevention and mitigation for infrastructure: Advances, challenges, and opportunities. Nat. Hazards 2022, 112, 1–36. [Google Scholar] [CrossRef]
- Othman, S.H.; Beydoun, G. Model-driven disaster management. Inf. Manag. 2013, 50, 218–228. [Google Scholar] [CrossRef]
- Srivas, T.; Artés, T.; de Callafon, R.A.; Altintas, I. Wildfire spread prediction and assimilation for FARSITE using ensemble Kalman filtering. Procedia Comput. Sci. 2016, 80, 897–908. [Google Scholar] [CrossRef]
- Finegan, D.P.; Zhu, J.; Feng, X.; Keyser, M.; Ulmefors, M.; Li, W.; Bazant, M.Z.; Cooper, S.J. The application of data-driven methods and physics-based learning for improving battery safety. Joule 2021, 5, 316–329. [Google Scholar] [CrossRef]
- Zhang, D.; del Rio-Chanona, E.A.; Petsagkourakis, P.; Wagner, J. Hybrid physics-based and data-driven modeling for bioprocess online simulation and optimization. Biotechnol. Bioeng. 2019, 116, 2919–2930. [Google Scholar] [CrossRef]
- Barricelli, B.R.; Casiraghi, E.; Fogli, D. A survey on digital twin: Definitions, characteristics, applications, and design implications. IEEE Access 2019, 7, 167653–167671. [Google Scholar] [CrossRef]
- Schleich, B.; Anwer, N.; Mathieu, L.; Wartzack, S. Shaping the digital twin for design and production engineering. CIRP Ann. 2017, 66, 141–144. [Google Scholar] [CrossRef]
- Boschert, S.; Heinrich, C.; Rosen, R. Next generation digital twin. In Proceedings of the Tmce, Las Palmas de Gran Canaria, Spain, 7–11 May 2018. [Google Scholar]
- Zhao, R.; Yan, D.; Liu, Q.; Leng, J.; Wan, J.; Chen, X.; Zhang, X. Digital twin-driven cyber-physical system for autonomously controlling of micro punching system. IEEE Access 2019, 7, 9459–9469. [Google Scholar] [CrossRef]
- Steindl, G.; Kastner, W. Semantic Microservice Framework for Digital Twins. Appl. Sci. 2021, 11, 5633. [Google Scholar] [CrossRef]
- Finney, M.A. FARSITE, Fire Area Simulator--Model Development and Evaluation (No. 4); US Department of Agriculture, Forest Service, Rocky Mountain Research Station: Ogden, UT, USA, 1998. [Google Scholar]
- Yen, T.H.; Wu, C.C.; Lien, G.Y. Rainfall Simulations of Typhoon Morakot with Controlled Translation Speed Based on EnKF Data Assimilation. Terr. Atmos. Ocean. Sci. 2011, 22, 647–660. [Google Scholar] [CrossRef]
- Radke, D.; Hessler, A.; Ellsworth, D. FireCast: Leveraging Deep Learning to Predict Wildfire Spread. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 4575–4581. [Google Scholar]
- Zou, H.; Hastie, T.; Tibshirani, R. Sparse principal component analysis. J. Comput. Graph. Stat. 2016, 15, 265–286. [Google Scholar] [CrossRef]
- Landfire. Available online: https://landfire.gov/ (accessed on 28 March 2022).
- Finco, M.; Quayle, B.; Zhang, Y.; Lecker, J.; Megown, K.A.; Brewer, C.K. Monitoring trends and burn severity (MTBS): Monitoring wildfire activity for the past quarter century using Landsat data. In Proceedings of the Forest Inventory and Analysis (FIA) Symposium 2012, Baltimore, MD, USA, 4–6 December 2012; pp. 222–228. [Google Scholar]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Koppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- NWCG Terminology. Available online: https://www.nwcg.gov/term/glossary/size-class-of-fire (accessed on 28 March 2022).






| Features | Physics-Based Model | Data-Driven Model | Hybrid Model | Proposed Hybrid Model |
|---|---|---|---|---|
| Accuracy | Low | High in trained scenario | High | High |
| Data independency | O | X | △ | O |
| Adaptability | X | O | O | O |
| Symbol | Description |
|---|---|
| Model for data-driven error correction FE | |
| Idle time of hybrid model-based digital twin | |
| Threshold of idle time of hybrid model-based digital twin | |
| Simulation time of hybrid model-based digital twin | |
| Simulation end time of hybrid model-based digital twin | |
| Simulation time step size of hybrid model-based digital twin | |
| Attr | Digital twin attributes |
| F | Feature vector of digital twin |
| N | Name of digital twin |
| S | Size of training data for hybrid modeling |
| Symbol | Description |
|---|---|
| Error amounts of type of model on disaster name | |
| The width and height of the data | |
| Prediction result for coordination i,j | |
| Observation data for coordination i,j | |
| Prediction error increments ratio on the untrained data | |
| Prediction error on trained wildfires | |
| Prediction error on untrained wildfires | |
| Prediction error with randomly selected wildfire dataset | |
| Prediction error with similarity-based hybrid modeling | |
| Prediction error ratio for wf wildfire |
| Size Class | Köppen Climate Classification | ||||||
|---|---|---|---|---|---|---|---|
| BS | BW | Cf | Cs | Df | Ds | ||
| Small | B | az_sunflower | - | ga_chimney_top al_caney_head | or_mr_068_blue_top | co_silver_creek | id_gleason |
| C | az_jack co_long_draw az_juniper az_pivot_rock | az_skeleton | al_half_way al_lookout_mountain ga_burrell_42 ga_creek_road ar_whitaker_point | or_gold_canyon ca_ash | co_old_stump co_rosebud | id_freeman | |
| D | az_maple az_fresnal az_fuller az_airstrip | ga_burrell ga_irwin_mill | - | id_moose co_freeman id_comet co_starwood id_black | - | ||
| Large | E | ca_cedar_sqf co_happy_hollow az_choulic az_mormon | az_tenderfoot | fl_taylor ga_tatum_gulf al_power_horn ga_rocky_face ga_rock_mountain | or_draw id_pioneer id_john_doe | co_spring_creek_2 co_cold_springs | id_dry_creek id_buck |
| F | az_brown az_cowboy nv_horseshoe | - | nv_pinto ga_fox_mountain_fire | nv_little_valley or_rail ca_chimney_cnd | id_lone_pine co_hayden_pass | - | |
| G | nv_maggie | - | - | or_rattlesnake | - | - | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yun, S.-J.; Kwon, J.-W.; Kim, W.-T. A Novel Digital Twin Architecture with Similarity-Based Hybrid Modeling for Supporting Dependable Disaster Management Systems. Sensors 2022, 22, 4774. https://doi.org/10.3390/s22134774
Yun S-J, Kwon J-W, Kim W-T. A Novel Digital Twin Architecture with Similarity-Based Hybrid Modeling for Supporting Dependable Disaster Management Systems. Sensors. 2022; 22(13):4774. https://doi.org/10.3390/s22134774
Chicago/Turabian StyleYun, Seong-Jin, Jin-Woo Kwon, and Won-Tae Kim. 2022. "A Novel Digital Twin Architecture with Similarity-Based Hybrid Modeling for Supporting Dependable Disaster Management Systems" Sensors 22, no. 13: 4774. https://doi.org/10.3390/s22134774
APA StyleYun, S.-J., Kwon, J.-W., & Kim, W.-T. (2022). A Novel Digital Twin Architecture with Similarity-Based Hybrid Modeling for Supporting Dependable Disaster Management Systems. Sensors, 22(13), 4774. https://doi.org/10.3390/s22134774






