Dynamic Deformation Reconstruction of Variable Section WING with Fiber Bragg Grating Sensors
Abstract
1. Introduction
2. A Deformation–Reconstruction Model for Wing with Variable Cross-Section
2.1. Inverse Finite Element Model for Variable Cross-Section Beam
2.2. Calculation of Section Strain of Variable Section Beam Element
3. Strain Error Correction
3.1. SSILSVRFN Structure Learning
3.2. SSILSVRFN Parameter Learning
3.2.1. Consequent Parameter Learning
3.2.2. Antecedent Parameter Learning
4. Verifications through Simulations and Experimentation
4.1. Simulation Test
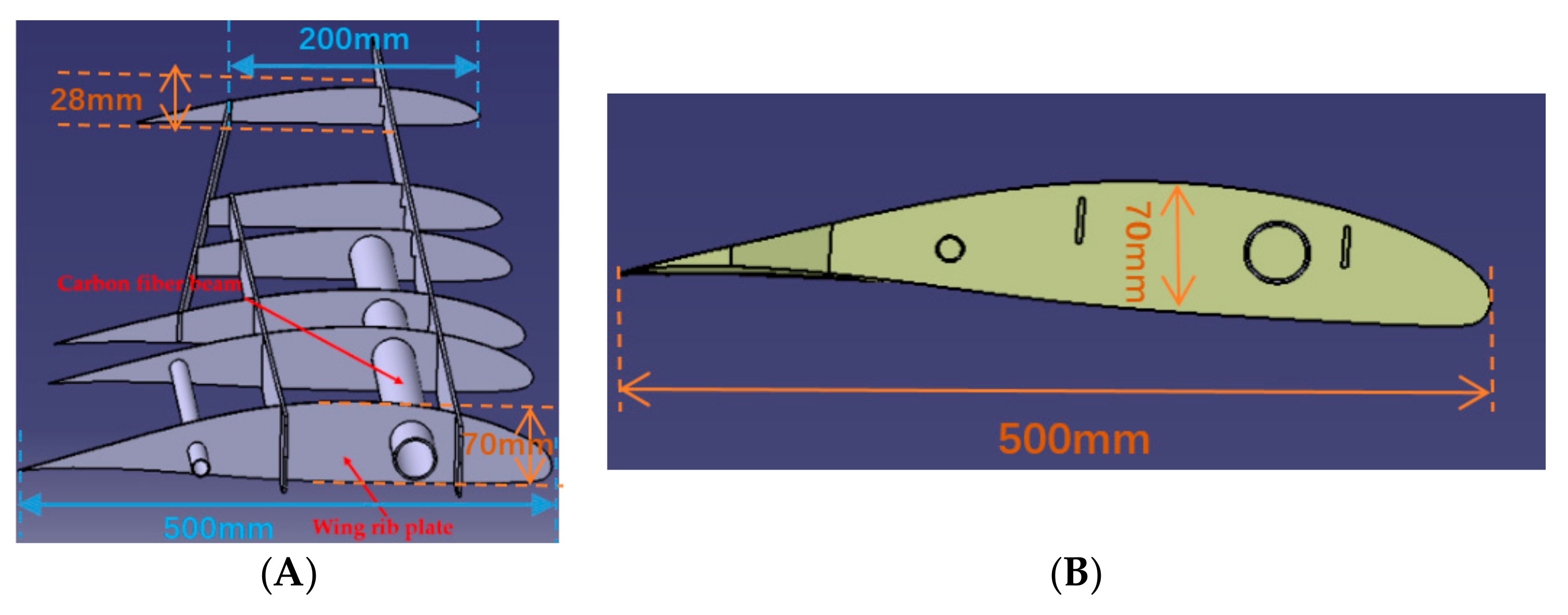
4.2. Physical Model Test
- By comparing between the FE analysis and the reconstructing with using IFEM, numerical studies show that the percent error of the deformation reconstruction along the main direction remains below 6.0%.
- Because of the strain measurement system error and the model error, experimental studies show that the percent error of the deformation reconstruction along the main direction computed from the unmodified strain measurements with iFEM remains below 13%.
- Experimental application of the proposed method shows that: the percent error of the deformation reconstruction along the main direction computed from the modified strain measurements remains below 6.7%.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A

References
- Xie, C.; Wu, Z.; Yang, C. Aeroelastic analysis of flexible wing with high aspect ratio. J. Beijing Univ. Aeronaut. Astronaut. 2003, 29, 1087–1090. [Google Scholar]
- Shang, B.; Song, B.; Wan, F. Application of optical fiber sensor in structural health monitoring of aircraft. Fiber Opt. Cable Appl. Technol. 2008, 3, 7–10. [Google Scholar]
- Foss, G.; Haugse, E. Using modal test results to develop strain to displacement transformations. In Proceedings of the 13th International Conference on Modal Analysis, Nashville, TN, USA, 13–19 February 1995; pp. 112–128. [Google Scholar]
- Gherlone, M.; Cerracchio, P.; Mattone, M.; di Sciuva, M.; Tessler, A. Shape sensing of 3D frame structures using an inverse Finite Element Method. Int. J. Solids Struct. 2012, 49, 3100–3112. [Google Scholar] [CrossRef]
- Van Tran Fleischer, W.L.K. Extension of ko Straight-Beam Displacement Theory to Deformed Shape Predictions of Slender Curved Structures; NASA: Edwards, CA, USA, 2011.
- Jutte, C.V.; Ko, W.L.; Stephens, C.A.; Stephens, C.A.; Bakalyar, J.A.; Rechards, W.L.; Parker, A.R. Deformed Shape Calculation of a Full-Scale Wing Using Fiber Optic Strain Data from a Ground Loads Test; NASA: Hampton, VA, USA, 2011.
- Jan, L.; Spangler, A.T. A Variational Principle for Reconstruction of Elastic Deformations in Shear Deformable Plates and Shells; NASA CASI: Hampton, VA, USA, 2003.
- Gherlone, M.; Cerracchio, P.; Mattone, M.; Di Sciuva, M.; Tessler, A. Beam shape sensing using inverse finite element method: Theory and experimental validation. In Proceedings of the 8th International Workshop on Structural Health Monitoring, Stanford, CA, USA, 13–15 September 2011. [Google Scholar]
- Kefal, A.; Oterkus, E. Displacement and stress monitoring of a Panamax containership using inverse finite element method. Ocean Eng. 2016, 119, 16–29. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E. Displacement and stress monitoring of a chemical tanker based on inverse finite element method. Ocean Eng. 2016, 112, 33–46. [Google Scholar] [CrossRef]
- Tessler, A.; Roy, R.; Esposito, M.; Surace, C.; Gherlone, M. Shape Sensing of Plate and Shell Structures Undergoing Large Displacements Using the Inverse Finite Element Method. Shock Vib. 2018, 2018, 8076085. [Google Scholar] [CrossRef]
- Gherlone, M.; Cerracchio, P.; Mattone, M. Shape sensing methods: Review and experimental comparison on a wing-shaped plate. Prog. Aerosp. Sci. 2018, 99, 14–26. [Google Scholar] [CrossRef]
- Cerracchio, P.; Gherlone, M.; di Sciuva, M.; Tessler, A. A novel approach for displacement and stress monitoring of sandwich structures based on the inverse Finite Element Method. Compos. Struct. 2015, 127, 69–76. [Google Scholar] [CrossRef]
- Zhao, Y.; Du, J.; Bao, H.; Xu, Q. Optimal Sensor Placement for Inverse Finite Element Reconstruction of Three Dimensional Frame Deformation. Int. J. Aerosp. Eng. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Zhao, Y.; Du, J.; Bao, H.; Xu, Q. Optimal Sensor Placement based on Eigenvalues Analysis for Sensing Deformation of Wing Frame. Sensors 2018, 18, 2424. [Google Scholar] [CrossRef] [PubMed]
- Zhao, F.; Bao, H.; Xue, S.; Xu, Q. Multi Objective Particle Swarm Optimization of Sensor Distribution Scheme with Consideration ofthe Accuracy and the Robustness for Deformation Reconstruction. Sensors 2019, 19, 1306. [Google Scholar] [CrossRef] [PubMed]
- Pan, X.; Bao, H.; Zhang, X. The in situ strain measurements modification based on Fuzzy nets for frame deformation reconstruction. J. Vib. Meas. Diagn. 2018, 38, 360–364. [Google Scholar]
- Gherlone, M.; Cerracchio, P.; Mattone, M. An inverse finite element method for beam shape sensing: theoretical framework and experimental validation. Smart Mater. Struct. 2014, 23, 045027. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, Z.; Chen, Z. A test method suitable for flexible UAV wing deformation. Comput. Meas. Control 2012, 20, 2894–2896. [Google Scholar]
- Forgit, C.; Lemoine, B.; le Marrec, L. A Timoshenko-like model for the study of three-dimensional vibrations of an elastic ring of general cross-section. Acta Mech. 2016, 227, 2543–2575. [Google Scholar] [CrossRef]
- Chuan, G.; Chen, Y.; Tong, G. Element Stiffness Matrix of Timoshenko Beam with Variable Section. Chin. J. Comput. Mech. 2014, 31, 266–272. [Google Scholar]
- Lurie, A.I. Theory of Elasticity; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2005. [Google Scholar]
- Mainçon, P. Inverse FEM I: load and response estimates from measurements. In Proceedings of the 2nd International Conference on Structural Engineering, Mechanics and Computation, Cape Town, South Africa, 5–7 July 2004. [Google Scholar]
- Feng, S. Research on the Fuzzy Network Method for Measuring the Deformation of the Long Flexible Base Antenna of the Base Wing. Master’s Thesis, Xi’an University, Xi’an, China, 2015. [Google Scholar]















| Loading | |||||||
|---|---|---|---|---|---|---|---|
| 135 N | FE analysis | 0.81 | 2.43 | 124.06 | −0.1292 | 0.0039 | 0.0011 |
| IFEM | 0.63 | 2.08 | 116.93 | −0.0846 | 0.0035 | 0.0032 | |
| Absolute error | 0.18 | 0.35 | 7.13 | 0.0446 | 0.0004 | 0.0021 | |
| Percent error | 22.2% | 14.4% | 5.7% | 34.5% | 10.3% | 190.9% | |
| 200 N | FE analysis | 1.52 | 4.27 | 168.18 | −0.2154 | 0.0066 | 0.0018 |
| IFEM | 1.17 | 3.72 | 158.09 | −0.1492 | 0.0058 | 0.0047 | |
| Absolute error | 0.35 | 0.55 | 10.09 | 0.0662 | 0.0008 | 0.0029 | |
| Percent error | 23.0% | 12.8% | 6.0% | 30.7% | 12.1% | 161.1% |
| Time/s | Measured Strain | Actual Strain | Modified Strain | Percentage Error | |||
|---|---|---|---|---|---|---|---|
| 0.04 | 0.001671 | 0.002137 | 0.002183 | 132.01 | 149.16 | 138.89 | 6.7% |
| 0.14 | 0.001428 | 0.001945 | 0.00187 | 113.07 | 127.52 | 124.97 | 5.2% |
| 0.24 | 0.001334 | 0.001659 | 0.001603 | 95.32 | 105.29 | 99.72 | 4.5% |
| 0.34 | 0.001079 | 0.001271 | 0.001261 | 78.48 | 89.13 | 86.29 | 4.2% |
| 0.44 | 0.001235 | 0.001357 | 0.001391 | 67.86 | 76.11 | 69.70 | 5.3% |
| 0.54 | 0.000934 | 0.001099 | 0.001087 | 57.46 | 64.37 | 62.79 | 5.6% |
| 0.64 | 0.00083 | 0.001075 | 0.001035 | 48.95 | 56.28 | 52.86 | 4.5% |
| 0.75 | 0.000644 | 0.000723 | 0.000714 | 46.53 | 53.30 | 49.95 | 5.1% |
| 0.85 | 0.000654 | 0.000779 | 0.000742 | 38.67 | 44.32 | 40.75 | 3.9% |
| 0.95 | 0.000627 | 0.000696 | 0.0007 | 33.83 | 37.78 | 36.58 | 5.2% |
| Time/s | Percentage Error | Percentage Error | ||||||
|---|---|---|---|---|---|---|---|---|
| 0.04 | 1.82 | 1.26 | 1.42 | 12.70% | 4.75 | 3.87 | 4.11 | 6.20% |
| 0.14 | 1.54 | 0.89 | 1.03 | 15.73% | 2.37 | 1.92 | 2.06 | 7.29% |
| 0.24 | 1.46 | 0.92 | 0.99 | 7.61% | 3.29 | 2.87 | 3.15 | 9.76% |
| 0.34 | 1.27 | 0.75 | 0.82 | 9.33% | 2.46 | 2.14 | 2.33 | 8.88% |
| 0.44 | 1.14 | 0.67 | 0.73 | 8.96% | 2.34 | 2.03 | 2.18 | 7.39% |
| 0.54 | 1.08 | 0.56 | 0.65 | 16.07% | 2.26 | 1.98 | 2.09 | 5.56% |
| 0.64 | 1.03 | 0.51 | 0.6 | 17.65% | 2.12 | 1.85 | 1.97 | 6.49% |
| 0.75 | 0.89 | 0.47 | 0.52 | 10.64% | 2.06 | 1.74 | 1.88 | 8.05% |
| 0.85 | 0.82 | 0.43 | 0.51 | 18.60% | 1.84 | 1.58 | 1.69 | 6.96% |
| 0.95 | 0.78 | 0.37 | 0.44 | 18.92% | 1.79 | 1.62 | 1.72 | 6.17% |
| Node | Maximum Percentage Error | |||
|---|---|---|---|---|
| 1 | 132.01 | 149.06 | 138.97 | 6.7% |
| 2 | 79.57 | 94.38 | 88.63 | 6.0% |
| 3 | 41.6 | 55.42 | 52.83 | 4.6% |
| 4 | 19.41 | 29.31 | 27.79 | 5.1% |
| 5 | 9.78 | 11.5 | 10.96 | 4.7% |
| 6 | 3.66 | 4.77 | 4.57 | 4.1% |
| Time/s | Percentage Reduced | ||
|---|---|---|---|
| 0.04 | 12.01 | 3.97 | 66.8% |
| 0.14 | 11.13 | 3.18 | 71.4% |
| 0.24 | 10.22 | 3.38 | 66.9% |
| 0.34 | 9.42 | 3.71 | 60.5% |
| 0.44 | 9.51 | 3.20 | 66.3% |
| 0.54 | 9.31 | 3.29 | 64.6% |
| 0.64 | 7.05 | 2.16 | 69.4% |
| 0.75 | 6.21 | 2.03 | 67.2% |
| 0.85 | 6.15 | 2.50 | 59.2% |
| 0.95 | 5.83 | 2.18 | 62.5% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Z.; Zhao, Y.; Bao, H.; Zhao, F. Dynamic Deformation Reconstruction of Variable Section WING with Fiber Bragg Grating Sensors. Sensors 2019, 19, 3350. https://doi.org/10.3390/s19153350
Fu Z, Zhao Y, Bao H, Zhao F. Dynamic Deformation Reconstruction of Variable Section WING with Fiber Bragg Grating Sensors. Sensors. 2019; 19(15):3350. https://doi.org/10.3390/s19153350
Chicago/Turabian StyleFu, Zhen, Yong Zhao, Hong Bao, and Feifei Zhao. 2019. "Dynamic Deformation Reconstruction of Variable Section WING with Fiber Bragg Grating Sensors" Sensors 19, no. 15: 3350. https://doi.org/10.3390/s19153350
APA StyleFu, Z., Zhao, Y., Bao, H., & Zhao, F. (2019). Dynamic Deformation Reconstruction of Variable Section WING with Fiber Bragg Grating Sensors. Sensors, 19(15), 3350. https://doi.org/10.3390/s19153350




