A Quest for the Origin of Barrier to the Internal Rotation ofHydrogen Peroxide (H2O2) and Fluorine Peroxide (F2O2)
Abstract
:1. Introduction
 Trans and Staggered
Trans and Staggered  Eclipsed conformers is in fact a rotational isomerization process and can be viewed as resulting from reorganization and redistribution of electron density among the atoms in a molecule, so that the total number of electrons is conserved even though there may be an intramolecular charge transfer process [9,10]. Thus the physical process of the dynamics of internal rotation initiates the isomerization reaction, which generates infinite number of conformations between the extreme conformations stated above. We [11] have demonstrated, by a density partitioning analysis, that no new force is appearing during the physical process of evolution of molecular conformations rather the forces responsible for molecular binding and antibinding are deciding the conformational behaviour. The efficacy of Pople’s [12,13] approximate SCF theory to compute the conformational isomers is well demonstrated [14,15]. It was also demonstrated that, in the context of study of molecular conformations of hydrogen peroxide, that Pople’s approximate method, compared to ab initio methods, was more reliable in computing the conformational isomers [16,17,18,19]. However, in the present day scenario of computational chemistry, the sophisticated methods can be easily invoked to calculate the barrier heights very accurately. But, perhaps, Pople’s approximate SCF method is the only method that provides with a scope of decomposition of the total energy into one- and two-center components and such components can be further decomposed into meaningful physical components. Although, more recently, there are also claims of partitioning the total SCF energy into one- and two center components in ab initio methods [20], but such fuzzy atom dissection of total energy appears to calculate the total one- and two-center interaction energies only and decomposition of such energy terms into meaningful physical components are, probably, yet to be furnished [20]. We have recently demonstrated that the Pople’s energy partitioning scheme can be invoked in the significant elucidation of the origin of the barrier to the physical process of inversion [21,22] and intramolecular rotation [23,24], and such an effort is a meaningful venture. In the present venture, we shall invoke the energy partitioning scheme of Pople in the elucidation of the origin of barrier to internal rotation of hydrogen peroxide (H2O2) and its analogue fluorine peroxide (F2O2). It is well known to the chemists that both hydrogen peroxide and fluorine peroxide have two barriers –cis barrier and trans barrier, and the equilibrium conformations are non-planar skew conformation instead of expected trans form. The fact that the equilibrium geometries of the molecules are not the trans form rather a non-planar skew form, is itself an intriguing phenomenon and a clear departure from a normal behaviour of the phenomenon of structural isomerism of chemistry. But why the preferred conformations of the molecules are the non-planar gauche forms and not the usual trans forms and also the origin of barrier are required to be completely elucidated. It seems that there is yet no theoretical correlation of the preferred conformations and the origin of barrier of the instant molecules. In the above premise, we propose to make a detailed study of the elucidation of the origin of barrier and justifying the preferred conformations of the hydrogen peroxide and fluorine peroxide molecules in terms of the energy partitioning analysis in the present investigation.
Eclipsed conformers is in fact a rotational isomerization process and can be viewed as resulting from reorganization and redistribution of electron density among the atoms in a molecule, so that the total number of electrons is conserved even though there may be an intramolecular charge transfer process [9,10]. Thus the physical process of the dynamics of internal rotation initiates the isomerization reaction, which generates infinite number of conformations between the extreme conformations stated above. We [11] have demonstrated, by a density partitioning analysis, that no new force is appearing during the physical process of evolution of molecular conformations rather the forces responsible for molecular binding and antibinding are deciding the conformational behaviour. The efficacy of Pople’s [12,13] approximate SCF theory to compute the conformational isomers is well demonstrated [14,15]. It was also demonstrated that, in the context of study of molecular conformations of hydrogen peroxide, that Pople’s approximate method, compared to ab initio methods, was more reliable in computing the conformational isomers [16,17,18,19]. However, in the present day scenario of computational chemistry, the sophisticated methods can be easily invoked to calculate the barrier heights very accurately. But, perhaps, Pople’s approximate SCF method is the only method that provides with a scope of decomposition of the total energy into one- and two-center components and such components can be further decomposed into meaningful physical components. Although, more recently, there are also claims of partitioning the total SCF energy into one- and two center components in ab initio methods [20], but such fuzzy atom dissection of total energy appears to calculate the total one- and two-center interaction energies only and decomposition of such energy terms into meaningful physical components are, probably, yet to be furnished [20]. We have recently demonstrated that the Pople’s energy partitioning scheme can be invoked in the significant elucidation of the origin of the barrier to the physical process of inversion [21,22] and intramolecular rotation [23,24], and such an effort is a meaningful venture. In the present venture, we shall invoke the energy partitioning scheme of Pople in the elucidation of the origin of barrier to internal rotation of hydrogen peroxide (H2O2) and its analogue fluorine peroxide (F2O2). It is well known to the chemists that both hydrogen peroxide and fluorine peroxide have two barriers –cis barrier and trans barrier, and the equilibrium conformations are non-planar skew conformation instead of expected trans form. The fact that the equilibrium geometries of the molecules are not the trans form rather a non-planar skew form, is itself an intriguing phenomenon and a clear departure from a normal behaviour of the phenomenon of structural isomerism of chemistry. But why the preferred conformations of the molecules are the non-planar gauche forms and not the usual trans forms and also the origin of barrier are required to be completely elucidated. It seems that there is yet no theoretical correlation of the preferred conformations and the origin of barrier of the instant molecules. In the above premise, we propose to make a detailed study of the elucidation of the origin of barrier and justifying the preferred conformations of the hydrogen peroxide and fluorine peroxide molecules in terms of the energy partitioning analysis in the present investigation. 2. Method of Computation
2.1 Coordinate System
2.2 Necessary Algorithm
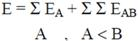
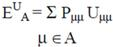

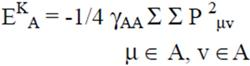
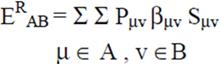
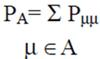
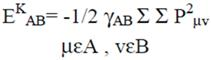
3. Results and Discussion
3.1 Hydrogen Peroxide, H2O2
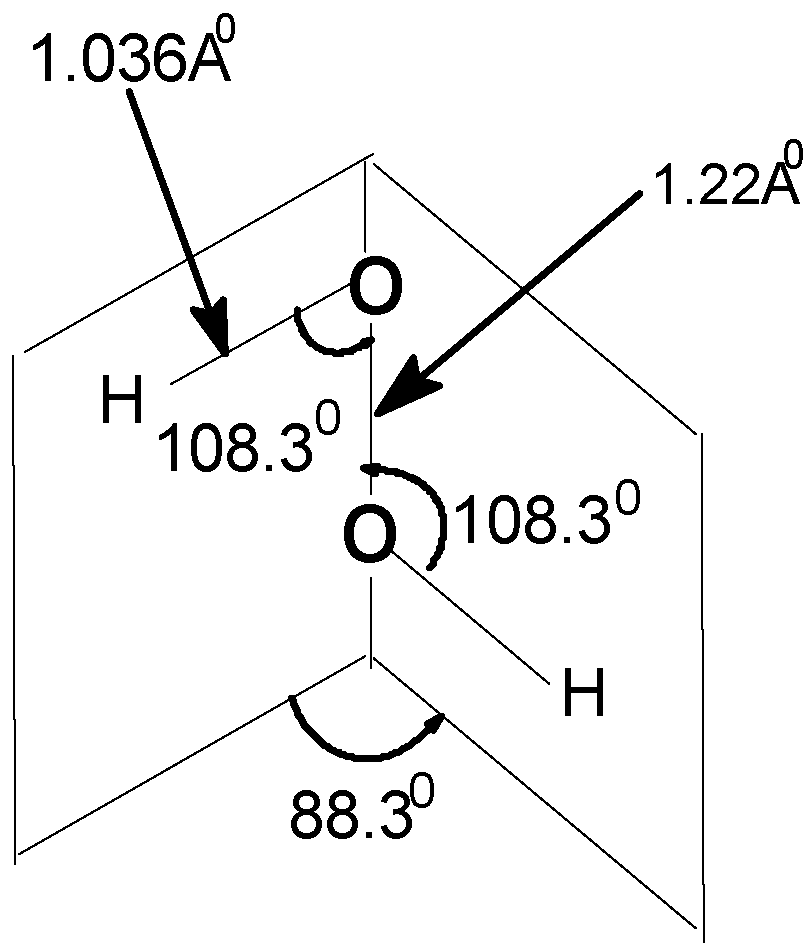
| Angle of torsion (θ) (degrees) | O–O (A0) | O–H (A0) | ∠HOO (degree) |
|---|---|---|---|
| 0(cis) | 1.22 | 1.034 | 108.9 |
| 20 | 1.22 | 1.036 | 108.8 |
| 40 | 1.22 | 1.037 | 108.5 |
| 60 | 1.22 | 1.038 | 108.3 |
| 80 | 1.22 | 1.039 | 108.3 |
| 88.3 | 1.22 | 1.036 | 108.3 |
| 100 | 1.22 | 1.038 | 106.5 |
| 120 | 1.22 | 1.038 | 106.2 |
| 140 | 1.22 | 1.039 | 105.9 |
| 160 | 1.22 | 1.039 | 105.7 |
| 180(trans) | 1.22 | 1.034 | 108.3 |
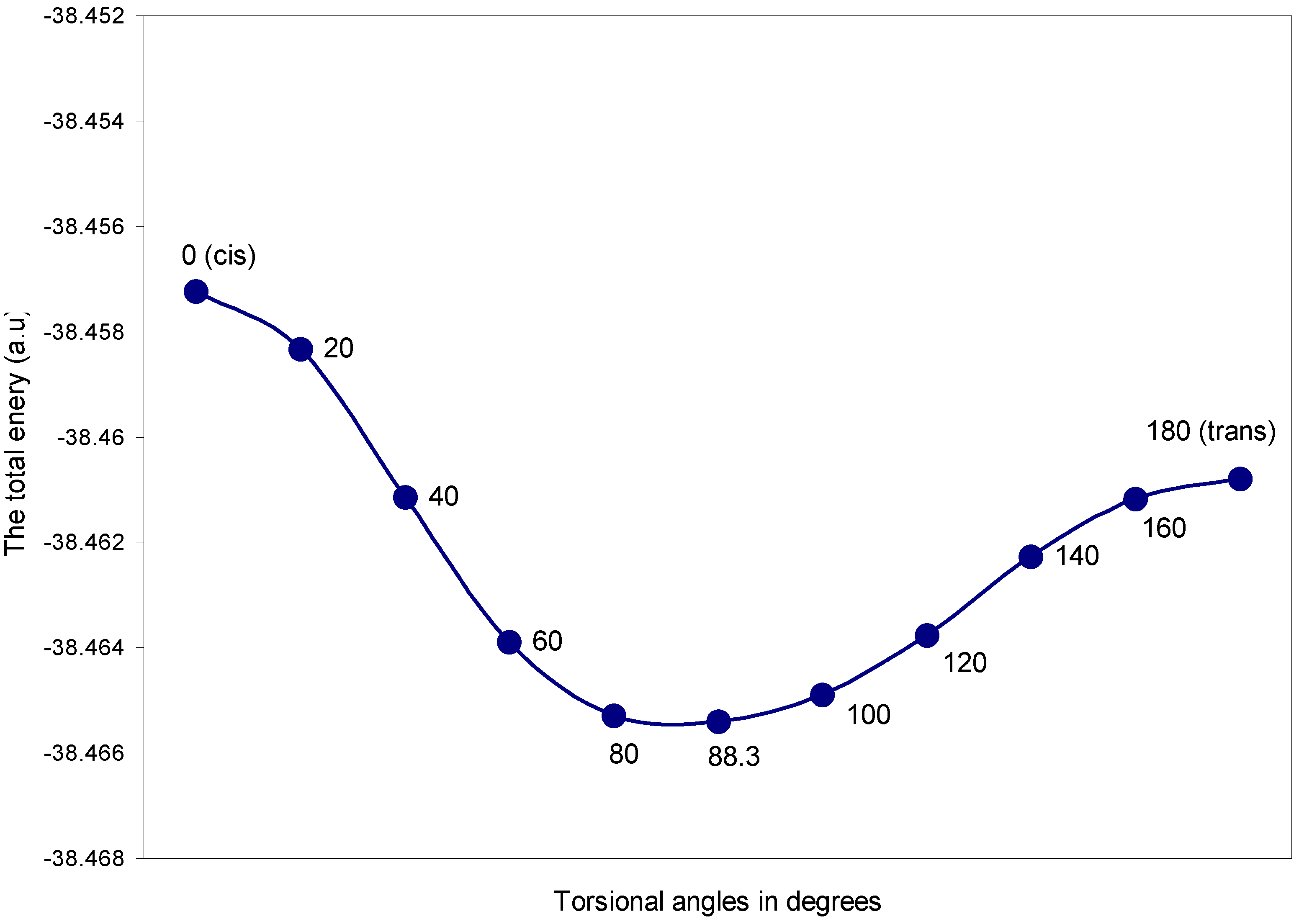
| Torsional angles (θ) in degrees | Total Energy | q (O) | q (H) |
|---|---|---|---|
| 0 (cis) | -38.45722 | 6.1209 | 0.8791 |
| 20 | -38.45833 | 6.1192 | 0.8808 |
| 40 | -38.46114 | 6.1161 | 0.8839 |
| 60 | -38.46388 | 6.1135 | 0.8865 |
| 80 | -38.46528 | 6.1129 | 0.8870 |
| 88.3 | -38.46540 | 6.1136 | 0.8864 |
| 100 | -38.46489 | 6.1156 | 0.8844 |
| 120 | -38.46375 | 6.1202 | 0.8798 |
| 140 | -38.46226 | 6.1260 | 0.8739 |
| 160 | -38.46116 | 6.1307 | 0.8693 |
| 180 (trans) | -38.46078 | 6.1326 | 0.8674 |
- (i)
- Two one-center interactions – one on O atoms and the other on H atoms,
- (ii)
- Two bonding interactions– ‘O–O’ bond and ‘O–H’ bond,
- (iii)
- Two nonbonding interactions–‘H------H’ and ‘H-----O’,
The two-center bonding interactions:
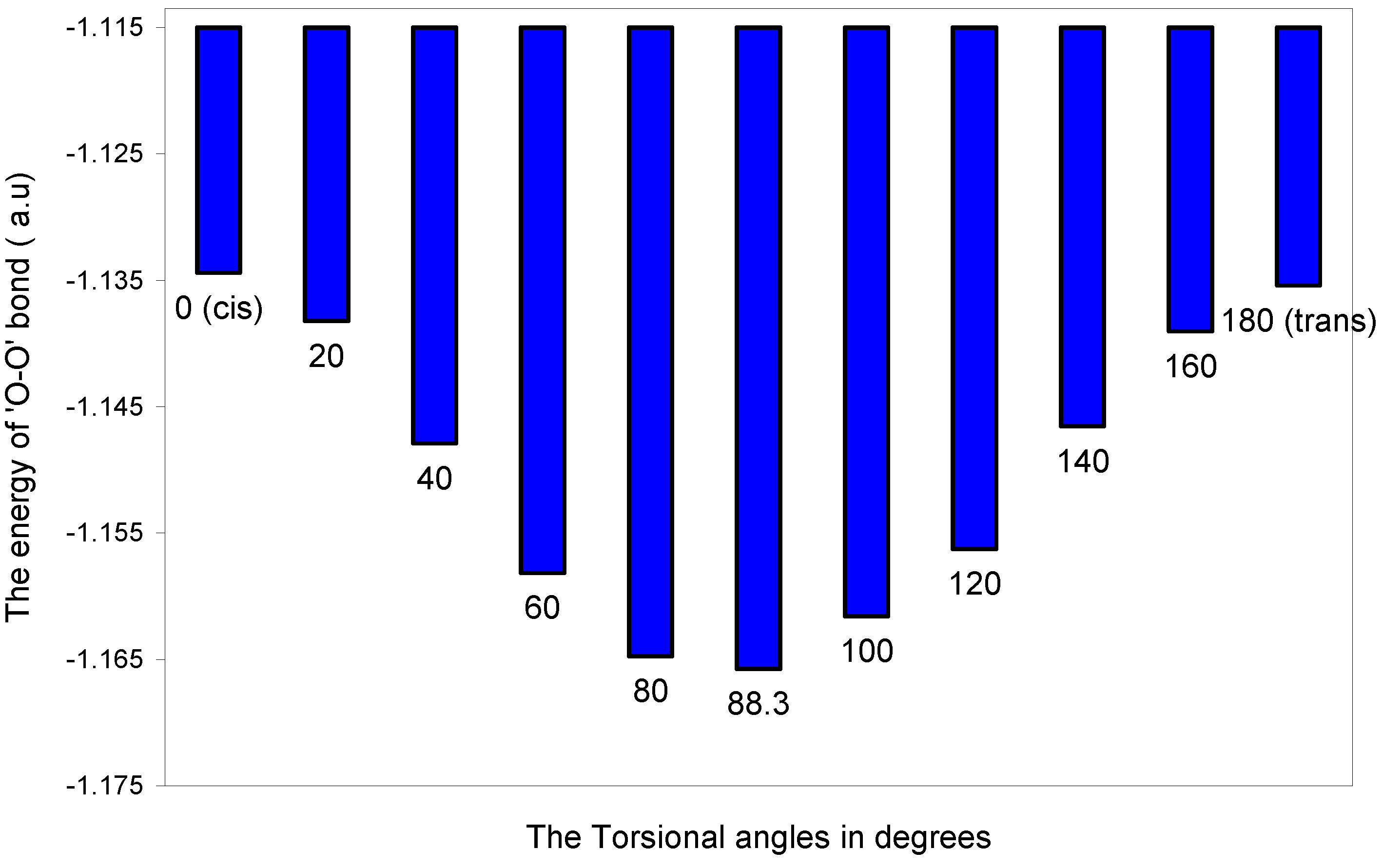
| Angle of torsion (θ) in degrees | EJ | EN | EV | EK | ER | ETotal |
|---|---|---|---|---|---|---|
| 0 (cis) | 15.91141 | 15.61476 | -31.19410 | -0.21828 | -1.24820 | -1.13441 |
| 20 | 15.90245 | 15.61476 | -31.18532 | -0.21855 | -1.25157 | -1.13823 |
| 40 | 15.88630 | 15.61476 | -31.16948 | -0.21924 | -1.26023 | -1.14789 |
| 60 | 15.87288 | 15.61476 | -31.15631 | -0.21990 | -1.26957 | -1.15814 |
| 80 | 15.86996 | 15.61476 | -31.15344 | -0.22024 | -1.27578 | -1.16474 |
| 88.3 | 15.87327 | 15.61476 | -31.15669 | -0.22024 | -1.27686 | -1.16576 |
| 100 | 15.88354 | 15.61476 | -31.16677 | -0.21971 | -1.27342 | -1.16160 |
| 120 | 15.90754 | 15.61476 | -31.19031 | -0.21921 | -1.26903 | -1.15625 |
| 140 | 15.93793 | 15.61476 | -31.22009 | -0.21848 | -1.26067 | -1.14655 |
| 160 | 15.96217 | 15.61476 | -31.24382 | -0.21801 | -1.25414 | -1.13904 |
| 180 (trans) | 15.97208 | 15.61476 | -31.25352 | -0.21778 | -1.25096 | -1.13542 |
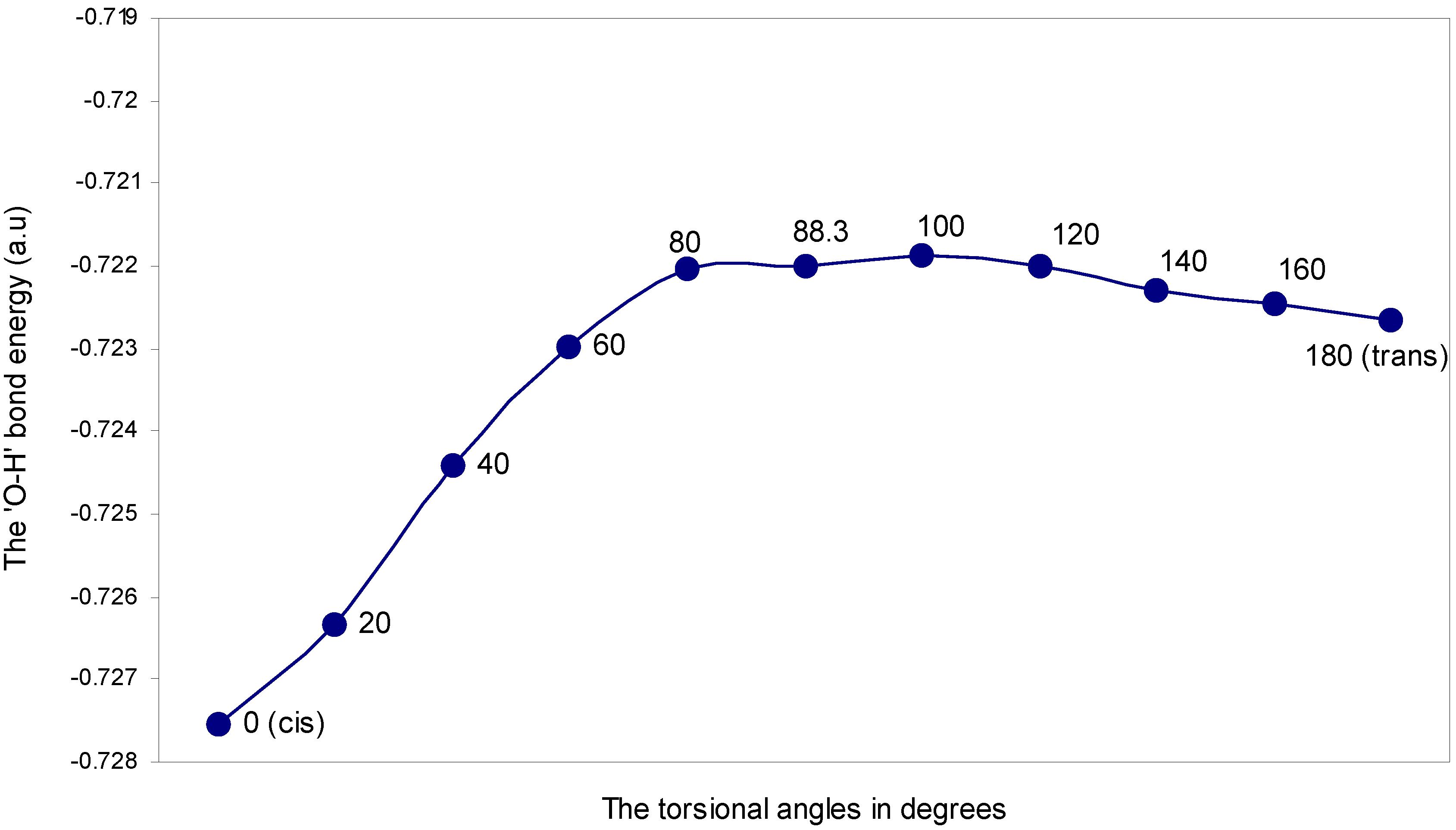
| Angle of torsion (θ) in degrees | EJ | EN | EV | EK | ER | ETotal |
|---|---|---|---|---|---|---|
| 0 (cis) | 2.55283 | 3.07061 | -5.40644 | -0.22832 | -0.71623 | -0.72755 |
| 20 | 2.55349 | 3.06467 | -5.40288 | -0.22806 | -0.71356 | -0.72634 |
| 40 | 2.55942 | 3.06173 | -5.40647 | -0.22797 | -0.71113 | -0.72442 |
| 60 | 2.56401 | 3.05878 | -5.40878 | -0.22786 | -0.70914 | -0.72299 |
| 80 | 2.56358 | 3.05582 | -5.40627 | -0.22768 | -0.70749 | -0.72204 |
| 88.3 | 2.56201 | 3.05582 | -5.40478 | -0.22764 | -0.70740 | -0.72199 |
| 100 | 2.55891 | 3.05875 | -5.40388 | -0.22790 | -0.70774 | -0.72186 |
| 120 | 2.54750 | 3.05878 | -5.39300 | -0.22753 | -0.70774 | -0.72199 |
| 140 | 2.53478 | 3.06173 | -5.38296 | -0.22718 | -0.70865 | -0.72228 |
| 160 | 2.52316 | 3.06170 | -5.37190 | -0.22664 | -0.70879 | -0.72247 |
| 180 (trans) | 2.52022 | 3.06468 | -5.37121 | -0.22660 | -0.70970 | -0.72266 |
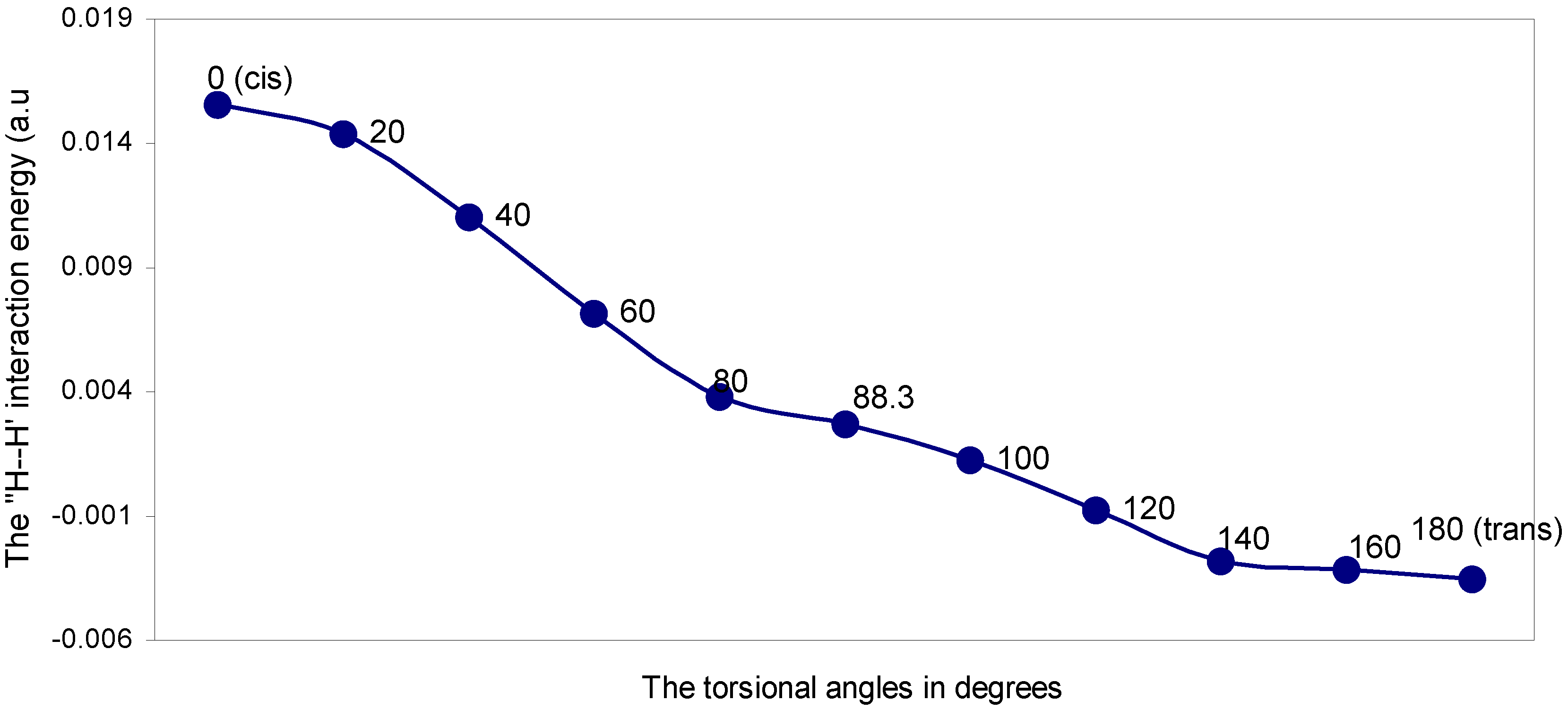
| Angle of torsion (θ) in degrees | EJ | EN | EV | EK | ER | ETotal |
|---|---|---|---|---|---|---|
| 0 (cis) | 0.21388 | 0.27849 | -0.48660 | -0.00177 | 0.01156 | 0.01556 |
| 20 | 0.21276 | 0.27586 | -0.48312 | -0.00149 | 0.01038 | 0.01439 |
| 40 | 0.20631 | 0.26526 | -0.46682 | -0.00088 | 0.00718 | 0.01105 |
| 60 | 0.19600 | 0.25015 | -0.44219 | -0.00028 | 0.00349 | 0.00717 |
| 80 | 0.18398 | 0.23424 | -0.41482 | -0.00000 | 0.00042 | 0.00382 |
| 88.3 | 0.17893 | 0.22806 | -0.40372 | -0.00001 | -0.00058 | 0.00273 |
| 100 | 0.17470 | 0.22362 | -0.39506 | -0.00016 | -0.00185 | 0.00125 |
| 120 | 0.16414 | 0.21221 | -0.37313 | -0.00067 | -0.00325 | -0.00073 |
| 140 | 0.15635 | 0.20482 | -0.35780 | -0.00146 | -0.00473 | -0.00282 |
| 160 | 0.15102 | 0.19994 | -0.34746 | -0.00212 | -0.00454 | -0.00316 |
| 180 (trans) | 0.14937 | 0.19861 | -0.34441 | -0.00239 | -0.00469 | -0.00351 |
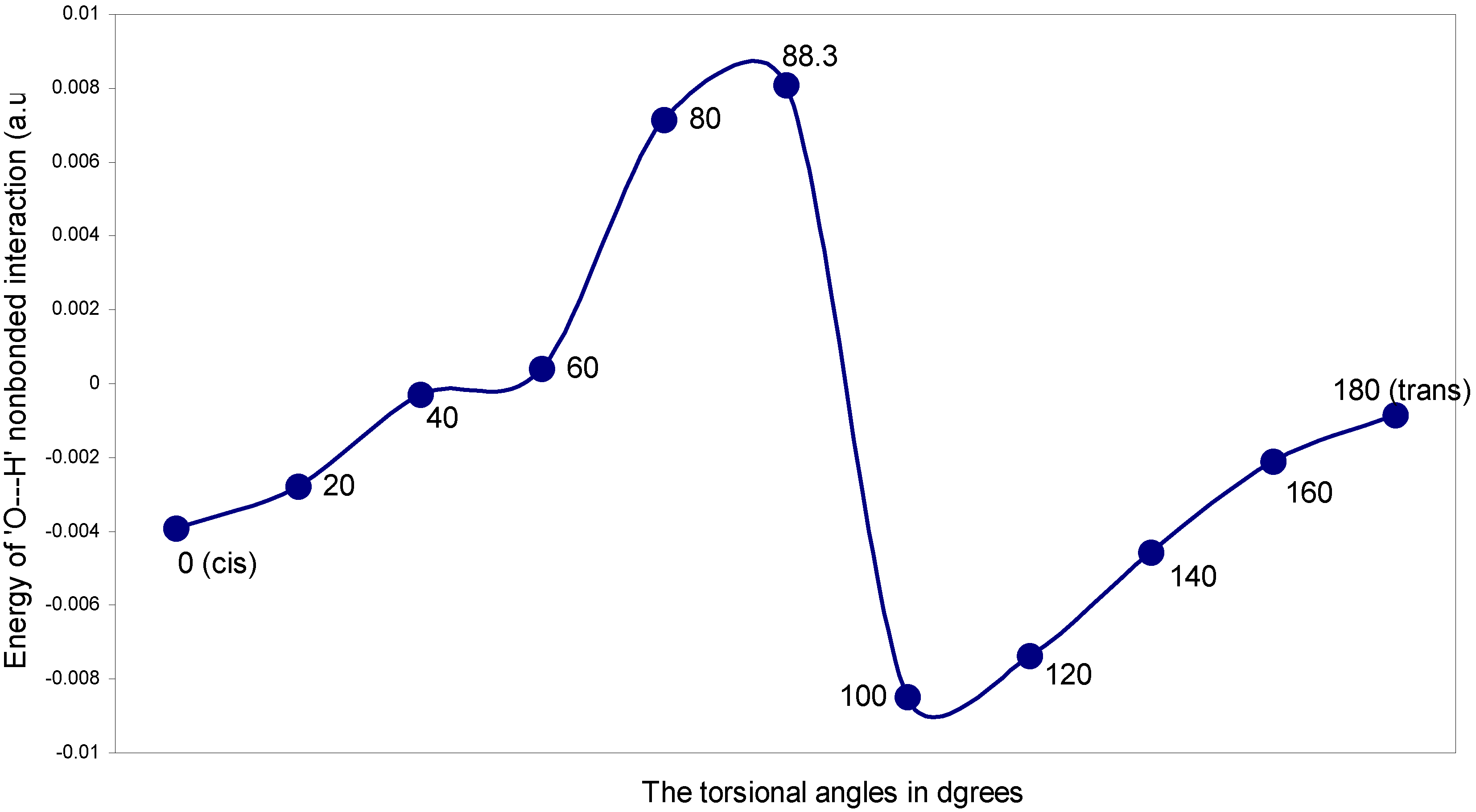
| Angle of torsion (θ) in degrees | EJ | EN | EV | EK | ER | ETotal |
|---|---|---|---|---|---|---|
| 0 (cis) | 1.54113 | 1.72512 | -3.26385 | -0.00145 | -0.00487 | -0.00392 |
| 20 | 1.54614 | 1.72791 | -3.27145 | -0.00174 | -0.00364 | -0.00278 |
| 40 | 1.55299 | 1.73040 | -3.28050 | -0.00243 | -0.00018 | -0.00028 |
| 60 | 1.55812 | 1.73183 | -3.28684 | -0.00311 | 0.00401 | 0.000401 |
| 80 | 1.55926 | 1.73217 | -3.28828 | -0.00345 | 0.00746 | 0.00716 |
| 88.3 | 1.55831 | 1.73217 | -3.28737 | -0.00345 | 0.00843 | 0.00809 |
| 100 | 1.57236 | 1.75172 | -3.32050 | -0.00317 | 0.00848 | -0.00848 |
| 120 | 1.56830 | 1.75513 | -3.32005 | -0.00250 | 0.00824 | -0.00736 |
| 140 | 1.56692 | 1.76390 | -3.32759 | -0.00148 | 0.00632 | -0.00457 |
| 160 | 1.56174 | 1.76622 | -3.32499 | -0.00062 | 0.00446 | -0.00211 |
| 180 (trans) | 1.56145 | 1.76930 | -3.32783 | -0.00026 | -0.00350 | -0.00084 |
| Angle of torsion (θ) in degrees | EU | EN | EK | ETotal | |
|---|---|---|---|---|---|
| O | -30.88718 | 15.48207 | -2.11602 | -17.52113 | |
| O | -30.87981 | 15.47336 | -2.11456 | -17.52101 | |
| O | -30.86588 | 15.45764 | -2.11157 | -17.51981 | |
| O | -30.85435 | 15.44459 | -2.10884 | -17.51860 | |
| O | -30.85220 | 15.44175 | -2.10780 | -17.51825 | |
| O | -30.85527 | 15.44496 | -2.10811 | -17.51902 | |
| O | -30.86622 | 15.45495 | -2.10980 | -17.52107 | |
| O | -30.88852 | 15.47830 | -2.11348 | -17.52370 | |
| O | -30.91689 | 15.50788 | -2.11851 | -17.52752 | |
| O | -30.93918 | 15.53148 | -2.12257 | -17.53027 | |
| O | -30.94835 | 15.54111 | -2.12428 | -17.53152 | |
The two-center nonbonding interactions:
The ‘H---H’ nonbonding interaction:
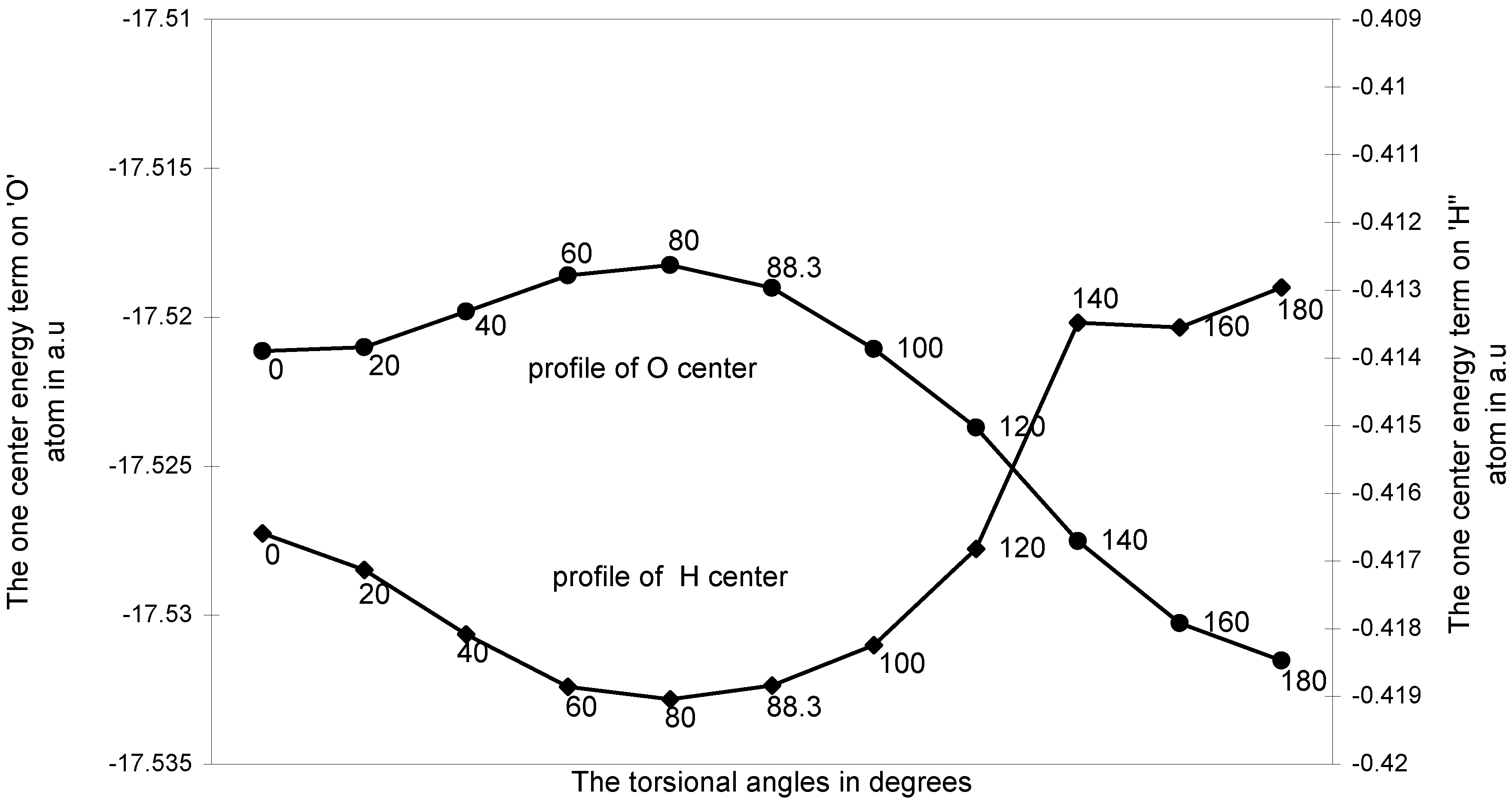
The ‘O---H’ nonbonding interaction:
The one-center components:
3.2 Fluorine Peroxide, F2O2
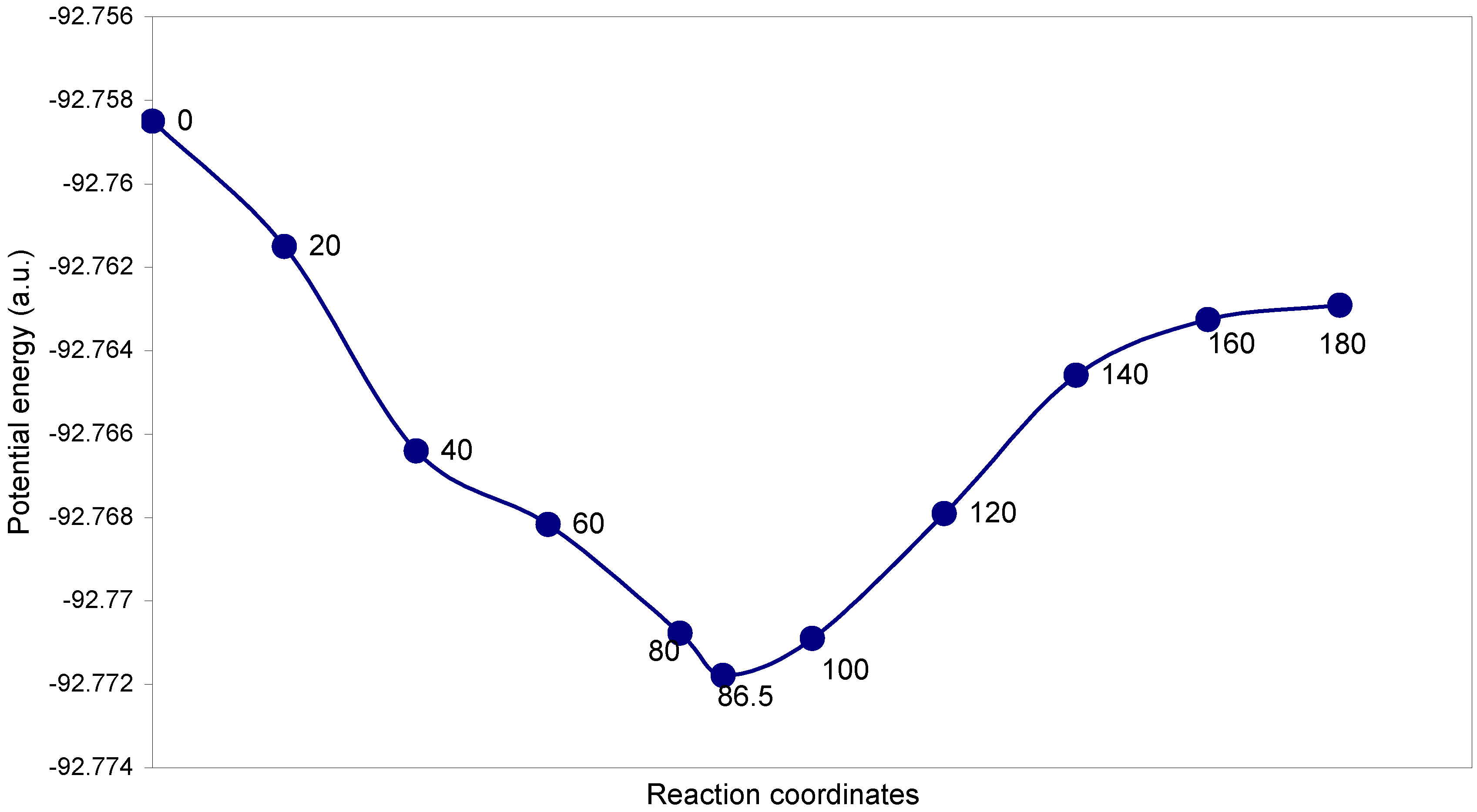
| Angle of torsion (θ, degrees) | O–O (A0) | O–F (A0) | ∠FOO (degree) | Total energy (a.u) |
|---|---|---|---|---|
| 0(cis) | 1.22 | 1.18 | 109.0 | -92.7585 |
| 20 | 1.22 | 1.18 | 108.6 | -92.76151 |
| 40 | 1.22 | 1.18 | 108.5 | -92.76641 |
| 60 | 1.22 | 1.18 | 108.4 | -92.76817 |
| 80 | 1.22 | 1.18 | 108.4 | -92.77078 |
| 86.5 | 1.22 | 1.18 | 108.3 | -92.77179 |
| 100 | 1.22 | 1.18 | 108.2 | -92.7709 |
| 120 | 1.22 | 1.18 | 108.0 | -92.76791 |
| 140 | 1.22 | 1.18 | 107.8 | -92.76459 |
| 160 | 1.22 | 1.18 | 107.7 | -92.76326 |
| 180(trans) | 1.22 | 1.18 | 106.9 | -92.76291 |
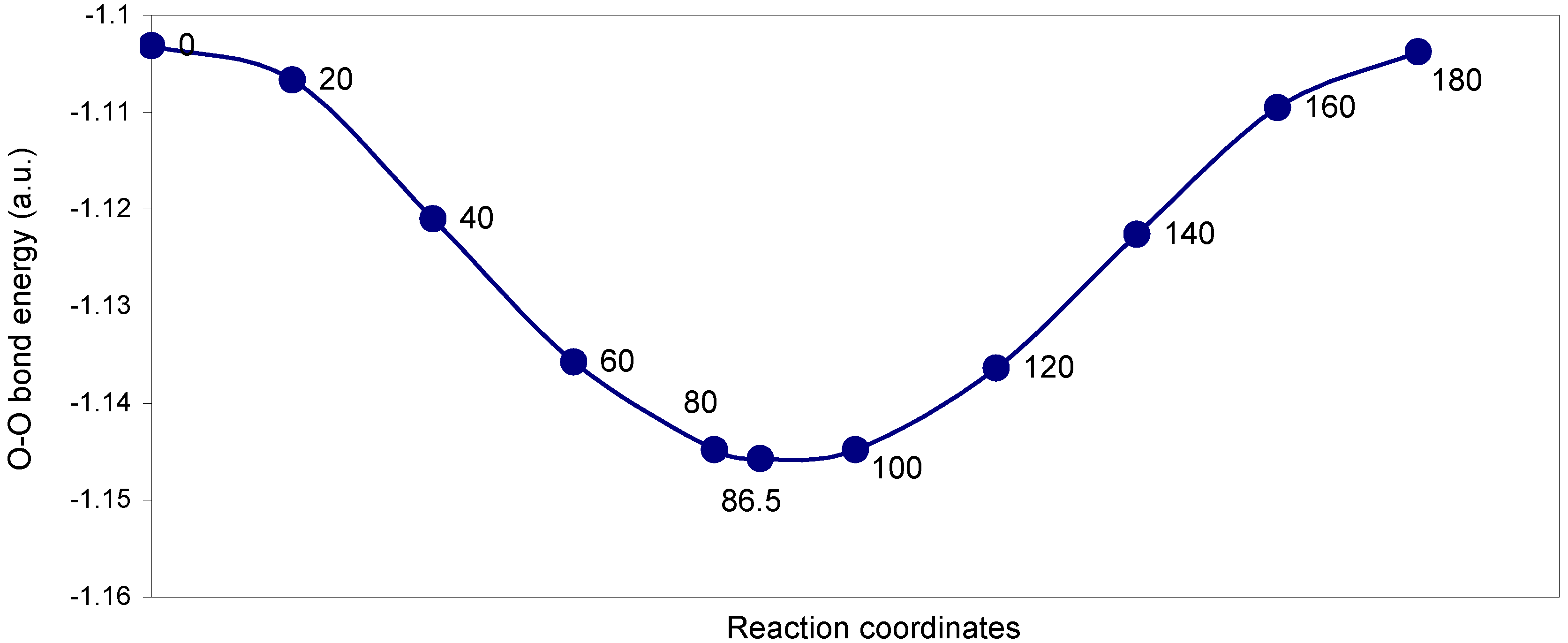
| Angle of torsion (degrees) | EJ | EN | EV | EK | ER | E (O – O) |
|---|---|---|---|---|---|---|
| 0 | 14.99701 | 15.61476 | -30.28450 | -0.21060 | -1.21983 | -1.10316 |
| 20 | 14.98779 | 15.61476 | -30.27520 | -0.21096 | -1.22312 | -1.10670 |
| 40 | 14.96508 | 15.61476 | -30.25225 | -0.21256 | -1.23603 | -1.12099 |
| 60 | 14.94054 | 15.61476 | -30.22744 | -0.21414 | -1.24950 | -1.13577 |
| 80 | 14.92515 | 15.61476 | -30.21186 | -0.21497 | -1.25789 | -1.14480 |
| 86.5 | 14.92252 | 15.61476 | -30.20920 | -0.21503 | -1.25876 | -1.14571 |
| 100 | 14.92265 | 15.61476 | -30.20933 | -0.21480 | -1.25809 | -1.14480 |
| 120 | 14.93427 | 15.61476 | -30.22109 | -0.21367 | -1.25066 | -1.13638 |
| 140 | 14.95472 | 15.61476 | -30.24178 | -0.21201 | -1.23830 | -1.12260 |
| 160 | 14.97323 | 15.61476 | -30.26048 | -0.21050 | -1.22655 | -1.10954 |
| 180 | 14.97831 | 15.61476 | -30.26562 | -0.21000 | -1.22121 | -1.10376 |
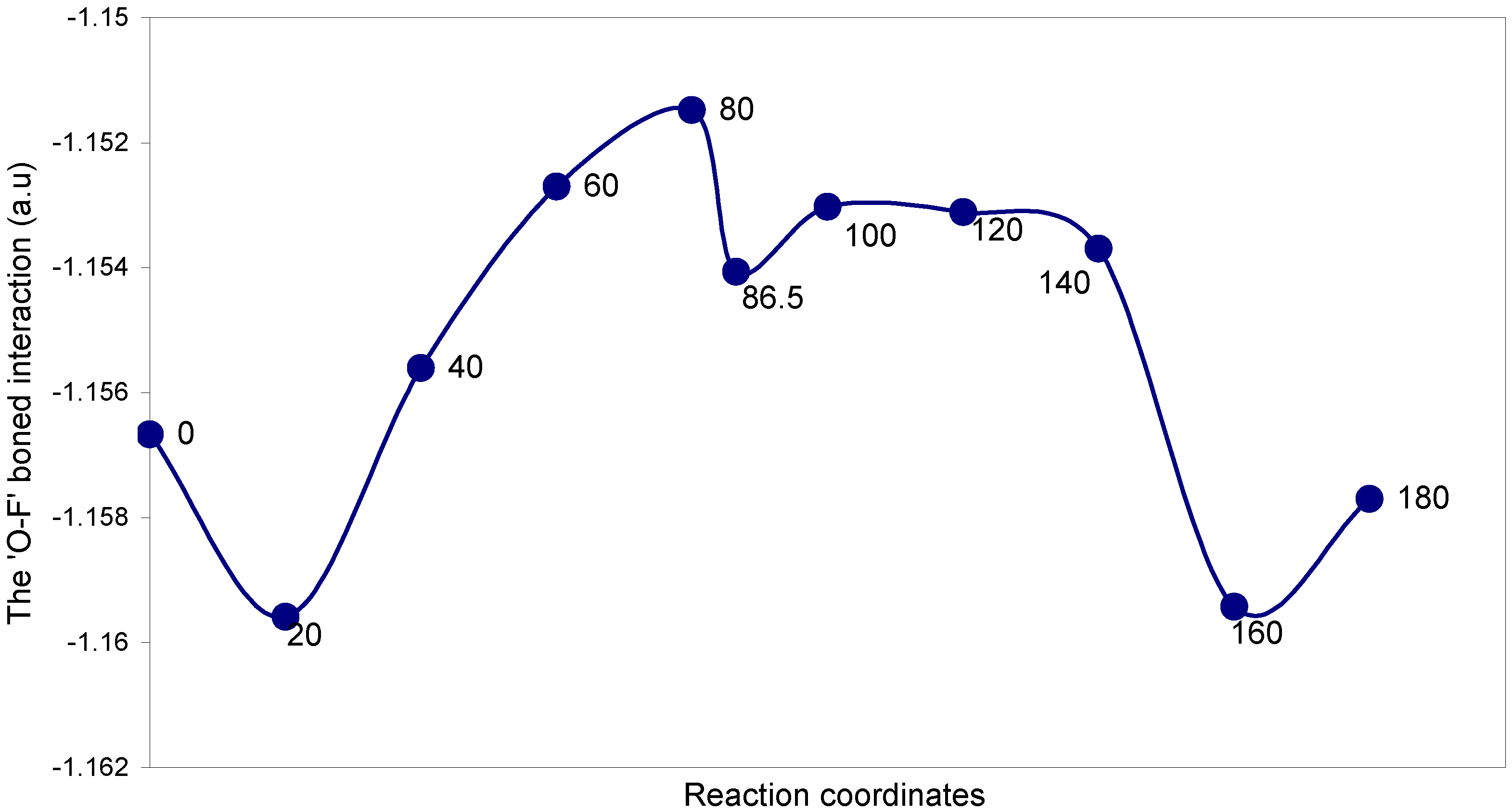
| Angles of torsion (degrees) | EJ | EN | EV | EK | ER | E (O – F) |
|---|---|---|---|---|---|---|
| 0 | 18.47503 | 18.83479 | -36.97840 | -0.21876 | -0.26932 | -1.15667 |
| 20 | 18.47439 | 18.83472 | -36.97814 | -0.21892 | -1.27163 | -1.15959 |
| 40 | 18.47219 | 18.83478 | -36.97603 | -0.21843 | -1.26812 | -1.15561 |
| 60 | 18.46986 | 18.83484 | -36.97414 | -0.21800 | -1.26526 | -1.15270 |
| 80 | 18.46846 | 18.83484 | -36.97293 | -0.21780 | -1.26406 | -1.15148 |
| 86.5 | 18.46793 | 18.83479 | -36.97261 | -0.21781 | -1.26636 | -1.15407 |
| 100 | 18.46778 | 18.83469 | -36.97215 | -0.21785 | -1.26550 | -1. 15303 |
| 120 | 18.46913 | 18.83471 | -36.97341 | -0.21807 | -1.26547 | -1.15311 |
| 140 | 18.47110 | 18.83480 | -36.97494 | -0.21835 | -1.26631 | -1.15370 |
| 160 | 18.47285 | 18.83476 | -36.97693 | -0.21862 | -1.27150 | -1.15943 |
| 180 | 18.47343 | 18.83475 | -36.97723 | -0.21863 | -1.27002 | -1.15770 |

| Angle (degree) | EJ | EN | EV | EK | ER | E (O----F) |
|---|---|---|---|---|---|---|
| 0 | 11.35484 | 11.37403 | -22.72726 | -0.00268 | 0.01163 | 0.01056 |
| 20 | 11.38287 | 11.40249 | -22.78372 | -0.00286 | 0.01238 | 0.01116 |
| 40 | 11.38838 | 11.40963 | -22.79651 | -0.00339 | 0.01516 | 0.01327 |
| 60 | 11.39405 | 11.41684 | -22.80954 | -0.00394 | 0.01850 | 0.01592 |
| 80 | 11.39314 | 11.41684 | -22.80874 | -0.00428 | 0.02102 | 0.01798 |
| 86.5 | 11.40049 | 11.42401 | -22.82326 | -0.00431 | 0.02146 | 0.01838 |
| 100 | 11.40744 | 11.43117 | -22.83765 | -0.00424 | 0.02156 | 0.01875 |
| 120 | 11.42248 | 11.44566 | -22.86675 | -0.00382 | 0.01978 | 0.01735 |
| 140 | 11.43807 | 11.46022 | -22.89671 | -0.00317 | 0.01640 | 0.01481 |
| 160 | 11.44670 | 11.46750 | -22.91246 | -0.00259 | 0.01310 | 0.01224 |
| 180 | 11.50568 | 11.52655 | -23.03028 | -0.00231 | 0.011538 | 0.01118 |
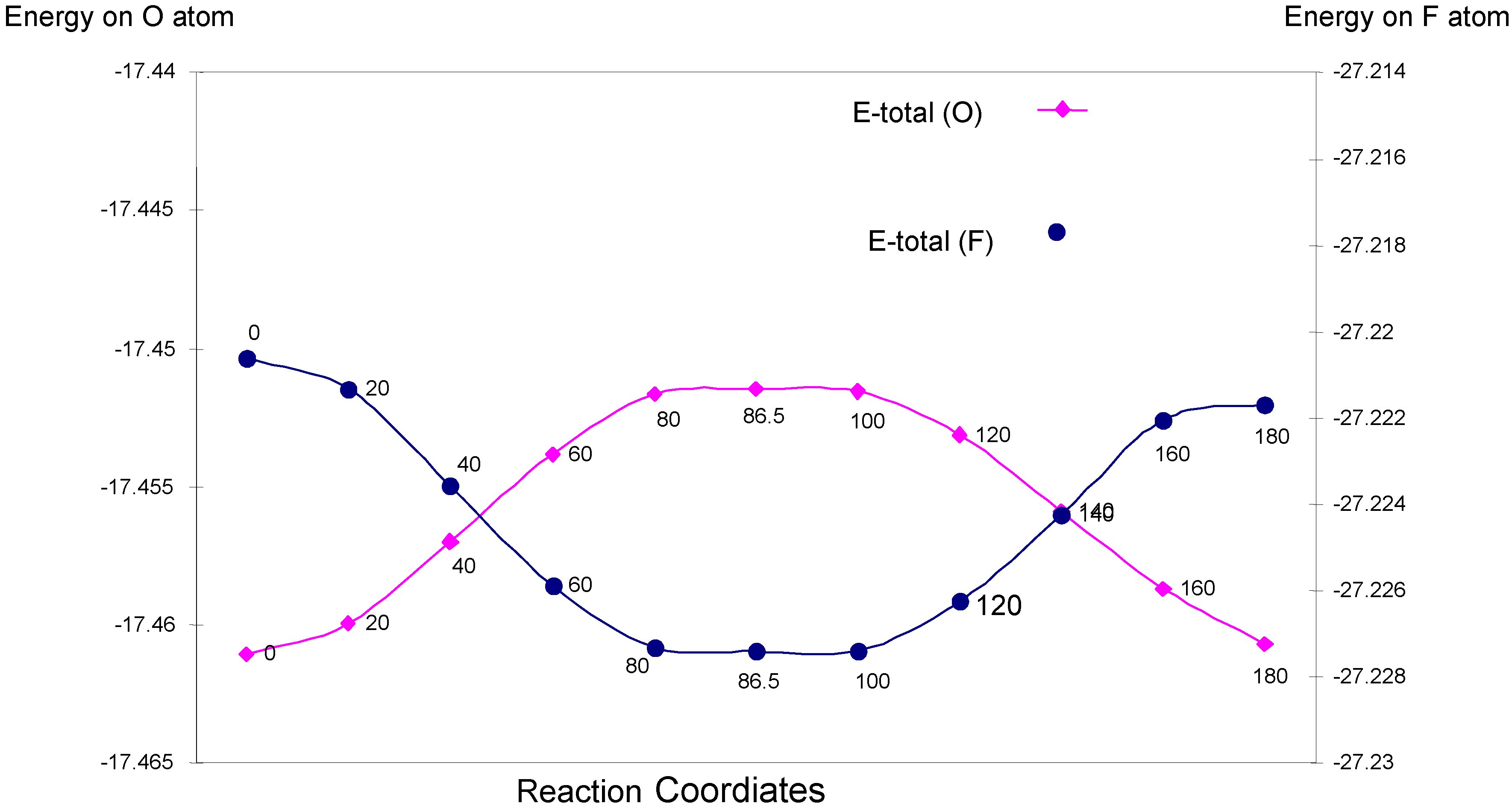
| Angle of torsion (degree) | EJ | EN | EV | EK | ER | E (F----F) |
|---|---|---|---|---|---|---|
| 0 | 13.25494 | 13.04062 | -26.29378 | -0.00160 | 0.00172 | 0.00190 |
| 20 | 13.11500 | 12.89617 | -26.0095 | -0.00122 | 0.00316 | 0.00360 |
| 40 | 12.49931 | 12.27473 | -24.77267 | -0.00078 | 0.00212 | 0.00272 |
| 60 | 11.69137 | 11.46525 | -23.15543 | -0.00034 | 0.00089 | 0.00177 |
| 80 | 10.86469 | 10.64529 | -21.50883 | -0.00008 | -0.00007 | 0.00100 |
| 86.5 | 10.62738 | 10.41123 | -21.03749 | -0.00006 | -0.00027 | 0.00080 |
| 100 | 10.16482 | 9.95815 | -20.12190 | -0.00010 | -0.00056 | 0.00041 |
| 120 | 9.60835 | 9.41914 | -19.02654 | -0.00036 | -0.00073 | -0.00015 |
| 140 | 9.21064 | 9.03963 | -18.24946 | -0.00077 | -0.00075 | -0.00073 |
| 160 | 8.97035 | 8.81296 | -17.78260 | -0.00115 | -0.00074 | -0.00119 |
| 180 | 8.92889 | 8.77469 | -17.70291 | -0.00131 | -0.00076 | -0.00140 |
| Angle of torsion (degree) | EU | EJ | EK | E-total (O) |
|---|---|---|---|---|
| 0 | -30.01181 | 14.59213 | -2.04136 | -17.46105 |
| 20 | -30.00353 | 14.58349 | -2.03991 | -17.45995 |
| 40 | -29.98211 | 14.56124 | -2.03611 | -17.45698 |
| 60 | -29.95901 | 14.53732 | -2.03213 | -17.45381 |
| 80 | -29.94439 | 14.52249 | -2.02975 | -17.45165 |
| 86.5 | -29.94209 | 14.52006 | -2.02942 | -17.45146 |
| 100 | -29.94190 | 14.52007 | -2.02972 | -17.45155 |
| 120 | -29.95228 | 14.53138 | -2.03221 | -17.45312 |
| 140 | -29.97086 | 14.55118 | -2.03622 | -17.45590 |
| 160 | -29.98796 | 14.56911 | -2.03984 | -17.45869 |
| 180 | -29.99364 | 14.57413 | -2.04118 | -17.46069 |
| Angle of torsion (degree) | EU | EJ | EK | E-total (F) |
|---|---|---|---|---|
| 0 | -47.65292 | 23.52328 | -3.09099 | -27.22062 |
| 20 | -47.66415 | 23.53484 | -3.09200 | -27.22132 |
| 40 | -47.69464 | 23.56556 | -3.09450 | -27.22358 |
| 60 | -47.72680 | 23.59800 | -3.09710 | -27.22589 |
| 80 | -47.74717 | 23.61854 | -3.09869 | -27.22732 |
| 86.5 | -47.74923 | 23.62065 | -3.09883 | -27.22741 |
| 100 | -47.74965 | 23.62107 | -3.09884 | -27.22741 |
| 120 | -47.73466 | 23.60600 | -3.09760 | -27.22627 |
| 140 | -47.70818 | 23.57941 | -3.09546 | -27.22424 |
| 160 | -47.68243 | 23.55371 | -3.09333 | -27.22205 |
| 180 | -47.67638 | 23.54765 | -3.09296 | -27.22168 |
- (i)
- Two ‘O–O’ and ‘O–F’ bonding interactions bonds;
- (ii)
- Two ‘O----F’ and ‘F-----F’ nonbonding interactions;
- (iii)
- Two different one-center interactions –one on ‘O’ atoms and the second on ‘F’ atoms.
Two-center bonding interactions:
The two-center ‘O–O’ bonding interaction:
The two-center ‘O–F’ bonding interaction:
The two-center nonbonding interactions:
- (i)
- O----F’
- (ii)
- F-----F’
(i): ‘O-------F’ ; the two center ‘oxygen----fluorine’ nonbonding interaction
(ii): ‘F-----F’ ;. The two-center fluorine ---fluorine nonbonding interaction
One-center interactions:
4. Conclusion
References
- Greenwood, N.N.; Earnshaw, A. Chemistry of the Elements, 2nd eds.; Butterworth–Heinemann: Oxford, U.K., 1997. [Google Scholar]
- March, J. Advanced Organic Chemistry, 4th eds.; Wiley: New York, 1992. [Google Scholar]
- Hess, W.T. Hydrogen Peroxide, in Kirk–Other Encyclopaedia of Chemical Technology, 4th Ed. edWiley: New York, 1995; Vol. 13, pp. 961–995. [Google Scholar]
- CA Cancer Jclin. 1993 Jan-Feb; 43 (1): 47-56, “ Questionable Methods of Cancer Management: Hydrogen Peroxide and other ‘ hyper oxygenation’ therapies.” PMID 8422605.
- Pitzer, R. M. The barrier to Internal Rotation in Ethane. Acc. Chem. Res. 1983, 16, 207–210. [Google Scholar] [CrossRef]
- Lowe, J.P. Prog. Phys. Chem. 1968, 6, 1, (ibid), The Barrier to Internal Rotation in Ethane: A Qualitative, Intuitively Useful Explanation Emerges from a Comparision of Different Theoretical Approaches, Science 1973, 179, 527-532..
- Schleyer, P.v.R.; Kaupp, M. ; Hampel, F.; Bremer, M.; Mislow, K. Relationships in the Rotational Barriers of All Group 14 Ethane Congeners H3X–YH3 (X, Y= C, Si, Ge, Sn, Pb). Comparison of ab Initio Pseudopotential and All-Electron results. J. Am. Chem. Soc. 1992, 114, 6791–6797. [Google Scholar] [CrossRef]
- Freeman, F.; Tsegai, Z. M.; Kasner, M. L.; Hehre, W. A Comparison of the ab initio Calculated and Experimental Conformational Energies of Alkyl Cyclohexanes. J. Chem. Educ. 2000, 77, 661–667. [Google Scholar] [CrossRef]
- Cárdenas-Jirón, G. I; Toro-Labbé, A. Hardness Profile and Activation Hardness for Rotational Isomerization Process 2. The Maximum Hardness Principle. J. Phys. Chem. 1995, 99, 12730–12738. [Google Scholar] [CrossRef]
- Cárdenas-Jirón, G. I.; Labsen, J; Toro-Labbé, A. Hardness Profile and Activation Hardness for Rotational Isomerization Process .1. Application to Nitrous Acid and Hydrogen Persulfide. 2. J. Phys. Chem. 1995, 99, 5325–5330. [Google Scholar] [CrossRef]
- Ghosh, D. C.; Rahman, M. A. A Study of the Origin of Barrier to Internal Rotation of Molecules. Chem. Environ. Res. 1996, 5, 73–88. [Google Scholar]
- (a) Pople, J.A.; Santry, D.P.; Segal, G.A. Approximate Self-Consistent Molecular Orbital Theory. I Invariant Procedure. J. Chem. Phys. 43, 1965, S129–S135. [Google Scholar] (b) Pople, J.A.; Santry, D.P.; Segal, G.A. Approximate Self-Consistent Molecular Orbital Theory.II Calculation With Complete Neglect of Differential Overlap. J. Chem. Phys. 43, 1965, S136–S151. [Google Scholar]
- Pople, J. A.; Beveridge, D. L. Approximate Molecular Orbital Theory. In J. Am. Chem. Soc.; McGraw-Hill Book Company, 1970. [Google Scholar]
- Gordon, M. S. Molecular Orbital Study of Internal Rotation. J. Am. Chem. Soc. 1969, 91, 3122–3130. [Google Scholar] [CrossRef]
- Ghosh, D. C. Density Functional and Frontier Orbital Study of the Physical Process of Conformational Isomerism of Ethane. J. Indian Chem. Soc. 2002, 79, 240–248. [Google Scholar]
- Pederson, L.; Morokuma, K. Ab Initio Calculations of Barriers to Internal Rotations of CH3 CH3, CH3NH2, CH3OH, N2 H4, H2O2 and NH2 OH. J. Chem. Phys. 1967, 46, 3941–3947. [Google Scholar]
- (a) Fink, W. H; Allen, L. C. Origin of Rotational Barriers I. Many-Electron Molecular Orbital Wave Functions for Ethane, Methyl Alcohol, Hydrogen Peroxide. J. Chem. Phys. 1967, 46, 2261–2275. [Google Scholar] [CrossRef] (b) ibid, Origin of Rotational Barriers II. Methyl amine and Improved Wave Functions for Hydrogen Peroxide. J. Chem. Phys. 1967, 46, 2276–2284.
- Kaldor, U; Shavitt, I. LCAO-SCF Computations for Hydrogen Peroxide. J. Chem. Phys. 1966, 44, 1823–1829. [Google Scholar] [CrossRef]
- Palke, W. E. ; Pitzer, R. M. On the Internal Rotation Potential in H2O2. J. Chem. Phys. 1967, 46, 3948–3950. [Google Scholar] [CrossRef]
- Salvador, P.; Mayer, I. Energy Partitioning for “fuzzy atoms. J. Chem. Phys. 2004, 120, 5046. [Google Scholar] [CrossRef]
- Ghosh, D. C. ; Jana, J.; Biswas, R. Quantum Chemical Study of the Umbrella Inversion of the Ammonia Molecule. Int. J. Quantum Chem. 2000, 80, 1–26. [Google Scholar] [CrossRef]
- Ghosh, D. C. ; Jana , J.; Bhattacharya, S. Density Functional and Molecular Orbital Study of Physical Process of Inversion of Nitrogen Trifluoride (NF3) Molecule. Int. J. Quantum Chem. 2002, 87, 111–134. [Google Scholar] [CrossRef]
- Ghosh , D. C.; Bhattacharya, S. Molecular Orbital and Density Functional Study of the Formation, Charge Transfer, Bonding and the Conformational of the Boron Trifluoride (BF3) and Ammonia (NH3) Donor-Acceptor Complexe. Int. J. Mol. Sci. 2004, 5, 239–264. [Google Scholar] [CrossRef]
- Ghosh, D. C. A. Density Functional and Molecular Orbital study of the Methylamine Conformers. Internet. Elect. J. Mol. Design 2005, 4, 31–58. [Google Scholar]
- Roothaan, C. C. J. A Study of Two-Center Integrals Useful in Calculation on Molecular Structure. J. Chem. Phys. 1951, 19, 1445–1457. [Google Scholar] [CrossRef]
- Fischer , H.; Kollmar, H. Energy Partitioning with the CNDO Method. Theor. Chim. Acta. 1970, 16, 163–184. [Google Scholar] [CrossRef]
- Hunt, R.H.; Leacock, R. A.; Peters, C. W; Hecht, K. T. Internal Rotation of Hydrogen Peroxide: The Far-Infrared Spectrum and the Determination of the hindering Potential. J. Chem. Phys. 1965, 42, 1931–1946. [Google Scholar]
- Oelfke, W. C.; Gordy, W. Millimeter-Wave Spectrum of Hydrogen Peroxide. J. Chem. Phys. 1969, 51, 5336–5343. [Google Scholar]
- Douglas, B.; Mc Daniel, D.; Alexander, J. ‘Concepts and Models of Inorganic Chemistry’, 3rd Edition edJohn Wiley & Sons, Inc.: New York, 1994. [Google Scholar]
- Dunning, T. H., Jr.; Winter, N. W. Theoretical Determination of the Barriers to Internal Rotation in Hydrogen Peroxide. J. Chem. Phys. 1975, 63, 1847–1855. [Google Scholar]
- Jackson, R. H. J. Chem. Soc. 1962, 4585–4592.
- Amos, R. D.; Murray, C. W.; Handy, N. C. Structure and Vibrational FOOF and FONO using Density Functional Theory. Chem. Phys. Letts. 1993, 202, 489–494. [Google Scholar]
- Scuseria, G. E. Analytic Ebaluation of Energy Gradients for the Singles and Doubles Coupled Cluster Method Including Perturbative Triple Excitations: Theory and Apllication to FOOF and Cr2. J. Chem. Phys. 1991, 94, 442–447. [Google Scholar]
- Allen Clabo, D., Jr.; Schaefer III, H. F. Fluorine Peroxide (F2O2): A Continuing Problem for Normally Reliable Theoretical Methods. Int. J. Quantum Chem. 1987, 31, 429–433. [Google Scholar]
- Mack, H. G.; Oberhammer, H. An Improved ab inition Structure for Fluorine Peroxide. Chem. Phys. Lett. 1988, 145, 121–124. [Google Scholar]
- Lee, T. J.; Rice, J.E.; Scuseria, G.E.; Schaefer III, H. F. F. Theor. Chim. Acta 1989, 75, 81.
- Rohlfing, C. M ; Hay, P. J. Structure and Bonding of F2O2. J. Chem. Phys. 1987, 86, 4518–4522. [Google Scholar]
- Ahlrichs, R.; Taylor, P. R. The Structure of F2O2; Theoretical Predictions and Comparison with F2 and F2 O. Chem. Phys. 1982, 72, 287–292. [Google Scholar]
- Raghavachari, K.; Trucks, G. W. Highly Correlated Systems. Structure and Harmonic Force Field of F2O2. Chem. Phys. Lett. 1989, 62, 511–516. [Google Scholar]
- Fukui, K. Role of Frontier Orbitals in Chemical Reactions. Science 1982, 218, 747–754. [Google Scholar]
- Pearson, R. G. Hard and Soft Acids and Bases. J. Am. Chem. Soc. 1963, 85, 3533–3539. [Google Scholar]
- Pasha, F.A.; Srivastava, H.K.; Singh, P.P. QSAR Study of Estrogens with the Help of PM3–based Descriptors. Int. J. Quantum Chem. 2005, 104, 87–100. [Google Scholar]
© 2006 by MDPI (http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Ghosh, D.C. A Quest for the Origin of Barrier to the Internal Rotation ofHydrogen Peroxide (H2O2) and Fluorine Peroxide (F2O2). Int. J. Mol. Sci. 2006, 7, 289-319. https://doi.org/10.3390/i7080289
Ghosh DC. A Quest for the Origin of Barrier to the Internal Rotation ofHydrogen Peroxide (H2O2) and Fluorine Peroxide (F2O2). International Journal of Molecular Sciences. 2006; 7(8):289-319. https://doi.org/10.3390/i7080289
Chicago/Turabian StyleGhosh, Dulal C. 2006. "A Quest for the Origin of Barrier to the Internal Rotation ofHydrogen Peroxide (H2O2) and Fluorine Peroxide (F2O2)" International Journal of Molecular Sciences 7, no. 8: 289-319. https://doi.org/10.3390/i7080289
APA StyleGhosh, D. C. (2006). A Quest for the Origin of Barrier to the Internal Rotation ofHydrogen Peroxide (H2O2) and Fluorine Peroxide (F2O2). International Journal of Molecular Sciences, 7(8), 289-319. https://doi.org/10.3390/i7080289




