Dating the Origin and Spread of Plastids and Chromatophores
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Set Preparation
2.2. Phylogenetic and Molecular Clock Analyses
2.3. Comparison of Molecular Clocks and Calibration Sets
3. Results and Discussion
3.1. Phylogenetic Analyses
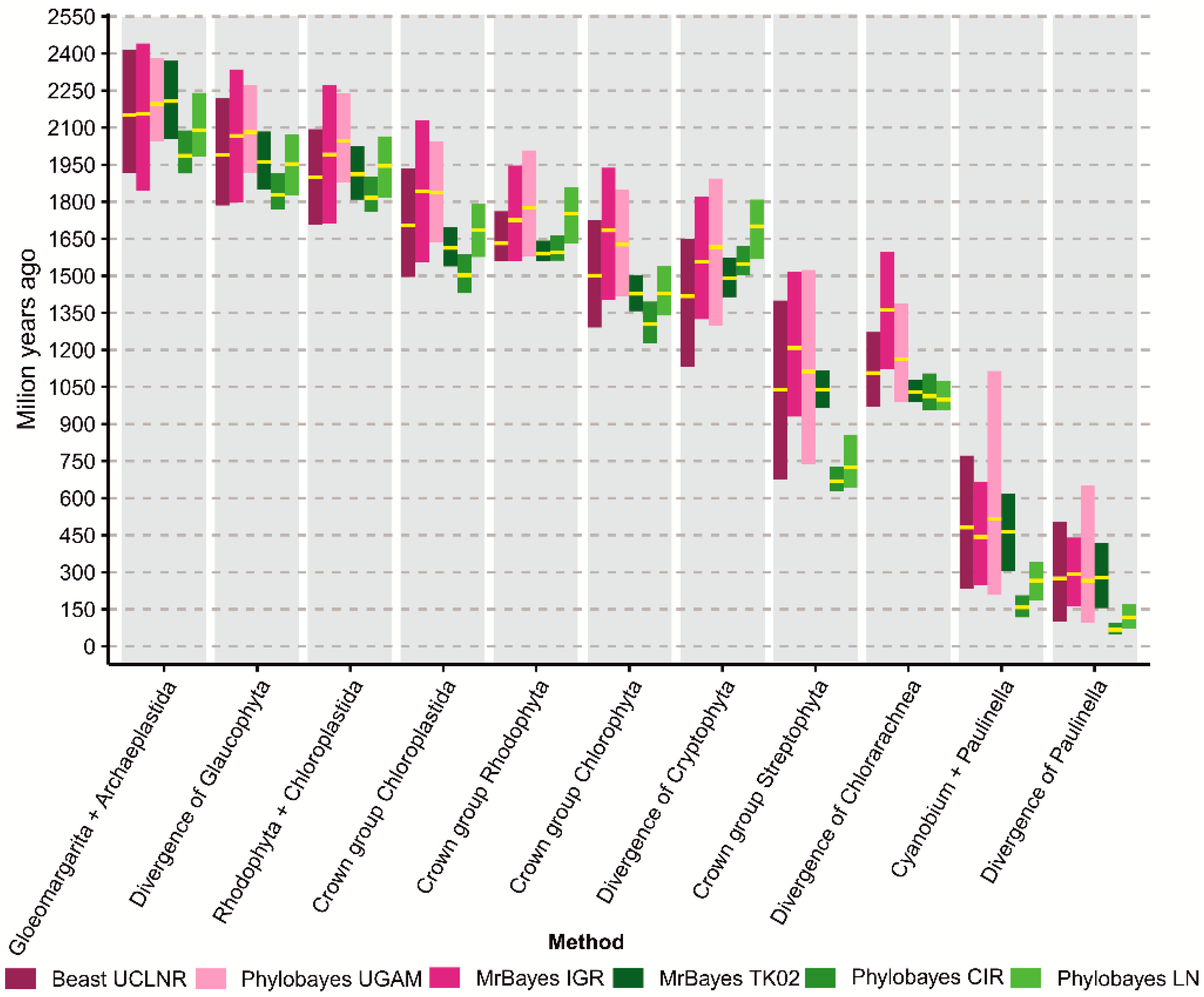
3.2. Molecular Dating Analyses
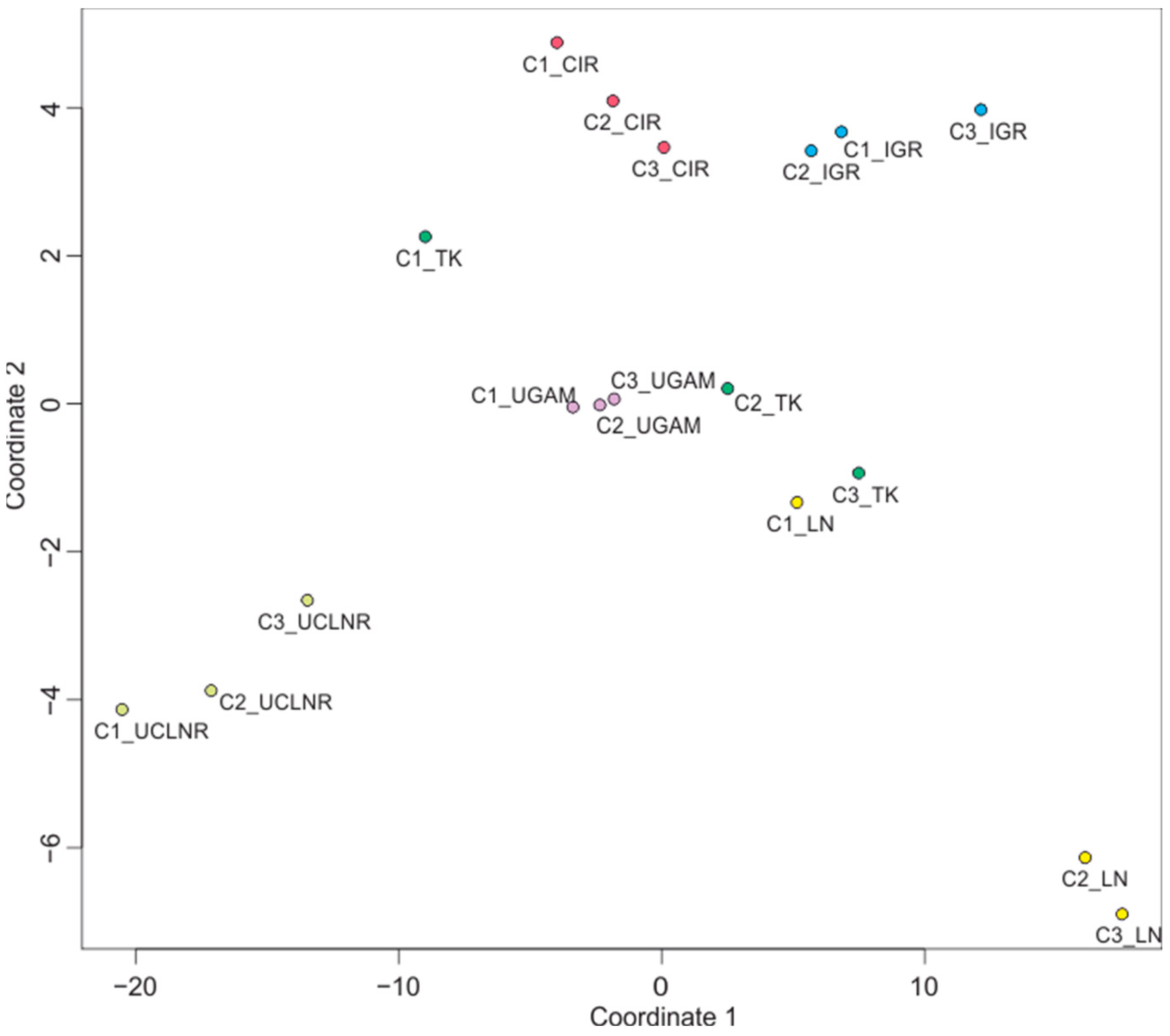
3.3. The Impact of Molecular Clocks and Calibration Sets on Age Estimations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lyons, T.W.; Reinhard, C.T.; Planavsky, N.J. The Rise of Oxygen in Earth’s Early Ocean and Atmosphere. Nature 2014, 506, 307–315. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Baracaldo, P.; Bianchini, G.; Wilson, J.D.; Knoll, A.H. Cyanobacteria and Biogeochemical Cycles through Earth History. Trends Microbiol. 2022, 30, 143–157. [Google Scholar] [CrossRef] [PubMed]
- Ponce-Toledo, R.I.; Deschamps, P.; López-García, P.; Zivanovic, Y.; Benzerara, K.; Moreira, D. An Early-Branching Freshwater Cyanobacterium at the Origin of Plastids. Curr. Biol. 2017, 27, 386–391. [Google Scholar] [CrossRef] [PubMed]
- Löffelhardt, W. The Single Primary Endosymbiotic Event. In Endosymbiosis; Löffelhardt, W., Ed.; Springer: Vienna, Austria, 2014; pp. 39–52. ISBN 978-3-7091-1303-5. [Google Scholar]
- Archibald, J.M. Genomic Perspectives on the Birth and Spread of Plastids. Proc. Natl. Acad. Sci. USA 2015, 112, 10147–10153. [Google Scholar] [CrossRef]
- Nowack, E.C.M. Paulinella chromatophora-Rethinking the Transition from Endosymbiont to Organelle. Acta Soc. Bot. Pol. 2014, 83, 387–397. [Google Scholar] [CrossRef]
- Gagat, P.; Sidorczuk, K.; Pietluch, F.; Mackiewicz, P. The Photosynthetic Adventure of Paulinella spp. In Symbiosis: Cellular, Molecular, Medical and Evolutionary Aspects; Springer: Cham, Switzerland, 2020; pp. 353–386. [Google Scholar]
- Nowack, E.C.M.; Melkonian, M.; Glöckner, G. Chromatophore Genome Sequence of Paulinella Sheds Light on Acquisition of Photosynthesis by Eukaryotes. Curr. Biol. 2008, 18, 410–418. [Google Scholar] [CrossRef]
- Bar-On, Y.M.; Phillips, R.; Milo, R. The Biomass Distribution on Earth. Proc. Natl. Acad. Sci. USA 2018, 115, 6506–6511. [Google Scholar] [CrossRef]
- Mackiewicz, P.; Gagat, P. Monophyly of Archaeplastida Supergroup and Relationships among Its Lineages in the Light of Phylogenetic and Phylogenomic Studies. Are We Close to a Consensus? Acta Soc. Bot. Pol. 2014, 83, 263–280. [Google Scholar] [CrossRef]
- Irisarri, I.; Strassert, J.F.H.; Burki, F. Phylogenomic Insights into the Origin of Primary Plastids. Syst. Biol. 2022, 71, 105–120. [Google Scholar] [CrossRef]
- Bengtson, S.; Sallstedt, T.; Belivanova, V.; Whitehouse, M. Three-Dimensional Preservation of Cellular and Subcellular Structures Suggests 1.6 Billion-Year-Old Crown-Group Red Algae. PLoS Biol. 2017, 15, e2000735. [Google Scholar] [CrossRef]
- Tang, Q.; Pang, K.; Yuan, X.; Xiao, S. A One-Billion-Year-Old Multicellular Chlorophyte. Nat. Ecol. Evol. 2020, 4, 543–549. [Google Scholar] [CrossRef] [PubMed]
- Altschul, S.F.; Madden, T.L.; Schäffer, A.A.; Zhang, J.; Zhang, Z.; Miller, W.; Lipman, D.J. Gapped BLAST and PSI-BLAST: A New Generation of Protein Database Search Programs. Nucleic Acids Res. 1997, 25, 3389–3402. [Google Scholar] [CrossRef] [PubMed]
- Pruitt, K.D.; Tatusova, T.; Maglott, D.R. NCBI Reference Sequence (RefSeq): A Curated Non-Redundant Sequence Database of Genomes, Transcripts and Proteins. Nucleic Acids Res. 2005, 33, D501–D504. [Google Scholar] [CrossRef] [PubMed]
- Sayers, E.W.; Cavanaugh, M.; Clark, K.; Pruitt, K.D.; Schoch, C.L.; Sherry, S.T.; Karsch-Mizrachi, I. GenBank. Nucleic Acids Res. 2021, 49, D92–D96. [Google Scholar] [CrossRef]
- Katoh, K.; Standley, D.M. MAFFT Multiple Sequence Alignment Software Version 7: Improvements in Performance and Usability. Mol. Biol. Evol. 2013, 30, 772–780. [Google Scholar] [CrossRef]
- Larsson, A. AliView: A Fast and Lightweight Alignment Viewer and Editor for Large Datasets. Bioinformatics 2014, 30, 3276–3278. [Google Scholar] [CrossRef]
- Capella-Gutiérrez, S.; Silla-Martínez, J.M.; Gabaldón, T. trimAl: A Tool for Automated Alignment Trimming in Large-Scale Phylogenetic Analyses. Bioinformatics 2009, 25, 1972–1973. [Google Scholar] [CrossRef]
- Vaidya, G.; Lohman, D.J.; Meier, R. SequenceMatrix: Concatenation Software for the Fast Assembly of Multi-Gene Datasets with Character Set and Codon Information. Cladistics 2011, 27, 171–180. [Google Scholar] [CrossRef]
- Doyle, J.J. Defining Coalescent Genes: Theory Meets Practice in Organelle Phylogenomics. Syst. Biol. 2022, 71, 476–489. [Google Scholar] [CrossRef]
- Minh, B.Q.; Schmidt, H.A.; Chernomor, O.; Schrempf, D.; Woodhams, M.D.; von Haeseler, A.; Lanfear, R. IQ-TREE 2: New Models and Efficient Methods for Phylogenetic Inference in the Genomic Era. Mol. Biol. Evol. 2020, 37, 1530–1534. [Google Scholar] [CrossRef]
- Stamatakis, A. RAxML Version 8: A Tool for Phylogenetic Analysis and Post-Analysis of Large Phylogenies. Bioinformatics 2014, 30, 1312–1313. [Google Scholar] [CrossRef] [PubMed]
- Lartillot, N.; Rodrigue, N.; Stubbs, D.; Richer, J. PhyloBayes MPI: Phylogenetic Reconstruction with Infinite Mixtures of Profiles in a Parallel Environment. Syst. Biol. 2013, 62, 611–615. [Google Scholar] [CrossRef] [PubMed]
- Ronquist, F.; Teslenko, M.; van der Mark, P.; Ayres, D.L.; Darling, A.; Höhna, S.; Larget, B.; Liu, L.; Suchard, M.A.; Huelsenbeck, J.P. MrBayes 3.2: Efficient Bayesian Phylogenetic Inference and Model Choice Across a Large Model Space. Syst. Biol. 2012, 61, 539–542. [Google Scholar] [CrossRef]
- Bouckaert, R.; Heled, J.; Kühnert, D.; Vaughan, T.; Wu, C.-H.; Xie, D.; Suchard, M.A.; Rambaut, A.; Drummond, A.J. BEAST 2: A Software Platform for Bayesian Evolutionary Analysis. PLoS Comput. Biol. 2014, 10, e1003537. [Google Scholar] [CrossRef]
- Kalyaanamoorthy, S.; Minh, B.Q.; Wong, T.K.F.; von Haeseler, A.; Jermiin, L.S. ModelFinder: Fast Model Selection for Accurate Phylogenetic Estimates. Nat. Methods 2017, 14, 587–589. [Google Scholar] [CrossRef]
- Lanfear, R.; Frandsen, P.B.; Wright, A.M.; Senfeld, T.; Calcott, B. PartitionFinder 2: New Methods for Selecting Partitioned Models of Evolution for Molecular and Morphological Phylogenetic Analyses. Mol. Biol. Evol. 2017, 34, 772–773. [Google Scholar] [CrossRef]
- Naser-Khdour, S.; Minh, B.Q.; Zhang, W.; Stone, E.A.; Lanfear, R. The Prevalence and Impact of Model Violations in Phylogenetic Analysis. Genome Biol. Evol. 2019, 11, 3341–3352. [Google Scholar] [CrossRef]
- Sánchez-Baracaldo, P.; Raven, J.A.; Pisani, D.; Knoll, A.H. Early Photosynthetic Eukaryotes Inhabited Low-Salinity Habitats. Proc. Natl. Acad. Sci. USA 2017, 114, E7737. [Google Scholar] [CrossRef]
- Gibson, T.M.; Shih, P.M.; Cumming, V.M.; Fischer, W.W.; Crockford, P.W.; Hodgskiss, M.S.; Wörndle, S.; Creaser, R.A.; Rainbird, R.H.; Skulski, T.M.; et al. Precise Age of Bangiomorpha Pubescens Dates the Origin of Eukaryotic Photosynthesis. Geology 2018, 46, 135–138. [Google Scholar] [CrossRef]
- Bekker, A.; Holland, H.D.; Wang, P.-L.; Rumble, D.; Stein, H.J.; Hannah, J.L.; Coetzee, L.L.; Beukes, N.J. Dating the Rise of Atmospheric Oxygen. Nature 2004, 427, 117–120. [Google Scholar] [CrossRef]
- Crowe, S.A.; Døssing, L.N.; Beukes, N.J.; Bau, M.; Kruger, S.J.; Frei, R.; Canfield, D.E. Atmospheric Oxygenation Three Billion Years Ago. Nature 2013, 501, 535–538. [Google Scholar] [CrossRef] [PubMed]
- Demoulin, C.F.; Lara, Y.J.; Cornet, L.; François, C.; Baurain, D.; Wilmotte, A.; Javaux, E.J. Cyanobacteria Evolution: Insight from the Fossil Record. Free Radic. Biol. Med. 2019, 140, 206–223. [Google Scholar] [CrossRef]
- Zhang, Y. Proterozoic Stromatolitic Micro-Organisms from Hebei, North China: Cell Preservation and Cell Division. Precambrian Res. 1988, 38, 165–175. [Google Scholar] [CrossRef]
- Page, R.W.; Jackson, M.J.; Krassay, A.A. Constraining Sequence Stratigraphy in North Australian Basins: SHRIMP U–Pb Zircon Geochronology between Mt Isa and McArthur River. Aust. J. Earth Sci. 2000, 47, 431–459. [Google Scholar] [CrossRef]
- Tomitani, A.; Knoll, A.H.; Cavanaugh, C.M.; Ohno, T. The Evolutionary Diversification of Cyanobacteria: Molecular–Phylogenetic and Paleontological Perspectives. Proc. Natl. Acad. Sci. USA 2006, 103, 5442–5447. [Google Scholar] [CrossRef]
- Sims, P.A.; Mann, D.G.; Medlin, L.K. Evolution of the Diatoms: Insights from Fossil, Biological and Molecular Data. Phycologia 2006, 45, 361–402. [Google Scholar] [CrossRef]
- Hedges, S.B.; Blair, J.E.; Venturi, M.L.; Shoe, J.L. A Molecular Timescale of Eukaryote Evolution and the Rise of Complex Multicellular Life. BMC Evol. Biol. 2004, 4, 2. [Google Scholar] [CrossRef]
- Xiao, S.; Knoll, A.H.; Yuan, X.; Pueschel, C.M. Phosphatized Multicellular Algae in the Neoproterozoic Doushantuo Formation, China, and the Early Evolution of Florideophyte Red Algae. Am. J. Bot. 2004, 91, 214–227. [Google Scholar] [CrossRef]
- Kooistra, W.H.; Medlin, L.K. Evolution of the Diatoms (Bacillariophyta): IV. A Reconstruction of Their Age from Small Subunit rRNA Coding Regions and the Fossil Record. Mol. Phylogenet. Evol. 1996, 6, 391–407. [Google Scholar] [CrossRef]
- Rubinstein, C.V.; Gerrienne, P.; de la Puente, G.S.; Astini, R.A.; Steemans, P. Early Middle Ordovician Evidence for Land Plants in Argentina (Eastern Gondwana). New Phytol. 2010, 188, 365–369. [Google Scholar] [CrossRef]
- Morris, J.L.; Puttick, M.N.; Clark, J.W.; Edwards, D.; Kenrick, P.; Pressel, S.; Wellman, C.H.; Yang, Z.; Schneider, H.; Donoghue, P.C. The Timescale of Early Land Plant Evolution. Proc. Natl. Acad. Sci. USA 2018, 115, E2274–E2283. [Google Scholar] [CrossRef] [PubMed]
- Steemans, P.; Le Hérissé, A.; Melvin, J.; Miller, M.A.; Paris, F.; Verniers, J.; Wellman, C.H. Origin and Radiation of the Earliest Vascular Land Plants. Science 2009, 324, 353. [Google Scholar] [CrossRef] [PubMed]
- Turnau, E.; Zavialova, N.; Prejbisz, A. Wall Ultrastructure in Some Dispersed Megaspores and Seed-Megaspores from the Middle Devonian of Northern Poland. Rev. Palaeobot. Palynol. 2009, 156, 14–33. [Google Scholar] [CrossRef]
- Hughes, N.F.; McDougall, A.B.; Chapman, J.L. Exceptional New Record of Cretaceous Hauterivian Angiospermid Pollen from Southern England. J. Micropalaeontol. 1991, 10, 75–82. [Google Scholar] [CrossRef][Green Version]
- Friis, E.M.; Pedersen, K.R.; Crane, P.R. Cretaceous Angiosperm Flowers: Innovation and Evolution in Plant Reproduction. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2006, 232, 251–293. [Google Scholar] [CrossRef]
- Soltis, P.S.; Soltis, D.E. The Origin and Diversification of Angiosperms. Am. J. Bot. 2004, 91, 1614–1626. [Google Scholar] [CrossRef]
- Mullins, G.L.; Servais, T. The Diversity of the Carboniferous Phytoplankton. Rev. Palaeobot. Palynol. 2008, 149, 29–49. [Google Scholar] [CrossRef]
- Lartillot, N.; Lepage, T.; Blanquart, S. PhyloBayes 3: A Bayesian Software Package for Phylogenetic Reconstruction and Molecular Dating. Bioinformatics 2009, 25, 2286–2288. [Google Scholar] [CrossRef]
- Gagat, P.; Mackiewicz, P. Protein translocons in photosynthetic organelles of Paulinella chromatophora. Acta Soc. Bot. Pol. 2014, 83, 399–407. [Google Scholar] [CrossRef]
- Lemieux, C.; Otis, C.; Turmel, M. A Clade Uniting the Green Algae Mesostigma viride and Chlorokybus atmophyticus Represents the Deepest Branch of the Streptophyta in Chloroplast Genome-Based Phylogenies. BMC Biol. 2007, 5, 2. [Google Scholar] [CrossRef]
- Jackson, C.; Knoll, A.H.; Chan, C.X.; Verbruggen, H. Plastid Phylogenomics with Broad Taxon Sampling Further Elucidates the Distinct Evolutionary Origins and Timing of Secondary Green Plastids. Sci. Rep. 2018, 8, 1523. [Google Scholar] [CrossRef] [PubMed]
- Strassert, J.F.H.; Irisarri, I.; Williams, T.A.; Burki, F. A Molecular Timescale for Eukaryote Evolution with Implications for the Origin of Red Algal-Derived Plastids. Nat. Commun. 2021, 12, 1879. [Google Scholar] [CrossRef] [PubMed]
- Pietluch, F.; Mackiewicz, P.; Ludwig, K.; Gagat, P. A New Model and Dating for the Evolution of Complex Plastids of Red Alga Origin. Genome Biol. Evol. 2024, 16, evae192. [Google Scholar] [CrossRef]
- Blank, C.E. Origin and Early Evolution of Photosynthetic Eukaryotes in Freshwater Environments: Reinterpreting Proterozoic Paleobiology and Biogeochemical Processes in Light of Trait Evolution. J. Phycol. 2013, 49, 1040–1055. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Du, W. The Long-Ranging Macroalga Grypania spiralis from the Ediacaran Doushantuo Formation, Guizhou, South China. Alcheringa Australas. J. Palaeontol. 2016, 40, 303–312. [Google Scholar] [CrossRef]
- Parfrey, L.W.; Lahr, D.J.G.; Knoll, A.H.; Katz, L.A. Estimating the Timing of Early Eukaryotic Diversification with Multigene Molecular Clocks. Proc. Natl. Acad. Sci. USA 2011, 108, 13624–13629. [Google Scholar] [CrossRef]
- Delaye, L.; Valadez-Cano, C.; Pérez-Zamorano, B. How Really Ancient Is Paulinella Chromatophora? PLoS Curr. 2016, 8, ecurrents.tol.e68a099364bb1a1e129a17b4e06b0c6b. [Google Scholar] [CrossRef]
- Lhee, D.; Ha, J.-S.; Kim, S.; Park, M.G.; Bhattacharya, D.; Yoon, H.S. Evolutionary Dynamics of the Chromatophore Genome in Three Photosynthetic Paulinella Species. Sci. Rep. 2019, 9, 2560. [Google Scholar] [CrossRef]
- Karkar, S.; Facchinelli, F.; Price, D.C.; Weber, A.P.M.; Bhattacharya, D. Metabolic Connectivity as a Driver of Host and Endosymbiont Integration. Proc. Natl. Acad. Sci. USA 2015, 112, 10208–10215. [Google Scholar] [CrossRef]
- Moore, K.R.; Magnabosco, C.; Momper, L.; Gold, D.A.; Bosak, T.; Fournier, G.P. An Expanded Ribosomal Phylogeny of Cyanobacteria Supports a Deep Placement of Plastids. Front. Microbiol. 2019, 10, 1612. [Google Scholar] [CrossRef]
- Brown, M.W.; Heiss, A.A.; Kamikawa, R.; Inagaki, Y.; Yabuki, A.; Tice, A.K.; Shiratori, T.; Ishida, K.-I.; Hashimoto, T.; Simpson, A.G.B.; et al. Phylogenomics Places Orphan Protistan Lineages in a Novel Eukaryotic Super-Group. Genome Biol. Evol. 2018, 10, 427–433. [Google Scholar] [CrossRef] [PubMed]
- Gawryluk, R.M.R.; Tikhonenkov, D.V.; Hehenberger, E.; Husnik, F.; Mylnikov, A.P.; Keeling, P.J. Non-Photosynthetic Predators Are Sister to Red Algae. Nature 2019, 572, 240–243. [Google Scholar] [CrossRef] [PubMed]
- Lax, G.; Eglit, Y.; Eme, L.; Bertrand, E.M.; Roger, A.J.; Simpson, A.G.B. Hemimastigophora Is a Novel Supra-Kingdom-Level Lineage of Eukaryotes. Nature 2018, 564, 410–414. [Google Scholar] [CrossRef]
- Strassert, J.F.H.; Jamy, M.; Mylnikov, A.P.; Tikhonenkov, D.V.; Burki, F. New Phylogenomic Analysis of the Enigmatic Phylum Telonemia Further Resolves the Eukaryote Tree of Life. Mol. Biol. Evol. 2019, 36, 757–765. [Google Scholar] [CrossRef]
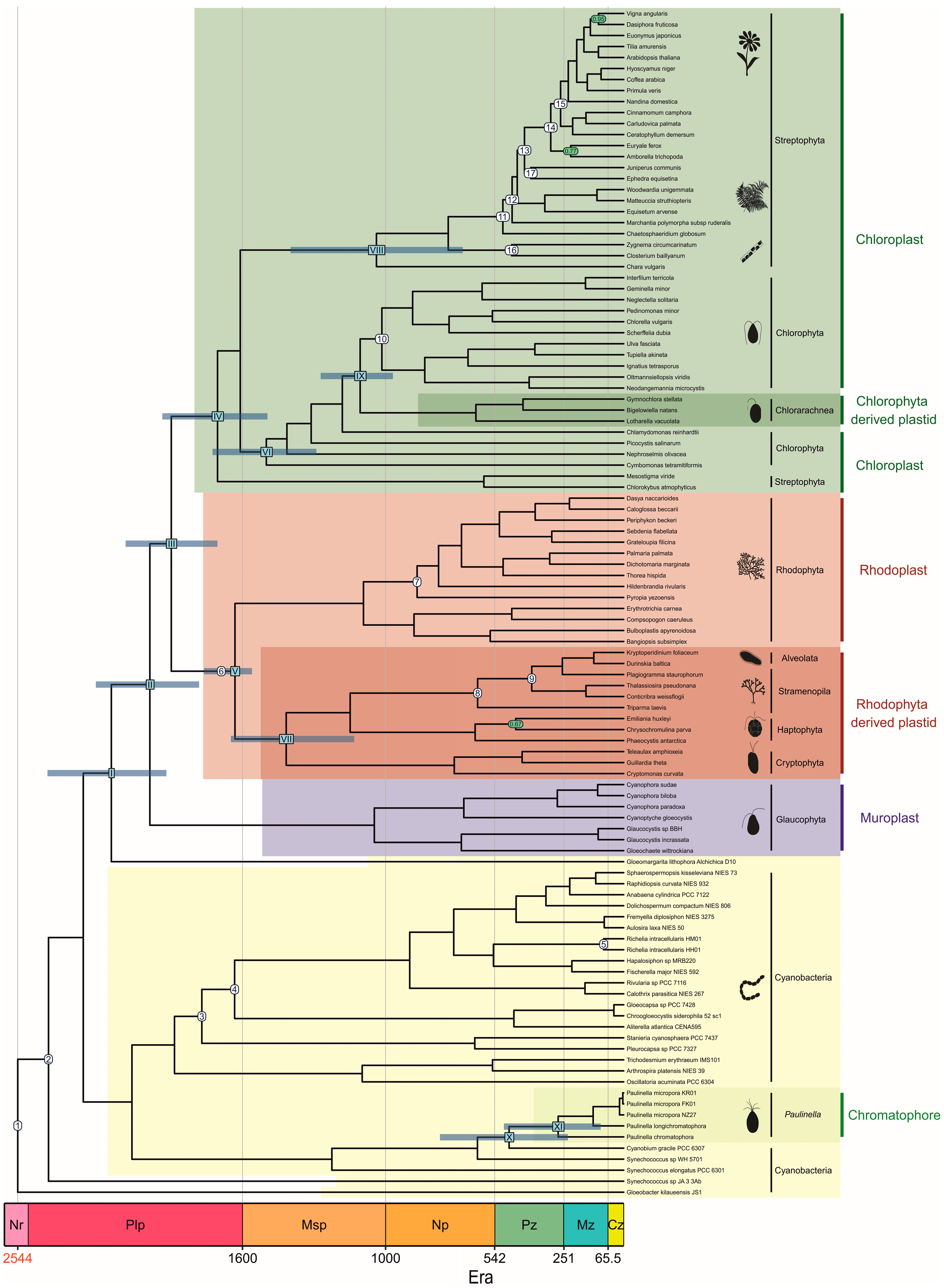
| Node No. | Node Name | Min. | Max. | Ref. | |||||
|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C1 | C2 | C3 | Min. | Max. | ||
| Cyanobacteria | |||||||||
| 1 | Great Oxidation Event | 2320 | 2320 | 2320 | 3000 | 3000 | 3000 | [32] | [33] |
| 2 | Earliest cyanobacteria | 1900 | 1900 | 1900 | 3000 | 3000 | 3000 | [34] | [33] |
| 3 | Pleurocapsales | 1700 | 1640 | 1640 | 1900 | 3000 | 3000 | [35] | [33,34] |
| 4 | Nostocales | 1600 | 1580 | 1580 | 1900 | 3000 | 3000 | [36,37] | [33,34] |
| 5 | Richelia | 110 | 110 | 110 | 3000 | 3000 | 3000 | [38] | [33] |
| Rhodoplast | |||||||||
| 6 | Earliest Rhodophyta | 1050 | 1030 | 1560 | 3000 | 2300 | 2300 | [12,31] | [33,39] |
| 7 | Floridiophyceae | 600 | 595 | 595 | 3000 | 2300 | 2300 | [40] | [33,39] |
| Rhodophyta-derived plastid | |||||||||
| 8 | Earliest diatom | 190 | 185 | 185 | 3000 | 2300 | 2300 | [41] | [33,39] |
| 9 | Bacillariophytina | 110 | 110 | 110 | 3000 | 2300 | 2300 | [38] | [33,39] |
| Chloroplast | |||||||||
| 10 | Ulvophyceae | 635 | 948 | 948 | 3000 | 2300 | 2300 | [13] | [33,39] |
| 11 | Earliest land plants | 475 | 471 | 471 | 501 | 515 | 515 | [42] | [30,43] |
| 12 | Tracheophyta | 446 | 446 | 446 | 501 | 515 | 515 | [44] | [30,43] |
| 13 | Angiosperms/Gymnosperms | 385 | 385 | 385 | 501 | 515 | 515 | [45] | [30,43] |
| 14 | Angiosperms | 130 | 130 | 130 | 501 | 515 | 515 | [46,47] | [30,43] |
| 15 | Eudicots | 125 | 125 | 125 | 501 | 515 | 515 | [48] | [30,43] |
| 16 | Zygnemataceae | 345 | 345 | 345 | 3000 | 2300 | 2300 | [49] | [33,39] |
| 17 | Gymnosperms | 385 | 385 | 385 | 501 | 515 | 515 | [45] | [30,43] |
| A: Impact of Calibration Sets on Dating for a Given Clock | B: Impact of Molecular Clocks on Dating for a Given Calibration Set | |||||
|---|---|---|---|---|---|---|
| Calibration Set | Calibration Set | |||||
| Clock | C1 | C2 | C3 | C1 | C2 | C3 |
| Beast UCLNR (UC) | −3.57 | −0.33 | 3.9 | −17.93 | −18.58 | −18.05 |
| MrBayes IGR (UC) | −1.3 | −2.47 | 3.77 | 13.16 | 6.51 | 9.79 |
| MrBayes TK02 (AC) | −9.3 | 1.9 | 7.4 | −5.61 | 0.49 | 2.21 |
| PhyloBayes CIR (AC) | −2.06 | 0.05 | 2.01 | −0.15 | −3.19 | −4.29 |
| PhyloBayes LN (AC) | −8.32 | 3.24 | 5.08 | 13.03 | 20.96 | 19.14 |
| PhyloBayes UGAM (UC) | −0.84 | 0.14 | 0.69 | −2.5 | −6.19 | −8.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pietluch, F.; Mackiewicz, P.; Sidorczuk, K.; Gagat, P. Dating the Origin and Spread of Plastids and Chromatophores. Int. J. Mol. Sci. 2025, 26, 5569. https://doi.org/10.3390/ijms26125569
Pietluch F, Mackiewicz P, Sidorczuk K, Gagat P. Dating the Origin and Spread of Plastids and Chromatophores. International Journal of Molecular Sciences. 2025; 26(12):5569. https://doi.org/10.3390/ijms26125569
Chicago/Turabian StylePietluch, Filip, Paweł Mackiewicz, Katarzyna Sidorczuk, and Przemysław Gagat. 2025. "Dating the Origin and Spread of Plastids and Chromatophores" International Journal of Molecular Sciences 26, no. 12: 5569. https://doi.org/10.3390/ijms26125569
APA StylePietluch, F., Mackiewicz, P., Sidorczuk, K., & Gagat, P. (2025). Dating the Origin and Spread of Plastids and Chromatophores. International Journal of Molecular Sciences, 26(12), 5569. https://doi.org/10.3390/ijms26125569







