Abstract
The variable Zagreb vM2 index is introduced and applied to the structure-boiling point modeling of benzenoid hydrocarbons. The linear model obtained (the standard error of estimate for the fit model Sfit=6.8 oC) is much better than the corresponding model based on the original Zagreb M2 index (Sfit=16.4 oC). Surprisingly, the model based on the variable vertex-connectivity index (Sfit=6.8 oC) is comparable to the model based on vM2 index. A comparative study with models based on the vertex-connectivity index, edge-connectivity index and several distance indices favours models based on the variable Zagreb vM2 index and variable vertex-connectivity index. However, the multivariate regression with two-, three- and four-descriptors gives improved models, the best being the model with four-descriptors (but vM2 index is not among them) with Sfit=5 oC, though the four-descriptor model contaning vM2 index is only slightly inferior (Sfit=5.3 oC).
Introduction
The concept of the variable molecular descriptors was proposed as an alternative way of characterizing heteroatoms in molecules [1,2], but also to assess the structural differences, such as, for example, the relative role of carbon atoms of acyclic and cyclic parts in alkylcycloalkanes [3]. The idea behind the variable molecular descriptors is that the variables are determined during the regression so that the standard error of estimate for a studied property is as small as possible.
Several molecular descriptors have already been tested in their variable forms in QSPR and QSAR [4,5,6,7,8,9,10,11,12]. Here we report the use of the variable Zagreb vM2 index in the structure-boiling point modeling of benzenoid hydrocarbons. We selected benzenoid hydrocarbons because there are several structure-boiling point models of these compounds already published [13,14]. Due to this fact, we were also able to carry out a comparative study of the model based on vM2 index against the models based on the standard vertex-connectivity index, variable vertex-connectivity index, edge-connectivity index and several distance indices. Since the Zagreb index in its original form was derived using graph-theoretical concepts and terminology [15], we will use these in the present report. Graphs will be generated from molecules in the usual way by replacing atoms with vertices and bonds with edges [16]. Besides, graphs that we will use will represent only carbon skeletons of benzenoid hydrocarbons. Therefore, benzenoid hydrocarbons in this report will be presented as various arrangements of hexagons in the plane.
The Zagreb M2 index and Its Variable Form vM2
Originally, the Zagreb M2 index together with the Zagreb M1 index appeared in the topological formula for the total π-electron energy of conjugated molecules [17]:
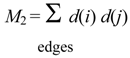 where d(i) is the degree of vertex i and d(i) d(j) is the weight of edge i-j. This index was first used as a branching index [18] and later as a useful molecular descriptor in various forms in QSPR and QSAR studies [19,20,21,22,23].
where d(i) is the degree of vertex i and d(i) d(j) is the weight of edge i-j. This index was first used as a branching index [18] and later as a useful molecular descriptor in various forms in QSPR and QSAR studies [19,20,21,22,23].
The easiest way to introduce the variable Zagreb vM2 index is by means of an example. For this purpose we will use a graph G representing the carbon skeleton of naphthalene (see Figure 1).
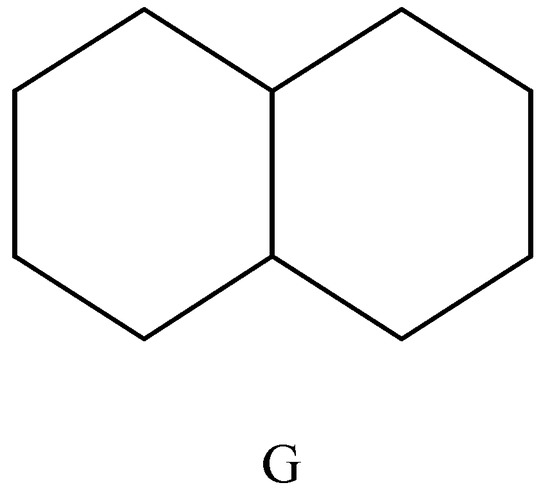
Figure 1.
Graph G representing the carbon skeleton of naphthalene
Since it is known from the chemistry of benzenoid hydrocarbons [24,25] that the carbon atoms with two adjacent carbon atoms possess different characteristics then the carbon atoms with three adjacent atoms, we assess their relative roles by differentiating these two groups with variable parameters. Using the graph-theoretical approach, the difference between the two groups of carbon atoms is expressed by means of the degrees of the corresponding vertices plus the variables. Hence, the vertex-degree of the carbon atom adjacent to two other carbon atoms is taken to be:
and likewise the vertex-degree of the carbon atom adjacent to three other carbon atoms is given by:
d = 2 + x
d = 3 + y
Putting (2) and (3) into (1), one obtains the following Zagreb vM2 index for naphthalene as a function of the variables x and y:
vM2 = 6 (2 + x)2 + 4 (2 + x) (3 + y) + (3 + y)2
In general, the variable Zagreb vM2i index of a benzenoid hydrocarbon i can be given as:
We denote the boiling point of a benzenoid hydrocarbon i (i=1,…,21) by bpi. Thus, for naphthalene (i=1), bp1=218°C and c11, c21 and c31 are respectively 6, 4 and 1. In Table 1 we give bpi, c1i, c2i and c3i values for 21 benzenoid hydrocarbons whose graphs are given in Figure 2.
vM2i = c1i (2 + x)2 + c2i (2 + x) (3 + y) + c3i (3 + y)2
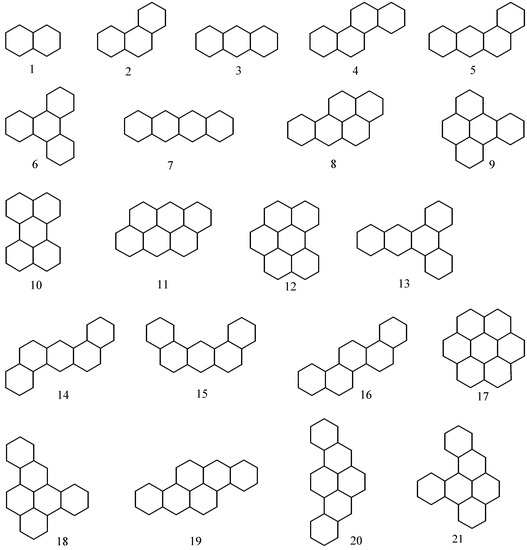
Figure 2.
Graphs corresponding to studied benzenoid hydrocarbons

Table 1.
The values of experimental boiling points (bpi in oC, i=1,…,21) and coefficients (c1i, c2i and c3i) of the variable Zagreb vM2 indices of 21 benzenoid hydrocarbons.
| Benzenoid hydrocarbon | bpi | vM2 index | ||
|---|---|---|---|---|
| c1i | c2i | c3i | ||
| 1 | 218 | 6 | 4 | 1 |
| 2 | 338 | 7 | 6 | 3 |
| 3 | 340 | 6 | 8 | 2 |
| 4 | 431 | 8 | 8 | 5 |
| 5 | 425 | 7 | 10 | 4 |
| 6 | 429 | 9 | 6 | 6 |
| 7 | 440 | 6 | 12 | 3 |
| 8 | 496 | 7 | 10 | 7 |
| 9 | 493 | 8 | 8 | 8 |
| 10 | 497 | 8 | 8 | 8 |
| 11 | 547 | 6 | 12 | 9 |
| 12 | 542 | 7 | 10 | 10 |
| 13 | 535 | 9 | 10 | 7 |
| 14 | 536 | 8 | 12 | 6 |
| 15 | 531 | 8 | 12 | 6 |
| 16 | 519 | 9 | 10 | 7 |
| 17 | 590 | 6 | 12 | 12 |
| 18 | 592 | 9 | 10 | 10 |
| 19 | 596 | 8 | 12 | 9 |
| 20 | 594 | 8 | 12 | 9 |
Experimental values of boiling points of considered benzenoid hydrocarbons are taken from Randić [13].
Expression (5) for x=0 and y=0 reduces to:
which is the formula for computing the original Zagreb M2 index of a given benzenoid i.It should also be noted that the variable connectivity index vχi is related to the Zagreb vM2i index with the same set of coefficients:
M2i = 22 c1i + 2·3 c2i + 32 c3i
vχi = c1i (2 + x)-1 + c2i [(2 + x) (3 + y)]-1/2 + c3i (3 + y)-1
For x=0 and y=0, eq. (7) reduces to one for computing the vertex-connectivity index of a benzenoid hydrocarbon i:
vχi = 2-1 c1i + (2·3)-1/2 c2i + 3-1 c3i
Results and Discussion
In order to find optimal variable Zagreb vM2 index, the values of x were varied in the range between –2 and 2 and values of y were varied in the range between –3 and 3, both in steps of 0.1. This range of x and y values was imposed by the degrees of valences in benzenoid graphs. In non-optimized Zagreb index (M2), the values of variables x and y are equal to 0.0. We want to see are there optimal values of x and y near their non-optimized values (0.0, 0.0) for which the standard error of estimate of the structure-boiling point model reaches minimum. For each pair (x, y) in the given range, coefficients a0 and a1 in the linear regression model:
were computed using the least square fitting procedure as implemented in the CROMRsel program [26,27,28]. The quality of models is expressed by fitted (descriptive) statistical parameters: the correlation coefficient Rfit, the standard error of estimate Sfit and F, the Fisher´s values. Sfit was computed with N and N-I-1 in the denominator, where N is the number of considered benzenoid hydrocarbons and I is the number of descriptors used in the model. In addition, the models were cross(internally)-validated using the leave-one-out method. Statistical parameters for the cross-validated models are denoted by Rcv and Scv, where cv denotes the cross-validation.
bp = a0 + a1 vM2
The linear structure-boiling point model based on the Zagreb vM2 index with the optimum values of x (0.0) and y (-1.2) is as follows:
bp = - 11.0 (± 8.2) + 5.767 (± 0.093) vM2
N=21 Rfit =0.998 Sfit(N)=6.8 Sfit(N-I-1)=7.2 Rcv =0.997 Scv(N)=8.0 Scv(N-I-1)=8.4 F=3866
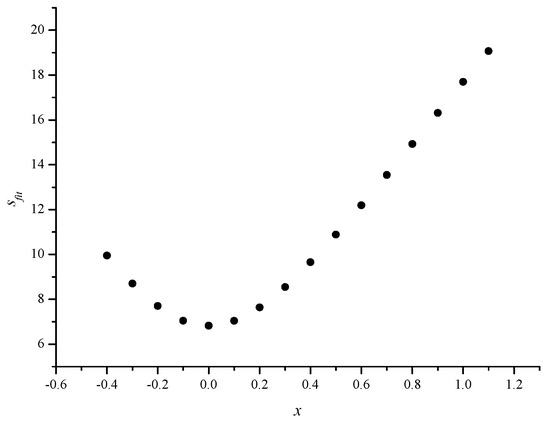
Figure 3.
Scatter plot between the fit standard error of estimate (Sfit(N)) and x values in the range from –0.4 to +1.1 for the optimum value of y (-1.2)
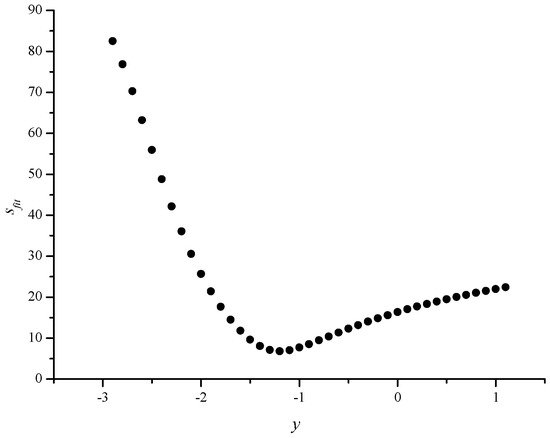
Figure 4.
Scatter plot between the fit standard error of estimate (Sfit(N)) and y values in the range from –3 to +1.1 for the optimum value of x (0.0)
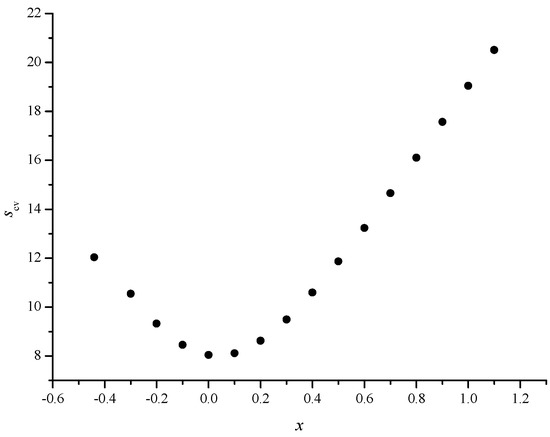
Figure 5.
Scatter plot between the cross validated standard errors of estimate (Scv(N)) and x values in the range from –0.4 to +1.1 for the optimum value of y (-1.2)
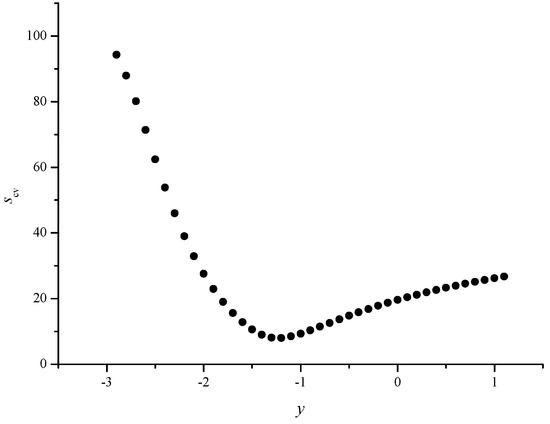
Figure 6.
Scatter plot between the cross validated standard errors of estimate (Scv(N)) and y values in the range from –3 to +1.1 for the optimum value of x (0.0)
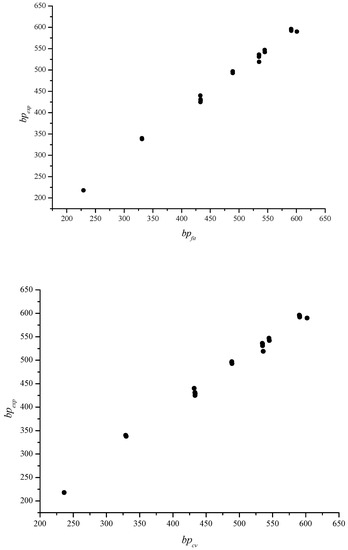
Figure 7.
Scatter plots between the experimental (bpexp) and calculated values of the fit (bpfit) and cross-validated (bpcv) models, respectively
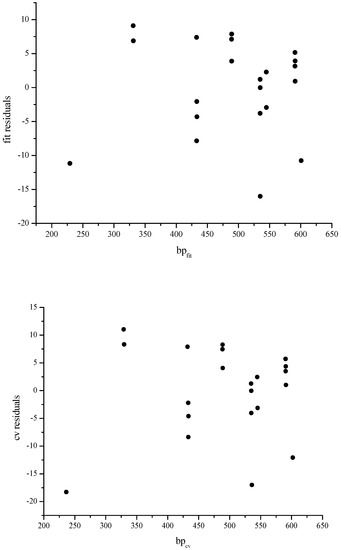
Figure 8.
Scatter plots of fit residuals versus fitted values (bpfit) and of cross validated residuals versus cross validated values (bpcv), respectively
In Figure 3, we give the scatter plot between Sfit(N) and x values for the optimum value of y (–1.2) and in Figure 4, we give the scatter plot between Sfit(N) and y values for the optimum value of x (0.0). The results for the fitted models were supported by the results for the cross-validated models (see Figure 5 and Figure 6).
In Figure 7, we give plots between the experimental and calculated boiling points for fit and cross-validated models and in Figure 8 we give the scatter plots of fit residuals against the fitted values and cross-validated residuals against cross-validated boiling points, respectively.
Model (10) is much superior to the linear model based on the original M2 index:
bp = 98 (± 16) + 2.63 (± 0.10) M2
N=21 Rfit=0.986 Sfit(N)=16.4 Sfit(N-I-1)=17.2 Rcv=0.980 Scv(N)=19.6 Scv(N-I-1)=20.6 F=656
We also derived the structure-boiling point model using the variable vertex-connectivity index vχ and the CROMRsel procedure. The following linear model is obtained for the optimum parameters x (0.0) and y (0.5):
bp = - 11.5 (± 8.2) + 46.27 (± 0.74) vχ
N=21 Rfit =0.998 Sfit(N)=6.8 Sfit(N-I-1)=7.2 Rcv =0.997 Scv(N)=8.0 Scv(N-I-1)=8.4 F=3866
Both models, (10) and (12), possess practically identical statistical parameters. This is unexpected results, since the vertex-connectivity index [29] is superior to the Zagreb M2 index in building QSPR models, though there are indications [22] that the various variable forms of these two indices lead to the models of the same quality regarding the statistical parameters. However, that is so because both eqs. (5) and (7) are based on the same coefficients c1i, c2i and c3i at constant factors.
We also considered the following linear model:
where c1i, c2i and c3i are taken from Table 1.
bpi = b0 + b1 c1i + b2 c2i + b3 c3i
The resulting model:
possesses fit statistical parameters Rfit and Sfit(N) almost identical to those in the models (10) and (12). These parameters would be exactly the same if x and y were obtained more accurately. Because of the greater number of descriptors used in model (14) its Sfit(N-I-1), Scv(N), Scv(N-I-1), Rcv and F values are somewhat worse.
bp = - 11.2 (± 14.2) + 22.8 (± 1.6) c1 + 21.2 (± 0.9) c2 + 18.4 (± 0.7) c3
N=21 Rfit =0.998 Sfit(N)=6.8 Sfit(N-I-1)=7.5 Rcv =0.996 Scv(N)=9.2 Scv(N-I-1)=10.2 F=1176
Models (10) and (14) are related by:
Similar relationships exist also between models (12) and (14).
b0 = a0
b1 = a1 (2 + x)2
b2 = a1 (2 + x) (3 + y)
b3 = a1 (3 + y)2
Models (10) and (12) possess better statistical properties than the models we found in the literature. Below we give the models based on the vertex-connectivity index [13,14] and the edge-connectivity index [14], respectively:
where χ denotes the vertex-connectivity index [29], while ε denotes the edge-connectivity index [30]. Both models (19) and (20) are fitted models − they were not cross-validated.
bp = - 34.4 (± 9.7) + 52.58 (± 0.95) χ
N=21 Rfit =0.997 Sfit(N-I-1)=8.1 F=3045
bp = 13.9 (± 8.6) + 40.07 (± 0.71) ε
N=21 Rfit =0.997 Sfit(N-I-1)=7.9 F=3179
The quadratic models with χ and ε do not represent an improvement and they also have not been cross-validated [13,14]:
bp = - 50 (± 35) + 56.3 (± 8.1) χ - 0.21 (± 0.45) χ2
N=21 Rfit =0.997 Sfit(N-I-1)=8.2 F=1460
bp = - 36 (± 26) + 50.0 (± 5.0) ε - 0.47 (± 0.23) ε2
N=21 Rfit =0.998 Sfit(N-I-1)=7.3 F=1848
The multivariate regression with two descriptors (ε and ws) also does not represent the improvement over the models (10) and (18) [14]:
where ws is a Wiener-like index [31], obtained from the quotient matrix Δ/D. Δ is the detour matrix [32,33] and D is the distance matrix [34].
bp = - 32 (± 22) + 48.0 (± 3.5) ε + 3.6 (± 1.6) ws
N = 21 Rfit = 0.998 Sfit(N-I-1)= 7.2 F = 1944
We also carried out the multivariate regression with two, three and four descriptors using the CROMRsel procedure and the obtained fitted model were cross-validated. Descriptors we considered were vM2, χ, ε and three distance indices (the Wiener sum index WS, ws, the detour index ω). The WS index is a Wiener-like index, obtained from the quotient matrix D/Δ [35] and ω is equal to the half-sum of the elements of the detour matrix [32,36]. We considered χ, ε, WS, ws and ω indices because they have been used in the previous structure-boiling point studies of benzenoid hydrocarbons [13,14]. Below we give the best obtained models followed by the best models containing the vM2 index − in the case of the two-descriptor model the best model contains the vM2 index:
- (i)
- The two-descriptor modelbp = - 40 (± 22) + 6.42 (± 0.46) vM2 – 0.021 (± 0.014) wsN=21 Rfit =0.998 Sfit(N)=6.5 Sfit(N-I-1)=7.0 Rcv =0.996 Scv(N)=8.4 Scv(N-I-1)=8.9 F=2048
- (ii)
- The three-descriptor modelsbp = - 46 (± 18) + 52.7 (± 3.3) ε – 0.167 (± 0.044) ws + 0.037 (± 0.012) ωN=21 Rfit =0.999 Sfit(N)=5.3 Sfit(N-I-1)=5.9 Rcv =0.997 Scv(N)=7.5 Scv(N-I-1)=8.2 F=1936bp = - 47 (± 24) + 37.9 (± 3.4) vM2 – 0.32 (± 0.45) ws - 0.024 (± 0.015) WSN=21 Rfit =0.998 Sfit(N)=6.3 Sfit(N-I-1)=7.0 Rcv =0.996 Scv(N)=8.6 Scv(N-I-1)=9.4 F=1338
- (iii)
- The four-descriptor modelsbp = - 62 (± 22) + 59.2 (± 5.8) ε – 0.72 (± 0.54) WS – 0.242 (± 0.071) ws + 0.057 (± 0.019) ωN=21 Rfit =0.999 Sfit(N)=5.0 Sfit(N-I-1)=5.7 Rcv =0.997 Scv(N)=7.6 Scv(N-I-1)=8.5 F=1518bp = - 88 (± 26) + 8.62 (± 0.91) vM2 – 1.77 (± 0.68) WS – 0.207 (± 0.073) ws + 0.051 (± 0.020) ωN=21 Rfit =0.999 Sfit(N)=5.3 Sfit(N-I-1)=6.1 Rcv =0.997 Scv(N)=7.7 Scv(N-I-1)=8.7 F=1330
The model (27) possesseses the lowest values of the standard errors of estimate, but the linear models based on the variable Zagreb M2 index (10) and the variable connectivity index (18) are also very good models with the standard errors of estimate for the fit and cross-validated models of 6.8 (7.2) oC and 8.0 (8.4) oC, respectively.
We also considered the intercorrelation between the descriptors used in building up models (24) – (28). The intercorrelation matrix reflecting the pairwise linear correlation between vM2, ε, WS, ws and ω computed for 21 benzenoid is given in Table 2.

Table 2.
The intercorrelation matrix
| vM2 | 1.000 | 0.999 | 0.946 | 0.981 | 0.973 |
| ε | 1.000 | 0.936 | 0.983 | 0.974 | |
| WS | 1.000 | 0.912 | 0.920 | ||
| ws | 1.000 | 0.997 |
The intercorrelation-degree is appraised by the correlation coefficient R. Pairs of indices with R ≥ 0.97 are regarded highly correlated, those with 0.90 ≤ R ≤ 0.97 appreciably correlated, those with 0.50 ≤ R ≤ 0.89 weakly correlated and the pairs of descriptors with low values of R (< 0.50) not correlated [37]. It appears that, according to the above classification, all the considered descriptors are either highly correlated (vM2,ε; vM2,ws; vM2,ω;ε, ws; ε,ω; ws, ω ) or appreciably correlated (vM2,WS; ε,WS; WS, ws; WS,ω). However, as Randić [e.g., 38] pointed out, the intercorrelation criterion should not be always used for filtering descriptors to be used in building up the QSPR models.
Conclusions
The variable Zagreb M2 index was used in the structure-boiling point modeling of benzenoid hydrocarbons. The obtained model is practically identical to the model based on the variable vertex-connectivity index and this is due to close relationship between the formulas for the two indices.
Comparative analysis of models based on several descriptors favoured the multivariate models with three and four descriptors. The best models with three and four descriptors did not include vM2 index. However, the next best three- and four-descriptor models contain the vM2 index. The best two-descriptor model contains vM2 index. The standard errors of estimate for the fit and cross-validated models listed in this report are in the 5.0 oC–9.4 oC range and this is a very good result since it shows that the boiling points of benzenoid hydrocarbons can be predicted within an error range of 0.8– 4.3%.
Acknowledgments.
This work was supported by Grant No. 0098034 rewarded by the Ministry of Science and Technology of Croatia. We thank the reviewers for very helpful and detailed comments.
References and Notes
- Randić, M. Novel graph theoretical approach to heteroatoms in QSAR. Chemometrics Intel. Lab. Syst. 1991, 10, 213–227. [Google Scholar]
- Randić, M. On computation of optimal parameters for multivariate analysis of structure-property relationship. J. Chem. Inf. Comput. Sci. 1991, 31, 970–980. [Google Scholar]
- Randić, M.; Plavšić, D.; Lerš, N. Variable connectivity index for cycle-containing structures. J. Chem. Inf. Comput. Sci. 2001, 41, 657–662. [Google Scholar]
- Randić, M.; Basak, S.C. Multiple regression analysis with optimal molecular descriptors. SAR QSAR Environ. Res. 2000, 11, 1–23. [Google Scholar]
- Randić, M.; Pompe, M. The variable molecular descriptors based on the distance matrix. J. Chem. Inf. Comput. Sci. 2001, 41, 575–581. [Google Scholar]
- Randić, M.; Basak, S.C. On use of the variable connectivity index 1χf in QSAR: Toxicity of aliphatic ethers. J. Chem. Inf. Comput. Sci. 2001, 41, 614–618. [Google Scholar]
- Randić, M.; Pompe, M. The variable connectivity index 1χf versus traditional molecular descriptors: A comparative study of 1χf against descriptors of CODESSA. J. Chem. Inf. Comput. Sci. 2001, 41, 631–638. [Google Scholar]
- Nikolić, S.; Plavšić, D.; Trinajstić, N. On the Balaban-like topological indices. MATCH ‒ Comm. Math. Comput. Chem. 2001, 44, 361–386. [Google Scholar]
- Amić, D.; Lučić, B.; Nikolić, S.; Trinajstić, N. Predicting inhibition of microsomal p-hydroxylation of aniline by aliphatic alcohols: A QSAR approach based the weighted path numbers. Croat. Chem. Acta 2001, 74, 237–250. [Google Scholar]
- Amić, D.; Basak, S.C.; Lučić, B.; Nikolić, S.; Trinajstić, N. Structure-water solubility of aliphatic alcohols using the weighted path numbers. SAR QSAR Environ. Res. 2002, 13, 281–295. [Google Scholar]
- Lučić, B.; Miličević, A.; Nikolić, S.; Trinajstić, N. On variable Wiener index. Ind. J. Chem. 2003, 42A, 1279–1282. [Google Scholar]
- Miličević, A.; Nikolić, S. On variable Zagreb indices. Croat. Chem. Acta 2004, 77, 97–1001. [Google Scholar]
- Randić, M. Quantitative structure-property relationship. Boiling points of planar benzenoids. New J. Chem. 1996, 20, 1001–1009. [Google Scholar]
- Plavšić, D.; Trinajstić, N.; Amić, D.; Šoškić, M. Comparison between the structure-boiling point relationships with different descriptor for condensed benzenoids. New J. Chem. 1998, 22, 1075–1078. [Google Scholar]
- Harary, F. Graph Theory, 2nd printing; Addison-Wesley: Reading (MA, U.S.A.), 1971. [Google Scholar]
- Trinajstić, N. Chemical Graph Theory, 2nd edition; CRC Press: Boca Raton (FL, U.S.A.), 1992. [Google Scholar]
- Gutman, I.; Trinajstić, N. Graph theory and molecular orbitals. Total π-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 1972, 17, 535–537. [Google Scholar]
- Gutman, I.; Ruščić, B.; Trinajstić, N.; Wilcox, C.F., Jr. Graph theory and molecular orbitals. XII. Acyclic polyenes. J. Chem. Phys. 1975, 62, 3399–3405. [Google Scholar]
- Devillers, J.; Balaban, A.T. (Eds.) Topological Indices and Related Descriptors in QSAR and QSPR; Gordon & Breach: Amsterdam (The Netherlands), 1999.
- Todeschini, R.; Consonni, V. Handbook of Molecular Descriptors. Wiley-VCH: Weinheim (Germany), 2000. [Google Scholar]
- Nikolić, S.; Kovačević, G.; Miličević, A.; Trinajstić, N. The Zagreb indices 30 years after. Croat. Chem. Acta 2003, 76, 113–124. [Google Scholar]
- Vukičević, D.; Trinajstić, N. Modified Zagreb M2 index - Comparison with the Randić connectivity index for benzenoid systems. Croat. Chem. Acta 2003, 76, 183–187. [Google Scholar]
- Miličević, A.; Nikolić, S.; Trinajstić, N. On reformulated Zagreb indices. Molecular Diversity 2004, in press. [Google Scholar]
- Clar, E. Polycyclic Hydrocarbons; Academic Press: London (U.K.), 1964. [Google Scholar]
- Gutman, I.; Cyvin, S.J. Introduction to the Theory Benzenoid Hydrocarbons; Springer-Verlag: Berlin (Germany), 1989. [Google Scholar]
- Lučić, B.; Trinajstić, N. Multivariate regression outperforms several robust architectures of neural networks. J. Chem. Inf. Comput. Sci. 1999, 39, 121–132. [Google Scholar]
- Lučić, B.; Trinajstić, N.; Sild, S.; Karelson, M.; Katritzky, A.R. A new efficient approach for variable selection based on multiregression: Prediction of gas chromatographic retention times and response factors. J. Chem. Inf. Comput. Sci. 1999, 39, 610–621. [Google Scholar]
- Lučić, B.; Amić, D.; Trinajstić, N. Nonlinear multivariate regression outperforms several concisely designed neural networks on three QSPR data sets. J. Chem. Inf. Comput. Sci. 2000, 40, 403–413. [Google Scholar]
- Randić, M. On characterization of molecular branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar]
- Estrada, E. Edge adjacency relationships and a novel topological index related to molecular volume. J. Chem. Inf. Comput. Sci. 1995, 35, 31–33. [Google Scholar]
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–209. [Google Scholar]
- Amić, D.; Trinajstić, N. On the detour matrix. Croat. Chem. Acta 1995, 68, 53–62. [Google Scholar]
- Trinajstić, N.; Nikolić, S.; Lučić, B.; Amić, D.; Mihalić, Z. The detour matrix in chemistry. J. Chem. Inf. Comput. Sci. 1997, 37, 631–638. [Google Scholar]
- Mihalić, Z.; Veljan, D.; Amić, D.; Nikolić, S.; Plavšić, D.; Trinajstić, N. The distance matrix in chemistry. J.Math. Chem. 1992, 11, 223–258. [Google Scholar]
- Randić, M. On characterization of cyclic structures. J. Chem. Inf. Comput. Sci. 1997, 37, 1063–1071. [Google Scholar]
- Lukovits, I. The detour index. Croat. Chem. Acta 1996, 69, 873–883. [Google Scholar]
- Trinajstić, N.; Nikolić, S.; Basak, S.C.; Lukovits, I. Distances indices and their hypercounterparts: Intercorrelation and use in the structure-property modeling. SAR QSAR Environ. Res. 2001, 12, 31–54. [Google Scholar]
- Randić, M. The connectivity index 25 years after. J. Mol. Graph. Model. 2001, 20, 19–35. [Google Scholar]
© 2004 by MDPI (http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.