Abstract
New valence topological charge-transfer indices are applied to the calculation of dipole moments. The algebraic and vector semisum charge-transfer indices are defined. The combination of the charge-transfer indices allows the estimation of the dipole moments. The model is generalized for molecules with heteroatoms. The ability of the indices for the description of the molecular charge distribution is established by comparing them with the dipole moments of a homologous series of phenyl alcohols. Linear and non-linear correlation models are obtained. The new charge-transfer indices improve the multivariable non-linear regression equations for the dipole moment. When comparing with previous results, the variance decreases 92%. No superposition of the corresponding Gk–Jk and  –
–  pairs is observed. This diminishes the risk of co-linearity. Inclusion of the oxygen atom in the π-electron system is beneficial for the description of the dipole moment, owing to either the role of the additional p orbitals provided by the heteroatom or the role of steric factors in the π-electron conjugation. Linear and non-linear correlations between the fractal dimension and various descriptors point not only to a homogeneous molecular structure but also to the ability to predict and tailor drug properties.
pairs is observed. This diminishes the risk of co-linearity. Inclusion of the oxygen atom in the π-electron system is beneficial for the description of the dipole moment, owing to either the role of the additional p orbitals provided by the heteroatom or the role of steric factors in the π-electron conjugation. Linear and non-linear correlations between the fractal dimension and various descriptors point not only to a homogeneous molecular structure but also to the ability to predict and tailor drug properties.
 –
–  pairs is observed. This diminishes the risk of co-linearity. Inclusion of the oxygen atom in the π-electron system is beneficial for the description of the dipole moment, owing to either the role of the additional p orbitals provided by the heteroatom or the role of steric factors in the π-electron conjugation. Linear and non-linear correlations between the fractal dimension and various descriptors point not only to a homogeneous molecular structure but also to the ability to predict and tailor drug properties.
pairs is observed. This diminishes the risk of co-linearity. Inclusion of the oxygen atom in the π-electron system is beneficial for the description of the dipole moment, owing to either the role of the additional p orbitals provided by the heteroatom or the role of steric factors in the π-electron conjugation. Linear and non-linear correlations between the fractal dimension and various descriptors point not only to a homogeneous molecular structure but also to the ability to predict and tailor drug properties.Introduction
The rationale for transdermal drug delivery needs to be carefully identified [1]. There has been great interest in developing systems for controlled delivery of drugs and other bioactive substances [2]. One technique is to attach a specialized patch on the skin with uncoated polymer matrices containing the embedded drug [3]. Other technique involves covering most of the matrix with an impermeable material [4]. The pathways that exist in a porous membrane used to deliver drugs over a continuous period form a percolating path with usual fractal structures [5,6].
Percutaneous penetration depends essentially on the lipophilicity of the substances tested [7]. The use of homologous series of compounds made it possible to establish behaviour models that allow predicting the percutaneous absorption capacity of chemically related substances [8,9]. Much of the theoretical background information on percutaneous absorption was developed from studies of nonelectrolytic permeating species [10,11]. However, the vehicle’s pH may have a profound influence upon the percutaneous delivery from topical products [12]. Depending on the pKa of the compound and on the pH of the vehicle, an equilibrium mixture of ionized and unionized species would be present in the immediate vicinity of the skin [13]. The permeation of ionized drugs through the skin must be taken into account [14]. Penetration enhancers may act by either interacting with the highly ordered lipid structure or modifying the partitioning of the drug into the tissue [15,16].
Different phenyl alcohols are included in many pharmaceutical and cosmetic products, e.g., bacteriostatic agents and essential oils. Benzyl alcohol, which is used as a bacteriostatic agent and also as a solvent, was evaluated as a percutaneous enhancer [17]. López et al. assessed other phenyl alcohols as enhancers for 5-fluorouracil [8], which was used in in vitro diffusion experiments [18]. Other authors employed dipalmitoylphosphatidylcholine as enhancer for azone [19].
In previous papers, molecular topological charge-transfer indices were applied to the calculation of the molecular dipole moment of hydrocarbons [20]. New valence charge-transfer indices were introduced to take into account the presence of heteroatoms in the molecules and applied to valence-isoelectronic series of benzene and styrene [21]. In this paper, the method has been applied to the calculation of the dipole moment of a homologous series of phenyl alcohols. In the next section, the topological charge-transfer indices are revised. Next, the valence charge-transfer indices for heteroatoms are presented. Following that, the calculation results are discussed. The last section summarizes my conclusions.
Topological charge-transfer indices
The two most important matrices that delineate the labelled chemical graph are the adjacency ( 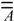 ) [22,23,24] and the distance (
) [22,23,24] and the distance ( 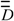 ) matrices, wherein Dij = Iij if i=j, “0” otherwise; lij is the shortest edge count between vertices i and j [25]. In
) matrices, wherein Dij = Iij if i=j, “0” otherwise; lij is the shortest edge count between vertices i and j [25]. In 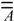 , Aij = 1 if vertices i and j are adjacent, “0” otherwise. The
, Aij = 1 if vertices i and j are adjacent, “0” otherwise. The 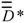 matrix is the matrix whose elements are the squares of the reciprocal distances
matrix is the matrix whose elements are the squares of the reciprocal distances 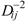 [26]. Now, the intermediate matrix
[26]. Now, the intermediate matrix 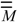 is defined as the matrix product of
is defined as the matrix product of 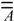 by
by 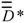 :
:
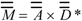 The charge-transfer matrix
The charge-transfer matrix 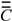 is defined as
is defined as 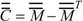 , where
, where 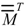 is the transpose of
is the transpose of 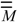 [27]. By agreement, Cii = Mii. For i ≠ j, the Cij terms represent a measure of the intramolecular net charge transferred from atom j to i.
[27]. By agreement, Cii = Mii. For i ≠ j, the Cij terms represent a measure of the intramolecular net charge transferred from atom j to i.
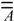 ) [22,23,24] and the distance (
) [22,23,24] and the distance ( 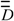 ) matrices, wherein Dij = Iij if i=j, “0” otherwise; lij is the shortest edge count between vertices i and j [25]. In
) matrices, wherein Dij = Iij if i=j, “0” otherwise; lij is the shortest edge count between vertices i and j [25]. In 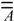 , Aij = 1 if vertices i and j are adjacent, “0” otherwise. The
, Aij = 1 if vertices i and j are adjacent, “0” otherwise. The 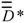 matrix is the matrix whose elements are the squares of the reciprocal distances
matrix is the matrix whose elements are the squares of the reciprocal distances 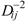 [26]. Now, the intermediate matrix
[26]. Now, the intermediate matrix 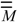 is defined as the matrix product of
is defined as the matrix product of 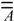 by
by 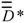 :
:
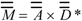
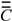 is defined as
is defined as 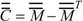 , where
, where 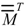 is the transpose of
is the transpose of 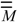 [27]. By agreement, Cii = Mii. For i ≠ j, the Cij terms represent a measure of the intramolecular net charge transferred from atom j to i.
[27]. By agreement, Cii = Mii. For i ≠ j, the Cij terms represent a measure of the intramolecular net charge transferred from atom j to i.Gálvez et al. defined the topological charge-transfer indices Gk as the sum, in absolute value, of the Cij terms defined for the vertices i,j placed at a topological distance Dij equal to k:
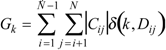 where N is the number of vertices in the graph, Dij are the entries of the
where N is the number of vertices in the graph, Dij are the entries of the 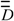 matrix, and δ is the Kronecker δ, being δ = 1 for i = j and δ = 0 for i ≠ j. Gk represents the sum of all the Cij terms, for every pair of vertices i and j at topological distance k. Gálvez et al. also introduced other topological charge-transfer index, Jk, as
matrix, and δ is the Kronecker δ, being δ = 1 for i = j and δ = 0 for i ≠ j. Gk represents the sum of all the Cij terms, for every pair of vertices i and j at topological distance k. Gálvez et al. also introduced other topological charge-transfer index, Jk, as
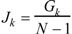 This index represents the mean value of the charge transfer for each edge, since the number of edges for acyclic compounds is N-1. The Gk and Jk indices were applied to the calculation of the molecular dipole moment of hydrocarbons, the boiling temperature of hydrocarbons and alcohols, the vaporization enthalpy of alkanes, the activity of drugs [28,29,30], the capacity and separation factors in chromatographic chiral separations of biomolecules [31], the resonance energy of hydrocarbons, the log IC50 of the D2 dopamine receptor and the σ receptor of piperidines and the sedative character of chiral barbiturates [32].
This index represents the mean value of the charge transfer for each edge, since the number of edges for acyclic compounds is N-1. The Gk and Jk indices were applied to the calculation of the molecular dipole moment of hydrocarbons, the boiling temperature of hydrocarbons and alcohols, the vaporization enthalpy of alkanes, the activity of drugs [28,29,30], the capacity and separation factors in chromatographic chiral separations of biomolecules [31], the resonance energy of hydrocarbons, the log IC50 of the D2 dopamine receptor and the σ receptor of piperidines and the sedative character of chiral barbiturates [32].
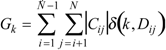
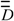 matrix, and δ is the Kronecker δ, being δ = 1 for i = j and δ = 0 for i ≠ j. Gk represents the sum of all the Cij terms, for every pair of vertices i and j at topological distance k. Gálvez et al. also introduced other topological charge-transfer index, Jk, as
matrix, and δ is the Kronecker δ, being δ = 1 for i = j and δ = 0 for i ≠ j. Gk represents the sum of all the Cij terms, for every pair of vertices i and j at topological distance k. Gálvez et al. also introduced other topological charge-transfer index, Jk, as
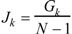
The algebraic semisum charge-transfer index μalg is defined as
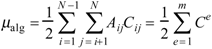 where Ce is the Cij index for vertices i and j connected by edge e. In the first equation, the sum extends for all pairs of adjacent vertices in the molecular graph. In the second expression, the sum extends for the m edges in the molecular graph. Therefore, μalg is intended as a measure of the molecular dipole moment calculated by algebraic semisum of Ce.
where Ce is the Cij index for vertices i and j connected by edge e. In the first equation, the sum extends for all pairs of adjacent vertices in the molecular graph. In the second expression, the sum extends for the m edges in the molecular graph. Therefore, μalg is intended as a measure of the molecular dipole moment calculated by algebraic semisum of Ce.
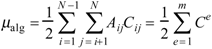
An edge-to-edge analysis of μ suggests that each edge dipole moment μe connecting vertices i and j can be evaluated from the corresponding edge Ce index as
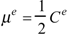 Each edge dipole can be associated with a vector
Each edge dipole can be associated with a vector 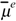 in space. This vector has magnitude μe, lies in the edge e connecting vertices i and j, and its direction is from j to i. The molecular dipole moment vector results the vector sum of the edge dipole moments as
in space. This vector has magnitude μe, lies in the edge e connecting vertices i and j, and its direction is from j to i. The molecular dipole moment vector results the vector sum of the edge dipole moments as
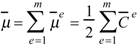 summed for all the m edges in the molecular graph. The vector semisum charge-transfer index μvec is defined as the norm of
summed for all the m edges in the molecular graph. The vector semisum charge-transfer index μvec is defined as the norm of 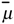 :
:
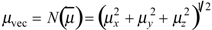 Therefore, μvec is intended as a measure of the molecular dipole moment calculated by vector semisum of edge
Therefore, μvec is intended as a measure of the molecular dipole moment calculated by vector semisum of edge 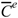 .
.
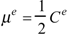
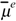 in space. This vector has magnitude μe, lies in the edge e connecting vertices i and j, and its direction is from j to i. The molecular dipole moment vector results the vector sum of the edge dipole moments as
in space. This vector has magnitude μe, lies in the edge e connecting vertices i and j, and its direction is from j to i. The molecular dipole moment vector results the vector sum of the edge dipole moments as
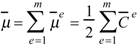
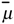 :
:
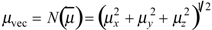
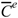 .
.As μvec is associated with a vector in space, the three-dimensional structure of the molecule is needed. The method followed to get it is outlined as follows.
- 1.
- Read the Cartesian coordinates of the atoms.
- 2.
- Determine which atoms are bonded to which other atoms. The distance between two atoms is calculated and, if it is less than a certain value, a bond is assumed to exist between the two atoms.
- 3.
- Build the charge transfer terms Cij.
- 4.
- Calculate the vector semisum dipole moment μvec.
Therefore, μvec is not a pure topological index. It is rather a linear combination of topological indices, but the coefficients are geometric descriptors.
Valence charge-transfer indices for heteroatoms
In valence charge-transfer indices terms, the presence of each heteroatom is taken into account by introducing its electronegativity value in the corresponding entry of the main diagonal of the adjacency matrix 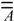 . For each heteroatom X, its entry Aii is redefined as
. For each heteroatom X, its entry Aii is redefined as
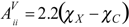 to give a modified
to give a modified 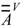 matrix, where xx and xc are the electronegativities of heteroatom X and carbon, respectively, in Pauling units. Notice that the subtractive term keeps
matrix, where xx and xc are the electronegativities of heteroatom X and carbon, respectively, in Pauling units. Notice that the subtractive term keeps 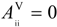 for the carbon atom (Equation 5). Moreover, the multiplicative factor reproduces
for the carbon atom (Equation 5). Moreover, the multiplicative factor reproduces 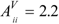 for oxygen, which was taken as standard in previous works. From the modified
for oxygen, which was taken as standard in previous works. From the modified 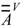 matrix, the valence
matrix, the valence 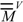 and
and 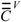 matrices,
matrices, 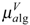 ,
, 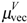 and topological charge-transfer indices
and topological charge-transfer indices 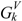 and
and 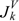 can be calculated by following the former procedure with the
can be calculated by following the former procedure with the 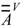 matrix. The
matrix. The 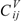 ,
, 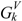 and
and 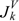 descriptors are graph invariants. The main difference between μvec and
descriptors are graph invariants. The main difference between μvec and 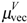 is that μvec is sensitive only to the steric effect of the heteroatoms while is sensitive to both electronic and steric effects.
is that μvec is sensitive only to the steric effect of the heteroatoms while is sensitive to both electronic and steric effects.
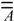 . For each heteroatom X, its entry Aii is redefined as
. For each heteroatom X, its entry Aii is redefined as
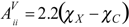
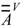 matrix, where xx and xc are the electronegativities of heteroatom X and carbon, respectively, in Pauling units. Notice that the subtractive term keeps
matrix, where xx and xc are the electronegativities of heteroatom X and carbon, respectively, in Pauling units. Notice that the subtractive term keeps 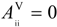 for the carbon atom (Equation 5). Moreover, the multiplicative factor reproduces
for the carbon atom (Equation 5). Moreover, the multiplicative factor reproduces 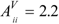 for oxygen, which was taken as standard in previous works. From the modified
for oxygen, which was taken as standard in previous works. From the modified 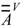 matrix, the valence
matrix, the valence 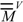 and
and 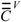 matrices,
matrices, 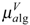 ,
, 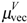 and topological charge-transfer indices
and topological charge-transfer indices 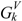 and
and 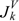 can be calculated by following the former procedure with the
can be calculated by following the former procedure with the 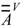 matrix. The
matrix. The 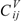 ,
, 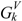 and
and 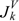 descriptors are graph invariants. The main difference between μvec and
descriptors are graph invariants. The main difference between μvec and 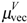 is that μvec is sensitive only to the steric effect of the heteroatoms while is sensitive to both electronic and steric effects.
is that μvec is sensitive only to the steric effect of the heteroatoms while is sensitive to both electronic and steric effects.Calculation results and discussion
The molecular charge-transfer indices Gk, Jk, 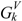 and
and 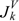 (with k < 6) for a series of 13 phenyl alcohols (8 form a homologous series and 5 are congeneric) are reported in Table 1. In the homologous series, G1 and G2 are sensitive to the presence of the alkyl chain. G3, G4 and G5 indicate the presence of at least 2, 3 and 4 carbon atoms in the alkyl chain, respectively.
(with k < 6) for a series of 13 phenyl alcohols (8 form a homologous series and 5 are congeneric) are reported in Table 1. In the homologous series, G1 and G2 are sensitive to the presence of the alkyl chain. G3, G4 and G5 indicate the presence of at least 2, 3 and 4 carbon atoms in the alkyl chain, respectively. 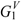 is influenced by the presence of the alkyl chain.
is influenced by the presence of the alkyl chain. 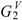 –
– 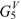 point out the presence of at least 2–5 carbon atoms in the alkyl chain.
point out the presence of at least 2–5 carbon atoms in the alkyl chain.
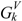 and
and 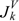 (with k < 6) for a series of 13 phenyl alcohols (8 form a homologous series and 5 are congeneric) are reported in Table 1. In the homologous series, G1 and G2 are sensitive to the presence of the alkyl chain. G3, G4 and G5 indicate the presence of at least 2, 3 and 4 carbon atoms in the alkyl chain, respectively.
(with k < 6) for a series of 13 phenyl alcohols (8 form a homologous series and 5 are congeneric) are reported in Table 1. In the homologous series, G1 and G2 are sensitive to the presence of the alkyl chain. G3, G4 and G5 indicate the presence of at least 2, 3 and 4 carbon atoms in the alkyl chain, respectively. 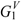 is influenced by the presence of the alkyl chain.
is influenced by the presence of the alkyl chain. 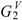 –
– 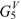 point out the presence of at least 2–5 carbon atoms in the alkyl chain.
point out the presence of at least 2–5 carbon atoms in the alkyl chain.
Table 1.
Values of the Gk and Jk charge-transfer indices up to the fifth order for a homologous series of phenyl alcohols.
| Molecule | N | G1 | G2 | G3 | G4 | G5 | ||||
| Phenol | 7 | 2.0000 | 0.8889 | 0.3750 | 0.2222 | 0.0000 | ||||
| benzyl alcohol | 8 | 1.2500 | 6.7778 | 0.8125 | 0.4133 | 0.1250 | ||||
| 2-phenyl-1-ethanol | 9 | 1.2500 | 6.7778 | 0.8750 | 0.5644 | 0.2431 | ||||
| 3-phenyl-1-propanol | 10 | 1.2500 | 6.7778 | 0.8750 | 0.6044 | 0.3333 | ||||
| 4-phenyl-1-butanol | 11 | 1.2500 | 6.7778 | 0.8750 | 0.6044 | 0.3611 | ||||
| 5-phenyl-1-pentanol | 12 | 1.2500 | 6.7778 | 0.8750 | 0.6044 | 0.3611 | ||||
| 6-phenyl-1-hexanol | 13 | 1.2500 | 6.7778 | 0.8750 | 0.6044 | 0.3611 | ||||
| 7-phenyl-1-heptanol | 14 | 1.2500 | 6.7778 | 0.8750 | 0.6044 | 0.3611 | ||||
| 1-phenyl-2-propanol | 10 | 2.2500 | 6.7778 | 0.9375 | 0.7156 | 0.3611 | ||||
| 2-phenyl-2-propanol | 10 | 2.7500 | 7.2222 | 1.5625 | 0.7956 | 0.3750 | ||||
| 3-phenyl-2-propen-1-ol | 10 | 1.2500 | 8.2222 | 0.8750 | 0.4844 | 0.2708 | ||||
| 1-phenyl-1-pentanol | 12 | 1.7500 | 7.1111 | 1.3125 | 0.8756 | 0.4861 | ||||
| 1-phenyl-2-pentanol | 12 | 2.2500 | 7.0000 | 1.0625 | 0.7556 | 0.4792 | ||||
| Molecule | J1 | J2 | J3 | J4 | J5 | |||||
| phenol | 0.3333 | 0.1481 | 0.0625 | 0.0370 | 0.0000 | |||||
| benzyl alcohol | 0.1786 | 0.9683 | 0.1161 | 0.0590 | 0.0179 | |||||
| 2-phenyl-1-ethanol | 0.1563 | 0.8472 | 0.1094 | 0.0706 | 0.0304 | |||||
| 3-phenyl-1-propanol | 0.1389 | 0.7531 | 0.0972 | 0.0672 | 0.0370 | |||||
| 4-phenyl-1-butanol | 0.1250 | 0.6778 | 0.0875 | 0.0604 | 0.0361 | |||||
| 5-phenyl-1-pentanol | 0.1136 | 0.6162 | 0.0795 | 0.0549 | 0.0328 | |||||
| 6-phenyl-1-hexanol | 0.1042 | 0.5648 | 0.0729 | 0.0504 | 0.0301 | |||||
| 7-phenyl-1-heptanol | 0.0962 | 0.5214 | 0.0673 | 0.0465 | 0.0278 | |||||
| 1-phenyl-2-propanol | 0.2500 | 0.7531 | 0.1042 | 0.0795 | 0.0401 | |||||
| 2-phenyl-2-propanol | 0.3056 | 0.8025 | 0.1736 | 0.0884 | 0.0417 | |||||
| 3-phenyl-2-propen-1-ol | 0.1389 | 0.9136 | 0.0972 | 0.0538 | 0.0301 | |||||
| 1-phenyl-1-pentanol | 0.1591 | 0.6465 | 0.1193 | 0.0796 | 0.0442 | |||||
| Molecule | 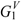 | 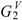 | 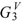 | 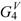 | 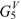 | |||||
| phenol | 2.2000 | 1.1000 | 0.3639 | 0.0847 | 0.0000 | |||||
| benzyl alcohol | 2.9500 | 6.6611 | 0.5625 | 0.2533 | 0.0370 | |||||
| 2-phenyl-1-ethanol | 2.9500 | 7.1056 | 0.7444 | 0.4044 | 0.1319 | |||||
| 3-phenyl-1-propanol | 2.9500 | 7.1056 | 0.9944 | 0.5019 | 0.2222 | |||||
| 4-phenyl-1-butanol | 2.9500 | 7.1056 | 0.9944 | 0.6619 | 0.2824 | |||||
| 5-phenyl-1-pentanol | 2.9500 | 7.1056 | 0.9944 | 0.6619 | 0.3936 | |||||
| 6-phenyl-1-hexanol | 2.9500 | 7.1056 | 0.9944 | 0.6619 | 0.3936 | |||||
| 7-phenyl-1-heptanol | 2.9500 | 7.1056 | 0.9944 | 0.6619 | 0.3936 | |||||
| 1-phenyl-2-propanol | 3.4500 | 7.6556 | 0.8069 | 0.5556 | 0.2500 | |||||
| 2-phenyl-2-propanol | 3.4500 | 8.2056 | 1.3125 | 0.6356 | 0.2870 | |||||
| 3-phenyl-2-propen-1-ol | 2.9500 | 8.3278 | 0.6306 | 0.3819 | 0.1597 | |||||
| 1-phenyl-1-pentanol | 2.9500 | 7.3222 | 1.1819 | 0.7731 | 0.4861 | |||||
| Molecule | 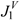 | 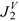 | 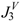 | 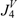 | 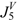 | |||||
| phenol | 0.3637 | 0.1833 | 0.0606 | 0.0141 | 0.0000 | |||||
| benzyl alcohol | 0.4214 | 0.9516 | 0.0804 | 0.0362 | 0.0053 | |||||
| 2-phenyl-1-ethanol | 0.3688 | 0.8882 | 0.0931 | 0.0506 | 0.0165 | |||||
| 3-phenyl-1-propanol | 0.3278 | 0.7895 | 0.1105 | 0.0558 | 0.0247 | |||||
| 4-phenyl-1-butanol | 0.2950 | 0.7106 | 0.0994 | 0.0662 | 0.0282 | |||||
| 5-phenyl-1-pentanol | 0.2682 | 0.6460 | 0.0904 | 0.0602 | 0.0358 | |||||
| 6-phenyl-1-hexanol | 0.2458 | 0.5921 | 0.0829 | 0.0552 | 0.0328 | |||||
| 7-phenyl-1-heptanol | 0.2269 | 0.5466 | 0.0765 | 0.0509 | 0.0303 | |||||
| 1-phenyl-2-propanol | 0.3833 | 0.8506 | 0.0897 | 0.0617 | 0.0278 | |||||
| 2-phenyl-2-propanol | 0.3833 | 0.9117 | 0.1458 | 0.0706 | 0.0319 | |||||
| 3-phenyl-2-propen-1-ol | 0.3278 | 0.9253 | 0.0701 | 0.0424 | 0.0177 | |||||
| 1-phenyl-1-pentanol | 0.2682 | 0.6657 | 0.1074 | 0.0703 | 0.0442 | |||||
| 1-phenyl-2-pentanol | 0.3136 | 0.6960 | 0.0956 | 0.0666 | 0.0335 | |||||
The molecular dipole moments μ (experimental and calculated as vector semisums of Cij or 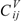 ) are listed in Table 2. As experimental values are not available for all the series, some reference values are calculated with program MOPAC-AM1. The reliability of the results has been tested with the first four entries in Table 2, for which experimental data are available. AM1 calculations adequately reproduce the oscillatory behaviour of the experimental data, mimicking two minima for phenol and 2-phenyl-1-ethanol and two maxima for benzyl alcohol and 3-phenyl-1-propanol. This test suggests that AM1 allows a good approximation, at least for the general performance of the homologous series as a whole, and that the error is sufficiently constant throughout the homologous series. The number of compounds in the homologous series has not been increased because longer phenyl alcohols are not percutaneous enhancers owing to their lower transdermal penetration. In particular, 3-phenyl-2-propen-1-ol has been chosen in order to compare the influence of a double bound in the alkyl chain region of a phenyl alcohol. The experimental μ decreases ca. 3% from that of 3-phenyl-1-propanol due to the presence of the double bond. The presence of an enol group (conjugated double bond in β position with respect to the -OH group) lends 3-phenyl-2-propen-1-ol to particular structural characteristics (greater rigidity than for 3-phenyl-1-propanol) with a lower μ. For the three phenyl propanols, μexperiment decreases 5% from 3-phenyl-1-propanol (primary alcohol) to 1-phenyl-2-propanol (secondary alcohol) and 11% to 2-phenyl-2-propanol (tertiary alcohol). For the three phenyl pentanols, μexperiment increases 7% from 5-phenyl-1-pentanol (primary alcohol) to 1-phenyl-1-pentanol (secondary alcohol with both –phenyl and –OH groups in terminal position) and decreases 8% to 1-phenyl-2-pentanol (secondary alcohol).
) are listed in Table 2. As experimental values are not available for all the series, some reference values are calculated with program MOPAC-AM1. The reliability of the results has been tested with the first four entries in Table 2, for which experimental data are available. AM1 calculations adequately reproduce the oscillatory behaviour of the experimental data, mimicking two minima for phenol and 2-phenyl-1-ethanol and two maxima for benzyl alcohol and 3-phenyl-1-propanol. This test suggests that AM1 allows a good approximation, at least for the general performance of the homologous series as a whole, and that the error is sufficiently constant throughout the homologous series. The number of compounds in the homologous series has not been increased because longer phenyl alcohols are not percutaneous enhancers owing to their lower transdermal penetration. In particular, 3-phenyl-2-propen-1-ol has been chosen in order to compare the influence of a double bound in the alkyl chain region of a phenyl alcohol. The experimental μ decreases ca. 3% from that of 3-phenyl-1-propanol due to the presence of the double bond. The presence of an enol group (conjugated double bond in β position with respect to the -OH group) lends 3-phenyl-2-propen-1-ol to particular structural characteristics (greater rigidity than for 3-phenyl-1-propanol) with a lower μ. For the three phenyl propanols, μexperiment decreases 5% from 3-phenyl-1-propanol (primary alcohol) to 1-phenyl-2-propanol (secondary alcohol) and 11% to 2-phenyl-2-propanol (tertiary alcohol). For the three phenyl pentanols, μexperiment increases 7% from 5-phenyl-1-pentanol (primary alcohol) to 1-phenyl-1-pentanol (secondary alcohol with both –phenyl and –OH groups in terminal position) and decreases 8% to 1-phenyl-2-pentanol (secondary alcohol).
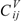 ) are listed in Table 2. As experimental values are not available for all the series, some reference values are calculated with program MOPAC-AM1. The reliability of the results has been tested with the first four entries in Table 2, for which experimental data are available. AM1 calculations adequately reproduce the oscillatory behaviour of the experimental data, mimicking two minima for phenol and 2-phenyl-1-ethanol and two maxima for benzyl alcohol and 3-phenyl-1-propanol. This test suggests that AM1 allows a good approximation, at least for the general performance of the homologous series as a whole, and that the error is sufficiently constant throughout the homologous series. The number of compounds in the homologous series has not been increased because longer phenyl alcohols are not percutaneous enhancers owing to their lower transdermal penetration. In particular, 3-phenyl-2-propen-1-ol has been chosen in order to compare the influence of a double bound in the alkyl chain region of a phenyl alcohol. The experimental μ decreases ca. 3% from that of 3-phenyl-1-propanol due to the presence of the double bond. The presence of an enol group (conjugated double bond in β position with respect to the -OH group) lends 3-phenyl-2-propen-1-ol to particular structural characteristics (greater rigidity than for 3-phenyl-1-propanol) with a lower μ. For the three phenyl propanols, μexperiment decreases 5% from 3-phenyl-1-propanol (primary alcohol) to 1-phenyl-2-propanol (secondary alcohol) and 11% to 2-phenyl-2-propanol (tertiary alcohol). For the three phenyl pentanols, μexperiment increases 7% from 5-phenyl-1-pentanol (primary alcohol) to 1-phenyl-1-pentanol (secondary alcohol with both –phenyl and –OH groups in terminal position) and decreases 8% to 1-phenyl-2-pentanol (secondary alcohol).
) are listed in Table 2. As experimental values are not available for all the series, some reference values are calculated with program MOPAC-AM1. The reliability of the results has been tested with the first four entries in Table 2, for which experimental data are available. AM1 calculations adequately reproduce the oscillatory behaviour of the experimental data, mimicking two minima for phenol and 2-phenyl-1-ethanol and two maxima for benzyl alcohol and 3-phenyl-1-propanol. This test suggests that AM1 allows a good approximation, at least for the general performance of the homologous series as a whole, and that the error is sufficiently constant throughout the homologous series. The number of compounds in the homologous series has not been increased because longer phenyl alcohols are not percutaneous enhancers owing to their lower transdermal penetration. In particular, 3-phenyl-2-propen-1-ol has been chosen in order to compare the influence of a double bound in the alkyl chain region of a phenyl alcohol. The experimental μ decreases ca. 3% from that of 3-phenyl-1-propanol due to the presence of the double bond. The presence of an enol group (conjugated double bond in β position with respect to the -OH group) lends 3-phenyl-2-propen-1-ol to particular structural characteristics (greater rigidity than for 3-phenyl-1-propanol) with a lower μ. For the three phenyl propanols, μexperiment decreases 5% from 3-phenyl-1-propanol (primary alcohol) to 1-phenyl-2-propanol (secondary alcohol) and 11% to 2-phenyl-2-propanol (tertiary alcohol). For the three phenyl pentanols, μexperiment increases 7% from 5-phenyl-1-pentanol (primary alcohol) to 1-phenyl-1-pentanol (secondary alcohol with both –phenyl and –OH groups in terminal position) and decreases 8% to 1-phenyl-2-pentanol (secondary alcohol).
Table 2.
Molecular dipole moment values, μ (D), for a series of phenyl alcohols with charge-transfer indices.
| Molecule | Number of carbon atoms in alkyl chain | Vector semisum | Valence vector semisum | Experimenta |
|---|---|---|---|---|
| phenol | 0 | 0.737 | 2.431 | 1.400 (1.233b) |
| benzyl alcohol | 1 | 0.589 | 2.487 | 1.700 (1.568b) |
| 2-phenyl-1-ethanol | 2 | 0.700 | 2.257 | 1.590 (1.497b) |
| 3-phenyl-1-propanol | 3 | 0.573 | 2.519 | 1.640 (1.597b) |
| 4-phenyl-1-butanol | 4 | 0.702 | 2.249 | 1.345b |
| 5-phenyl-1-pentanol | 5 | 0.573 | 2.519 | 1.626b |
| 6-phenyl-1-hexanol | 6 | 0.702 | 2.250 | 1.346b |
| 7-phenyl-1-heptanol | 7 | 0.573 | 2.518 | 1.634b |
| 1-phenyl-2-propanol | 3 | 0.923 | 2.347 | 1.564b |
| 2-phenyl-2-propanol | 3 | 0.780 | 2.821 | 1.463b |
| 3-phenyl-2-propen-1-ol | 3 | 0.561 | 2.495 | 1.591b |
| 1-phenyl-1-pentanol | 5 | 0.426 | 2.794 | 1.746b |
| 1-phenyl-2-pentanol | 5 | 0.895 | 2.367 | 1.496b |
a Taken from Reference 60.b Calculations carried out with program MOPAC-AM1.
Figure 1 illustrates how the dipole moment of the homologous phenyl alcohols fluctuates with the number of C atoms in the alkyl chain, n. Experimental μ and calculated 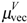 vary in an alternate fashion: for odd n, μ is greater than for even n. However, μvec presents the opposite tendency. As μvec is not sensitive to the electronic effect of the oxygen atom, it is clear that the steric (μvec) and electronic (
vary in an alternate fashion: for odd n, μ is greater than for even n. However, μvec presents the opposite tendency. As μvec is not sensitive to the electronic effect of the oxygen atom, it is clear that the steric (μvec) and electronic ( 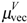 ) factors are antagonistic, and that the electronic effect dominates over the steric one. The μexperiment decreases ca. 4% either from to 6 or from to 7.
) factors are antagonistic, and that the electronic effect dominates over the steric one. The μexperiment decreases ca. 4% either from to 6 or from to 7.
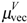 vary in an alternate fashion: for odd n, μ is greater than for even n. However, μvec presents the opposite tendency. As μvec is not sensitive to the electronic effect of the oxygen atom, it is clear that the steric (μvec) and electronic (
vary in an alternate fashion: for odd n, μ is greater than for even n. However, μvec presents the opposite tendency. As μvec is not sensitive to the electronic effect of the oxygen atom, it is clear that the steric (μvec) and electronic ( 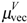 ) factors are antagonistic, and that the electronic effect dominates over the steric one. The μexperiment decreases ca. 4% either from to 6 or from to 7.
) factors are antagonistic, and that the electronic effect dominates over the steric one. The μexperiment decreases ca. 4% either from to 6 or from to 7.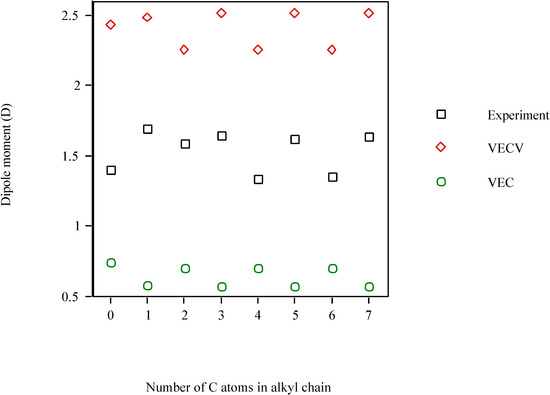
Figure 1.
Dipole moment of homologous phenyl alcohols as a function of the number of C atoms in alkyl chain.
The experimental dipole moments and charge-transfer indices have been correlated for the homologous series. The best linear regression results:
 The mean absolute percentage error (MAPE) is 4.53% and the approximation error variance (AEV) is 0.5087. All other models with greater MAPE and AEV have been discarded. The presence of charge-transfer (G3) and valence (
The mean absolute percentage error (MAPE) is 4.53% and the approximation error variance (AEV) is 0.5087. All other models with greater MAPE and AEV have been discarded. The presence of charge-transfer (G3) and valence ( 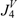 ) indices is representative of charge-transfer processes and clearly conditions the polar character of the correlated compounds. The best non-linear model for μ does not improve the results.
) indices is representative of charge-transfer processes and clearly conditions the polar character of the correlated compounds. The best non-linear model for μ does not improve the results.

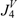 ) indices is representative of charge-transfer processes and clearly conditions the polar character of the correlated compounds. The best non-linear model for μ does not improve the results.
) indices is representative of charge-transfer processes and clearly conditions the polar character of the correlated compounds. The best non-linear model for μ does not improve the results.If the congeneric set is included in the model of phenyl alcohols, the best linear regression for all μ results:
 and AEV increases 21%. The best non-linear model for μ does not improve the results.
and AEV increases 21%. The best non-linear model for μ does not improve the results.

If all μ are calculated with AM1, the best linear regression results:
 and AEV augments 12%. The best non-linear model for μ does not improve the results.
and AEV augments 12%. The best non-linear model for μ does not improve the results.

If μvec is included in the model of phenyl alcohols, the best linear regression for μ results:
 and AEV decreases 72%. Notice that the negative sign of the μvec coefficient is due to the opposite trend of μvec and μexperiment. The best non-linear model for μ results:
and AEV decreases 72%. Notice that the negative sign of the μvec coefficient is due to the opposite trend of μvec and μexperiment. The best non-linear model for μ results:
 and AEV diminishes 86%.
and AEV diminishes 86%.


If 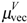 is included in the model, the best linear regression for μ results:
is included in the model, the best linear regression for μ results:
 and AEV drops 73%. The non-linear model with
and AEV drops 73%. The non-linear model with 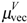 results:
results:
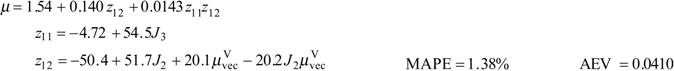 and AEV decreases 92%. Due to the complexity of Equations 8 and 10, a Fortran program has been written to calculate μ. The program is available from the author at Internet (Francisco.Torrens@uv.es).
and AEV decreases 92%. Due to the complexity of Equations 8 and 10, a Fortran program has been written to calculate μ. The program is available from the author at Internet (Francisco.Torrens@uv.es).
 is included in the model, the best linear regression for μ results:
is included in the model, the best linear regression for μ results:

 results:
results:
No superposition of the corresponding Gk–Jk and  –
– 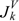 pairs is observed in Equations 6–10. This diminishes the risk of co-linearity in the fit, given the close relationship between each pair Gk, Jk in Equation 2 [33].
pairs is observed in Equations 6–10. This diminishes the risk of co-linearity in the fit, given the close relationship between each pair Gk, Jk in Equation 2 [33].
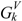 –
– 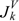 pairs is observed in Equations 6–10. This diminishes the risk of co-linearity in the fit, given the close relationship between each pair Gk, Jk in Equation 2 [33].
pairs is observed in Equations 6–10. This diminishes the risk of co-linearity in the fit, given the close relationship between each pair Gk, Jk in Equation 2 [33].The correlation coefficient found between cross-validated representatives and the property values Rcv has been calculated with the leave-n-out procedure for Equations 6–10 [34]. The procedure furnishes a new method for selecting the best set of descriptors according to the criterion of maximization of the value of Rcv. The Rcv calculations for a homologous series of phenyl alcohols are given in Table 3 for 1 ≤ n ≤ 5. In general, Rcv decreases with n. In particular, Equations 9-10 give greater Rcv than Equations 7-8 (2%) and than Equation 6 (86%) for the whole range of n given in Table 3, although the results for Equations 7 and 9 are rather similar. The corresponding interpretation is that Equations 9-10 are more predictive than Equations 7-8 or 6.

Table 3.
Cross-validation correlation coefficient in a leave-n-out procedure for a homologous series of phenyl alcohols.
| n | Equation 6 | Equation 7 | Equation 8 | Equation 9 | Equation 10 |
|---|---|---|---|---|---|
| 1 | 0.477 | 0.834 | 0.915 | 0.823 | 0.956 |
| 2 | – | 0.827 | 0.916 | 0.821 | 0.954 |
| 3 | – | 0.819 | 0.916 | 0.821 | 0.951 |
| 4 | – | 0.806 | 0.915 | 0.820 | 0.935 |
| 5 | – | – | 0.890 | 0.823 | -0.951 |
In the rest of this section, new parameters are calculated to illustrate the importance of linear and non-linear models in pharmacology. Another intramolecular property related with charge-transfer is the quadrupole moment tensor Θ, defined by
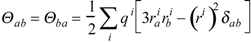 where
where 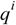 is the i-th element of charge at the point
is the i-th element of charge at the point 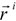 relative to an origin fixed at the centre of mass in the molecule [35]. The δab stands for the Kronecker δ. The subscripts a, b… denote vector or tensor components and can be equal to the Cartesian components x, y, z. Tensor Θ is calculated with our program POLAR [36,37]. The fractal dimension D of the solvent-accessible surface As of the phenyl alcohols may then be obtained according to Lewis and Rees as
relative to an origin fixed at the centre of mass in the molecule [35]. The δab stands for the Kronecker δ. The subscripts a, b… denote vector or tensor components and can be equal to the Cartesian components x, y, z. Tensor Θ is calculated with our program POLAR [36,37]. The fractal dimension D of the solvent-accessible surface As of the phenyl alcohols may then be obtained according to Lewis and Rees as
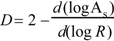 where R is the radius of a probe representing the solvent [38]. It is calculated with our program TOPO. The fractal dimension D provides a quantitative indication of the degree of surface accessibility toward different solvents [39,40,41,42,43,44,45,46]. In previous papers, the fractal dimension of transdermal-delivery drug models (phenyl alcohols [47] and 4-alkylanilines [48]) was calculated. A linear model for the molecular quadrupole moment of the homologous phenyl alcohols vs. fractal dimension is shown in Figure 2.
where R is the radius of a probe representing the solvent [38]. It is calculated with our program TOPO. The fractal dimension D provides a quantitative indication of the degree of surface accessibility toward different solvents [39,40,41,42,43,44,45,46]. In previous papers, the fractal dimension of transdermal-delivery drug models (phenyl alcohols [47] and 4-alkylanilines [48]) was calculated. A linear model for the molecular quadrupole moment of the homologous phenyl alcohols vs. fractal dimension is shown in Figure 2.
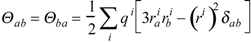
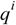 is the i-th element of charge at the point
is the i-th element of charge at the point 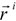 relative to an origin fixed at the centre of mass in the molecule [35]. The δab stands for the Kronecker δ. The subscripts a, b… denote vector or tensor components and can be equal to the Cartesian components x, y, z. Tensor Θ is calculated with our program POLAR [36,37]. The fractal dimension D of the solvent-accessible surface As of the phenyl alcohols may then be obtained according to Lewis and Rees as
relative to an origin fixed at the centre of mass in the molecule [35]. The δab stands for the Kronecker δ. The subscripts a, b… denote vector or tensor components and can be equal to the Cartesian components x, y, z. Tensor Θ is calculated with our program POLAR [36,37]. The fractal dimension D of the solvent-accessible surface As of the phenyl alcohols may then be obtained according to Lewis and Rees as
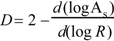
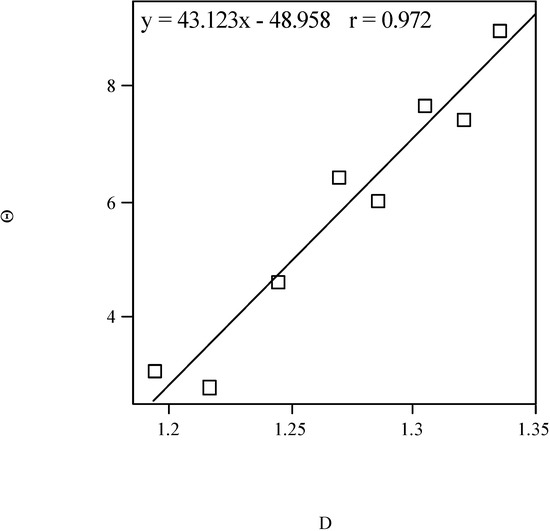
Figure 2.
Quadrupole moment of homologous phenyl alcohols vs. the fractal dimension.
The 1-octanol–water partition coefficient of a substance soluble in 1-octanol and water is defined as
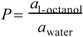 where a1-octanol and awater are the activities of the solute in 1-octanol and water, respectively [49]. P is calculated with the equation:
where a1-octanol and awater are the activities of the solute in 1-octanol and water, respectively [49]. P is calculated with the equation:
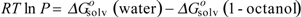 at a given T, which is taken as 298K. R is the gas constant, and
at a given T, which is taken as 298K. R is the gas constant, and 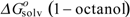 and
and 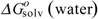 (in kJ·mol-1) are the standard-state free energies of solvation of a given solute considered in 1-octanol and water, respectively. The solvation energies are calculated with our program SCAP [50,51,52,53,54,55]. A non-linear model for of the homologous phenyl alcohols vs. fractal dimension is illustrated in Figure 3.
(in kJ·mol-1) are the standard-state free energies of solvation of a given solute considered in 1-octanol and water, respectively. The solvation energies are calculated with our program SCAP [50,51,52,53,54,55]. A non-linear model for of the homologous phenyl alcohols vs. fractal dimension is illustrated in Figure 3.
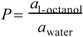
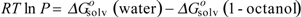
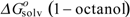 and
and 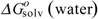 (in kJ·mol-1) are the standard-state free energies of solvation of a given solute considered in 1-octanol and water, respectively. The solvation energies are calculated with our program SCAP [50,51,52,53,54,55]. A non-linear model for of the homologous phenyl alcohols vs. fractal dimension is illustrated in Figure 3.
(in kJ·mol-1) are the standard-state free energies of solvation of a given solute considered in 1-octanol and water, respectively. The solvation energies are calculated with our program SCAP [50,51,52,53,54,55]. A non-linear model for of the homologous phenyl alcohols vs. fractal dimension is illustrated in Figure 3.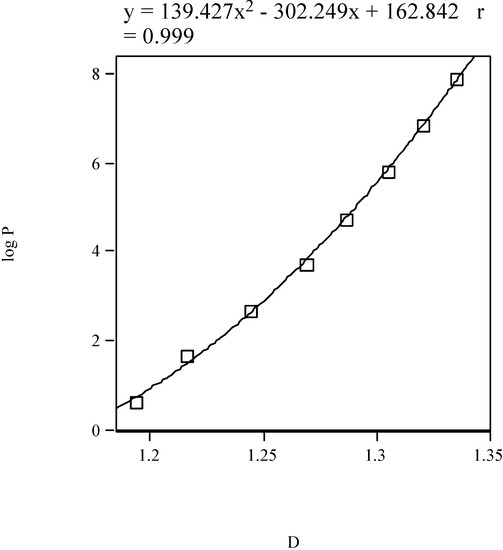
Figure 3.
1-Octanol–water partition coefficient of homologous phenyl alcohols vs. the fractal dimension.
The molar concentration necessary to produce a 1:1 complex with bovine serum albumin (BSA) via equilibrium dialysis, C, provides information on the binding and conformational perturbation of macromolecules by smaller compounds [56]. It is calculated with SCAP. A non-linear model of for the homologous phenyl alcohols vs. fractal dimension is illustrated in Figure 4.
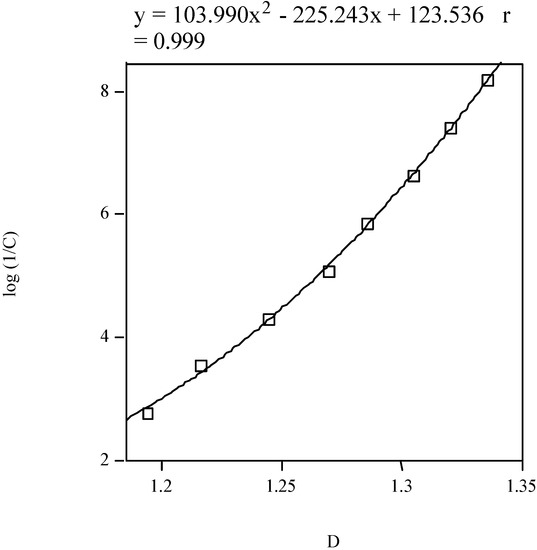
Figure 4.
Molar concentration of homologous phenyl alcohols necessary to produce a 1:1 complex with BSA via equilibrium dialysis vs. the fractal dimension.
The hydrophile–lipophile balance (HLB) is a scale that characterizes surfactants in emulsions as solubilizers, emulsifiers, wetting agents or antifoaming agents [57,58]. It is calculated with SCAP. A non-linear model of HLB for the homologous phenyl alcohols vs. fractal dimension is shown in Figure 5.
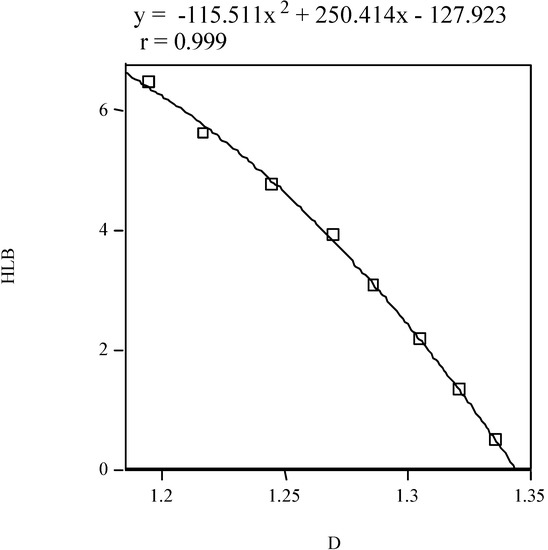
Figure 5.
Hydrophile–lipophile balance of homologous phenyl alcohols vs. the fractal dimension.
The best linear model for the fractal dimension of the phenyl alcohols vs. a series of physicochemical parameters results:
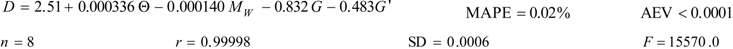 where MW is the molecular weight, G is the molecular globularity and G’ is the molecular rugosity. Index G is calculated as G = Se/S, where Se is the surface area of a sphere whose volume is equal to the molecular volume V, and S is the molecular surface area. Index G’ is calculated as G’ = S/V. All the descriptors are calculated with TOPO. Notice that Equation 15 contains five parameters versus only eight data, allowing three degrees of freedom. The statistical significance of the fit is that the error introduced by fitting is much lower than the error due to the individual points and can be disregarded. Therefore, the data points can be replaced by the fit without adding an appreciable error. The very question is the predictive power of the fit for points out of the fitting set [59]. However, it is not the case because longer phenyl alcohols in the aromatic series are not percutaneous enhancers owing to their lower transdermal penetration. On the other hand, the best non-linear model for the fractal dimension does not improve the results.
where MW is the molecular weight, G is the molecular globularity and G’ is the molecular rugosity. Index G is calculated as G = Se/S, where Se is the surface area of a sphere whose volume is equal to the molecular volume V, and S is the molecular surface area. Index G’ is calculated as G’ = S/V. All the descriptors are calculated with TOPO. Notice that Equation 15 contains five parameters versus only eight data, allowing three degrees of freedom. The statistical significance of the fit is that the error introduced by fitting is much lower than the error due to the individual points and can be disregarded. Therefore, the data points can be replaced by the fit without adding an appreciable error. The very question is the predictive power of the fit for points out of the fitting set [59]. However, it is not the case because longer phenyl alcohols in the aromatic series are not percutaneous enhancers owing to their lower transdermal penetration. On the other hand, the best non-linear model for the fractal dimension does not improve the results.
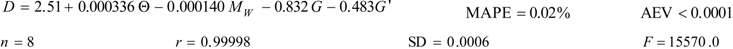
Conclusions
From the preceding results the following conclusions can be drawn:
- 1
- Inclusion of the oxygen atom in the π-electron system is beneficial for the description of the dipole moment, owing to either the role of the additional p orbitals provided by the heteroatom or the role of steric factors in the π-electron conjugation. The analysis of both electronic and steric factors in μ caused by the presence of the oxygen atom shows that the two factors are antagonistic, and that the electronic factor dominates over the steric one.
- 2
- In 3-phenyl-2-propen-1-ol, the double bond in the side chain lends to a more rigid structure with a lower dipole moment.
- 3
- Linear and non-linear correlation models have been obtained for the molecular dipole moments of phenyl alcohols. The new μvec and
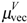 charge-transfer indices have improved the multivariable regression equations for μ, diminishing the risk of co-linearity in the fit.
charge-transfer indices have improved the multivariable regression equations for μ, diminishing the risk of co-linearity in the fit. - 4
- The linear correlation between D and Θ, and various non-linear correlations between D, log P, log 1/C and HLB point not only to a homogeneous molecular structure of the phenyl alcohols but also to the ability to predict and tailor drug properties. The latter is nontrivial in pharmacology.
Work is in progress on the calculation of the dipole moments of a homologous series of 4-alkylanilines, which are also percutaneous enhancers.
Acknowledgements
I wish to thank Dr. E. Besalú for providing me several versions of his full linear leave-many-out program prior to publication, and Drs. Gálvez and de Julián-Ortiz for their kind comments. The author acknowledges financial support of the Spanish MCT (Plan Nacional I+D+I, Project No. BQU2001-2935-C02-01).
References
- Naik, A.; Kalia, Y. N.; Guy, R. H. Transdermal Drug Delivery: Overcoming the Skin’s Barrier Function. Pharm. Sci. Technol. Today 2000, 3, 318–326. [Google Scholar]
- Langer, R. S. Drug Therapy 1983, 31, 217.
- Langer, R. S.; Folkman, J. Polymers for the Sustained Release of Proteins and Other Macromolecules. Nature (London) 1976, 263, 797–800. [Google Scholar]
- Langer, R. S. Chem. Eng. Commun. 1980, 6, 1.
- Bunde, A.; Havlin, S.; Nossal, R.; Stanley, H. E.; Weiss, G. H. On Controlled Diffusion-Limited Drug Release from a Leaky Matrix. J. Chem. Phys. 1985, 83, 5909–5913. [Google Scholar]
- Kaye, B. H. Fine Particle Characterization Aspects of Predictions Affecting the Efficiency of Microbiological Mining Techniques. Powder Technol. 1987, 50, 177–191. [Google Scholar]
- López, A.; Morant, M. J.; Guzmán, D.; Borrás-Blasco, J.; Díez-Sales, O.; Herráez, M. Skin Permeation Model of Phenylalkylcarboxylic Homologous Acids and Their Enhancer Effect on Percutaneous Penetration of 5-Fluorouracil. Int. J. Pharm. 1996, 139, 205–213. [Google Scholar]
- López, A.; Pellett, M. A.; Llinares, F.; Díez-Sales, O.; Herráez, M.; Hadgraft, J. The Enhancer Effect of Several Phenyl Alcohols on Percutaneous Penetration of 5-Fluorouracil. Pharm. Res. 1997, 14, 681–685. [Google Scholar]
- López, A.; Faus, V.; Díez-Sales, O.; Herráez, M. Skin Permeation Model of Phenyl Alcohols: Comparison of Experimental Conditions. Int. J. Pharm. 1998, 173, 183–191. [Google Scholar]
- Yalkowsky, S. H.; Flynn, G. L. Transport of Alkyl Homologues Across Synthetic and Biological Membranes: A New Model for Chain Length-Activity Relationships. J. Pharm. Sci. 1973, 62, 210–216. [Google Scholar]
- Flynn, G. L.; Yalkowsky, S. H.; Roseman, T. J. Mass Transport Phenomena and Models: Theoretical Concepts. J. Pharm. Sci. 1974, 63, 479–509. [Google Scholar]
- Irwin, W. J.; Sanderson, F. D.; Po, A. L. W. Int. J. Pharm. 1990, 66, 193.
- Swarbrick, J.; Lee, G.; Brom, J.; Gensmantel, N. P. J. Pharm. Sci. 1984, 73, 1352–1355.
- Banerjee, P. S.; Ritschel, W. A. Int. J. Pharm. 1989, 49, 189.
- Lewis, D.; Hadgraft, J. Int. J. Pharm. 1990, 65, 211.
- Williams, A. C.; Barry, B. W. Pharm. Res. 1991, 8, 17.
- Saitoh, I.; Ikeda, K.; Takagishi, Y. Effect of Benzyl Alcohol on Rat Skin as a Solvent of Liquid Droplet Dispersion Ointment. Biol. Pharm. Bull. 1995, 18, 321–325. [Google Scholar]
- Díez-Sales, O.; Watkinson, A. C.; Herráez-Domínguez, M.; Javaloyes, C.; Hadgraft, J. A Mechanistic Investigation of the in-Vitro Human Skin Permeation Enhancing Effect of Atone®. Int. J. Pharm. 1996, 129, 33–40. [Google Scholar]
- Rolland, A.; Brzokewicz, A.; Shroot, B.; Jamoulle, J. Int. J. Pharm. 1991, 76, 217.
- Torrens, F. A New Topological Index to Elucidate Apolar Hydrocarbons. J. Comput.-Aided Mol. Design 2002, 15, 709–719. [Google Scholar]
- Torrens, F. Valence Topological Charge-Transfer Indices for Dipole Moments. J. Mol. Struct. (Theochem). in press.
- Randi, M. On Characterization of Molecular Branching. J. Am. Chem. Soc. 1975, 97, 6609–6615. [Google Scholar]
- Murray, W. J.; Kier, L. B.; Hall, L. H. Molecular Connectivity III: Relationship to Partition Coefficients. J. Pharm. Sci. 1975, 64, 1978–1981. [Google Scholar]
- Balaban, A. T. Using Real Numbers as Vertex Invariants for Third-Generation Topological Indexes. J. Chem. Inf. Comput. Sci. 1992, 32, 23–28. [Google Scholar]
- Hosoya, H. Topological Index. A Newly Proposed Quantity Characterizing Topological Nature of Structural Isomers of Saturated Hydrocarbons. Bull. Chem. Soc. Jpn. 1971, 44, 2332–2339. [Google Scholar]
- Plavsic, D.; Nikolic, S.; Trinajstic, N. On the Harary Index for the Characterization of Chemical Graphs. J. Math. Chem. 1993, 12, 235–250. [Google Scholar]
- Gálvez, J.; García, R.; Salabert, M. T.; Soler, R. Charge Indexes. New Topological Descriptors. J. Chem. Inf. Comput. Sci. 1994, 34, 520–525. [Google Scholar]
- Gálvez, J.; García-Domenech, R.; de Julián-Ortiz, J. V.; Soler, R. Topological Approach to Drug Design. J. Chem. Inf. Comput. Sci. 1995, 35, 272–284. [Google Scholar]
- Gálvez, J.; García-Domenech, R.; de Gregorio-Alapont, C.; de Julián-Ortiz, J. V.; Popa, L. Pharmacological Distribution Diagrams: A Tool for de Novo Drug Design. J. Mol. Graphics 1996, 14, 272–276. [Google Scholar]
- Ponce, A. M.; Blanco, S. E.; Molina, A. S.; García-Domenech, R.; Gálvez, J. Study of the Action of Flavonoids on Xanthine-Oxidase by Molecular Topology. J. Chem. Inf. Comput. Sci. 2000, 40, 1039–1045. [Google Scholar]
- De Julián-Ortiz, J. V.; García-Domenech, R.; Gálvez-Alvarez, J.; Soler-Roca, R.; García-March, F. J.; Antón-Fos, G. M. Use of Topological Descriptors in Chromatographic Chiral Separations. J. Chromatogr. A 1996, 719, 37–44. [Google Scholar]
- De Julián-Ortiz, J. V.; de Gregorio-Alapont, C.; Ríos-Santamarina, I.; García-Domenech, R.; Gálvez, J. Prediction of Properties of Chiral Compounds by Molecular Topology. J. Mol. Graphics Mod. 1998, 16, 14–18. [Google Scholar]
- Hocking, R. R. The Analysis and Selection of Variables in Linear Regression. Biometrics 1976, 32, 1–49. [Google Scholar]
- Besalú, E. Fast Computation of Cross-Validated Properties in Full Linear Leave-Many-Out Procedures. J. Math. Chem. 2001, 29, 191–203. [Google Scholar]
- Buckingham, A. D. Permanent and Induced Molecular Moments and Long-Range Intermolecular Forces. Adv. Chem. Phys. 1967, 12, 107–142. [Google Scholar]
- Torrens, F.; Sánchez-Marín, J.; Nebot-Gil, I. Interacting Induced Dipoles Polarization Model for Molecular Polarizabilities. Reference Molecules, Amino Acids and Model Peptides. J. Mol. Struct. (Theochem) 1999, 463, 27–39. [Google Scholar]
- Torrens, F. Molecular Polarizability of Fullerenes and Endohedral Metallofullerenes. J. Phys. Org. Chem. 2002, 15, 742–749. [Google Scholar]
- Lewis, M.; Rees, D. C. Fractal Surfaces of Proteins. Science 1985, 230, 1163–1165. [Google Scholar]
- Torrens, F. Fractal Hybrid Orbitals in Biopolymer Chains. Russ. J. Phys. Chem. (Engl. Transl.) 2000, 74, 115–120. [Google Scholar]
- Torrens, F.; Sánchez-Marín, J.; Nebot-Gil, O. New Dimension Indices for the Characterization of the Solvent-Accessible Surface. J. Comput. Chem. 2001, 22, 477–487. [Google Scholar]
- Torrens, F. Fractals for Hybrid Orbitals in Protein Models. Complexity Int. 2001, 8. torren01. [Google Scholar]
- Torrens, F. Fractal Hybrid Orbitals Analysis of the Tertiary Structure of Protein Molecules. Molecules 2002, 7, 26–37. [Google Scholar]
- Torrens, F. Fractal Dimension of Different Structural-Type Zeolites and of the Active Sites. Top. Catal. 2002, 18, 291–297. [Google Scholar]
- Torrens, F. Fractal Dimension of Zeolite Catalysts. Mol. Phys. 2002, 100, 3105–3109. [Google Scholar]
- Torrens, F. Fractal Dimension of Zeolite Catalysts. Mol. Cryst. Liq. Cryst. submitted for publication.
- Torrens, F. Fractal Hybrid-Orbital Analysis of the Protein Tertiary Structure. Complexity Int. submitted for publication.
- Torrens, F. Fractal Dimension of Transdermal-Delivery Drug Models. J. Sci. Libanais. submitted for publication.
- Torrens, F. Fractal Dimension of Transdermal-Delivery Drug Models: 4-Alkylanilines. Int. J. Quantum Chem. submitted for publication.
- Fujita, T.; Iwasa, J.; Hansch, C. A New Substitutent Constant, π, Derived from Partition Coefficient. J. Am. Chem. Soc. 1964, 86, 5175–5180. [Google Scholar]
- Torrens, F.; Sánchez-Marín, J.; Nebot-Gil, I. Universal Model for the Calculation of All Organic Solvent–Water Partition Coefficients. J. Chromatogr. A 1998, 827, 345–358. [Google Scholar]
- Torrens, F. Universal Organic Solvent-Water Partition Coefficient Model. J. Chem. Inf. Comput. Sci. 2000, 40, 236–240. [Google Scholar]
- Torrens, F. Calculation of Partition Coefficient and Hydrophobic Moment of the Secondary Structure of Lysozyme. J. Chromatogr. A 2001, 908, 215–221. [Google Scholar]
- Torrens, F. Free Energy of Solvation and Partition Coefficients in Methanol–Water Binary Mixtures. Chromatographia 2001, 53, S199–S203. [Google Scholar]
- Torrens, F.; Soria, V. Stationary-Mobile Phase Distribution Coefficient for Polystyrene Standards. Sep. Sci. Technol. 2002, 37, 1653–1665. [Google Scholar]
- Torrens, F. Calculation of Organic Solvent–Water Partition Coefficients of Iron–Sulphur Protein Models. Polyhedron 2002, 21, 1357–1361. [Google Scholar]
- Helmer, F.; Kiehs, K.; Hansch, C. The Linear Free-Energy Relationship Between Partition Coefficients and the Binding and Conformational Perturbation of Macromolecules by Small Organic Compounds. Biochemistry 1968, 7, 2858–2863. [Google Scholar]
- Griffin, W. C. Classification of Surface-Active Agents by “HLB”. J. Soc. Cosmet. Chem. 1949, 1, 311–326. [Google Scholar]
- Griffin, W. C. Calculation of HLB Values of Non-ionic Surfactants. J. Soc. Cosmet. Chem. 1954, 5, 249–256. [Google Scholar]
- Randi, M. The Connectivity Index 25 Years After. J. Mol. Graphics Mod. 2001, 20, 19–35. [Google Scholar]
- McClellan, A. L. Tables of Experimental Dipole Moments; Freeman: San Francisco, 1963. [Google Scholar]
© 2003 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.