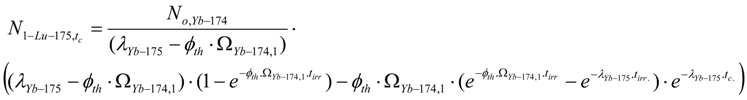Abstract
The conventional reaction yield evaluation for radioisotope production is not sufficient to set up the optimal conditions for producing radionuclide products of the desired radiochemical quality. Alternatively, the specific radioactivity (SA) assessment, dealing with the relationship between the affecting factors and the inherent properties of the target and impurities, offers a way to optimally perform the irradiation for production of the best quality radioisotopes for various applications, especially for targeting radiopharmaceutical preparation. Neutron-capture characteristics, target impurity, side nuclear reactions, target burn-up and post-irradiation processing/cooling time are the main parameters affecting the SA of the radioisotope product. These parameters have been incorporated into the format of mathematical equations for the reaction yield and SA assessment. As a method demonstration, the SA assessment of 177Lu produced based on two different reactions, 176Lu (n,γ)177Lu and 176Yb (n,γ) 177Yb (β- decay) 177Lu, were performed. The irradiation time required for achieving a maximum yield and maximum SA value was evaluated for production based on the 176Lu (n,γ)177Lu reaction. The effect of several factors (such as elemental Lu and isotopic impurities) on the 177Lu SA degradation was evaluated for production based on the 176Yb (n,γ) 177Yb (β- decay) 177Lu reaction. The method of SA assessment of a mixture of several radioactive sources was developed for the radioisotope produced in a reactor from different targets.
1. Introduction
State-of-the-art radiopharmaceutical development requires radioisotopes of specific radioactivity (SA) as high as possible to overcome the limitation of in vivo uptake of the entity of living cells for the peptide and/or monoclonal antibody based radiopharmaceuticals which are currently used in the molecular PET/CT imaging and endo-radiotherapy. The medical radioisotopes of reasonable short half-life are usually preferred because they have, as a rule of thumb, higher SA. These radioisotopes can be produced from cyclotrons, radionuclide generators and nuclear reactors. The advantage of the last one lies in its large production capacity, comfortable targetry and robustness in operation. This ensures the sustainable supply and production of key, medically useful radioisotopes such as 99Mo/99mTc for diagnostic imaging and 131I, 32P, 192Ir and 60Co for radiotherapy. The high SA requirement for these radioisotopes was not critically considered with respect to their effective utilization in nuclear medicine, except for 99Mo. The current wide expansion of targeting endo-radiotherapy depends very much on the availability of high SA radionuclides which can be produced from nuclear research reactor such as 153Sm, 188W/188Re, 90Y and 177Lu. As an example, as high as 20 Ci per mg SA 177Lu is a prerequisite to formulate radiopharmaceuticals targeting tumors in different cancer treatments [1,2].
So far in radioisotope production, reaction yield has been the main parameter to be concerned with rather than SA assessment and unfortunately, the literature of detailed SA assessment is scarcely to be found [3,4]. The SA assessment of radioisotopes produced in a reactor neutron–activated target is a complex issue. This is due to the influence of the affecting factors such as target burn-up, reaction yield of expected radionuclide and unavoidable side-reactions. All these depend again on the available neutron fluxes and neutron spectrum, which are not always adequately recorded. Besides, the reactor power-on time and target self-shielding effect is usually poorly followed up. Certainly, the SA of target radionuclides has been a major concern for a long time, especially for the production of radioisotopes, such as 60Co and 192Ir, used in industry and radiotherapy. In spite of the target burn-up parameter present in the formula of reaction yield calculation to describe the impact of target depression, the SA assessment using the reaction yield was so significantly simplified that the target mass was assumed to be an invariable value during the reactor activation. Critically, this simplification was only favored by virtue of an inherent advantageous combination of the low neutron capture cross section (37 barns) of the target nuclide 59Co and the long half-life of 60Co (which keeps the amount of elemental Co unchanged during neutron bombardment) [4].
The targets used in the production of short-lived medical radioisotopes, however, have high neutron capture cross sections to obtain as high as possible SA values. This fact causes a high “real” burn-up of the target elemental content. Especially, the short half-life of the beta emitting radioisotope produced in the target hastens the chemical element transformation of the target nuclide and strongly affects the SA of the produced radioisotope. The triple factors influencing the production mentioned above (target, neutron flux and short half-life of produced radionuclide) are also critical with respect to the influence of the nuclear side-reactions and impurities present in the target. Moreover, the SA of a radionuclide produced in nuclear reactor varies with the irradiation and post-irradiation processing time as well. All these issues should be considered for a convincing SA assessment of the producible radioisotope for any state-of-the-art nuclear medicine application. As an example, a theoretical approach to the SA assessment reported together with an up-to-date application for 177Lu radioisotope production is presented in this paper. This assessment can also play a complementary or even substantial role in the quality management regarding certifying the SA of the product, when it may be experimentally unfeasible due to radiation protection and instrumentation difficulties in the practical measurement of very low elemental content in a small volume solution of high radioactivity content.
High SA nuclides can be produced by (n, γ) reaction using high cross section targets such as the 176Lu (n, γ)177Lu reaction (б = 2,300 barns). 177Lu is a radioisotope of choice for endo-radiotherapy because of its favorable decay characteristics, such as a low energy beta decay of 497 keV (78.6%) and half-life of 6.71 day. It also emits gamma rays of 113 keV (6.4%) and 208 keV (11%) which make it useful for imaging in-vivo localization with a gamma camera.
177Lu can be produced by two different routes, a direct route with the 176Lu (n, γ)177Lu reaction and an indirect route via the 176Yb (n, γ) 177Yb (β- decay) 177Lu nuclear reaction-transformation. The direct route could be successfully performed in high neutron flux nuclear reactors but these are available in only a handful of countries in the world. Additionally, large burn-up of the target nuclide during high neutron flux irradiation may cause a degradation of the SA value of the produced nuclide if the target contains isotopic impurities. No-carrier-added (n.c.a) radioisotopes of higher SA can be produced via an indirect route with a nuclear reaction- followed –by- radioactive transformation process, such as in the process of neutron capture-followed-by- β- decay , 176Yb (n, γ) 177Yb (β- decay) 177Lu. In this case, the same reduction in SA is also be experienced if the target contains isotopic and/or elemental Lu impurities.
177Lu production has been reported in many publications [5,6,7,8,9], but until now the product quality, especially the evaluation of 177Lu specific radioactivity in the product, has not been sufficiently analyzed. Based on the theoretical SA assessment results obtained in this report, the optimal conditions for the 177Lu production were set up to produce 177Lu product suitable for radiopharmaceutical preparations for targeting endo-radiotherapy.
1.1. Units of specific radioactivity, their conversion and SA of carrier-free radionuclide
The specific radioactivity is defined by different ways. In our present paper we apply the percentage of the hot atom numbers of a specified radioactive isotope to the total atom numbers of its chemical element present in the product as the specific radioactivity. This is denoted as atom %.
The following denotation will be used for further discussion. NRi(A) is the hot atom numbers of radioisotope Ri of the chemical element A and λRi(A), its decay constant. NA is the atom numbers of the chemical element A and T1/2 (sec) the half-life of radioisotope Ri.
The SA unit of atom % is defined as follows:
which can be formulated as follows:
SA in units Bq /Mol and Bq/g are more currently used in practice. The conversion between the SA units is the following:
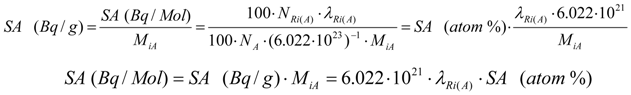 where MiA is the atomic weight of the target or radioactive material of given isotopic composition of the chemical element A.
where MiA is the atomic weight of the target or radioactive material of given isotopic composition of the chemical element A.
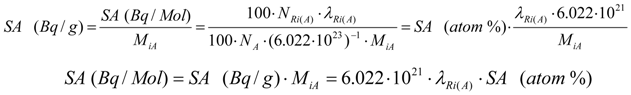
For a radioactive material containing n isotopes of the element A:
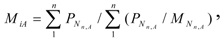 where and are the weight percentage and atomic weight of the isotope Nn,A, respectively. The specific radioactivity of the carrier-free radioisotope Ri is calculated as below:
where and are the weight percentage and atomic weight of the isotope Nn,A, respectively. The specific radioactivity of the carrier-free radioisotope Ri is calculated as below:
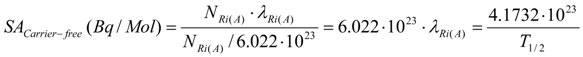
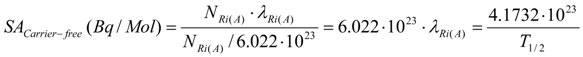
Identifying eq.2 with eq.3 (individualizing MiA as the atomic weight of the concerned radioisotope), it is clear that the SA of a carrier-free radionuclide in unit atom % is 100%.
2. Theoretical Approach and Assessment Methods
Reactor-based radioisotope preparation usually involves two main nuclear reactions. The first one is the thermal neutron capture (n, γ) reaction. This reaction doesn’t lead to a radioisotope of another chemical element, but the following radioactive β− decay of this isotope during target activation results in a decrease in both the reaction yield and atom numbers of the target chemical element. The second reaction is the thermal neutron capture followed by radioactive transformation S (n, γ) Rx (β− decay) Ri. This reaction leads to a carrier-free radioisotope of another chemical element than the target chemical element.
The SA assessment in the radioisotope production using the first reaction (with a simple target system) is simple. Careful targetry could avoid the side reaction S (n, γ) Rx (β− decay) Ri which could result in the isotopic impurities for the radioisotope intended to be produced using the first reaction. In this case the SA assessment in (n, γ) reaction based production process can be simplified by investigation of the SA degrading effect of target nuclide burn-up, chemical element depression due to radioactive decay and isotopic impurities present in the target.
On the other hand the SA assessment in the radioisotope production using the second reaction (with complex target system) is more complicated. The complexity of the targetry used in S (n, γ) Rx (β- decay) Ri reaction based isotope production requires an analysis of the combined reaction system. This system is influenced by both (n, γ) reaction and neutron-capture- followed-by-radioactive transformation S (n, γ) Rx (β- decay) Ri. So the effect of side nuclear reactions in this target system will be assessed in addition to the three above mentioned factors that are involved in the simple target system. In this case the SA assessment is best resolved by a method of SA calculation used for the mixture of several radioactive sources of variable SA, which is referred to as a radioisotope dilution process.
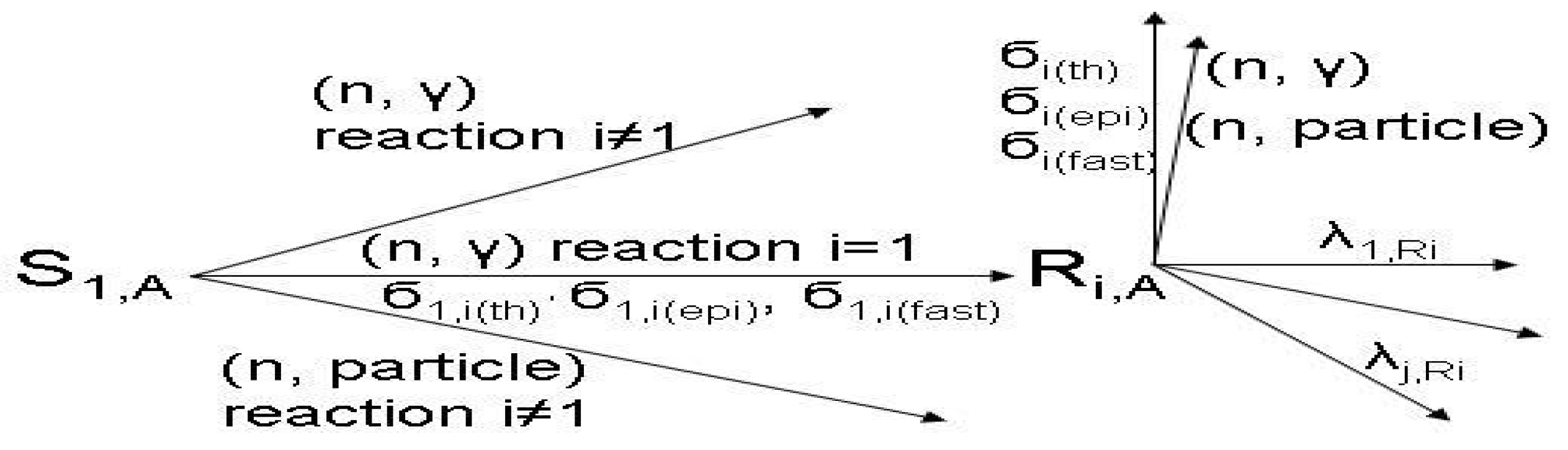
For the calculation of SA and reaction yield of the radioisotope Ri in the two above mentioned reactions, the following reaction schemes are used for further discussion.
Reaction scheme 1:
Reaction scheme 2:
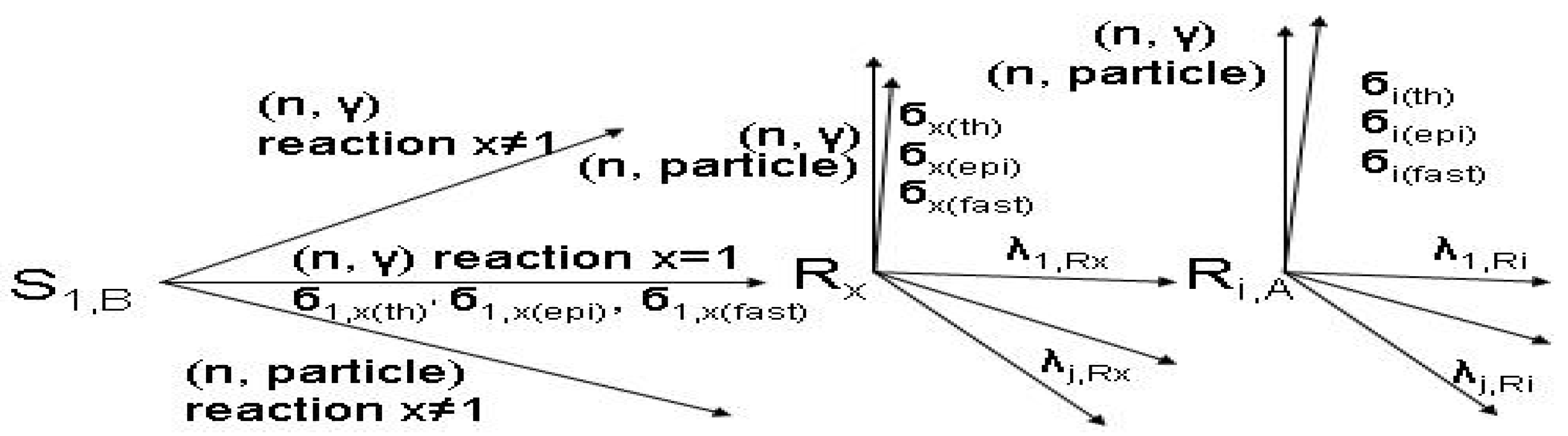
Reaction scheme 3:
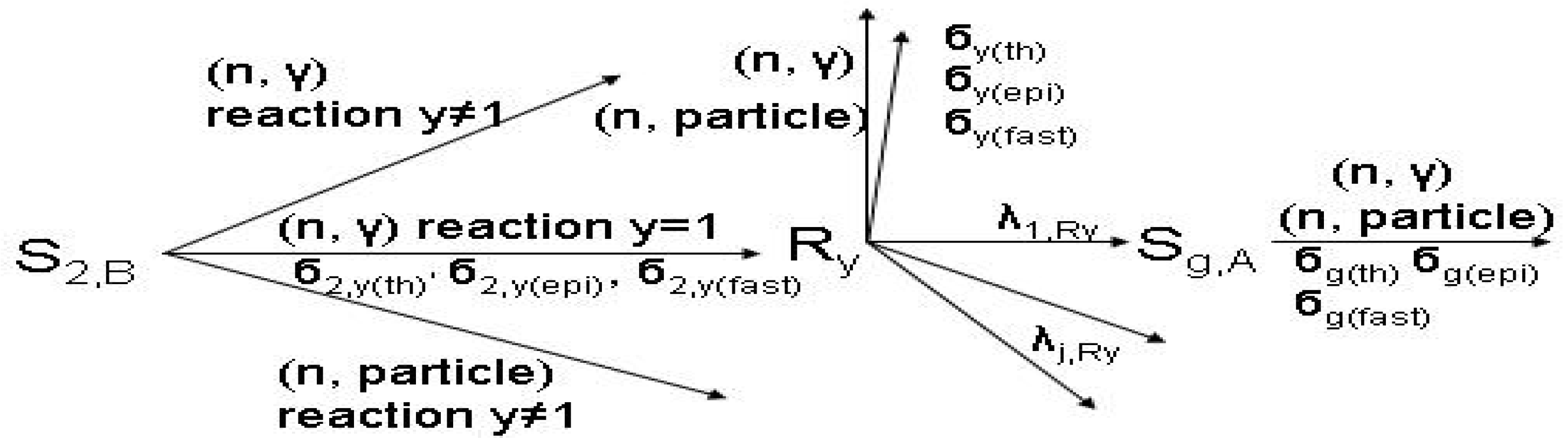
- S1,A is the target stable isotope of element A in the target; Sg,A (with g ≥ 2) is the impure stable isotope of element A originally presented or produced in the target.
- S1,B is the target stable isotope of element B in the target; S2,B is the stable isotope of element B in the target.
- Ri,A or Ri is the wanted radioisotope of element A produced in the target from stable isotope S1,A.
- Rx and Ry are the radioisotopes of element B produced in the target.
- The particle emitted from reaction (n, particle) may be proton or alpha.
- σ(th), σ(epi) and σ(fast) are reaction cross sections for thermal, epi-thermal and fast neutrons, respectively.
- σ1,i(th), σ2,x(th), σ2,y(th),. are cross sections of thermal neutrons for the formation of isotopes i, x, y,. from stable isotope 1, 2, 2, respectively.
- λ is the decay constant.
The (n, γ) reaction yield and the specific radioactivity calculated from it depends on the neutron flux and reaction cross-section which is variable with neutron energy (En) or velocity (vn). In the thermal neutron region, the cross-section usually varies linearly as 1/vn (so called 1/vn reaction), where vn is velocity of neutrons. The cross section-versus-velocity function of many nuclides is, however, not linear as 1/vn in the thermal region (so called non − 1/vn reaction.). As the energy of neutrons increases to the epithermal region, the cross section shows a sharp variation with energy, with discrete sharp peaks called resonance.
On other hand, the cross section values of the (n, γ) reactions tabulated in the literature present as σ0 given for thermal neutrons of En = 0.0253 eV and vn = 2200 m/s and as I0 (infinite dilution resonance integral in the neutron energy region from ECd = 0.55 eV to 1.0 MeV) given for epithermal neutrons.
The symbols σth and σepi used in this paper are identified with the thermal neutron activation cross-section σ0 and the infinite dilution resonance integral I0, respectively, for the case of 1/vn (n,γ)-reaction carried out with a neutron source of pure 1/En epithermal neutron spectrum (Epithermal flux distribution parameter α = 0). Unfortunately, this condition is not useful any more for practical reaction yield and SA calculations.
In practice the target is irradiated by reactor neutrons of epithermal neutron spectrum, so the value of Ωi presenting as a sum σ1,i(th) + Repi.σ1,i(epi) in all the equations below has to be replaced by σeff(1/v) for the “1/vn”- named (n,γ) reaction and by σeff(non − 1/v) for the “non − 1/vn” - named (n,γ)- reaction. The detailed description of these σeff values can be found in the ‘Notes on Formalism’ at the end of this section.
For the isotope production based on (n,γ) reactions the neutron bombardment is normally carried out in a well-moderated nuclear reactor where the thermal and epithermal neutrons are dominant. The fast neutron flux is insignificant compared to thermal and epithermal flux (e.g. <107 n.cm−2.s−1 fast neutron flux compared to >1014 n.cm−2.s−1 thermal one in the Rigs LE7-01 and HF-01 of OPAL reactor-Australia). Besides, the milli-barn cross-section of (n,γ) ,(n,p) and (n,α) reactions induced by fast neutrons is negligible compared to that of (n,γ) reaction with thermal neutron [11]. So the reaction rate of the fast neutron reactions is negligible. Nevertheless, for the generalization purposes the contribution of the fast neutron reaction is also included in the calculation methods below described. It can be ignored in the practical application of SA assessment without significant error.
2.1. The specific radioactivity of radionuclide Ri in the simple target system for the (n, γ) reaction based radioisotope production
2.1.1. Main characteristics of the simple target system
The simple target system contains several isotopes of the same chemical element. Among them only one radioisotope Ri is intended to be produced from stable isotope S1,A via a (n, γ) reaction i = 1 as described above in reaction scheme 1. Other stable Sg,A isotopes ( with g ≥ 2) of the target are considered as impure isotopes.
2.1.1.1. The target burn-up for each isotope in simple target system
The burn-up of the isotope S1,A is the sum of the burn-up caused by different (n,γ) and (n, particle) reactions from reaction i = 1 to i = k, the cross sections of which are different б1,i values. This total burn up rate could be formulated as follows:
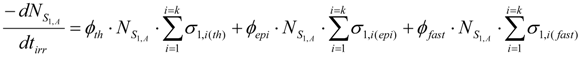 σ1,i(th), σ1,i(epi) and σ1,i(fast) are the thermal, epithermal and fast neutron cross section of the S1,i nuclide for the reaction i, respectively. ϕth, ϕepi and ϕfast are the thermal, epithermal and fast neutron flux, respectively. tirr is the irradiation time. is the atom numbers of the isotope S1,A. By putting Repi = ϕepi/ϕth and Rfast = ϕfast/ϕth ratios into eq.4, the following is deduced.
σ1,i(th), σ1,i(epi) and σ1,i(fast) are the thermal, epithermal and fast neutron cross section of the S1,i nuclide for the reaction i, respectively. ϕth, ϕepi and ϕfast are the thermal, epithermal and fast neutron flux, respectively. tirr is the irradiation time. is the atom numbers of the isotope S1,A. By putting Repi = ϕepi/ϕth and Rfast = ϕfast/ϕth ratios into eq.4, the following is deduced.
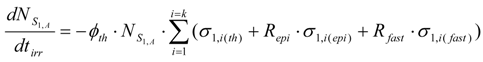
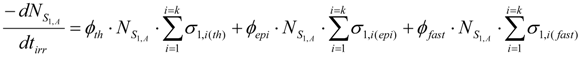
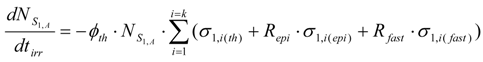
By substituting:
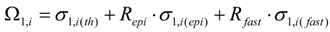 and:
and:
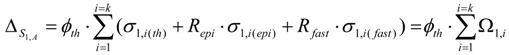 the above differential equation is simplified as follows:
the above differential equation is simplified as follows:
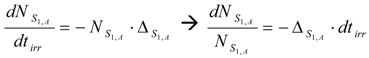
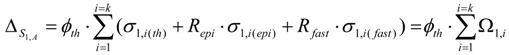
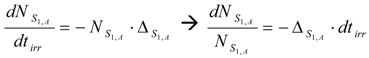
The un-burned atom numbers of the isotope S1,A at any tirr values () is achieved by the integration of eq.7 with the condition of at tirr = 0. The result is:
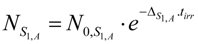 From this equation, the burned-up atom numbers of the isotope S1,A () is:
From this equation, the burned-up atom numbers of the isotope S1,A () is:
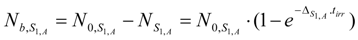 The same calculation process is performed for any isotope Sg,A.
The same calculation process is performed for any isotope Sg,A.
Half-burn-up time of the target nuclide. At half-burn-up time T1/2-B a half of the original atom numbers of the isotope S1,A are burned. Putting into eq. 8, the T1/2-B value is achieved as follows:
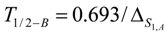
2.1.1.2. Reaction yield of radioisotope Ri in the simple target system
By taking into consideration the un-burned atom numbers of the isotope S1,A (eq. 8) , the reaction rate of any isotope in reaction scheme 1 will be evaluated as follows. In this reaction process the depression of the atom numbers of radioisotope Ri is caused by beta radioactive decays and (n, γ)/(n, particle) reaction-related destruction. The depression factor of the radioisotope Ri in reaction scheme 1 is formulated as follows:
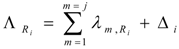 where Δi = ϕth·ΣΩi and Ωi = σi(th) + Repi·σi(epi) + Rfast·σi(fast)
where Δi = ϕth·ΣΩi and Ωi = σi(th) + Repi·σi(epi) + Rfast·σi(fast)
Taking into account eq.5, Ri radioisotope formation rate is the following:
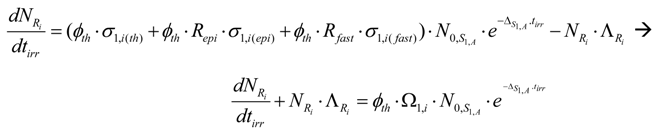
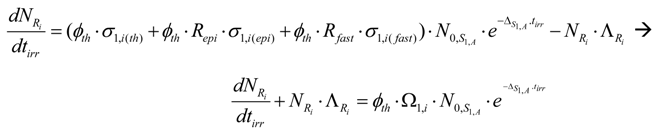
By multiplying both sides of this equation with and manipulating with the mathematical tool , this equation is converted into the following form:
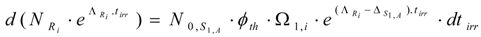
By integrating this equation and assuming NRi = 0 at tirr = 0, the yield of radioisotope Ri at the irradiation time tirr is the following:
The Ri atom numbers (NRi):
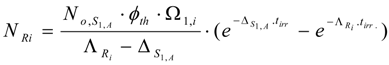
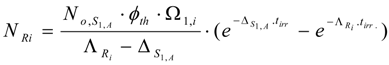
The Ri isotope radioactivity (ARi):
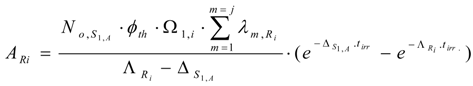
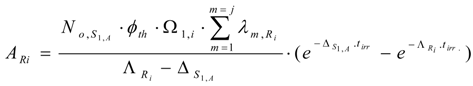
These equations can be deduced from the well known Bateman equation [3,12]. The Ri atom numbers and radioactivity at the post-irradiation time tc ( NRi,tc and ARi,tc, respectively) are calculated by multiplying eqs.13 and 14 with the factor .
Maximum yield of radioisotope Ri. At the irradiation time (denoted as tirr-max) where , Ri radioactivity reaches maximum (ARi−max). By differentiating eq.14 and making it equal to zero:
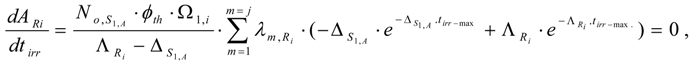 the tirr-max is deduced as follows:
the tirr-max is deduced as follows:
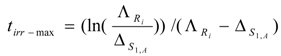
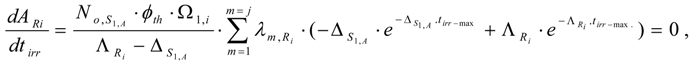
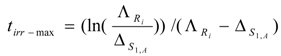
Equation (15) is useful for irradiation optimization to produce Ri radioisotope of highest yield. By introducing the value tirr-max into eqs.13 and 14, we achieve the maximum yield of radioisotope Ri ( NRi-max and ARi-max) as follows:
The maximum atom numbers NRi-max is:
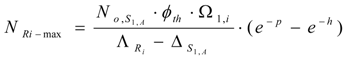
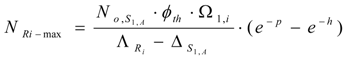
The maximum radioactivity ARi-max is:
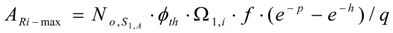 where
where
As shown the maximum yield of radioisotope Ri is a function of the variable D.
2.1.2. The SA assessment of radionuclide Ri in the simple target for (n, γ) reaction based radioisotope production
2.1.2.1. General formula of SA calculation for the simple multi-isotope target
The simplification in the calculation is based on the fact that the target isotope Si,A captures neutrons to form the wanted radioisotope Ri and the isotopic impurities in the target don’t get involved in any nuclear reactions whatsoever. The isotopic impurities may participate in some nuclear reactions to generate either stable isotopes of the target element or an insignificant amount of the isotopes of other chemical element than the target one. This simplified calculation process is supported by a careful targetry study regarding minimizing the radioactive isotopic impurities in the radioisotope product. The following is the SA of radioisotope Ri formed in a target composed of different stable isotopes:
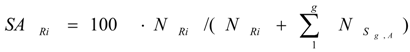 is the sum of the remaining (unburned) atom numbers of g different stable isotopes of the same chemical element in the target. By placing the values of different stable isotopes of the target from eq.8 into this equation, the following general formula is obtained for the SA of radioisotope Ri:
is the sum of the remaining (unburned) atom numbers of g different stable isotopes of the same chemical element in the target. By placing the values of different stable isotopes of the target from eq.8 into this equation, the following general formula is obtained for the SA of radioisotope Ri:
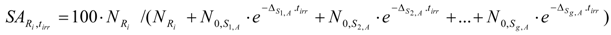 where
where
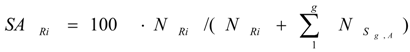
If the target contains impure isotopes of another chemical element, more stable isotopes of chemical element A generated via reaction scheme 3 above could be present in the denominator of this formula. This amount may cause additional depression of . This small impurity will, however, bring about an insignificant amount of stable isotope Sg,A and its depression effect will be ignored.
The eq.19 is set up with an ignorance of insignificant amount of not-really-burned impure stable isotope which captures neutron, but not yet transformed into the isotope of other chemical element via a radioactive decay).
If the impure isotope Sg,A doesn’t participate in any nuclear reaction or its neutron capture generates a stable isotope of the target element, then zero value will be given to the parameter ΔSg,A of eq.(19).
2.1.2.2. SA of radioisotope Ri in the simple two-isotope target
From the practical point of view, the target composed of two stable isotopes is among the widely used ones for radioisotope production. For this case the SA calculation is performed as follows:
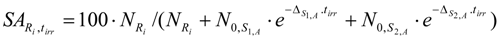 where , Ri is the radioisotope expected to be produced from the stable isotope S1,A . P1 and M1, the weight percentage and atomic weight of the isotope S1,A, respectively. P2 and M2 are for the isotope S2,A, m is the weight of the target.
where , Ri is the radioisotope expected to be produced from the stable isotope S1,A . P1 and M1, the weight percentage and atomic weight of the isotope S1,A, respectively. P2 and M2 are for the isotope S2,A, m is the weight of the target.
By replacing , and the value from eq.(13) into eq.(20), SA of radioisotope Ri in a two isotope target at the end of neutron bombardment, , is the following:
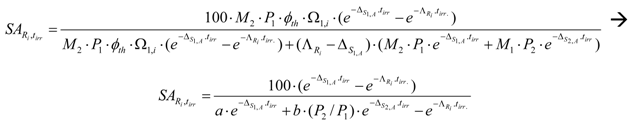 where
where
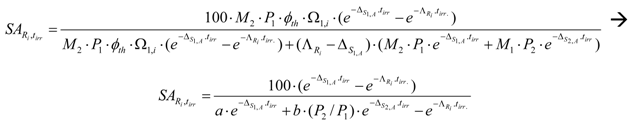
SA at the post- bombardment time tc, , is:


Maximum SA of radioisotope Ri in the simple two-isotope target. Rendering the differential of eq. 21 equal to zero offers the way to calculate the irradiation time at which the SA of nuclide Ri reaches maximum value ():
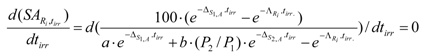
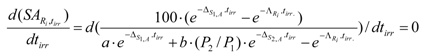
The irradiation time where the SA reaches maximum is denoted as . The equation for the calculation of the value, which is derived from the above differential equation, is the following:
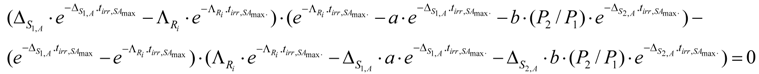
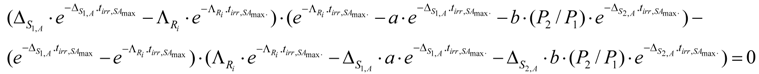
The solution of this equation performed by the computer software MAPLE-10 x gives the value . The analysis of the equation 24 and MAPLE-10 calculation results confirmed that the SA of nuclide Ri reaches maximum at a defined characteristic irradiation time except for the case of P2=0 or very large value, which will be investigated in the following sections.
SA of radioisotope Ri in the simple two-isotope target at the maximum reaction yield. Replacing tirr of eqs.(21) and (22) with the tirr-max from eq.15 is to calculate SA at the maximum reaction yield (achieved at the irradiation time tirr-max):
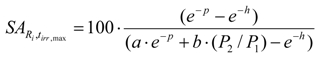 where
where
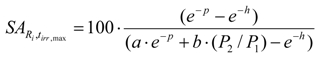
These parameters are identical to that of the eq.(17) and (21).
SA of radioisotope Ri in the target which is considered as a simple two-isotope target. It is also a matter of fact that another very commonly used target system contains more than two stable isotopes (simple multi-isotope target system, g ≥ 2). Except S1,A as shown in reaction scheme 1, all the impure isotopes of the same chemical element in the target don’t get involved in any nuclear reactions or they may participate in with very low rate giving insignificant burn-up ().This system is considered as a special two-isotope target system for which the non-depression of impure isotopes () and the combined impure isotope percentage (Pimp,A) and molecular weight (Mimp,A) are applied. We will have the relevant equations for the calculation of the specific SA value of this target by putting , and into eqs. (21)-(25) ( and are the weight percentage and atomic weight of impure stable isotopes Sg,A, respectively).
2.1.2.3. SA of radioisotope Ri in the simple one-isotope target system
By introducing P2 = 0 into eq.(21), the SA of radioisotope Ri in the simple one-isotope target is the following:
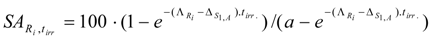
This equation doesn’t give the maximum value of .The result is confirmed by a calculation with MAPLE 10 software. A double check is made by putting the differential of eq. (26) equal to zero to investigate whether a maximum SA could be found:
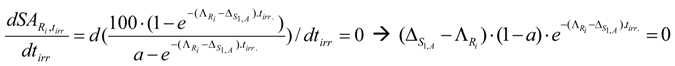
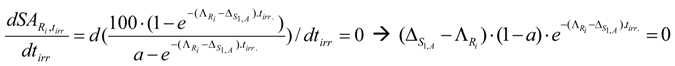
It is shown that the achieved differential eq. (27) has no solution with the variable tirr and gives a correct solution when tirr value approaches to infinity .When then a = 1 (as shown in eq.25), hence the differential value is not defined, so the specific radioactivity has no maximum value at any time. This means that the SA of nuclide Ri in the stable isotope target of 100% isotopic purity never reaches maximum at any irradiation time.
It is also worth mentioning that when the value of or is very large, eq. (21) is converted to eq. (26). It means that the high burn-up of impure stable isotope Sg,A makes a multi-isotope target system change to a one-isotope target one. So, no maximum SA will be expected with this type of multi-isotope target system too.
As shown in eq. (26) the SA of these target systems increases with tirr. This fact teaches us that a compromise between maximum yield achievable at tirr,max and favorable higher SA at the time tirr> tirr,max is subject to the priority of the producer.
2.2. The specific radioactivity of radionuclide Ri in a complex target system for the S(n, γ) Rx (β- decay) Ri reaction based radioisotope production
2.2.1. Main characteristics of the complex target system
The complex target system contains several isotopes of different chemical elements. Among them only one radioisotope Ri is intended to be produced from stable isotope S1,B of chemical element B via a S1,B (n, γ) Rx (β- decay) Ri reaction i = 1 as described above in reaction scheme 2. Other stable Sg,B isotopes ( with g ≥ 2) of the element B are considered as impure isotopes and they could be transformed into other isotopes (except Ri ) of the chemical element A as described above in reaction scheme 3. Besides, the target could contain different isotopes of the element A as impure isotopes which could be involved in different nuclear reactions during target irradiation.
2.2.1.1. The yield of S1B(n, γ) Rx (β- decay) Ri reaction
This reaction generates a carrier-free radioisotope Ri . The SARi value is 100 atom %. As shown in reaction scheme 2, the atom numbers (NRi) and the radioactivity (ARi) of Ri radioisotope of chemical element A are calculated based on the general Bateman equation[3,12]. This is detailed in the following equation:
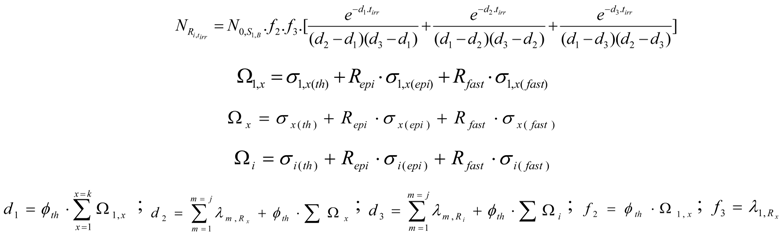
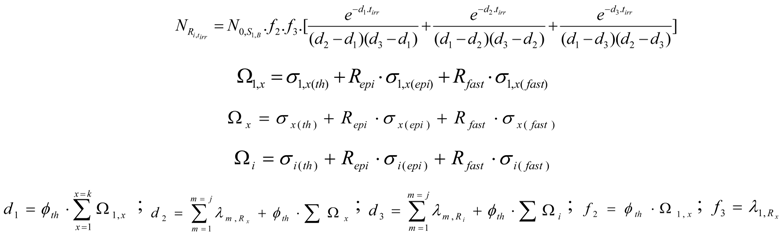
The Ri atom numbers present at post-irradiation time tc is achieved by multiplying the value with the decay factor .
The ARi value is simply derived by multiplying the NRi values with
2.2.1.2. SA-degradation effect of impure stable isotope generated from S2,B(n, γ) Ry(β- decay) Sg,Areaction
Referred to reaction scheme 3 involving the impure stable isotope S2,B in the S1,B target , reaction S2,B(n, γ) Ry (β- decay) Sg,A generates an amount of stable isotope Sg,A of the same chemical element to the wanted radionuclide Ri,A. This fact makes the SA of radionuclide Ri,A produced from stable isotope S1,B lower, so the atom numbers of the stable isotope Sg,A should be evaluated for the purpose of SA assessment. The atom numbers of Sg,A is determined based on the activity of radioisotope Ry. Identifying eqs. (13) and (14) described for reaction scheme 1 with the process of reaction scheme 3, we get the following equations.
The atom numbers () and the radioactivity () of radionuclide Ry at irradiation time tirr are calculated in the same manner as in Section 2.1.1.2 above (using eqs. (13) and (14)):
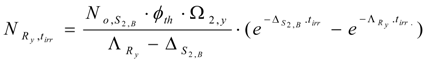
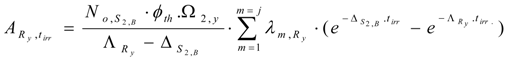 is for stable isotope S2,B and
is for stable isotope S2,B and
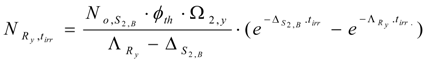
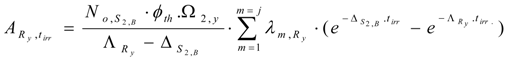
where
for radionuclide Ry and , where
The partial radioactivity of radionuclide Ry for the formation of Sg,A isotope is denoted as . This quantity is calculated by either multiplying eq. (30) with a branch decay ratio or using an individual decay constant as follows:
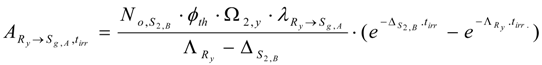
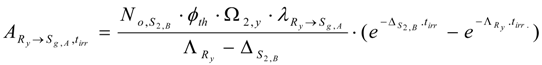
The Sg,A content () formed during neutron activation of the impure stable isotope S2,B is calculated by integrating Ry nuclide radioactivity for the neutron irradiation time tirr as below.
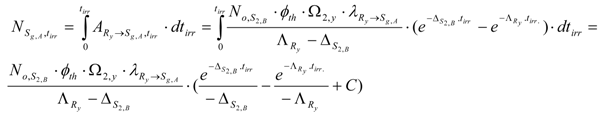
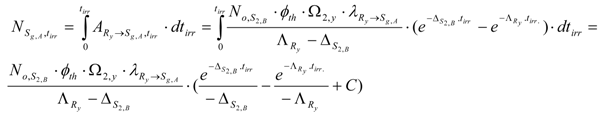
At tirr = 0, , then . Putting C value into the above equation we get:
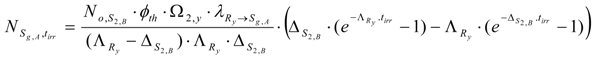
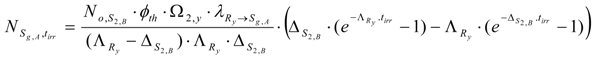
At post-irradiation time (tc) Ry radioactivity decreases as below:

The radioactivity is equal to the formation rate of Sg,A during decay time. By integrating this formation rate we get the Sg,A atom numbers () collected at the time tc. Because the of nuclide Ry at the end-of- neutron-bombardment (E.O.B) time tirr is independent on the variable tc, we get the following integral:
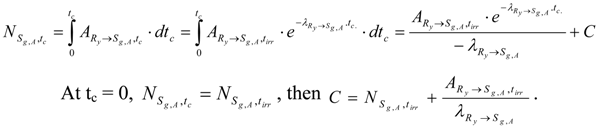
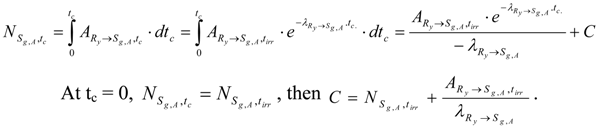
Putting the C value into the above equation we have:


Further putting the value of eq. (31) and of eq. (32) into this equation, we get the result below:


As shown in this equation, the Sg,A content () formed in the target from the S2,B impure stable isotope is composed of a partial amount formed during neutron activation () of isotope Sg,A and its another part formed during post-irradiation decay of Ry induced in the target.
The SA of Ri in the above mentioned target containing both S1,B and S2,B (as described in reaction schemes 2 and 3) is calculated using eqs. (28) and (33b) as follows:
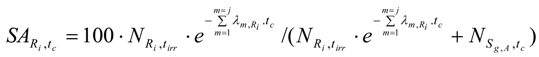
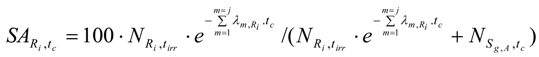
As a result of the analysis of the above equations, minimizing post-irradiation cooling/processing time is recommended to reduce the SA-degradation effect of the impure isotopes.
2.2.1.3. SA-degradation effect of impure isotopes of the chemical element A
The assessment of SA in system containing these impure isotopes can be found in the Section 2.1 for the simple target system.
2.2.2. The SA assessment of radionuclide Ri in a complex target system
The radioisotope dilution is involved in SA depression in a complex target system in which both the wanted radioisotope Ri and its unfavorable stable isotope are generated from different nuclear reactions of both the target isotope and impurities. The complex target system is considered as a mixture of several radioactive sources of variable SA. The method of SA assessment for this mixture is formulated as below.
SAj,Ri is the SA of Ri in the radioactive source Sj the Ri radioactivity of which is Aj,Ri .The radioactive source Sj is produced in the target from a given nuclear reaction such as S (n, γ) Rx (β- decay) Ri reaction (reaction scheme 2) or (n, γ) reaction (reaction scheme 1). There are n different radioactive sources Sj (j=1…n) in the target. So the target is a mixture of radioactive sources. The SA of this radioactive source mixture (SAMix,Ri) is calculated as follows:
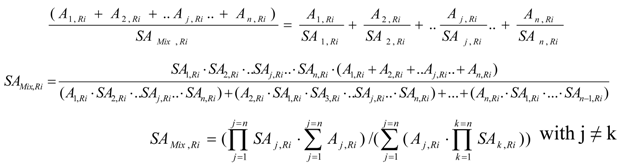 where is in unit of atom %. is either the hot Ri atom numbers or Ri radioactivity of the relevant radioactive source j.
where is in unit of atom %. is either the hot Ri atom numbers or Ri radioactivity of the relevant radioactive source j.
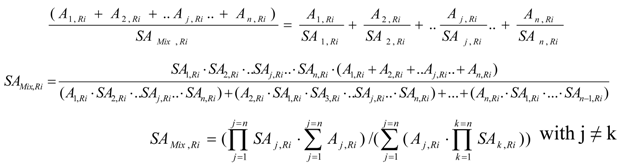
This equation is valuable for all values of SA, except SAj,Ri = 0. This situation excludes the unfavorable effect of some (n, γ) reaction which generates a stable brother isotope Sg,A of radioisotope Ri in the target system ( Reaction scheme 3). To solve this problem we have to combine the atom numbers of this stable brother isotope with the atom numbers of one specified radioactive source of the mixture to generate a new radioactive source of SA ≠ 0, e.g. the combination of radioactive sources produced from the reactions in the scheme 2 and 3. This treatment will be detailed in a practical application for the 176Yb target system in the following section.
2.3. Notes on formalism
During neutron bombardment of the target in the nuclear reactor of epithermal neutron spectrum, the rate of (n,γ) reactions is calculated based on either Westcott or Hogdahl formalism [13] depending on the excitation function of the target nuclide ( the dependence of the reaction cross section on the neutron energy).
For the “non − 1/vn” - named (n,γ) reactions the modified Westcott formalism can be used to improve the accuracy of reaction yield calculation and the reaction rate in both thermal and epithermal neutron region for a diluted sample (both the thermal and epithermal neutron self-shielding factors are set equal to 1 or very close to unity) is:
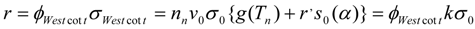 (where , k-factor k = {g(Tn) + r’S0(α} and ).
(where , k-factor k = {g(Tn) + r’S0(α} and ).
In case that Westcott’s factor g(Tn) = 1 the Westcott values are and .Under this condition, the reaction rate is:
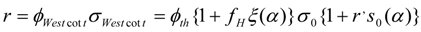
Westcott did not define a thermal neutron flux, but only a conventional (total) neutron flux was mentioned instead. It is the ascertainment from Westcott and Hogdahl formalism that:
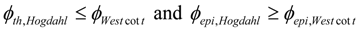
Practically, the values and (usually known as thermal neutron flux and epi-thermal neutron flux , respectively) are determined by a specified nuclide (so called monitor) reaction based measurement of neutron flux in the spectral area below and above the cadmium cut-off energy (ECd = 0.55 eV), respectively, while the Westcott neutron flux values and are not usually available.
For the evaluation of the practical value of versus , the ratio was calculated using the extreme values of epithermal flux distribution parameter α, the neutron energy E0 = 0.0253 eV and ECd = 0.55 eV and the Hogdahl ratio fH = 0.02 (Rig LE7-01 of Australian OPAL reactor).
The values of () ratio of 1.011 for α = −0.15 and 1.006 for α = 0.3 were achieved. These results suggest that the “non − 1/vn” - named (n,γ) reaction yield will be around 1% less than the real value if is used in the Westcott formalism based calculation. So the value can be safely used in placement of . This is agreed with calculation performed by other authors [5].
The k-factor in eq. N.1 is, however, generated from any values of Westcott’s factor g(Tn), so eq. (N.2) can be re-written as follows:
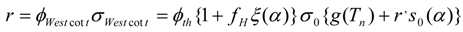
Because as mentioned above, the reaction rate for the “non − 1/vn” - named (n,γ) reactions can be calculated as:
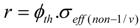
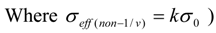
For the “1/vn”- named (n,γ) reactions, the reaction rate in both thermal and epithermal neutron region calculated based on the Hogdahl convention ion is:
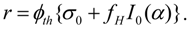 with it is written as:
with it is written as:

For the above equations, or is Hogdahl convention thermal neutron flux, is so-called Hogdahl conventional neutron flux ratio or epithermal to thermal (subcadmium) neutron flux ratio ( in this paper Repi is used instead i.e fH = Repi). Q0 = I0/σ0 is infinite dilution resonance integral I0 per thermal neutron activation cross-section σ0 at the corresponding energy E0 = 0.0253eV;
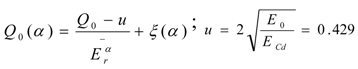
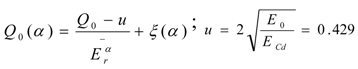
is for the cadmium cut-off energy ECd = 0.55 eV correction,
α is epithermal flux distribution parameter, its extreme values −0.15 < α < +0.3,
σeff(1/v) is Hogdahl convention effective cross-section. nn is total neutron density.
vn is neutron velocity and v0 is the most probable neutron velocity at 20 °C (2200 m/s).
g(Tn) is Westcott’s g-factor for neutron temperature Tn, g(Tn) ≠ 1 for “non − 1/vn” reactions.
r is a measure for the epithermal to total neutron density ratio in the Westcott formalism,
S0 is ratio of the modified reduced resonance integral (1/vn − tail subtracted) to the thermal cross-section σ0,
and
is Westcott conventional (total) neutron flux,
is Westcott convention effective cross-section,
is “non − 1/vn” effective cross-section,
3. Experimental
3.1. Reagents and materials
The isotopically enriched 176Yb2O3 and 176Lu2O3 targets for neutron activation were purchased from Trace-Sciences International Inc.USA [10]. The 176Yb2O3 target isotopic compositions were 176Yb (97.6%), 174Yb (1.93%), 173Yb (0.18%), 172Yb (0.22%), 171Yb (0.07%), 170Yb (<0.01%) and 168Yb (<0.01%). The main Lanthanide impurities of this target were Er (50 p.p.m), Tm (50 p.p.m) and Lu (50 p.p.m). The 176Lu2O3 target isotopic compositions were 176Lu (74.1 %), 175Lu (25.9%). The main Lanthanide impurities of this target were La (66 p.p.m), Yb (13 p.pm), Tm (<1 p.p.m), Er (17 p.p.m), Dy (4 p.p.m), Gd (6 p.p.m), Eu (20 p.p.m), Sm (2 p.p.m) and Nd (1 p.p.m).
3.2. Targets, reactor irradiations, chemical separation, elemental analysis and radioactivity calibration
The radioactive 177Lu + 175Yb solutions were obtained by the reactor thermal neutron irradiation of 176Yb2O3 and/or 176Lu2O3 targets. A quartz ampoule containing an adequate amount of 176Yb2O3 or 176Lu2O3 target was irradiated with a thermal neutron flux in HIFAR reactor (Australia). A 24-hour cooling period was needed to let all 177Yb (T1/2 = 1.911 hours) radionuclides (which formed via 176Yb (n, γ) 177Yb) to be transformed to 177Lu via beta particle decay. The irradiated target was then dissolved in HCl solution and the radiochemical separation of 177Lu from the target solution was performed as reported in our previous papers [8,9]. The radioactivity of the different radioisotopes was calibrated using a CAPINTEC Dose calibrator and gamma-ray spectrometer coupled with ORTEC HP Ge detector. The gamma ray energy and counting efficiency calibration of this analyzer system were performed using a radioactive standard source of 152Eu solution. Lutetium element and other metal content in the completely decayed 177Lu solutions (at least > 10 half-lives) was analyzed using ICP-MS instrument.
4. Results and Discussion
The methods developed in the above sections were evaluated and used for the assessment of SA values of two typical isotope target systems, enriched 176Lu and 176Yb targets. 177Lu produced from these targets is a representative for the state-of-the-art radioisotopes of high specific radioactivity used in targeted endo-radiotherapy.
4.1. The specific radioactivity of 177Lu radioisotope produced via 176Lu (n, γ)177Lu reaction
The 176Lu enriched target is used for 177Lu production. The main nuclear characteristics and nuclear reactions/ radioactive transformations of the 176Lu and 175Lu isotope are listed in Table 1. The production of 177Lu radioisotope is based on the reaction Lu-1. As shown in this data list, the target composes of two stable isotopes, 176Lu and 175Lu. In the reactions Lu-6 and Lu-3 the neutron captures yield the isotopes of another chemical element, so these reactions may cause a depression in elemental Lu atom numbers of the target during neutron bombardment.

Table 1.
Nuclear characteristics of the radionuclides produced in the 176Lu enriched target [11].
However, the effect of these reactions is ignored due to their low cross sections. The reactions Lu-2, Lu-4 and Lu-5 yield long –lived and stable isotopes of the Lutetium element, so the elemental Lu atom numbers of these isotopes are likely to be unchanged during neutron irradiation. This condition shows a similarity between the 176Lu enriched target and the multi-isotope target system of depression factor ΔS2,A = 0 as described in Section 2.1.2.2 (Third bullet). So, eqs. 20–25 are adopted for the 177Lu specific radioactivity assessment of the Lu target. For this SA assessment process the relevant parameters should be identified to individualize the selected equations for the above mentioned 177Lu production reaction. These parameters are the following:
S1,A is 176Lu and re-denoted as S1,Lu. S2,A is 175Lu and re-denoted as S2,Lu. Ri is 177Lu.
P1 is the weight percentage of 176Lu. Pimp,A is weight percentage of 175Lu and re-denoted as Pimp,Lu . M1 is atomic weight of 176Lu. Mimp,A is atomic weight of 175Lu and re-denoted as Mimp,Lu. is for isotope 176Lu.
Because 176Lu has three neutron capture reactions (i=1, 2, 3) as listed in Tab. 1, the value is
where or or
Because the 176Lu is a typical non-1/υn nuclide, the σ1,i(th) cross section (of reaction Lu-1 in Table 1), which is tabulated for neutron of E= 0.0253 eV and υn = 2,200 m/s, should be multiplied with a so called k-factor which is based on the Westcott convention equation as discussed in Section 2.3 [5,6]. The k values ranging from 1.67 at 10 °C to 1.9 at 40 °C were calculated for the Munich reactor [5]. As generally accepted, we use the value k = 1.74 tabulated in reference [11] for our further calculation.
or
(the item can be ignored due to the insignificant value of fast neutron flux)
is for isotope 175Lu and
where
is for radionuclide 177Lu and
where and
177Lu specific radioactivities as a function of the target isotopic composition, neutron flux and irradiation time were formulated and calculated (as shown in Figure 1 and Figure 2). The maximum values of 177Lu specific radioactivity and irradiation time were evaluated. These were used as optimal conditions for carrier-containing 177Lu production.
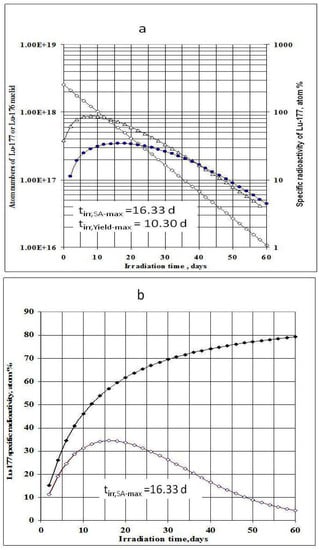
Figure 1.
a- 176Lu target nuclide depression, 177Lu build-up and 177Lu specific radioactivity in the 176Lu enriched target vs. irradiation time (Thermal neutron flux: 2.5·1014 n·cm−2·s−1; Target composition: 74.1% 176Lu + 25.9% 175Lu; Target weight: 1.0 mg), : Specific radioactivity of 177Lu; Δ–Δ–Δ: Atom numbers of 177Lu; ◊-◊-◊: Atom numbers 176Lu target nuclide. b- 177Lu specific radioactivity in the 176Lu enriched target vs. irradiation time and 176Lu enrichment of the target (Thermal neutron flux: 2.5·1014 n·cm−2·s−1), ♦-♦-♦: 100% purity 176Lu target; ◊-◊-◊: Target composition: 74.1% 176Lu + 25.9 % 175Lu.

Figure 2.
177Lu specific radioactivity as a function of irradiation time and 176Lu isotopic purity in the target (Thermal neutron flux of 1.7·1014 n·cm−2·s−1 was applied. Nuclear data was extracted from literatures [11]).
As shown in Figure 1a, the irradiation time for maximum yield (tirr,Yield-max) and that for maximum specific radioactivity (tirr,SA-max) are different. The results presented in Figure 3a state that the higher the 176Lu enrichment of the target, the bigger the difference between values tirr,Yield-max and tirr,SA-max. The ratio of these times varies with thermal neutron flux applied and reaches a maximum value at the flux value of around 3·1014 n·cm−2·s−1 for all the 176Lu enrichment values of the target.
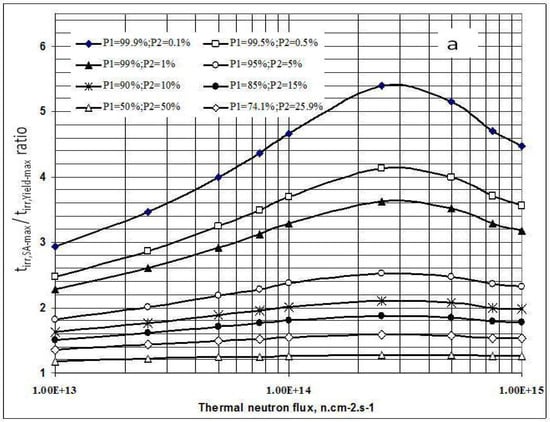
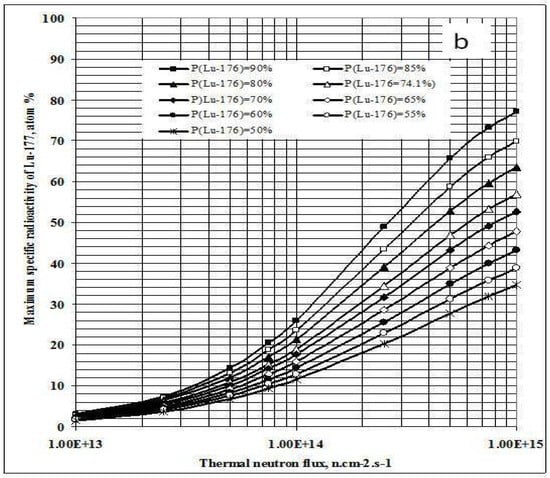
Figure 3.
a- Irradiation time ratio (tirr,SA-max / tirr,Yield-max) vs. thermal neutron flux and target composition.b- Maximum specific radioactivity of 177Lu vs. thermal neutron flux and target composition.
This result is quite interesting in respect to the optimization of neutron flux utilization, irradiation time and target enrichment. Based on the result of further analysis of eqs. (15) and (24) the conclusion can be drawn that the coincident interaction based on the target burn-up / product depression ratio (ΔS1,A/ΛRi) plays an important role in the creation of this maximum value of tirr,Yield-max and tirr,SA-max / tirr,Yield-max ratio at a specified neutron flux value specific for a given target system.. Although the higher neutron flux irradiation gives the higher SA as shown in Figure 3b, the bigger difference between values tirr,Yield-max and tirr,SA-max. makes the outcomes of maximum yield and maximum SA incompatible.
This is to say that the production of 177Lu via 176Lu (n,γ) 177Lu reaction with neutron flux of around 3·1014 n·cm−2·s−1 could be awkward. Hence the production yield and desired SA should be compromised to achieve a cost effective production of clinically useful 177Lu product. The tirr,SA-max values increase with the 176Lu enrichment on the target (Figure 2) and the 100% purity 176Lu target showed no-maximum SA value during neutron activation as seen in Figure 1b. This is confirmed by the analysis of differential equation 27, which was described in Section 2.1.2.3 above.
4.2. The specific radioactivity of 177Lu radioisotope produced via neutron- capture- followed- by- radioactive transformation, 176Yb (n, γ) 177Yb (β- decay) 177Lu
The 176Yb enriched target is used for 177Lu radioisotope production. Based on the isotopic compositions of the elemental Lu -contaminated 176Yb2O3 target and the possible nuclear reactions listed in Table 1 and Table 2, the total 177Lu radioactivity in this activated 176Yb target composes of one part (denoted as A1-Lu-177) induced from the 176Yb target nuclide via reaction176Yb (n, γ) 177Yb (β- decay) 177Lu and another part (denoted as A2-Lu-177) from the176Lu impurity via 176Lu (n, γ) 177Lu reaction. As shown in Table 2, the Lu-free 176Yb target contains 174Yb impure isotope, so the 175Lu induced via reaction174Yb (n, γ) 175Yb (β- decay) 175Lu increases the atom numbers of elemental Lu in the target during neutron activation. Especially, due to long-lived175Yb, the 175Lu generation from beta decay of 175Yb will be continued during post-irradiation processing/cooling of the target. The SA degradation effect of 174Yb and Lu impurities on the carrier-free 177Lu producible from an isotopically pure176Yb target is demonstrably predictable. The assessment of this effect measure is a showcase example for a complex target system in which a stable brother isotope of radioisotope Ri may be generated from the elemental impurities.

Table 2.
Nuclear characteristics of radionuclides produced in 176Yb target matrix [11].
Specific radioactivity SALu-177 achievable in the Lu- and 174Yb-contaminated 176Yb target will be calculated based on “isotopic dilution” equation (35) which is applied for a multi radioactive source system. The 176Yb enriched target discussed in this report is referred to as a system composed of two 177Lu radioactive sources, S1 and S2. The source S1 refers to the radioisotopes induced in the elementally pure (Lu impurity-free) Yb target, while S2 is the radioactive part produced from the Lu impurity in the target.
4.2.1. 177Lu radioactive source 1 (S1): Radioactivity (A1-Lu--177) and specific radioactivity (SA1-Lu--177) of 177Lu isotope in the elementally pure (Lu impurity-free) Yb target
As shown in Table 2, the target is composed of seven stable Yb isotopes. Among them only 176Yb and 174Yb are involved in the neutron capture reactions (reactions Yb-1 and Yb-2, respectively) to produce the Lu isotopes (177Lu and 175Lu). It is obvious that in the elementally pure (Lu impurity-free) Yb target, the 177Lu radioactivity is generated from reaction Yb-1. The elemental Lu atom numbers, however, result from both reactions Yb-1 and Yb-2. The following parameters should be evaluated for the SA assessment of 177Lu isotope in the given Yb target.
Radioactivity of carrier-free 177Lu ( A1-Lu—177 ) from the reaction Yb-1 in the Lu -free Yb target.
Radioactivity at post-irradiation time tc (A1-Lu-177,tc) can be calculated using eq.28. The carrier-free 177Lu activity is the following:
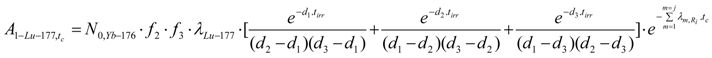
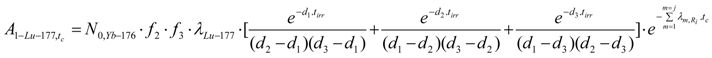
The relevant parameters should be identified to individualize this equation for the reaction Yb-1 mentioned in Table 2. Individualizing eq.28 with Ω1,1 for ΩYb-176,1 (or ΩYb-176,Yb-177),Ωx for ΩYb-177 and Ωi for ΩLu-177, these parameters are the following:
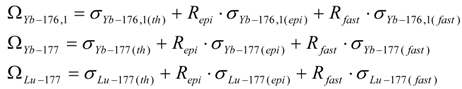 (Rfast·σYb-176,1(fast), Rfast·σYb-177(fast)and Rfast·σLu-177(fast) can be ignored due to the insignificant value of fast neutron flux)
(Rfast·σYb-176,1(fast), Rfast·σYb-177(fast)and Rfast·σLu-177(fast) can be ignored due to the insignificant value of fast neutron flux)
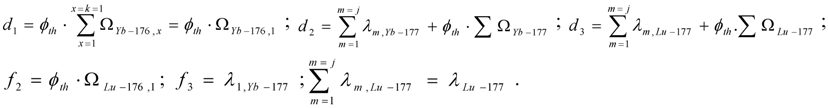 N0,Yb-176 denotes the atom numbers of 176Yb in the m grams weight target.
N0,Yb-176 denotes the atom numbers of 176Yb in the m grams weight target.
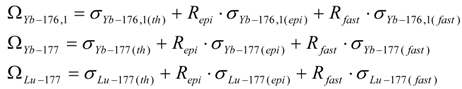
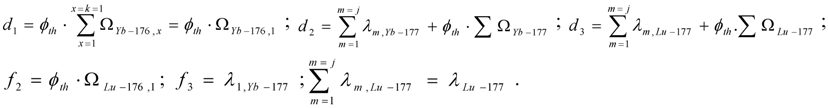
N0,Yb-176=6.02·1023·m·PYb-176/(100·176), where PYb-176 is the weight percentage of 176Yb in the 176Yb enriched target.
Total elemental Lu atom numbers N1-Lu in the Lu impurity-free 176Yb target. This amount is the sum of the Lu atom numbers of carrier-free 177Lu radioisotope (N1-Lu-177,tc) from reaction Yb-1 and Lu atom numbers generated from the 174Yb impurity of the target (N1-Lu-175,tc) from reaction Yb-2.

N1-Lu-177,tc is calculated by a quotient of eq.36 and λLu-177:
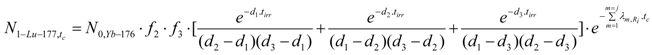
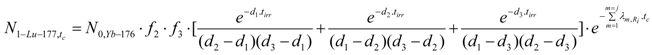
Individualizing eq. (33b) for the 175Lu isotope generated from 174Yb, the following is identified.
S2,B is stable isotope174Yb. is re-denoted as for isotope 174Yb. Because 174Yb has only one neutron capture reaction (y = 1) as shown in Tab. 2, the value is , where . (The items can be ignored due to the insignificant value of fast neutron flux).
is re-denoted as for radioisotope 175Yb and .
is re-denoted as , as and as for radionuclide Yb175 and . For simplification, is applied and value is ignored due to unavailability of value. So we get . is the initial 174Yb atom numbers . This quantity is . P Yb-174 is the weight percentage of 174Yb impurity in the 176Y target.
177Lu specific radioactivity of the Lu impurity-free 176Yb target. The specific radioactivity of 177Lu source (the 177Lu radioactive source 1) generated from the elemental Lu impurity-free 176Yb target is the following:

4.2.2. 177Lu radioactive source 2 (S2): Radioactivity A2-Lu-177) and specific radioactivity SA2-Lu-177 of 177Lu generated from 176Lu (n, γ) 177Lu reaction of the elemental Lu-impurity in the Lu-contaminated 176Yb target
Specific radioactivity. SA2-Lu-177 of 177Lu radioisotope produced in this target is calculated using the same process as described in the previous Section 4.1 ‘The specific radioactivity of 177Lu radioisotope produced via 176Lu (n, γ)177Lu reaction’ of Results and Discussion. In this case the impure Lu content in the 176Yb target is assumed to have natural abundance, so the values P1 = 2.59% for 176Lu and Pimp,Lu-175 = 97.41% for 175Lu are put into calculation.
Radioactivity. Radioactivity of 177Lu from the elemental Lu impurity in the 176Yb target at post-irradiation time tc is calculated using eq. (14):
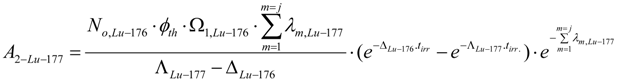 P 1 =2.59 % is natural abundance of 176Lu. m is the weight of elemental Lu impurity in the 176Y target.
P 1 =2.59 % is natural abundance of 176Lu. m is the weight of elemental Lu impurity in the 176Y target.
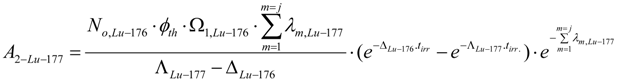
4.2.3. 177Lu specific radioactivity SALu-177 and 177Lu radioactivity ALu-177 in the Lu-contaminated 176Yb target as a combination of 177Lu radioactive source S1 and S2
177Lu specific radioactivity SALu-177. The method of SA assessment of the mixture of several radioactive sources (referred to Section 2.2.2) is used for the SA calculation. The 177Lu specific radioactivity SALu-177 in the Lu-contaminated 176Yb target is calculated using eq. (35) with relevant parameters of the mixture of two 177Lu radioactive sources S1 and S2 as described above,
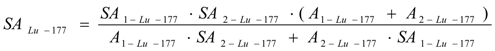
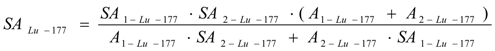
177Lu radioactivity. Total 177Lu radioactivity in the target is ALu-177 = A1-Lu-177 + A2-Lu-177. 175Lu isotope generated from 174Yb (n, γ) 175Yb (β- decay) 175Lu process and elemental Lu impurities remaining in the 177Lu product (which is chemically separated from 176Yb target) makes the SA value of 177Lu strongly decreased.
Rendering the differential of eq. (42) equal to zero offers the way to calculate the irradiation time at which the SA of 177Lu reaches maximum value (SALu-177,max). The maximum SA is predicted based on the opposite tendency of SA variation of elementally pure and Lu-contaminated Yb targets. This argument is supported by the results obtained below.
The SA of 177Lu radioisotope produced by the 176Yb (n, γ) 177Yb (β- decay) 177Lu process as a function of the elemental and isotopic impurities of the 176Yb enriched target and the times tirr and tc is shown in Figure 4 and Figure 5. The experimental results reported in our previous publications agree well with the theoretical calculation results shown in Figure 5. The maximum SA value present on the curve D of Figure 4 shows a combined effect of 174Yb- and elemental Lu- impurities on the SA degradation. This tells us that the irradiation time should be optimized to obtain the highest SA for 177Lu produced via 176Yb (n, γ) 177Yb (β- decay) 177Lu reaction. While being the best theoretical way to produce carrier-free 177Lu, with this reaction we always obtain a 177Lu product of much lower SA due to the use of an isotopically/elementally impure target. The maximum SA value mentioned above is characterized for a specific target composition and its neutron irradiation conditions, so the theoretical assessment of SA developed in this paper is important before starting the neutron activation process. This avoids over-bombardment destroying the SA of 177Lu product and wasting expensive reactor operation time. Moreover, the post-irradiation processing time should be minimized to keep the SA as high as possible, the effect of which is shown in Figure 5.
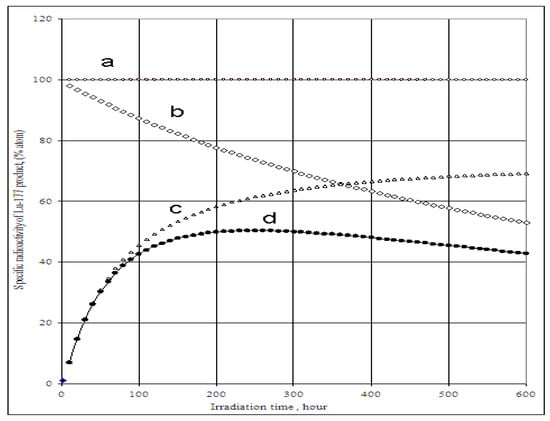
Figure 4.
Specific radioactivity of 177Lu radioisotope in the 176 Yb target vs. irradiation time and content of 174Yb- and elemental Lu- impurities.(Thermal neutron flux: 5·1013 n·cm−2·s−1, Nuclear data extracted from literatures [11]).
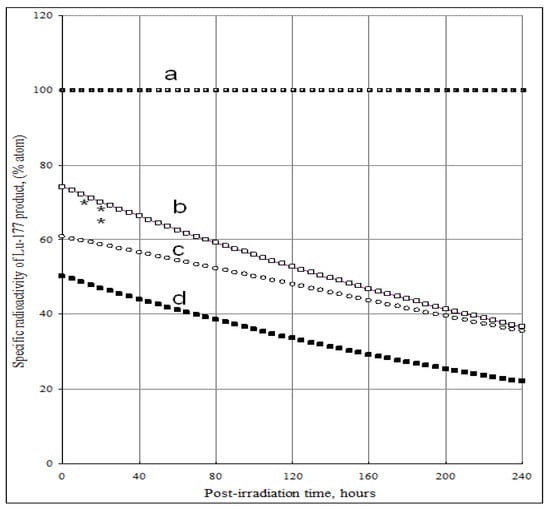
Figure 5.
Specific radioactivity of 177Lu in the 176 Yb target vs. post-irradiation time and content of 174Yb and elemental Lu impurities. (Thermal neutron flux: 5·1013 n·cm−2·s−1; Irradiation time: 240 hours; Nuclear data extracted from literatures [11]).
5. Conclusions
Several factors affect SA of the radionuclide product which can be produced either by neutron capture reaction or by neutron-capture-followed- by -radioactive transformation processes. Among them the target composition (elemental and isotopic impurities), target nuclide and produced radioisotope depression causes (including target nuclide burn-up, reaction rate of target nuclide and the decay property of produced radionuclide) and the activation or post-irradiation time are most accounted for. With the method of SA assessment of multi radioactive source system the SA of a radioisotope produced in a reactor from different targets can be evaluated. The theoretical SA assessment of a radioactive nuclide has definitely given us a firm basis to set up an optimized process for the production of clinically useful radioisotopes and to evaluate the quality of the radionuclide product. A useful computer code based on the above developed SA assessment methods can be set up for a convenient daily use in the reactor-based production of medical radioisotopes such as 177Lu, 153Sm, 169Yb, 165Dy, 153Gd... This evaluation plays a complementary or even substantial role in the quality management system regarding certifying the SA of the product which may be experimentally inaccessible due to radiation protection and instrumentation difficulties in the practical measurement of very low elemental content (<0.01 μg/mCi·μL) of a radioactive solution of very high specific volume and specific radioactivity.
Acknowledgments
The author would like to thank Australian Nuclear Science and Technology Organization for the financial support for this Project (RRI-0168). The author also acknowledges his thanks to Natalie Nha Truc Le (Cochlear Limited, PQ Box 692, Lane Cove NSW 2066, Australia) for her mathematical contribution and to Hien P.T. Do and to Tim Jackson for English revision.
References
- Knapp, F.F., Jr.; Mirzadeh, S.; Beets, A.L.; Du, M. Production of therapeutic radioisotopes in the ORNL High Flux Isotope Reactor (HFIR) for applications in nuclear medicine, oncology and interventional cardiology. J. Radioanal. Nucl. Chem. 2005, 263, 503–509. [Google Scholar] [CrossRef]
- Pillai, M.R.A.; Chakraborty, S.; Das, T.; Venkatesh, M.; Ramamoorthy, N. Production logistics of 177Lu for radionuclide therapy. Appl. Radiat. Isot. 2003, 59, 109–118. [Google Scholar] [CrossRef]
- Mirzadeh, S.; Walsh, P. Numerical evaluation of the production of radionuclides in a nuclear reactor (Part I). Appl. Radiat. Isot. 1998, 49, 379–382. [Google Scholar] [CrossRef]
- International Atomic Energy Agency. Manual for reactor produced radioisotopes, IAEA-TECDOC-1340; IAEA: Vienna, Austria, 2003; pp. 121–124. [Google Scholar]
- Dvorakova, Z.; Henkelmann, R.; Lin, X.; Turler, A.; Gerstenberg, H. Production of 177Lu at the new research reactor FRM-II: Irradiation yield of 176Lu (n, γ)177Lu. Appl. Radiat. Isot. 2008, 66, 147–151. [Google Scholar] [CrossRef] [PubMed]
- Zhernosekov, K.P.; Perego, R.C.; Dvorakova, Z.; Henkelmann, R.; Turler, A. Target burn-up corrected specific activity of 177Lu produced via of 176Lu (n, γ)177Lu nuclear reactions. Appl. Radiat. Isot. 2008, 66, 1218–1220. [Google Scholar] [CrossRef] [PubMed]
- Mikolajczak, R.; Parus, J.L.; Pawlak, D.; Zakrzewska, E.; Michalak, W.; Sasinowska, I. Reactor produced 177Lu of specific activity and purity suitable for medical applications. J. Radioanal. Nucl. Chem. 2003, 257, 53–57. [Google Scholar] [CrossRef]
- Le, V.S.; Morcos, N.; Zaw, M.; Pellegrini, P.; Greguric, I. Alternative chromatographic processes for no-carrier added 177Lu radioisotope separation. Part I. Multi-column chromatographic process for clinically applicable. J. Radioanal. Nucl. Chem. 2008, 277, 663–673. [Google Scholar]
- Le, V.S.; Morcos, N.; Zaw, M.; Pellegrini, P.; Greguric, I.; Nevissi, A. Alternative chromatographic processes for no-carrier added 177Lu radioisotope separation. Part II. The conventional column chromatographic separation combined with HPLC for high purity. J. Radioanal. Nucl. Chem. 2008, 277, 675–683. [Google Scholar]
- Trace Sciences International Inc. Certificate of Analysis #1, Jan, 2003. Trace Sciences International Corp.: Richmond Hill, ON L4B 3N6, Canada.
- Parrington, J.R.; Knox, H.D.; Breneman, S.L.; Baum, E.M.; Feiner, F. Nuclides and Isotopes, 15th ed.; KAPL, Inc. and General Electric Co. Press: California, USA, 1996; pp. 7–51. [Google Scholar]
- Rubinson, W. The equations of radioactive transformation I a neutron flux. J. Chem. Phys. 1949, 17, 542–547. [Google Scholar] [CrossRef]
- Verheijke, M.L. Relation between the Hogdahl convention and the modified Westcott formalism for (n, γ) reactions with a pure 1/vn cross-section behavior. J. Radioanal. Nucl. Chem. 2008, 183, 293–299. [Google Scholar] [CrossRef]
Sample Availability: Not available. |
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).