An Online Prediction Method for Transient Frequency Response in New Energy Grids Based on Deep Integration of WAMS Data and Physical Model
Abstract
1. Introduction
- (1)
- A physics-based frequency response analysis model incorporating the frequency regulation characteristics of multiple heterogeneous resources is developed to provide critical physical features for data-driven approaches.
- (2)
- Information entropy theory is introduced to perform quantitative assessment and adaptive weighting of physical features, thereby enhancing the contribution of critical features in the model input.
- (3)
- A physics-guided machine learning framework is proposed, which integrates the weighted physical features along with the complete frequency curve predicted by the physical model into the prediction process.
- (4)
- An MLP-GRU-Attention hybrid model is designed as the data-driven engine, and a physical consistency constraint is incorporated into the loss function, thereby ensuring that the prediction results strictly adhere to physical laws.
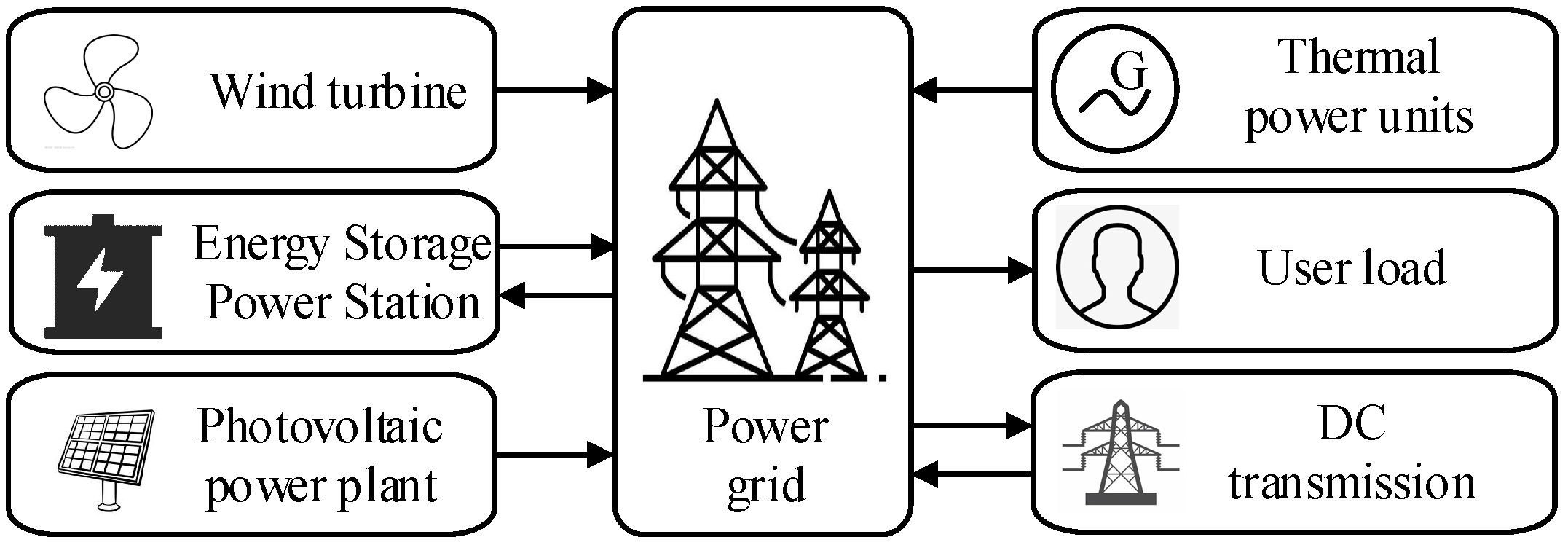
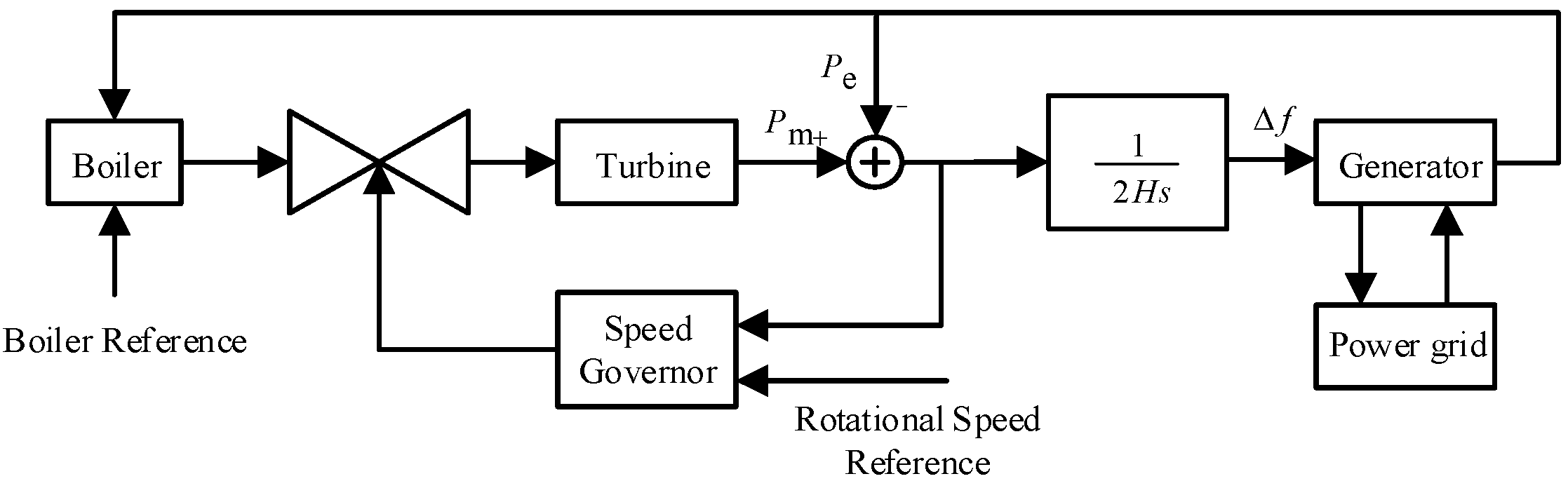
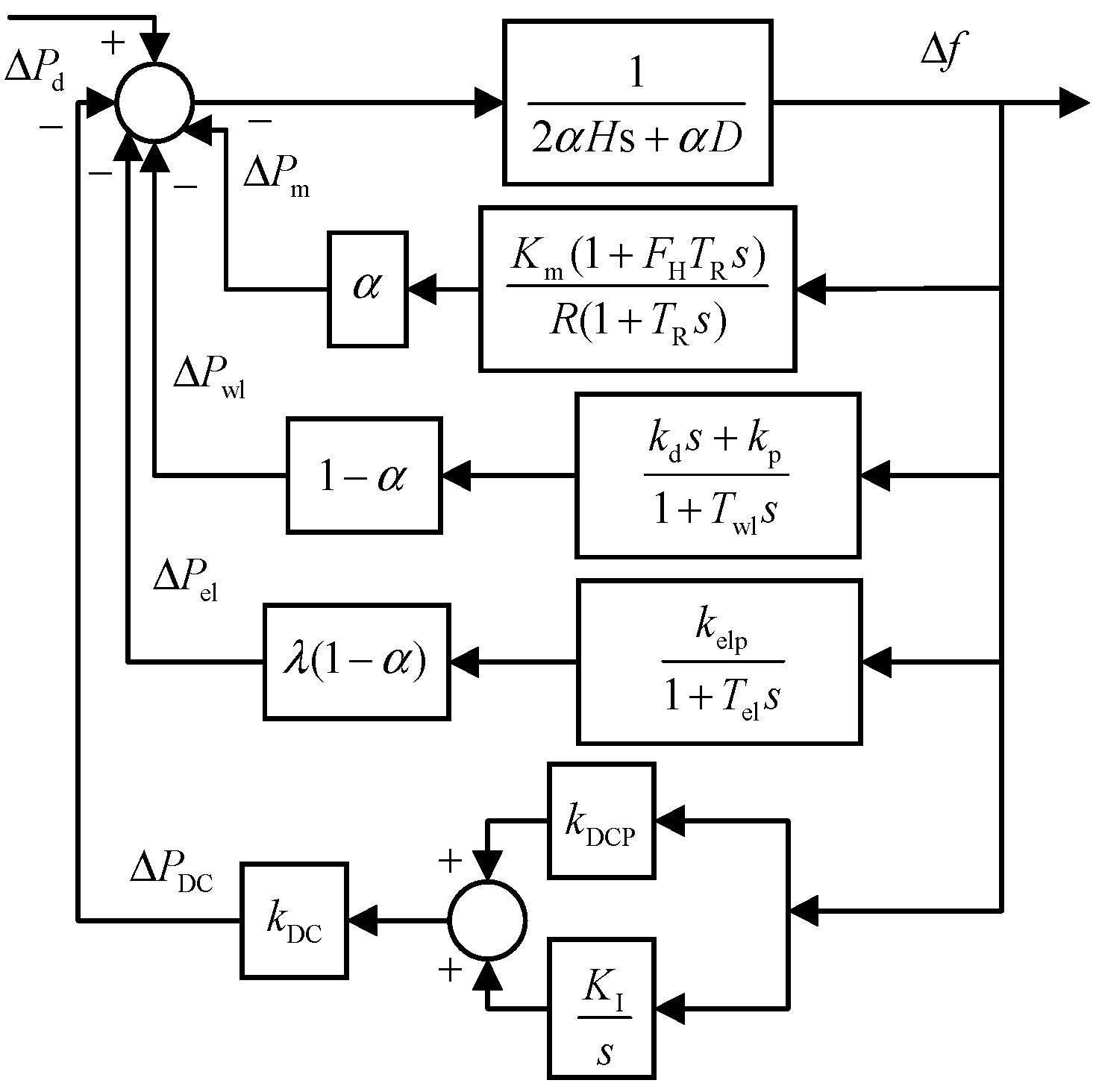
2. Physical Model Analysis of Dynamic Frequency Response in New Energy Grids
2.1. New Energy Grid Frequency Response Model
2.2. Key Characteristics of Frequency Response in New Energy Grids
3. A Frequency Prediction Architecture Integrating WAMS Information with Physical Model
3.1. Principles of the MLP-GRU-Attention Model
3.2. Information Entropy-Based Weighting Method for Physical Features
3.3. Construction of the Weighted Physical Feature Vector
4. Online Prediction Method for Transient Frequency Response Based on the Fusion of WAMS Data and Physical Model
- (1)
- Offline Training
- (2)
- Online Prediction
5. Analysis of the Algorithm
5.1. Example System
5.2. Performance Evaluation Index
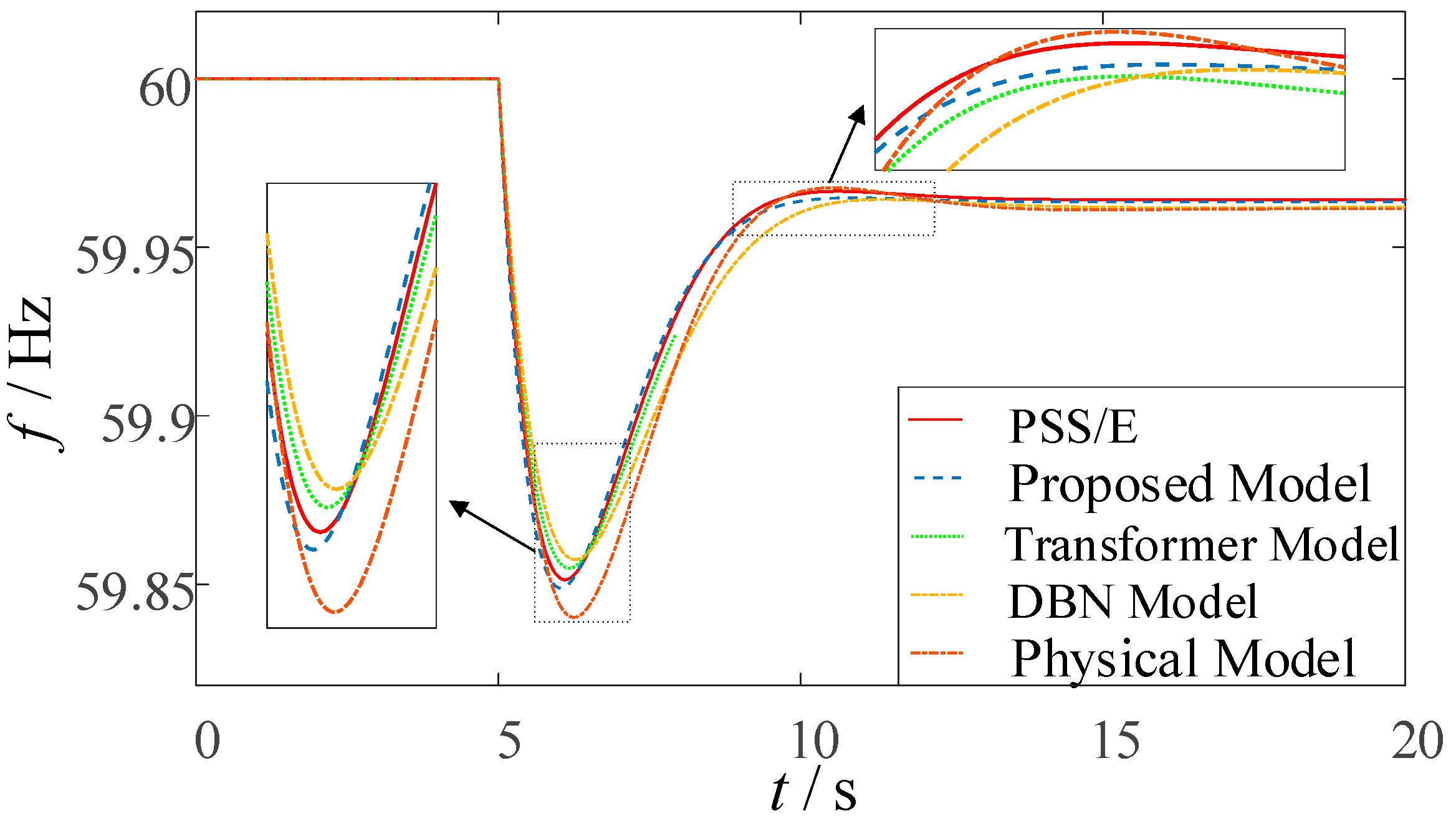
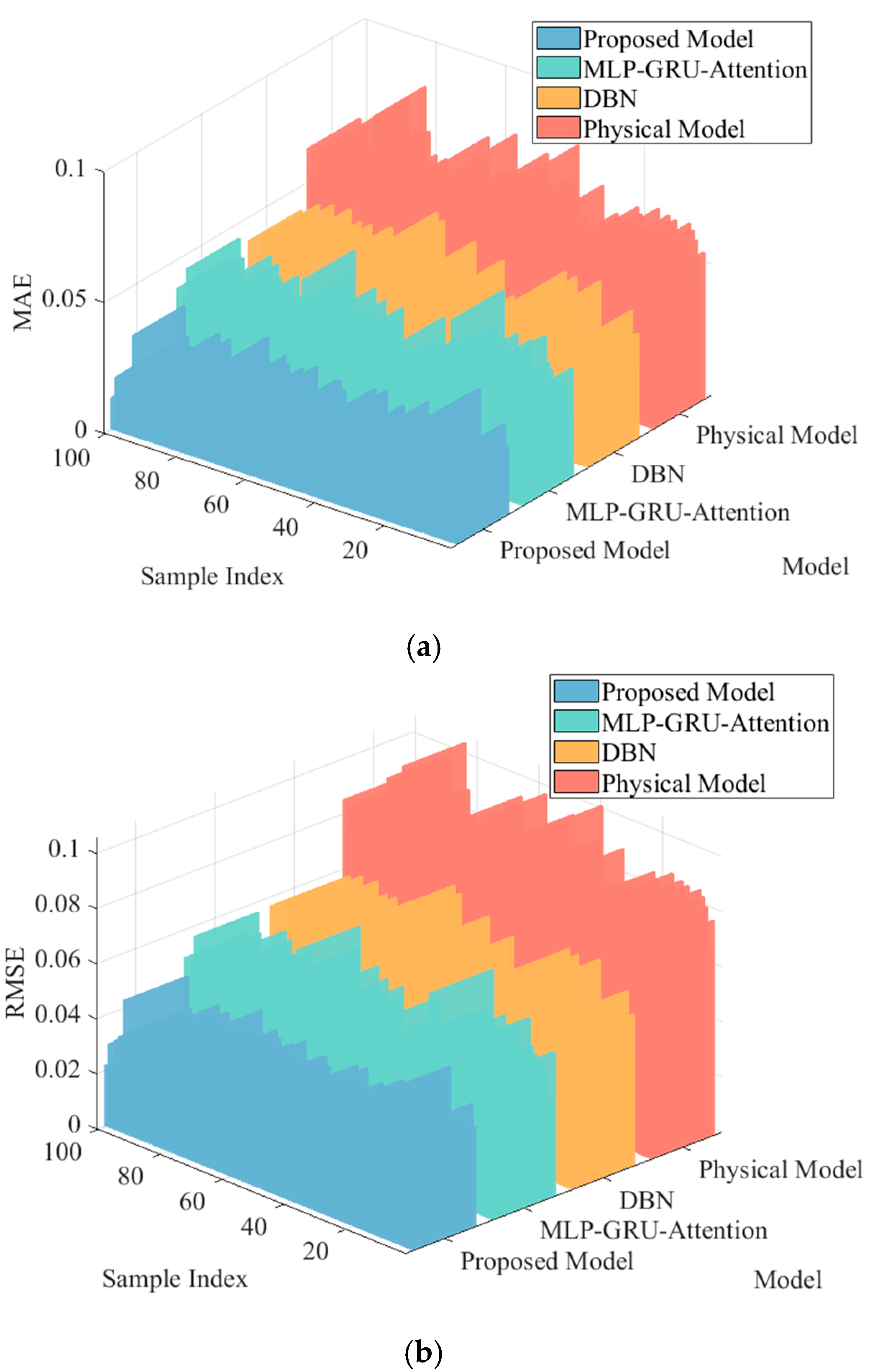
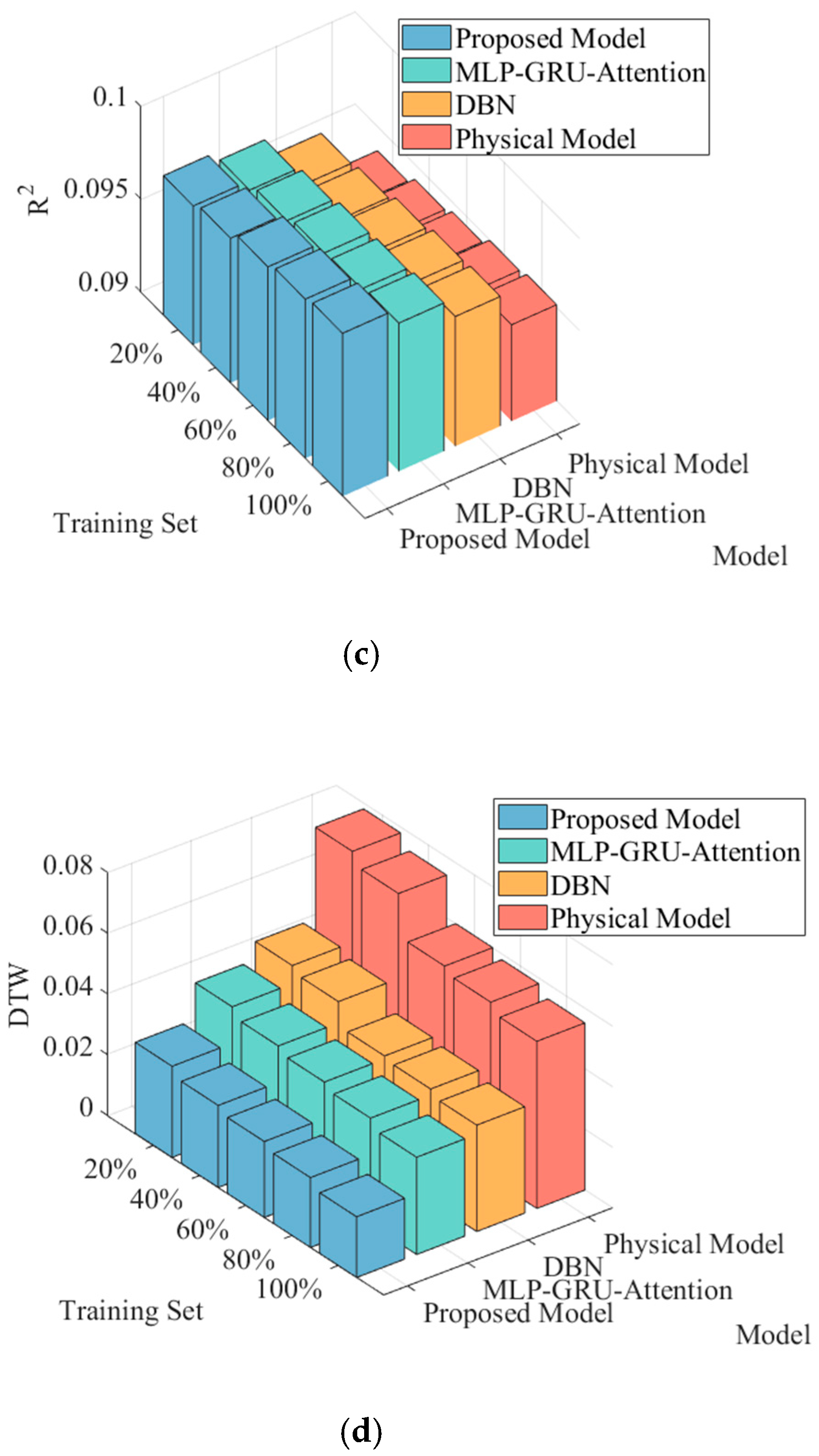
5.3. Prediction Performance Analysis
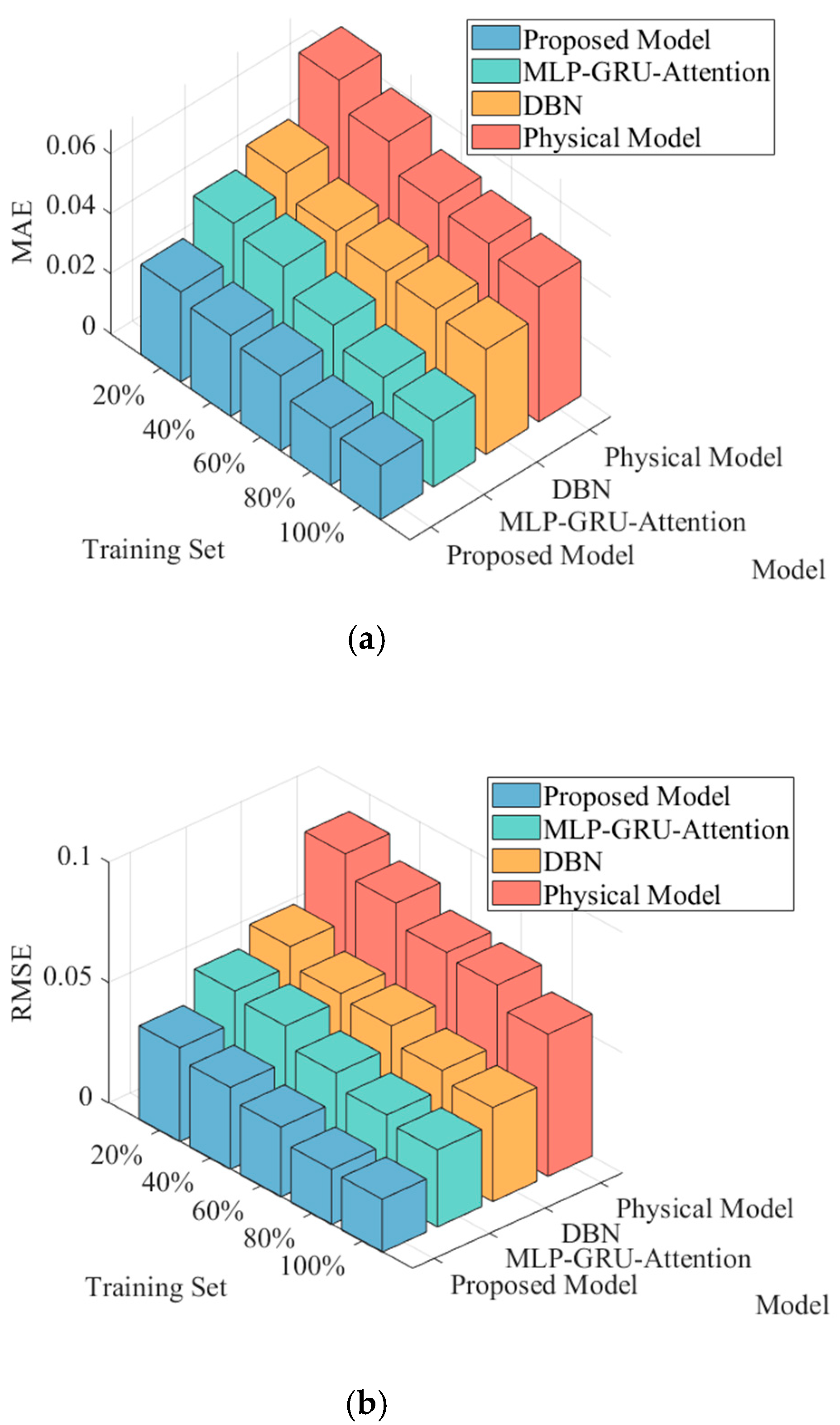
5.4. Evaluation of Model Generalization Ability for Small Samples
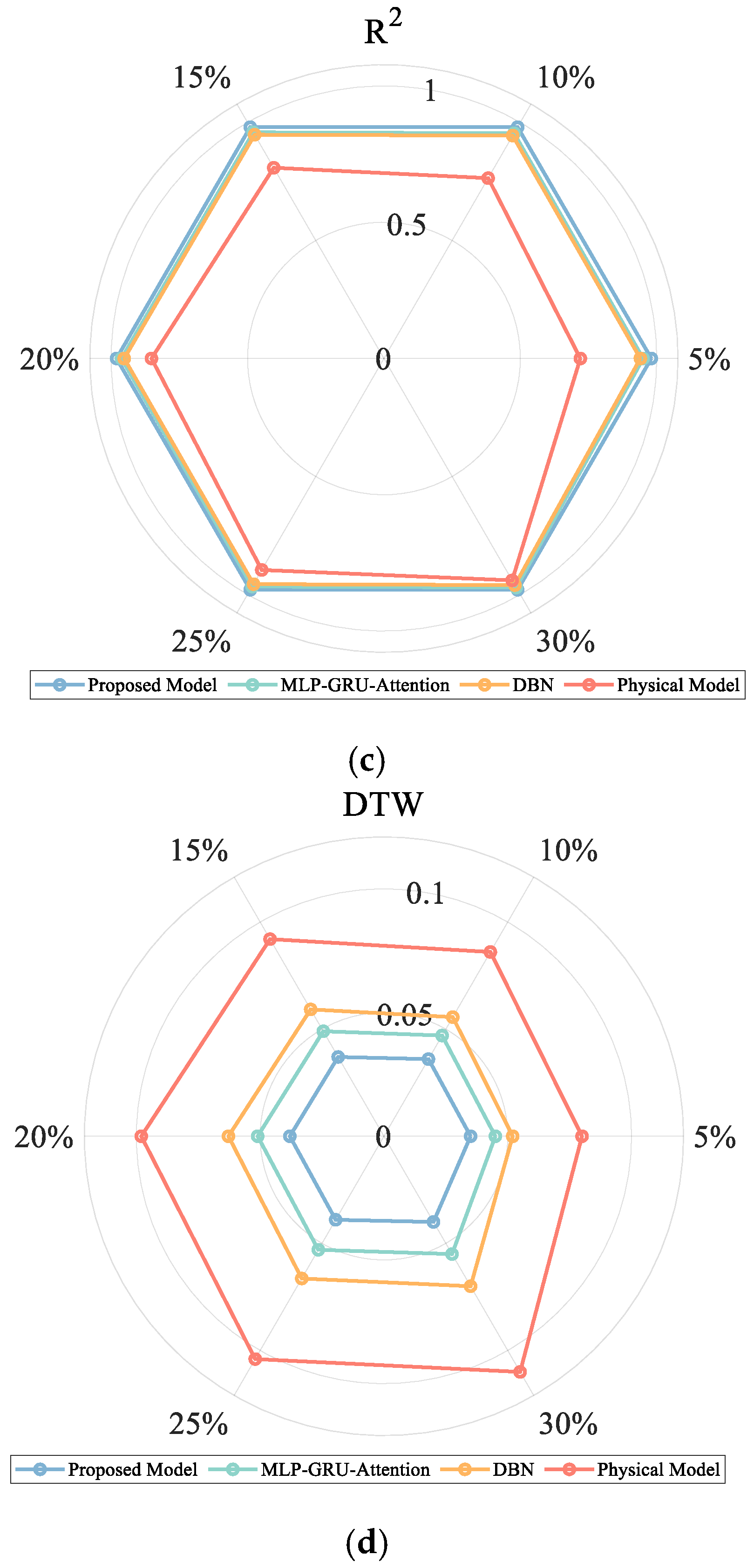
5.5. Model Noise Resistance Evaluation
6. Conclusions
- (1)
- The physics–data fusion method proposed in this paper effectively integrates the mechanistic interpretability of physical models with the high-precision learning capability of data-driven approaches through information entropy-weighted fusion of system-level key features extracted from the average frequency model and multi-bus measurement data provided by WAMS. As evidenced by simulation results, the proposed method demonstrates highly accurate reproduction of actual system frequency dynamics benchmarked against PSS/E simulations, exhibiting superior accuracy and reliability throughout the entire transient frequency response prediction process.
- (2)
- By introducing the information entropy-weighted physical feature fusion and the physics-guided machine learning framework, the generalization ability of the model under small sample conditions is significantly improved, and its applicability in extreme disturbance scenarios is enhanced.
- (3)
- The proposed method shows good robustness in the presence of WAMS measurement noise, and the embedding of physical knowledge effectively suppresses noise interference, maintains the stability and consistency of the prediction results, and provides reliable technical support for the online sensing and control of frequency security in new energy power grids.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FM | Frequency Modulation |
| SFR | System Frequency Response |
| WAMS | Wide-Area Measurement System |
| SME | Single-Machine Equivalent |
| HVDC | High Voltage Direct Current Transmission |
| RoCoF | Rate of Change of Frequency |
| UFLS | Under-Frequency Load Shedding |
| FLC | Frequency Limiting Controller |
| PI | Proportional-Integral |
| PV | Photovoltaic |
| MLP | Multilayer Perceptron |
| GRU | Gated Recurrent Unit |
| DBN | Deep Belief Network |
| RNN | Recurrent Neural Network |
| 1D-CNN | One-Dimensional Convolutional Neural Network |
| TFAM | Temporal-Feature Attention Module |
| FSPM | Frequency Security Predictor Model |
| FDL | Frequency Danger Level |
| TSM | Time Security Margin |
| LSTM | Long Short-Term Memory |
| WOA | Whale Optimization Algorithm |
| NAR | Nonlinear AutoRegressive |
| MSE | Mean Squared Error |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Square Error |
| MRE | Mean Relative Error |
| R2 | Coefficient of Determination |
| DTW | Dynamic Time Warping |
| PMU | Phasor Measurement Unit |
References
- Yu, L.; Zhang, L.; Meng, G.; Zhang, F.; Liu, W. Research on Multi-Objective Reactive Power Optimization of Power Grid with High Proportion of New Energy. IEEE Access 2022, 10, 116443–116452. [Google Scholar] [CrossRef]
- Luo, Y.; Cai, L.; Zhang, N. Doubly-Fed Pumped Storage Units Participation in Frequency Regulation Control Strategy for New Energy Power Systems Based on Model Predictive Control. Energy Eng. 2025, 122, 765–783. [Google Scholar] [CrossRef]
- Dhara, P.K.; Rather, Z.H. A Novel Approach to Determine and Maintain Area-Wise Minimum Inertia in Renewable Energy Dominated Power Systems. IEEE Trans. Sustain. Energy 2025, 16, 1084–1097. [Google Scholar] [CrossRef]
- Cao, Y.; Wu, Q.; Zhang, H.; Li, C.; Zhang, X. Chance-Constrained Optimal Configuration of BESS Considering Uncertain Power Fluctuation and Frequency Deviation Under Contingency. IEEE Trans. Sustain. Energy 2022, 13, 2291–2303. [Google Scholar] [CrossRef]
- Hao, L.; Ji, J.; Xie, D.; Wang, H.; Li, W.; Asaah, P. Scenario-based Unit Commitment Optimization for Power System with Large-scale Wind Power Participation in primary Frequency Regulation. J. Mod. Power Syst. Clean Energy 2022, 8, 1259–1267. [Google Scholar] [CrossRef]
- Alves, E.F.; Polleux, L.; Guerassimoff, G.; Korpås, M.; Tedeschi, E. Allocation of Spinning Reserves in Autonomous Grids Considering Frequency Stability Constraints and Short-Term Solar Power Variations. IEEE Access 2023, 11, 29896–29908. [Google Scholar] [CrossRef]
- Dai, D.; Liu, J. Human powered wireless charger for low-power mobile electronic devices. IEEE Trans. Consum. Electron. 2012, 58, 767–774. [Google Scholar] [CrossRef]
- Tan, D.; Novosel, D. Energy challenge, power electronics & systems (PEAS) technology and grid modernization. CPSS Trans. Power Electron. Appl. 2017, 2, 3–11. [Google Scholar] [CrossRef]
- Meng, L.; Zafar, J.; Khadem, S.K.; Collinson, A.; Murchie, K.C.; Coffele, F.; Burt, G.M. Fast Frequency Response From Energy Storage Systems—A Review of Grid Standards, Projects and Technical Issues. IEEE Trans. Smart Grid 2020, 11, 1566–1581. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, M.; Wu, Z.; Liu, S.; Guo, Z.; Li, G. A Frequency Security Constrained Scheduling Approach Considering Wind Farm Providing Frequency Support and Reserve. IEEE Trans. Sustain. Energy 2022, 13, 1086–1100. [Google Scholar] [CrossRef]
- Azman, S.K.; Isbeih, Y.J.; Moursi, M.S.E. A Unified Online Deep Learning Prediction Model for Small Signal and Transient Stability. IEEE Trans. Power Syst. 2020, 35, 4585–4598. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Zhou, G.; Wang, L.; Li, B.; Li, K. Integrating Physical and Data-Driven System Frequency Response Modelling for Wind-PV-Thermal Power Systems. IEEE Trans. 2024, 39, 217–228. [Google Scholar] [CrossRef]
- Belforte, P.; Spina, D.; Lombardi, L.; Antonini, G.; Dhaene, T. Automated Framework for Time-Domain Piecewise-Linear Fitting Method Based on Digital Wave Processing of S-Parameters. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 235–248. [Google Scholar] [CrossRef]
- Wu, F.; Qian, J.; Ju, P.; Zhang, X.; Jin, Y.; Xu, D.; Sterling, M. Transfer function based equivalent modeling method for wind farm. J. Mod. Power Syst. Clean Energy 2019, 7, 549–557. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Z.; Liu, X.; Li, W.; Li, Q.; Zhang, Y.; Chen, Q.; Guo, S.; Xu, Z. Frequency response mode prediction of power system after large disturbances based on deep belief neural network. IEEE Access 2023, 11, 113653–113666. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Li, H.; Zhou, G.; Li, B.; Wang, L.; Li, K. SFR modeling for hybrid power systems based on deep transfer learning. IEEE Trans. Ind. Inform. 2023, 20, 399–410. [Google Scholar] [CrossRef]
- Li, L.; Wu, J.; Zhao, P.; Li, B.; Shi, F.; Wang, Y. Online transient frequency safety prediction machine of power system based on time-feature attention module. IEEE Trans. Power Syst. 2022, 38, 3952–3964. [Google Scholar] [CrossRef]
- Li, X.; Xiao, N.; Peng, B.; Ai, Z.; Wang, Y. Frequency prediction after disturbance of grid-connected wind power systems based on WOA and Attention-LSTM. Energy Rep. 2023, 9, 208–216. [Google Scholar] [CrossRef]
- Ahakonye, L.A.C.; Nwakanma, C.I.; Lee, J.-M.; Kim, D.-S. Low computational cost convolutional neural network for smart grid frequency stability prediction. Internet Things 2024, 25, 101086. [Google Scholar] [CrossRef]
- Chamorro, H.R.; Orjuela-Cañón, A.D.; Ganger, D.; Persson, M.; Gonzalez-Longatt, F.; Alvarado-Barrios, L.; Sood, V.K.; Martinez, W. Data-Driven Trajectory Prediction of Grid Power Frequency Based on Neural Models. Electronics 2021, 10, 151. [Google Scholar] [CrossRef]
- Xu, L.; Li, L.; Wang, M.; Wang, X.; Li, Y.; Li, W.; Zhou, K. Online Prediction Method for Power System Frequency Response Analysis Based on Swarm Intelligence Fusion Model. IEEE Access 2023, 11, 13519–13532. [Google Scholar] [CrossRef]
- Wang, Q.; Li, F.; Tang, Y.; Xu, Y. Integrating Model-Driven and Data-Driven Methods for Power System Frequency Stability Assessment and Control. IEEE Trans. Power Syst. 2019, 34, 4557–4568. [Google Scholar] [CrossRef]
- Wang, S.; Wang, R.; Yang, J.; Hao, L. Online Incremental Dynamic Modeling Using Physics-Informed Long Short-Term Memory Networ for the Pneumatic Artificial Muscle. IEEE Robot. Autom. Lett. 2024, 9, 8435–8442. [Google Scholar] [CrossRef]
- Tan, Y.; Chen, Y.; Li, Y.; Cao, Y. Linearizing Power Flow Model: A Hybrid Physical Model-Driven and Data-Driven Approach. IEEE Trans. Power Syst. 2020, 35, 2475–2478. [Google Scholar] [CrossRef]
- Remon, D.; Cantarellas, A.M.; Rodriguez, P. Equivalent Model of Large-Scale Synchronous Photovoltaic Power Plants. IEEE Trans. Ind. Appl. 2016, 52, 5029–5040. [Google Scholar] [CrossRef]
- Yang, L.; Zhou, N.; Zhou, G.; Chi, Y.; Chen, N.; Wang, L.; Wang, Q.; Chang, D. Day-ahead Optimal Dispatch Model for Coupled System Considering Ladder-type Ramping Rate and Flexible Spinning Reserve of Thermal Power Units. J. Mod. Power Syst. Clean Energy 2022, 10, 1482–1493. [Google Scholar] [CrossRef]
- Sun, M.; Min, Y.; Chen, L. Optimal auxiliary frequency control of wind turbine generators and coordination with synchronous generators. CSEE J. Power Energy Syst. 2021, 7, 78–85. [Google Scholar]
- Kakimoto, N.; Takayama, S.; Satoh, H. Power Modulation of Photovoltaic Generator for Frequency Control of Power System. IEEE Trans. Energy Convers. 2009, 24, 943–949. [Google Scholar] [CrossRef]
- Hoke, A.F.; Shirazi, M.; Chakraborty, S. Rapid Active Power Control of Photovoltaic Systems for Grid Frequency Support. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1154–1163. [Google Scholar] [CrossRef]
- Muyeen, S.M.; Takahashi, R.; Tamura, J. Operation and Control of HVDC-Connected Offshore Wind Farm. IEEE Trans. Sustain. Energy 2010, 1, 30–37. [Google Scholar] [CrossRef]
- Dai, J.; Tang, Y.; Wang, Q.; Jiang, P. Aggregation Frequency Response Modeling for Wind Power Plants with Primary Frequency Regulation Service. IEEE Access 2019, 7, 108561–108570. [Google Scholar] [CrossRef]
- Zhang, B.; Xiong, D.; Xie, J.; Su, J. Neural Machine Translation with GRU-Gated Attention Model. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4688–4698. [Google Scholar] [CrossRef]
- Hasanat, S.M.; Ullahet, K.; Yousafal, H.; Munir, K.; Abid, S.; Bokhari, S.A.S.; Aziz, M.M.; Naqvi, S.F.M.; Ullah, Z. Enhancing Short-Term Load Forecasting with a CNN-GRU Hybrid Model: A Comparative Analysis. IEEE Access 2024, 12, 184132–184141. [Google Scholar] [CrossRef]
- Chen, W.; Zhou, H.; Cheng, L.; Xia, M. Wind Turbine Blade Icing Diagnosis Using Convolutional LSTM-GRU with Improved African Vultures Optimization. IEEE Open J. Instrum. Meas. 2022, 1, 1–9. [Google Scholar] [CrossRef]
- Yang, J.; He, H.; Zhao, X.; Wang, J.; Yao, T.; Cao, H.; Wan, M. Day-Ahead PV Power Forecasting Model Based on Fine-Grained Temporal Attention and Cloud-Coverage Spatial Attention. IEEE Trans. Sustain. Energy 2024, 15, 1062–1073. [Google Scholar] [CrossRef]
- Bian, J.; Wang, L.; Scherer, R.; Wozniak, M.; Zhang, P.; Wei, W. Abnormal Detection of Electricity Consumption of User Based on Particle Swarm Optimization and Long Short Term Memory with the Attention Mechanism. IEEE Access 2021, 34, 1653–1656. [Google Scholar] [CrossRef]

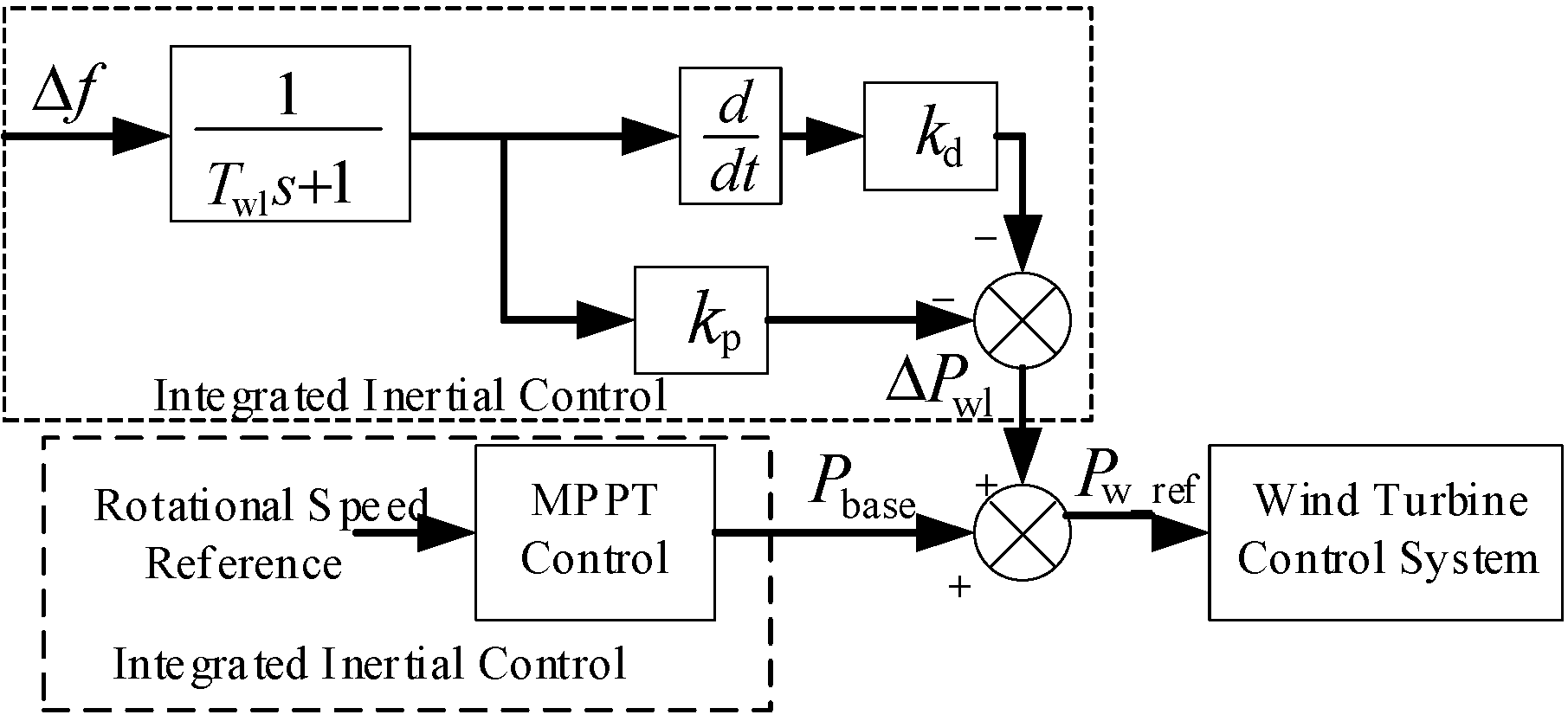

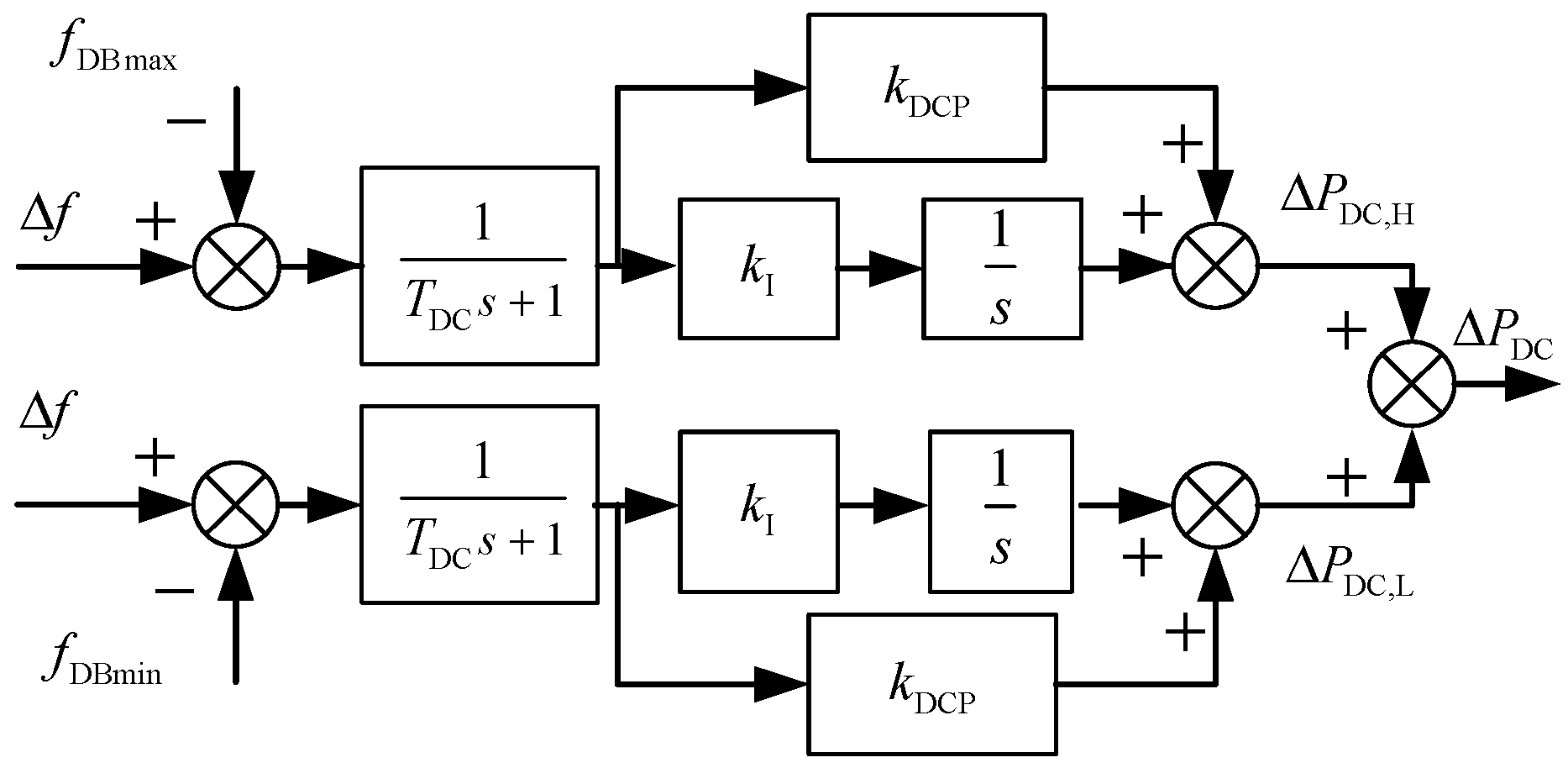





| Control Measures | Auxiliary Power Transfer Function |
|---|---|
| Synchronous Generator Governor | |
| Virtual Inertia Control for Fans | |
| Photovoltaic and Energy Storage Droop Control | |
| DC Transmission FLC |
| Methodologies | Initial Frequency Rate of Change (Hz/s) | Minimum Frequency (Hz) | Minimum Frequency Arrival Time (s) | Steady State Frequency (Hz) | ||||
|---|---|---|---|---|---|---|---|---|
| AE | AE | AE | AE | |||||
| Methodology of this paper | 0.124 | 0.004 | 59.849 | 0.003 | 6.02 | 0.07 | 59.963 | 0.001 |
| MLP-GRU-Attention modeling approach | 0.111 | 0.009 | 59.859 | 0.007 | 6.17 | 0.08 | 59.959 | 0.005 |
| DBN modeling approach | 0.116 | 0.004 | 58.864 | 0.012 | 6.30 | 0.21 | 59.962 | 0.002 |
| physical model | 0.131 | 0.011 | 59.836 | 0.016 | 6.31 | 0.22 | 59.961 | 0.003 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, K.; Hu, Y.; Xu, H.; Huang, T.; Long, Y.; Wang, T. An Online Prediction Method for Transient Frequency Response in New Energy Grids Based on Deep Integration of WAMS Data and Physical Model. Entropy 2025, 27, 1145. https://doi.org/10.3390/e27111145
Yan K, Hu Y, Xu H, Huang T, Long Y, Wang T. An Online Prediction Method for Transient Frequency Response in New Energy Grids Based on Deep Integration of WAMS Data and Physical Model. Entropy. 2025; 27(11):1145. https://doi.org/10.3390/e27111145
Chicago/Turabian StyleYan, Kailin, Yi Hu, Han Xu, Tao Huang, Yang Long, and Tao Wang. 2025. "An Online Prediction Method for Transient Frequency Response in New Energy Grids Based on Deep Integration of WAMS Data and Physical Model" Entropy 27, no. 11: 1145. https://doi.org/10.3390/e27111145
APA StyleYan, K., Hu, Y., Xu, H., Huang, T., Long, Y., & Wang, T. (2025). An Online Prediction Method for Transient Frequency Response in New Energy Grids Based on Deep Integration of WAMS Data and Physical Model. Entropy, 27(11), 1145. https://doi.org/10.3390/e27111145






