ADP-Based Fault-Tolerant Control with Stability Guarantee for Nonlinear Systems
Abstract
1. Introduction
- (1)
- A stability-aware weight update mechanism with an auxiliary stabilizing term is proposed to evaluate real-time system stability and correct the learning process of the critic NN, which ensures the system stability in the absence of the initial stabilizing control.
- (2)
- By designing a fault observer, the unknown actuator fault is estimated accurately and compensated based on the nominal optimal control, thereby eliminating the influence of the actuator fault.
2. Problem Statement and Preliminaries
2.1. Problem Formulation
2.2. Nominal Optimal Control
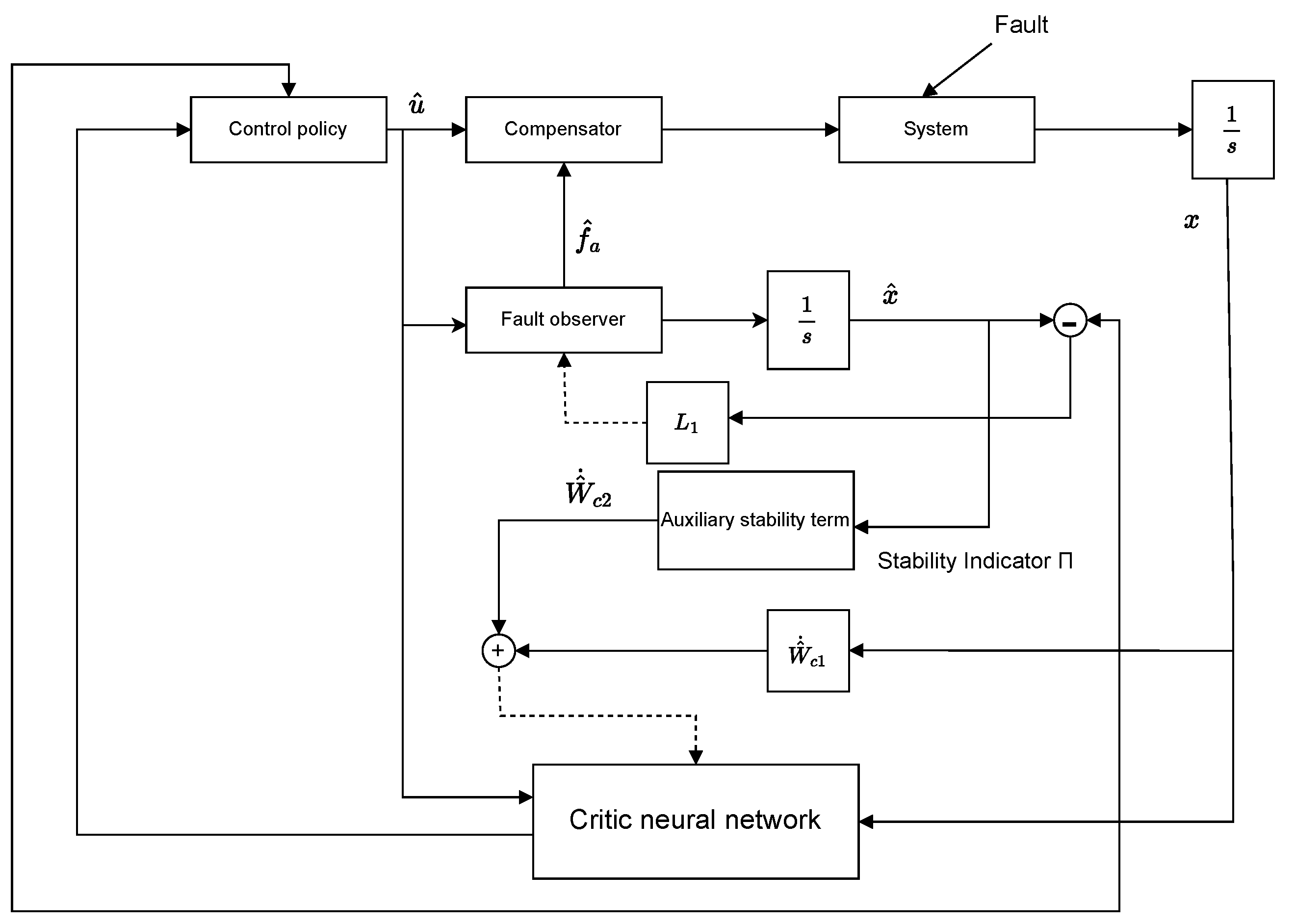
3. Stability-Guaranteed ADP-Based FTC Without IAP
3.1. Fault Observer Design
3.2. Nominal Optimal Control via Critic Neural Network
3.3. Stability-Aware Weight Update Mechanism
3.4. Fault Compensation Design
3.5. Stability Analysis
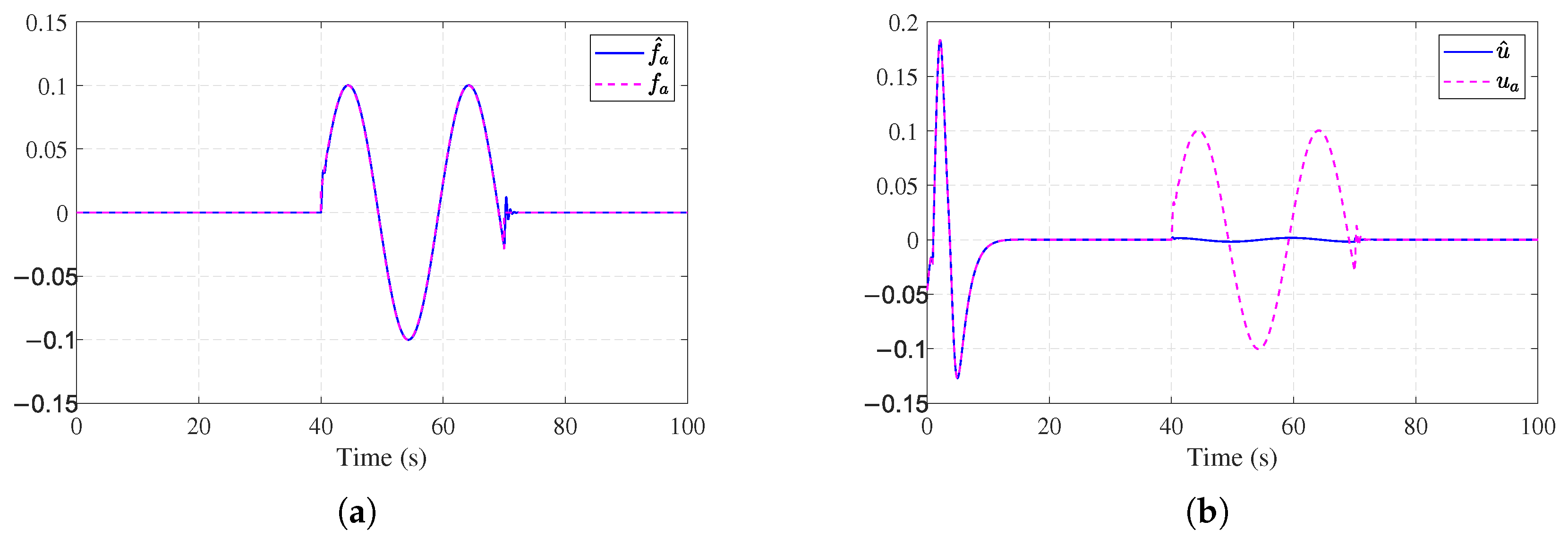
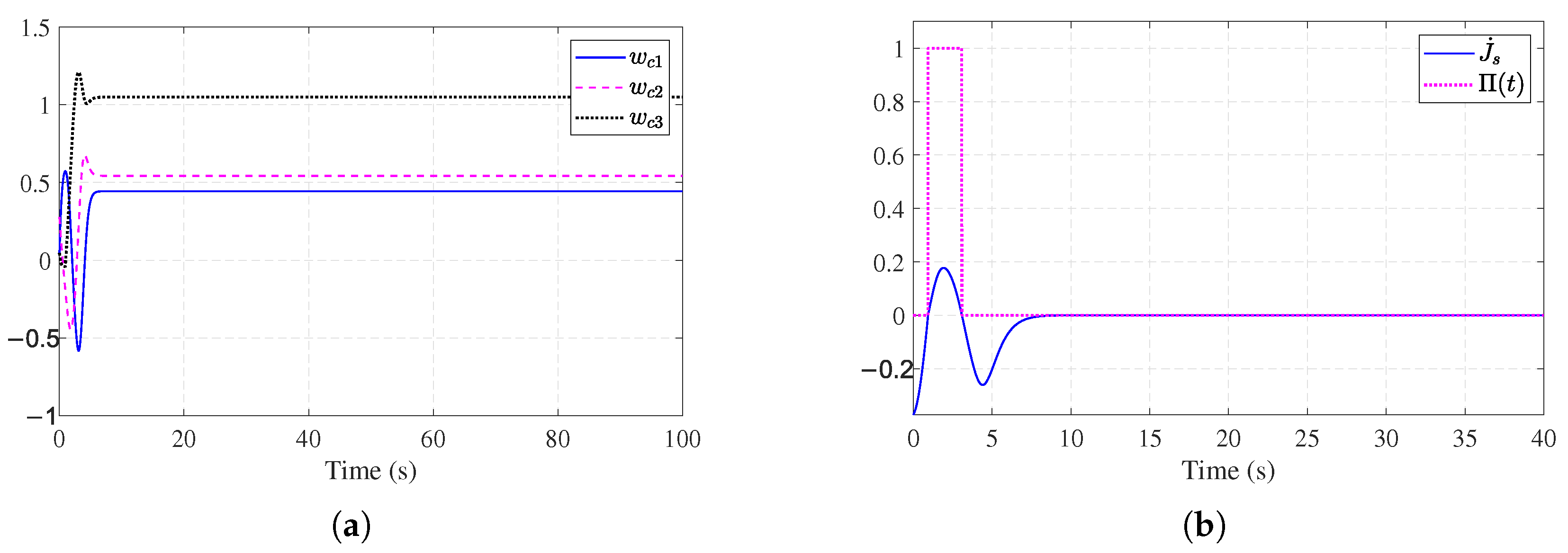
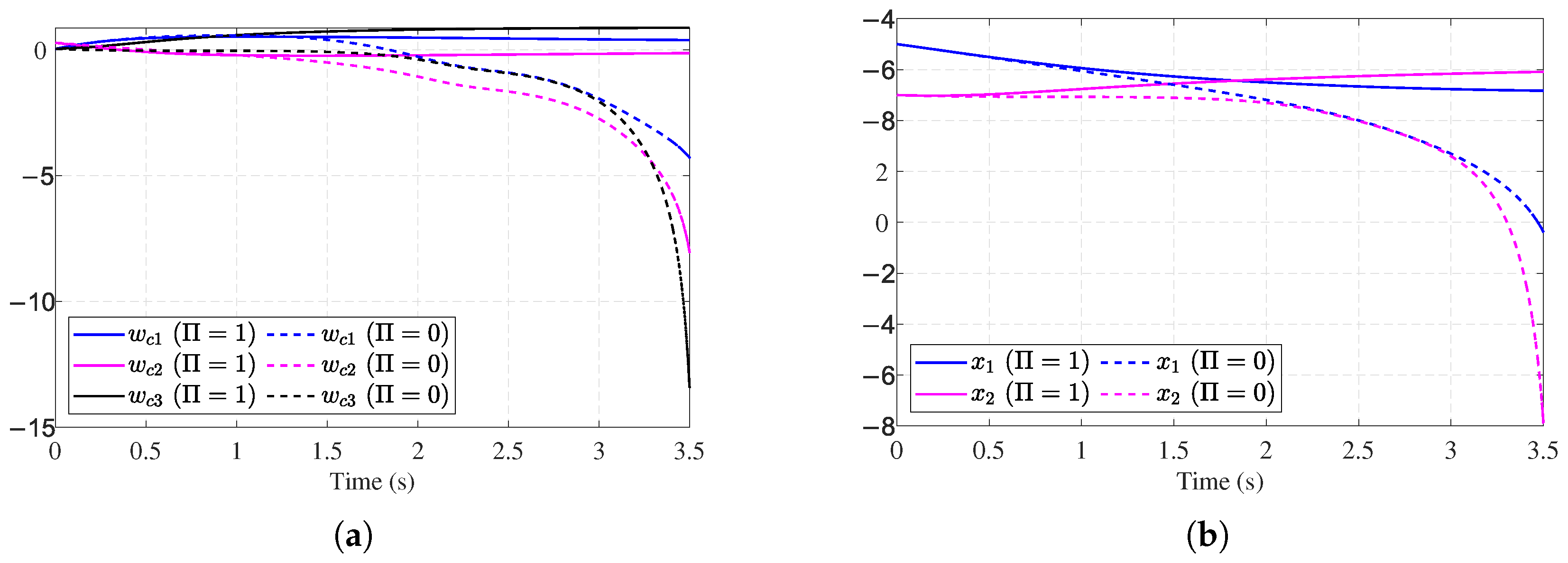
4. Simulation
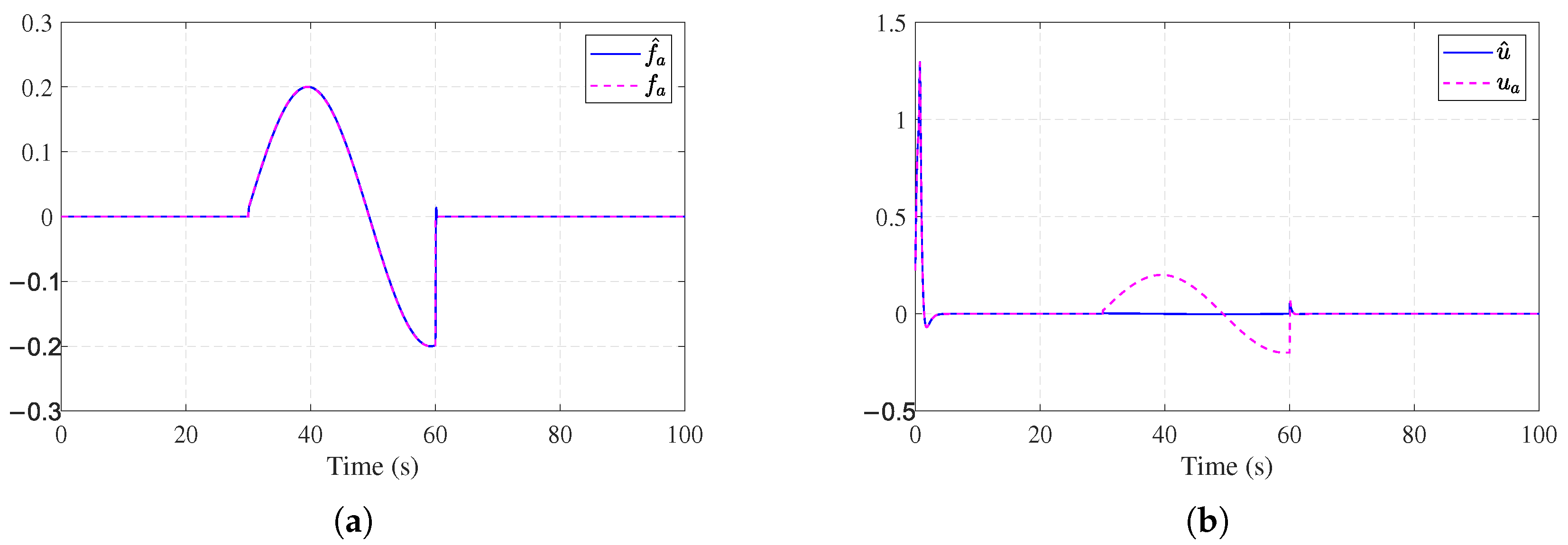
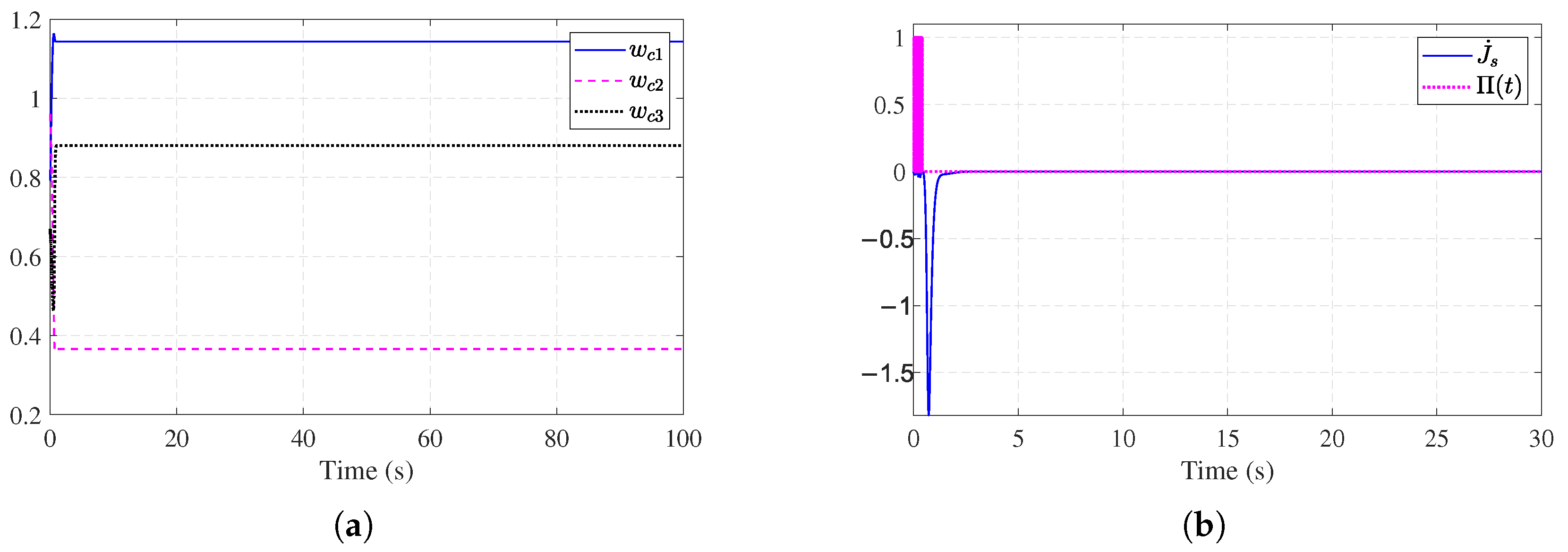
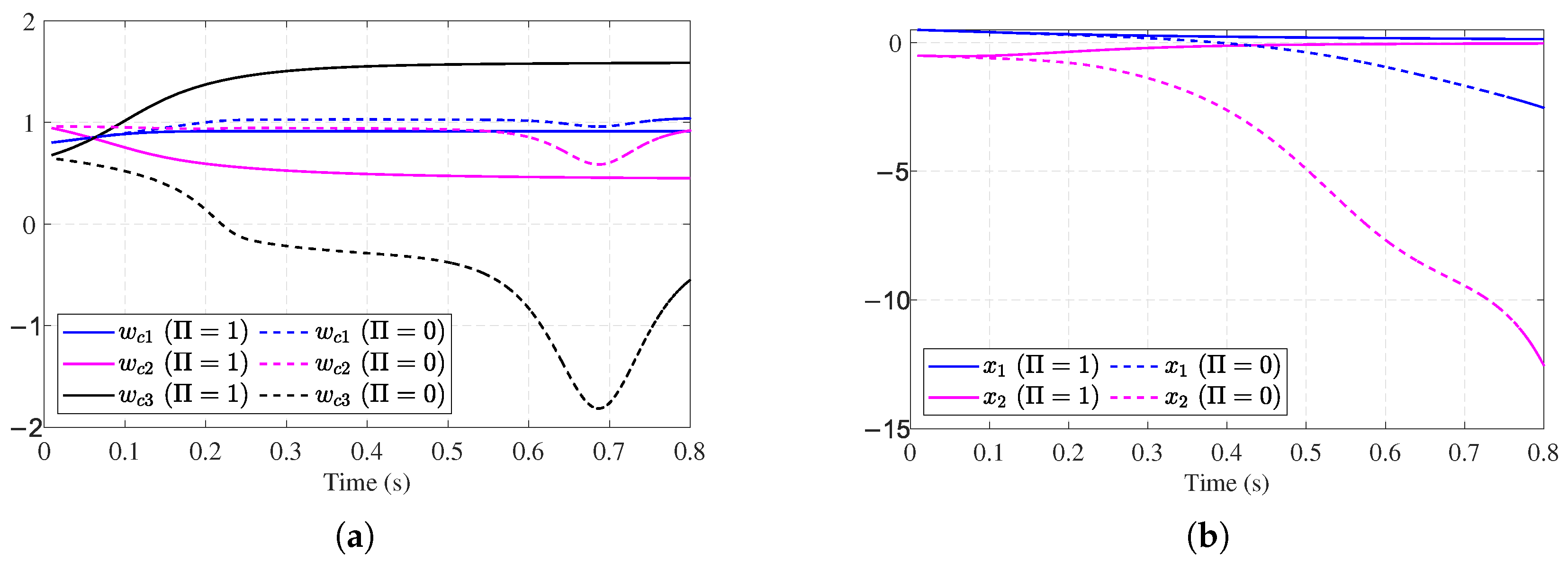
4.1. Example 1
4.2. Example 2
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, Z.; Liu, G.; Zhou, M. A robust mean-field actor-critic reinforcement learning against adversarial perturbations on agent states. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 14370–14381. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, H.; Sun, J.; Yue, X. ADP-based fault-tolerant control for multiagent systems with semi-Markovian jump parameters. IEEE Trans. Cybern. 2024, 54, 5952–5962. [Google Scholar] [CrossRef] [PubMed]
- Mu, C.; Wang, K. Aperiodic adaptive control for neural-network-based nonzero-sum differential games: A novel event-triggering strategy. ISA Trans. 2019, 92, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Ding, D.; Dong, H.; Zhang, X.-M. Neural-network-based control for discrete-time nonlinear systems with input saturation under stochastic communication protocol. IEEE/CAA J. Autom. Sin. 2021, 8, 766–778. [Google Scholar] [CrossRef]
- Xiao, G.; Zhang, H. Convergence analysis of value iteration adaptive dynamic programming for continuous-time nonlinear systems. IEEE Trans. Cybern. 2024, 54, 1639–1650. [Google Scholar] [CrossRef]
- Ha, M.; Wang, D.; Liu, D. Novel discounted adaptive critic control designs with accelerated learning formulation. IEEE Trans. Cybern. 2024, 54, 3003–3016. [Google Scholar] [CrossRef]
- Duan, J.; Li, J.; Ge, Q.; Li, S.E.; Bujarbaruah, M.; Ma, F. Relaxed actor-critic with convergence guarantees for continuous-time optimal control of nonlinear systems. IEEE Trans. Intell. Veh. 2023, 8, 3299–3313. [Google Scholar] [CrossRef]
- Luo, B.; Yang, H.; Wu, H.-N.; Huang, T. Balancing value iteration and policy iteration for discrete-time control. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 3948–3958. [Google Scholar] [CrossRef]
- Guo, Z.; Yao, D.; Bai, W.; Li, H.; Lu, R. Event-triggered guaranteed cost fault-tolerant optimal tracking control for uncertain nonlinear system via adaptive dynamic programming. Int. J. Robust Nonlinear Control 2021, 31, 2572–2592. [Google Scholar] [CrossRef]
- Teng, J.; Li, C.; Feng, Y.; Yang, T.; Zhou, R. Adaptive observer based fault tolerant control for sensor and actuator faults in wind turbines. Sensors 2021, 21, 8170. [Google Scholar] [CrossRef]
- Sheng, N.; Liu, Y.; Chi, R. Adaptive observer-based finite-time fault tolerant control for non-strict feedback systems. J. Syst. Sci. Complex. 2024, 37, 1526–1544. [Google Scholar] [CrossRef]
- Vazquez Trejo, J.A.; Ponsart, J.-C.; Adam-Medina, M.; Valencia-Palomo, G.; Vazquez Trejo, J.A.; Theilliol, D. Distributed observer-based fault-tolerant leader-following control of multi-agent systems. IFAC-PapersOnLine 2022, 55, 209–221. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, T.; Lin, Z.; Zhao, Z.; Zhang, X. Actuator fault tolerant control of variable cycle engine using sliding mode control scheme. Actuators 2021, 10, 24. [Google Scholar] [CrossRef]
- Du, Z.; Li, J.; Ye, H.; Li, J. Integral sliding mode control for nonlinear networked cascade control systems with multiple delays. J. Frankl. Inst. 2025, 362, 107680. [Google Scholar] [CrossRef]
- Liu, C.; Jiang, B.; Patton, R.J.; Zhang, K. Decentralized output sliding-mode fault-tolerant control for heterogeneous multiagent systems. IEEE Trans. Cybern. 2020, 50, 4934–4945. [Google Scholar] [CrossRef]
- Yan, W.; Tu, H.; Qin, P.; Zhao, T. Interval type-II fuzzy fault-tolerant control for constrained uncertain 2-DOF robotic multi-agent systems with active fault detection. Sensors 2023, 23, 4836. [Google Scholar] [CrossRef]
- Sun, K.; Ma, Z.; Dong, G.; Gong, P. Adaptive fuzzy fault-tolerant control of uncertain fractional-order nonlinear systems with sensor and actuator faults. Fractal Fract. 2023, 7, 862. [Google Scholar] [CrossRef]
- Zhai, D.; Xi, C.; Dong, J.; Zhang, Q. Adaptive fuzzy fault-tolerant tracking control of uncertain nonlinear time-varying delay systems. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 1840–1849. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, B.; Liu, D. Fault tolerant tracking control for nonlinear systems with actuator failures through particle swarm optimization-based adaptive dynamic programming. Appl. Soft Comput. 2020, 97, 106766. [Google Scholar] [CrossRef]
- Zeng, C.; Zhao, B.; Liu, D. Fault tolerant control for a class of nonlinear systems with multiple faults using neuro-dynamic programming. Neurocomputing 2023, 553, 126502. [Google Scholar] [CrossRef]
- Rahimi, F. Adaptive dynamic programming-based fault tolerant control for nonlinear time-delay systems. Chaos Solit. Fractals 2024, 188, 115544. [Google Scholar] [CrossRef]
- Rahimi, F. Fault-tolerant control for nonlinear time-delay systems using neural network observers. Int. J. Dyn. Control 2025, 13, 33. [Google Scholar] [CrossRef]
- Guo, Z.; Zhou, Q.; Ren, H.; Ma, H.; Li, H. ADP-based fault-tolerant consensus control for multiagent systems with irregular state constraints. Neural Netw. 2024, 180, 106737. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Li, T.; Yang, Y.; Tong, S.; Chen, C.L.P. Simplified ADP for event-triggered control of multiagent systems against FDI attacks. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 4672–4685. [Google Scholar] [CrossRef]
- Lin, H.; Zhao, B.; Liu, D.; Alippi, C. Data-based fault tolerant control for affine nonlinear systems through particle swarm optimized neural networks. IEEE/CAA J. Autom. Sin. 2020, 7, 954–964. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Li, S.; Luo, X.; Guan, X. Off-policy reinforcement-learning-based fault-tolerant H∞ control for topside separation systems with time-varying uncertainties. ISA Trans. 2025, 156, 11–19. [Google Scholar] [CrossRef]
- Wang, D.; Hu, L.; Li, X.; Qiao, J. Online fault-tolerant tracking control with adaptive critic for nonaffine nonlinear systems. IEEE/CAA J. Autom. Sin. 2025, 12, 215–227. [Google Scholar] [CrossRef]
- Wu, Q.; Zhao, B.; Liu, D.; Polycarpou, M. Event-triggered adaptive dynamic programming for decentralized tracking control of input constrained unknown nonlinear interconnected systems. Neural Netw. 2023, 157, 336–349. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, T.; Zhao, Y.; Yu, S.; Zhou, F. Adaptive dynamic programming-based multi-fault tolerant control of reconfigurable manipulator with input constraint. Complex Intell. Syst. 2024, 10, 8341–8353. [Google Scholar] [CrossRef]
- Zhao, B.; Liu, D.; Li, Y. Observer based adaptive dynamic programming for fault tolerant control of a class of nonlinear systems. Inf. Sci. 2017, 384, 21–33. [Google Scholar] [CrossRef]
- Wang, D.; Liu, D.; Mu, C.; Zhang, Y. Neural Network Learning and Robust Stabilization of Nonlinear Systems With Dynamic Uncertainties. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 1342–1351. [Google Scholar] [CrossRef]
- Ren, H.; Zhang, C.; Ma, H.; Li, H. Cloud-based distributed group asynchronous consensus for switched nonlinear cyber-physical systems. IEEE Trans. Ind. Inform. 2025, 21, 693–701. [Google Scholar] [CrossRef]
- Ma, H.; Zhou, Q.; Ren, H.; Wang, Z. Distributed estimator-based fuzzy containment control for nonlinear multiagent systems with deferred constraints. IEEE Trans. Fuzzy Syst. 2025, 33, 2074–2083. [Google Scholar] [CrossRef]
- Du, Z.; Di, M.; Li, C.; Ye, H.; Li, J. Improved event-triggered controller design for nonlinear networked cascade control system under cyber attacks. Nonlinear Dyn. 2025. [Google Scholar] [CrossRef]

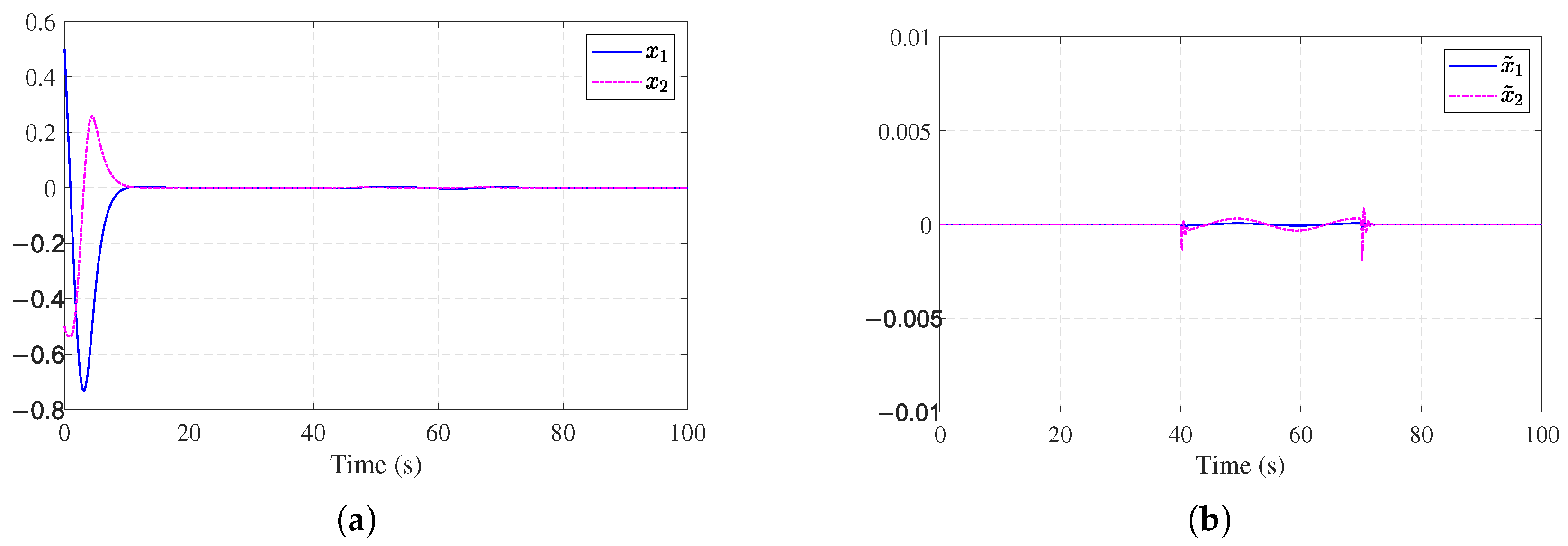
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Lv, J.; Lin, H.; Zhan, R.; Wu, L. ADP-Based Fault-Tolerant Control with Stability Guarantee for Nonlinear Systems. Entropy 2025, 27, 1028. https://doi.org/10.3390/e27101028
Liu L, Lv J, Lin H, Zhan R, Wu L. ADP-Based Fault-Tolerant Control with Stability Guarantee for Nonlinear Systems. Entropy. 2025; 27(10):1028. https://doi.org/10.3390/e27101028
Chicago/Turabian StyleLiu, Luojia, Junhong Lv, Haowei Lin, Ruidian Zhan, and Liming Wu. 2025. "ADP-Based Fault-Tolerant Control with Stability Guarantee for Nonlinear Systems" Entropy 27, no. 10: 1028. https://doi.org/10.3390/e27101028
APA StyleLiu, L., Lv, J., Lin, H., Zhan, R., & Wu, L. (2025). ADP-Based Fault-Tolerant Control with Stability Guarantee for Nonlinear Systems. Entropy, 27(10), 1028. https://doi.org/10.3390/e27101028




