Logical Entropy of Information Sources

Abstract

In this paper, we present the concept of the logical entropy of order m, logical mutual information, and the logical entropy for information sources. We found upper and lower bounds for the logical entropy of a random variable by using convex functions. We show that the logical entropy of the joint distributions $X_1$ and $X_2$ is always less than the sum of the logical entropy of the variables $X_1$ and $X_2$. We define the logical Shannon entropy and logical metric permutation entropy to an information system and examine the properties of this kind of entropy. Finally, we examine the amount of the logical metric entropy and permutation logical entropy for maps.

1. Introduction and Basic Notions

Entropy is an influential quantity that has been explored in a wide range of studies, from applied to physical sciences. In the 19th century, Carnot and Clausius diversified the concept of entropy into three main directions—entropy associated with heat engines (where it behaves similar to a thermal charge), statistical entropy, and (according to Boltzmann and Shannon) entropy in communications channels and information security. Thus, the theory of entropy plays a key role in mathematics, statistics, dynamical systems (where complexity is mostly measured by entropy), information theory [1], chemistry [2], and physics [3] (see also [4,5,6]).

In recent years, other information source entropies have been studied [7,8,9]. Butt et al. in [10,11] introduced new bounds for Shannon, relative, and Mandelbrot entropies via interpolating polynomials. Amig and colleagues defined entropy as a random process and the permutation entropy of a source [1,12].

Ellerman [13] was the first to take credit for introducing a detailed introduction to the concept of logical entropy and establishing its relationship with the renowned Shannon entropy. In recent years, many researchers have focused on extending the notion of logical entropy in new directions/perspectives. Markechová et al. [14] proposed the study of logical entropy and logical mutual information of experiments in the intuitionistic fuzzy case. Ebrahimzadeh [15] proposed the logical entropy of a quantum dynamical system and investigated its ergodic properties. However, the logical entropy of a fuzzy dynamical system was investigated in [7] (see also [16]). Tamir et al. [17] extended the idea of logical entropy over the quantum domain and expressed it in terms of the density matrix. In [18], Ellerman defined logical conditional entropy and logical relative entropy. In fact, logical entropy is a particular case of Tsallis entropy when $q=2$. Logical entropy resembles the information measure introduced by Brukner and Zeilinger [19]. In [13], Ellerman introduced the concept of logical entropy for a random variable. He studied the logical entropy of the joint distribution $p(x,y)$ over $X\times Y$ as:

$$\begin{array}{c}\hfill h(x,y)=1-\sum _{x,y}{\left[p(x,y)\right]}^2.\end{array}$$

The motive of this study was to extend the concept of logical entropy presented in [13] to information sources. Since estimating entropy from the information source can be difficult [20], we defined the logical metric permutation entropy of a map and used it to apply for an information source.

In the article, $(\Gamma ,\mathcal{G},\mu )$ is a measurable probability space (i.e., $\Gamma \ne \varnothing$ and $\mathcal{G}$ enjoys the structure of $\sigma$-algebra of subsets of $\Gamma$ with $\mu (\Gamma )=1$). Further, if X is a random variable of $\Gamma$ possessing discrete finite state space $A=\{a_1,\dots ,a_n\}$, then the function $p:A\to [0,1]$ defined by

$$\begin{array}{c}\hfill p(x)=\mu \{\gamma \in \Gamma :X(\gamma )=x\}\end{array}$$

is a probability function. $H_{\mu }(X)=-{\sum }_{x\in A}p(x)logp(x)$ denotes the Shannon entropy of X [1]. If ${(X_n)}_{n=1}^{\infty }$ is a sequence of the random variables on $\Gamma$, the sequence $X_n$ is called an information source (also called the stochastic process [$\mathbf{S}.\mathbf{P}$]). Similarly, if $m\ge 1$, then we define $p:A^m\to [0,1]$ by

$$\begin{array}{c}\hfill p(x_1,\dots ,x_m)=\mu \left\{\gamma \in \Gamma :X_1(\gamma )=x_1,\dots ,X_m(\gamma )=x_m\right\}.\end{array}$$

We know that

$$\begin{array}{c}\hfill \sum _{x_1,\dots ,x_m\in A}p(x_1,\dots ,x_m)=\mu (\Gamma )=1\end{array}$$

for every natural number m. A finite space $\mathbf{S}.\mathbf{P}$, $\mathbf{X}={(X_n)}_{n=1}^{\infty }$ can be recalled as a stationary finite space $\mathbf{S}.\mathbf{P}$ if

$$\begin{array}{c}\hfill p(x_1,\dots ,x_m)=\mu \left\{\gamma \in \Gamma :X_{k+1}(\gamma )=x_1,\dots ,X_{k+m}(\gamma )=x_m\right\},\end{array}$$

for every $m,k\in \mathbb{N}$. In an information–theoretical setting, one may assume a stationary $\mathbf{S}.\mathbf{P}$, $\mathbf{X}$ as a data source. A finite space $\mathbf{S}.\mathbf{P}$, $\mathbf{X}$ is strictly a stationary finite space $\mathbf{S}.\mathbf{P}$ if

$$\begin{array}{c}\hfill p(x_1,\dots ,x_m)=\mu \left\{\gamma \in \Gamma :X_{k_1}(\gamma )=x_1,\dots ,X_{k_m}(\gamma )=x_m\right\},\end{array}$$

for every $\{k_1,\dots ,k_m\}\subseteq \mathbb{N}$. The Shannon entropy of order m of source $\mathbf{X}$ is defined by [1,12]

$$\begin{array}{c}\hfill H_{\mu }(X_1^m)=-\sum _{x_1,\dots ,x_m\in A}p(x_1,\dots ,x_m)logp(x_1,\dots ,x_m).\end{array}$$

The Shannon entropy of source $\mathbf{X}$ is defined by $h_{\mu }(\mathbf{X})={lim}_{m\to \infty }(\frac{1}{m}{H}_{\mu }(X_1^m)).$ If we assume that the alphabet A from source $\mathbf{X}$ accepts an order ≤, so that $(A,\le )$ is a totally ordered set, then define another order ≺ on A by [1]

$$\begin{array}{c}\hfill t_i\prec t_j\iff t_i<t_j\mathrm{or}(t_i=t_j\mathrm{and}i<j).\end{array}$$

We say that a length-m sequence $t_k^{k+m-1}=(t_k,\dots ,t_{k+m-1})$ has an order pattern $\pi$ if, $t_{k+\pi (0)}\prec t_{k+\pi (1)}\prec \dots \prec t_{k+\pi (m-1)},$ where $t_i,t_j\in A$, $k\in N$ and $i\ne j$. To a $\mathbf{S}.\mathbf{P}$, $\mathbf{X}={(X_n)}_{n\in N_0}$ we associate a probability process $\mathbf{R}={(R_n)}_{n\in N_0}$ defined by $R_m(\gamma )={\sum }_{i=0}^m\delta (X_i(\gamma )\le X_m(\gamma )).$ The sequence $\mathbf{R}$ defines a discrete-time process that is non-stationary. The metric permutation entropy of order m and the metric permutation entropy of source $\mathbf{X}$ are, respectively, defined by [1,12]

$$\begin{array}{c}\hfill H_{\mu }^{★}(X_0^{m-1})=H_{\mu }(R_0^{m-1})=\frac{-1}{m-1}\sum _{r_0,\dots ,r_{m-1}}p(r_0^{m-1})logp(r_0^{m-1}),\end{array}$$

and $h_{\mu }^{★}(\mathbf{X})={lim\; sup}_{m\to \infty }{H}_{\mu }^{★}(X_0^{m-1}).$

2. Main Results

In this section, we use the symbol $x_1^m$ for $(x_1,\dots ,x_m)$ to simplify the notation.

Definition 1.

Reference [13]. Let X be a random variable on Γ with discrete finite state space $A=\{a_1,\dots ,a_n\}$. Then,

$$\begin{array}{c}\hfill H_{\mu l}(X)=\sum _{x\in A}p(x)[1-p(x)]=1-\sum _{x\in A}{\left[p(x)\right]}^2\end{array}$$

is called the logical Shannon entropy of X.

Theorem 1.

Reference [21] If f is convex on I and $\zeta ={min}_{1\le i\le n}\left\{y_i\right\}$, $\eta ={max}_{1\le i\le n}\left\{y_i\right\}$, then

$$\begin{array}{c}\hfill \frac{f(\zeta )+f(\eta )-2f(\frac{\zeta +\eta }{2})}{n}\le \frac{{\sum }_{i=1}^{n}f(y_i)}{n}-f(\frac{{\sum }_{i=1}^n{y}_i}{n})\le f(\zeta )+f(\eta )-2f(\frac{\zeta +\eta }{2}).\end{array}$$

Theorem 2.

Suppose that X is a random variable on Γ with a discrete finite state space $A=\{a_1,\dots ,a_n\}$, $\zeta ={min}_{1\le i\le n}\left\{p(a_i)\right\}$ and $\eta ={max}_{1\le i\le n}\left\{p(a_i)\right\}$, then

$$\begin{array}{c}\hfill 0\le \Delta (\zeta ,\eta ):=\frac{{(\zeta -\eta )}^2}{4}\le \frac{n-1}{n}-H_{\mu l}(X)\le n\frac{{(\zeta -\eta )}^2}{4}=n\Delta (\zeta ,\eta ).\end{array}$$

Proof. 

Applying Theorem 1 with $f(x)=x^2-x$, we obtain

$$\begin{array}{cc}\hfill & \frac{1}{n}(({\zeta }^2-\zeta )+({\eta }^2-\eta )-2({(\frac{\zeta +\eta }{2})}^2-\frac{\zeta +\eta }{2}))\hfill \\ \hfill & \le \frac{1}{n}\sum _{i=1}^n(x_i^2-x_i)-({(\frac{{\sum }_1^n{x}_i}{n})}^2-(\frac{{\sum }_1^n{x}_i}{n}))\hfill \\ \hfill & \le ({\zeta }^2-\zeta )+({\eta }^2-\eta )-2({(\frac{\zeta +\eta }{2})}^2-\frac{\zeta +\eta }{2}).\hfill \end{array}$$

Putting $y_i=p(a_i)$, it follows that

$$\begin{array}{cc}\hfill & \frac{1}{n}(({\zeta }^2-\zeta )+({\eta }^2-\eta )-2({(\frac{\zeta +\eta }{2})}^2-\frac{\zeta +\eta }{2}))\hfill \\ \hfill & \le \frac{1}{n}\sum _{i=1}^n({(p(a_i))}^2-p(a_i))-({(\frac{{\sum }_1^{n}p(a_i)}{n})}^2-(\frac{{\sum }_1^{n}p(a_i)}{n}))\hfill \\ \hfill & \le ({\zeta }^2-\zeta )+({\eta }^2-\eta )-2({(\frac{\zeta +\eta }{2})}^2-\frac{\zeta +\eta }{2}).\hfill \end{array}$$

Thus,

$$\begin{array}{cc}\hfill & \frac{1}{n}(({\zeta }^2-\zeta )+({\eta }^2-\eta )-2({(\frac{\zeta +\eta }{2})}^2-\frac{\zeta +\eta }{2}))\hfill \\ \hfill & \le \frac{1}{n}\sum _{i=1}^n{(p(a_i))}^2-\frac{1}{n}\sum _{i=1}^{n}p(a_i)-(\frac{1}{n^2}-\frac{1}{n})\hfill \\ \hfill & \le ({\zeta }^2-\zeta )+({\eta }^2-\eta )-2({(\frac{\zeta +\eta }{2})}^2-\frac{\zeta +\eta }{2}).\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill & \frac{1}{n}(({\zeta }^2-\zeta )+({\eta }^2-\eta )-2({(\frac{\zeta +\eta }{2})}^2-\frac{\zeta +\eta }{2}))\hfill \\ \hfill & \le \frac{1}{n}(1-H_{\zeta l}(X))-\frac{1}{n}-(\frac{1}{n^2}-\frac{1}{n})\hfill \\ \hfill & \le ({\zeta }^2-\zeta )+({\eta }^2-\eta )-2({(\frac{\zeta +\eta }{2})}^2-\frac{\zeta +\eta }{2}).\hfill \end{array}$$

After some calculations, it turns out that

$$\begin{array}{c}\hfill \Delta (\zeta ,\eta ):=\frac{{(\zeta -\eta )}^2}{4}\le \frac{n-1}{n}-H_{\mu l}(X)\le n\frac{{(\zeta -\eta )}^2}{4}.\end{array}$$

□

Lemma 1.

Let X be a random variable with alphabet $A=\{a_1,\dots ,a_n\}$. Then, $0\le H_{\mu l}(X)\le \frac{n-1}{n}$, and equality holds if and only if $p(a_i)=p(a_j)$ for every $1\le i,j\le n$.

Proof. 

Using Theorem 2, we obtain $0\le H_{\mu l}(X)\le \frac{n-1}{n}$. Now, let $H_{\mu l}(X)=\frac{n-1}{n}$, by the use of Theorem 2, we have $M(\zeta ,\eta )=\frac{{(\zeta -\eta )}^2}{4}=0$ and, thus, $\zeta =\eta$. Therefore, ${max}_{1\le i\le n}\left\{p(a_i)\right\}={min}_{1\le i\le n}\left\{p(a_i)\right\}$. Thus, $p(a_i)=p(a_j)$ for every $1\le i,j\le n$. On the other hand, if $p(a_i)=p(a_j)$ for every $1\le i,j\le n$, then $\zeta =\eta$, so $M(\zeta ,\eta )=0$ and by the use of Theorem 2, we obtain $H_{\mu l}(X)-\frac{n-1}{n}=0$. Hence, $H_{\mu l}(X)=\frac{n-1}{n}$. □

Definition 2.

The logical Shannon entropy of order m of source $\mathbf{X}$ is defined by

$$\begin{array}{cc}\hfill H_{\mu l}(X_1^m)=H_{\mu l}(X_1,\dots ,X_m)& :=\sum _{x_1,\dots ,x_m\in A}p(x_1,\dots ,x_m)(1-p(x_1,\dots ,x_m)),\hfill \\ & =1-\sum _{x_1,\dots ,x_m\in A}(p(x_1,\dots ,x_m){)}^2\hfill \end{array}$$

It is easy to see that may be $p(x_1,x_2)\ne p(x_2,x_1)$ but for every two random variables $x_1,x_2$ we have $H_{\mu l}(x_1,x_2)=H_{\mu l}(x_2,x_1)$.

Definition 3.

Let m be a natural number and $1\le i_1,\dots ,i_m\le n$. We define the sets ${\mathcal{A}}_{i_1{i}_2\dots i_m}$ by

$$\begin{array}{c}\hfill {\mathcal{A}}_{i_1{i}_2\dots i_m}=\{\gamma \in \Gamma :X_1(\gamma )=a_{i_1},X_2(\gamma )=a_{i_2},\dots ,X_m(\gamma )=a_{i_m}\}.\end{array}$$

and $\mu ({\mathcal{A}}_{i_1{i}_2\dots i_m}):=a_{i_1{i}_2\dots i_m}$.

Moreover, ${\mathcal{A}}_{i_1{i}_2\dots i_m}\cap {\mathcal{A}}_{j_1{j}_2\dots j_m}=\varnothing$ for every $(i_1,i_2,\dots ,i_m)\ne (j_1,j_2,\dots ,j_m)$ and for every $m\in \mathbb{N}$. Furthermore, if $\gamma \in {\bigcup }_{j=1}^n{\mathcal{A}}_{i_1{i}_2\dots i_{m}j}$, then $\gamma \in {\mathcal{A}}_{i_1{i}_2\dots i_m{j}_0}$ for some $j_0\in \{1,\dots ,n\}$. Hence,

$$\begin{array}{c}\hfill X_1(\gamma )=a_{i_1},\dots ,X_m(\gamma )=a_{i_m},X_{m+1}(\gamma )=a_{j_0}\end{array}$$

for some $j_0\in \{1,\dots ,n\}$ and, thus, $\gamma \in {\mathcal{A}}_{i_1{i}_2\dots i_m}$. Moreover, if $\gamma \in {\mathcal{A}}_{i_1{i}_2\dots i_m}$, then

$$\begin{array}{c}\hfill X_1(\gamma )=a_{i_1},\dots ,X_m(\gamma )=a_{i_m}.\end{array}$$

Define $X_{m+1}(\gamma )=a_{j_0}$. Therefore,

$$\begin{array}{c}\hfill X_1(\gamma )=a_{i_1},\dots ,X_m(\gamma )=a_{i_m},X_{m+1}(\gamma )=a_{j_0}.\end{array}$$

Hence, $\gamma \in {\mathcal{A}}_{i_1{i}_2\dots i_m{j}_0}$ for some $j_0\in \{1,\dots ,n\}$ and, thus, $\gamma \in {\bigcup }_{j=1}^n{\mathcal{A}}_{i_1{i}_2\dots i_{m}j}$. So,

$$\begin{array}{c}\hfill {\mathcal{A}}_{i_1{i}_2\dots i_m}=\bigcup _{j=1}^n{\mathcal{A}}_{i_1{i}_2\dots i_{m}j}\end{array}$$

and, therefore, $\Gamma ={\bigcup }_{i_1,i_2,\dots ,i_m}{\mathcal{A}}_{i_1{i}_2\dots i_m}$. Hence, we obtain

$$\begin{array}{c}\hfill \sum _{i_1{i}_2\dots i_m}{a}_{i_1{i}_2\dots i_m}=1\end{array}$$

and

$$\begin{array}{cc}\hfill a_{i_1{i}_2\dots i_m}& =\mu ({\mathcal{A}}_{i_1{i}_2\dots i_m})=\mu ({\cup }_{j=1}^n{\mathcal{A}}_{i_1{i}_2\dots i_{m}j})\hfill \\ \hfill & =\sum _{j=1}^n\mu ({\mathcal{A}}_{i_1{i}_2\dots i_{m}j})=\sum _{j=1}^n{a}_{i_1{i}_2\dots i_{m}j}\hfill \end{array}$$

(1)

for every $1\le i_1,i_2,\dots ,i_m\le n$.

We now prove the following Theorem by employing Lemma A1 (see Appendix A):

Theorem 3.

If $X_1$ and $X_2$ are two random variables on Γ, then

$$\begin{array}{c}\hfill max\{H_{\mu l}(X_1),H_{\mu l}(X_2)\}\le H_{\mu l}(X_1,X_2)\le H_{\mu l}(X_1)+H_{\mu l}(X_2).\end{array}$$

(2)

Proof. 

Suppose $A=\{a_1,\dots ,a_n\}$. For every $1\le i,j\le n$, we consider

$$\begin{array}{cc}\hfill & {\mathcal{B}}_i=\{\gamma \in \Gamma :X_1(\gamma )=a_i\},{\mathcal{C}}_j=\{\gamma \in \Gamma :X_2(\gamma )=a_j\},{\mathcal{A}}_{ij}={\mathcal{B}}_i\cap {\mathcal{C}}_j,\hfill \\ \hfill & b_i=\mu ({\mathcal{B}}_i),c_j:=\mu ({\mathcal{C}}_j),a_{ij}=\mu ({\mathcal{A}}_{ij}).\hfill \end{array}$$

Moreover, ${\mathcal{C}}_i\cap {\mathcal{C}}_j=\varnothing$ and ${\mathcal{B}}_i\cap {\mathcal{B}}_j=\varnothing$ for every $1\le i\ne j\le n$; thus, ${\mathcal{A}}_{ij}\cap {\mathcal{A}}_{kl}=\varnothing$ for every ordered pair $(i,j)\ne (k,l)$. For obvious reasons, ${\mathcal{B}}_i={\cup }_{j=1}^n{\mathcal{A}}_{ij}$ for each $1\le i\le n$ and ${\mathcal{C}}_j={\cup }_{i=1}^n{\mathcal{A}}_{ij}$ for each $1\le j\le n$, and $\Gamma ={\cup }_{i,j}{\mathcal{A}}_{ij}$. So, we have ${\sum }_{i,j}{a}_{ij}=1$ and for every $1\le i,j\le n$,

$$\begin{array}{c}\hfill b_i=\mu ({\mathcal{B}}_i)=\mu (\bigcup _{j=1}^n{\mathcal{A}}_{ij})=\sum _{j=1}\mu ({\mathcal{A}}_{ij})=\sum _{j=1}^n{a}_{ij},\end{array}$$

and

$$\begin{array}{c}\hfill c_j=\mu ({\mathcal{C}}_j)=\mu ({\cup }_{i=1}^n{\mathcal{A}}_{ij})=\sum _{i=1}\mu ({\mathcal{A}}_{ij})=\sum _{i=1}^n{a}_{ij}.\end{array}$$

With the use of Lemma A1, we have

$$\begin{array}{c}\hfill \sum _{i=1}^n{(\sum _{j=1}^n{a}_{ij})}^2+\sum _{j=1}^n{(\sum _{i=1}^n{a}_{ij})}^2\le 1+\sum _{i,j}{a}_{ij}^2.\end{array}$$

Therefore,

$$\begin{array}{c}\hfill \sum _{i=1}^n{b}_i^2+\sum _{j=1}^n{c}_j^2\le 1+\sum _{i,j}{a}_{ij}^2.\end{array}$$

Consequently,

$$\begin{array}{c}\hfill \sum _{i=1}^n{(\mu ({\mathcal{B}}_i))}^2+\sum _{j=1}^n{(\mu ({\mathcal{C}}_j))}^2\le 1+\sum _{i,j}{(\mu ({\mathcal{A}}_{ij}))}^2,\end{array}$$

and

$$\begin{array}{c}\hfill -\sum _{i,j}{(\mu ({\mathcal{A}}_{ij}))}^2\le 1-\sum _{i=1}^n{(\mu ({\mathcal{B}}_i))}^2-\sum _{j=1}^n{(\mu ({\mathcal{C}}_j))}^2.\end{array}$$

Hence,

$$\begin{array}{c}\hfill 1-\sum _{i,j}{(\mu ({\mathcal{A}}_{ij}))}^2\le (1-\sum _{i=1}^n{(\mu ({\mathcal{B}}_i))}^2)+(1-\sum _{j=1}^n{(\mu ({\mathcal{C}}_j))}^2),\end{array}$$

it follows that $H_{\mu l}(X_1,X_2)\le H_{\mu l}(X_1)+H_{\mu l}(X_2).$

Now, we prove the left-hand inequality. Since

$$\begin{array}{c}\hfill b_i=\mu ({\mathcal{B}}_i)=\mu (\bigcup _{j=1}^n{\mathcal{A}}_{ij})=\sum _{j=1}\mu ({\mathcal{A}}_{ij})=\sum _{j=1}^n{a}_{ij}\end{array}$$

for every $1\le i\le n$, $b_i^2={({\sum }_{j=1}^n{a}_{ij})}^2\ge {\sum }_{j=1}^n{a}_{ij}^2$. Therefore,

$$\begin{array}{c}\hfill {(\mu ({\mathcal{B}}_i))}^2\ge \sum _{j=1}^n{(\mu ({\mathcal{A}}_{ij}))}^2,\end{array}$$

and, thus,

$$\begin{array}{c}\hfill \sum _{i=1}^n{(\mu ({\mathcal{B}}_i))}^2\ge \sum _{i=1}^n\sum _{j=1}^n{(\mu ({\mathcal{A}}_{ij}))}^2.\end{array}$$

So, $H_{\mu l}(X_1)\le H_{\mu l}(X_1,X_2)$.

Similarly, $H_{\mu l}(X_2)\le H_{\mu l}(X_1,X_2)$. Consequently,

$$\begin{array}{c}\hfill max\{H_{\mu l}(X_1),H_{\mu l}(X_2)\}\le H_{\mu l}(X_1,X_2).\end{array}$$

□

Corollary 1.

If $\mathbf{X}$ is an information source, then

$$\begin{array}{c}\hfill max\{H_{\mu l}(X_i):1\le i\le k\}\le H_{\mu l}(X_1,\dots ,X_k)\le \sum _{i=1}^k{H}_{\mu l}(X_i),(\forall k\in \mathbb{N}).\end{array}$$

Proof. 

This follows from Theorem 3. □

Definition 4.

The logical metric permutation entropy of order m of source $\mathbf{X}=\{X_0,X_1,\dots \}$ defined by

$$\begin{array}{c}\hfill H_{\mu l}^{★}(X_0^{m-1})=H_{\mu l}(R_0^{m-1})=1-\sum _{r_0,\dots ,r_{m-1}}{(p(r_0^{m-1}))}^2.\end{array}$$

Lemma 2.

For a $\mathbf{S}.\mathbf{P}$, $\mathbf{X}$, the sequence of ${\left\{H_{\mu l}(X_1^m)\right\}}_m$ increases. Thus, ${lim}_{m\to \infty }{H}_{\mu l}(X_1^m)$ exists.

Proof. 

According to (1),

$$\begin{array}{c}\hfill p(x_1,\dots ,x_m)=\sum _{x_{m+1}}p(x_1,\dots ,x_m,x_{m+1})\end{array}$$

for every $m\in \mathbb{N}$. Therefore,

$$\begin{array}{cc}\hfill {(p(x_1,\dots ,x_m))}^2& ={(\sum _{x_{m+1}}p(x_1,\dots ,x_m,x_{m+1}))}^2\hfill \\ \hfill & \le \sum _{x_{m+1}}{(p(x_1,\dots ,x_m,x_{m+1}))}^2,\hfill \end{array}$$

and

$$\begin{array}{c}\hfill \sum _{x_1^m}{(p(x_1,\dots ,x_m))}^2\le \sum _{x_1^{m+1}}{(p(x_1,\dots ,x_m,x_{m+1}))}^2.\end{array}$$

This means that

$$\begin{array}{cc}\hfill H_{\mu l}(X_1^m)& =1-\sum _{x_1^m}{(p(x_1,\dots ,x_m))}^2\hfill \\ \hfill & \ge 1-\sum _{x_1^{m+1}}{(p(x_1,\dots ,x_m,x_{m+1}))}^2=H_{\mu l}(X_1^{m+1}).\hfill \end{array}$$

□

Definition 5.

The logical Shannon entropy of source $\mathbf{X}=\{X_1,X_2,\dots \}$ is defined by

$$\begin{array}{c}\hfill h_{\mu l}(\mathbf{X})=\underset{m\to \infty }{lim}(H_{\mu l}(X_1^m)).\end{array}$$

Definition 6.

The logical metric permutation entropy of source $\mathbf{X}=\{X_0,X_1,\dots \}$ is defined by

$$\begin{array}{c}\hfill h_{\mu l}^{★}(\mathbf{X})=\underset{m\to \infty }{lim}{H}_{\mu l}^{★}(X_0^{m-1}).\end{array}$$

Remark 1.

Let m be a positive integer number. Then $0\le H_{\mu l}(X_1^m)\le 1$ and $0\le h_{\mu l}(\mathbf{X})\le 1$.

Lemma 3.

Let $\mathbf{X}=(X_1,X_1,X_1,\dots )$ be an information source. Then the following holds:

1. 

$H_{\mu l}(\underset{mtimes}{\underbrace{X_1,X_1,\dots ,X_1}})=H_{\mu l}(X_1),$for every$m\in \mathbb{N}$.

2. 

$h_{\mu l}(\mathbf{X})=H_{\mu l}(X_1)$.

Proof. 

• If $\mathbf{X}=(X_1,X_1,X_1,\dots )$, then

  $$\begin{array}{c}\hfill p(x_1,x_2,\dots ,x_m)=\left\{\begin{array}{cc}p(x_1)\hfill & x_1=x_2=\dots =x_m\hfill \\ 0\hfill & x_i\ne x_j,\mathrm{for}\mathrm{some}1\le i\ne j\le m.\hfill \end{array}\right.\end{array}$$
  Hence,

  $$\begin{array}{cc}\hfill H_{\mu l}(X_1,\dots ,X_m)& =\sum _{x_1,\dots ,x_m\in A}p(x_1,\dots ,x_m)(1-p(x_1,\dots ,x_m))\hfill \\ \hfill & =\sum _{x_1\in A}p(x_1)(1-p(x_1))\hfill \\ \hfill & =H_{\mu l}(X_1).\hfill \end{array}$$

  (3)
• We derive from (3) that

  $$\begin{array}{cc}\hfill h_{\mu l}(\mathbf{X})& =\underset{m\to \infty }{lim}{H}_{\mu l}(X_1,\dots ,X_m)\hfill \\ \hfill & =\underset{m\to \infty }{lim}{H}_{\mu l}(X_1,\dots ,X_1)\hfill \\ \hfill & =\underset{m\to \infty }{lim}{H}_{\mu l}(X_1)=H_{\mu l}(X_1).\hfill \end{array}$$

□

Theorem 4.

Suppose that $\mathbf{X}$ represents an information source on Γ with the discrete finite state space $A=\{a_1,\dots ,a_n\}$.

1. 

If ${\zeta }_m={min}_{x_1^m\in A}\left\{p(x_1^m)\right\}$ and ${\eta }_m={max}_{x_1^m\in A}\left\{p(x_1^m)\right\}$, then

$$\begin{array}{cc}\hfill 0\le \Delta ({\zeta }_m,{\eta }_m)\le \frac{n^m-1}{n^m}-H_{\mu l}(x_1^m)& \le n^m\Delta ({\zeta }_m,{\eta }_m),\hfill \end{array}$$

(4)

2. 

${lim}_{m\to \infty }\Delta ({\zeta }_m,{\eta }_m)\le 1-h_{\mu l}(\mathbf{X})\le {lim}_{m\to \infty }{n}^m\Delta ({\zeta }_m,{\eta }_m).$

Proof. 

• The result follows from Theorem 2.
• Taking the limit as $m\to \infty$ in (4), consequently (2) holds.

□

Lemma 4.

Let $\mathbf{X}$ represent an information source on Γ with the discrete finite state space $A=\{a_1,\dots ,a_n\}$, then $0\le H_{\mu l}(X_1^m)\le \frac{n^m-1}{n^m}$, and equality holds if and only if $p(x_1^m)=p(t_1^m)$ for every $x_1^m,t_1^m\in A^m$.

Proof. 

By Theorem 4, $0\le H_{\mu l}(X_1^m)\le \frac{n^m-1}{n^m}$. If $H_{\mu l}(X_1^m)=\frac{n^m-1}{n^m}$, then by the use of Theorem 4 we obtain $\Delta ({\zeta }_m,{\eta }_m)=\frac{{({\zeta }_m-{\eta }_m)}^2}{4}=0$. Hence ${\zeta }_m={\eta }_m$. Therefore ${max}_{x_1^m\in A}\left\{p(x_1^m)\right\}$$={min}_{x_1^m\in A}\left\{p(x_1^m)\right\}$. Thus $p(x_1^m)=p(t_1^m)$ for every $x_1^m,t_1^m\in A^m$. On the other hand if $p(x_1^m)=p(t_1^m)$ for every $x_1^m,t_1^m\in A^m$, then ${\zeta }_m={\eta }_m$. Therefore $\Delta ({\zeta }_m,{\eta }_m)=0$ and by Theorem 4 has $H_{\mu l}(X_1^m)-\frac{n^m-1}{n^m}=0$ and thus $H_{\mu l}(X_1^m)=\frac{n^m-1}{n^m}$. □

Definition 7.

Let $p(x)\ne 0$, the conditional probability function defined by $p(y|x):=\frac{p(x,y)}{p(x)}$. In general, for $p(x_1,\dots ,x_n)\ne 0$, the conditional probability function is defined by $p(x_1|x_2,\dots ,x_{n+1}):=\frac{p(x_1,x_2,\dots ,x_{n+1})}{p(x_2,x_3,\dots ,x_n)}$.

Lemma 5.

Let $x_1,x_2,\dots ,x_{n+1}$ be a word. Then

$$\begin{array}{c}\hfill p(x_{m+1},x_m,\dots ,x_1)=\prod _{i=1}^{m+1}p(x_i|x_{i-1},\dots ,x_1),\end{array}$$

where $m\in \mathbb{N}$ and $p(x_1|x_0):=p(x_1)$.

Proof. 

We prove the lemma by induction. If $m=1$, have $p(x_1,x_2)=p(x_1)\times p(x_1|x_2)$. Thus, the statement is true for $m=1$. Now suppose the statement is true for $m=k-1$, we give reasons for $m=k$.

$$\begin{array}{cc}\hfill \prod _{i=1}^{k+1}p(x_i|x_{i-1},\dots ,x_1)& =\prod _{i=1}^{k}p(x_i|x_{i-1},\dots ,x_1)\times p(x_{k+1}|x_k,\dots ,x_1)\hfill \\ \hfill & =p(x_k,x_{k-1},\dots ,x_1)\times p(x_{k+1}|x_k,\dots ,x_1)\hfill \\ \hfill & =p(x_k,x_{k-1},\dots ,x_1)\times \frac{p(x_{k+1},x_k,\dots ,x_1)}{p(x_k,x_{k-1},\dots ,x_1)}\hfill \\ \hfill & =p(x_{k+1},x_k,\dots ,x_1),\hfill \end{array}$$

which completes the proof. □

Definition 8.

Let $X_1$ and $X_2$ be two random variables on Γ. We define the conditional logical entropy of $X_2$ given $X_1$ by

$$\begin{array}{c}\hfill H_{\mu l}(X_2|X_1):=\sum _{x_1,x_2}{(p(x_1))}^2(p(x_2)-{(p(x_2|x_1))}^2).\end{array}$$

Note: if $p(x_1)=0$, define ${(p(x_1))}^2(p(x_2)-{(p(x_2|x_1))}^2=0$.

Definition 9.

Suppose $X_1,X_2,\dots ,X_m$ are m random variables on Γ. Define the conditional logical entropy of $X_m$ given $X_1,\dots ,X_{m-1}$ by

$$\begin{array}{cc}\hfill H_{\mu l}(X_m|X_{m-1},\dots ,X_2,X_1):& =\sum _{x_1^m}{(p(x_{m-1},\dots ,x_2,x_1))}^2\hfill \\ \hfill & [p(x_m)-{(p(x_m|x_{m-1},\dots ,x_1))}^2].\hfill \end{array}$$

Lemma 6.

Suppose $X_1,X_2,\dots ,X_m$ are m random variables on Γ, then

$$\begin{array}{cc}\hfill & H_{\mu l}(X_m|X_{m-1},\dots ,X_2,X_1)\hfill \\ \hfill & =\sum _{x_1^{m-1}}{(p(x_{m-1},\dots ,x_2,x_1))}^2-\sum _{x_1^m}{(p(x_m,\dots ,x_2,x_1))}^2\hfill \\ \hfill & =H_{\mu l}(X_m,X_{m-1},\dots ,X_2,X_1)-H_{\mu l}(X_{m-1},\dots ,X_2,X_1).\hfill \end{array}$$

Proof. 

According to Definition 9, we obtain

$$\begin{array}{cc}\hfill & H_{\mu l}(X_n|X_{m-1},\dots ,X_2,X_1)\hfill \\ \hfill & =\sum _{x_1^m}{(p(x_{m-1},\dots ,x_2,x_1))}^2(p(x_m)-{(p(x_m|x_{m-1},\dots ,x_1))}^2)\hfill \\ \hfill & =\sum _{x_1^m}p(x_{m-1},\dots ,x_2,x_1){)}^{2}p(x_m)\hfill \\ \hfill & -\sum _{x_1^m}p(x_{m-1},\dots ,x_2,x_1){)}^2{(p(x_m|x_{m-1},\dots ,x_1))}^2\hfill \\ \hfill & ={(\sum _{x_1^{m-1}}p(x_{m-1},\dots ,x_2,x_1))}^2)(\sum _{x_m}p(x_m))\hfill \\ \hfill & -\sum _{x_1^m}p(x_{m-1},\dots ,x_2,x_1){)}^2{(\frac{p(x_m,x_{m-1},\dots ,x_1)}{p(x_{m-1},\dots ,x_1)})}^2\hfill \\ \hfill & =\sum _{x_1^{m-1}}{(p(x_{m-1},\dots ,x_2,x_1))}^2-\sum _{x_1^m}{(p(x_m,\dots ,x_2,x_1))}^2.\hfill \end{array}$$

□

Lemma 7.

Let $\mathbf{X}$ be a stationary finite space $\mathbf{S}.\mathbf{P}$, then

$$\begin{array}{c}\hfill \sum _{x_2^n}{(p(x_n,\dots ,x_2))}^2=\sum _{x_1^{n-1}}{(p(x_{n-1},\dots ,x_2,x_1))}^2.\end{array}$$

(5)

Proof. 

Since $\mathbf{X}$ is stationary,

$$\begin{array}{cc}\hfill \sum _{x_2^n}{(p(x_n,\dots ,x_2))}^2& =\sum _{x_2^n}{(\mu (\{\gamma \in \Gamma :X_n(\gamma )=x_n,\dots ,X_2(\gamma )=x_2\}))}^2\hfill \\ \hfill & =\sum _{x_2^n}{(\mu (\{\gamma \in \Gamma :X_{n-1}(\gamma )=x_n,\dots ,X_1(\gamma )=x_2\}))}^2\hfill \\ \hfill & =\sum _{x_1^{n-1}}{(p(x_{n-1},\dots ,x_2,x_1))}^2,\hfill \end{array}$$

which yields (5). □

Theorem 5.

Let $\mathbf{X}$ be a stationary finite space $\mathbf{S}.\mathbf{P}$, with discrete finite state space $A=\{a_1,\dots ,a_n\}$. Then the sequence of conditional logical entropies $H_{\mu l}(X_m|X_{m-1},\dots ,X_1)$ decreases.

Proof. 

Under the notation of Definition 3, define

$$\begin{array}{c}\hfill \{{\mathcal{A}}_{i_1{i}_2\dots i_m}:1\le i_1,i_2,\dots ,i_m\le n\}=\{{\mathcal{D}}_1,{\mathcal{D}}_2,\dots ,{\mathcal{D}}_M\},\end{array}$$

and $\mu ({\mathcal{D}}_r)=d_r$ where $M=n^m$. Furthermore, assume that

$$\begin{array}{c}\hfill {\mathcal{D}}_{ij}={\mathcal{D}}_i\bigcap \{\gamma \in \Gamma :x_j(\gamma )=a_j\},\mu ({\mathcal{D}}_{ij})=d_{ij},\end{array}$$

$$\begin{array}{c}\hfill {\mathcal{D}}_{ijk}={\mathcal{D}}_{ij}\bigcap \{\gamma \in \Gamma :x_k(\gamma )=a_k\},\mu ({\mathcal{D}}_{ijk})=d_{ijk},\end{array}$$

where $1\le i\le M$ and $1\le j,k\le n$. It is easy to see that ${\mathcal{D}}_i\cap {\mathcal{D}}_j=\varnothing$ for every $1\le i\ne j\le n$, and ${\mathcal{D}}_{ij}\cap {\mathcal{D}}_{rs}=\varnothing$ for every ordered pair $(i,j)\le (r,s)$. Therefore, ${\mathcal{D}}_{ijk}\cap {\mathcal{D}}_{rst}=\varnothing$ for every $(i,j,k)\ne (r,s,t)$. For obvious reasons, ${\mathcal{D}}_i={\cup }_{j=1}^n{\mathcal{D}}_{ij}$ for each $1\le i\le n$, ${\mathcal{D}}_{ij}={\cup }_{k=1}^n{\mathcal{D}}_{ijk}$ for every $1\le i,j\le n$ and $\Gamma ={\cup }_{i,j,k}{\mathcal{D}}_{ijk}$. Consequently, ${\sum }_{i,j,k}{d}_{ijk}=1$ and

$$\begin{array}{c}\hfill d_i=\mu ({\mathcal{D}}_i)=\mu (\bigcup _{j=1}^n{\mathcal{D}}_{ij})=\sum _{j=1}^n\mu ({\mathcal{D}}_{ij})=\sum _{j=1}^n{d}_{ij}\end{array}$$

and

$$\begin{array}{c}\hfill d_{ij}=\mu ({\mathcal{D}}_{ij})=\mu (\bigcup _{k=1}^n{\mathcal{D}}_{ijk})=\sum _{k=1}^n\mu ({\mathcal{D}}_{ijk})=\sum _{k=1}^n{d}_{ijk}\end{array}$$

for every $1\le j\le M,1\le i\le n$.

Using Theorem A1 and Lemma 7, we deduce that

$$\begin{array}{cc}\hfill & \sum _{x_1^{m+2}}{(p(x_{m+2},\dots ,x_2,x_1))}^2=\sum _{i=1}^M\sum _{j=1}^n\sum _{k=1}^n{d}_{ijk}^2=\sum _{i,j,k}{d}_{ijk}^2\hfill \\ \hfill & \sum _{x_1^{m+1}}{(p(x_{m+1},\dots ,x_2,x_1))}^2=\sum _{i=1}^M\sum _{j=1}^n{d}_{ij}^2=\sum _{i,j}{d}_{ij}^2=\sum _{i,j}{(\sum _{k=1}^n{d}_{ijk})}^2\hfill \\ \hfill & \sum _{x_1^m}{(p(x_m,\dots ,x_2,x_1))}^2=\sum _{i=1}^M{d}_i^2=\sum _{i=1}^M{(\sum _{j,k=1}^n{d}_{ijk})}^2\hfill \\ \hfill & \sum _{x_2^{m+2}}{(p(x_{m+2},\dots ,x_2))}^2=\sum _{x_1^{m+1}}{(p(x_{m+1},\dots ,x_2,x_1))}^2=\sum _{i,j}{d}_{ij}^2.\hfill \end{array}$$

With the use of Theorem A1, we obtain

$$\begin{array}{cc}\hfill & H_{\mu l}(X_{m+2}|X_{m+1},\dots ,X_2,X_1)\hfill \\ \hfill & =\sum _{x_1^{m+1}}{(p(x_{m+1},\dots ,x_2,x_1))}^2-\sum _{x_1^{m+2}}{(p(x_{m+2},\dots ,x_2,x_1))}^2.\hfill \\ \hfill & =\sum _{i,j,k}{d}_{ijk}^2-\sum _{i,j}{(\sum _{k=1}^n{d}_{ijk})}^2\hfill \\ \hfill & \ge \sum _{i,j}{(\sum _{k=1}^n{d}_{ijk})}^2-\sum _{i=1}^M{(\sum _{j,k=1}^n{d}_{ijk})}^2\hfill \\ \hfill & =\sum _{x_1^m}{(p(x_m,\dots ,x_2,x_1))}^2-\sum _{x_1^{m+1}}{(p(x_{m+1},\dots ,x_2,x_1))}^2\hfill \\ \hfill & =H_{\mu l}(X_{m+1}|X_m,\dots ,X_2,X_1),\hfill \end{array}$$

this means that the sequence of conditional logical entropies

$$\begin{array}{c}\hfill H_{\mu l}(X_m|X_{m-1},\dots ,X_1)\end{array}$$

is decreasing, so

$$\begin{array}{c}\hfill 0\le \dots \le H_{\mu l}(X_{m+1}|X_m,\dots ,X_1)\le H_{\mu l}(X_m|X_{m-1},\dots ,X_1)\le \dots \le H_{\mu l}(X_1).\end{array}$$

□

Corollary 2.

Let $\mathbf{X}=(X_1,X_2,X_3,\dots )$ be a source. Then the limit ${lim}_{n\to \infty }{H}_{\mu l}(X_n|X_{n-1},\dots ,X_1)$ exists.

Lemma 8.

Let $\mathbf{X}={(X_m)}_{m=1}^{\infty }$ be a stationary finite space $\mathbf{S}.\mathbf{P}$. Then

$$\begin{array}{cc}\hfill \sum _{x_2^{m+1}}{(p(x_{m+1}|x_m,\dots ,x_2))}^2& =\sum _{x_1^m}{(p(x_m|x_{m-1},\dots ,x_1))}^2.\hfill \end{array}$$

Proof. 

Since $\mathbf{X}$ is stationary,

$$\begin{array}{cc}\hfill & \sum _{x_2^{m+1}}{(p(x_{m+1}|x_m,\dots ,x_2))}^2\hfill \\ \hfill & =\sum _{x_2^{m+1}}{(\frac{p(x_{m+1},x_m,\dots ,x_2)}{p(x_m,\dots ,x_2)})}^2\hfill \\ \hfill & =\sum _{x_2^{m+1}}{(\frac{\mu (\{\gamma \in \Gamma :x_{m+1}(\gamma )=x_{m+1},\dots ,x_2(\Gamma )=x_2\})}{\mu (\{\Gamma \in \Gamma :x_m(\Gamma )=x_m,\dots ,x_2(\gamma )=x_2\})})}^2\hfill \\ \hfill & =\sum _{x_2^{m+1}}{(\frac{\mu (\{\gamma \in \Gamma :x_m(\gamma )=x_{m+1},\dots ,x_1(\gamma )=x_2\})}{\mu (\{\gamma \in \Gamma :x_{m-1}(\gamma )=x_m,\dots ,x_1(\gamma )=x_2\})})}^2\hfill \\ \hfill & =\sum _{x_1^m}{(p(x_m|x_{m-1},\dots ,x_1))}^2,\hfill \end{array}$$

which completes the proof. □

Theorem 6.

Let $\mathbf{X}={(X_n)}_{n=1}^{\infty }$ be a stationary finite space $\mathbf{S}.\mathbf{P}$. Then

$$\begin{array}{c}\hfill H_{\mu l}(X_{m+1}|X_m,\dots ,X_2)=H_{\mu l}(X_m|X_{m-1},\dots ,X_1)\end{array}$$

Proof. 

According to Lemma 7,

$$\begin{array}{cc}\hfill H_{\mu l}(X_{m+1}|X_m,\dots ,X_2)& =\sum _{x_2^m}{(p(x_m,\dots ,x_2))}^2-\sum _{x_2^{m+1}}{(p(x_m,\dots ,x_2))}^2\hfill \\ \hfill & =\sum _{x_1^{m-1}}{(p(x_{m-1},\dots ,x_1))}^2-\sum _{x_1^m}{(p(x_m,\dots ,x_1))}^2\hfill \\ \hfill & =H_{\mu l}(X_m|X_{m-1},\dots ,X_2,X_1).\hfill \end{array}$$

Theorem 6 is thus proved. □

Theorem 7.

Let $X_1$ and $X_2$ be two random variables on Γ. Then the following hold:

1. 

$H_{\mu l}(X_2|X_1)=H_{\mu l}(X_1,X_2)-H_{\mu l}(X_1).$

2. 

$H_{\mu l}(X_2|X_1)+H_{\mu l}(X_1)=H_{\mu l}(X_1|X_2)+H_{\mu l}(X_2)$.

Proof. 

• Using the definition of condition logical entropy, we deduce

  $$\begin{array}{cc}\hfill H_{\mu l}(X_2|X_1)& =(\sum _{x_1}{(p(x_1))}^2)-\sum _{x_1,x_2}{(p(x_1,x_2))}^2\hfill \\ \hfill & =(1-\sum _{x_1,x_2}{(p(x_1,x_2))}^2)-(1-\sum _{x_1}{(p(x_1))}^2)\hfill \\ \hfill & =H_{\mu l}(X_1,X_2)-H_{\mu l}(X_1),\hfill \end{array}$$

  which completes the proof.
• From the previous part, and since $H_{\mu l}(X_1,X_2)=H_{\mu l}(X_2,X_1)$, we have

  $$\begin{array}{cc}\hfill H_{\mu l}(X_2|X_1)+H_{\mu l}(X_1)& =H_{\mu l}(X_1,X_2)\hfill \\ \hfill & =H_{\mu l}(X_2,X_1)\hfill \\ \hfill & =H_{\mu l}(X_1|X_2)+H_{\mu l}(X_2).\hfill \end{array}$$

□

Theorem 8.

Let $\mathbf{X}=(X_1,X_1,X_1,\dots )$ be an information source. Then

$$\begin{array}{c}\hfill H_{\mu l}(X_1,\dots ,X_m)=\sum _{i=1}^m{H}_{\mu l}(X_i|X_{i-1},\dots ,X_1),\end{array}$$

where $H_{\mu l}(X_1|X_0):=H_{\mu l}(X_1)$.

Proof. 

According to Lemma 6, we obtain

$$\begin{array}{cc}\hfill & \sum _{i=1}^m{H}_{\mu l}(X_i|X_{i-1},\dots ,X_1)\hfill \\ \hfill & =H_{\mu l}(X_1)+\sum _{i=2}^m(H_{\mu l}(X_i,\dots ,X_1)-H_{\mu l}(X_{i-1},\dots ,X_1))\hfill \\ \hfill & =H_{\mu l}(X_1,\dots ,X_m),\hfill \end{array}$$

hence the theorem is proven. □

Theorem 9.

Let $\mathbf{X}=(X_1,X_2,X_3,\dots )$ be an information source. Then

$$\begin{array}{c}\hfill h_{\mu l}(\mathbf{X})=\sum _{i=1}^{\infty }{H}_{\mu l}(X_i|X_{i-1},\dots ,X_1).\end{array}$$

Proof. 

By the use of Theorem 8, we obtain

$$\begin{array}{c}\hfill h_{\mu l}(\mathbf{X})=\underset{n\to \infty }{lim}\sum _{i=1}^n{H}_{\mu l}(X_i|X_{i-1},\dots ,X_1)=\sum _{i=1}^{\infty }{H}_{\mu l}(X_i|X_{i-1},\dots ,X_1),\end{array}$$

which completes the proof. □

Definition 10.

An independent information source, $\mathbf{X}=(X_1,X_2,X_3,\dots )$, is a source with the following property

$$\begin{array}{c}\hfill p(x_1,x_2,\dots ,x_m)=\prod _{i=1}^{m}p(x_i)\end{array}$$

for all $x_1^m$.

Theorem 10.

Let $\mathbf{X}=(X_1,X_2,X_3,\dots )$ be an independent information source. Then

$$\begin{array}{c}\hfill H_{\mu l}(X_{m+1}|X_m,\dots ,X_1)=(1-H_{\mu l}(X_m,\dots ,X_1))H_{\mu l}(X_{m+1})\end{array}$$

for every $m\in \mathbb{N}$.

Proof. 

Since $\mathbf{X}=(X_1,X_2,X_3,\dots )$ is an independent random variables, we have

$$\begin{array}{cc}\hfill & H_{\mu l}(X_{m+1}|X_m,\dots ,X_1)\hfill \\ \hfill & =\sum _{x_1^{m+1}}{(p(x_m,\dots ,x_1))}^{2}p(x_{m+1})-\sum _{x_1^{m+1}}{(p(x_{m+1},\dots ,x_1))}^2\hfill \\ \hfill & =\sum _{x_1^{m+1}}{(p(x_m,\dots ,x_1))}^{2}p(x_{m+1})-\sum _{x_1^{m+1}}{(p(x_{m+1},\dots ,x_1))}^2\hfill \\ \hfill & =\sum _{x_1^{m+1}}{(p(x_m,\dots ,x_1))}^{2}p(x_{m+1})-\sum _{x_1^{m+1}}{(p(x_m,\dots ,x_1))}^2{(p(x_{m+1}))}^2\hfill \\ \hfill & =\sum _{x_1^{m+1}}{(p(x_m,\dots ,x_1))}^2(p(x_{m+1})-{(p(x_{m+1}))}^2)\hfill \\ \hfill & =(\sum _{x_1^m}{(p(x_m,\dots ,x_1))}^2)(\sum _{x_{m+1}}(p(x_{m+1})-{(p(x_{m+1}))}^2))\hfill \\ \hfill & =(1-H_{\mu l}(X_m,\dots ,X_1))H_{\mu l}(X_{m+1}).\hfill \end{array}$$

(6)

The result follows from (6). □

Theorem 11.

Suppose that $\mathbf{X}=(X_1,X_2,X_3,\dots )$ is an independent information source and ${lim}_n{H}_{\mu l}(X_n)\ne 0$. Then $h_{\mu l}(\mathbf{X})=1$.

Proof. 

In view of Theorem 10 and Lemma A2, we conclude that

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim}{H}_{\mu l}(X_{n+1}|X_n,\dots ,X_1)& =\underset{n\to \infty }{lim}(1-H_{\mu l}(X_n,\dots ,X_1))H_{\mu l}(X_{n+1})\hfill \\ \hfill & =\underset{n}{lim}(1-H_{\mu l}(X_n,\dots ,X_1))\times \underset{n}{lim}{H}_{\mu l}(X_{n+1})=0.\hfill \end{array}$$

Since ${lim}_n{H}_{\mu l}(X_n)\ne 0$, ${lim}_n(1-H_{\mu l}(X_n,\dots ,X_1))=0$. Hence,

$$\begin{array}{c}\hfill h_{\mu l}(\mathbf{X})=\underset{n\to \infty }{lim}{H}_{\mu l}(X_n,\dots ,X_1)=1.\end{array}$$

□

Theorem 12.

Let $\mathbf{X}=(X_1,X_2,X_3,\dots )$ be an independent information source. Then

$$\begin{array}{c}\hfill H_{\mu l}(X_m,\dots ,X_1)=1-\prod _{i=1}^m(1-H_{\mu l}(X_i))\end{array}$$

for every $m\in \mathbb{N}$.

Proof. 

Since $\mathbf{X}$ is an independent source,

$$\begin{array}{cc}\hfill H_{\mu l}(X_m,\dots ,X_1)& =1-\sum _{x_1,\dots ,x_m}(p(x_1,\dots ,x_m){)}^2\hfill \\ \hfill & =1-\sum _{x_1,\dots ,x_m}{(\prod _{i=1}^{m}p(x_i))}^2=1-\sum _{x_1,\dots ,x_m}{(\prod _{i=1}^m(p(x_i))}^2)\hfill \\ \hfill & =1-\prod _{i=1}^m(\sum _{x_i}{(p(x_i))}^2)=1-\prod _{i=1}^m(1-H_{\mu l}(X_i)),\hfill \end{array}$$

which is the desired result. □

Theorem 13.

If $\mathbf{X}=(X_1,X_2,X_3,\dots )$ is an independent information source, then

1. 

${lim}_{n\to \infty }{\prod }_{i=1}^n(1-H_{\mu l}(X_i))=1-h_{\mu l}(\mathbf{X}).$

2. 

If there exists $k\in \mathbb{N}$, such that $H_{\mu l}(X_k)=1$, then $h_{\mu l}(\mathbf{X})=1$.

Proof. 

• This follows from Theorem 12.
• Let $H_{\mu l}(X_k)=1$ for some $k\in \mathbb{N}$. Since $H_{\mu l}(X_k)=1$,

  $$\begin{array}{c}\hfill 1-h_{\mu l}(\mathbf{X})=\underset{n\to \infty }{lim}\prod _{i=1}^n(1-H_{\mu l}(X_i))=0.\end{array}$$

Hence, $h_{\mu l}(\mathbf{X})=1$. □

Definition 11.

Let $X_1$ and $X_2$ be two random variables on Γ. Define the logical mutual information of $X_2$ and $X_1$ by

$$\begin{array}{c}\hfill I_{\mu l}(X_1,X_2):=H_{\mu l}(X_1)-H_{\mu l}(X_1|X_2).\end{array}$$

Lemma 9.

Let $X_1$ and $X_2$ be two random variables on Γ. Then the following hold:

1. 

$I_{\mu l}(X_1,X_2)=H_{\mu l}(X_2)-H_{\mu l}(X_2|X_1)$.

2. 

$I_{\mu l}(X_1,X_2)=H_{\mu l}(X_1)+H_{\mu l}(X_2)-H_{\mu l}(X_1,X_2)$.

3. 

$I_{\mu l}(X_1,X_2)=I_{\mu l}(X_2,X_1)$.

4. 

$I_{\mu l}(X_1,X_1)=H_{\mu l}(X_1)$.

5. 

If $X_1$ and $X_2$ are independent random variables, then

$$\begin{array}{c}\hfill I_{\mu l}(X_1,X_2)=H_{\mu l}(X_1)H_{\mu l}(X_2).\end{array}$$

Proof. 

1–3.

follows from Definition 11 and Theorem 7.

4.

According to Lemma 3, $H_{\mu l}(X_1,X_1)=H_{\mu l}(X_1)$. Therefore,

$$\begin{array}{cc}\hfill I_{\mu l}(X_1,X_1)& =H_{\mu l}(X_1)+H_{\mu l}(X_1)-H_{\mu l}(X_1,X_1)\hfill \\ \hfill & =2H_{\mu l}(X_1)-H_{\mu l}(X_1))=H_{\mu l}(X_1).\hfill \end{array}$$

5.

It follows from Lemma 12 that

$$\begin{array}{cc}\hfill H_{\mu l}(X_1,X_2)& =1-(1-H_{\mu l}(X_1))(1-H_{\mu l}(X_2))\hfill \\ \hfill & =H_{\mu l}(X_1)+H_{\mu l}(X_2)-H_{\mu l}(X_1)H_{\mu l}(X_2).\hfill \end{array}$$

Hence, the result follows from 2. □

Definition 12.

Let $\mathbf{X}=(X_1,X_2,X_3,\dots )$ be an information source. Define the logical mutual information of $X_1$,…,$X_m$ by

$$\begin{array}{c}\hfill I_{\mu l}(X_1,\dots ,X_m):=\sum _{i=1}^m{H}_{\mu l}(X_i)-H_{\mu l}(X_1,\dots ,X_m).\end{array}$$

Lemma 10.

Let $X_1$ and $X_2$ be two random variables on Γ. Then

$$\begin{array}{c}\hfill 0\le H_{\mu l}(X_2|X_1)\le H_{\mu l}(X_2).\end{array}$$

Proof. 

It follows from Theorem 8 that

$$\begin{array}{c}\hfill H_{\mu l}(X_1,X_2)=H_{\mu l}(X_1)+H_{\mu l}(X_2|X_1)\end{array}$$

and from Theorem 3 that $H_{\mu l}(X_1,X_2)\le H_{\mu l}(X_1)+H_{\mu l}(X_2)$. Hence,

$$\begin{array}{c}\hfill H_{\mu l}(X_1)+H_{\mu l}(X_2|X_1)\le H_{\mu l}(X_1)+H_{\mu l}(X_2).\end{array}$$

This means that $H_{\mu l}(X_2|X_1)\le H_{\mu l}(X_2).$ □

Theorem 14.

Let $X_1$ and $X_2$ be two random variables on Γ. Then the following holds:

$$\begin{array}{c}\hfill 0\le I_{\mu l}(X_1,X_2)\le min\{H_{\mu l}(X_1),H_{\mu l}(X_1)\}.\end{array}$$

Proof. 

From Lemma 9, it follows that

$$\begin{array}{c}\hfill I_{\mu l}(X_1,X_2)=H_{\mu l}(X_1)+H_{\mu l}(X_2)-H_{\mu l}(X_1,X_2).\end{array}$$

Furthermore, Theorem 3 yields $H_{\mu l}(X_2)\le H_{\mu l}(X_1,X_2)$. Hence,

$$\begin{array}{cc}\hfill I_{\mu l}(X_1,X_2)& =H_{\mu l}(X_1)+H_{\mu l}(X_2)-H_{\mu l}(X_1,X_2)\hfill \\ \hfill & \le H_{\mu l}(X_1)+H_{\mu l}(X_1,X_2)-H_{\mu l}(X_1,X_2)\hfill \\ \hfill & =H_{\mu l}(X_1).\hfill \end{array}$$

Similarly, $I_{\mu l}(X_1,X_2)\le H_{\mu l}(X_2)$; therefore,

$$\begin{array}{c}\hfill I_{\mu l}(X_1,X_2)\le min\{H_{\mu l}(X_1),H_{\mu l}(X_1)\}.\end{array}$$

On the other hand, (2) yields

$$\begin{array}{c}\hfill H_{\mu l}(X_2)+H_{\mu l}(X_2)-H_{\mu l}(X_1,X_2)\ge 0.\end{array}$$

Therefore, $I_{\mu l}(X_1,X_2)\ge 0$ and, thus,

$$\begin{array}{c}\hfill 0\le I_{\mu l}(X_1,X_2)\le min\{H_{\mu l}(X_1),H_{\mu l}(X_1)\}.\end{array}$$

□

3. Logical Entropy of Maps

Definition 13.

Let $f:\Gamma ⟶\Gamma$ be a measurable function and $\alpha =\{{\alpha }_1,\dots ,{\alpha }_n\}$ be a partition of Γ. The logical metric entropy of order m of f with respect to the partition α is defined by

$$\begin{array}{c}\hfill h_{\mu l,m}(f,\alpha )=1-\sum _{1\le x_0,\dots ,x_m\le n}(\mu {({\alpha }_{x_0}\cap f^{-1}({\alpha }_{x_1})\cap \dots \cap f^{-m}(({\alpha }_{x_m})))}^2,\end{array}$$

(7)

and the logical metric entropy of f with respect to the partition α is defined by

$$\begin{array}{c}\hfill h_{\mu l}(f,\alpha )=\underset{m\to \infty }{lim}{h}_{\mu l,m}(f,\alpha ).\end{array}$$

(8)

The limits in (7) and (8) exist (see Theorem 15). The logical metric entropy of f is defined by $h_{\mu l}(f)={sup}_{\alpha }{h}_{\mu l}(f,\alpha )$.

Remark 2.

$0\le h_{\mu l}(f)\le 1$.

Let I be an interval, $h:I⟶I$ be a function and $x\in I$. For the finite orbit $\{h^n(x):0\le n\le L-1\}$, we say that x is of type ordinal L-pattern $\pi =\pi (x)=({\pi }_0,\dots ,{\pi }_{L-1})$ if

$$\begin{array}{c}\hfill h^{{\pi }_0}(x)<h^{{\pi }_1}(x)<\dots <h^{{\pi }_{L-1}}(x).\end{array}$$

We denote $P_{\pi }$ the set of $x\in I$ that are of type $\pi$.

Definition 14.

The logical metric permutation entropy of order m of f is defined by

$$\begin{array}{c}\hfill H_{\mu l,m}^{★}(f):=1-\sum _{\pi \in {\mathcal{S}}_m}{(\mu (p_{\pi }))}^2,\end{array}$$

and the logical metric permutation entropy of f is defined by

$$\begin{array}{c}\hfill h_{\mu l}^{*}(f):=\underset{m\to \infty }{lim}{H}_{\mu l,m}^{★}(f)=1-\underset{m\to \infty }{lim}\sum _{\pi \in {\mathcal{S}}_m}{(\mu (p_{\pi }))}^2.\end{array}$$

Theorem 15.

Given $A=\{0,1,\dots ,n-1\}$ with $X_m:[0,1]⟶A$, is defined as follows:

$$\begin{array}{c}\hfill X_m(x)=i⟺f^m(x)\in {\alpha }_i.\end{array}$$

Then $h_{\mu l}(f,\alpha )=h_{\mu l}(\mathbf{X})$ where $\mathbf{X}$ is a stationary process $(X_0,X_1,\dots )$.

Proof. 

Since

$$\begin{array}{cc}\hfill H_{\mu l}(X_m)& =1-\sum _{i=0}^{n-1}{(\mu (\{x:f^m(x)\in {\alpha }_i\}))}^2\hfill \\ \hfill & =1-\sum _{i=0}^{n-1}{(\mu (f^{-m}{\alpha }_i))}^2,\hfill \end{array}$$

we have

$$\begin{array}{cc}\hfill p(x_0,\dots ,x_m)& =\mu (\{x:x_0(x)=x_0,\dots ,x_m(x)=x_m\})\hfill \\ \hfill & =\mu (\{x:x\in {\alpha }_{x_0},\dots ,f^m(x)\in {\alpha }_{x_m}\})\hfill \\ \hfill & =\mu ({\alpha }_{x_0}\bigcap f^{-1}({\alpha }_{x_1})\cap \dots \bigcap f^{-m}(({\alpha }_{x_m})).\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill H_{\mu l}(X_0^m)& =1-\sum _{x_0^m}(\mu {({\alpha }_{x_0}\bigcap f^{-1}({\alpha }_{x_1})\bigcap \dots \bigcap f^{-m}(({\alpha }_{x_m})))}^2,\hfill \end{array}$$

(9)

and so (9) implies that $h_{\mu l}(f,\alpha )=h_{\mu l}(\mathbf{X})$. □

4. Examples and Applications in Logistic and Tent Maps

Example 1.

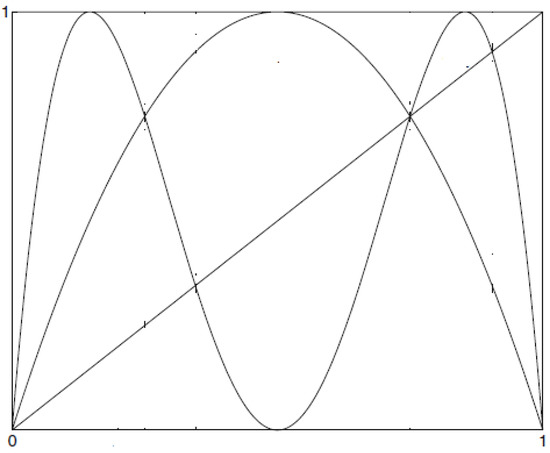
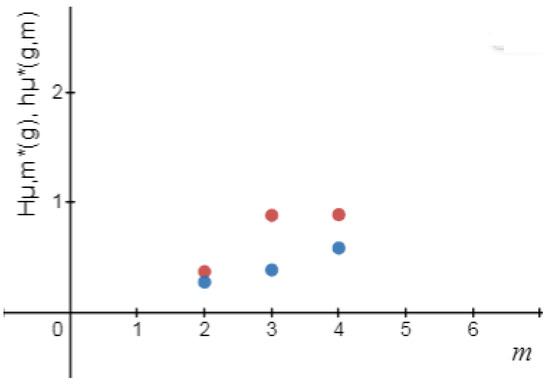
Let $g(x)=4x(1-x):[0,1]⟶[0,1]$ be the logistic map (see Figure 1 and Figure 2 and Table 1). Then

$$\begin{array}{cc}\hfill & p_{(0,1)}=(0,\frac{3}{4}),p_{(1,0)}=(\frac{3}{4},1),\hfill \\ \hfill & p_{(0,1,2)}=(0,\frac{1}{4}),p_{(0,2,1)}=(\frac{1}{4},\frac{5-\sqrt{5}}{8}),p_{(2,0,1)}=(\frac{5-\sqrt{5}}{8},\frac{3}{4}),\hfill \\ \hfill & p_{(1,0,2)}=(\frac{3}{4},\frac{5+\sqrt{5}}{8}),p_{(1,2,0)}=(\frac{5+\sqrt{5}}{8},1),p_{(2,1,0)}=\varnothing .\hfill \end{array}$$

Figure 1. $x,g(x),\mathrm{and}{g}^2(x)$.

Figure 2. $H_{\mu l,m}^{★}(g),\mathrm{and}{h}_{\mu }^{★}(g,m)$.

Table 1. Logical metric permutation entropy and metric permutation entropy [1] for the logistic map up to order $m=3$.

m	1	2	3
$H_{\mu l,m}^{★}(g)$	0	0/375	0/888
$h_{\mu }^{★}(g,m)$	0	0/28	0/39

Therefore,

$$\begin{array}{cc}\hfill & \sum _{\pi \in {\mathcal{S}}_2}{(\mu (p_{\pi }))}^2={(\frac{3}{4})}^2+{(\frac{1}{4})}^2=\frac{5}{8},\hfill \\ \hfill & H_{\mu l,2}^{★}(g)=1-\frac{5}{8}=0/375,\hfill \end{array}$$

$$\begin{array}{cc}\hfill \sum _{\pi \in {\mathcal{S}}_3}{(\mu (p_{\pi }))}^2& ={(\frac{1}{4})}^2+{(\frac{3-\sqrt{5}}{8})}^2+{(\frac{1+\sqrt{5}}{8})}^2+{(\frac{\sqrt{5}-1}{8})}^2+{(\frac{3-\sqrt{5}}{8})}^2,\hfill \\ \hfill & =\frac{17-6\sqrt{5}}{32}\hfill \end{array}$$

and

$$\begin{array}{c}\hfill H_{\mu l,3}^{★}(g)=1-\frac{17-6\sqrt{5}}{32}=\frac{15+6\sqrt{5}}{32}\simeq 0/888.\end{array}$$

Example 2.

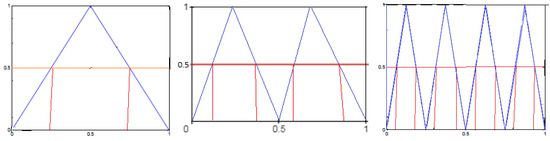
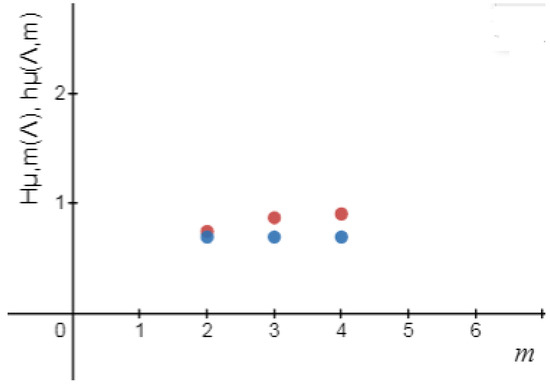
Ref. [1] Let $\alpha =\{{\alpha }_0=[0,\frac{1}{2}],{\alpha }_1=(\frac{1}{2},1]\}$. We consider the tent map (see Figure 3 and Figure 4 and Table 2) $\Lambda :[0,1]⟶[0,1]$ by

$$\begin{array}{c}\hfill \Lambda (x)=\left\{\begin{array}{cc}2x\hfill & 0\le x\le \frac{1}{2},\hfill \\ 2-2x\hfill & \frac{1}{2}\le x\le 1,\hfill \end{array}.\right.\end{array}$$

Figure 3. $\Lambda ,{\Lambda }^2\mathrm{and}{\Lambda }^3$.

Figure 4. $H_{\mu l,m}(\Lambda ),\mathrm{and}{h}_{\mu }(\Lambda ,m)$.

Table 2. Logical metric entropy and metric entropy [1] for the tent map up to order $m=3$.

m	1	2	3	…	m
$H_{\mu l,m}(\Lambda )$	0	0/75	0.875	…	$1-\frac{1}{2^m}$
$h_{\mu }^{★}(\Lambda ,m)$	0	$ln2$	$ln2$	…	$ln2$

Define $X_m:[0,1]⟶\{0,1\}$ via

$$\begin{array}{c}\hfill X_m(x)=\left\{\begin{array}{cc}0\hfill & \mathrm{if}{\Lambda }^m(x)\in {\alpha }_0,\hfill \\ 1\hfill & \mathrm{if}{\Lambda }^m(x)\in {\alpha }_1,\hfill \end{array}\right.\end{array}$$

for every $m\ge 0$. Let

$$\begin{array}{cc}\hfill & {\alpha }_{00}=[0,\frac{1}{4}]=\{x\in {\alpha }_0:\Lambda (x)\in {\alpha }_0\},{\alpha }_{01}=(\frac{1}{4},\frac{1}{2}]=\{x\in {\alpha }_0:\Lambda (x)\in {\alpha }_1\},\hfill \\ \hfill & {\alpha }_{10}=[\frac{3}{4},1]=\{x\in {\alpha }_1:\Lambda (x)\in {\alpha }_0\},{\alpha }_{11}=(\frac{1}{2},\frac{3}{4})=\{x\in {\alpha }_1:\Lambda (x)\in {\alpha }_1\}.\hfill \end{array}$$

Given ${\alpha }_{i_1\dots i_m}$, where $m\in \mathbb{N}$, set

$$\begin{array}{c}\hfill {\alpha }_{i_1\dots i_{m}0}={\alpha }_{i_1\dots i_m}\bigcap \{x\in [0,1]:{\Lambda }^m(x)\in {\alpha }_0\},\end{array}$$

$$\begin{array}{c}\hfill {\alpha }_{i_1\dots i_{m}1}={\alpha }_{i_1\dots i_m}\bigcap \{x\in [0,1]:{\Lambda }^m(x)\in {\alpha }_1\},\end{array}$$

and

$$\begin{array}{c}\hfill {\alpha }_{i_0{i}_1\dots i_m}=\bigcap _{k=0}^m{\Lambda }^{-k}{\alpha }_{i_k}.\end{array}$$

Therefore,

$$\begin{array}{cc}\hfill & {\alpha }_{000}=[0,\frac{1}{8}],{\alpha }_{001}=(\frac{1}{8},\frac{1}{4}],{\alpha }_{010}=[\frac{3}{8},\frac{1}{2}],{\alpha }_{011}=(\frac{1}{4},\frac{3}{8}),\hfill \\ \hfill & {\alpha }_{100}=[\frac{7}{8},1],{\alpha }_{101}=[\frac{3}{4},\frac{7}{8}),{\alpha }_{110}=(\frac{1}{2},\frac{5}{8}],{\alpha }_{111}=(\frac{5}{8},\frac{3}{4}),\hfill \\ \hfill & {\alpha }_{0000}=[0,\frac{1}{16}],{\alpha }_{0001}=(\frac{1}{16},\frac{1}{8}],{\alpha }_{0010}=[\frac{3}{16},\frac{1}{4}],{\alpha }_{0011}=(\frac{1}{8},\frac{3}{16}),\hfill \\ \hfill & {\alpha }_{0100}=[\frac{7}{16},\frac{1}{2}],{\alpha }_{0101}=[\frac{3}{8},\frac{7}{16}),{\alpha }_{0110}=(\frac{1}{4},\frac{5}{16}],{\alpha }_{0111}=(\frac{5}{16},\frac{3}{8}),\hfill \\ \hfill & {\alpha }_{1000}=[\frac{15}{16},1],{\alpha }_{1000}=[\frac{7}{8},\frac{15}{16}),{\alpha }_{1010}=[\frac{3}{4},\frac{13}{16}],{\alpha }_{1011}=(\frac{13}{16},\frac{7}{8}),\hfill \\ \hfill & {\alpha }_{1100}=(\frac{1}{2},\frac{9}{16}],{\alpha }_{1101}=(\frac{9}{16},\frac{5}{8}],{\alpha }_{1110}=[\frac{11}{16},\frac{3}{4}),{\alpha }_{1111}=(\frac{5}{8},\frac{3}{4}).\hfill \end{array}$$

The sets $\left\{{\alpha }_{i_0\dots i_{m-1}}\right\}$ are identical to the binary sequences of 0, 1 in length m.

Hence, $\mu ({\alpha }_{i_0\dots i_{m-1}})=\frac{1}{2^m}$ and, thus,

$$\begin{array}{cc}\hfill H_{\mu l}(X_0^{m-1})& =1-\sum _{i_0\dots i_{m-1}}{(\mu ({\alpha }_{i_1\dots i_m}))}^2=1-\sum _{i_0^{m-1}}{(\frac{1}{2^m})}^2\hfill \\ \hfill & =1-2^m\times \frac{1}{2^{2m}}=\frac{2^m-1}{2^m}.\hfill \end{array}$$

So, $h_{\mu l}(\mathbf{X})=1$, $h_{\mu l}(\Lambda ,\alpha )=1$ and $h_{\mu l}(\Lambda )=1$. Furthermore, if

$$\begin{array}{c}\hfill \mathbf{X}=(X_1,X_1,X_1,\dots ),\end{array}$$

then $H_{\mu l}(X_1,\dots ,X_1)=H_{\mu l}(X_1)$ and $h_{\mu l}(\mathbf{X})=\frac{1}{2}$.

Example 3.

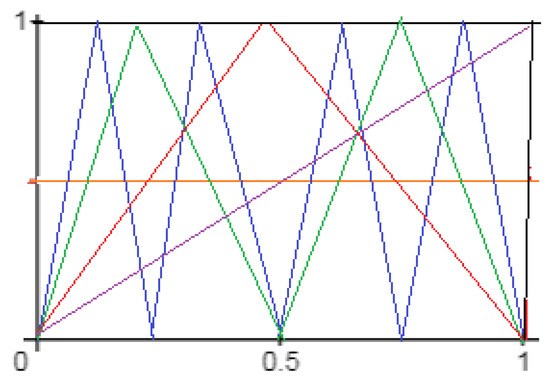
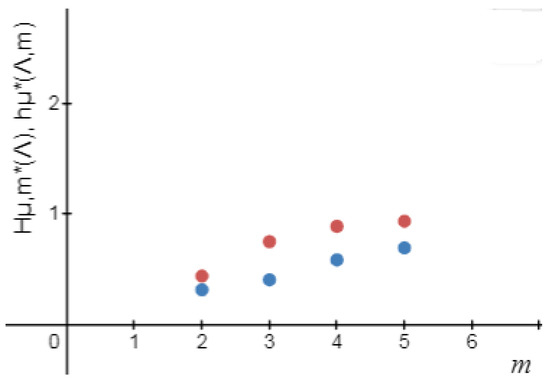
Reference [1]. Consider the symmetric tent map in Example 2, we obtain (Figure 5 and Figure 6 and Table 3)

$$\begin{array}{cc}\hfill & p_{(0,1)}=(0,\frac{2}{3}),p_{(1,0)}=(\frac{2}{3},1),\hfill \\ \hfill & p_{(0,1,2)}=(0,\frac{1}{3}),p_{(0,2,1)}=(\frac{1}{3},\frac{2}{5}),p_{(2,0,1)}=(\frac{2}{5},\frac{2}{3}),\hfill \\ \hfill & p_{(1,0,2)}=(\frac{2}{3},\frac{4}{5}),p_{(1,2,0)}=(\frac{4}{5},1),p_{(2,1,0)}=\varnothing ,\hfill \\ \hfill & p_{(0,1,2,3)}=(0,\frac{1}{6}),p_{(0,1,3,2)}=(\frac{1}{6},\frac{1}{5}),p_{(0,3,1,2)}=(\frac{1}{5},\frac{2}{9})\cup (\frac{2}{7},\frac{1}{3}),\hfill \\ & p_{(3,0,1,2)}=(\frac{2}{9},\frac{2}{7}),p_{(0,2,1,3)}=(\frac{1}{3},\frac{2}{5}),p_{(2,0,3,1)}=(\frac{2}{5},\frac{4}{9})\cup (\frac{4}{7},\frac{3}{5}),\hfill \\ \hfill & p_{(2,3,0,1)}=(\frac{4}{9},\frac{4}{7}),p_{(2,0,1,3)}=(\frac{3}{5},\frac{2}{3}),p_{(3,1,0,2)}=(\frac{2}{3},\frac{4}{5}),\hfill \\ \hfill & p_{(1,3,2,0)}=(\frac{4}{5},\frac{5}{6}),p_{(1,2,0,3)}=(\frac{6}{7},\frac{8}{9}),p_{(1,2,3,0)}=(\frac{5}{6},\frac{6}{7})\cup (\frac{8}{9},1).\hfill \end{array}$$

Figure 5. $x,\Lambda (x),{\Lambda }^2(x)\mathrm{and}{\Lambda }^3(x)$.

Figure 6. $H_{\mu l,m}^{*}(\Lambda ),\mathrm{and}{h}_{\mu }^{*}(\Lambda ,m)$.

Table 3. Logical metric permutation entropy and metric permutation entropy [1] for the tent map up to order $m=4$.

m	1	2	3	4
$H_{\mu l,m}^{★}(\Lambda )$	0	0/444	0/756	0/894
$h_{\mu }^{★}(\Lambda ,m)$	0	0/32	0/41	0/59

Therefore,

$$\begin{array}{cc}\hfill & \sum _{\pi \in {\mathcal{S}}_2}{(\mu (p_{\pi }))}^2={(\frac{2}{3})}^2+{(\frac{1}{3})}^2=\frac{5}{9}\simeq 0/556,\hfill \\ \hfill & H_{\mu l,2}^{★}(\Lambda )=1-\frac{5}{9}=\frac{4}{9}\simeq 0/444,\hfill \\ \hfill & \sum _{\pi \in {\mathcal{S}}_3}{(\mu (p_{\pi }))}^2={(\frac{1}{3})}^2+{(\frac{1}{15})}^2+{(\frac{4}{15})}^2+{(\frac{2}{15})}^2+{(\frac{1}{5})}^2=\frac{11}{45}\simeq 0/244,\hfill \\ \hfill & H_{\mu l,3}^{★}(\Lambda )=1-\frac{11}{45}=\frac{34}{45}\simeq 0/756,\hfill \\ \hfill & \sum _{\pi \in {\mathcal{S}}_4}{(\mu (p_{\pi }))}^2\simeq 0.106,\hfill \\ \hfill & H_{\mu l,4}^{★}(\Lambda )\simeq 0/894.\hfill \end{array}$$

Furthermore,

$$\begin{array}{c}\hfill h_{\mu l}^{★}(\Lambda )=\underset{m\to \infty }{lim}{H}_{\mu l,m}^{★}(\Lambda )=1=h_{\mu l}(\Lambda ).\end{array}$$

Example 4.

Let $I=[0,1]$ endowed with the measure ν,

$$\begin{array}{c}\hfill \nu (A)={\chi }_A(\frac{1}{2})=\left\{\begin{array}{cc}1\hfill & if\frac{1}{2}\in A\hfill \\ 0\hfill & if\frac{1}{2}\notin A,\hfill \end{array}\right.\end{array}$$

and let $f:[0,1]⟶[0,1]$ be a function. Then $h_{\nu l}(f,\alpha )=0$ for every partition α. Hence, $h_{\nu l}(f)=0$.

5. Concluding Remarks

We introduced the concept of the logical entropy of random variables. In addition, we found a bound for the logical entropy of a random variable. We also extended the Shannon and permutation entropies to information sources. Finally, we used these results to estimate the logical entropy of the maps. In this article, we only introduced the concept of logical entropy for information systems. In future studies, researchers can find methods that calculate or estimate the numerical value of this type of entropy. It is pertinent to mention that, in the future, Rényi’s metric entropy and Rényi’s permutation entropy can be generalized for information sources. Another important problem is to extend this idea for quantum logical entropy, as it is a good direction to investigate the existence of such results.