Information Bottleneck Signal Processing and Learning to Maximize Relevant Information for Communication Receivers
Abstract
:1. Introduction
2. The Information Bottleneck Method and Coarsely Quantized Information Bottleneck Signal Processing
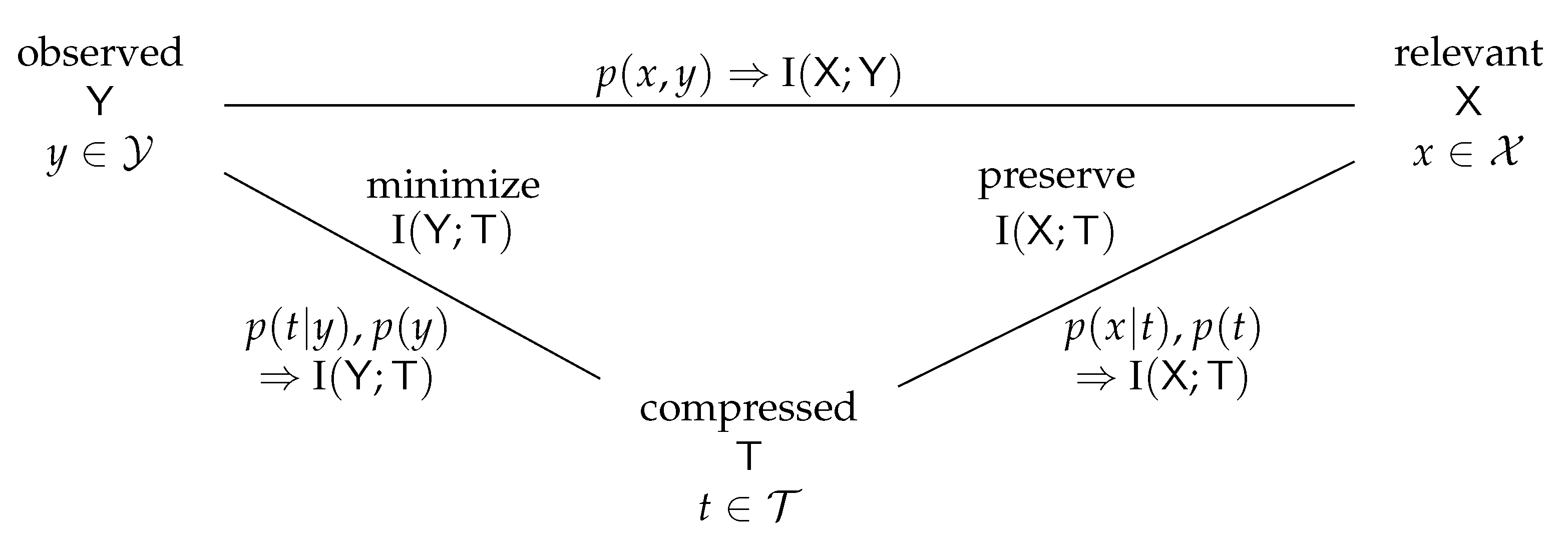
2.1. The Information Bottleneck Method
- Conduct a lossy compression of the realizations to a compressed realization to yield a compact compressed representation of the observation . The information theoretical notion of such a compression is the minimization of the compression information I (i.e., the transmission rate, relating to rate–distortion theory).
- While conducting the compression mentioned above, preserve the relevant information .
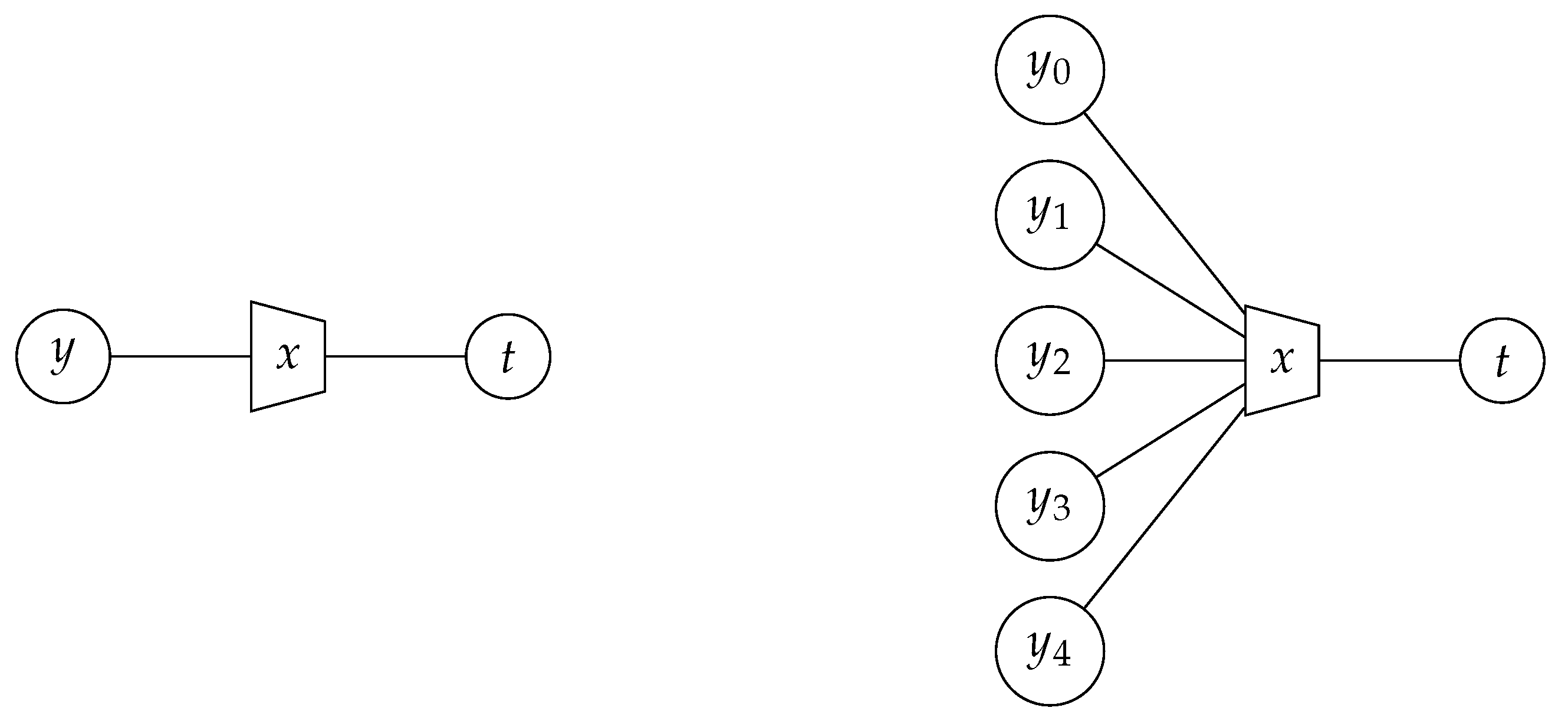
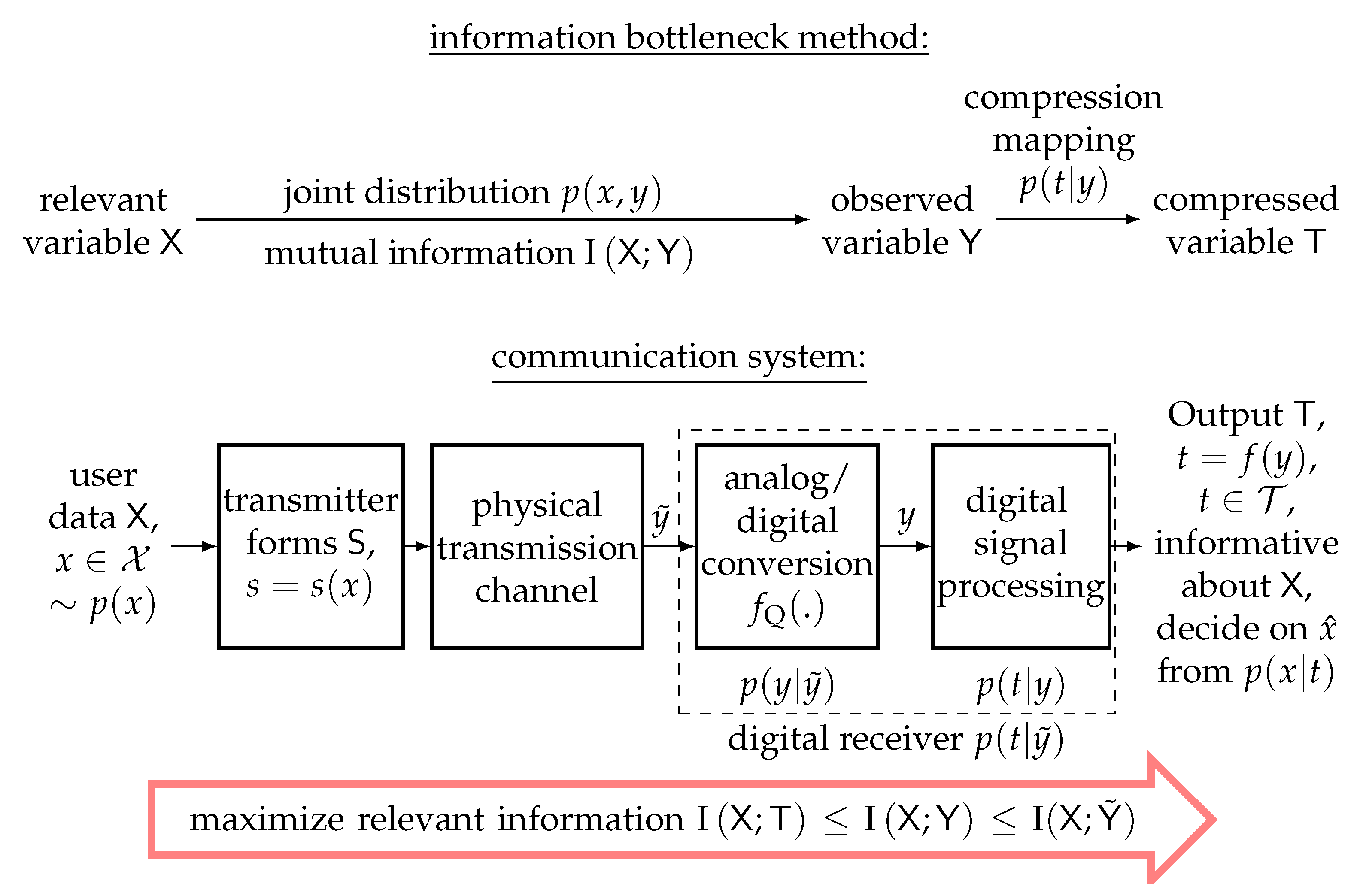
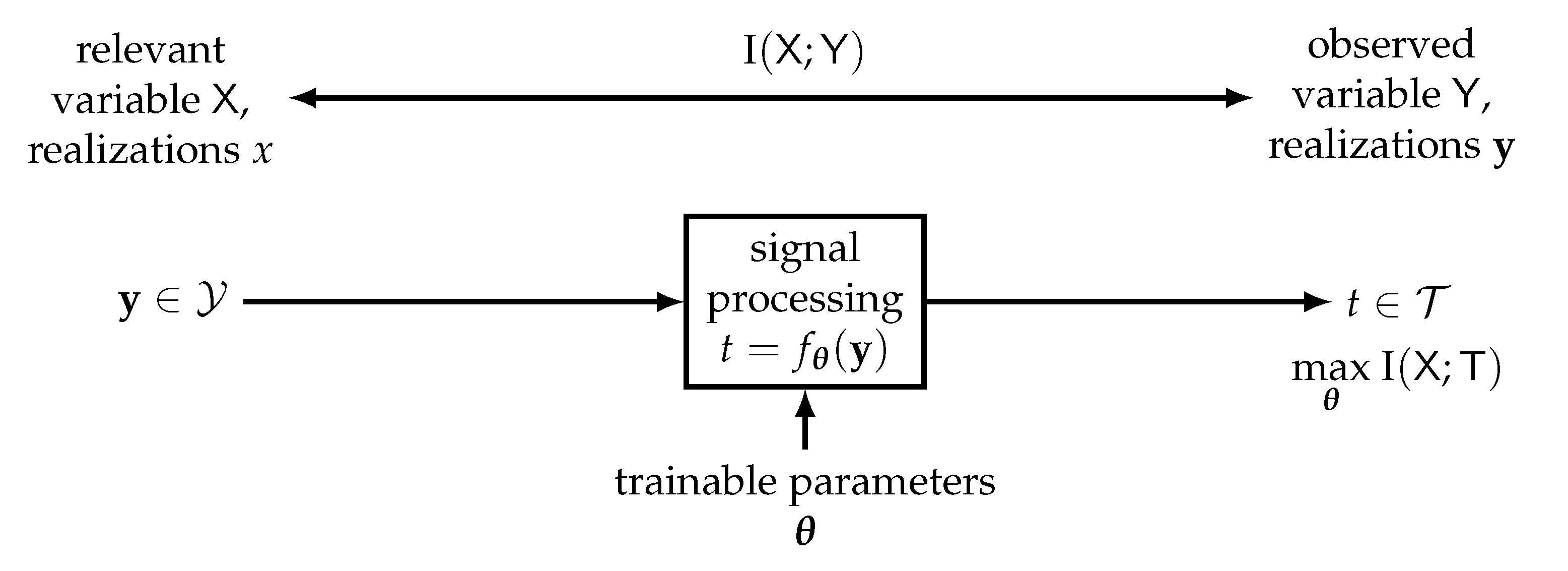
2.2. General View on Information Bottleneck Signal Processing for Receiver Design
2.3. An Example of Information Bottleneck Receiver Design with Iterative Detection and Decoding
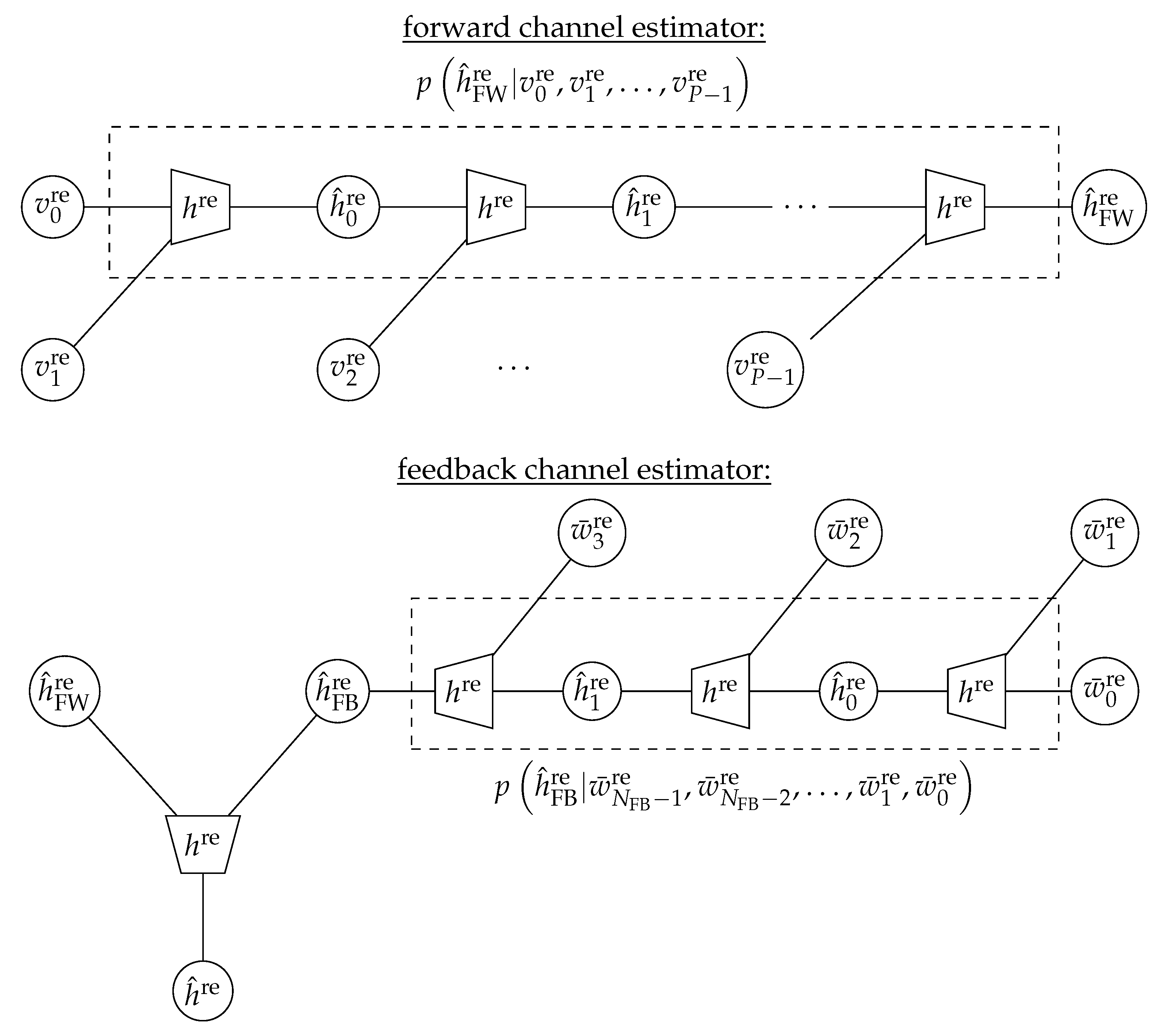
2.3.1. Information Bottleneck Channel Estimation
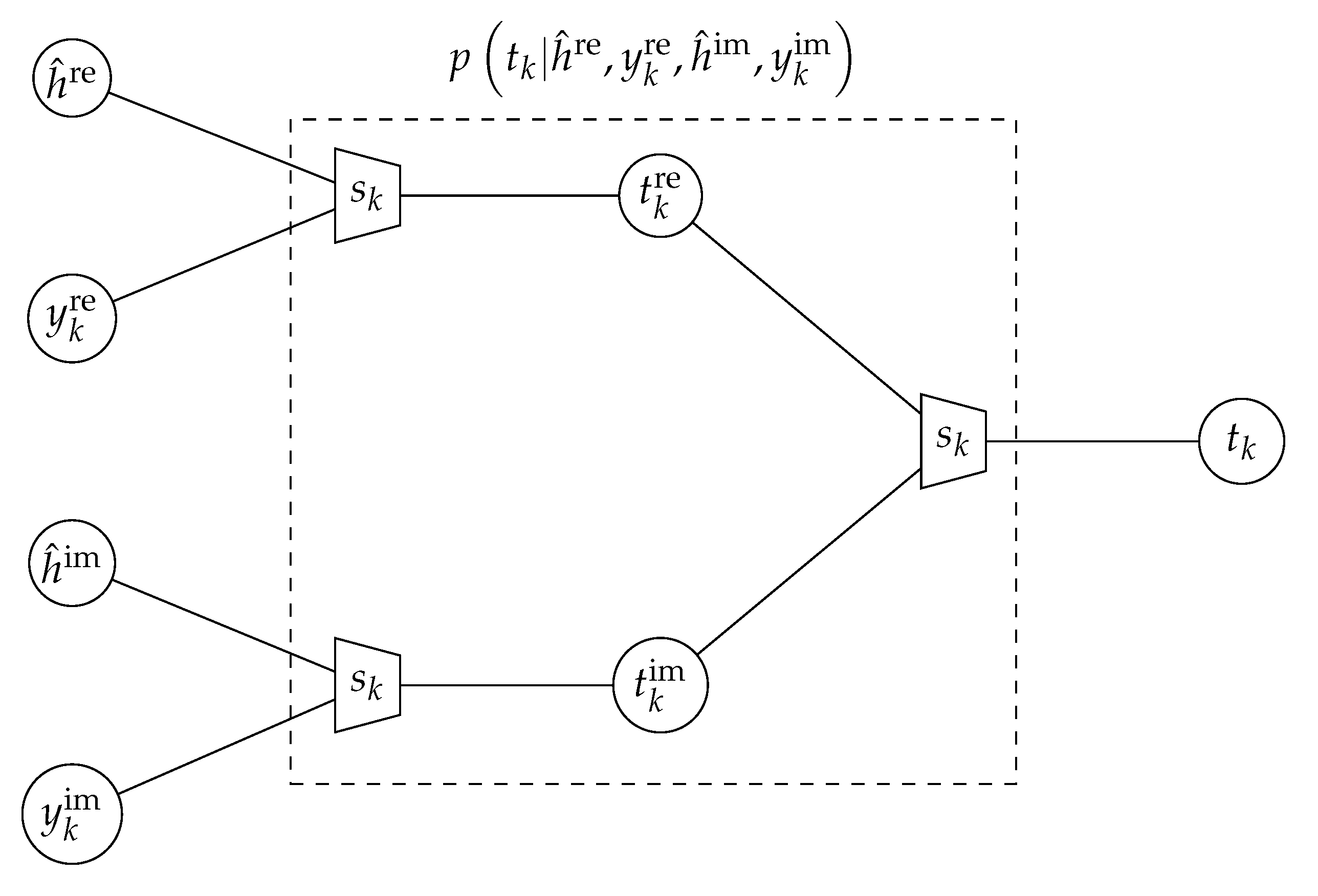
2.3.2. Information Bottleneck Detection
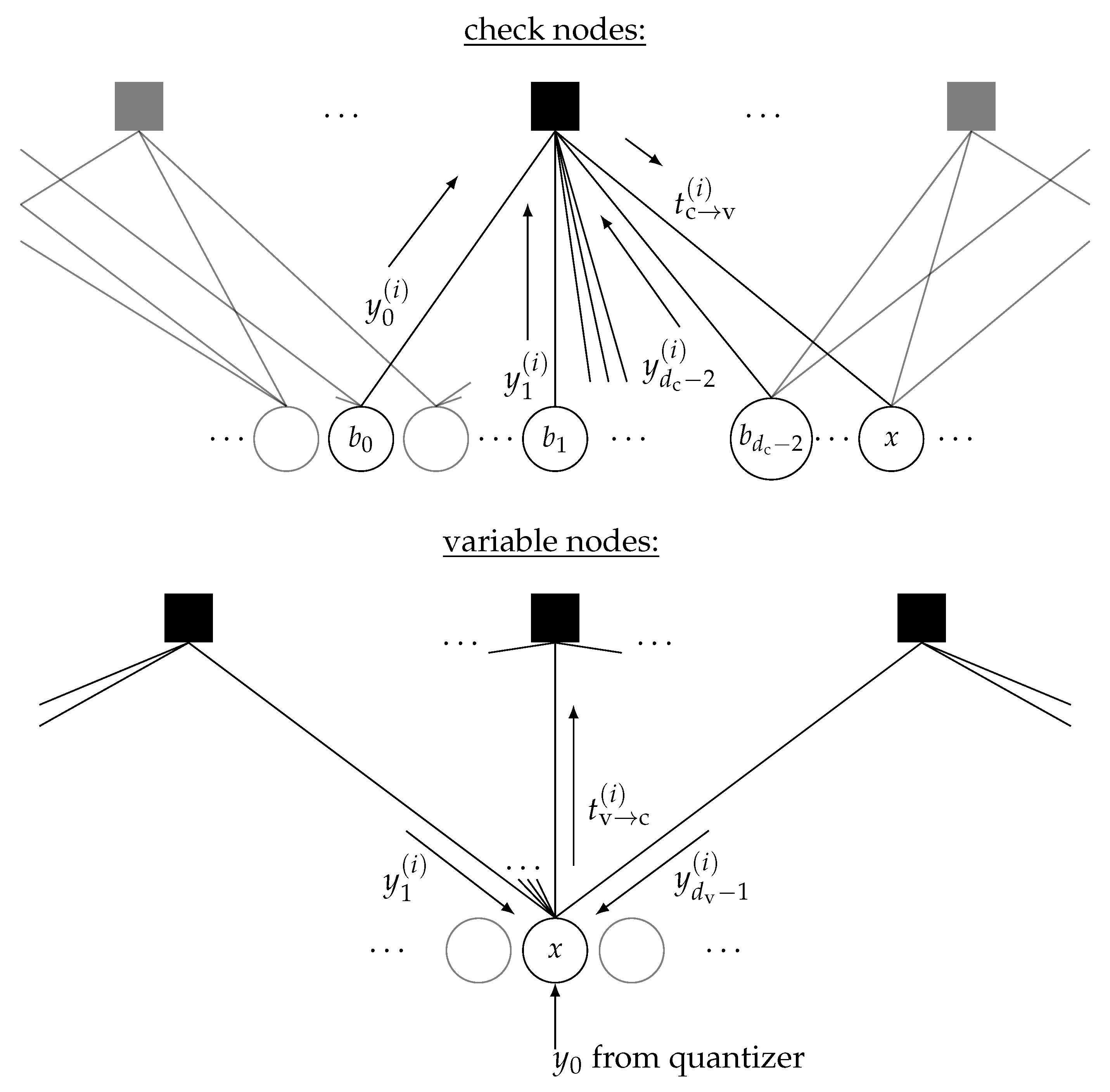
2.3.3. Information Bottleneck LDPC Decoder Design
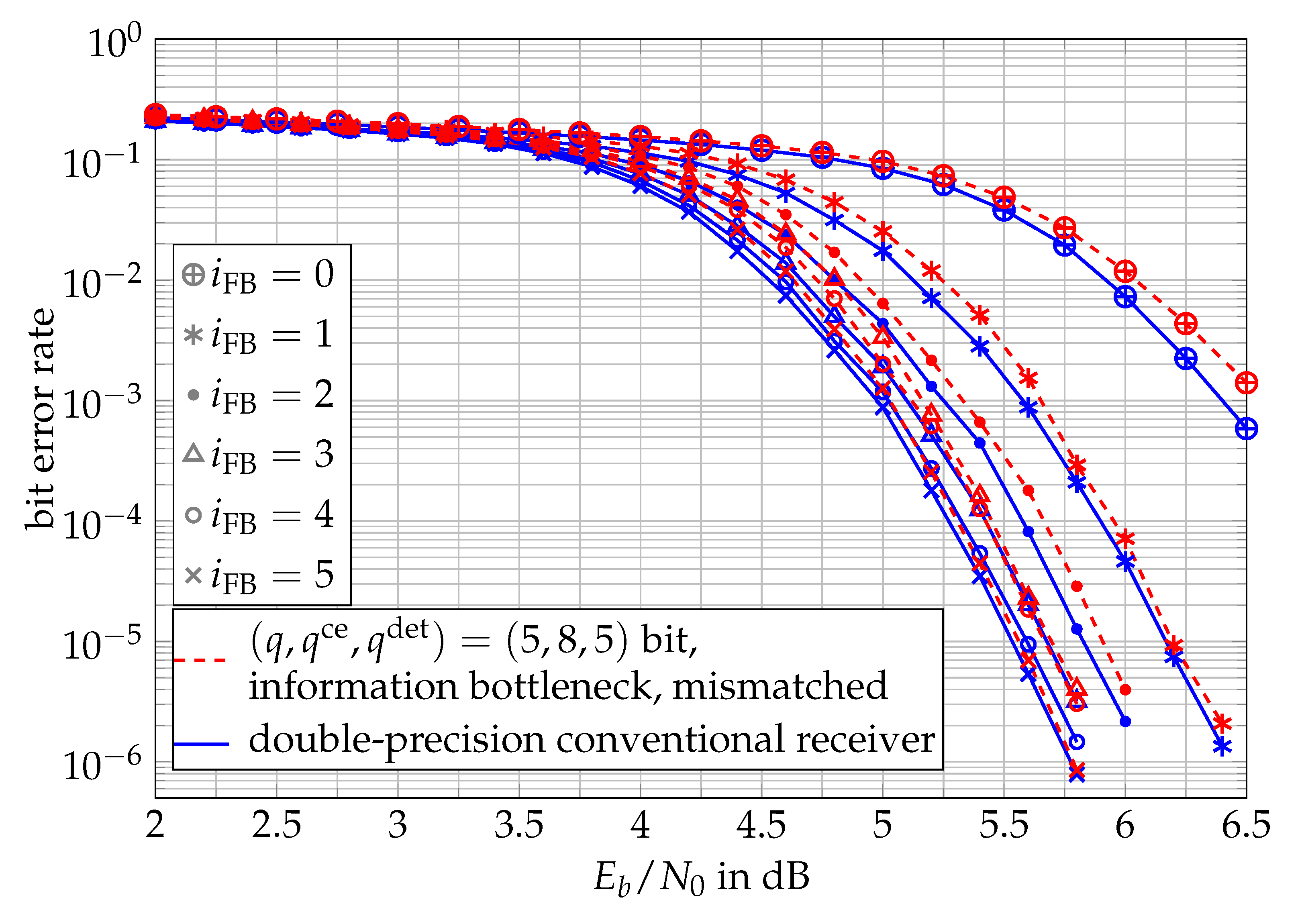
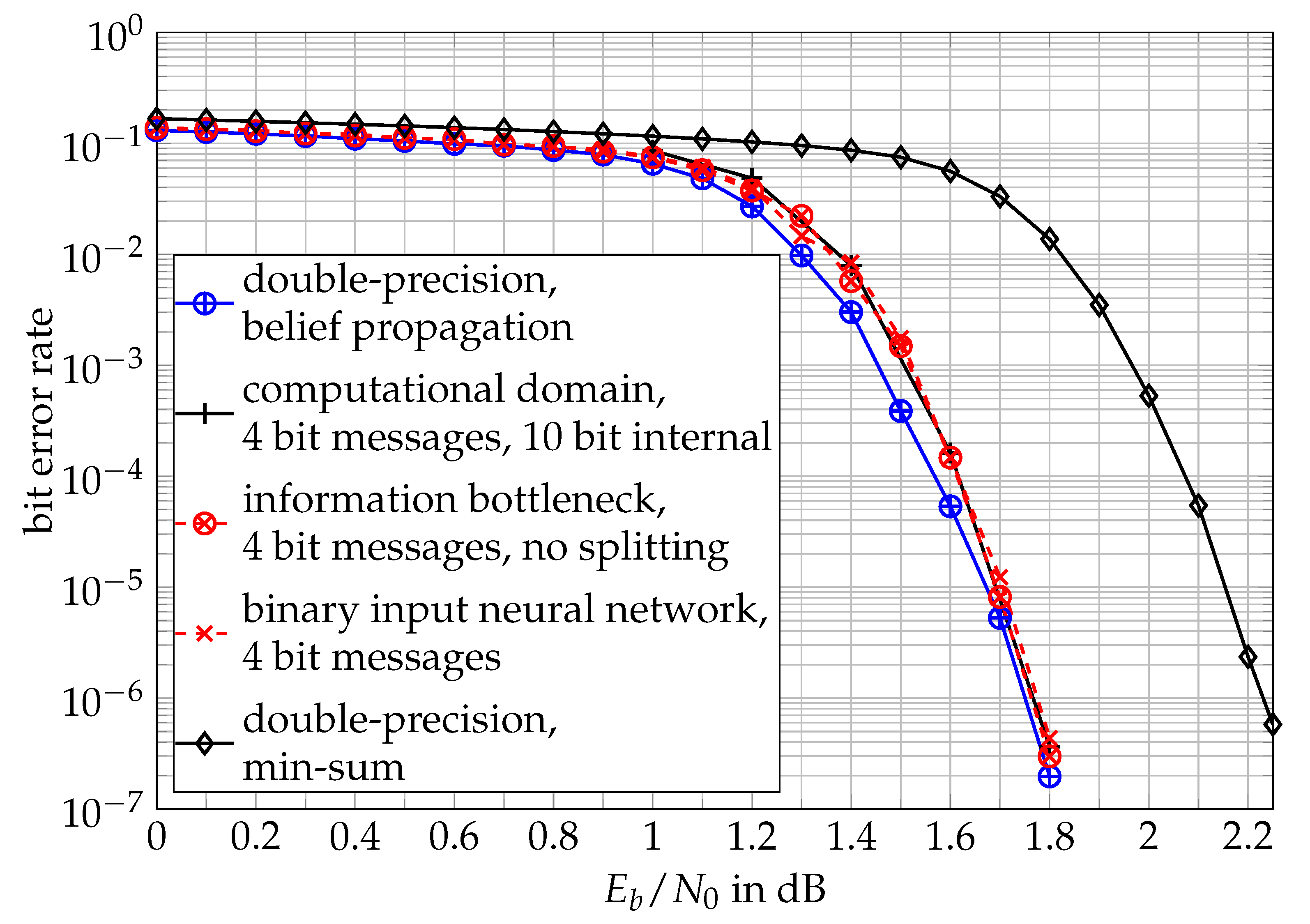
2.3.4. Comparison of Iterative Receiver Performances
3. Parameter Learning of Trainable Functions to Maximize the Relevant Information
3.1. Lookup Tables
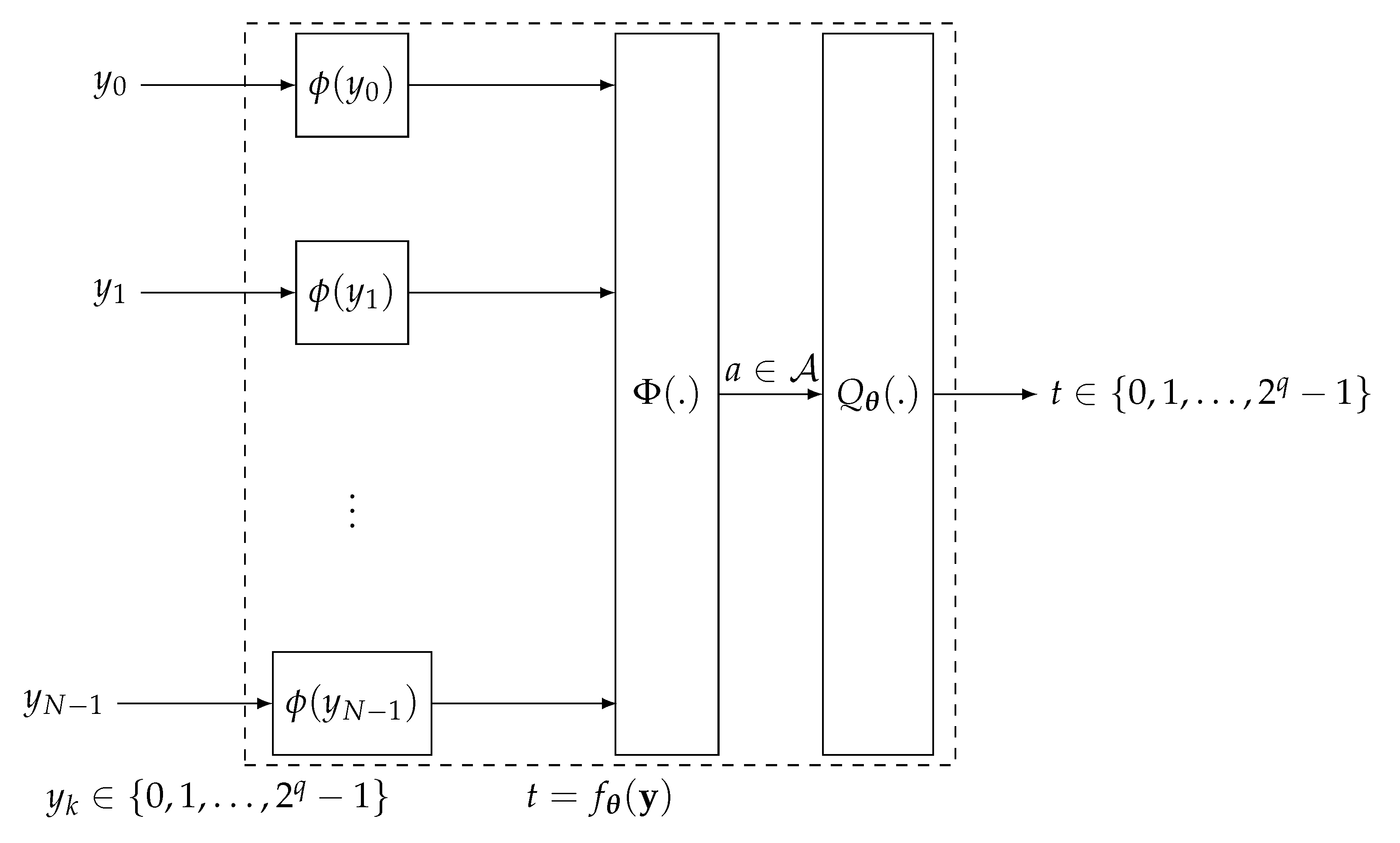
3.2. Computational Domain Technique
- Use a predefined reconstruction function to transfer the incoming messages to numbers in a computational domain ;
- Use a function to process the numbers in the computational domain and to map them onto a single number ;
- Apply a scalar quantizer with ordered thresholds on a that quantizes back to the set .
3.3. Neural Networks
3.4. Further Discussion, Other Approaches and Future Work
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Tishby, N.; Pereira, F.C.; Bialek, W. The information bottleneck method. In Proceedings of the 37th Allerton Conference on Communication and Computation, Monticello, NY, USA, 22–24 September 1999; pp. 368–377. [Google Scholar]
- Slonim, N. The Information Bottleneck: Theory and Applications. Ph.D. Thesis, Hebrew University, Jerusalem, Israel, 2002. [Google Scholar]
- Slonim, N.; Somerville, R.; Tishby, N.; Lahav, O. Objective classification of galaxy spectra using the information bottleneck method. Mon. Not. R. Astron. Soc. 2001, 323, 270–284. [Google Scholar] [CrossRef] [Green Version]
- Bardera, A.; Rigau, J.; Boada, I.; Feixas, M.; Sbert, M. Image segmentation using information bottleneck method. IEEE Trans. Image Process. 2009, 18, 1601–1612. [Google Scholar] [CrossRef] [Green Version]
- Buddha, S.; So, K.; Carmena, J.; Gastpar, M. Function identification in neuron populations via information bottleneck. Entropy 2013, 15, 1587–1608. [Google Scholar] [CrossRef] [Green Version]
- Zaidi, A.; Agueri, I.-E.; Shamai, S. On the information bottleneck problems, connections, applications and information theoretic views. Entropy 2020, 22, 151. [Google Scholar] [CrossRef] [Green Version]
- Goldfeld, Z.; Polyanskiy, Y. The information bottleneck problem and its applications in machine learning. IEEE J. Sel. Areas Inf. Theory 2020, 1, 19–38. [Google Scholar] [CrossRef]
- Zeitler, G. Low-precision analog-to-digital conversion and mutual information in channels with memory. In Proceedings of the 2010 48th Annual Allerton Conference on Communication, Control, and Computing (Allerton’2010), Monticello, NY, USA, 29 September–1 October 2010; pp. 745–752. [Google Scholar]
- Zeitler, G.; Singer, A.C.; Kramer, G. Low-precision A/D conversion for maximum information rate in channels with memory. IEEE Trans. Commun. 2012, 60, 2511–2521. [Google Scholar] [CrossRef]
- Kurkoski, B.M.; Yagi, H. Quantization of binary-input discrete memoryless channels. IEEE Trans. Inf. Theory 2014, 60, 4544–4552. [Google Scholar] [CrossRef]
- Kurkoski, B.M.; Yamaguchi, K.; Kobayashi, K. Noise thresholds for discrete LDPC decoding mappings. In Proceedings of the 2008 IEEE Global Telecommunications Conference (GLOBECOM’2008), New Orleans, LA, USA, 30 November–4 December 2008; pp. 1–5. [Google Scholar]
- Meidlinger, M.; Balatsoukas-Stimming, A.; Burg, A.; Matz, G. Quantized message passing for LDPC codes. In Proceedings of the 2015 49th Asilomar Conference on Signals, Systems and Computers (ACSSC’2015), Pacific Grove, CA, USA, 8–11 November 2015; pp. 1606–1610. [Google Scholar]
- Lewandowsky, J.; Bauch, G. Trellis based node operations for LDPC decoders from the information bottleneck method. In Proceedings of the 2015 9th International Conference on Signal Processing and Communication Systems (ICSPCS’2015), Cairns, Australia, 14–16 December 2015; pp. 1–10. [Google Scholar]
- Romero, F.J.C.; Kurkoski, B.M. LDPC decoding mappings that maximize mutual information. IEEE J. Sel. Areas Commun. 2016, 34, 2391–2401. [Google Scholar] [CrossRef]
- Lewandowsky, J.; Stark, M.; Bauch, G. Optimum message mapping LDPC decoders derived from the sum-product algorithm. In Proceedings of the 2016 IEEE International Conference on Communications (ICC’2016), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–5. [Google Scholar]
- Meidlinger, M.; Matz, G. On irregular LDPC codes with quantized message passing decoding. In Proceedings of the 2017 IEEE 18th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC’2017), Sapporo, Japan, 3–6 July 2017; pp. 1–5. [Google Scholar]
- Lewandowsky, J.; Bauch, G. Information-optimum LDPC decoders based on the information bottleneck method. IEEE Access 2018, 6, 4054–4071. [Google Scholar] [CrossRef]
- Stark, M.; Lewandowsky, J.; Bauch, G. Information-optimum LDPC decoders with message alignment for irregular codes. In Proceedings of the 2018 IEEE Global Communications Conference (GLOBECOM’2018), Abu Dhabi, United Arab Emirates, 9–13 December 2018; pp. 1–6. [Google Scholar]
- Stark, M.; Lewandowsky, J.; Bauch, G. Information-bottleneck decoding of high-rate irregular LDPC codes for optical communication using message alignment. Appl. Sci. 2018, 8, 1884. [Google Scholar] [CrossRef] [Green Version]
- Stark, M.; Bauch, G.; Lewandowsky, J. Decoding of non-binary LDPC codes using the information bottleneck method. In Proceedings of the 2019 IEEE International Conference on Communications (ICC’2019), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar]
- Meidlinger, M.; Matz, G.; Burg, A. Design and decoding of irregular LDPC codes based on discrete message passing. IEEE Trans. Commun. 2019, 68, 1329–1343. [Google Scholar] [CrossRef]
- Lewandowsky, J.; Bauch, G.; Tschauner, M.; Oppermann, P. Design and evaluation of information bottleneck LDPC decoders for digital signal processors. IEICE Trans. Commun. 2019, E102-B, 1363–1370. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Cai, K.; Mei, Z. Mutual information-maximizing quantized belief propagation decoding of regular LDPC codes. arXiv 2019, arXiv:1904.0666. [Google Scholar]
- He, X.; Cai, K.; Mei, Z. On mutual information-maximizing quantized belief propagation decoding of LDPC codes. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM’2019), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar]
- Stark, M.; Bauch, G.; Wang, L.; Wesel, R. Information bottleneck decoding of rate-compatible 5G-LDPC codes. In Proceedings of the 2020 IEEE International Conference on Communications (ICC’2020), Taipei, Taiwan, 7–11 December 2020; pp. 1–6. [Google Scholar]
- Stark, M.; Bauch, G.; Wang, L.; Wesel, R. Decoding rate-compatible 5G-LDPC codes with coarse quantization using the information bottleneck method. IEEE Open J. Commun. Soc. 2020, 1, 646–660. [Google Scholar] [CrossRef]
- Stark, M.; Lewandowsky, J.; Bauch, G. Neural information bottleneck decoding. In Proceedings of the 2020 14th International Conference on Signal Processing and Communication Systems (ICSPCS’2020), Adelaide, Australia, 14–16 December 2020; pp. 1–7. [Google Scholar]
- Stark, M. Machine Learning for Reliable Communication under Coarse Quantization. Ph.D. Dissertation, Hamburg University of Technology, Hamburg, Germany, 2021. [Google Scholar]
- Mohr, P.; Bauch, G. Coarsely Quantized Layered Decoding Using the Information Bottleneck Method. In Proceedings of the 2021 IEEE International Conference on Communications (ICC’2021), Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]
- Wang, L.; Terrill, C.; Stark, M.; Li, Z.; Chen, S.; Hulse, C.; Kuo, C.; Wesel, R.; Bauch, G. Reconstruction-Computation-Quantization (RCQ): A Paradigm for Low Bit Width LDPC Decoding. IEEE Trans. Commun. 2022, 70, 2213–2226. [Google Scholar] [CrossRef]
- Stark, M.; Shah, A.; Bauch, G. Polar code construction using the information bottleneck method. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference Workshops (WCNCW’2018), Barcelona, Spain, 15–18 April 2018; pp. 7–12. [Google Scholar]
- Shah, S.A.A.; Stark, M.; Bauch, G. Design of quantized decoders for polar codes using the information bottleneck method. In Proceedings of the 12th International ITG Conference on Systems, Communications and Coding 2019 (SCC’2019), Rostock, Germany, 11–14 February 2019; pp. 1–6. [Google Scholar]
- Shah, S.A.A.; Stark, M.; Bauch, G. Coarsely Quantized Decoding and Construction of Polar Codes Using the Information Bottleneck Method. Algorithms 2019, 12, 192. [Google Scholar] [CrossRef] [Green Version]
- Lewandowsky, J.; Stark, M.; Bauch, G. Information bottleneck graphs for receiver design. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT’2016), Barcelona, Spain, 10–15 July 2016; pp. 1–5. [Google Scholar]
- Lewandowsky, J.; Stark, M.; Bauch, G. Message alignment for discrete LDPC decoders with quadrature amplitude modulation. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT’2017), Aachen, Germany, 25–30 June 2017; pp. 2925–2929. [Google Scholar]
- Lewandowsky, J.; Stark, M.; Mendrzik, R.; Bauch, G. Discrete channel estimation by integer passing in information bottleneck graphs. In Proceedings of the 2017 11th International ITG Conference on Systems, Communications and Coding (SCC’2017), Hamburg, Germany, 6–9 February 2017; pp. 1–6. [Google Scholar]
- Bauch, G.; Lewandowsky, J.; Stark, M.; Oppermann, P. Information-optimum discrete signal processing for detection and decoding. In Proceedings of the 2018 IEEE 87th Vehicular Technology Conference (VTC Spring), Porto, Portugal, 3–6 June 2018; pp. 1–6. [Google Scholar]
- Hassanpour, S.; Monsees, T.; Wübben, D.; Dekorsy, A. Forward-aware information bottleneck-based vector quantization for noisy channels. IEEE Trans. Commun. 2020, 68, 7911–7926. [Google Scholar] [CrossRef]
- Hassanpour, S.; Wübben, D.; Dekorsy, A. Forward-aware information bottleneck-based vector quantization: Multiterminal extensions for parallel and successive retrieval. IEEE Trans. Commun. 2021, 69, 6633–6646. [Google Scholar] [CrossRef]
- Zeitler, G.; Koetter, R.; Bauch, G.; Widmer, J. Design of network coding functions in multihop relay networks. In Proceedings of the 5th International Symposium on Turbo Codes and Related Topics (ISTC’2008), Lausanne, Switzerland, 1–5 September 2008; pp. 249–254. [Google Scholar]
- Zeitler, G.; Koetter, R.; Bauch, G.; Widmer, J. On quantizer design for soft values in the multiple-access relay channel. In Proceedings of the IEEE International Conference on Communications (ICC’2009), Dresden, Germany, 14–18 June 2009; pp. 1–5. [Google Scholar]
- Winkelbauer, A.; Matz, G. Joint network-channel coding for the asymmetric multiple-access relay channel. In Proceedings of the IEEE International Conference on Communications (ICC’2012), Ottawa, ON, Canada, 10–15 June 2012; pp. 2485–2489. [Google Scholar]
- Winkelbauer, A.; Matz, G. Joint network-channel coding in the multiple-access relay channel: Beyond two sources. In Proceedings of the 5th International Symposium on Communications, Control and Signal Processing, Rome, Italy, 2–4 May 2012; pp. 1–5. [Google Scholar]
- Kern, D.; Kühn, V. Practical aspects of compress and forward with BICM in the 3-node relay channel. In Proceedings of the 20th International ITG Workshop on Smart Antennas (WSA), Munich, Germany, 9–11 March 2016; pp. 1–7. [Google Scholar]
- Kern, D.; Kühn, V. On compress and forward with multiple carriers in the 3-node relay channel exploiting information bottleneck graphs. In Proceedings of the 11th International ITG Conference on Systems, Communications and Coding (SCC’2017), Hamburg, Germany, 6–9 February 2017; pp. 1–6. [Google Scholar]
- Kern, D.; Kühn, V. On implicit and explicit channel estimation for compress and forward relaying OFDM schemes designed by information bottleneck graphs. In Proceedings of the 21th International ITG Workshop on Smart Antennas (WSA’2017), Berlin, Germany, 15–17 March 2017; pp. 1–6. [Google Scholar]
- Chen, D.; Kühn, V. Alternating information bottleneck optimization for the compression in the uplink of C-RAN. In Proceedings of the 2016 IEEE International Conference on Communications (ICC’2016), Kuala Lumpur, Malaysia, 22–27 May 2016; pp. 1–7. [Google Scholar]
- Stark, M.; Lewandowsky, J.; Bauch, G. Iterative message alignment for quantized message passing between distributed sensor nodes. In Proceedings of the 2018 IEEE 87th Vehicular Technology Conference (VTC Spring’2018), Porto, Portugal, 3–6 June 2018; pp. 1–6. [Google Scholar]
- Steiner, S.; Kühn, V. Distributed compression using the information bottleneck principle. In Proceedings of the 2021 IEEE International Conference on Communications (ICC’2021), Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]
- Steiner, S.; Kühn, V.; Stark, M.; Bauch, G. Reduced-complexity greedy distributed information bottleneck algorithm. In Proceedings of the 2021 IEEE Statistical Signal Processing Workshop (SSP’2021), Rio de Janeiro, Brazil, 11–14 July 2021; pp. 361–365. [Google Scholar]
- Steiner, S.; Kühn, V.; Stark, M.; Bauch, G. Reduced-complexity optimization of distributed quantization using the information bottleneck principle. IEEE Open J. Commun. Soc. 2021, 2, 1267–1278. [Google Scholar] [CrossRef]
- Steiner, S.; Aminu, A.D.; Kühn, V. Distributed quantization for partially cooperating sensors using the information bottleneck method. Entropy 2022, 24, 438. [Google Scholar] [CrossRef] [PubMed]
- Aguerri, I.-E.; Zaidi, A. Distributed variational representation learning. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 120–138. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moldoveanu, M.; Zaidi, A. On In-network learning. A comparative study with federated and split learning. In Proceedings of the 2021 IEEE 22nd International Workshop on Signal Processing Advances in Wireless Communications (SPAWC’2021), Lucca, Italy, 27–30 September 2021; pp. 221–225. [Google Scholar]
- Moldoveanu, M.; Zaidi, A. In-network learning for distributed training and inference in networks. In Proceedings of the 2021 IEEE Globecom Workshops (GC Wkshps’2021), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar]
- Zhang, J.A.; Kurkoski, B.M. Low-complexity quantization of discrete memoryless channels. In Proceedings of the 2016 International Symposium on Information Theory and Its Applications (ISITA), Monterey, CA, USA, 30 October–2 November 2016; pp. 448–452. [Google Scholar]
- Hassanpour, S.; Wübben, D.; Dekorsy, A. On the equivalence of double maxima and KL-means for information bottleneck-based source coding. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018; pp. 1–6. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Lewandowsky, J.; Stark, M.; Bauch, G. A discrete information bottleneck receiver with iterative decision feedback channel estimation. In Proceedings of the 2018 IEEE 10th International Symposium on Turbo Codes and Iterative Information Processing (ISTC’2018), Hong Kong, China, 25–29 November 2018; pp. 1–5. [Google Scholar]
- Lewandowsky, J. The Information Bottleneck Method in Communications. Ph.D. Thesis, Hamburg University of Technology, Hamburg, Germany, 2020. [Google Scholar]
- Genz, A. Numerical computation of multivariate normal probabilities. J. Comput. Graph. Stat. 1992, 1, 141–149. [Google Scholar]
- MacKay, D.J.C. Encyclopedia of Sparse Graph Codes. Available online: http://www.inference.phy.cam.ac.uk/mackay/codes/data.html (accessed on 14 November 2017).
- Lewandowsky, J.; Dongare, S.J.; Adrat, M.; Schrammen, M.; Jax, P. Optimizing parametrized information bottleneck compression mappings with genetic algorithms. In Proceedings of the 2020 14th International Conference on Signal Processing and Communication Systems (ICSPCS’2020), Adelaide, Australia, 14–16 December 2020; pp. 1–8. [Google Scholar]
- Lewandowsky, J.; Dongare, S.J.; Martín Lima, R.; Adrat, M.; Schrammen, M.; Jax, P. Genetic Algorithms to Maximize the Relevant Mutual Information in Communication Receivers. Electronics 2021, 10, 1434. [Google Scholar] [CrossRef]
- Coley, D.A. An Introduction to Genetic Algorithms for Scientists and Engineers; World Scientific Publishing Co., Inc.: Singapore, 1998. [Google Scholar]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lewandowsky, J.; Bauch, G.; Stark, M. Information Bottleneck Signal Processing and Learning to Maximize Relevant Information for Communication Receivers. Entropy 2022, 24, 972. https://doi.org/10.3390/e24070972
Lewandowsky J, Bauch G, Stark M. Information Bottleneck Signal Processing and Learning to Maximize Relevant Information for Communication Receivers. Entropy. 2022; 24(7):972. https://doi.org/10.3390/e24070972
Chicago/Turabian StyleLewandowsky, Jan, Gerhard Bauch, and Maximilian Stark. 2022. "Information Bottleneck Signal Processing and Learning to Maximize Relevant Information for Communication Receivers" Entropy 24, no. 7: 972. https://doi.org/10.3390/e24070972
APA StyleLewandowsky, J., Bauch, G., & Stark, M. (2022). Information Bottleneck Signal Processing and Learning to Maximize Relevant Information for Communication Receivers. Entropy, 24(7), 972. https://doi.org/10.3390/e24070972







