Information Fragmentation, Encryption and Information Flow in Complex Biological Networks
Abstract
1. Introduction
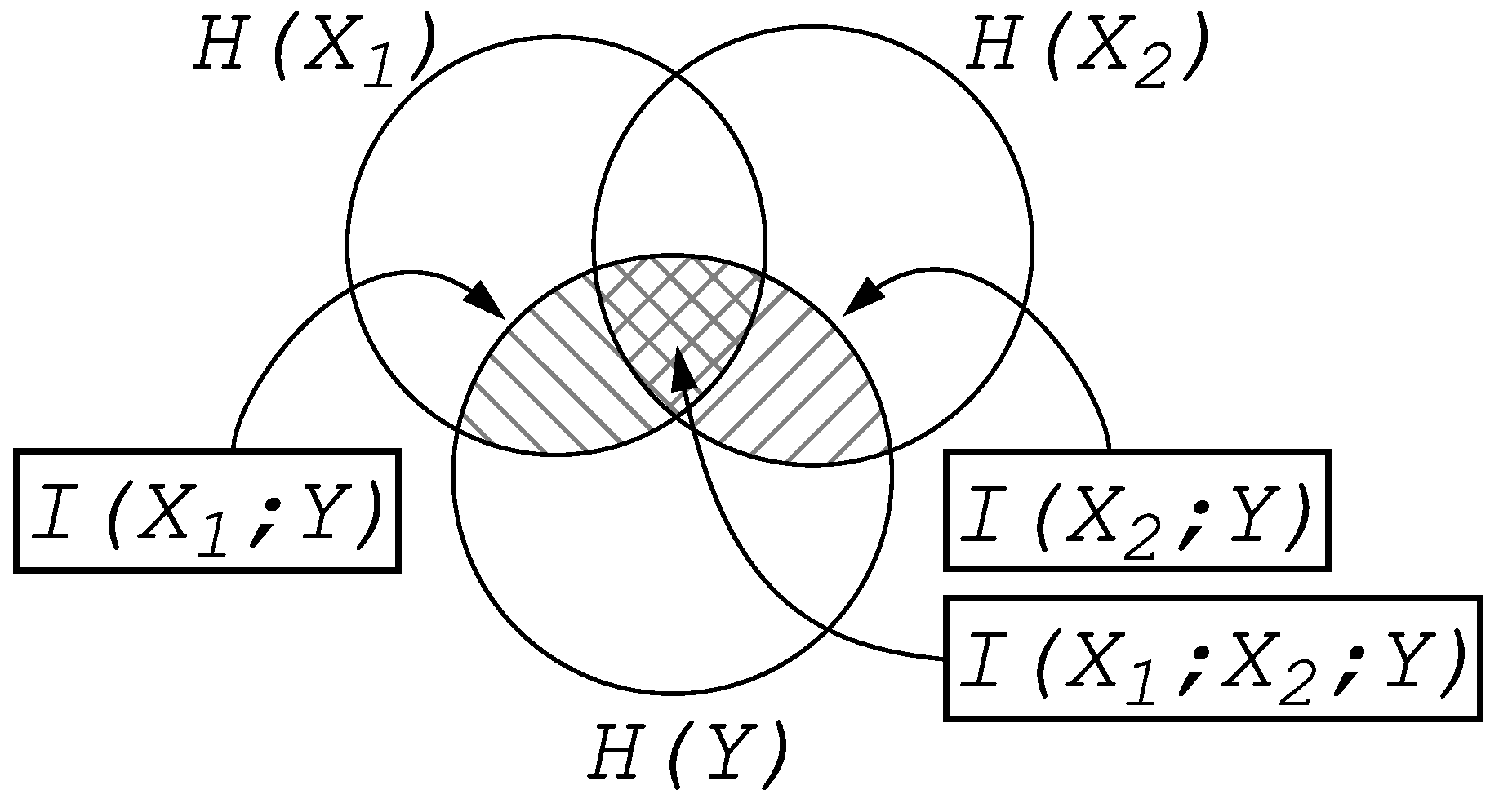
Entropy and Information
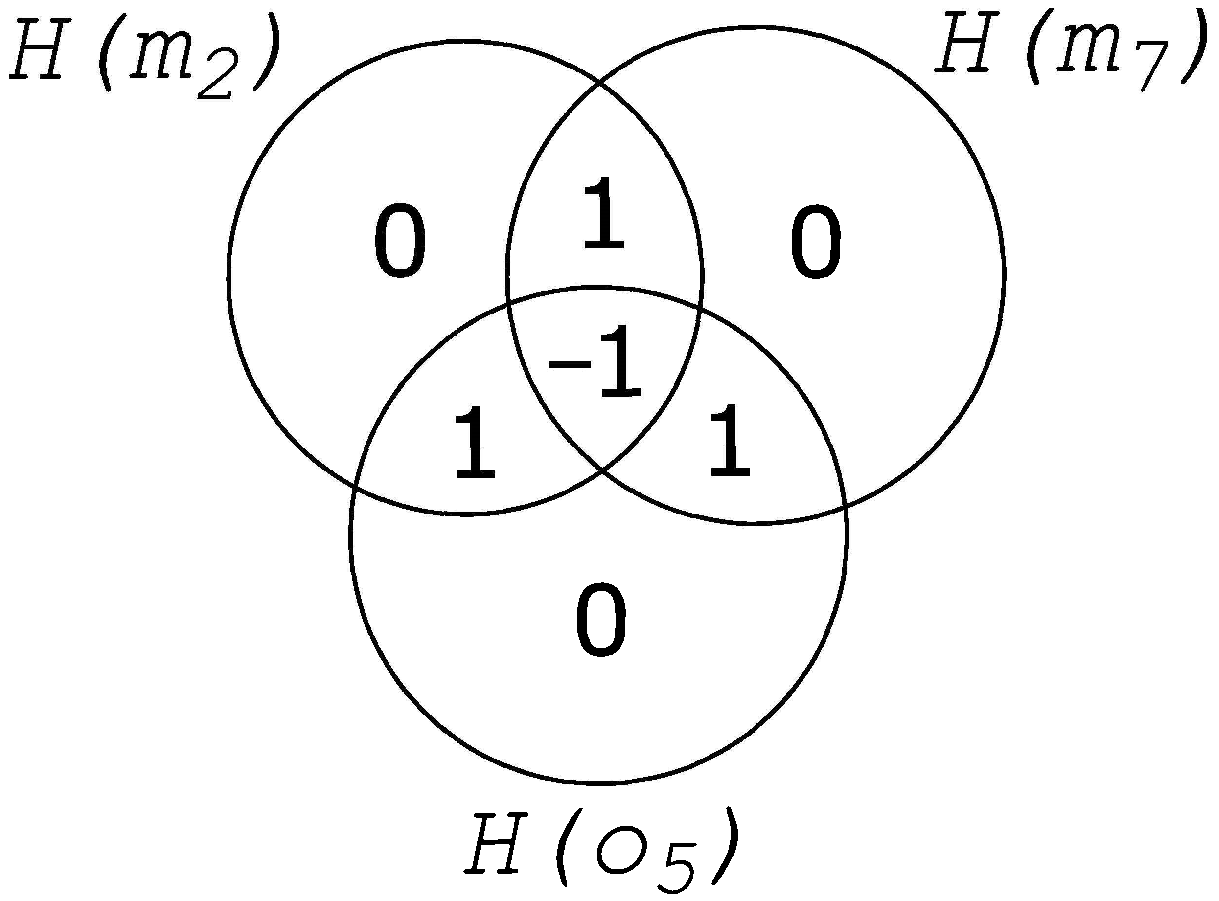
2. Information Fragmentation
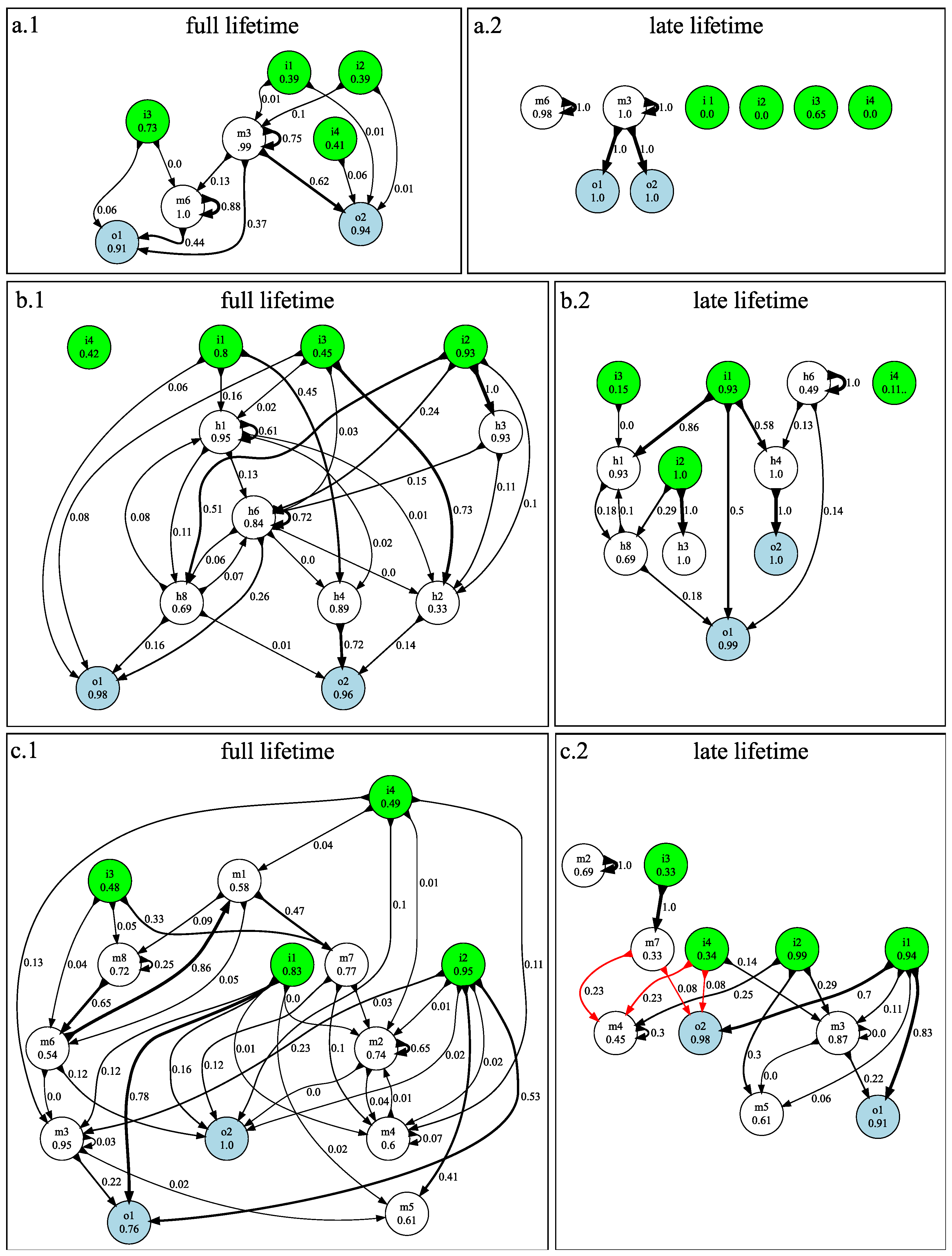
3. Results
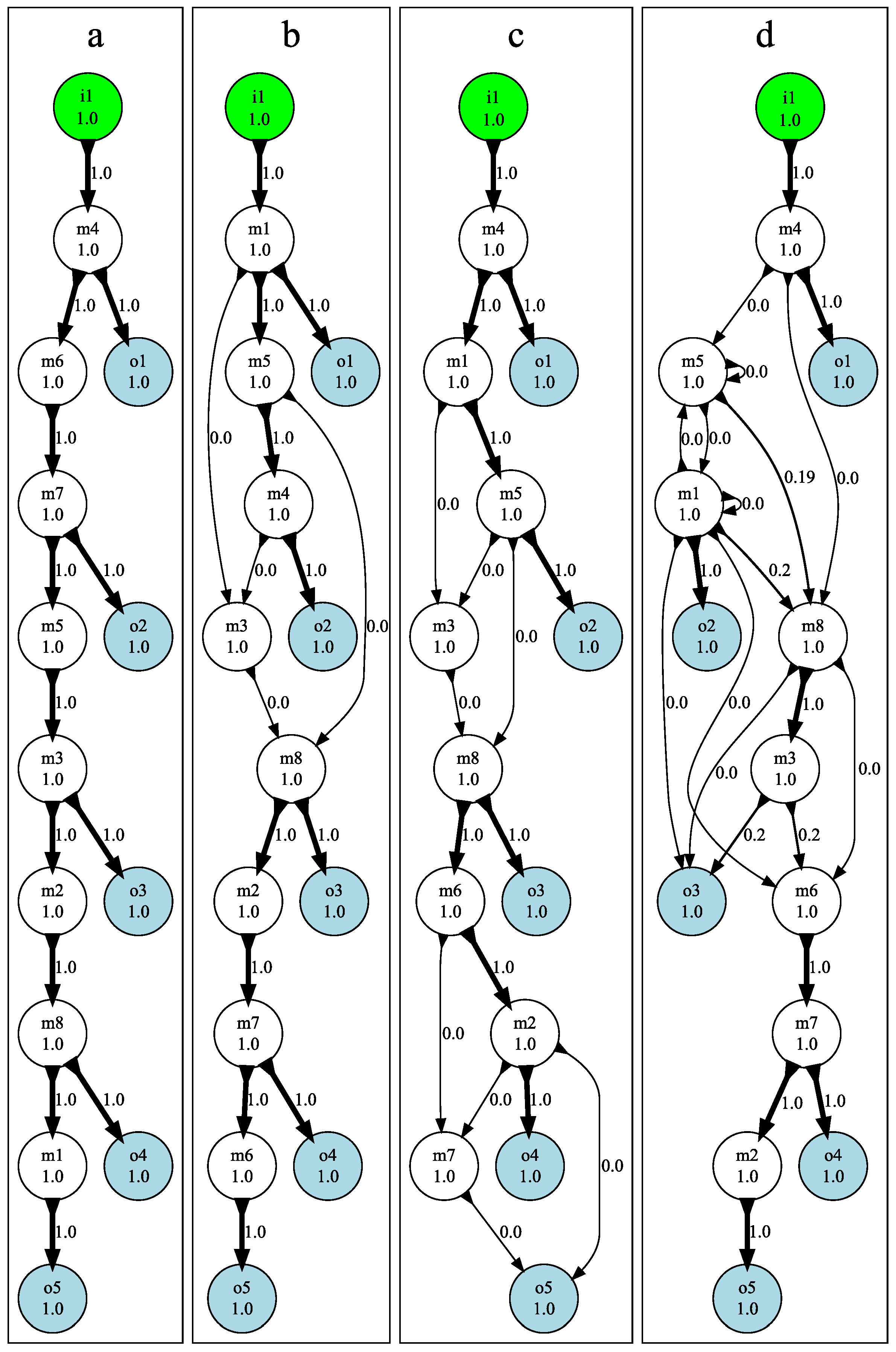
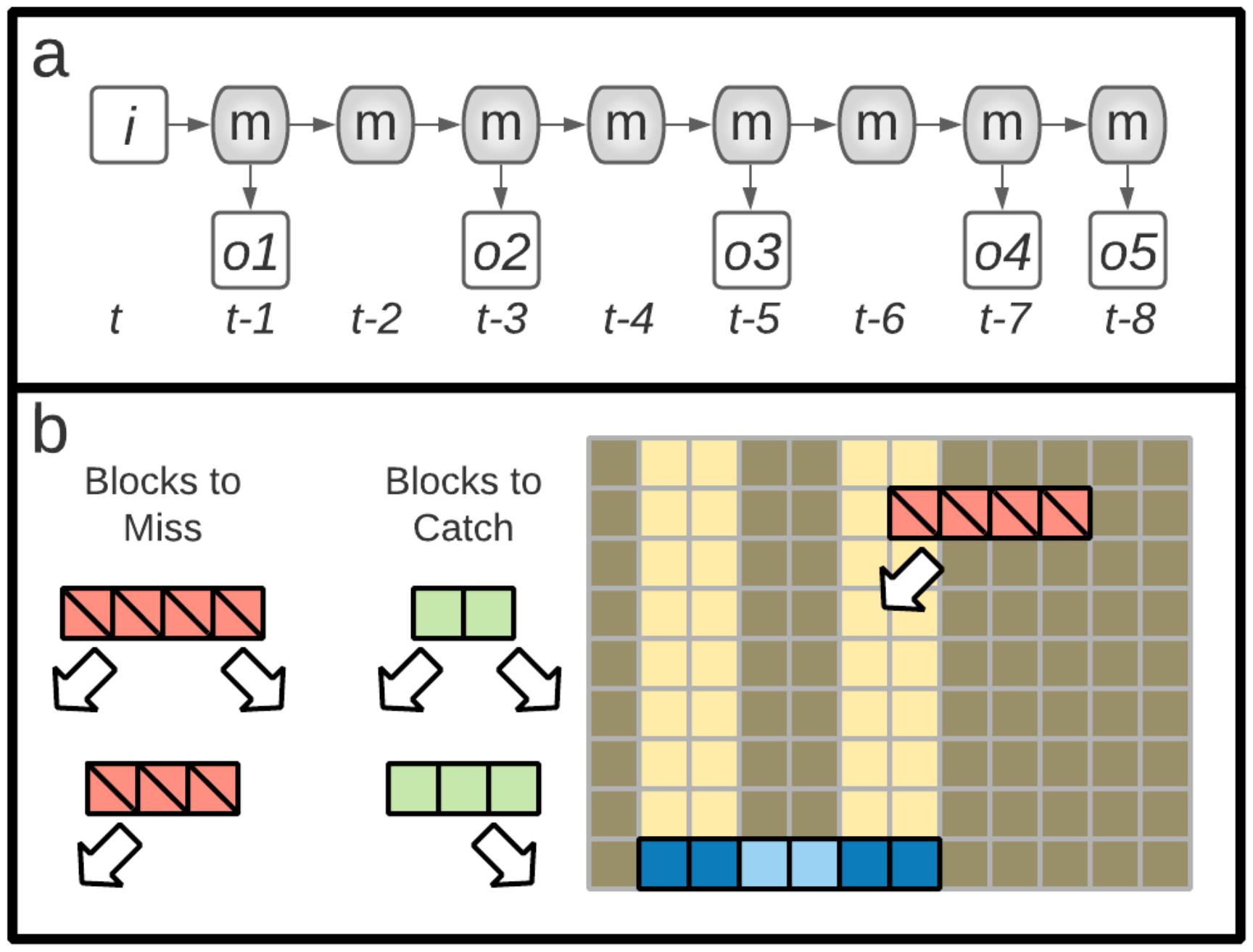
3.1. n-Back Task
3.2. Block Catch Task
3.3. Mutational Robustness of Evolved Networks
4. Discussion
5. Methods
5.1. Fragmentation, Fragmentation Matrices and Information Flow
5.1.1. Data Collection and Formatting
5.1.2. Generating Information Fragmentation Matrices
5.1.3. Determining Fragmentation
5.1.4. Visualizing Information Flow
5.2. Digital Evolution System
5.2.1. Tasks: n-Back
5.2.2. Tasks: Block Catch
5.3. Cognitive Systems
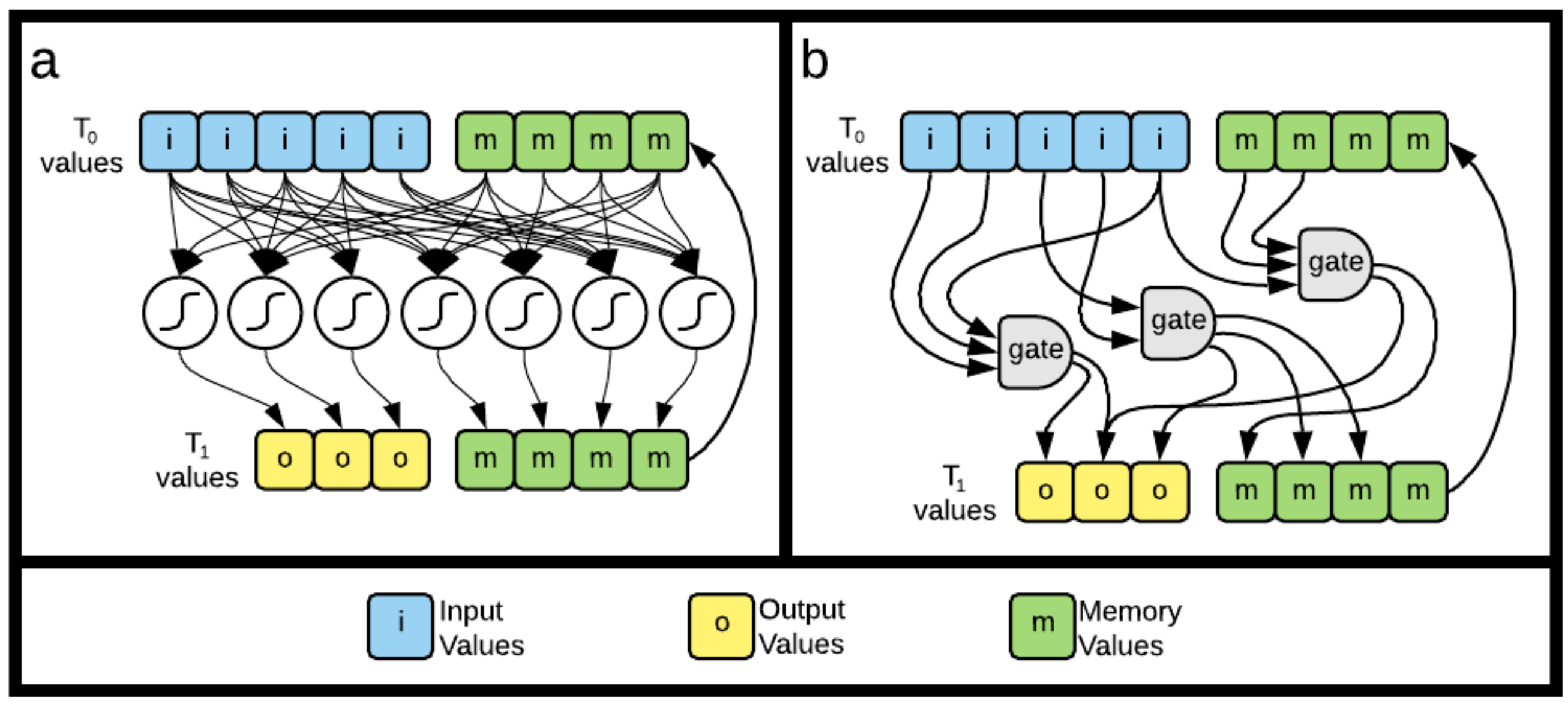
5.3.1. Recurrent Neural Networks
5.3.2. Markov Brains
5.4. Evolutionary Algorithm
5.5. Testing Mutational Robustness
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ACP | Active Categorical Perception |
| MABE | Modular Agent Based Evolver |
| DIS | Distinct Informative Set |
| RNN | Recurrent Neutral Network |
| XOR | Exclusive OR |
References
- Reid, A.T.; Headley, D.B.; Mill, R.D.; Sanchez-Romero, R.; Uddin, L.Q.; Marinazzo, D.; Lurie, D.J.; Valdés-Sosa, P.A.; Hanson, S.J.; Biswal, B.B.; et al. Advancing functional connectivity research from association to causation. Nat. Neurosci. 2019, 22, 1751–1760. [Google Scholar] [CrossRef]
- Ioannidis, J.P.A.; Thomas, G.; Daly, M.J. Validating, augmenting and refining genome-wide association signals. Nat. Rev. Genet. 2009, 10, 318–329. [Google Scholar] [CrossRef]
- Borst, A.; Theunissen, F.E. Information theory and neural coding. Nat. Neurosci. 1999, 2, 947–957. [Google Scholar] [CrossRef]
- Beer, R.D.; Williams, P.L. Information processing and dynamics in minimally cognitive agents. Cogn. Sci. 2015, 39, 1–38. [Google Scholar] [CrossRef]
- Williams, P.L.; Beer, R.D. Nonnegative decomposition of multivariate information. arXiv 2010, arXiv:1004.251. [Google Scholar]
- Timme, N.; Alford, W.; Flecker, B.; Beggs, J.M. Synergy, redundancy, and multivariate information measures: An experimentalist’s perspective. J. Comput. Neurosci. 2014, 36, 119–140. [Google Scholar] [CrossRef]
- DeWeese, M.R.; Meister, M. How to measure the information gained from one symbol. Netw. Comput. Neural Syst. 1999, 10, 325–340. [Google Scholar] [CrossRef]
- Zwick, M. An overview of reconstructability analysis. Kybernetes 2004, 33, 877–905. [Google Scholar] [CrossRef]
- Clark, E. Dynamic patterning by the Drosophila pair-rule network reconciles long-germ and short-germ segmentation. PLoS Biol. 2017, 15, e2002439. [Google Scholar] [CrossRef]
- Adami, C. What is information? Philos. Trans. A 2016, 374, 20150230. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Griffith, V.; Koch, C. Quantifying synergistic mutual information. arXiv 2012, arXiv:1205.4265. [Google Scholar]
- Schneidman, E.; Still, S.; Berry, M.J., 2nd; Bialek, W. Network information and connected correlations. Phys. Rev. Lett. 2003, 91, 238701. [Google Scholar] [CrossRef]
- Gigerenzer, G.; Goldstein, D.G. Reasoning the fast and frugal way: Models of bounded rationality. Psychol. Rev. 1996, 103, 650–669. [Google Scholar] [CrossRef]
- Hintze, A.; Edlund, J.A.; Olson, R.S.; Knoester, D.B.; Schossau, J.; Albantakis, L.; Tehrani-Saleh, A.; Kvam, P.; Sheneman, L.; Goldsby, H.; et al. Markov brains: A technical introduction. arXiv 2017, arXiv:1709.05601. [Google Scholar]
- Bohm, C.; Kirkpatrick, D.; Hintze, A. Understanding memories of the past in the context of different complex neural network architectures. Neural Comput. 2022, 34, 754–780. [Google Scholar] [CrossRef]
- Beer, R. Toward the evolution of dynamical neural networks for minimally cognitive behavior. In Proceedings of the 4th International Conference on Simulation of Adaptive Behavior; Maes, P., Mataric, M.J., Meyer, J., Pollack, J., Wilson, S.W., Eds.; MIT Press: Cambridge, MA, USA, 1996; pp. 421–429. [Google Scholar]
- Beer, R. The dynamics of active categorical perception in an evolved model agent. Adapt. Behav. 2003, 11, 209–243. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Granger, C.W. Investigating causal relations by econometric models and cross-spectral methods. Econom. J. Econom. Soc. 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef]
- Lizier, J.T.; Prokopenko, M. Differentiating information transfer and causal effect. Eur. Phys. J. B 2010, 73, 605–615. [Google Scholar] [CrossRef]
- James, R.G.; Barnett, N.; Crutchfield, J.P. Information flows? A critique of transfer entropies. Phys. Rev. Lett. 2016, 116, 238701. [Google Scholar] [CrossRef]
- Bossomaier, T.; Barnett, L.; Harré, M.; Lizier, J.T. An Introduction to Transfer Entropy; Springer International: Cham, Switzerland, 2015. [Google Scholar]
- Tehrani-Saleh, A.; Adami, C. Can transfer entropy infer information flow in neuronal circuits for cognitive processing? Entropy 2020, 22, 385. [Google Scholar] [CrossRef]
- Van Dartel, M.; Sprinkhuizen-Kuyper, I.; Postma, E.; van den Herik, J. Reactive agents and perceptual ambiguity. Adapt. Behav. 2005, 13, 227–242. [Google Scholar] [CrossRef]
- Marstaller, L.; Hintze, A.; Adami, C. The evolution of representation in simple cognitive networks. Neural Comput. 2013, 25, 2079–2107. [Google Scholar] [CrossRef]
- Hutchins, E. Cognition in the Wild; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Kirsh, D.; Maglio, P. On distinguishing epistemic from pragmatic actions. Cogn. Sci. 1994, 18, 513–549. [Google Scholar] [CrossRef]
- Stoltzfus, A. On the possibility of constructive neutral evolution. J. Mol. Evol. 1999, 49, 169–181. [Google Scholar] [CrossRef]
- Stoltzfus, A. Constructive neutral evolution: Exploring evolutionary theory’s curious disconnect. Biol. Direct 2012, 7, 35. [Google Scholar] [CrossRef]
- Liard, V.; Parsons, D.P.; Rouzaud-Cornabas, J.; Beslon, G. The complexity ratchet: Stronger than selection, stronger than evolvability, weaker than robustness. Artif. Life 2020, 26, 38–57. [Google Scholar] [CrossRef]
- Tawfik, D.S. Messy biology and the origins of evolutionary innovations. Nat. Chem. Biol. 2010, 6, 692–696. [Google Scholar] [CrossRef]
- Beslon, G.; Liard, V.; Parsons, D.; Rouzaud-Cornabas, J. Of evolution, systems and complexity. In Evolutionary Systems: Advances, Questions, and Opportunities, 2nd ed.; Crombach, A., Ed.; Springer: Cham, Switzerland, 2021; pp. 1–18. [Google Scholar]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef] [PubMed]
- Downward, J. Targeting RAS signalling pathways in cancer therapy. Nat. Rev. Cancer 2003, 3, 11–22. [Google Scholar] [CrossRef] [PubMed]
- Wan, P.T.C.; Garnett, M.J.; Roe, S.M.; Lee, S.; Niculescu-Duvaz, D.; Good, V.M.; Jones, C.M.; Marshall, C.J.; Springer, C.J.; Barford, D.; et al. Mechanism of activation of the RAF-ERK signaling pathway by oncogenic mutations of B-RAF. Cell 2004, 116, 855–867. [Google Scholar] [CrossRef]
- Holderfield, M.; Merritt, H.; Chan, J.; Wallroth, M.; Tandeske, L.; Zhai, H.; Tellew, J.; Hardy, S.; Hekmat-Nejad, M.; Stuart, D.D.; et al. RAF inhibitors activate the MAPK pathway by relieving inhibitory autophosphorylation. Cancer Cell 2013, 23, 594–602. [Google Scholar] [CrossRef] [PubMed]
- Herberholz, J.; Issa, F.A.; Edwards, D.H. Patterns of neural circuit activation and behavior during dominance hierarchy formation in freely behaving crayfish. J. Neurosci. 2001, 21, 2759–2767. [Google Scholar] [CrossRef]
- Grant, R.I.; Doncheck, E.M.; Vollmer, K.M.; Winston, K.T.; Romanova, E.V.; Siegler, P.N.; Holman, H.; Bowen, C.W.; Otis, J.M. Specialized coding patterns among dorsomedial prefrontal neuronal ensembles predict conditioned reward seeking. eLife 2021, 10, e65764. [Google Scholar] [CrossRef]
- Bohm, C.; Hintze, A. MABE (Modular Agent Based Evolver): A framework for digital evolution research. In Proceedings of the European Conference of Artificial Life, Lyon, France, 4–8 September 2017; pp. 76–83. [Google Scholar]
- Albantakis, L.; Hintze, A.; Koch, C.; Adami, C.; Tononi, G. Evolution of integrated causal structures in animats exposed to environments of increasing complexity. PLoS Comput. Biol. 2014, 10, e1003966. [Google Scholar] [CrossRef]
- Kirkpatrick, D.; Hintze, A. The evolution of representations in genetic programming trees. In Genetic Programming Theory and Practice XVII; Springer: Berlin/Heidelberg, Germany, 2020; pp. 121–143. [Google Scholar]
- Albani, S.; Ackles, A.L.; Ofria, C.; Bohm, C. The comparative hybrid approach to investigate cognition across substrates. In Proceedings of the 2021 Conference on Artificial Life (ALIFE 2021), Prague, Czech Republic, 19–23 July 2021; Čejková, J., Holler, S., Soros, L., Witkowski, O., Eds.; MIT Press: Cambridge, MA, USA, 2021; pp. 232–240. [Google Scholar]
- Lenski, R.E.; Ofria, C.; Pennock, R.T.; Adami, C. The evolutionary origin of complex features. Nature 2003, 423, 139–144. [Google Scholar] [CrossRef]
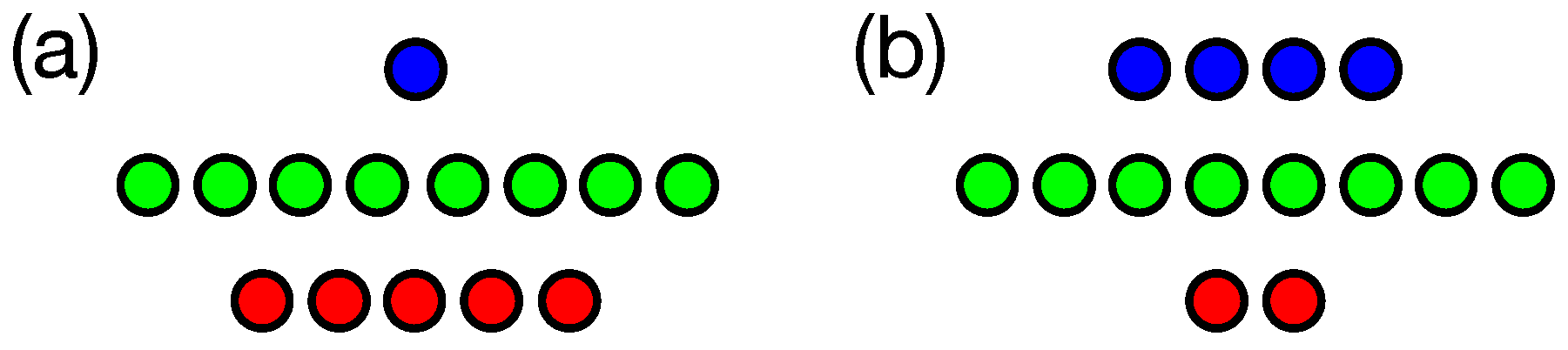



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bohm, C.; Kirkpatrick, D.; Cao, V.; Adami, C. Information Fragmentation, Encryption and Information Flow in Complex Biological Networks. Entropy 2022, 24, 735. https://doi.org/10.3390/e24050735
Bohm C, Kirkpatrick D, Cao V, Adami C. Information Fragmentation, Encryption and Information Flow in Complex Biological Networks. Entropy. 2022; 24(5):735. https://doi.org/10.3390/e24050735
Chicago/Turabian StyleBohm, Clifford, Douglas Kirkpatrick, Victoria Cao, and Christoph Adami. 2022. "Information Fragmentation, Encryption and Information Flow in Complex Biological Networks" Entropy 24, no. 5: 735. https://doi.org/10.3390/e24050735
APA StyleBohm, C., Kirkpatrick, D., Cao, V., & Adami, C. (2022). Information Fragmentation, Encryption and Information Flow in Complex Biological Networks. Entropy, 24(5), 735. https://doi.org/10.3390/e24050735







