Abstract
In quantum information science, it is very important to solve the eigenvalue problem of the Gram matrix for quantum signals. This allows various quantities to be calculated, such as the error probability, mutual information, channel capacity, and the upper and lower bounds of the reliability function. Solving the eigenvalue problem also provides a matrix representation of quantum signals, which is useful for simulating quantum systems. In the case of symmetric signals, analytic solutions to the eigenvalue problem of the Gram matrix have been obtained, and efficient computations are possible. However, for asymmetric signals, there is no analytic solution and universal numerical algorithms that must be used, rendering the computations inefficient. Recently, we have shown that, for asymmetric signals such as amplitude-shift keying coherent-state signals, the Gram matrix eigenvalue problem can be simplified by exploiting its partial symmetry. In this paper, we clarify a method for simplifying the eigenvalue problem of the Gram matrix for quadrature amplitude modulation (QAM) signals, which are extremely important for applications in quantum communication and quantum ciphers. The results presented in this paper are applicable to ordinary QAM signals as well as modified QAM signals, which enhance the security of quantum cryptography.
1. Introduction
The efficient computations and evaluations of quantities such as the error probability, mutual information, channel capacity, and reliability function are extremely important in quantum communication, quantum radar, and quantum cipher systems [1,2,3,4,5]. The computation of these quantities is essential not only for evaluating the reliability of quantum communication and the sensitivity of quantum radar but also for guaranteeing the security of quantum cryptography. In particular, because the security of a quantum stream cipher relies on the difference between the quantum optimum receiving capabilities of the legitimate receiver and the eavesdropper, it is essential to evaluate the optimum quantum receiver performance of the eavesdropper to guarantee security [6,7]. In quantum stream ciphers, the number of signals usually runs to several hundreds or thousands [8,9]. However, recent experiments have shown that some cases may contain millions or even billions of signals [10,11].
The eigenvalues and eigenvectors of the Gram matrix are very useful for computing various quantities that evaluate system performance. By solving the eigenvalue problem of the Gram matrix and finding its square root, the channel matrix given by the so-called square-root measurement (SRM) [12,13,14,15,16] can be computed. This implies that the error probability and mutual information using SRM can be directly calculated. SRM is asymptotically optimal for any quantum state signals with respect to minimizing the error probability, and it is used in the proof of the quantum channel coding theorem [14]. Moreover, SRM is strictly optimal for symmetric pure-state signals with uniform a priori probabilities [12,13,14,15,17,18,19]. Actually, SRM is also strictly optimal for some asymmetric pure-state signals with not necessarily uniform a priori probabilities [20]. As each component of the square root of the Gram matrix corresponds to the inner product of a signal quantum state and a measurement state of the SRM, a matrix representation of the signal quantum state can be obtained when the signal quantum states are linearly independent [21]. This representation is known to be useful for analyzing quantum systems (e.g., [21]). Furthermore, even if the quantum state is a vector in an infinite-dimensional Hilbert space, such as a coherent state or squeezed state, the matrix form allows numerical calculations to be performed because it provides a representation in a finite-dimensional subspace (e.g., [22]). Because the Gram matrix is a matrix representation of the density operator of the quantum information source, the Holevo capacity [14] and the upper and lower bounds of the reliability function [23,24] can be directly calculated by using its eigenvalues.
In general, the Gram matrix is for M-ary pure-state signals. Therefore, if we use a universal numerical algorithm to compute the eigenvalues and eigenvectors of the Gram matrix, the computation is hard when M is large. However, if the signals are symmetric, the analytic solutions of the Gram matrix eigenvalues and eigenvectors can be obtained by using well-known operations in linear algebra. In addition, by using the character [25] of a group, analytic solutions [26] can be obtained for narrow-sense group covariant signals [27], which are a generalization of symmetric signals. Narrow-sense group covariant signals are important in applications such as phase-shift keying (PSK) coherent-state signals and coded symmetric signals. Unfortunately, however, several important asymmetric signals are not narrow-sense group covariant, such as amplitude-shift keying (ASK) coherent-state signals and quadrature amplitude modulation (QAM) coherent-state signals [27]. QAM coherent-state signals are extremely important for quantum communication [28] and quantum ciphers [29]; moreover, QAM signals almost achieve the quantum channel capacity under energy constraints [30].
Recently, we showed that the eigenvalue problem of the Gram matrix can be simplified by using its partial symmetry for ASK coherent-state signals and amplitude-modulated phase-modulated (AMPM) signals, which belong to a class of asymmetric signals [31,32,33]. In this paper, we show that the eigenvalue problem of the Gram matrix can also be simplified by using its partial symmetry for QAM signals, which are more important for applications than ASK and AMPM signals. The method in this paper is applicable to ordinary QAM signals as well as modified QAM signals, which enhance the security of quantum stream ciphers [29]. Note that the signals considered in this paper belong to a class of asymmetric signals defined in Ref. [20], where the class is referred to as “the multiple constellations of geometrical uniform symmetry (GUS) state”. The results of this paper are closely related to Ref. [20].
The remainder of this paper is organized as follows. In Section 2, we introduce some preliminaries and basic theory. First, we define quantum signals and measurements, and then we explain various quantities such as the error probability, mutual information, and Holevo capacity. Next, we introduce the Gram matrix, SRM, and symmetric signals, which are the subject of this paper. In Section 3, we present the main results. For the eigenvalue problem of the Gram matrix of QAM signals, we show that the size of the problem can be reduced by using the partial symmetry of the signals. In Section 4, we show examples for the simplest case of and provide specific forms of eigenvalues and eigenvectors for the smaller matrices than the Gram matrix. In Section 5, we provide numerical experiments as examples of applications for the main result. Finally, in Section 6, we summarize the conclusions to this study.
2. Basic Theory
2.1. Quantum Signals and Measurements
Let be the Hilbert space of a quantum system. The set of M-ary pure-state signals is represented by the following:
where . Let be the a priori probability of state . Then, the pair is referred to as a quantum information source or a quantum ensemble.
In general, a quantum measurement is mathematically described by a positive operator-valued measure (POVM). The POVM is described as follows:
where is a Hermitian operator on satisfying the following.
Here, is the identity operator on . Although POVM is a mathematical representation of a quantum measurement, it may be called a quantum measurement. The conditional probability that the result j is obtained when performing the measurement on quantum state is as follows.
2.2. Error Probability, Mutual Information, and Holevo Capacity
Suppose we measure the quantum information source by a POVM . Using Equation (3), the average error probability is defined as follows:
which is also simply called the error probability. Then, the following is the case:
and it is referred to as the minimum error probability and the set that attains is called the optimum POVM. The mutual information is defined as follows:
and its maximization with respect to quantum measurements is the following:
which is called accessible information. For , the following is the case:
and it is called the density operator of the quantum information source. Using the density operator, we define von Neumann entropy as follows.
When the signals are pure states, the maximization of with respect to is the so-called Holevo capacity.
Let be the eigenvalues of corresponding to the that attains C. Then, the Holevo capacity can be calculated as follows.
2.3. Gram Matrix
For an M-ary pure-state signal set , the Gram matrix is defined as follows.
The Gram matrix is an matrix in which the -th element is the inner product between quantum state signals (Note that the Gram matrix is sometimes defined by using the inner products between weighted quantum state signals [20,34]). By definition, the Gram matrix is Hermitian; moreover, it is non-negative [35]. Because the norm of the quantum state vector is unity, so are all diagonal components of the Gram matrix, and the sum of the diagonal components is M. The Gram matrix is very useful in the theoretical treatment of M-ary pure-state signal systems. First, for a quantum information source for which its a priori probabilities are uniform, is a matrix representation of its density operator. That is, and are isomorphic.
In this case, the eigenvalues of the Gram matrix and those of the density operator are identical, and the von Neumann entropy can be calculated using the eigenvalues of the Gram matrix. For symmetric signals, the Holevo capacity can be calculated directly from the eigenvalues of the Gram matrix, because the Holevo capacity is attained with uniform a priori probabilities [36]. A similar statement can be made for the upper and lower bounds of the quantum reliability function [37,38]. Furthermore, the Gram matrix is closely related to the theory of SRM, as described below.
2.4. Square-Root Measurement
The SRM is a quantum measurement defined using the quantum states that are being transmitted. For a set of M-ary pure-state signals , the POVM of the SRM is defined as follows:
where vector is the measurement state or measurement quantum state (e.g., [4]). For linearly independent signal systems, the set of measurement quantum states is an orthonormal system and is an orthonormal basis of the space spanned by signal quantum states [34]. Although SRM appeared in papers in the 1970s (e.g., Belavkin [12] and earlier papers by Holevo), the name SRM has only been used since 1996, when Hausladen et al. presented the quantum channel coding theorem [14]. They proved that the inner product between quantum states and in Equation (15) is equal to the -th element of the square root of the Gram matrix, , and called this the “square-root” measurement. Specifically, they showed the following.
The existence of is always guaranteed because the Gram matrix is non-negative and Hermitian, as mentioned above. Therefore, Equation (17) denotes a component of the matrix representation of the signal quantum state using the orthonormal basis . Thus, as the signal quantum state can be represented in matrix form based on the square-root of the Gram matrix, computing is very useful for simulating systems such as quantum communication, quantum radar, and quantum ciphers. From Equation (3), we have the following.
Because the matrix in which the -th elements are equal to is the channel matrix and obtaining allows the error probability and mutual information to be calculated using Equations (4) and (6). Therefore, if the square root of the Gram matrix can be computed efficiently, it is easy to compute the error probability and mutual information when SRM is applied. In general, the square root of a matrix can be computed using its eigenvalues and eigenvectors. Thus, being able to efficiently compute the eigenvalues and eigenvectors of a Gram matrix is extremely important.
2.5. Coherent-State Signals
Coherent states are the most fundamental optical quantum states used in macroscopic quantum communication or quantum ciphers. They are the stable states of light that can be realized by an ideal laser. The coherent state with the complex amplitude is given by the following:
where is the photon number state, and n is the number of photons. The inner product between two coherent states and is as follows:
where * denotes complex conjugation. If and are both real numbers, the value of is real. In this paper, we assume that the signal quantum state is a coherent state.
Note that the coherent state is completely characterized by its complex amplitude , as shown in Equation (19). A complex number is graphically described by a point on the complex plane, and so a coherent state signal is also described by a point on the complex plane. In this case, the complex plane is often called the phase plane.
2.6. Symmetric Signals
In the field of quantum information science, Davies defined a group covariant signal [39] with symmetry corresponding to the symmetry of the group, which is sometimes simply called a symmetric signal. Although Davies’ definition of group covariant signals applies to a broader class of signals than the pure-state signals treated in this paper, we adopt the following narrow definition of group covariant signals [27], which is applicable only to simpler pure-state signals.
Definition 1
(Narrow-sense group covariant signals [27]). Let be a finite group with the operation ∘. A set of quantum state signals is called (narrow-sense) group covariant with respect to the group if the following is the case:
where is a unitary operator.
Narrow-sense group covariant signals have the following necessary and sufficient conditions.
Proposition 1
(Necessary and sufficient conditions for narrow-sense group covariant signals [27]). A set of quantum state signals is narrow-sense group covariant with respect to if and only if the following is the case.
From this proposition, we can easily show that signals such as arbitrary binary pure-state signals and arbitrary M-ary PSK coherent-state signals are narrow-sense group covariant. In addition, for narrow-sense group covariant signals, analytic solutions for the eigenvalues and eigenvectors of the Gram matrix have been presented, indicating that narrow-sense group covariant signals are very useful for communication and cipher systems. In this study, we apply this knowledge to QAM signals that are not group-covariant.
3. Eigenvalues and Eigenvectors of -ary QAM Signals and Their Gram Matrix
In this section, we consider the eigenvalues and eigenvectors of the Gram matrix corresponding to -ary QAM signals. First, -ary QAM signals are defined and the corresponding Gram matrix is explained. Next, we state that the Gram matrix can be block-partitioned and clarify that it has the structure of the sum of tensor products. Finally, we show that the scale of the computation can be reduced.
3.1. -ary QAM Signals
This subsection describes the -ary QAM signals treated in this paper. QAM is a major modulation scheme used in digital communication, such as for coherent optical communication [40], and QAM signals are important for applications in quantum technologies such as quantum communication and quantum ciphers. Ordinary QAM signals are placed in a square lattice on the phase plane. As an example, Figure 1a shows the signal constellation of 256QAM on the phase plane. In quantum ciphers, modified QAM signals in which signals near the origin are removed have been proposed for higher security [29]. As an example, Figure 1b shows the signal constellation of the modified 156QAM on the phase plane. For 256QAM signals, the number of signals is and , while for modified 156QAM signals, it is and .

Figure 1.
Examples of QAM signals presented in [29]. (a) 256QAM. (b) Modified 156QAM.
In this paper, we consider the signals defined below, which include both the ordinary QAM of Figure 1a and the modified QAM of Figure 1b, and we call them QAM signals.
Definition 2
(-ary QAM Signals). Let be any m-ary set of complex amplitudes for which its arguments lie in the range . That is, the complex amplitudes correspond to points in the first quadrant. Here, and are assumed. For each , let , , , and , where . Then, we call the following set of coherent states “-ary QAM coherent-state signals” (-ary QAM signals for short):
where are sets of coherent states defined as follows.
The rotation operator [4] that rotates the phase by an angle in the phase plane is represented as follows:
where and are photon annihilation and creation operators, respectively. Rewriting as simply , becomes the following.
Here, we have the following.
The -ary QAM signals defined above obviously include both ordinary QAM signals (e.g., Figure 1a) and modified QAM signals (e.g., Figure 1b). Although -ary QAM signals are not symmetric signals, each subset is symmetric, group covariant, and geometrical uniform symmetric (GUS). Moreover, we should mention that -ary QAM signals in Definition 2 satisfy the definition of the multiple constellations of GUS state [20], which is a particularization of the concept of compound geometrical uniform (CGU) states [41]. Hence, -ary QAM signals are practical examples of the multiple constellations of GUS state and CGU states. The following results are also applicable when considering non-coherent states , such as squeezed states, instead of in Equation (26).
3.2. Gram Matrix of -ary QAM Signals
As shown in Equation (23), -ary QAM signals are partitioned into m subsets . Let be the matrix for which its entries are the inner product between two signals, where one of the two signals is chosen from the subset , and the other is chosen from the subset . Then, the Gram matrix of the -ary QAM signals can be represented in block-partitioned form as follows.
From Equation (26), the -th element of is as follows.
This implies that is cyclic.
Denoting the components of the first row of as and , the submatrix is described as follows:
where the following is the case.
3.3. Decomposition of Submatrices
Here, we consider the common properties of each by performing a spectral decomposition of each submatrix introduced in the previous section. Because is cyclic according to Equation (30), the analytic expressions of its eigenvalues and eigenvectors are well known. The expressions are as follows.
As eigenvectors are orthonormal, can be spectrally decomposed as follows:
where denotes the conjugate transpose of .
3.4. Decomposition of Gram Matrix
In this subsection, we decompose the Gram matrix into a sum of tensor products using the spectral decomposition of submatrices . All have common eigenvectors independent of k and l. Substituting Equation (31) into Equation (28), we obtain the following:
where the following is the case.
In the following, we show that each matrix consisting of the eigenvalues of is Hermitian. As is the Gram matrix (and is therefore Hermitian), its submatrices satisfy the following.
From Equation (31), we have the following:
and from Equation (34), it coincides with the following.
Thus, we have
Hence, all of Equation (33) are Hermitian.
Therefore, each is spectrally decomposable. Let and be the eigenvalues and corresponding orthonormalized eigenvectors of . Then, the spectral decomposition form of is as follows.
Substituting this into Equation (32), we obtain the following.
3.5. Eigenvalues and Eigenvectors of Gram Matrix
In this subsection, we derive the eigenvalues and eigenvectors from the decomposition form (40) of the Gram matrix . Because both and are orthonormal, we have the following:
and the eigenvalues and eigenvectors of the Gram matrix of -ary QAM signals are listed in Table 1.

Table 1.
Eigenvalues and eigenvectors of .
Therefore, to compute the eigenvalues and eigenvectors of the matrix , it is sufficient to consider the eigenvalue problem of the smaller matrices .
3.6. Relation of the Results in the Relevant Literature
In this subsection, we consider the relation between the results in this paper and those in Ref. [20]. As examples of the multiple constellations of GUS state, the new signals were introduced [20]. They are called a double quantum binary phase shift keying (BPSK) and a double quantum pulse position modulation (PPM). As mentioned in Section 3.1, -ary QAM signals also belong to the class of the multiple constellations of GUS state. The signals are not new, but they are rather traditional, and they are well known to be useful. Therefore, it is worth noticing that the results in Ref. [20] are also applicable to -ary QAM signals. The most significant result is the optimality of SRM. That is, SRM can be an optimal measurement for -ary QAM signals with certain a priori probabilities. Furthermore, various results had been obtained in Ref. [20] while they had shown the optimality of SRM. They provided the block-partitioned form of the Gram matrix and showed that each submatrix is diagonalizable by the Fourier matrix. These results correspond to the results in Section 3.2 and Section 3.3. Then, they considered a transformation of the matrix block-partitioned by diagonal submatrices into a block diagonal matrix. This result is closely related to the result in Section 3.4. Although they had not mentioned the eigenvalues and eigenvectors, one may connect their discussion for the square-root of the Gram matrix to the results in this section. We would like to emphasize here a reduction in computational costs, whereas they did not explicitly state a reduction.
4. Examples for the Case of
Here, we consider the simplest case of as examples.
4.1. Submatrices
From Equation (33), each consists of the eigenvalues of . Since is a weighted sum of the inner products , and , it is convenient to describe the forms of the inner product for coherent states by using Equation (20):
where we set and . Using the above forms, we have the following:
where we write the following.
From Equations (41)–(44), we obtain for the case of :
where ∘ denotes the Hadamard product, and the following is the case.
The remaining task is to calculate the eigenvalues and eigenvectors of the matrices ∼. Although it is possible to calculate eigenvalues and eigenvectors of a matrix, the general form may be slightly complicated. In the following, we consider simple two cases.
4.2. Case of
This case corresponds to phase-mismatching PSK signals. The signals are similar to the double quantum BPSK with a misalignment or a systematic bias error in the angle defining one of the two constellations [20]. Note that the number of signals is different. In this case, from the following:
“” in Equations (45)–(48) becomes simply a scalar product “”. Therefore, each has the following form:
where a is a real number and b is a complex number. The eigenvalues and the corresponding orthonormal eigenvectors of the above form are the following:
where . Therefore, the eigenvalues of are as follows:
where we set .
The eigenvectors of are as follows:
where the following is the case.
4.3. Case of
The signals in this case are similar to the four-pulse amplitude modulation (PAM) [20]. Note that the number of signals is eight in this case, but four for the 4-PAM. In this case, the form of is as follows:
where , and c are real numbers. The eigenvalues of the matrix with this form are as follows:
and the corresponding orthogonal eigenvectors are the following.
We obtain the orthonormal eigenvectors by normalizing them. Using the above equations, we can obtain the explicit forms of and as the same manner in Section 4.2.
5. Numerical Experiments
Here, we provide numerical experiments as examples of application for the results in Section 3. We consider 16QAM signals (the case of ) in this section. Set , . The average number of photons of 16QAM coherent-state signals is as follows:
and it is proportional to . Hence, in the following, we show numerical results of some quantities with respect to .
5.1. Von Neumann Entropy
First, we consider the von Neumann entropy, which is calculated by using eigenvalues of the Gram matrix. Since the Holevo capacity is the maximization of the von Neumann entropy with respect to a priori probabilities, the von Neumann entropy is a lower bound on the capacity. Let be the density operator of 16QAM signals. Then, the von Neumann entropy (9) is calculated by the eigenvalues of as follows.
Each is equal to an eigenvalue of from Equation (13). According to the results in Section 3, the following is the case:
where are eigenvalues of the matrices described in Section 3, and we numerically calculate . Note that we only need numerical calculation of eigenvalues for smaller matrices than the original Gram matrix .
Figure 2 shows the von Neumann entropy of 16QAM signals with respect to . The blue line is drawn by using the results in Section 3, while the red dots are plotted by using direct calculation of eigenvalues for the Gram matrix. From Figure 2, we can confirm that both results are identical.
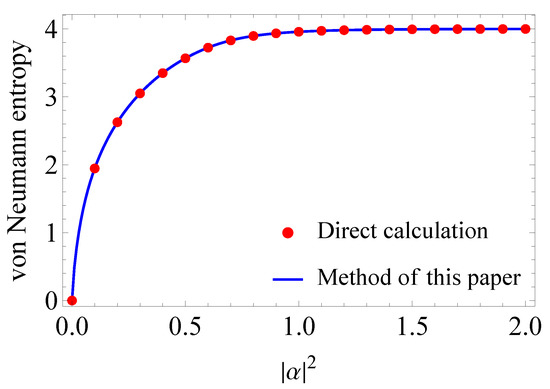
Figure 2.
von Neumann entropy of 16QAM signals with respect to . The blue line is drawn by using the results in Section 3, while the red dots are plotted by using direct calculation of eigenvalues for the Gram matrix.
5.2. Error Probability
Now, we consider the error probability by using the SRM. To compute the error probability, both eigenvalues and eigenvectors of the Gram matrix are needed. As explained in Section 2, the error probability is as follows.
From Equation (40), we have the following.
Then, numerically calculating the eigenvalues and the eigenvectors for matrices , and substituting them into the above equation, we obtain the error probability.
Figure 3 shows the error probability of 16QAM signals with respect to . The blue line and the red dots have the same meaning as in Figure 2. From Figure 3, we can confirm that both results are identical.
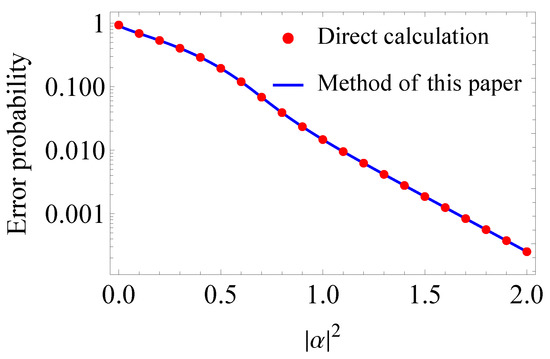
Figure 3.
Error probability of 16QAM signals with respect to . The blue line is drawn by using the results in Section 3, while the red dots are plotted by using direct calculation of the matrix square-root for the Gram matrix.
6. Conclusions
In this paper, we have described the simplification of the Gram matrix eigenvalue problem for QAM coherent-state signals and shown that the scale of the computation can be reduced. As explained in Section 2, by solving the eigenvalue problem of the Gram matrix, it is possible to calculate quantities such as the error probability, mutual information, Holevo capacity, and the upper and lower bounds of the reliability function, which are important for evaluating the performance of quantum communication, quantum radar, and the security of quantum cryptography. The QAM signals treated in this study are very versatile, being applicable not only to ordinary QAM signals but also to any signals generated by rotation in the first quadrant of the phase plane. The quantum state used is typically but not necessarily the coherent state. In fact, the QAM signals defined in this paper belong to the class of the multiple constellations of GUS [20] and CGU states [41]. Therefore, the results in the literature are also applicable to QAM signals. Moreover, some results in Ref. [20] are closely related to the results in this paper, as explained in Section 3.6.
The most significant challenge for the future is the further simplification of the eigenvalue problem of the Gram matrix. For this purpose, the regularity of the signal constellation in the first quadrant of the phase plane should be taken into account. Therefore, carefully determining the order of signals in the first quadrant is important, even if they are the same signals. Another challenge is to apply the methods of this study to actual problems, whereas we have shown simple examples for 16QAM. For this purpose, the combined use of numerical algorithms (e.g., [42]) for the matrix calculations should be considered.
Author Contributions
Conceptualization, T.S.U.; methodology, R.M.; validation, T.W.; formal analysis, R.M.; investigation, R.M.; writing—original draft preparation, R.M.; writing—review and editing, T.W. and T.S.U.; supervision, T.S.U.; project administration, T.S.U.; funding acquisition T.W. and T.S.U. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by JSPS KAKENHI (grant number JP20K20397, JP20H00581, and JP21K04064) and research grants from the Marubun Research Promotion Foundation and the Nitto Foundation.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank S. Takahira and M. Yoshida for valuable discussions during this and previous research studies. We thank Stuart Jenkinson, PhD, from Edanz (https://jp.edanz.com/ac, accessed on 12 April 2022) for editing a draft of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SRM | Square-root measurement; |
| PSK | Phase shift keying; |
| ASK | Amplitude shift keying; |
| QAM | Quadrature amplitude modulation; |
| AMPM | Amplitude-modulated phase-modulated; |
| POVM | Positive operator-valued measure. |
References
- Helstrom, C.W. Detection theory and quantum mechanics. Inform. Control 1967, 10, 254–291. [Google Scholar] [CrossRef]
- Holevo, A.S. Statistical decision theory for quantum systems. J. Multivar. Anal. 1973, 3, 337–394. [Google Scholar] [CrossRef]
- Yuen, H.P.; Kennedy, R.S.; Lax, M. Optimum testing of multiple hypotheses in quantum detection theory. IEEE Trans. Inform. Theory 1975, 21, 125–134. [Google Scholar] [CrossRef]
- Helstrom, C.W. Quantum Detection and Estimation Theory; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Hirota, O.; Ikehara, S. Minimax strategy in the quantum detection theory and its application to optical communication. Trans. IECE 1982, 65, 627–633. [Google Scholar]
- Yuen, H.P. KCQ: A new approach to quantum cryptography I. General principles and key generation. arXiv 2004, arXiv:quant-ph/0311061. [Google Scholar]
- Yuen, H.P. Key generation: Foundations and a new quantum approach. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 1630–1645. [Google Scholar] [CrossRef]
- Corndorf, E.; Liang, C.; Kanter, G.S.; Kumar, P.; Yuen, H.P. Quantum-noise randomized data encryption for wavelength-division-multiplexed fiber-optic networks. Phys. Rev. A 2005, 71, 062326. [Google Scholar] [CrossRef]
- Hirota, O.; Sohma, M.; Fuse, M.; Kato, K. Quantum stream cipher by Yuen 2000 protocol: Design and experiment by intensity modulation scheme. Phys. Rev. A 2005, 72, 022335. [Google Scholar] [CrossRef]
- Tanizawa, K.; Futami, F. Digital coherent PSK Y-00 quantum stream cipher with 217 randomized phase levels. Opt. Express 2019, 27, 1071–1079. [Google Scholar] [CrossRef]
- Chen, X.; Tanizawa, K.; Winzer, P.; Dong, P.; Cho, J.; Futami, F.; Kato, K.; Melikyan, A.; Kim, K.W. Experimental demonstration of 4,294,967,296-QAM based Y-00 quantum stream cipher template carrying 160-Gb/s 16-QAM signals. Opt. Express 2021, 29, 5658–5664. [Google Scholar] [CrossRef]
- Belavkin, V.P. Optimal multiple quantum statistical hypothesis testing. Stochastics 1975, 1, 315–345. [Google Scholar] [CrossRef]
- Belavkin, V.P. Optimal distinction of non-orthogonal quantum signals. Radio Eng. Electron. Phys. 1975, 20, 39–47. [Google Scholar]
- Hausladen, P.; Jozsa, R.; Schumacher, B.; Westmoreland, M.; Wootters, W.K. Classical information capacity of a quantum channel. Phys. Rev. A 1996, 54, 1869–1876. [Google Scholar] [CrossRef] [PubMed]
- Eldar, Y.C.; Forney, G.D., Jr. On quantum detection and the square-root measurement. IEEE Trans. Inform. Theory 2001, 47, 858–872. [Google Scholar] [CrossRef]
- Kato, K.; Hirota, O. Square-root measurement for quantum symmetric mixed state signals. IEEE Trans. Inform. Theory 2003, 49, 3312–3317. [Google Scholar] [CrossRef]
- Ban, M.; Kurokawa, K.; Momose, R.; Hirota, O. Optimum measurements for discrimination among symmetric quantum states and parameter estimation. Int. J. Theor. Phys. 1997, 36, 1269–1288. [Google Scholar] [CrossRef]
- Usuda, T.S.; Takumi, I.; Hata, M.; Hirota, O. Minimum error detection of classical linear code sending through a quantum channel. Phys. Lett. A 1999, 256, 104–108. [Google Scholar] [CrossRef]
- Usuda, T.S.; Usami, S.; Takumi, I.; Hata, M. Superadditivity in capacity of quantum channel for q-ary linearly dependent real symmetric-state signals. Phys. Lett. A 2002, 305, 125–134. [Google Scholar] [CrossRef]
- Dalla Pozza, N.; Pierobon, G. Optimality of square-root measurements in quantum state discrimination. Phys. Rev. A 2015, 91, 042334. [Google Scholar] [CrossRef]
- Osaki, M.; Usuda, T.S.; Hirota, O. Group covariant detection for a three-phase shift keyed signal. Phys. Lett. A 1998, 245, 189–196. [Google Scholar] [CrossRef]
- Takeuchi, H.; Yamaguchi, S.; Usuda, T.S. Entanglement-assisted classical communication using quasi Bell states. In Proceedings of the 1st International Workshop on Entangled Coherent State and Its Application to Quantum Information Science—Towards Macroscopic Quantum Communications, Tokyo, Japan, 26–28 November 2012; pp. 115–119. [Google Scholar]
- Burnashev, M.V.; Holevo, A.S. On reliability function of quantum communication channel. Probl. Peredachi Inform. 1998, 34, 1–13. [Google Scholar]
- Dalai, M. Lower bounds on the probability of error for classical and classical-quantum channels. IEEE Trans. Inform. Theory 2013, 59, 8027–8056. [Google Scholar] [CrossRef]
- Isaacs, I.M. Character Theory of Finite Groups; Academic Press: New York, NY, USA; London, UK, 1976. [Google Scholar]
- Usuda, T.S.; Shiromoto, K. Analytical expression of s-th power of Gram matrix for group covariant signals and its application. In Quantum Communication, Measurement and Computing (QCMC), AIP Conference Proceedings; American Institute of Physics: New York, NY, USA, 2011; Volume 1363, pp. 97–100. [Google Scholar]
- Usuda, T.S.; Takumi, I. Group covariant signals in quantum information theory. In Quantum Communication, Computing, and Measurement 2; Plenum Press: New York, NY, USA, 2000; pp. 37–42. [Google Scholar]
- Kato, K.; Osaki, M.; Sasaki, M.; Hirota, O. Quantum detection and mutual information for QAM and PSK signals. IEEE Trans. Commun. 1999, 47, 248–254. [Google Scholar] [CrossRef]
- Kato, K.; Hirota, O. Quantum quadrature amplitude modulation system and its applicability to coherent-state quantum cryptography. In Proceedings of the SPIE, Quantum Communications and Quantum Imaging III, San Diego, CA, USA, 31 July 2005; Volume 5893. [Google Scholar]
- Ishida, Y.; Kato, K.; Usuda, T.S. Capacity of attenuated channel with discrete-valued input. In Proceedings of the 8th International Conference on Quantum Communication, Measurement and Computing, Tsukuba, Japan, 28 November–3 December 2006; NICT Press: Tokyo, Japan, 2007; pp. 323–326. [Google Scholar]
- Miyazaki, R.; Yoshida, M.; Usuda, T.S. Simplification of calculation of channel matrix for 2m-ary ASK coherent-state signals. In Proceedings of the 2019 Tokai-Section Joint Conference on Electrical, Electronics, Information, and Related Engineering, Nagoya, Japan, 9–10 September 2019. No. F5-4. (In Japanese). [Google Scholar]
- Miyazaki, R.; Yoshida, M.; Wang, T.; Usuda, T.S. Simplification of the calculation of the channel matrix for AMPM coherent-state signals. In Proceedings of the 2020 International Symposium on Information Theory and Its Applications (ISITA2020), Hawai’i, HI, USA, 24–27 October 2020; pp. 121–125. [Google Scholar]
- Miyazaki, R.; Yoshida, M.; Wang, T.; Takahira, S.; Usuda, T.S. Simplification of calculation of channel matrix for non-symmetric signals. IEICE Trans. Commun. 2022, J105-B, 74–87. (In Japanese) [Google Scholar]
- Sasaki, M.; Kato, K.; Izutsu, M.; Hirota, O. Quantum channels showing superadditivity in classical capacity. Phys. Rev. A 1998, 58, 146–158. [Google Scholar] [CrossRef]
- Horn, R.A.; Jonson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Kato, K.; Osaki, M.; Hirota, O. Derivation of classical capacity of quantum channel for discrete information source. Phys. Lett. A 1999, 251, 157–163. [Google Scholar] [CrossRef]
- Kato, K. Error exponents of quantum communication system with M-ary PSK coherent state signal. Tamagawa Univ. Quantum ICT Res. Inst. Bull. 2011, 1, 33–40. [Google Scholar]
- Kato, K. A note on the reliability function for M-ary PSK coherent state signal. Tamagawa Univ. Quantum ICT Res. Inst. Bull. 2018, 8, 21–25. [Google Scholar]
- Davies, E.B. Information and quantum measurement. IEEE Trans. Inform. Theory 1978, IT-24, 596–599. [Google Scholar] [CrossRef]
- Kikuchi, K. Digital coherent optical communication systems: Digital coherent optical communication systems. IEICE Electron. Express 2011, 8, 1642–1662. [Google Scholar] [CrossRef]
- Eldar, Y.C.; Megretski, A.; Verghese, G. Optimal detection of symmetric mixed quantum states. IEEE Trans. Inform. Theory 2004, 50, 1198–1207. [Google Scholar] [CrossRef]
- Mizuno, S.; Moriizumi, Y.; Usuda, T.S.; Sogabe, T. An initial guess of Newton’s method for the matrix square root based on a sphere constrained optimization problem. JSIAM Lett. 2016, 8, 17–20. [Google Scholar] [CrossRef][Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).