1. Introduction
The introduction around three decades ago of the view and methods of statistical physics into economics and finance signaled the appearance of a new interdisciplinary aspect of physics, which is sometimes called “econophysics” [
1,
2,
3]. The fact that financial prices are random with sudden and uncontrollable ups and downs has been long-known; however, the first step towards a systematic mathematical analysis of price randomness was taken by Bachelier in 1900, who proposed a model for the market dynamics in which the prices follow ordinary Brownian motion [
4].
However, Bachelier’s model is not completely satisfactory because, in such a representation, prices can be either positive or negative, contradicting one of the most fundamental tenets of economics, the “principle of limited liability”, which affirms that prices cannot attain negative values. This limitation in Bachelier’s model was remedied more than six decades later by Osborne [
5] by assuming the geometric Brownian motion where prices are described by the exponential of the ordinary Brownian motion and, hence, they can never attain negative values.
Let us denote by
a speculative price (or an economic index) at time
t. In the continuous time framework, the geometric Brownian motion assumes that
where
is the price at some initial time
and
, the so-called return, is described by the ordinary Brownian motion, that is to say, by the stochastic differential equation
where
is the standard Wiener process with zero mean and unit variance. Note that the return is assumed to be a diffusion process with constant drift
m and diffusion coefficient
. In this model, the return is a Gaussian process with the mean and variance given, respectively, by
m and
. The price is, hence, a log-normal process, and the geometric Brownian motion is also called the log-normal model.
Despite the log-normal model being used in countless financial applications, it has certain limitations [
6], which have given rise to several generalizations. One of them assumes that the return is a more complex diffusion process obeying a stochastic equation of the form
which is interpreted in the sense of Itô. In this case, returns, and hence prices, are driven by an external “force” and by multiplicative noise, which, in the most general case, depend explicitly on the time and on the return level. Function
drives prices, and function
modulates the intensity of the fluctuations around the deterministic motion set by
. In any case, and regardless of the values taken by
, the prices given by Equation (
1) are always nonnegative, thus, keeping the principle of limited liability.
Another significant shortcoming of the geometric Brownian motion model is the absence of both “fat tails” and skewness in the distribution of log-prices (i.e., returns). Indeed, empirical distributions of log-prices not only show fat tails—meaning that extreme losses and profits have a higher probability than those of the log-normal model—but also an asymmetric shape in the sense that losses are usually more probable than profits [
6]. In order to address these and other problems, intense research has been prompted both in mathematics and physics, which, among others, may involve the use of the Lévy process as driving noise (instead of the Wiener process). One of the most popular alternative financial models—proposed by Mandelbrot [
7] and Fama [
8] in the early 1960s—is provided by substituting the Wiener process by the Lévy process, which can take into account the appearance of fat tails in the probability distribution of prices, a widely accepted empirical fact [
6]. A major inconvenience of the non-Poissonian Lévy jump processes is, however, their lack of finite moments apart from (at most) the first one, which does not seem to be case in empirical data [
6]. or models in which the variance
(or the noise intensity
g) is a random process, such as in the so-called “stochastic volatility models” [
9,
10,
11].
In economics and finance, one of the most consequential developments is that of “discounting”, which essentially attempts to answer the crucial question of what the price will be in the future. In other words, discounting weighs the future relative to the present. Traditionally, the weighting procedure has been performed through a decreasing exponential. Thus, under a constant interest rate
r, continuously compounded, a dollar invested today at time
yields
dollars at time
t [
12]; hence, one dollar in any future time
t is worth
today. This statement is true under constant and fixed rates; however, in real life, rates are random, and this uncertainty makes it completely unrealistic to represent rates by constant quantities or even by deterministic functions of time, and, as a consequence, random models for rates must be addressed.
The problem of discounting is widely known in finance where it has been thoroughly studied closely related to bond pricing particularly over short periods of time [
13]. Discounting, particularly in the long run, is of importance not only in the context of finance but to many other aspects of the global economy. For instance, we may consider the long-term environmental planning, which is certainly sensitive in relation to climate action. Thus, in an oversimplified way, an environmental problem, which costs
X to fix at a time
t is worth an investment of
today.
This analysis assumes that the interest rate remains constant between today and the distant future
t. The rate
r becomes a key magnitude to decide whether it becomes more beneficial to take action today with a significant investment or whether the discount gives negligible value to today’s investment. The choice of discount rate is perhaps the biggest factor influencing the debate on the urgency of the response to global warming as it relates today’s investments with potential climate-related losses in future [
14]. No wonder that, in recent years, obtaining a long-run discount rate valid for decades ahead has been the object of intense controversy.
Thus, Nicholas Stern, in an influential report commissioned by the UK government, advocated for a long-run discount of 1.4% [
15], which on a 100-year horizon implies a present value of 25% (meaning that the future is worth 25% as much as the present). On the other hand, Willian Nordhaus proposed a discount rate of 4% [
16] (implying a present value of 2%) and even the higher value of 6% [
17], which implies a present value of 0.3%. Stern has been widely criticized for using such a low rate [
18,
19,
20], and the question is far from being settled.
Economists present a variety of reasons for discounting, particularly for environmental problems in the long run. These reasons include, among others, ethical considerations [
21,
22], impatience, economic growth [
23] and arguments based on the maximization of utility functions that are mostly chosen for mathematical convenience [
24], all of them ingrained in a phenomenological expression called the Ramsey formula [
25], which constitutes the standard approach to discounting in the economics literature (particularly in the long-run) [
14].
From an empirical point of view, any practical economist involved in environmental debates might consider the average of historical interest rates, which occurred in the last 200 hundred years to estimate the forward discount rate (which is 2.7% in the less unstable countries [
26]) or take the average of Wall Street forward looking models, with price bonds of maturity as long as 30 years. Unfortunately, due to historical fluctuations of real interest rates, the appropriate rate is considerably below such averages [
26].
In econophysics, the problem of discounting, despite its relevance, is virtually unknown. The main purpose of this paper is to offer a survey of the problem devoid of excessive formalism and abstraction as well as to review some of our recent work on the problem [
26,
27,
28,
29,
30]
3. Pricing Bonds—The Term Structure of Interest Rates
Pricing bonds is a traditional objective in finance and intimately related to the problem of discounting. It constitutes a vast subject with countless studies, many of them rather abstract, which have appeared in the mathematical finance literature over the last decades. We present a short and intentionally simple, yet rigorous, introduction to the subject devoid as much as possible of technicalities and mathematical subtleties and refer the interested reader to more specialized works for further information [
13].
A bond is a financial instrument that one purchases now and that provides a payment in the future. From a more technical point of view, we say that a (discount) bond is a default-free claim on a specified sum of money to be delivered at a given future date called the maturity time. Such claims are bought and issued by investors. Let us denote by
the price at time
of a discount bond maturing at time
, with unit maturity value,
Let us incidentally note that, if the final maturity price is not 1 (say,
) then the price of the bond at
would be
.
Bonds are classified according to the
time interval to maturity defined as
Thus, if years, we talk about a 10-year bond that is traded at (for instance, today) with price and that, after 10 years, has unit value. Similarly for a 3-year bond, 3-month bond, etc.
The central question is to know the backward evolution of the bond price, from unit maturity to the initial purchasing price . Note that the problem is virtually identical to the problem of discounting discussed in Sect. II, with the sole difference that, in discounting, we look for the forward evolution from a known initial value to an unknown final value, while, in bond pricing, the situation is reversed, since we know the final value but not the initial one.
In order to proceed further, we define the
instantaneous rate of return (also called
forward rate) as the relative time variation of the bond price (compare with Equation (
5))
The knowledge of the forward rate
allows us to relate the initial price
and the maturing price
. Indeed, the integration of the above equation directly leads to
The close analogy between bond pricing and discounting is now apparent. Indeed, the comparison of Equation (
37) with Equation (
11) shows that
is the equivalent of the discount function
and that the forward rate
is the equivalent of the discount rate
. However, in what follows, we will use the notation
not for the forward rate
but for the so-called spot rate (also called nominal rate), which we define in Equation (
39).
Another quantity of interest is the
yield to maturity defined by
From (
37), we see that
that is to say, the yield is the time average of the forward rate over the maturity period
.
A final quantity is needed, the
spot or nominal rate, which is defined as the limit of the yield when the maturity tends to 0. In dealing with bonds, one sometimes uses, for the nominal rate, the notation
instead of
—the later reserved for real interest rates, which can be negative due to inflation (see
Section 3).
Solving the indeterminacy by expanding the integral in powers of
, we see that the spot rate is given in terms of the forward rate by
In other words, the spot rate is the instantaneous forward rate.
Let us finally note that a loan of amount
M subscribed at time
with an interest rate
(the spot rate) will, at time
, increase in value to
, where
Indeed, at any time
, the value of the spot rate
is the instantaneous increase of the loan value, that is,
(compare with Equation (
36)). All of this clearly heightens the close similarities with discounting mentioned above.
However, subsequent values of the spot rate are not necessarily certain. We will see next, the consequences of this fact on the time evolution of the bond price .
3.1. Dynamics of the Bond Price
Suppose the spot rate
is not deterministic but random. In such a case, and analogously to discounting, the usual assumption is that
is a Markovian random process with continuous trajectories; that is, a diffusion process obeying a stochastic differential equation of the form
where
is the standard Wiener process. We assumed that the drift and the noise intensity are independent of time, thus, the time dependence of these coefficients is implicit through
. We know that this implies invariance under time translations, and we can set
when needed without loss of generality.
We will now obtain the time evolution of the bond price
from the purchasing time
to maturity
t, and to this end, we follow Oldrich Vasicek [
33]. Let us first observe that the most natural hypothesis consists in assuming that the bond price
B is a function of the initial spot rate
and write
In this way,
represents the price of a bond issued at time
and maturing at time
t, given that the initial interest rate is
. The infinitesimal variation of the bond price is then defined by
We expand in Taylor series up to second order
Substituting for Equation (
42) and taking into account that
[
34,
39], we write
However,
(in mean square sense) [
34,
39], and, up to the first order in
, we obtain
Defining
and
we see from (
44) that the bond price satisfies the stochastic differential equation
showing that the bond price is also a diffusion process.
Averaging Equation (
47) and recalling that
, we see that
which proves that
is the average of the instantaneous rate of return [cf. Equation (
36)] at time
on a bond with maturing date
t, given that the current spot rate is
. In an analogous way, one can easily show that
is the variance [
33].
We therefore see from the above development that the bond price is a random quantity but with a final fixed price (the maturity price). The question is: what is the (initial) price that an investor has to buy (or sell) a bond at time maturing at time with the current spot rate ? One possible answer would be proceeding as in discounting to take the average over all possible realizations of the bond price. However, this procedure implies that the expected rate of return of a bond is invariant under risk variation—that is, under changes of the variance —a fact that investors always have in mind.
We explain next a procedure resulting in a deterministic bond price, which takes into account the risk aversion of investors (in practice this is only true to some extend because the mathematical procedure assumes that the market is driven by Gaussian white noise—that is, the Wiener process, which is an idealized noise presenting, among other shortcomings, no fat tails, a key characteristic of real markets [
6]).
3.2. The Market Price of Risk
Consider an investor who, at time
, sells an amount
of a bond maturing at time
and, at the same time, buys an amount
of another bond with a different maturing date
. The total worth of the
portfolio, thus, constructed is
. Note that each amount
(
) is a multiple of the bond price
(
) and, hence, they also obey the stochastic differential Equation (
47). That is,
As a consequence, the infinitesimal variation
of the worth of the portfolio changes over time according to
Suppose we choose the amounts
and
such that
where
and
(
). Hence
is proportional to
, while
is proportional to
. With this choice, we have
and the random term in Equation (
48) vanishes. This renders the portfolio composed of such amounts of the two bonds instantaneously riskless:
where
. The rate of return
of this portfolio is
In order to avoid
arbitrage opportunities—that is, making profits without taking any risk—the rate
must be equal to the spot rate
. If not, the portfolio can be purchased by taking funds borrowed at the spot rate, or otherwise sold and the profits lent out to accomplish a riskless arbitrage [
33]. Therefore (compare also Equation (
41) with Equation (
50))
Rearranging terms, we find
, so that
This equation is valid for arbitrary maturities
, it then follows that the ratio
must be independent of the maturity timet.
Let us denote by
the common value of such a ratio for a bond of any maturity date, given that the current spot rate (at time
) is
,
The quantity
is called the
market price of risk, as it gives the variation of the expected rate of return on a bond (specified by the
risk premium) per an additional unit risk (specified by the standard deviation
). The market price of risk
is the so-called Sharpe ratio [
40] of the excess return
.
Note that, if
, the spot rate
and the average rate of return
coincide.
meaning that the expected instantaneous rates of return on bonds are the same for all maturities.
3.3. The Term Structure Equation and the Risk-Neutral Measure
The introduction of the market price of risk implies a non-random bond price
, which, in turn, allows a deterministic equation for
B. In effect, rewriting Equation (
51) as
and substituting
and
for their definitions given in Equations (
45) and (
46), we have
which, after rearranging terms, yields
This equation, called the term structure equation, is a partial differential equation for
, that is obtained once we know the random character of the spot rate process
(through its drift
f and noise intensity
g) and once the market price of risk
is specified. Bond prices are thus obtained after solving the deterministic Equation (
52) with the final condition:
Let us observe that the term structure Equation (
52) for the bond price
B is identical to the Feynman–Kac Equation (
27) for the discount function
D as long as we make the following change of drift
On the other hand, as we have seen in
Section 2, the solution of the Feynman–Kac Equation (
27) for the discount function
is written as the average (cf. Equation (
15))
where
is the probability density function of the bidimensional diffusion process
defined by Equation (
16),
Now the analogy between the term structure Equation (
52) and the Feynman–Kac Equation (
29) suggests that we can write the bond price
as an average over the different realizations of the spot rate
. However, this averaging procedure is taken using a modified PDF called the
risk-free measure. Thus, it can be proven in a more rigorous way that [
32,
33]
where
is the risk-free measure that is the PDF of the bidimensional process
defined by the following pair of stochastic differential equations that include the market price of risk (see Equation (
54)):
That is,
is the solution to the FPE
with the initial condition
Since, as we have shown in
Section 2.2, the Feynman–Kac approach to discounting is equivalent to the Fourier method described in
Section 2.3, we can apply the latter to directly obtain the bond price knowing only the risk neutral PDF, without having to solve the Feynman–Kac Equation (
52) with condition (
23). Indeed, the characteristic function of the risk neutral density
is the joint Fourier transform
which, after comparing with Equation (
55), yields
Finally, once we know the bond price, the yield to maturity
(also called
the term structure of interest rates) is readily evaluated from Equation (
38):
The graphic representations of
as a function of
and for different values of the maturity interval
are called
yield curves and are of prime importance for practitioners.
4. Standard Models
Throughout the above development, it is clear that, in order to proceed further in the discounting process (as well as in pricing bonds), we need to identify the specific diffusion process chosen for modeling rates. Such a choice is mostly based on the analysis of empirical data [
26,
29]. Clearly, in any proposed market model, there are idealizations, otherwise a complete treatment of the problem would be very problematic, not to say impossible, not only analytically but computationally as well.
In addition to assuming a diffusive behavior for the market, the first of such idealizations is supposing that the market is stationary, i.e., the structural conditions of the market do not change over time. However, and in particular after the 1980s, market circumstances have largely changed due to a great increase of transaction volumes along with transparency and, to a lesser extend, changes in investor perspectives. In this review, we only address stationary models, although we are working on new models dealing with some non-stationary features of the market [
29,
35], and we refer the interested reader to these works for further information.
On the other hand, there is a property of the market that appears to be well founded on empirical grounds. This is the property of mean reversion meaning that prices tend to return to some fundamental value, called the normal level, which is typically identified as the long-time (i.e., stationary) mean value. The simplest method of introducing this feature in the diffusion market model is to assume a linear drift of the form , where is the strength of the reversion to the normal level, identified by m.
In such a case, the drift acts like a linear restoring force driving
towards
m as time increases. Despite that the introduction of mean reversion might create some arbitrage opportunities, the property of mean reversion is widely accepted in the literature [
6], and we previously discussed this issue in the context of option pricing when considering the Ornstein–Uhlenbeck model [
41].
4.1. Bonds and Real Rates
Before proceeding with the introduction of some standard models for the market evolution, we briefly explain the link between bonds and (real) interest rates.
Financial economists have developed a large number of models of interest rate processes to enable them to price bonds and other cash flows. In these models, interest rates are described by positive random processes since financial interest rates rarely take negative values. Although the models could be, in principle, extended to arbitrary horizons, they have only been studied carefully over time horizons of up to 30 years, since bonds are seldom issued for periods longer than this.
On the other hand, environmental economists are interested in the real behavior of the economic growth over longer horizons, in contrast to financial economists who are typically more interested in nominal rates over shorter periods of time. The behavior of real and nominal rates usually differ as, due to inflation, real rates can take on negative values. In this way, real rates
are generally defined by the so-called Fisher procedure:
where
is the inflation rate that is usually generated from consumer price indexes as we will explain in the next section. The quantity
represents nominal rates, which are typically constructed out of government bonds and are usually positive (even though, in recent years, nominal rates have taken slightly negative values). In order to explain the close relationship between nominal rates and bonds, let us first recall that nominal rates were called spot rates in the previous section on bond pricing where we used the notation
instead of
. We thus define the spot (i.e., nominal) rate as (see Equations (
39) and (
40))
where
is the forward rate for bonds defined in Equation (
36) (see also Equation (
37)), that is
where
is the price at time
of a (government) bond maturing at time
. Let us recall the definition of the yield to maturity
given in Equation (
38),
(
), so that
and comparing with Equation (
62), we see that, in terms of the yield nominal rates,
can be defined as
Thus, for empirical analysis, the yield can be used as an estimator of the nominal rates:
and the accuracy of such an estimator increases as
. We will return to this discussion in the next section.
In this way, taking nominal rates corrected by inflation as a proxy of economic growth, we recently demonstrated [
26,
29,
30] through a detailed empirical study on many countries that real interest rates are negative around 25% of the time (see next section). To understand how discounting depends on the random process used to characterize interest rates, we focused on three different models and obtained exact analytical expressions for the discount function [
27]. The three models describe to, varying degrees, a number of relevant characteristics observed in the data, while being simple enough to allow for complete analytical treatment. The main results are summarized in
Table 1.
The first model is based on the Ornstein–Uhlenbeck (OU) process—also called the Vasicek model in the financial literature [
13]—which allows for negative rates and is, therefore, suitable for pricing environmental problems. The model has a stationary probability distribution and exhibits reversion to the mean, which means that the process tends to return to its average stationary value. We will review this model below.
The second and third models that we considered are given by the Feller and log-normal processes, respectively. For these processes, the rates cannot be negative. The Feller process—also known as the Cox–Ingersoll–Ross (CIR) model [
42]—has reversion to the mean and stationary probability distribution.
This is one of the most popular models in finance [
13], and we recently reviewed the main properties of the Feller process in previous works [
27,
43]. A third model, also implying positive rates, is the log-normal process (occasionally called the Dotham model in the financial literature [
44]). The model does not have reversion to the mean nor a stationary distribution. Despite these shortcomings, the log-normal process has also been used in the financial literature mainly because it is positive and allows for analytical treatment [
13]. We refer the interested reader to our previous work [
27] for details on this model.
As remarked in the introduction, we are primarily interested in valuing the far future for environmental problems rather than the short time discount of finance, the latter implying positive interest rates, while the former involves positive as well as negative rates. For this reason, we next review in more detail the Vasicek model allowing for both positive and negative rates than the CIR and log-normal models of which we only present a sketched review.
4.2. The Vasicek (Ornstein–Uhlenbeck) Model
In this model, the rates are described by the Ornstein–Uhlenbeck process [
33], which is a diffusion model with linear drift and constant noise intensity:
where
is the rate and
is the Wiener process. The parameter
m (the normal level) is the mean value to which rates revert,
is the amplitude of fluctuations, and
is the strength of the reversion to the mean. These parameters have to be estimated from empirical data.
In this case, the Fokker–Planck equation for the joint density
of the bidimensional process
, given by Equation (
17), reads
with the initial condition
The joint Fourier transform of these equations results in a simpler initial-value problem for the joint characteristic function
, which can be readily solved to yield the Gaussian density [
27]
where
,
and
are given by [
27]
and
The characteristic function of the rate
is obtained by setting
in Equation (
68), which also results in the Gaussian density
and in the stationary state
), we have
which proves that the normal level
m is the stationary mean value,
It can also be shown that the correlation function of the process, defined as the average
(
) in the stationary state reads [
27]
which means that
is the correlation time,
, of the rate. Indeed,
Let us observe that the volatility,
, is independent of the normal level and given by
The discount function
is also obtained from Equations (
68)–(
71) although, in this case, after setting
and
(cf. Equation (
31)). We have
which, after rearranging terms, can be written as
where
is the initial rate. Note that, as
(in fact when
, i.e., for times much greater than the correlation time
) Equation (
77) shows at once that the discount function of the Vasicek model has the typical exponential decay
where
is the long-run discount rate. Let us note that the long-run rate can be defined as the limit
as long as the limit exists. Let us also note the important fact that
is smaller than the mean value of the return given by the normal level
m. This reduction is quantified by the “noise-to-signal” ratio
, which means that either a long persistence (recall that this is equivalent to long correlation time, i.e.,
small) or an increase of the noise fluctuations (i.e.,
k large) reduce the long-run discount rate as compared with the average rate
m.
Finally, we easily see from Equation (
77) that, as
, the discount function approximates to
, which would correspond to a fixed interest rate without random fluctuations or deterministic changes.
Risk Aversion
As mentioned above, risk aversion is taken into account by introducing the market price of risk
and changing the drift according to Equation (
32). For the Vasicek model, in which
and
, we have
and assuming
to be a constant independent of
r, we write
where
Since the modified drift
has the same form that
, we conclude that the adjusted-for-risk discount function will be given by Equation (
77) after the replacement
. In particular, the adjusted long-run discount now reads (cf. Equation (
79))
We thus see that the long-run discount depends on the historical rate
m; however, this is shifted by two terms. The first term raises the long-run rate due to the market price of risk. The second shift lowers it by an amount given by the ratio of uncertainty (as measured by
k) and persistence (as measured by
). We rewrite Equation (
84) as
This shows that the overall shift in the long-run discount rate will be positive or negative depending on the size of the market price of risk and on the noise-to-signal ratio between the volatility parameter and the reversion rate.
It is not surprising that the market price of risk raises the long term rate; however, it is not so obvious that uncertainty and persistence can lower it. Indeed, for any given mean interest rate m, by varying k and , the long-run discount rate can take on any value less than m, including negative values, while, at the same time, the standard deviation can also be made to take on any arbitrary positive value.
A negative long-run rate is due to the amplification of negative real interest rates . Computation of the discount function involves an average over exponentials, rather than the exponential of an average. As a result, periods where interest rates are negative are amplified and can easily dominate periods where interest rates are large and positive, even if the negative rates are rarer and weaker. It does not take many such periods to substantially reduce the long run interest rate.
To summarize, in the Vasicek model, and even taking into account risk aversion, the long-run discounting rate can be much lower than the mean and, indeed, can correspond to low interest rates that are rarely observed.
4.3. The Cox–Ingersoll–Ross (Feller) Model
In the financial literature, one of the most accepted models for interest rates is the Cox–Ingersoll–Ross (CIR) model [
42] where rates follow the Feller process described by drift and noise intensity given, respectively, by [
45]
The Feller model is thus a diffusion process described by the stochastic differential equation
where
is the standard Wiener process, and, as in the OU process,
represents the mean stationary rate (the
normal level), and
is the correlation time [
27]. Let us note that, in one-dimensional diffusions, the diffusion coefficient is given by the square of the noise intensity, and we thus see that the Feller process has a linear diffusion vanishing at the origin. This turns the origin into a singular boundary, which results in significant properties for the process [
43].
As in the Vasicek model, the linear drift results in a restoring force, which, in the absence of noise, makes the process decay toward the normal level m. On the other hand, the state-dependent noise intensity for large values of r magnifies the effect of noise, while when r goes to zero, this effect vanishes. Therefore, as the process approaches the origin, the drift drags r towards m. Hence, since , starting at some positive value the process cannot attain negative values with the overall result that the Feller process always remains positive.
Previous works [
27,
43] that we reviewed rather thoroughly presented the properties of the Feller process, and we refer the reader to these works for more detailed information. The process is not Gaussian, and the stationary PDF as
is the Gamma distribution [
27]
where
is a positive and dimensionless constant that combines all the parameters of the model into a single expression. As mentioned above, a major characteristic of the Feller process is that
cannot attain negative values, which makes the model a convenient tool for pricing bonds, which are never negative [
13].
In the Feller model, the joint density of the discounting process
defined in Equation (
16) obeys the Fokker–Planck equation (FPE) (cf. Equations (
17) and (
18))
with the initial condition
The joint Fourier transform, Equation (
30), turns Equations (
90)–(
91) into a more manageable problem:
Equation (
92) is a linear partial differential equation of first order whose solution can be obtained by the method of characteristics, and we refer the interested reader to our work [
27] for a detailed information. Once we know the solution
, the discount function is then obtained through Equation (
31) with the result [
27]
where
is defined in Equation (
89) and
Notice that
and the time scale represented by
is smaller than the correlation time
.
In this case, the long-run discount rate, defined by the limit (cf. Equation (
80))
is directly obtained from Equation (
94) with the result
and, as in the Vasicek model, the effective discount reduces to the expected exponential decay
Substituting into Equation (
96) the expressions for
and
given in Equations (
89) and (
95), we write
which clearly shows that the long-run discount rate is always smaller than the stationary average rate:
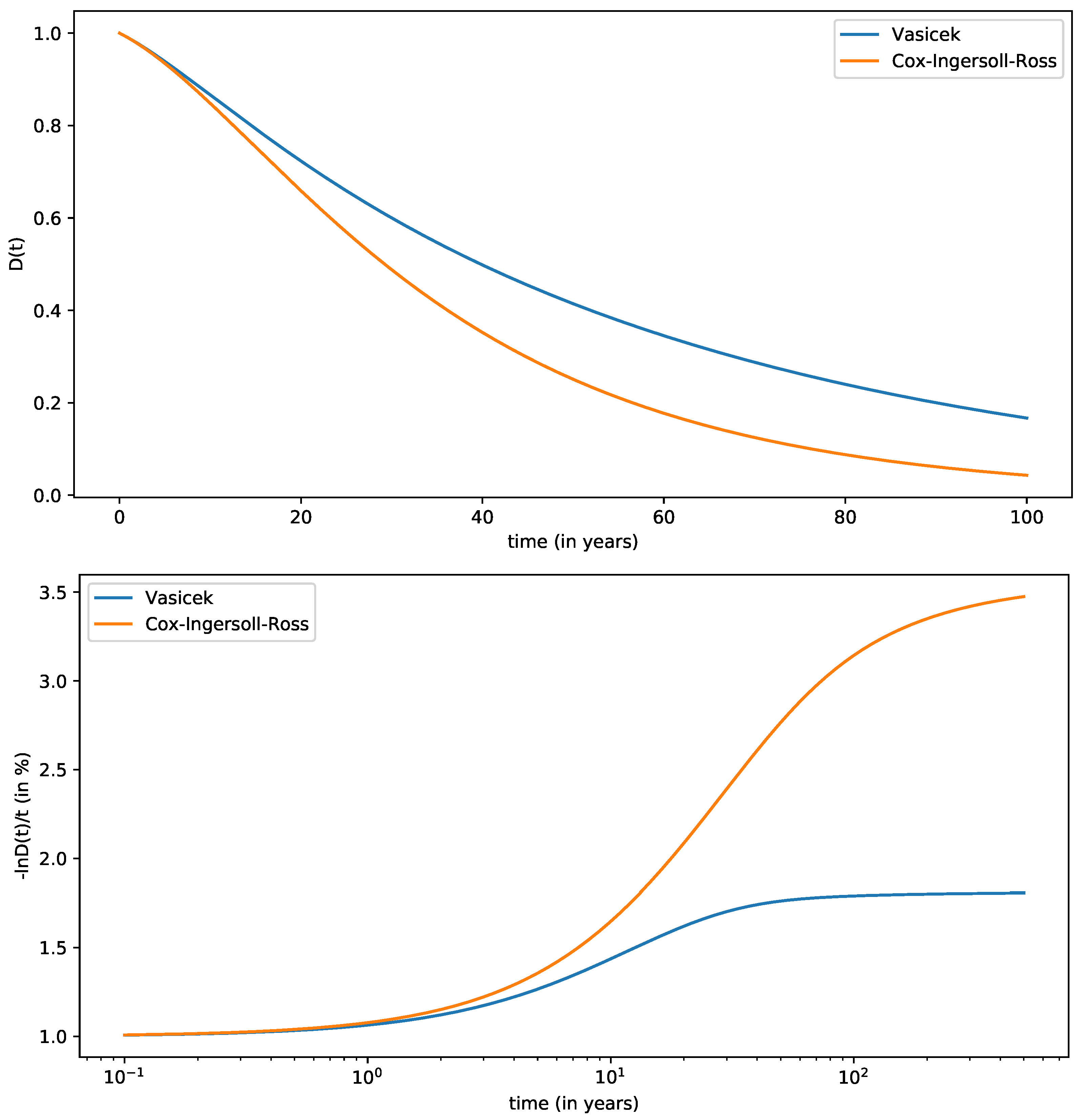
Figure 1 shows the discount function
along with the quantity
(cf. Equation (
80)) and compare them with the Vasicek model with equivalent parameters.
Risk Aversion
For the Feller process, the adjusted drift for risk defined in Equation (
54) reads
where
is the market price of risk as discussed in the previous section. For any function
(including a constant market price of risk
q), this adjusted drift leads to an unsolvable Fokker–Planck equation with no analytical expression for the adjusted discount and the long-run discount rate. It is, nonetheless, possible to obtain analytical expressions for these quantities if the market price of risk has the following functional form
where
is a positive quantity. In such a case, we may write
where
The adjusted drift has the same form as
. Therefore, the adjusted discount function will be given Equation (
94) with the replacements
and
, and the long-run discount is (cf. Equation (
98))
From the definitions of
and
, we easily see that
and
. Hence, writing
as
so that
, and, if the market price of risk has the form given in Equation (
100), then, in the CIR model, risk always increases the long-run discount rate regardless of the noise intensity and persistence.
4.4. The Log-Normal Model
In this model, rates are described by the the geometric Brownian motion (log-normal process), and the model is determined by the stochastic differential equation
where
r is the interest rate,
and
k are constant parameters.
may be positive or negative, whereas
k is always positive, and
is the standard Wiener process. Equation (
104) can be integrated at once yielding
showing that
is never negative (
). Therefore, the log-normal model is more suited for modeling nominal interest rates and bonds in finance than for the long-run real rates of environmental economics. Contrary to the OU and Feller processes, the log-normal process does not show reversion to the mean. Indeed, as
t increases, we see from Equation (
105) that the rate either diverges when
or goes to zero if
. In an equivalent way, one can also show from Equation (
105) that the mean and variance of the process are [
27]
The discount associated with the log-normal process model was studied in 1978 by L. U. Dothan [
44], and, in finance, it is sometimes refereed to as the Dothan model. As it allows for analytical treatment, it is one of the models used in the literature [
13]. For this model, the FPE for the joint density of the discounting processes
is given by (cf. Equation (
17))
with the usual initial condition given by Equation (
18). The Fourier transform of this expression leads to the following equation for the characteristic function
and the initial condition (
91). Equation (
106) is a partial differential equation of second order, which cannot be solved by the method of characteristics, and we refer the interested reader to our work [
27] for more information on how to solve Equation (
107) using the time–Laplace transform. Hence—and contrary to Vasicek and CIR models where it is possible to obtain exact expressions for the discount function
—for the log-normal case, we can only achieve the exact expression of its Laplace transform,
The resulting formula—written as an integral of special functions, the Kummer function—is rather intricate, and we will not write it here (see [
27] for more information). However, from the exact expression for
, we can obtain asymptotic expressions as
of the discount function
in real time. This is done using the so-called Tauberian theorems, which relate the small
s behavior of
with the long-time behavior of
[
46,
47]. The final result is the following asymptotic expression for the discount function
in the long run as
[
27]
The asymptotic form of the discount function thus depends on the values taken by the ratio between the strength of the constant deterministic drift and the amplitude of fluctuations given by (which can be considered the “signal-to-noise ratio” of this model).
(i) The case
corresponds to strong fluctuations, where the noise intensity
is greater than the drift parameter
. In this case, the discount tends to a constant value (for the actual value of this constant, see [
27]).
(ii) The case
corresponds to mild fluctuations for which the deterministic drift is stronger than noise. In such a case, the discount function has the expected exponential decay
with a long-run rate of discount given by [
27]
where
is a positive numerical factor that only depends on the ratio
and reads
where
is the digamma function.
Let us write Equation (
109) in a more characteristic form. Indeed, from Equation (
105), we see that
and, with the help of Equation (
109), we write Equation (
109) as
(
and
). Note that the average
is what a practitioner would take as an estimate of the discount rate up to time
t within the log-normal model. Since
, the analytical result (
112) shows that the actual long-run rate of the model is a fraction of the average rate. We indicated elsewhere that the long-run discount rate is at most 73% of the average rate [
26].
In this way, when
, the log-normal model follows a similar pattern to that of the OU and Feller models: In all of them, the long-run rate is smaller than the average rate. This general statement is a direct consequence of Jensen’s inequality, which states that the average of a convex function is greater than or equal to the function of the average; that is,
. Assuming
f to be the decreasing exponential and
X as the cumulative process
defined in Equation (
14), it follows immediately that the long-run rate
must be always less than or equal to the average rate. Nonetheless, our procedure quantifies the difference among averages [
27].
(iii) The critical case
, in which deterministic motion and fluctuations are balanced, leads to the hyperbolic discount function as obtained by Farmer and Geanakoplos [
48,
49]. The hyperbolic
is substantially greater than any exponential decaying function, showing that there is no long-run rate of interest in this case. In fact, the long-run rate of interest is 0; however, that does not convey as precise information as saying that
is approximately
for all large
t. Since the sum (i.e., the integral) of all these
is infinite, such
assigns infinite value to any permanent positive flow of consumption: the infinite future is infinitely valuable.
Risk Aversion
Let us very briefly comment on the inclusion of risk aversion in the Dothan model. For the log-normal process
and
and
Assuming a constant market price of risk,
, we have
Again,
has the same form than
, and all previous results will apply after making the replacement
.
5. Some Empirical Results
In order to choose an appropriate model for rates that would allow us to obtain realistic long-run discount functions, we performed a rather complete empirical study on interest rates combined with inflation. Our study follows the line partly initiated by Newell and Pizer [
50] (see also [
51]). To our knowledge, there are few empirical studies on real rates with some exceptions. We remark here the recent and excellent survey by Giglio et al. on the housing market in London and Singapore [
52,
53,
54], which allowed for a rather realistic estimation of long-run discount rates.
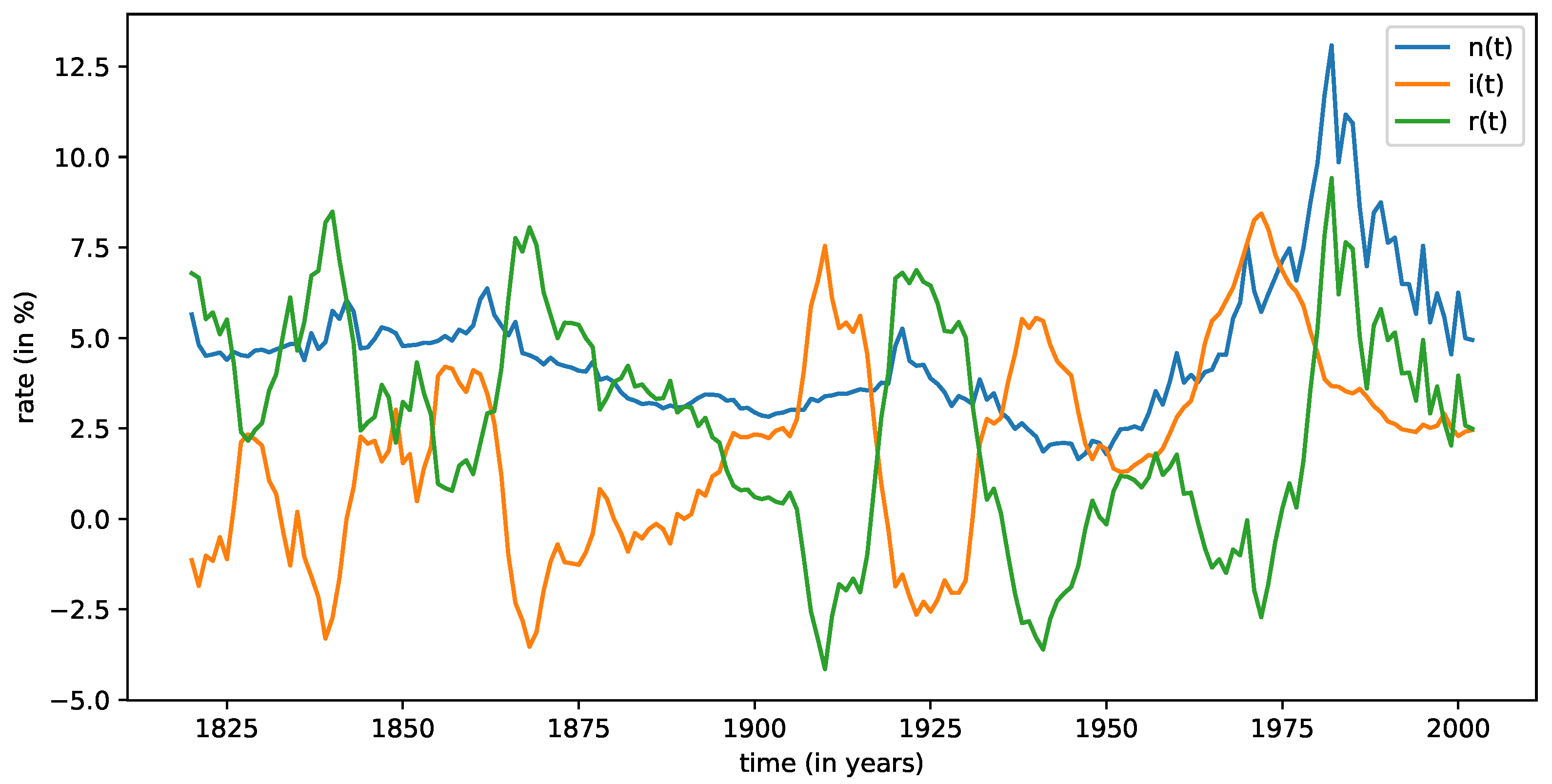
Our first concern was knowing how the discount process depended on the underlying random process that characterizes interest rates. To this end, we collected data for the nominal interest rates and inflation of fourteen countries over time spans ranging from 87 to 318 years [
26]. The countries in our sample are Argentina (ARG, 1864–1960), Australia (AUS, 1861–2012), Chile (CHL, 1925–2012), Germany (DEU, 1820–2012), Denmark (DNK, 1821–2012), Spain (ESP, 1821–2012), United Kingdom (GBR, 1694–2012), Italy (ITA, 1861–2012), Japan (JPN, 1921–2012), Netherlands (NLD, 1813–2012), Sweden (SWE, 1868–2012), the United States (USA, 1820–2012) and South Africa (ZAF, 1920–2012). The data are summarized in
Table 2.
Since all but two of our nominal interest rate processes are for 10-year government bonds, which pay out over a 10-year period, we smoothed out inflation rates with a 10-year moving average and subtracted the annualized inflation index from the annualized nominal rate to compute the real interest rate, as explained in the previous section by means of the Fisher’s procedure (cf. Equation (
61)),
where
is the nominal rate and
is the inflation rate. The particular case of the United States is plotted in
Figure 2.
In our empirical analysis, the nominal rates are determined by IG rates constructed from the 10-year Government Bond Yield
with
= 10 years. Thus, looking at Equations (
63) and (
64), we estimate the nominal rates by
Let us recall that denoting, by
, the government bond issued at time
t and maturing at time
with unit maturity,
, the yield
is defined as (cf. Equation (
38))
One can argue that
years is not a short period of time in order to consider
a very accurate estimator of
(cf. Equations (
63) and (
64)). Although this may be true, we must bear in mind that 10 year bonds are the shortest bonds available for most of the countries analyzed.
The inflation rate is estimated through the Consumer Price Index (CPI) as
where
is the aggregated inflation up to time
t, and
10 years. The relation between
and the Consumer Price Index (CPI) is
where
is the time series of the empirical CPI. The instantaneous rate of inflation
is, therefore, estimated by the quantity
, which is written in terms of the CPI reads
A remarkable characteristic observed for all countries is that real interest rates frequently become negative as the real interest rates are mostly dominated by inflation
(see
Figure 2). In some cases, as we can see in
Table 3 (see also
Figure 2), negative real rates show high frequency and long periods of time, and, on average, real interest rates are negative one quarter of the time.
This makes the Feller and log-normal models—as well as any other model assuming positive interest rates [
13]—less interesting or at least less appropriate to model real interest
instead of solely considering nominal rates
. It is, however, necessary to remember the fact that nominal rates can indeed become negative as has recently been observed in Western economies. We, therefore, confined the empirical work to the OU (Vasicek) model and then assumed the Local Expectation Hypothesis [
36,
37,
38], according to which, we live in a risk neutral world, and the market price of risk is zero. Let us recall, as explained in
Section 3, that the market price of risk
may be any function of the rate and time. There is, hence, no unique expression for it. Thus, in
Section 4, we presented several expressions of the long-run rate, which include risk in different forms for all market models analyzed. The usual assumption in the literature [
33,
38] is that the price of risk is a constant that is independent of time and the value of the rate but without any empirical justification. This is a sensitive issue since data is quite scarce, particularly in environmental applications, for obtaining a credible estimation of
q. Moreover, to our knowledge, in environmental problems, the estimations of the long-run rates do not take into account, nor even mention, the market price of risk [
14,
15,
16,
50,
54]. In any case, we do not lessen the importance of taking into account some kind of risk in estimating log-run rates; however, unfortunately, with the data available to us, we cannot make any reliable estimation of
q. For this reason, we have not taken into account the market price of risk, assuming risk-neutral investors and following the Local Expectation Hypothesis. In any case, the question is under consideration).
We can estimate the parameters
m,
and
k of the Vasicek model to each of the data series. There are several possible procedures. One of the possible methods is to deal with stationary averages. The parameter
m can be estimated through the stationary mean value of the rate (cf. Equation (
74))
Parameters
and
k can be estimated via the correlation function of the Ornstein–Uhlenbeck process. Thus, from Equation (
75), we have
The empirical correlation can then be fitted by an exponential, which in turn allows us to estimate
(measured in 1/year units) for each country. The parameter
k is obtained from the empirical standard deviation
, and for the Vasicek model, it is given by
The resulting parameters are shown in
Table 3. The minimum and maximum values for each country allows us to show that parameters may indeed fluctuate over different periods of time.
Finally, the long-run discount rate can be evaluated from Equation (
79),
For this calculation, we neglected the market price of risk as mentioned above.
The countries studied can be divided into two groups. Nine countries have long-run positive rates (boldface in
Table 3). The average historical rate for these nine countries is
% while the average long-run rate is
%, which, on average, is 29% lower than
. Five countries with less stable behavior have long-run negative rates and an exponentially increasing discount.
Four cases of this group have a negative average rate
m due to at least one period of runaway inflation; the exception is Spain, which has a (highly positive) mean real interest rate but still has a long-run negative rate. Convergence in this case to the long-run rate happens within 30 years and typically within less than a decade. This contrasts with other treatments, which assume that short term rates are always (or nearly always) positive and predict that the decrease in the discounting rate happens over a much longer timescale, which can be measured in hundreds of years [
50,
51,
55,
56,
57,
58].
Alternatively, we can estimate parameters using the well-established maximum likelihood procedure. For the Vasicek model, the maximum likelihood estimation is extensively documented in the financial mathematics literature (see for instance [
13]). The approach differs from the previous one as it focuses attention on two consecutive steps of our time series (generally consecutive years) and takes the conditional probability to perform the estimation.
Table 4 shows that the most inaccurate estimator is
, an unsurprising fact since the estimation of
is known to be quite difficult for the Vasicek model [
59]. The last two columns in
Table 4 include the long-run interest rate estimator
and its error calculated through error propagation.
Only four countries (the Netherlands, Sweden, the United Kingdom and the United States) show a positive long-run rate, . This estimation procedure leads to more negative . This feature can be attributed to the fact that, in most of the countries, estimating via the maximum likelihood brings smaller values, which in turn leads to more drastic corrections to the long-run rate as is inversely proportional to (remember that ). This effect is particularly relevant in most turbulent countries during last century (e.g., Germany) thus signaling a more intense lack of stationarity in empirical data. The averaged over all countries estimated via maximum likelihood is also sensitively smaller.
However, if we focus the attention on stable countries (with
) both estimation procedures bring quite similar results (see, for instance, the United States case in
Table 3 and
Table 4, 2.1% versus 1.8%). As in the previous estimation procedure, we also neglected the effects of risk aversion and the market price of risk.
The Vasicek model is therefore the only one among the three classic models allowing for negative rates, and for this reason, both the Feller and the log-normal models have been excluded from our analysis. However, for the Cox–Ingersoll–Ross (Feller) model, it is possible to redefine the model by shifting the process where .
The estimation through the maximum likelihood procedure and its error analysis is then possible [
59], and
Figure 1 includes the shifted Cox–Ingersoll–Ross discount and compares it with the equivalent result assuming the Vasicek model. We demonstrated in Ref. [
29] how to redefine the Feller process and how maximum likelihood estimation could be possible.
6. Discussion
We reviewed one of the most important aspects of economics and finance, i.e., the problem of discount, which weights the future relative to the present. The problem is clearly very relevant in finance over relatively short time spans; however, it is even more crucial for long-run planning in addressing environmental problems on how to act now with measures to mitigate the effects of climate change.
To our knowledge, this is a rather unknown issue to the econophysics community, and this review is particularly intended for this group. We thus addressed the problem with a simple approach and yet with a high level of rigor and generality. In this way, we also developed the traditional method used in mathematical finance to address the problem, i.e., the Feynman–Kac approach. In addition, we reviewed the bond pricing theory and its close similarity with discounting and presented a short introduction to the term structure of interest rates along with the market price of risk.
We obtained quantitative results on the problem by studying, in some detail, three standard models for the dynamical evolution of rates. These models are based on the Ornstein–Uhlenbeck process (the Vasicek model), thus, allowing for both positive and negative rates and also on the Feller and log-normal processes for positive rates. We presented the exact results for the discount function and asymptotic expressions as leading to the long-run discount rate, and we discussed the modifications of these expressions when the market price of risk is taken into account.
An important conclusion is that, for all models, the long-run discount rate is always less than the long-time average rate. This is a conclusion that necessarily has to have consequences in any long-run economic planning. Finally, we reviewed our recent empirical study on 14 different countries, which obtained numerical values for the parameters that appear in the Vasicek model. We demonstrated two different estimation procedures and briefly discussed their differences and similarities.