On the Thermal Capacity of Solids
Abstract
:1. Introduction
1.1. Energy and Entropy
1.2. Outline
2. Materials and Methods
3. Entropy Capacity
4. Entropy Capacity versus “Heat Capacity”
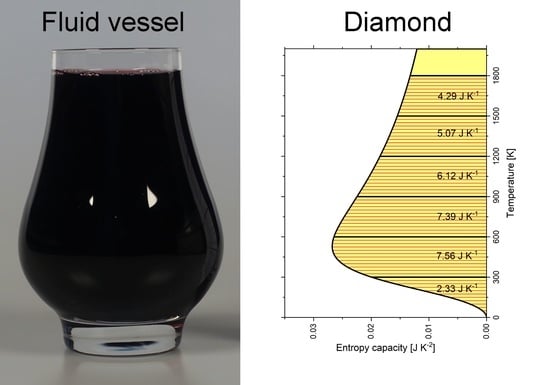
5. Analogy: Storage of a Fluid in a Vessel
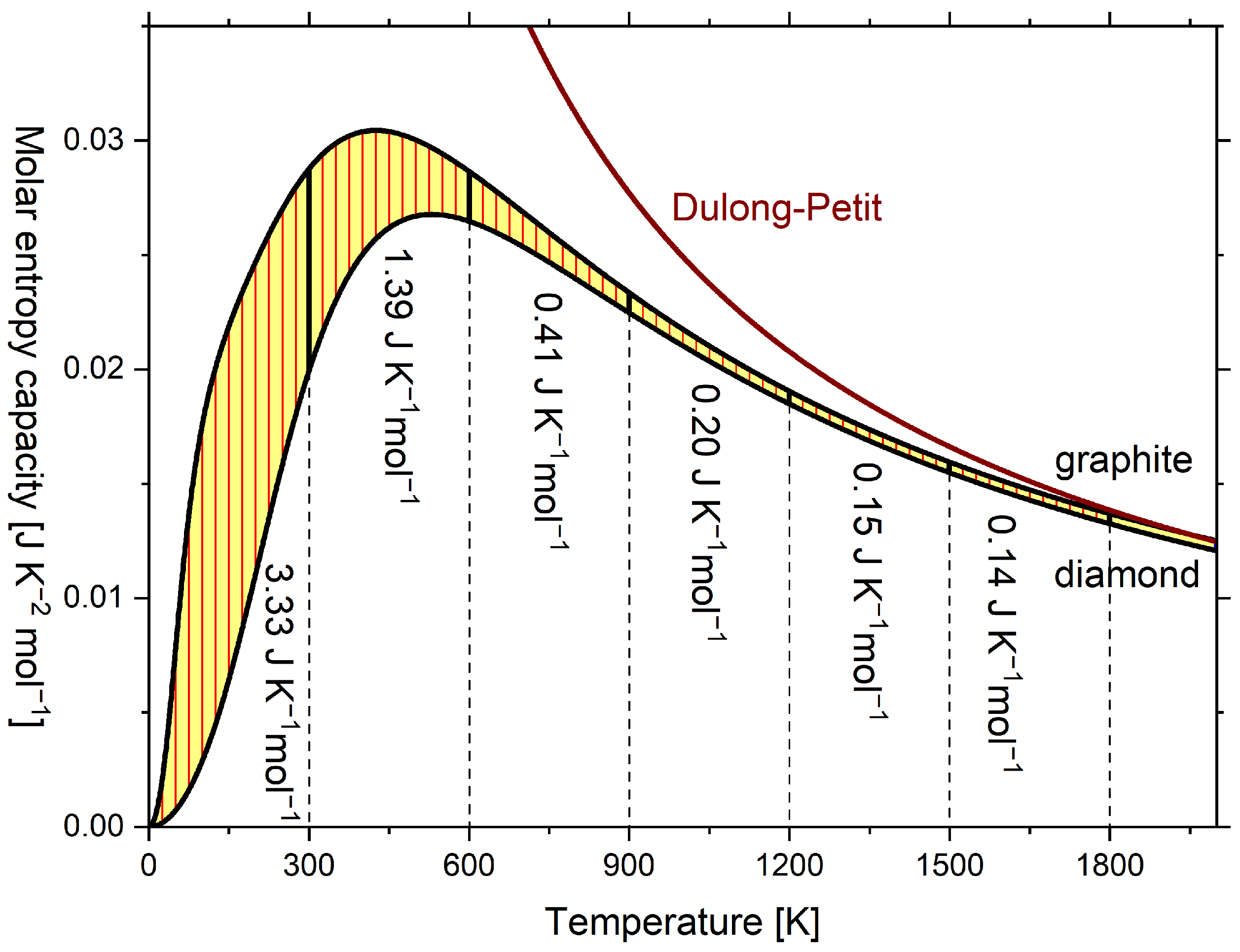
6. Entropy Capacity of Diamond and Graphite
7. Reaction Entropy
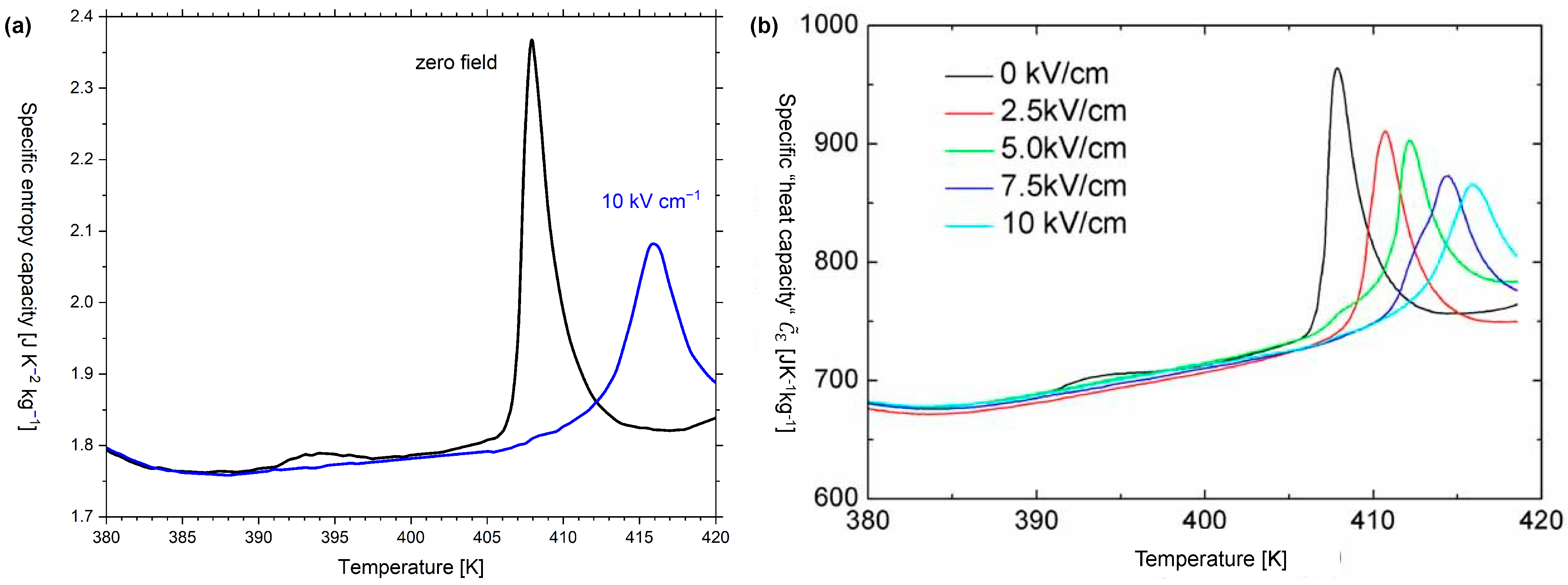
8. Caloric Materials
9. Thermoelectrics and Thermal Conductivity
10. Phononic Contributions to Entropy Capacity: Debye Model
11. Phononic and Electronic Contributions to Entropy Capacity
12. Discussion
12.1. Thermal Capacity
12.2. Units of Entropy and Entropy Capacity
12.3. Confusion and Resolution
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Symbols
| specific temperature coefficient of energy (at a constant electrical field) (specific “heat capacity” at a constant electrical field) | |
| temperature coefficient of energy (at constant volume) (“heat capacity” at constant volume) | |
| molar temperature coefficient of energy (molar “heat capacity” at constant volume) | |
| temperature coefficient of energy at a constant number of particles (“heat capacity” at constant volume and at a constant number of particles) | |
| temperature coefficient of enthalpy (“heat capacity” at constant pressure) | |
| molar temperature coefficient of enthalpy (molar “heat capacity” at constant pressure) | |
| specific temperature coefficient of enthalpy (specific isobaric “heat capacity”) | |
| temperature coefficient of enthalpy at a constant number of particles (“heat capacity” at constant pressure and at a constant number of particles) | |
| thermal diffusivity (diffusion coefficient of “heat”, diffusion coefficient of entropy) | |
| electronic density of states at the Fermi energy | |
| E | energy |
| Fermi energy | |
| electrical field | |
| f | dimensionless thermoelectric figure of merit (see also ) |
| H | enthalpy |
| Boltzmann’s constant | |
| entropy capacity at constant electrical field | |
| specific entropy capacity at constant electrical field | |
| entropy capacity at constant magnetic field | |
| entropy capacity at constant magnetisation | |
| entropy capacity at constant pressure (isobaric entropy capacity) | |
| molar isobaric entropy capacity | |
| molar isobaric entropy capacity of substance i | |
| molar isobaric entropy capacity of substance j | |
| entropy capacity at constant pressure and at a constant number of particles | |
| specific isobaric entropy capacity | |
| entropy capacity at constant (electrical) polarisation | |
| entropy capacity at constant volume (isochoric entropy capacity) | |
| entropy capacity at constant volume and at a constant number of particles | |
| molar isochoric entropy capacity | |
| entropy capacity at constant stress | |
| entropy capacity at constant strain | |
| N | amount of substance (number of particles), given in mol |
| p | pressure |
| P | (electrical) polarisation |
| R | universal gas constant |
| S | entropy |
| T | absolute temperature |
| V | volume |
| x | integration variable in Debye model |
| dimensionless thermoelectric figure of merit (see also f) | |
| molar isochoric entropy capacity of the electron gas (Sommerfeld coefficient) | |
| factor in the Debye model (low-temperature limit) | |
| reaction entropy | |
| molar reaction entropy | |
| temperature difference | |
| strain | |
| open-circuited specific “heat” conductivity | |
| open-circuited specific entropy conductivity | |
| stoichiometric coefficient of substance i | |
| stoichiometric coefficient of substance j | |
| density | |
| (mechanical) stress | |
| Debye temperature |
Appendix A. Entropy Capacity and “Heat Capacity” of Graphite and Diamond
Appendix A.1. “Heat Capacity” of Graphite and Diamond According to Vassiliev and Taldrik

Appendix A.2. Entropy Capacity and “Heat Capacity” of Diamond

Appendix A.3. Multiparameter Modelling of the Entropy Capacity and “Heat Capacity” of Graphite and Diamond
| Phase | a | b | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Diamond | 1366 | 0.031 | 1833.6 | 0.488 | 1968.7 | 0.482 | 1824.5 | 24.59 | 0.287 |
| Graphite | 282.6 | 0.773 | 1949.9 | 0.114 | 426.4 | 0.114 | 947.9 | 24.25 | 0.848 |
Appendix A.4. Comparison to Wiberg’s Book
| Temperature Interval | ||||||
|---|---|---|---|---|---|---|
| Wiberg [10] 1,2 | This work 3 | Wiberg [10] 1,2 | This Work 3 | Wiberg [10] 1,2 | This Work 3 | |
| 1500–1800 | N/A | 4.43 | N/A | 4.29 | N/A | 0.14 |
| 1200–1500 | N/A | 5.22 | N/A | 5.07 | N/A | 0.15 |
| 900–1200 | 6.28 | 6.32 | 6.28 | 6.12 | 0 | 0.20 |
| 600–900 | 7.49 | 7.80 | 7.49 | 7.39 | 0 | 0.41 |
| 300–600 | 8.83 | 8.95 | 7.95 | 7.56 | 0.88 | 1.39 |
| 0–300 | 5.78 | 5.66 | 2.43 | 2.33 | 3.35 | 3.33 |
Appendix B. Entropy Capacity and “Heat Capacity” of Barium Titanate
References and Notes
- For clarity, the traditional term “heat” is put into quotation marks when it addresses the thermal energy. When the term heat is left without quotation marks, it can be read as entropy. “Heat capacity” can be read either as temperature coefficient of energy or as temperature coefficient of enthalpy depending if isochoric or isobaric conditions apply.
- Zemansky, M. Heat and Thermodynamics; Mc Graw Hill: New York, NY, USA, 1951. [Google Scholar]
- Callen, H.B. Thermodynamics—An Introduction to the Physical Theories of Equilibrium Thermostatics and Irreversible Thermodynamics; John Wiley and Sons: New York, NY, USA, 1960. [Google Scholar]
- Strunk, C. Quantum transport of particles and entropy. Entropy 2021, 23, 1573. [Google Scholar] [CrossRef] [PubMed]
- Falk, G.; Ruppel, W. Energie und Entropie; Springer: Berlin, Germany, 1976. [Google Scholar] [CrossRef]
- The term energy form should not be taken literally. There is only one kind of energy.
- “Die Wärme ist aber kein Energieanteil, sondern eine Energieform....Daß aber Wärmeenergie nicht in einem System ‘drinsteckt’, sondern nur bei Energieaustausch auftritt, wie alle Energieformen, ist ein springender Punkt der Thermodynamik, auf den man nicht hartnäckig genug hinweisen kann.” (p. 92).
- Falk, G.; Herrmann, F.; Schmid, G. Energy forms or energy carriers? Am. J. Phys. 1983, 51, 1074–1077. [Google Scholar] [CrossRef]
- Callen’s famous book is dealing a lot with entropy as a central quantity in thermal phenomena.
- Wiberg, E. Die Chemische Affinität; Walter de Gruyter & Co: Berlin, Germany, 1951. [Google Scholar] [CrossRef]
- Debye, P. Zur Theorie der spezifischen Wärmen. Ann. Phys. 1912, 344, 789–839. [Google Scholar] [CrossRef] [Green Version]
- Lunn, A.C. The measurement of heat and the scope of Carnot’s principle. Phys. Rev. (Ser. I) 1919, 14, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Falk, G. Physik—Zahl und Realität, 1st ed.; Birkhäuser: Basel, Switzerland, 1990. [Google Scholar] [CrossRef] [Green Version]
- Here, Falk uses heat as a synonym for entropy. When it goes to heat capacity, the wording is the same regardless if entropy capacity is meant or the traditional term. Careful reading is required, but from the context it is obvious which term is meant in each case. Falk states that the traditional term “heat capacity” is semantically and conceptually a trap.
- Callendar, H. The caloric theory of heat and Carnot’s principle. Proc. Phys. Soc. Lond. 1911, 23, 153–189. [Google Scholar] [CrossRef] [Green Version]
- Falk, G. Entropy, a resurrection of caloric—A look at the history of thermodynamics. Eur. J. Phys. 1985, 6, 108–115. [Google Scholar] [CrossRef] [Green Version]
- Herrmann, F.; Pohlig, M. Which physical quantity deserves the name “quantity of heat”? Entropy 2021, 23, 1078. [Google Scholar] [CrossRef]
- Herrmann, F.; Hauptmann, H. (Eds.) The Karlsruhe Physics Course—Thermodynamics. 2019. Available online: http://www.physikdidaktik.uni-karlsruhe.de/Parkordner/transit/KPK%20Thermodynamics%20Sec%20II.pdf (accessed on 25 February 2022).
- Strunk, C. Moderne Thermodynamik—Band 1: Physikalische Systeme und ihre Beschreibung, 2nd ed.; De Gruyter: Berlin, Germany, 2018. [Google Scholar] [CrossRef]
- Strunk, C. Moderne Thermodynamik—Band 2: Quantenstatistik aus Experimenteller Sicht, 2nd ed.; De Gruyter: Berlin, Germany, 2018. [Google Scholar] [CrossRef]
- Mareŝ, J.; Hulík, P.; Ŝesták, J.; Ŝpiĉka, V.; Kriŝtofik, J.; Stávek, J. Phenomenological approach to the caloric theory of heat. Thermochim. Acta 2008, 474, 16–24. [Google Scholar] [CrossRef]
- Here, Mareŝ et al. use the term caloric capacity in place of entropy capacity.
- Job, G. Neudarstellung der Wärmelehre—Die Entropie als Wärme; Akademische Verlagsgesellschaft: Frankfurt, Germany, 1972. [Google Scholar]
- Here, Job calls entropy heat* with an asterisks to distinguish it from the traditional use of “heat”.
- Job, G.; Rüffler, R. Physical Chemistry from a Different Angle, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Job, G.; Rüffler, R. Physical Chemistry from a Different Angle Workbook, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Fuchs, H.U. The Dynamics of Heat—A Unified Approach to Thermodynamics and Heat Transfer, 1st ed.; Springer: New York, NY, USA, 1996. [Google Scholar] [CrossRef]
- Fuchs, H.U. Solutions Manual for The Dynamics of Heat, 1st ed.; Springer: New York, NY, USA, 1996. [Google Scholar] [CrossRef]
- Fuchs, H.U. The Dynamics of Heat—A Unified Approach to Thermodynamics and Heat Transfer, 2nd ed.; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Here, Fuchs uses heat and caloric as synonyms for entropy. He uses heat capacity as a synonym for entropy capacity. When the thermal energy or the temperature coefficient of energy is meant, he puts the terms “heat” or “heat capacity” into quotation marks. In the second issue of the book, Fuchs uses the term entropy capacitance instead of entropy capacity to underline analogies to other branches of physics.
- Fuchs, H.U.; D’Anna, M.; Corni, F. Entropy and the experience of heat. Entropy 2022. submitted. [Google Scholar]
- Here, Fuchs et al. use caloric as a synonym for entropy and caloric capacity as a synonym for entropy capacity.
- “Führt man einem chemischen Stoff Wärme zu, so vergrößert man seinen Entropiegehalt. Und in derselben Weise, in der sich beim Füllen eines Wassergefäßes mit Wasser der Flüssigkeitsspiegel im Behälter hebt, also die Höhe der eingefüllten Wassermenge, steigt auch beim Füllen irgendeines Entropiegefäßes (z.B. eines Gases oder einer Flüssigkeit) mit Entropie die Höhe des Entropiespiegels, d.h. die Temperatur des betreffenden Körpers. Die durch eine bestimmte Substanzmenge bewirkte Höhenzunahme hängt in beiden Fällen von der Gestalt des Behälters ab.” (p. 140).
- Buck, W.; Rudtsch, S. Chapter Thermal Properties. In Springer Handbook of Metrology and Testing; Springer: Berlin, Germany, 2011; pp. 453–484. [Google Scholar] [CrossRef]
- Vassiliev, V.P.; Taldrik, A.F. Description of the heat capacity of solid phases by a multiparameter family of functions. J. Alloys Compd. 2021, 872, 159682. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Harcourt College Publishers: Fort Worth, TX, USA, 1976. [Google Scholar]
- Bigdeli, S.; Chen, Q.; Selleby, M. A new description of pure C in developing the third generation of Calphad databases. J. Phase Equilibria Diffus. 2018, 39, 832–840. [Google Scholar] [CrossRef] [Green Version]
- Tohie, T.; Kuwabara, A.; Oba, F.; Tanaka, I. Debye temperature and stiffness of carbon and boron nitride polymorphs from first principles calculations. Phys. Rev. 2006, 73, 064304. [Google Scholar] [CrossRef] [Green Version]
- Schmalzried, H.; Navrotsky, A. Festkörperthermodynamik—Chemie des Festen Zustandes; Verlag Chemie: Weinheim, Germany, 1975. [Google Scholar]
- Voronin, G.F.; Kutsenok, I.B. Universal method for approximating the standard thermodynamic functions of solids. J. Chem. Eng. Data 2013, 58, 2083–2094. [Google Scholar] [CrossRef]
- Ohtani, H. Chapter The CALPHAD Method. In Springer Handbook of Metrology and Testing; Springer: Berlin, Germany, 2011; pp. 1061–1090. [Google Scholar] [CrossRef]
- Davies, G.; Evans, T. Graphitization of diamond at zero pressure and at a high pressure. Proc. R. Soc. A 1972, 382, 413–427. [Google Scholar] [CrossRef]
- Bundy, F. Direct conversion of graphite to diamond in static pressure apparatus. J. Chem. Phys. 1963, 38, 631–643. [Google Scholar] [CrossRef]
- Wentorf, R. Behavior of some carbonaceous materials at very high pressures and high temperatures. J. Phys. Chem. 1965, 69, 3063–3069. [Google Scholar] [CrossRef]
- Boldrin, D. Fantastic barocalorics and where to find them. Appl. Phys. Lett. 2021, 118, 170502. [Google Scholar] [CrossRef]
- Zarkevich, N.A.; Zverev, V.I. Viable materials with a giant magnetocaloric effect. Crystals 2020, 10, 815. [Google Scholar] [CrossRef]
- Chauhan, A.; Patel, S.; Vaish, R.; Bowen, C.R. A review and analysis of the elasto-caloric effect for solid-state refrigeration devices: Challenges and opportunities. MRS Energy Sustain. 2015, 2, E16. [Google Scholar] [CrossRef] [Green Version]
- Scott, J. Electrocaloric materials. Annu. Rev. Mater. Res. 2011, 41, 229–240. [Google Scholar] [CrossRef]
- Liu, Y.; Scott, J.F.; Dkhil, B. Direct and indirect measurements on electrocaloric effect: Recent developments and perspectives. Appl. Phys. Rev. 2016, 3, 031102. [Google Scholar] [CrossRef] [Green Version]
- Moya, X.; Stern-Taulats, E.; Crossley, S.; González-Alonso, D.; Kar-Narayan, S.; Planes, A.; Mañosa, L.; Mathur, N.D. Giant electrocaloric strength in single-crystal BaTiO3. Adv. Mater. 2013, 25, 1360–1365. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.X.; Li, Z.Y. Electrocaloric effect in BaTiO3 thin films. J. Appl. Phys. 2009, 106, 94104. [Google Scholar] [CrossRef]
- Bai, Y.; Ding, K.; Zheng, G.P.; Shi, S.Q.; Qiao, L. Entropy-change measurement of electrocaloric effect of BaTiO3 single crystal. Phys. Status Solidi A 2012, 209, 941–944. [Google Scholar] [CrossRef]
- Feldhoff, A. Thermoelectric material tensor derived from the Onsager–de Groot–Callen model. Energy Harvest. Syst. 2015, 2, 5–13. [Google Scholar] [CrossRef]
- Feldhoff, A. Power conversion and its efficiency in thermoelectric materials. Entropy 2020, 22, 803. [Google Scholar] [CrossRef] [PubMed]
- Corak, W.S. Atomic heat of copper, silver, and gold from 1 K to 5 K. Phys. Rev. 1955, 98, 1699–1708. [Google Scholar] [CrossRef]
- Phillips, N.E. Heat capacity of aluminum between 0.1 K and 4.0 K. Phys. Rev. 1959, 114, 676–686. [Google Scholar] [CrossRef]
- Herrmann, F. The Karlsruhe Physics Course. Eur. J. Phys. 2000, 21, 49–58. [Google Scholar] [CrossRef]
- Job, G. Der Zwiespalt zwischen Theorie und Anschauung in der heutigen Wärmelehre und seine geschichtlichen Ursachen. Sudhoffs Archiv. 1969, 53, 378–396. [Google Scholar]
- Ostwald, W. Die Energie; Verlag Johann Ambrosius Barth: Leipzig, Germany, 1908. [Google Scholar]
- Hermann and Pohlig provide an English translation of Ostwald’s note that entropy is concordant with Carnot’s caloric (heat).
- Hirshfeld, M.A. On “Some current misinterpretations of Carnot’s memoir”. Am. J. Phys. 1955, 23, 103. [Google Scholar] [CrossRef]
- Chen, M. Comment on ’A new perspective of how to understand entropy in thermodynamics’. Phys. Educ. 2021, 56, 028002. [Google Scholar] [CrossRef]
- Landolt, H.; Börnstein, R. Physikalisch-Chemische Tabellen, 5th ed.; Springer: Berlin, Germany, 1923. [Google Scholar]



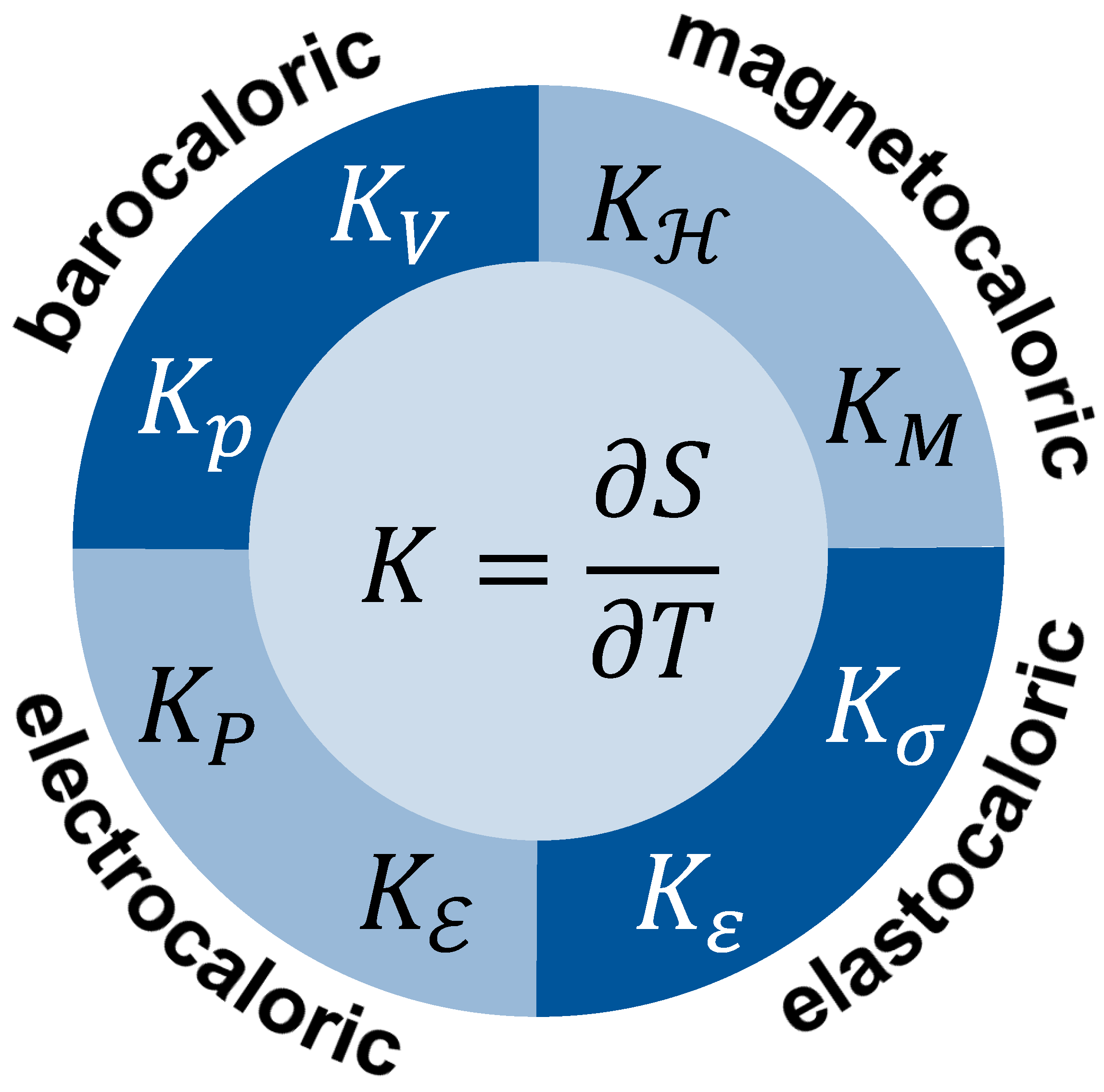
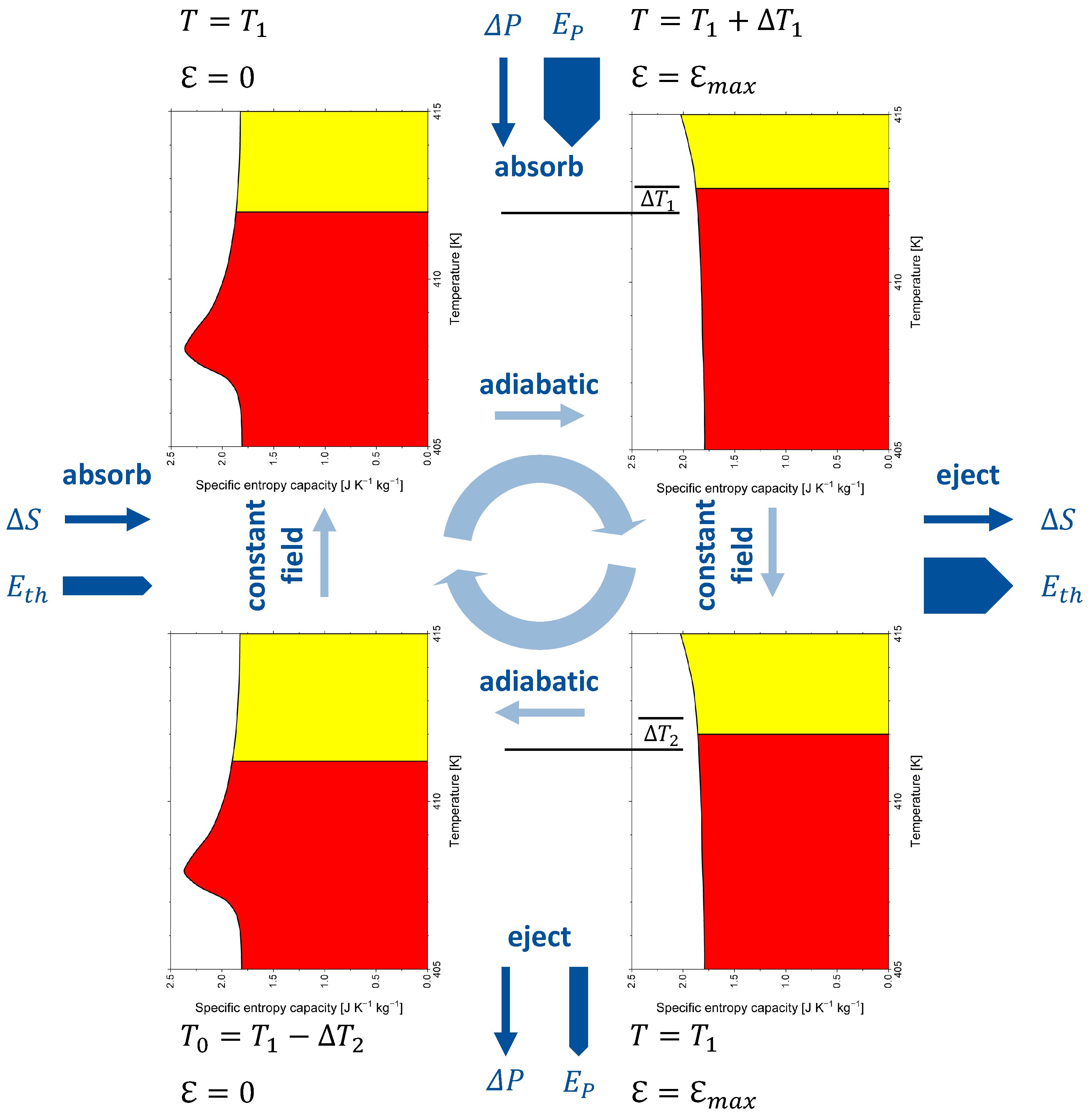
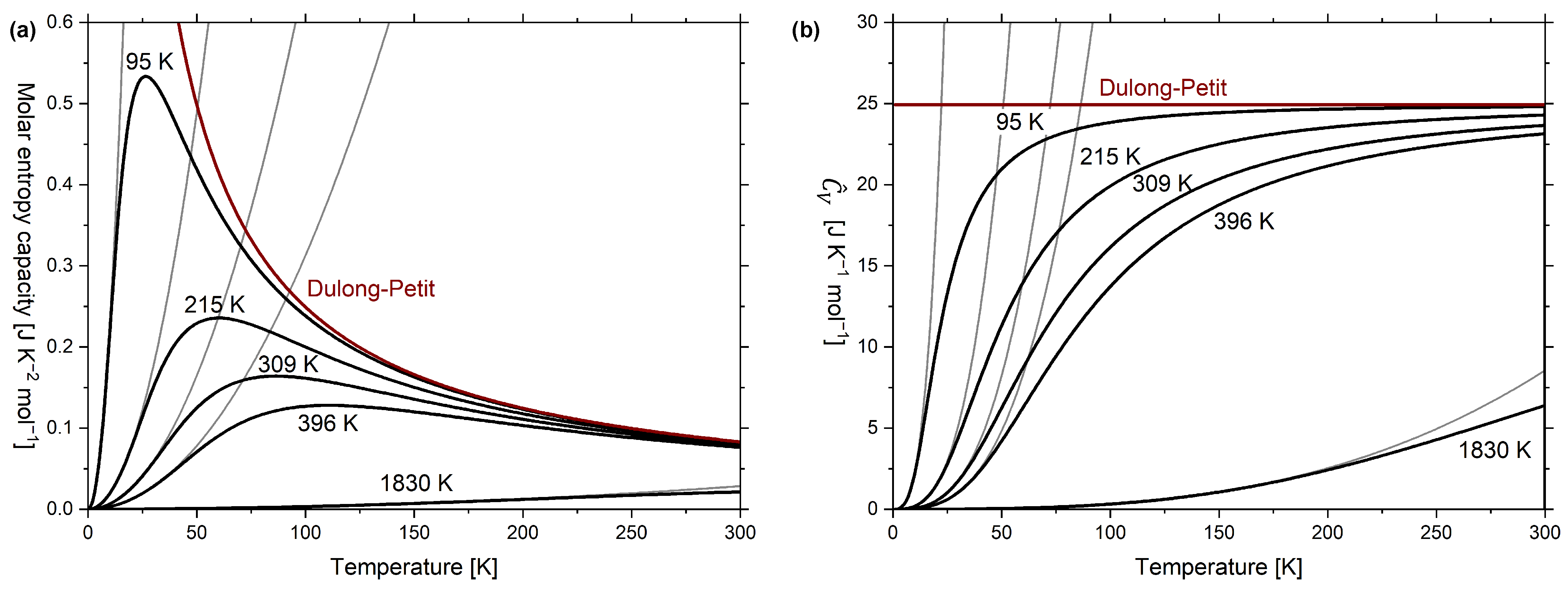
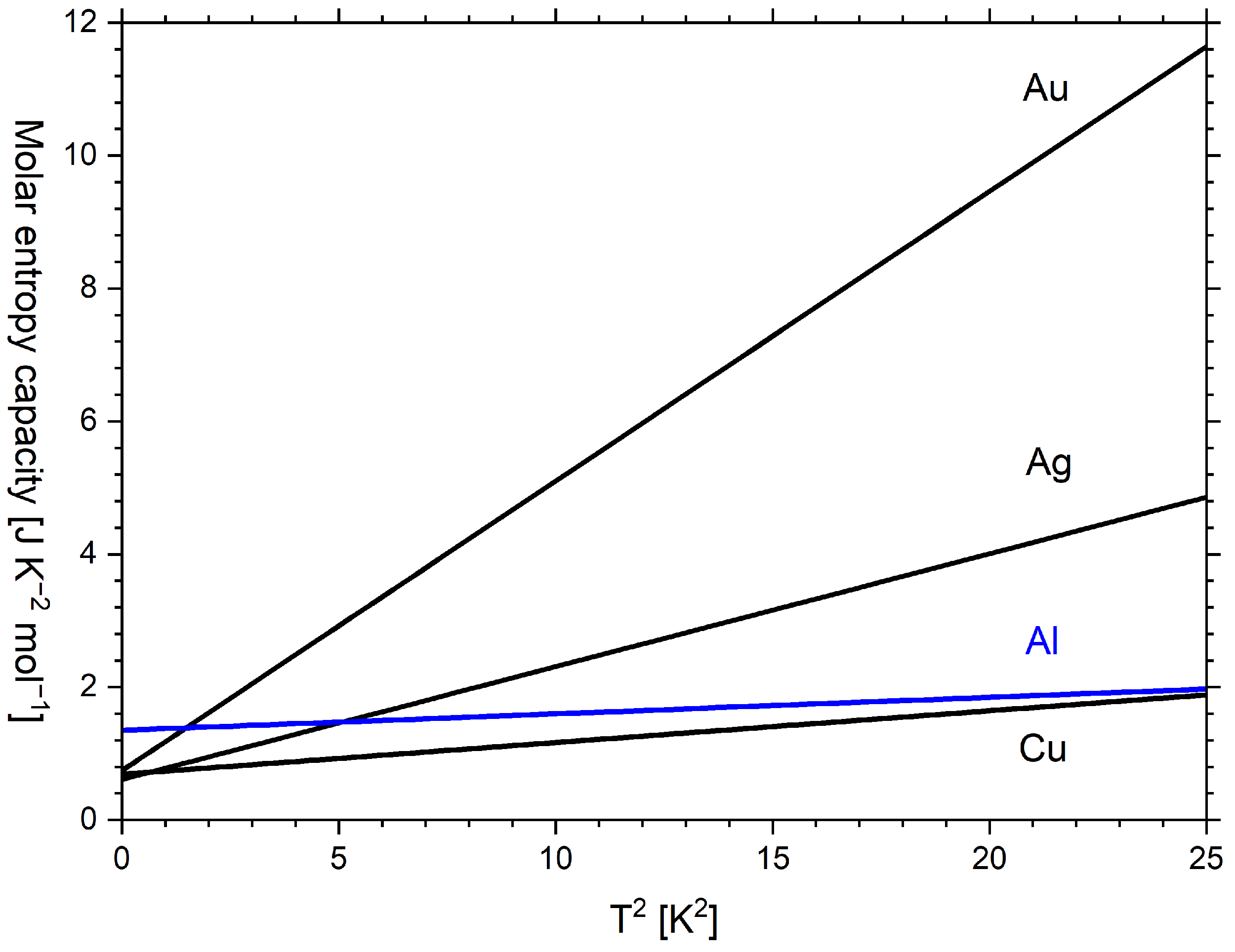
| Caloric Effect | Energy Form | Conjugated Quantities | |||
|---|---|---|---|---|---|
| Intensive Quantity | Extensive Quantity | ||||
| magnetocaloric | magnetisation energy | magnetic field | magnetisation | M | |
| elastocaloric | elastic energy | stress | strain | ||
| electrocaloric | polarisation energy | electrical field | polarisation | P | |
| barocaloric | compression energy | pressure | p | volume | V |
| all | thermal energy 1 | temperature | T | entropy | S |
| Substance | |||
|---|---|---|---|
| (mJ K mol) | (K) | (K) | |
| Au | 0.743 [55] 1 | 164.57 [55] 1 | N/A [11] |
| Ag | 0.610 [55] 1 | 225.3 [55] 1 | 215 [11] |
| Cu | 0.688 [55] 1 | 343.8 [55] 1 | 309 [11] |
| Al | 1.35 [56] 2 | 427.7 [56] 2 | 396 [11] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feldhoff, A. On the Thermal Capacity of Solids. Entropy 2022, 24, 479. https://doi.org/10.3390/e24040479
Feldhoff A. On the Thermal Capacity of Solids. Entropy. 2022; 24(4):479. https://doi.org/10.3390/e24040479
Chicago/Turabian StyleFeldhoff, Armin. 2022. "On the Thermal Capacity of Solids" Entropy 24, no. 4: 479. https://doi.org/10.3390/e24040479
APA StyleFeldhoff, A. (2022). On the Thermal Capacity of Solids. Entropy, 24(4), 479. https://doi.org/10.3390/e24040479