Abstract
Exploring the dynamics of a mobile impurity immersed in field excitations is challenging, as it requires to account for the entanglement between the impurity and the surrounding excitations. To this end, the impurity’s effective mass has to be considered as finite, rather than infinite. Here, we theoretically investigate the interaction between a finite-mass impurity and a dissipative soliton representing nonlinear excitations in the polariton Bose–Einstein condensate (BEC). Using the Lagrange variational method and the open-dissipative Gross–Pitaevskii equation, we analytically derive the interaction phase diagram between the impurity and a dissipative bright soliton in the polariton BEC. Depending on the impurity mass, we find the dissipative soliton colliding with the impurity can transmit through, get trapped, or be reflected. This work opens a new perspective in understanding the impurity dynamics when immersed in field excitations, as well as potential applications in information processing with polariton solitons.
1. Introduction
The motion of an impurity through a dynamical medium of field excitations is a fundamental problem. In his seminal paper [1,2], Landau first studied an electron dressed by phonons. Since then, such impurity problem has appeared in different incarnations, such as the Kondo [3] and Cherenkov [4,5,6] effects, the polaron physics [7], and the Landau criterion [8,9,10,11,12] for the sound speed of a superfluid. At present, there are great efforts and interest in studying a mobile impurity in a quantum medium in diverse areas [13,14,15,16,17,18,19].
Central to understanding the dynamics of an impurity in a quantum many-body medium is to include the entanglement between the impurity and the surrounding excitations on a wide range of energy scales. To achieve this task, one needs to consider the impurity’s effective mass as being finite, instead of infinite [8,9,10,11,12]. In addition, the excitations surrounding the impurity can be linear or nonlinear excitations. For instance, in ultracold quantum gases, the Bogoliubov modes are linear excitations, and dark (or bright) solitons are nonlinear excitations. Numerous theoretical studies [13,14,15,16,17,18,19] have already been carried out to study the interaction mechanism between the impurity and the excitations. These studies, however, mainly involve linear excitations and an impurity with an infinite mass [13,14,15,16,17,18,19] or finite effective mass [20]. Thus, it is highly desired to study the interaction mechanism between a quantum impurity with a finite effective mass and nonlinear excitations, such as the soliton, which is not only a key ingredient in the effective field theory, but also plays an important role in information processing [21]. In this largely unexplored area, we are interested in the interaction mechanism between an impurity and a moving bright soliton in the exciton–polariton Bose–Einstein condensate (BEC).
The exciton–polariton BEC has emerged as a novel platform for studying impurity-related problems. In comparison with previous systems [13,14,15,16,17,18,19], which mainly concerned equilibrium quantum media, the polariton condensates have fundamental novel aspects associated with their inherent nonequilibrium character and a strong nonlinearity. Firstly, because the polariton BEC is open-dissipative, the excitations of an homogeneous polariton condensate exhibit exotic properties. For instance, the linear excitations are provided by the diffusive Goldstone modes [22,23,24,25], with observable ghost branches of Bogoliubov excitations [26]. These have already triggered questions and studies on the definition of superfluidity and the characteristic observables in a nonequilibrium context, e.g., an extension of the standard Landau critical velocity has been proposed [11,12,27,28,29,30,31]. Novel kinds of nonlinear excitations have also been observed in recent experiments, such as oblique dark solitons and vortices [32,33,34], or bright spatial and temporal solitons [35]. Secondly, compared to the light-only solitons in optical setups, the excitonic component of the polariton leads to a weaker diffraction and stronger interparticle interactions, implying, respectively, a tighter localization and lower powers for nonlinear functionality. These appealing properties of polaritons can be used for quantum information processing [21] and quantum computation and simulation [36]. In particular, Ref. [37] engineered dissipative bright polariton solitons, whose picosecond response time made them more useful for ultrafast information processing than the light-only solitons of semiconductor cavity lasers. Thus, a timely question arises: In a nonequilibrium polariton BEC, what is the interaction mechanism between an impurity with a finite effective mass and a dynamical medium with nonlinear excitations?
In this work, we theoretically investigate the interaction between a finite-mass impurity and the dissipative bright soliton in a polariton BEC. By using the Lagrange variational method in the framework of the open-dissipative Gross–Pitaevskii equation, we analytically derive the interaction phase diagram. Depending on the impurity mass, we find that the dissipative soliton colliding with the impurity can have three fates, i.e., it can transmit through, get trapped, or be reflected. Our analytical analysis agrees well with numerical simulations based on the open-dissipative Gross–Pitaevskii equation.
The rest of the paper is organized as follows. In Section 2, we present the model which describes a polariton condensate. Furthermore, we derive the analytic expression of the interaction using the Lagrange variational method. Section 3 investigate the influence of the effective mass of the impurity on the interaction phase diagram between a soliton and an impurity in a polariton condensate, by means of a direct simulation of the motion equations of variational parameters and the Gross–Pitaevskii equation. Various interaction effects such as transmission, reflection, and trapping of the soliton by a repulsive impurity are described and verified by direct simulations of the equation. Finally, Section 4 provides a summary and conclusions for this research.
2. The Theoretical Model and Lagrangian Approach
We consider an exciton–polariton BEC under nonresonant pumping, which is created in a wire-shaped microcavity [38] that bounds the polaritons to a quasi-one-dimensional (1D) channel. In the mean field theory, the time evolution of the polariton field is governed by an effectively 1D driven-dissipative GPE for the condensate order parameter , which is coupled to a rate equation for the density of reservoir polaritons [25,39,40,41,42], i.e.,
In Equations (1) and (2), the m is the effective mass of lower polaritons, P is the off-resonant continuous-wave pumping rate, and denote the lifetimes of the condensate and reservoir polaritons, respectively, R is the stimulated scattering rate of reservoir polaritons into the condensate, characterizes the strengths of the polariton interaction, while denotes the interaction strength between the reservoir and the polaritons. The impurity potential [39,43] is , with the strength . The in Equation (1) and in Equation (2) are the incoherent pumping rates on the condensate and reservoir [44], respectively. The parameters , , and R have been rescaled into the one-dimensional case by the width d of the nanowire thickness, i.e., , , . We aim to investigate the interaction mechanism between the impurity and the nonlinear excitations.
As the first step, let us determine the steady state of Equations (1) and (2), which will provide the density background for the nonlinear excitations. Following Ref. [40], when the pumping rate P in Equation (2) exceeds the critical value , a stable condensate with the condensate density can be created. The corresponding steady-state reservoir density is , with .
By rescaling and denoting , Equations (1) and (2) can be recast into a dimensionless form as
where , , , and . The term with describes the impurity potential. Moreover, we have measured the time t and the space coordinate x in the units of and . Equations (3) and (4) are the starting point for our subsequent investigation of the interaction between the impurity and the nonlinear excitations in the polariton BEC. Note that the nonequilibrium nature of the model system is captured by the parameters of in Equation (3).
We are interested in the fast reservoir limit, where the reservoir density in Equation (4) can be written as [40]
where , with the constant pumping rate and the spatially dependent pumping rate . Following Ref. [40], we insert Equation (5) into Equation (3), and rewrite Equation (3) as
Here, we model as a spatially modulated Gaussian function with the power and width , i.e., ; the parameters and are referred to as the polariton loss rate and the gain saturation, respectively. In deriving Equation (6), the incoherent pumping of is adjusted to be within the current experimental capability [44,45,46]. Below, we investigate the interaction between a bright soliton and the impurity as captured by the term in Equation (6).
Equation (6) can be viewed as a nonlinear Schrödinger equation subjected to a time-dependent perturbation of the form . As a benchmark, let us recapitulate the unperturbed case without the open-dissipative effects: (i) for a vanishing nonlinearity in Equation (6), Equation (6) can be simplified into the linear Schrödinger equation with the delta-potential. It has the well-known exact solution with that describes the impurity; (ii) for a vanishing delta-potential , Equation (6) allows for the exact soliton solution with an arbitrary amplitude .
Next, we take into account the open-dissipative effects captured by in Equation (6). Since and are no longer the exact solutions of Equation (6), we exploit the Lagrangian approach of the perturbation theory to treat the open-dissipative effects. We assume a trial wave function as a combination of the bright soliton and impurity mode
where , z, , , a, , and are the variational parameters. Specifically, is the global phase of the trial wave function, and are the amplitudes and center position of the bright soliton, respectively, is referred to as the wavenumber of the soliton, and are associated with the strength of the variable function induced by the impurity, and is the relative phase between the soliton and impurity-induced function.
The key assumption underlying the ansatz (7) is that the functional forms of the soliton and the impurity-induced function are preserved in the presence of perturbation, whereas the corresponding parameters become slowly time-dependent. The time evolution of the parameters in Equation (7) can be obtained via the Euler-Lagrangian equations for the dissipative system [47,48,49,50,51]
with and , and labels the real part of the expression. In Equation (8), the Lagrangian is referred to as the average Lagrangian of Equation (6) with , where the Lagrangian density is given by
Inserting the ansatz (7) into Equation (9), we calculate the average Lagrangian L in Equation (8) as
Here, we have ignored the higher-order terms of , as inspired by Ref. [52]. Physically, this corresponds to ignoring the direct interaction between the soliton and the local mode, except for the energy exchange through the defect. This approximation will be justified a posteriori by comparing the analytical results from Equation (10) and the simulation results based on Equation (6).
By substituting Equation (10) into Equation (8), we obtain the equations of motion for the variational parameters , , , z, a, , and in Equation (8) as
Equations (11a)–(11g) are the key results of this work, which describe the interaction of an impurity and a bright soliton in the polariton condensate. Note that without the dissipation (i.e., ), the above equations obviously reproduce the result of Ref. [52]. According to Equations (11a)–(11c), the nonequilibrium nature of the polariton condensates will directly affect the soliton’s center position z and its amplitude , as well as the impurity’s amplitude . Since does not appear in Equations (11a) and (11b), the relevant equations for our study, Equation (11f) for is not important. Equation (11c), on the other hand, is crucial because it shows that the moving soliton excites the local mode. Note that Equation (11g) without the soliton () gives the correct value for the spatial decay of the impurity mode.
3. Interaction between an Impurity and a Bright Soliton
In the previous section, we used the Lagrangian approach to analytically derive Equations (11a)–(11g). Below, we construct the interaction phase diagram by solving Equations (11a)–(11g) and comparing the results with the exact numerical simulations of the dynamics governed by Equation (6), supplemented with the initial function of Equation (11b).
Let us first specify the initial conditions of Equations (11a)–(11g). We assume the soliton is initially at , far from the impurity at . The initial amplitude and velocity of the soliton are chosen as and , respectively. For other parameters (a, , and ), we set their initial values as 0.
We then solve the time-evolutions of the parameters z, a, , and from Equations (11b)–(11e). The soliton amplitude is determined by Equations (11a)–(11c), and is calculated from Equation (11g). In addition, Equation (11g) allows us to follow independently the evolution of the soliton and the impurity. The solutions to Equations (11a)–(11g) are plotted in the left column of Figure 1, Figure 2 and Figure 3. To validate our variational approach, we also show the numerical results from the direct solutions of Equation (6) on the right column of Figure 1, Figure 2 and Figure 3.
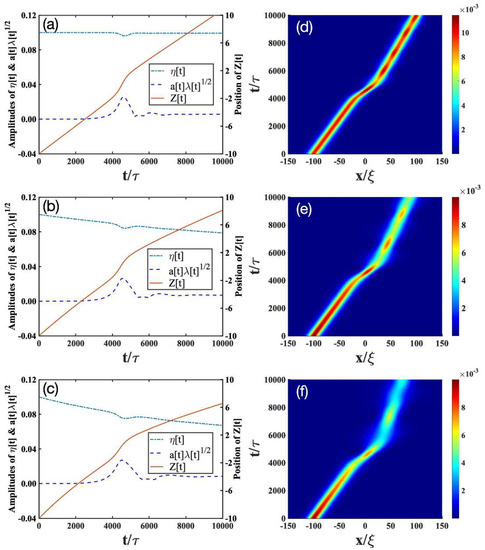
Figure 1.
Transmission scenario corresponding to the bright soliton with the initial value passing through the impurity with a strength of . The analytical results of Equations (11a)–(11g) and the numerical simulation based on Equation (6) are plotted in the left and right columns, respectively. In (a–c), the positions Z of the bright soliton are plotted by solid lines and scaled on the right axis; the amplitudes of the bright soliton are plotted by dash-dotted lines and scaled on the left axis; the impurity amplitudes of are plotted by the dashed lines and scaled on the left axis. The other parameters are given as follows: in (a,d); in (b,e); in (c,f).
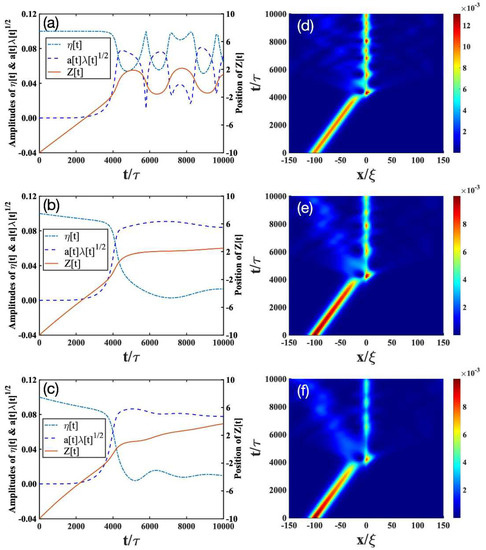
Figure 2.
Trapping scenario corresponding to the bright soliton with the initial value passing through the impurity with a strength of . The other parameters and descriptions about the figures are the same as the ones in Figure 1.
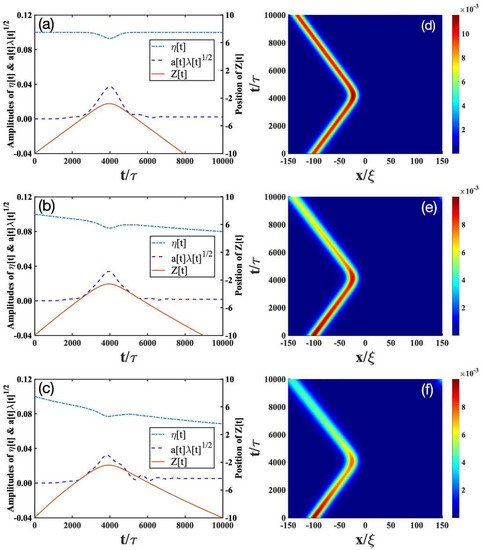
Figure 3.
Reflection scenario corresponding to the bright soliton with the initial value passing through the impurity with a strength of . The other parameters and descriptions about the figures are the same as the ones in Figure 1.
In understanding the interaction between the impurity and the quantum many-body medium, we emphasize the key role of the effective mass of the impurity [5,6]. For an infinite mass, corresponding to a pinned impurity [5,53], a kinematic scale is set up by the sound speed of the superfluid according to the Landau criterion. In contrast, an impurity with a finite mass is expected to recoil due to the interactions with the surrounding quantum gas, yielding novel physics beyond the kinematic picture [6]. Indeed, quantum fluctuations already become highly relevant to the dynamics for the slowly moving impurities with a finite mass.
Figure 1, Figure 2 and Figure 3 show the interaction diagrams between the impurity and a bright soliton under various impurity trap strengths . Different ’s correspond to different effective masses of the impurity [52]. For used in the plots, we have . In the following, we analyze how the impurity–soliton interaction is affected by the open-dissipative nature of the condensate, as captured by the parameters of , , and in Equation (6).
The results for in the absence of dissipation [52] are plotted in Figure 1a, Figure 2a, Figure 3a, respectively. Depending on , we find there exist three scenarios. (i) The transmission scenario (Figure 1a): when is small, the bright soliton directly transmits through the impurity. (ii) The trapping reflection scenario (Figure 2a): when increases, the bright soliton can be trapped by the impurity (see Figure 2a). (iii) The reflection scenario (Figure 3a): when is strong enough, the bright soliton is reflected by the impurity.
To compare the interaction of the soliton with the impurity in the presence and absence of dissipation, we change the dissipative parameters of , , and in each scenario:
- (i)
- Transmission scenario: As mentioned before, in the absence of dissipation (Figure 1a), the bright soliton can simply pass through a light impurity (), almost unaffected by the latter. The dotted lines in Figure 1a denotes the amplitude of the impurity. There, the appearance of the maximal amplitude of the impurity indicates that the impurity mode can be excited during the collision with the bright soliton, but after the collision, the excitation returns to a very small level. This analysis is consistent with Figure 1d obtained from the numerical simulation of Equation (6). Thus, we conclude that the analytical results in Equations (11a)–(11g) not only provide a good solution to Equation (6), but also allow us to follow independently the evolution of the bright soliton and the impurity. In the presence of dissipation, the amplitude of soliton gradually decreases after the collision with the impurity; see the solid lines in Figure 1b,c. These results are consistent with the full numerical simulations in Figure 1e,f. Comparing Figure 1b,c, therefore, we see that the soliton amplitude decays faster when the dissipation parameter increases.
- (ii)
- Trapping scenario: In the absence of dissipation (Figure 2a,d), the bright soliton can be trapped by an impurity with a moderate mass (), as indicated by the position of the bright soliton (solid lines in Figure 2a). Furthermore, the impurity mode (dashed lines in Figure 2a) is strongly excited and begins to oscillate, whereas the soliton amplitude (dashed-dotted lines in Figure 2a) decreases drastically. This result is verified by the numerical simulations in Figure 2d. In the presence of dissipation (Figure 2b,c,e,f), the bright soliton can still be trapped by the impurity, but the oscillating behavior of the bright soliton begins to disappear. This can be understood, as the dissipation will destroy the low-energy excitations generated from the collisions of the bright soliton and the impurity.
- (iii)
- Reflection scenario: In the absence of dissipation (Figure 3a,d), the bright soliton can be reflected by a heavy impurity (). In contrast to the above transmission and trapping scenarios, dissipation has relatively small effects on the reflection scenario, as shown in Figure 3b,d–f. This can be expected, because the heavier the impurity is, the less excitations are created from the collisions.
4. Conclusions
In summary, we investigated the interaction dynamics of a soliton with an impurity mode in the exciton–polariton condensates excited by a nonresonant pump. Our study was based on the Lagrange variational approach, which allowed us to analytically derive the equations of motion for each variational parameter. Depending on the interaction strength between the soliton and the impurity, we observed the occurrence of transmission, reflection, and trapping of the soliton by the impurity. We showed that these effects were weakened with the increase of dissipation. Our analytical results of the interaction phase diagram agreed well with the numerical results of the open-dissipative Gross–Pitaevskii equation. The present work goes beyond prior research studies in the context of equilibrium systems, opening a new perspective toward understanding the nonequilibrium dynamics of a mobile impurity immersed the field excitations.
Author Contributions
Conceptualization, Z.L.; Investigation, C.J.; Methodology, C.J. and Z.L.; software, C.J.; writing—original draft preparation, C.J.; writing—review and editing, Z.L.; supervision, Z.L.; All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Zhejiang Provincial Natural Science Foundation (grant no. LZ21A040001), the National Natural Science Foundation of China (grant no. 12074344) and the key projects of the Natural Science Foundation of China (grant no. 11835011).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank Yiling Zhang for stimulating discussions. This work was supported by the Zhejiang Provincial Natural Science Foundation (grant no. LZ21A040001), the National Natural Science Foundation of China (grant no. 12074344) and the key projects of the Natural Science Foundation of China (grant no. 11835011).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Landau, L.D. The Movement of Electrons in the Crystal Lattice. Phys. Z. Sowjetunion 1933, 3, 644. [Google Scholar]
- Landau, L.D.; Pekar, S.I. Effective Mass of a Polaron. J. Exp. Theor. Phys. 1948, 18, 419. [Google Scholar]
- Hewson, A.C. The Kondo Problem to Heavy Fermions; Cambridge University: Cambridge, UK, 1993. [Google Scholar]
- Bolotovskii, B.M. Vavilov–Cherenkov radiation: Its discovery and application. Phys.-Uspekhi 2009, 52, 1099–1110. [Google Scholar] [CrossRef]
- Carusotto, I.; Hu, S.X.; Collins, L.A.; Smerzi, A. Bogoliubov-Čerenkov Radiation in a Bose-Einstein Condensate Flowing against an Obstacle. Phys. Rev. Lett. 2006, 97, 260403. [Google Scholar] [CrossRef]
- Seetharam, K.; Shchadilova, Y.; Grusdt, F.; Zvonarev, M.B.; Demler, E. Dynamical Quantum Cherenkov Transition of Fast Impurities in Quantum Liquids. Phys. Rev. Lett. 2021, 127, 185302. [Google Scholar] [CrossRef]
- Mahan, G. Many-Particle Physics; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2000. [Google Scholar]
- Astrakharchik, G.E.; Boronat, J.; Casulleras, J.; Giorgini, S. Superfluidity versus Bose-Einstein condensation in a Bose gas with disorder. Phys. Rev. A 2002, 66, 23603. [Google Scholar] [CrossRef]
- Wouters, M.; Carusotto, I. Superfluidity and Critical Velocities in Nonequilibrium Bose-Einstein Condensates. Phys. Rev. Lett. 2010, 105, 20602. [Google Scholar] [CrossRef]
- Liang, Z.X.; Dong, X.; Zhang, Z.D.; Wu, B. Sound speed of a Bose-Einstein condensate in an optical lattice. Phys. Rev. A 2008, 78, 23622. [Google Scholar] [CrossRef]
- Amelio, I.; Carusotto, I. Perspectives in superfluidity in resonantly driven polariton fluids. Phys. Rev. B 2020, 101, 64505. [Google Scholar] [CrossRef]
- He, P.S.; Liang, Z. Drag force of an exciton-polariton condensate under nonresonant pumping. Phys. Rev. A 2021, 103, 13303. [Google Scholar] [CrossRef]
- Chevy, F.; Mora, C. Ultra-cold polarized Fermi gases. Rep. Prog. Phys. 2010, 73, 112401. [Google Scholar] [CrossRef]
- Massignan, P.; Zaccanti, M.; Bruun, G.M. Polarons, dressed molecules and itinerant ferromagnetism in ultracold Fermi gases. Rep. Prog. Phys. 2014, 77, 34401. [Google Scholar] [CrossRef]
- Adlong, H.S.; Liu, W.E.; Scazza, F.; Zaccanti, M.; Oppong, N.D.; Fölling, S.; Parish, M.M.; Levinsen, J. Quasiparticle Lifetime of the Repulsive Fermi Polaron. Phys. Rev. Lett. 2020, 125, 133401. [Google Scholar] [CrossRef]
- Schmidt, R.; Knap, M.; Ivanov, D.A.; You, J.S.; Cetina, M.; Demler, E. Universal many-body response of heavy impurities coupled to a Fermi sea: A review of recent progress. Rep. Prog. Phys. 2018, 81, 24401. [Google Scholar] [CrossRef]
- Jørgensen, N.B.; Wacker, L.; Skalmstang, K.T.; Parish, M.M.; Levinsen, J.; Christensen, R.S.; Bruun, G.M.; Arlt, J.J. Observation of Attractive and Repulsive Polarons in a Bose-Einstein Condensate. Phys. Rev. Lett. 2016, 117, 55302. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.G.; Van de Graaff, M.J.; Kedar, D.; Corson, J.P.; Cornell, E.A.; Jin, D.S. Bose Polarons in the Strongly Interacting Regime. Phys. Rev. Lett. 2016, 117, 55301. [Google Scholar] [CrossRef] [PubMed]
- Yan, Z.Z.; Ni, Y.; Robens, C.; Zwierlein, M.W. Bose polarons near quantum criticality. Science 2020, 368, 190–194. [Google Scholar] [CrossRef] [PubMed]
- Vashisht, A.; Richard, M.; Minguzzi, A. Bose polaron in a quantum fluid of light. SciPost Phys. 2022, 12, 8. [Google Scholar] [CrossRef]
- Flayac, H.; Solnyshkov, D.D.; Shelykh, I.A.; Malpuech, G. Transmutation of Skyrmions to Half-Solitons Driven by the Nonlinear Optical Spin Hall Effect. Phys. Rev. Lett. 2013, 110, 16404. [Google Scholar] [CrossRef]
- Wouters, M.; Carusotto, I. Excitations in a Nonequilibrium Bose-Einstein Condensate of Exciton Polaritons. Phys. Rev. Lett. 2007, 99, 140402. [Google Scholar] [CrossRef]
- Szymańska, M.H.; Keeling, J.; Littlewood, P.B. Nonequilibrium Quantum Condensation in an Incoherently Pumped Dissipative System. Phys. Rev. Lett. 2006, 96, 230602. [Google Scholar] [CrossRef]
- Byrnes, T.; Horikiri, T.; Ishida, N.; Fraser, M.; Yamamoto, Y. Negative Bogoliubov dispersion in exciton-polariton condensates. Phys. Rev. B 2012, 85, 75130. [Google Scholar] [CrossRef]
- Xu, X.; Hu, Y.; Zhang, Z.; Liang, Z. Spinor polariton condensates under nonresonant pumping: Steady states and elementary excitations. Phys. Rev. B 2017, 96, 144511. [Google Scholar] [CrossRef]
- Pieczarka, M.; Syperek, M.; Dusanowski, L.; Misiewicz, J.; Langer, F.; Forchel, A.; Kamp, M.; Schneider, C.; Höfling, S.; Kavokin, A.; et al. Ghost Branch Photoluminescence From a Polariton Fluid Under Nonresonant Excitation. Phys. Rev. Lett. 2015, 115, 186401. [Google Scholar] [CrossRef] [PubMed]
- Janot, A.; Hyart, T.; Eastham, P.R.; Rosenow, B. Superfluid Stiffness of a Driven Dissipative Condensate with Disorder. Phys. Rev. Lett. 2013, 111, 230403. [Google Scholar] [CrossRef] [PubMed]
- Keeling, J. Superfluid Density of an Open Dissipative Condensate. Phys. Rev. Lett. 2011, 107, 080402. [Google Scholar] [CrossRef] [PubMed]
- Van Regemortel, M.; Wouters, M. Negative drag in nonequilibrium polariton quantum fluids. Phys. Rev. B 2014, 89, 85303. [Google Scholar] [CrossRef]
- Gladilin, V.N.; Wouters, M. Normal and superfluid fractions of inhomogeneous nonequilibrium quantum fluids. Phys. Rev. B 2016, 93, 134511. [Google Scholar] [CrossRef]
- Juggins, R.T.; Keeling, J.; Szymańska, M.H. Coherently driven microcavity-polaritons and the question of superfluidity. Nat. Commun. 2018, 9, 4062. [Google Scholar] [CrossRef]
- Grosso, G.; Nardin, G.; Morier-Genoud, F.; Léger, Y.; Deveaud-Plédran, B. Soliton Instabilities and Vortex Street Formation in a Polariton Quantum Fluid. Phys. Rev. Lett. 2011, 107, 245301. [Google Scholar] [CrossRef]
- Akhmerov, A.R. Topological quantum computation away from the ground state using Majorana fermions. Phys. Rev. B 2010, 82, 20509. [Google Scholar] [CrossRef]
- Amo, A.; Pigeon, S.; Sanvitto, D.; Sala, V.G.; Hivet, R.; Carusotto, I.; Pisanello, F.; Lemenager, G.; Houdre, R.; Giacobino, E.; et al. Polariton Superfluids Reveal Quantum Hydrodynamic Solitons. Science 2011, 332, 1167–1170. [Google Scholar] [CrossRef] [PubMed]
- Barland, S.; Giudici, M.; Tissoni, G.; Tredicce, J.R.; Brambilla, M.; Lugiato, L.; Prati, F.; Barbay, S.; Kuszelewicz, R.; Ackemann, T.; et al. Solitons in semiconductor microcavities. Nat. Photonics 2012, 6, 204. [Google Scholar] [CrossRef]
- Sanvitto, D.; Kéna-Cohen, S. The road towards polaritonic devices. Nat. Mater. 2016, 15, 1061–1073. [Google Scholar] [CrossRef]
- Sich, M.; Krizhanovskii, D.N.; Skolnick, M.S.; Gorbach, A.V.; Hartley, R.; Skryabin, D.V.; Cerda-Méndez, E.A.; Biermann, K.; Hey, R.; Santos, P.V. Observation of bright polariton solitons in a semiconductor microcavity. Nat. Photonics 2012, 6, 50–55. [Google Scholar] [CrossRef]
- Wertz, E.; Ferrier, L.; Solnyshkov, D.D.; Johne, R.; Sanvitto, D.; Lemaître, A.; Sagnes, I.; Grousson, R.; Kavokin, A.V.; Senellart, P.; et al. Spontaneous formation and optical manipulation of extended polariton condensates. Nat. Phys. 2010, 6, 860–864. [Google Scholar] [CrossRef]
- Keeling, J.; Berloff, N.G. Spontaneous Rotating Vortex Lattices in a Pumped Decaying Condensate. Phys. Rev. Lett. 2008, 100, 250401. [Google Scholar] [CrossRef] [PubMed]
- Smirnov, L.A.; Smirnova, D.A.; Ostrovskaya, E.A.; Kivshar, Y.S. Dynamics and stability of dark solitons in exciton-polariton condensates. Phys. Rev. B 2014, 89, 235310. [Google Scholar] [CrossRef]
- Yu, Z.F.; Xue, J.K.; Zhuang, L.; Zhao, J.; Liu, W.M. Non-Hermitian spectrum and multistability in exciton-polariton condensates. Phys. Rev. B 2021, 104, 235408. [Google Scholar] [CrossRef]
- Sabari, S.; Kumar, R.K.; Radha, R.; Muruganandam, P. Stability window of trapless polariton Bose-Einstein condensates. Phys. Rev. B 2022, 105, 224315. [Google Scholar] [CrossRef]
- Cristofolini, P.; Dreismann, A.; Christmann, G.; Franchetti, G.; Berloff, N.G.; Tsotsis, P.; Hatzopoulos, Z.; Savvidis, P.G.; Baumberg, J.J. Optical Superfluid Phase Transitions and Trapping of Polariton Condensates. Phys. Rev. Lett. 2013, 110, 186403. [Google Scholar] [CrossRef] [PubMed]
- Sitnik, K.A.; Alyatkin, S.; Töpfer, J.D.; Gnusov, I.; Cookson, T.; Sigurdsson, H.; Lagoudakis, P.G. Spontaneous Formation of Time-Periodic Vortex Cluster in Nonlinear Fluids of Light. Phys. Rev. Lett. 2022, 128, 237402. [Google Scholar] [CrossRef] [PubMed]
- Cerna, R.; Sarchi, D.; Paraïso, T.K.; Nardin, G.; Léger, Y.; Richard, M.; Pietka, B.; El Daif, O.; Morier-Genoud, F.; Savona, V.; et al. Coherent optical control of the wave function of zero-dimensional exciton polaritons. Phys. Rev. B 2009, 80, 121309. [Google Scholar] [CrossRef]
- Wang, Y.; Sigurdsson, H.; Töpfer, J.D.; Lagoudakis, P.G. Reservoir optics with exciton-polariton condensates. Phys. Rev. B 2021, 104, 235306. [Google Scholar] [CrossRef]
- Kivshar, Y.S.; Królikowski, W. Lagrangian approach for dark solitons. Opt. Commun. 1995, 114, 353–362. [Google Scholar] [CrossRef]
- Theocharis, G.; Schmelcher, P.; Oberthaler, M.K.; Kevrekidis, P.G.; Frantzeskakis, D.J. Lagrangian approach to the dynamics of dark matter-wave solitons. Phys. Rev. A 2005, 72, 23609. [Google Scholar] [CrossRef]
- Zhang, Y.; Jia, C.; Liang, Z. Dynamics of Two Dark Solitons in a Polariton Condensate. Chin. Phys. Lett. 2022, 39, 20501. [Google Scholar] [CrossRef]
- Jia, C.Y.; Liang, Z.X. Dark Soliton of Polariton Condensates under Nonresonant PT-Symmetric Pumping. Chin. Phys. Lett. 2020, 37, 40502. [Google Scholar] [CrossRef]
- Xu, X.; Chen, L.; Zhang, Z.; Liang, Z. Dark–bright solitons in spinor polariton condensates under nonresonant pumping. J. Phys. B 2018, 52, 025303. [Google Scholar] [CrossRef]
- Forinash, K.; Peyrard, M.; Malomed, B. Interaction of discrete breathers with impurity modes. Phys. Rev. E 1994, 49, 3400–3411. [Google Scholar] [CrossRef]
- Astrakharchik, G.E.; Pitaevskii, L.P. Motion of a heavy impurity through a Bose-Einstein condensate. Phys. Rev. A 2004, 70, 13608. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).