Abstract
The states of the qubit, the basic unit of quantum information, are 2 × 2 positive semi-definite Hermitian matrices with trace 1. We contribute to the program to axiomatize quantum mechanics by characterizing these states in terms of an entropic uncertainty principle formulated on an eight-point phase space. We do this by employing Rényi entropy (a generalization of Shannon entropy) suitably defined for the signed phase-space probability distributions that arise in representing quantum states.
1. Introduction
The maximum entropy method was introduced into physics as a way of deriving the Boltzmann distribution of statistical mechanics (Jaynes [1]). In this paper, we apply entropy methods to characterize the basic unit of quantum information, namely, the qubit. Our work fits into the ongoing program to identify principles or axioms yielding quantum mechanics. This program goes back at least to Birkhoff and von Neumann [2] and their investigation of quantum mechanics as a non-classical logic. More recently, Hardy [3] reconstructed quantum theory from five axioms couched in terms of operations that can be conducted on a physical system. His work spurred many other axiomatizations based on communication complexity (Van Dam [4]), information causality (Pawlowski et al. [5]), information capacity (Dakić and Brukner [6]), and purification (Chiribella, et al. [7]), among other principles.
We aim to characterize the simplest quantum system, namely, a two-level system such as the spin of a particle. Empirically, the experimenter can observe a property such as spin in three arbitrarily chosen mutually orthogonal directions. In each direction, the outcome is binary (up or down). An empirical model gives the frequencies of these outcomes when identical copies of the same two-level system are prepared and one of the three measurements is performed on a given copy. We want to associate an entropy with an empirical model. This step is not immediate because entropy is a measure of the uncertainty in a single probability distribution, and an empirical model contains three distinct probability distributions (one for each direction). The solution is to move to phase space, where an empirical model is represented by a single probability distribution. Our phase space for a two-level system contains eight points, where each point specifies the outcome (up or down) of each of the three possible measurements. The possibility of a non-deterministic response to measurement—as in quantum mechanics—is allowed for by specifying a probability of each point in phase space. Later, we comment on the relationship between our phase-space framework and the finite-field representations due to Wootters and collaborators (e.g., Wootters [8]; Gibbons et al. [9]).
Our phase-space representation of an empirical model can be thought of as a particular (canonical) type of local hidden-variable model (Bell [10]), where the possible values of the hidden variable are precisely the possible points in phase space. It follows from Bell’s Theorem (Bell [10]) that there are empirical models which arise in quantum mechanics and which cannot be represented in phase space with ordinary probabilities. One answer is found in the Wigner distribution (Wigner [11]), which can take on negative values at certain locations in phase space. Dirac [12] and Feynman [13] also argued for admitting negative probabilities in quantum calculations. We emphasize that although we will allow phase-space probabilities to take negative values, the frequencies of all observable events remain non-negative. Further support for the use of negative probabilities comes from Abramsky and Brandenburger [14], who prove that the family of empirical models that can be represented in phase space this way is precisely the family of no-signaling theories (Popescu and Rohrlich [15]).
We are now ready to associate entropies with probability distributions on phase space. Within quantum mechanics, the most common entropy measure is the von Neumann entropy (von Neumann [16]). This is unsuitable for our purpose because it is defined within the quantum formalism, which we want to derive not assume. Shannon entropy (Shannon [17]) is also unsuitable when applied to probabilities in phase space, since, if the latter can be negative, then it would take complex values. Instead, we work with the more basic notion of Rényi entropy [18] and impose real-valuedness and smoothness. Rényi entropy satisfies the basic requirement of extensivity, i.e., it is additive across statistically independent systems. In fact, it is defined by this property together with some technical axioms (Daróczy [19]). Rényi entropy is used in various applications in quantum mechanics (Wehner and Winter [20]; Bialynicki-Birula and Rudnicki [21]; Coles et al. [22]).
The next step is to state an entropic uncertainty principle as an axiom on phase space. Note that different from other entropic uncertainty principles in quantum mechanics (Everett [23]; Hirschman [24]; Beckner [25]; Bialynicki-Birula and Mycielski [26]), our principle is formulated in phase space. Furthermore, we do not derive the principle from quantum mechanics but introduce it as an axiom. Our main result is that the set of probability distributions on phase space whose Rényi entropy exceeds a certain lower bound is exactly equal to the set of probability distributions that induce the qubit.
A paper that, broadly speaking, goes in the opposite direction to ours is Wootters and Sussman [27]. These authors work in a finite-field phase-space representation of discrete quantum systems and are able to identify certain minimum-uncertainty states. In particular, they show that a particular class of states (the “rotationally invariant states”) minimize Rényi 2-entropy (a special case of our family of entropy functionals, as we shall see).
We consider our axiomatization of the qubit as in line with the program enunciated by Fuchs [28] to find “deep physical principles” that yield quantum mechanics. This said, we do not claim that our axiom is self-evident. In relativity theory, the principle of light speed invariance is not an intuitive axiom—the point is that it is physically intelligible. (This comparison between quantum theory and relativity theory is also made in Onggadinata et al. [29].) Our interest in an uncertainty principle is similar. Ever since the initial formulation by Heisenberg [30], uncertainty principles have been viewed as one of the notably unintuitive features of quantum mechanics. However, even though they are mysterious at the everyday macroscopic level, uncertainty principles are physically interpretable, and they are evidently true of microscopic systems.
2. Preliminaries
A basis for the space of Hermitian matrices is given by , where is the identity matrix and , , are the Pauli matrices
A Hermitian matrix satisfies if and only if
for some vector .
Definition 1.
A Hermitian matrix with is called a potential quantum state. If, in addition, is positive semi-definite, then is a quantum state, or a state of the qubit. We also refer to the corresponding vectors as potential quantum states and quantum states.
This is the model of the simplest quantum system, namely a two-level system such as the spin of a particle. Empirically, the experimenter can observe a property such as spin in three arbitrarily chosen mutually orthogonal directions , , and . In each direction, the outcome of a measurement will be labeled or . The expectation of the outcome in direction i is (see, e.g., p. 181 in Sakurai and Napolitano [31]).
We want to associate an entropy with an empirical model. This step is not immediate because entropy is a measure of the uncertainty in a single probability distribution, and an empirical model contains three probability distributions (one for each direction). Our solution is to move to phase space, where an empirical model is represented by a single probability distribution. The phase space for a two-level system contains eight points,
where for the base-2 digits of . Each point in phase space specifies the outcome of each of the three possible measurements. Non-deterministic responses to measurement are incorporated by specifying probabilities over the points in phase space. Let
denote the set of all signed probability distributions on phase space. That is, we do not require the probabilities to be positive, only that they sum to 1. We define a map from Q to the set of potential quantum states by
where
The map gives the correct transformation from phase space to the space of potential quantum states, in the sense of preserving the empirical probabilities. This map is linear and it will be helpful to fix some notation surrounding a matrix representation. Note we have folded the condition that is a probability distribution in as the last equation in the definition of representation below.
Definition 2.
Let denote the matrix
For define . For and we say represents if .
3. Rényi Entropy
We are going to use phase space to formulate an entropic uncertainty principle as an axiom, and derive the quantum states this way. In particular, we will allow only those potential quantum states for which there is a phase-space representation whose entropy exceeds a lower bound. The non-classicality of the qubit becomes apparent because there are quantum states for which the only representations with entropy exceeding the bound are signed probability distributions. The use of negative probabilities on phase space to represent quantum systems goes back to the Wigner quasi-probability distribution (Wigner [11]). The first task then is to choose a suitable definition of entropy for signed probabilities.
We extend Rényi entropy ([18]) to signed probabilities and impose a smoothness condition that identifies a particular family of entropy functionals. Fix a finite set together with an ordinary (unsigned) probability distribution on X. Rényi entropy is the family of functionals
where is a free parameter. (Shannon entropy is the special case, via L’Hôpital’s rule, when .) We can preserve the real-valuedness of entropy under signed probabilities by taking absolute values
This formula can also be derived axiomatically. (see Brandenburger and La Mura [32] who modify the original axioms for Rényi entropy in Rényi [18] and Daróczy [19].) We next impose a smoothness condition, requiring that be smooth on the space of signed probabilities. That is, we require to be on . Now, if is not an integer let k be the least integer with . Then
where and for any q with . Thus, must be an integer. If is an odd integer then is undefined for q with . Therefore, Rényi entropy takes the following form under our smoothness assumption.
Definition 3.
Rényi entropy for signed probability distributions is the family of functionals
where is a free parameter.
Finally in this section, we give an example of a quantum state such that the only representatives with Rényi entropy satisfying the lower bound are signed probabilities. Consider the quantum state . Set . The (unique) maximum 2-entropy representation is
with negative final component. The 2-entropy of is 2, which is the lower bound we impose below, so we cannot find a representation with all non-negative components with sufficiently high 2-entropy. In fact any state with will have this property.
4. Main Theorem
We can now state an entropic uncertainty principle as an axiom on phase space. The axiom is inspired by the use of entropic uncertainty relations in quantum information (Wehner and Winter [20]; Bialynicki-Birula and Rudnicki [21]; Coles et al. [22]).
This says that we allow as potential quantum states only those states containing a minimum amount of uncertainty, as measured by the entropy of a corresponding probability distribution on phase space. Note that our Uncertainty Principle is a sequence of conditions, one for each k. This is because Rényi entropy itself is not a single functional but a sequence of functionals (indexed by k).Uncertainty Principle: A potential quantum state satisfies the Uncertainty Principle if for every k, there is a phase-space probability distribution that represents and satisfies .
Theorem 1.
The potential quantum states satisfying the Uncertainty Principle are precisely the states of the qubit.
Proof.
We first show that the potential quantum states satisfying the Uncertainty Principle at are the states of the qubit. Note that
For a general , the representation which maximizes 2-entropy is given by
Using the fact that we have
if and only if
and the result follows since the matrix is positive semi-definite if and only if .
We now show that if a potential state satisfies the Uncertainty Principle at then it satisfies the Uncertainty Principle at all k. This is the main mathematical argument. Fix and let be a state of the qubit. Choose a to maximize the -entropy of a representative of . We want to show which is equivalent to .
Observe that solves the norm minimization problem
The dual problem is
(see pp. 221–222 in Boyd and Vandenberghe [33].) Note that is the dual norm of . Strong duality holds so the values of the primal and dual problems are equal. Let be the maximizers of the dual problems for 2-entropy and -entropy, respectively. Let
and
Note that are both convex and, in fact, is the ball of radius . Let
be the projection of onto . Since , where is the angle between them, we must have and so
Since the values of the primal and dual problems are equal, these values are positive, so is equal to the ratio of the value of the general k problem to the value of the problem. By assumption
so it is enough to show
We will bound this expression by a function that can be explicitly maximized. Note that for every nonzero vector there are unique such that
and
This follows immediately from linearity, homogeneity, the fact that has full rank, and the fact that . Now let
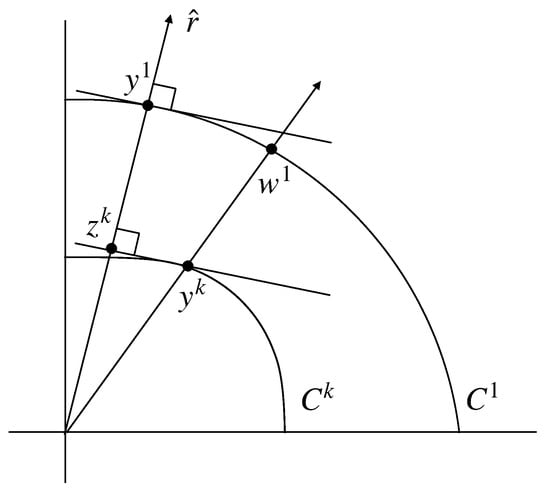
By the previous observation and the fact that for any nonzero scalar , we see that is the ratio of the distance to the boundary of along the ray through to the distance to the boundary of . Let belong to the boundary of . Figure 1 depicts the situation in the plane containing and .

Figure 1.
Comparing the maximizers of the dual problem.
Claim 1.
is bounded by a value off.
Proof.
We claim that
Note that
so the length of the projection of onto (call this vector ) cannot exceed the length of . By similar triangles then
so □
To complete the proof of Theorem 1, it suffices to show that
which we do in the Appendix A. □
5. Conclusions
We have shown that an entropic Uncertainty Principle formulated on an eight-point phase space characterizes the states of the qubit. We see our result as contributing to the program that aims to reconstruct quantum mechanics from physically interpretable axioms. Of course, our derivation is only for the simplest, two-level quantum system. We anticipate that to characterize an n-qubit system, methods will be needed that go beyond those in this paper. In particular, it may be necessary not only to extend our entropic Uncertainty Principle to the n-qubit case, but to identify new axioms. The Wootters and Sussman [27] analysis may be an important guide in this direction in that they are able to identify certain minimum-uncertainty states in an n-qubit system. A full characterization may be possible combining techniques across the two papers.
We re-emphasize that our paper is aimed at a derivation not a representation of the qubit. This explains why our phase space contains eight points while in Wootters [8] and Gibbons et al. [9] the phase space for a single qubit comprises four points. A four-point space is the appropriate domain for the discrete Wigner function, but we do not assume a Wigner representation.
A related derivation of the qubit is Onggadinata et al. [29]. Similar to our paper, they employ Rényi entropy, but fix . This instance of Rényi entropy is often called collision entropy. Their postulate is that the collision entropy is constant under any dynamics (not necessarily deterministic) on a finite one-dimensional lattice. From this, they recover the qubit with its full dynamics as defined on the Bloch sphere.
Both Wootters and Sussman [27] and Onggadinata et al. [29] work with Rényi 2-entropy. By contrast, we are able to obtain our results not just for 2-entropy, but for the entire family of -entropies, which we derived from basic principles. It would be interesting to see if our methods could be employed to generalize the results in these papers.
Author Contributions
A.B., P.L.M. and S.Z. did the research and prepared the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by NYU Stern School of Business, NYU Abu Dhabi, NYU Shanghai, J.P. Valles, the HHL—Leipzig Graduate School of Management, and the Deutsche Bundesbank.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
We are grateful to three referees and two associate editors for suggestions that importantly improved this paper. Samson Abramsky, Časlav Brukner, Matthew Deutsch, Christopher Fuchs, Leslie Greengard, Michael J.W. Hall, Jerry Keisler, Elliot Lipnowski, Kelvin Onggadinata, David Pine, Rui Soares Barbosa, Blake Stacey, Yuri Tschinkel, and Noson Yanofsky provided valuable input.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the writing of the manuscript; or in the decision to publish the results.
Appendix A
Let and . Let be defined by . Note that the critical points of f are the same as the critical points of
which are the solutions of the system of first-order conditions
where
and is the ith row of the matrix . It is helpful to write out the system with denoting for readability:
Claim A1.
The systemhas the following properties:
- 1.
- Ifis a solution then so isfor any.
- 2.
- Ifis a solution thenis a solution, whereis obtained fromby permuting coordinates.
Proof.
For (1) we have . For (2) we have
and
and similarly for . □
Claim A2.
Assume. Let. Then
Proof.
where is a multi-index,
and C is defined by
We may assume . For N sufficiently large we have where . Thus, the Taylor series expansion of at the point converges at . We have
Note that if and only if . Assume . We have
equivalently
Re-indexing we have
Collecting terms we have
equivalently
The key point is that
always has the same sign as . Thus, since we conclude that . □
Claim A3.
Ifthen.
Proof.
By Claim A1 and Claim A2 we may assume that and . We may further assume that . Thus, the equation for becomes
so
from which we conclude that as desired. □
We have thus shown that for every either or so we need only consider critical points with
for each . It is easy to check that the maximum of the original function f occurs when exactly two of the weights are 0 and this maximum value is , completing the proof of Theorem 1.
References
- Jaynes, E. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Birkhoff, G.; von Neumann, J. The Logic of Quantum Mechanics. Ann. Math. 1934, 37, 823–843. [Google Scholar] [CrossRef]
- Hardy, L. Quantum Theory from Five Reasonable Axioms. 2001. Available online: https://arxiv.org/abs/quant-ph/0101012 (accessed on 29 September 2022).
- Van Dam, W. Implausible Consequences of Superstrong Nonlocality. 2005. Available online: https://arxiv.org/abs/quant-ph/0501159 (accessed on 29 September 2022).
- Pawlowski, M.; Paterek, T.; Kaszlikowski, D.; Scarani, V.; Winter, A.; Zukowski, M. Information Causality as a Physical Principle. Nature 2009, 461, 1101–1104. [Google Scholar] [CrossRef]
- Dakić, B.; Brukner, Č. Quantum Theory and Beyond: Is Entanglement Special? In Deep Beauty: Understanding the Quantum World through Mathematical Innovation; Halvorson, H., Ed.; Cambridge University Press: Cambridge, UK, 2011; pp. 365–392. [Google Scholar]
- Chiribella, G.; D’Ariano, G.; Perinotti, P. Informational Derivation of Quantum Theory. Phys. Rev. A 2011, 84, 012311. [Google Scholar] [CrossRef]
- Wootters, W. A Wigner-Function Formulation of Finite-State Quantum Mechanics. Ann. Phys. 1987, 176, 1–21. [Google Scholar] [CrossRef]
- Gibbons, K.; Hoffman, M.; Wootters, W. Discrete Phase Space Based on Finite Fields. Phys. Rev. A 2004, 70, 062101. [Google Scholar] [CrossRef]
- Bell, J. On the Einstein–Podolsky-Rosen Paradox. Physics 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Wigner, E. On the Quantum Correction For Thermodynamic Equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Dirac, P. The Physical Interpretation of Quantum Mechanics. Proc. R. Soc. A 1942, 180, 1–40. [Google Scholar]
- Feynman, R. Negative Probability. In Quantum Implications: Essays in Honour of David Bohm; Hiley, B., Peat, F., Eds.; Routledge: London, UK, 1987; pp. 235–248. [Google Scholar]
- Abramsky, S.; Brandenburger, A. The Sheaf-Theoretic Structure of Non-Locality and Contextuality. New J. Phys. 2011, 13, 113036. [Google Scholar] [CrossRef]
- Popescu, S.; Rohrlich, D. Quantum Nonlocality as an Axiom. Found. Phys. 1994, 24, 379–385. [Google Scholar] [CrossRef]
- Von Neumann, J. Mathematische Grundlagen der Quantenmechanik; Springer: Berlin, Germany, 1932. [Google Scholar]
- Shannon, C. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423, 623–656. [Google Scholar] [CrossRef]
- Rényi, A. On Measures of Information and Entropy. In the 4th Berkeley Symposium on Mathematical Statistics and Probability; Neymann, J., Ed.; University of California Press: Berkeley, CA, USA, 1961; pp. 547–561. [Google Scholar]
- Daróczy, Z. Über die gemeinsame Charakterisierung der zu den nicht vollständigen Verteilungen gehörigen Entropien von Shannon und von Rényi. Z. Wahrscheinlichkeitstheorie Verwandte Geb. 1963, 1, 381–388. [Google Scholar] [CrossRef]
- Wehner, S.; Winter, A. Entropic Uncertainty Relations—A Survey. New J. Phys. 2010, 12, 025009. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I.; Rudnicki, Ł. Entropic Uncertainty Relations in Quantum Physics. In Statistical Complexity: Applications in Electronic Structure; Sen, K., Ed.; Springer: Berlin, Germany, 2011; pp. 1–34. [Google Scholar]
- Coles, P.; Beta, M.; Tomamichel, M.; Wehner, S. Entropic Uncertainty Relations and Their Applications. Rev. Mod. Phys. 2017, 89, 015002. [Google Scholar] [CrossRef]
- Everett, H. On the Foundations of Quantum Mechanics. Ph. D. Dissertation, Princeton University, Princeton, NJ, USA, 1957. [Google Scholar]
- Hirschman, I. A Note on Entropy. Am. J. Math. 1957, 79, 152–156. [Google Scholar] [CrossRef]
- Beckner, W. Inequalities in Fourier Analysis. Ann. Math. 1975, 102, 159–182. [Google Scholar] [CrossRef]
- Bialynicki-Birula, I.; Mycielski, J. Uncertainty Relations for Information Entropy in Wave Mechanics. Commun. Math. Phys. 1975, 44, 129–132. [Google Scholar] [CrossRef]
- Wootters, W.; Sussman, D. Discrete Phase Space and Minimum-Uncertainty States. 2007. Available online: https://arxiv.org/abs/0704.1277 (accessed on 29 September 2022).
- Fuchs, C. Quantum Mechanics as Quantum Information (and Only a Little More). In Quantum Theory: Reconsideration of Foundations; Khrennikov, A., Ed.; Växjö University Press: Växjö, Sweden, 2002; pp. 463–543. [Google Scholar]
- Onggadinata, K.; Kurzynski, P.; Kaszlikowski, D. Qubit from the Classical Collision Entropy. 2022. Available online: https://arxiv.org/abs/2205.00773 (accessed on 4 September 2022).
- Heisenberg, W. Über den anschulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 1927, 43, 172–198. [Google Scholar] [CrossRef]
- Sakurai, J.; Napolitano, J. Modern Quantum Mechanics, 2nd ed.; Addison-Wesley: Boston, MA, USA, 2011. [Google Scholar]
- Brandenburger, A.; La Mura, P. Axioms for Rényi Entropy with Signed Measures. 2019. Available online: www.adambrandenburger.com (accessed on 29 September 2022).
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).