1. Introduction
The concept of entropy has been useful in classical physics but extending it to quantum mechanics (QM) has been challenging. In classical physics Boltzmann entropy and Gibbs entropy and their respective H-theorems [
1] are formulated in the classical phase space, capturing the practical limitations of specifying the degrees of freedom (DOFs) of a classical state by describing it with randomness. Naturally, in quantum physics the DOFs specify a quantum state. Von Neumann entropy, analogously to the entropy in classical physics, quantifies the randomness of specifying the quantum state, expressed by the classical statistical coefficients of a mixture of quantum states.
Our goal for defining a quantum entropy is to quantify both (i) the inherit randomness of the observables and (ii) the randomness due to the limitations of specifying the DOFs of the quantum state. Our interest in entropy is to better understand the dynamics of quantum information and its impact in physics.
Quantum entropy is not an observable as there is no entropy operator, instead, entropy is a scalar function associated with a state. Thus, we also require quantum entropy to be a scalar invariant under special relativity, canonical transformations of coordinates, and CPT transformations.
We propose a definition of entropy in quantum phase spaces that satisfies those conditions. Quantum entropy has two components. One component is the coordinate-entropy, defined in the phase space of position and momentum. The other component is the spin entropy, which we study elsewhere [
2]. Here we focus on this coordinate-entropy of position and momentum and its time evolution, and our study is applicable to both QM and Quantum Field Theory (QFT).
1.1. Related Work
Von Neumann entropy [
3] captures the randomness associated with not-knowing precisely the quantum state, but does not capture the randomness associated with the observables. Thus, it requires the existence of classical statistics elements (mixed states) in order not to vanish. Wehrl entropy [
4] is based on Husimi’s [
5] quasiprobability distribution, rooted in projecting states to an overcomplete basis representation of coherent states. These quasiprobability distributions are not relativistic invariant. Note that no two coherent states are orthogonal to each other. Therefore, the Kolmogorov third axiom for a probability distribution, requiring that elementary events be mutually exclusive, is not satisfied. Consequently some probability properties, such as the monotonicity of probabilities and the complement rule, are not satisfied by Husimi’s quasiprobability distribution. These limitations prevent Wehrl entropy from correctly counting the random values of the observables. For example, a quantum state where the projection in position space is a Dirac delta function at
produces a non-zero value distribution for all possible position coordinates
x in the classical phase space coordinate
, where
p is the momentum coordinate. Clearly, this is not the description of the random position
x in QM. Indeed Wehrl [
6] referred to his proposed entropy as a classical entropy for the classical phase space.
The entropic uncertainty principle (EUP) [
7,
8,
9,
10] is an extension of the standard uncertainty principle [
11,
12] for a conjugate pair of observables, where the product of the variances of each observable is replaced by the sum of the entropies for each observable. It is a static statement. We view the sum of these two entropies as a single entropy in phase space, which evolves over time, and the EUP as a lower bound for our proposed entropy for pure states.
Works on quantum thermalization [
13,
14,
15,
16] and their references, suggest consideration of a quantum system as a bipartite set of environment states and a subsystem of interest and application of the von Neumann procedure of tracing out the density matrix for the environment states. Then, these works establish a relation between the von Neumann reduced density matrix of a subsystem of interest and the classical entropy. We argue that a complete quantification of randomness of the system, including the randomness of the observables, will lead to a more accurate understanding of the role of entropy in physics.
1.2. Our Contribution
Our starting points are pure states, where the DOFs associated with position and spin are precisely specified. We investigate the inherent quantum randomness associated with the observables. This randomness is fully captured by two conjugate pairs of observables satisfying the uncertainty principle [
11,
12], one associated with space and momentum, and the other associated with the internal spin state. The extension of the uncertainty principle to the entropic uncertainty principle (EUP) [
7,
8,
9,
10] suggests that the two entropy components associated with position and momentum play a role in physics. We propose a definition of entropy associated with a quantum pure state, and refer to it as coordinate-entropy. Furthermore, we extend the coordinate-entropy to mix states.
We study the coordinate-entropy’s time evolution for some physical systems, including a coherent state evolution through a potential free Dirac equation, and the hydrogen atom in an excited state transitioning to the ground state with a photon emission. In these scenarios the entropy increases. We also study a collision of two spinless particles. As they come close with each other, due to the superposition of the position wave functions and conservation laws, only the annihilation of these particles and the creation of new particles can prevent the entropy from decreasing. In the process of this analysis, we propose a property of the time evolution of the entropy associated with a potential free Dirac equation.
We then hypothesize an entropy law, universally applicable to particle physics, stating that in a closed physical system the entropy never decreases. The motivation is that the inverse of the amount of randomness, information, cannot be gained in a closed system. Such a law implies irreversibility of time for all physical scenarios where entropy does not stay constant. We complete the paper examining the consequences of such a law in physics.
2. Quantum Entropy in Quantum Phase Spaces
We now proceed to define a quantum entropy. An entropy is required to account for both types of DOFs: the coordinate DOFs and the internal DOFs (spin). It must quantify accurately all the randomness associated with the observables of a quantum state. Thus, the probability distributions that define the quantum entropy should express the uncertainty relations of the observables. Moreover, a quantum entropy must be invariant under (i) special relativity transformations, (ii) canonical transformations, and (iii) CPT transformations. Also when considering quantum mixed states, the quantum entropy must also quantify all the randomness associated with the specification of a quantum state.
We first address the coordinate-entropy associated with the coordinate DOFs. Then we mention briefly the spin-entropy associated the spin DOFs, as such study is developed elsewhere [
2].
2.1. Coordinate-Entropy
We associate with a state and its density operator their projection onto the QM eigenstates and of the operators and , respectively. Either one projection, or , is sufficient to recover the other one via a Fourier transform. However, to account for the randomness of the observables, both and , are needed. The quantum coordinate phase space is defined by projecting the density operator to obtain the probability densities and .
A time evolution of a density function according to a Hermitian Hamiltonian H is described by and so the evolution of a state in the quantum coordinate phase space is given by the pair of probability densities and .
Our formulation of the coordinate-entropy is motivated by previous work including Boltzmann and Gibbs [
1], Shanon [
17], Jaynes [
18], von Neumann entropy, Wehrl entropy, and it amounts to the sum of the two entropies in the EUP. More precisely, let the entropy associated only with the spatial coordinates be the differential entropy
. Let
be the spatial frequency (Fourier conjugate of
x),
the associated probability density, and
. Then we define the entropy associated with the quantum coordinate phase space distributions as
where
. The entropy is dimensionless and thus, invariant under changes of the units of measurements.
A natural extension of this entropy to an
N-particle QM system is
where
and
are defined in QM via the projection of the state
of
N particles (the product of
N Hilbert spaces) onto
and
coordinate systems.
Fields in QFT are described by the operators
, where
is the space-time, and their spatial Frequency transform
. They are written in terms of operators that create and the annihilate particles at a position and time
. A representation for a system of particles is based on Fock states with occupation number
, where
is the number of particles in a QM state
. The number of particles in a Fock state is then
, and a QFT state is described in a Fock space as
, where
m is an index over the configurations of a Fock state,
, and
. The QFT phase space state associated with an initial
and quantum fields
and
is then given by
, where the probability density operators for the spatial coordinates are
The QFT coordinate-entropy is then described by the same formulae (
1), but for QFT
and
.
The framework used, QM or QFT, will define which probability density operator is being employed and to which kind of state is being applied.
2.1.1. Uniqueness of the Phase Space and QFT
The variable x can be thought as the 3D space where a quantum field is defined and as the spatial frequency domain where the Fourier of the quantum field is defined. This makes them unique variables in QFT up to canonical transformations, Lorentz transformations, and CPT transformations.
2.1.2. Mixed Quantum States
We now extend the entropy (
1) to mixed states using the QM framework. Consider a mixed state formed from
pure quantum states
, defined by the density matrix
, where
and
.
Projecting each component of the density matrix onto the quantum coordinate phase space basis yields
, where
, which account for the observables probabilities as well as the probabilities associated with specifying the quantum state, namely the probabilities
. We define the coordinate-entropy associated with mixed states to be
where
is the entropy of each pure state. This entropy has two terms: the von Neumann entropy (
) and the average value of the entropies of the observables for each pure state weighted by the mixed coefficients
. Clearly, the proposed entropy is larger than the von Neumann entropy since it captures both type of randomness, the one associated with the DOFs of a quantum state plus the one associated with the observables. This entropy also differs from Wehrl entropy because it is based on a probability distribution of the observables and not on a quasiprobability distribution that lacks probability properties needed to characterize precisely the randomness of the observables.
When one is interested in quantifying just the randomness of the observables, then one must consider the probability densities and .
In this article we will focus on pure quantum states only as this is the setting of the main new contribution.
2.2. Spin-Entropy
It is not possible to know simultaneously the spin of a particle in all three dimensional directions, and this uncertainty, or randomness, was exploited in the Stern–Gerlach experiment [
19] to demonstrate the quantum nature of the spin. We explore elsewhere [
2] the entropy associated with the quantum spin phase space.
3. Entropy Invariant Properties
We now address invariant properties that the coordinate-entropy must satisfy to be considered a physical quantity of interest, namely it must be invariant under canonical transformations, under CPT transformation, and under Lorentz transformation.
QFT is constructed to be invariant under Lorentz transformation, e.g., see [
20]. We then adopt the QFT framework for proving the entropy invariance as listed above.
3.1. Canonical Transformations
In classical physics canonical transformations are studied for phase spaces mapping that preserves the form of Hamilton’s equations. We adopt the QFT description of canonical transformations, where the phase space coordinates are conjugate variables and not operators.
Theorem 1. Consider a canonical transformation of coordinates . The entropy is invariant under canonical transformations.
Proof. Let
be the entropy in phase-space relative to a conjugate Cartesian pair of coordinates
at time
t, and
to be the entropy of the the new pair of canonical variables
at time
t. The canonical transformations induce new operators
and
in phase space that must satisfy the property that probabilities in infinitesimal volumes are invariant. Thus,
Let
be the jacobian matrix of
. The infinitesimal volume invariance at any time
t gives
, and applying it to (
2) we get
Thus,
since for canonical transformations
. □
A special case of canonical transformations of the coordinates
, is known as point transformation. Attempts by [
21] to extend it to a quantum mechanics point transformation, where the conjugate variables become conjugate operators, are interesting. However, a large set of classical point transformations cannot yield a quantum point transformation, including the transformation from Cartesian coordinates to a spherical coordinate system [
22]. The case of translations is possible, and studied by [
23] as quantum reference frames. So now we adopt the QM representation, but it is not difficult to adapt it to a QFT representation. When a quantum reference frame is translated by
along
x, the state
in the position representation becomes
, where
, and where
is the momentum operator conjugate to
. When the reference frame is translated by
along
p, the state
in the momentum representation becomes
, where
, and where
is the position operator conjugate to
.
Theorem 2 (Frames of reference). The entropy of a state is invariant under a change of a quantum reference frame by translations along x and along p.
Proof. Let be a state and its entropy. We start by showing that is invariant under two types of translations:
- (i)
translations along
x by any
which is verified by changing variables.
- (ii)
translations along
p by any
implying
.
Similarly, by applying both translations to we conclude that is invariant under them too. Therefore is invariant under translations in both x and p. □
3.2. CPT Transformations
We will be focusing on fermions, and thus on the Dirac spinors equation, though the results apply to bosons as well. We return to the QFT represenation where the Dirac Hamiltonian is
A QFT solution satisfies and the C, P, and T symmetries provide new solutions from . As usual, , , , and . For completeness, we briefly review the three operations, Charge Conjugation, Parity Change, and Time Reversal.
Charge Conjugation transforms particles into antiparticles . As , is also a solution for the same Hamiltonian. In the standard representation, up to a phase. Parity Change , up to a sign, effects the transformation . Time Reversal effects and is carried by the operator , where applies conjugation. In the standard representation , up to a phase. For simplicity of notation we will drop for the QFT superscript of the probability density operator in the theorem that now follows.
Theorem 3 (Invariance of the entropy under CPT-transformations). Given a quantum field operator , its Fourier transform , and its entropy associated with any initial state, the entropies of , , , , , and their corresponding Fourier transforms are all equal to .
Proof. The probability densities of
,
,
,
, and
are
As the operator densities are equal, so are the associated entropies for any given initial state.
Equation (
3) also hold for
and its density. Thus, both entropies terms in
are invariant under all CPT transformations. □
3.3. Lorentz Transformations
Theorem 4. The entropy is invariant under Lorentz Transformations.
Proof. The probability elements
and
are invariant under Lorentz transformations because event probabilities do not depend on the frame of reference. Consider a slice of the phase space with frequency
. The volume elements
and
, are invariant under the Lorentz group [
20], that is,
and
, implying
, where
,
and
result from applying a Lorentz transformation to
x,
k, and
. Thus, from the probability-invariant elements we conclude that
and
are also invariant under the group. Thus, the phase space density
is an invariant under Lorentz transformations. Therefore, the entropy is a relativistic scalar. □
Note that in QFT, one scales the operator by , that is, one scales the creation and the annihilation operators and . In this way, the density operator scales with and becomes a relativistic scalar. Also, with such a scaling, the infinitesimal probability of finding a particle with momentum in the original reference frame is invariant under the Lorentz transformation, though it would be found with momentum .
4. The Minimum Entropy Value
The third law of thermodynamics establishes 0 as the minimum classical entropy. However, the minimum of the quantum entropy must be positive due to the uncertainty principle’s lower bound. Let be 1 for positive x and 0 elsewhere.
Theorem 5. The minimum entropy of a particle with spin s is .
Proof. The entropy is the sum of the coordinate-entropy and the spin-entropy. The coordinate-entropy (
1) is
. Due to the entropic uncertainty principle
as shown in [
7,
8,
10], with
. To complete the proof, by [
2], the minimum spin-entropy is
. □
Higgs bosons in coherent states have the lowest possible entropy .
The dimensionless element of volume of integration to define the entropy will not contain a particle unless
, due to the uncertainty principle, and this may be interpreted as a necessity of discretizing the phase space. We note that the minimum entropy of the discretization of (
1) is also
, as shown in [
24].
We point out that coherent states minimize the uncertainty principle, they also minimize the entropic uncertainty principle (and we show it in
Section 5.3) and they also minimize Wehrl entropy as shown by Lieb [
25].
5. Time Evolution of the Entropy
We now introduce a formalism and characterize time evolution behaviors of the entropy.
5.1. A Formalism for Entropy Evolution
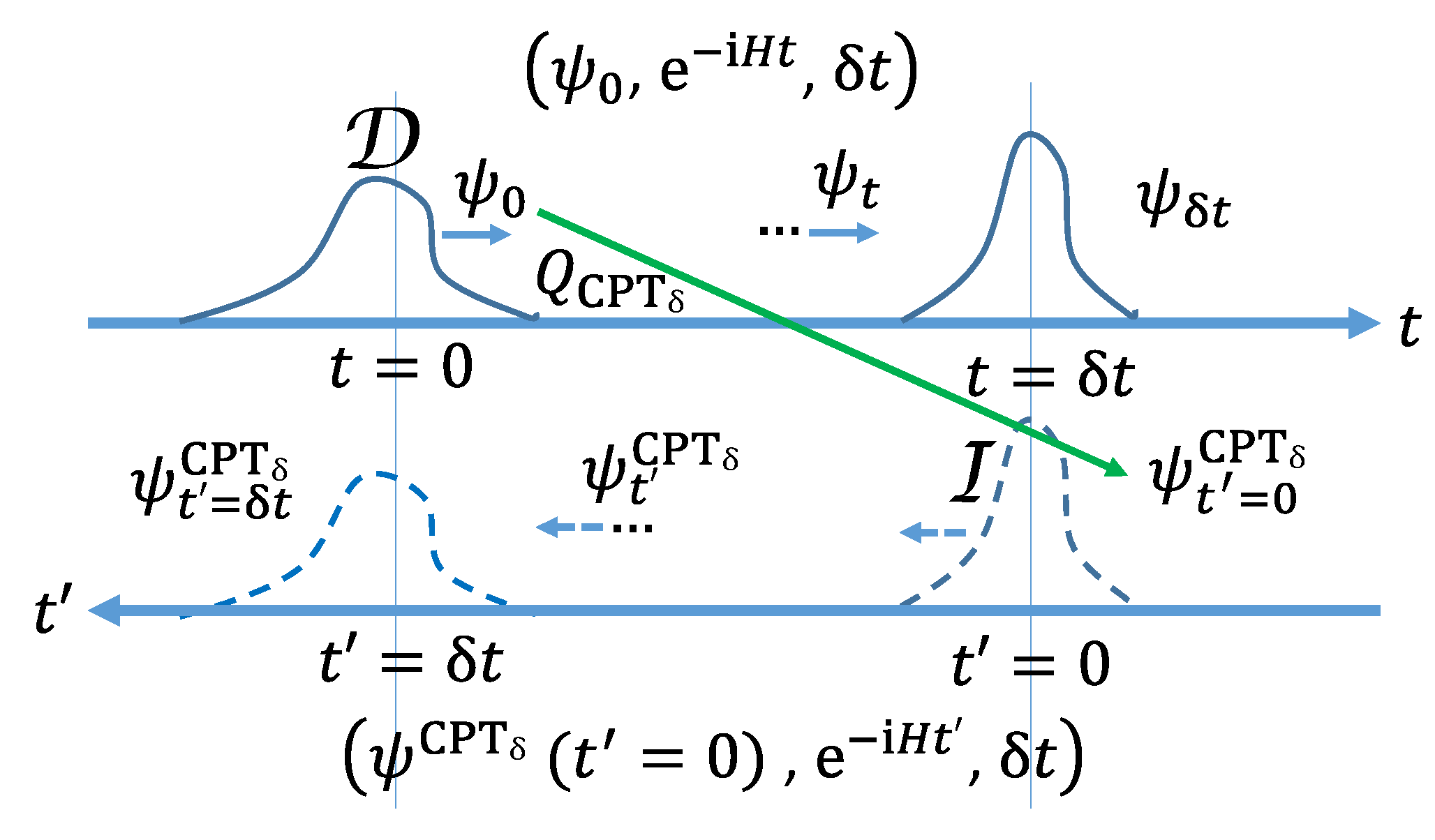
We introduce the concept of a QCurve to specify a curve (or path) in a Hilbert space parametrized by time. In QM a QCurve is represented by a triple where is the initial state, is the evolution operator, and is the time interval of the evolution. Of course, one may also represent the initial state by a triple , where is the density matrix. Alternatively, we can represent the initial state in the quantum coordinate phase space by or . In QFT the unitary evolution may be represented by the initial condition or by the initial phase space state .
We will use any of these representations to describe a QCurve as more convenient for manipulations for the problem at hand.
Definition 1 (Partition of ). Let to be the set of all the QCurves. We define a partition of based on the entropy evolution into four blocks:
- :
The set of QCurves for which the entropy is a constant.
- :
The set of QCurves for which the entropy is increasing, but it is not a constant.
- :
The set of QCurves for which the entropy is decreasing, but it is not a constant.
- :
The set of oscillating QCurves, with the entropy strictly increasing in some subinterval of and strictly decreasing in another subinterval of .
Consider stationary states with , where E is an energy eigenvalue of the Hamiltonian, and is the time-independent eigenstate of the Hamiltonian associated with E.
Theorem 6. All stationary states are in .
Proof. Follows from the time invariance of the probabilities . □
5.2. Dispersion of a Fermion Hamiltonian
Dirac’s free-particle Hamiltonian in QM [
26] is
It can be diagonalized in the spatial Fourier domain
basis to obtain
where
is the frequency component of the Hamiltonian. We focus on the positive energy solutions and so the group velocity becomes
In (
9) we will use the Taylor expansion of (
5) up to the second order, thus requiring the Hessian
, with the entries
for the positive energy solution. The three (positive) eigenvalues of
are
where
is the kinetic energy in mass units. The Hessian is positive definite for positive energy, and so it gives a measure of the dispersion of the wave.
We now consider initial solutions that are localized in space, , where is the mean value of x. Assume that the variance, , is finite, where . In a Cartesian representation, we can write the initial state in the spatial frequency domain as , where is the Fourier transform of , and so the variance of is also finite, with the mean in the spatial frequency center .
The time evolution of
according a Hamiltonian with a dispersion relation
, and written via the inverse Fourier transform, is
As
fades away exponentially from
, we expand (
5) in a Taylor series and approximate it by
where
,
, and
are the phase velocity
, the group velocity (6), and the Hessian (7) of the dispersion relation
, respectively. Then after inserting (9) into (8), we obtain the quantum dispersion transform
where
,
, with Fourier transform
; ∗ denotes a convolution,
and
normalize the amplitudes, and
is a normal distribution. Consequently,
is the spatial Fourier transform of
.
The probability densities associated with the probability amplitudes in (
10) are
Lemma 1 (Dispersion Transform and Reference Frames)
. The entropy associated with (11) is equal to the entropy associated with the simplified probability densities Proof. Consider (11). If the frame of reference is translating the position by
and the momentum by
, we get the simplified density functions (
12).
Theorem 2 shows that the entropy in position and momentum is invariant under translations of the position x and the spatial frequency k, and that completes the proof. □
The time invariance of the density , and therefore of , reflects the conservation law of momentum for free particles.
5.3. The Coordinate-Entropy of Coherent States Increases with Time
Coherent states, represented by state
, are eigenstates of the annihilator operator. The 1D quantum phase space of observables
can be constructed by the unitary operator
applied to zero-state
, that is, they can be constructed as
, where
. Projecting the state to position space yields
, where
. Squeeze states extend coherent states to all eigenstate solutions of the annihilator operator by allowing different variances to the Gaussian solution, and together their representation in 3D position and momentum space are
where
is the spatial covariance matrix.
Theorem 7. A QCurve with an initial coherent state (13) and evolving according to (4) is in . Proof. To describe the evolution of the initial states (
13), we apply (
10). Then, after applying Lemma 1,
where
. Then
As , the entropy increases over time. □
The theorem suggests that quantum physics has an inherent mechanism to increase entropy for free particles, due to the spatial dispersion property of the Hamiltonian. Note that at
a coherent state (
13) reaches the minimum possible coordinate-entropy value.
The dispersion properties of the Dirac and Schrödinger Hamiltonian equations have been studied in the past, and are already present in Feynmann path integral formulation for the free particle [
27], where an analytical solution is derived showing the dispersion of the initial localized particle.
5.4. A Conjecture on Entropy Evolution
Conjecture 1. For every single fermion state in Hilbert space, that is evolving under the free fermion Hamiltonian, there exist a finite time parameter T such that the coordinate-entropy will not decrease.
We present a motivation for this conjecture. The dispersion relation
for the free fermion Hamiltonian has a positive Hessian (7). Note that Schrödinger Hamiltonian also has a positive Hessian. We also observe some mathematical scenarios where the entropy can decrease temporarily. Given a fermion in a coherent state solution
evolving backwards for a time period
T. It will yield a solution
, with larger entropy than
. Then a starting solution
will evolve forward for a period
, until it reaches back to
, with entropy decreasing. However, for
the entropy of the evolution will increase forever. We discuss this scenario next in
Section 5.5. Another physical scenario where the entropy can decrease for a period
T is when the initial state is a sum of two coherent states,
, that is, these parameters model two components away from each other and moving towards each other. For large distances
, where the overlap of the two components is negligible, the entropy evolution of each component increases due to dispersion, and thus, the entropy increases. As the two components come closer to each other, the overlap increases, and the final probability contain a significant term from the interference of the components. Then, due to the interference, the entropy can decrease. Continuing the evolution, as the two components “pass through each other” and start to move away from each other, the entropy will again start to increase, and will increase forever. The parameter
T in this case represents the period of a large overlap between the two components up to when they “pass through each other”.
Note that for physical scenarios where the overlap is large enough for causing the entropy to decrease, there is a possible mechanism in nature, outside of the motion equation, to annihilate such solutions (such particles) and create new particles that satisfy the conservation laws that could have the entropy of the evolution to always increase.
5.5. Time Reflection
Consider a time-independent Hamiltonian. We investigate the discrete symmetries C and P, and propose that Time Reversal be augmented with Time Translation, say by
. We refer to the mapping
as Time Reflection, because as
t varies from 0 to
,
varies as a reflection from
to 0. We define the Time Reflection quantum field
Note that in contrast to the case of Time Reversal, , and the entropies associated with and are generally not equal. Thus, an instantaneous Time Reflection transformation will cause entropy changes.
We next consider a composition of the three transformation, Charge Conjugation, Parity Change, and Time Reflection.
Definition 2 (
)
. Let the quantum field bewhere η is the product of the phases of each operation, is the phase of time translation, and . Definition 3 (). Let be .
Theorem 8 (Time Reflection)
. Consider a invariant quantum field theory (QFT) with energy conservation, such as Standard Model or Wightman axiomatic QFT [28]. Let be a QCurve solution to such QFT. Then, is (i) a solution to such QFT, (ii) if is in , , , then is respectively in , , , , making , , , reflections of , , , , respectively. Proof. Let . The QCurve describes the evolution of during the period .
Since is a solution to a QFT that is CPT-invariant and time-translation invariant, is also a solution to the QFT, proving (i).
The time evolution of from 0 to is described by , and by (15) . Thus by Theorem 3, the evolution of as evolves from 0 to has the same entropies as . Since traverses the same path as but in the opposite time direction, we conclude that produces the time evolution states in the time interval traversing the same path and with the same entropies as , but in the opposite time directions.
Applying the above to a QCurve respectively in , , , , results in a QCurve respectively in , , , , proving (ii). □
5.6. Entropy Oscillations
Consider a Hamiltonian
, where
accounts for additional interactions, and the initial eigenstate
of
H associated with the eigenvalue
. The time evolution of
is
where
n is the number of the eigenvectors of
H. Fermi’s golden rule [
29,
30] approximates the coefficients of transition for
and short time intervals by
Theorem 9 (Entropy Oscillations). Consider the QCurve with the ground state value of H and . Assume that for and . Then the QCurve is in .
Proof. With the theorem’s assumptions, we can approximate the position and the momentum probability densities associated with
by
The time coefficients of and are the same, and they all return to the same values simultaneously after a period of T, and so the entropy will return to its previous value too. As the entropy is not a constant, it must be oscillating. □
Thus, when Fermi’s golden rule can be applied, the coefficients of the transition probabilities of the unitary evolution of a state oscillate, and the entropy associated with the evolution of such a state will also oscillate with the same period.
Theorem 10 (Coefficients for two states). Consider a particle in an eigenstate of a Hamiltonian H that has only two eigenstates and with eigenvalues and , respectively. Let this particle interact with an external field (such as the impact of a Gauge Field), requiring an additional Hamiltonian term to describe the evolution of this system.
Let , , , , and . Then, the probability of the particle to be in state at time t is Proof. The Hamiltonians in the basis
are
where the real values satisfy
as
is Hermitian. The eigenvalues of the symmetric matrix
are
, and so we can decompose it as
where
The time evolution of
is
, and projecting onto
, we get
. From (
16),
Thus,
and so
As , the probability of being in state at time t is . Using (17), completes the proof. □
If
,
, and
, then
, and the coefficient of transition becomes
, which is Fermi’s golden rule [
29,
30].
6. Entropy Evolution in Physical Scenarios
We now apply to physical scenarios the formalism developed for characterizing the time evolution of the entropy, including analysis of experiments conducted with particles and atoms.
6.1. A Two-Particle Collision
Consider a two-fermions or a two-massive-bosons system
where
is the normalization constant that may evolve over time and the signs “∓” represent fermions (“−”) and bosons (“+”). When
and
are orthogonal to each other,
. Projecting on
and on
,
The entropy of the two-particle system, discarding the spin-entropy which is constant throughout the collision, is then
Consider a collision of two particles, each one described by an initial coherent state with position variance
, centered at
and
, and moving towards each other along the
x-axis with center momenta
and
. They can be represented in position and momentum space as
Figure 2 shows that when the two particles are far apart, the entropy of the system is close to the sum of the two individual entropies, with each one increasing over time. The spatial entanglement decreases the uncertainty, and therefore the entropy too. The competition between the increase of the entropy of the individual particles and the decrease of the entropy due to entanglement results in an oscillation and the decrease in the total entropy when the two particles are close to each other.
6.2. The Hydrogen Atom and Photon Emission
The QED Hamiltonian for the hydrogen atom is
where the photon’s helicity
,
, the creation and the annihilation operators of photons satisfy
, and the electromagnetic vector potential is
and in the Coulomb Gauge (
), for
, the polarizations satisfy
and
.
The state of the atom can be described by , where are the quantum numbers of the electron , and q and are the momentum and the helicity of the photon . We next consider the Lyman-alpha transition, with the emission of a photon with wavelength .
We first evaluate the electron’s entropy at both states and . For simplicity, we consider the Schrödinger approximation to describe the electron state with the energy change in this transition of . We now compute the difference between the final and the initial state entropy in three steps.
- (i)
The position probability amplitudes described in [
31] and the associated entropies are
where
is the Bohr radius, and
.
- (ii)
The momentum probability amplitudes described in [
31] and the associated entropies are
where
.
- (iii)
Therefore,
Thus, the entropy of the electron is reduced by approximately during the transition .
We next evaluate the entropy associated with the randomness in the emission of the photon. Due to energy conservation, the energy must satisfy
, where
c is the speed of light. The associated energy uncertainty is very small. The main randomness for the photon is in specifying the direction of the emission. The angular momentum of the electron along
z (
) does not change between
and
. The spin 1 of the photon is along its motion, and conserves the total angular momentum of the system. Thus, to conserve angular momentum along
z, the photon must be moving perpendicularly to the
z axis, that is,
, and so the polarization vectors must be
and
. The angle
is completely unknown, with the entropy
. Then we observe that the entropy increases, as
Consider now an apparent time-reversing scenario in which an apparatus emitted photons with energy to strike a hydrogen atom with its electron in the ground state. The photon had to follow a precise direction towards the atom, and a very small uncertainty in the direction implies low photon entropy. Once the atom absorbs the photon, the energy of the electron in the ground state suffices for a jump into an excited state. The entropy increases again, as the entropy of the excited state is larger than the entropy of the ground state (accounting for the low photon entropy).
Experiments in a Reflective Cavity
More recent sophisticated experiments have addressed time reversibility of quantum mechanics, see, e.g., [
32,
33]. A cavity is created with nearly perfect mirrors and an atom with an electron in an excited state is placed inside the cavity. Then the atom goes to the ground state and a photon is emitted. Then, the cavity mirror reflects the photon, which carries the same phase as the emitted photon. The ground state atom absorbs the photon and the electron jumps back to the excited state, and the process restarts. The whole process is then apparently reversible, meaning it starts with the atom and the excited electron and ends with the atom and the excited electron.
We do not interpret this process as a demonstration of quantum time reversibility. Our reasoning follows. Let
denote the state of the atom with the electron in the excited state, while
denotes the state of the atom in the ground state. At the start of this process the atom state is
and once the electron goes to the ground state and emits a photon the new state is denoted by
, with a photon in the state
. More generally, the atom can be in a superposition of the two states,
and
. Note that the state
requires the atom to recoil due to momentum conservation. Since the photon is emitted to a random direction (constrain by the angular momentum conversation) the recoil of the atom must also have such randomness, and the pair of states
and
must be entangled by the motion direction variable (see for example [
34,
35] and references). If one observes the atom recoil direction one will know the direction of the photon emission. Next in the process, the photon is reflected by the cavity. After the photon is reflected, due to momentum conservation, the cavity must now be in a new quantum state,
, carrying twice the momentum the photon had when it was emitted. Since the photon emission direction is a random variable, so is the cavity motion direction. Then the three states
,
and
must now be entangled. Observing the momentum of the atom or of the cavity will reveal all other motion directions.
During this process, a flow of information also occurs, that is the entropy associated with the isolated states vary in time. The system evolved from the state , to the entangled state , then to the entangled state , and finally, after the atom absorbs the photon, it is in the entangled state . It is clear that the introduction of the cavity adds another quantum state to the system. For the initial state the cavity motion was assumed to be zero. For the final state there is an uncertainty in the motion direction of the atom entangled with the motion direction of the cavity. Thus, the final state has a larger entropy than the initial state and the process is not reversible.
7. An Entropy Law and a Time Arrow
In classical statistical mechanics, the entropy provides a time arrow through the second law of thermodynamics [
36]. We have shown that due to the dispersion property of the fermionic Hamiltonian, some states, such as coherent states, evolve with an increasing entropy. However, current quantum physics is time reversible, and it is possible to have state evolution where the entropy oscillates. This includes the scenario in the hydrogen atom studied earlier, where the excited state of the electron with no photon and the ground state of the electron with a photon emission are two possible states where quantum physics describe an oscillation which we showed leads to the entropy oscillation.
We hypothesize the following
Law (The Entropy Law). The entropy of an isolated quantum system is an increasing function of time.
It is an information-theoretic conjecture about isolated quantum states, whereby information (the inverse of the entropy) cannot be gained. We note that it does not require any observer making any measurement.
An evidence for such a law is the hydrogen atom scenario discussed earlier. According to QED, and due to photon fluctuations of the vacuum, the state of an electron in an excited state of the hydrogen atom is in a superposition with the ground state, and the entropy would decrease within a time interval . Instead, interrupting the oscillation, the electron jumps to the ground state and a photon is created/emitted, increasing the entropy. We hypothesize that the entropy law is the trigger for the photon creation.
We complete the paper wondering whether, in light of the hypothesized entropy law, all quantum states are indeed always in a superposition of all quantum states evolving according to the unitary evolution dictated by the Hamiltonian of the system as current QM asserts. In this case, no collapse of the wave function exists. Alternatively, and according to the QFT description, the creation and annihilation of particles occur and can interrupt the unitary evolution. In this QFT framework, if entropy oscillation scenarios can occur, e.g., as described by the Fermi Golden Rule transition [
29,
30], then the entropy law would trigger a collapse of a state to a new state where the entropy will increase during the following evolution. This could possibly describe the emission of the photon when the electron falls to the ground state in the hydrogen atom, or the collision of two particles, creating the new particles. In this case, like in the Copenhagen interpretation of QM, the collapse of the state would occur, but in contrast to the Copenhagen interpretation, it would not require a measurement (or an observer).
8. Conclusions
Capturing all the information of a quantum state requires specification of the parameters associated with the DOFs of a quantum state as well as the intrinsic randomness of the quantum state. The intrinsic randomness is associated with a conjugate pair of observables, satisfying the uncertainty principle. We proposed a coordinate-entropy defined in the quantum phase spaces, the space of all possible states projected in the Fourier conjugate basis of position, and spatial frequency. Even though these observables are the same variables used in the classical entropy, the motivation and quantification are quite different. For the classical case, the randomness originates in the practical difficulties in specifying the DOFs precisely, while for the quantum pure state case, the randomness is due to the intrinsic quantum state observables characterized by a pair of conjugate observables that satisfy the uncertainty principle.
This definition of the coordinate-entropy and quantum phase spaces possesses desirable properties, including invariance under canonical transformations, under Lorentz trasnformations, and under CPT transformations. We extended this entropy for the more general case where there is a randomness associated with specifying the quantum state, leading to a mixed quantum state. For mixed states, the entropy is always larger than von Neumann entropy due to the accounting for the randomness associated with the observables of each pure state.
We analyzed the entropy evolution through the partition of QCurves into the four sets , , , . We showed that the Dirac’s Hamiltonian disperses information due to its positive Hessian, causing coherent states time evolution to increase entropy. We proved that Time Reflection transforms QCurves in , , , into QCurves in , , , , respectively. We proved that an initial eigenstate of a Hamiltonian evolving with the addition of a Hamiltonian term not only causes a state oscillation (as suggested by Fermi’s golden rule when the appropriate approximations hold) but also causes entropy oscillation. We showed that the entropy increases when an electron in an excited state of the hydrogen atom falls to the ground state emitting a photon. We also showed that experiments with near perfect cavity with atoms in excited states do not describe reversible processes, but rather processes such that the information of the entanglement of the atom with a cavity motion direction cannot be neglected. We studied collisions of two particles, each evolving as a coherent state, and showed that as they come closer to each other the total system’s entropy oscillates.
We hypothesized an entropy law that the entropy of a closed quantum system increases with time. The motivation for the law is that information (inverse of the amount of randomness) cannot increase in a closed quantum system. This law implies the irreversibility of time for scenarios where the entropy is not constant.
The results are applicable to both the Quantum Mechanics (QM) and the Quantum Field Theory (QFT) settings, but we generally presented them in the more convenient setting.
For the oscillation scenarios, the entropy law triggers the collapse of a state to a new state where the new evolution will cause the entropy to increase. Such a collapse is accompanied by particle creation or annihilation. In this case, the entropy law determines that the event of particle creation and/or annihilation does occur, regardless of an observer performing a measurement. In this view, a measurement is a physical process that activates the hypothesized entropy law. Thus, for example, the phenomena described by the double slit experiment would imply that, at the sensors screen, the absorption (annihilation) of the particle passing through the double slit occurs, accompanied by the collapse of the particle state. However, a measurement is not required for the collapse of the state to occur.