Determination of Parameters for an Entropy-Based Atrial Fibrillation Detector
Abstract
:1. Introduction
2. Methods
2.1. Data
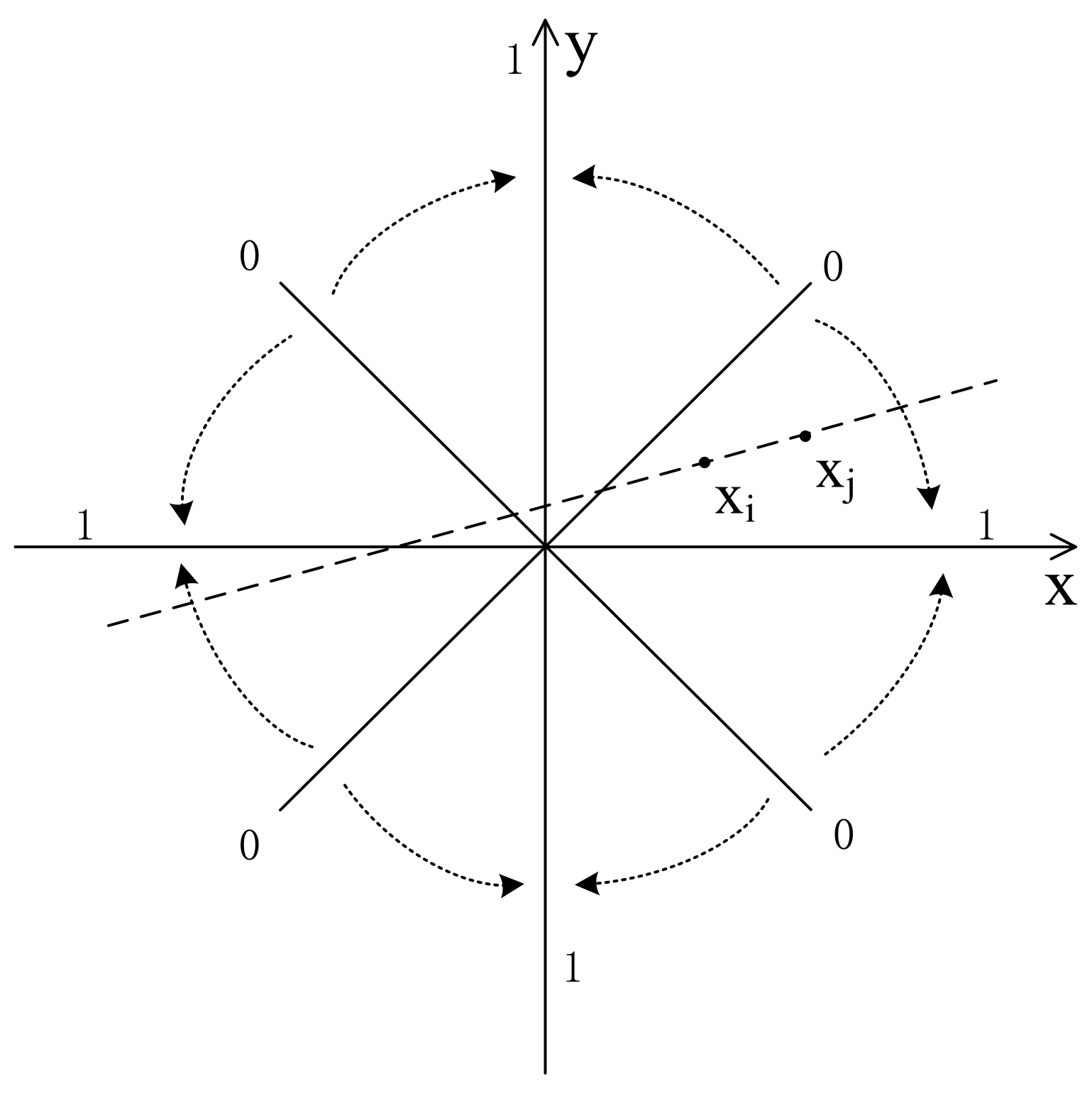
2.2. EntropyAF Method
2.3. Parameter Test
3. Results
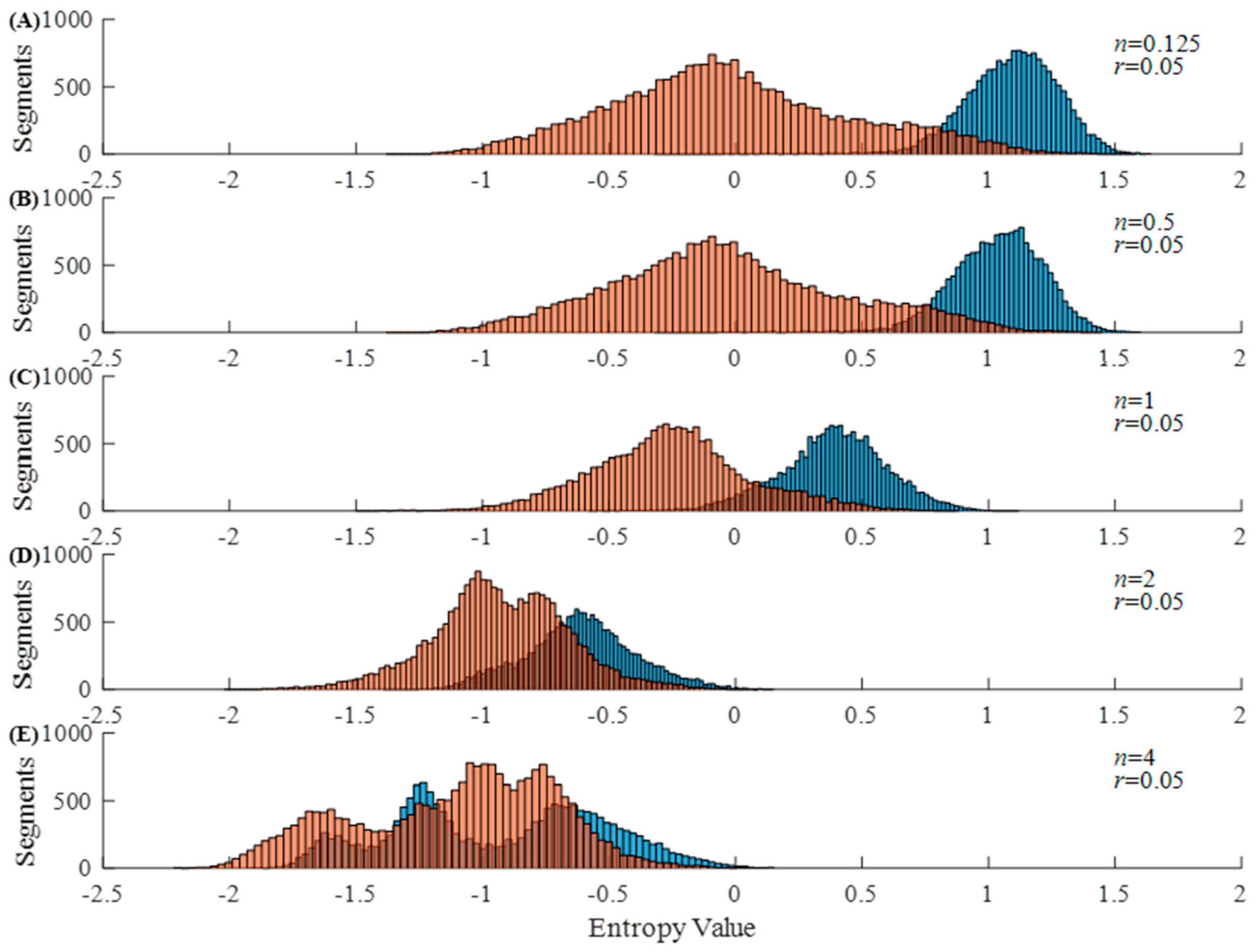
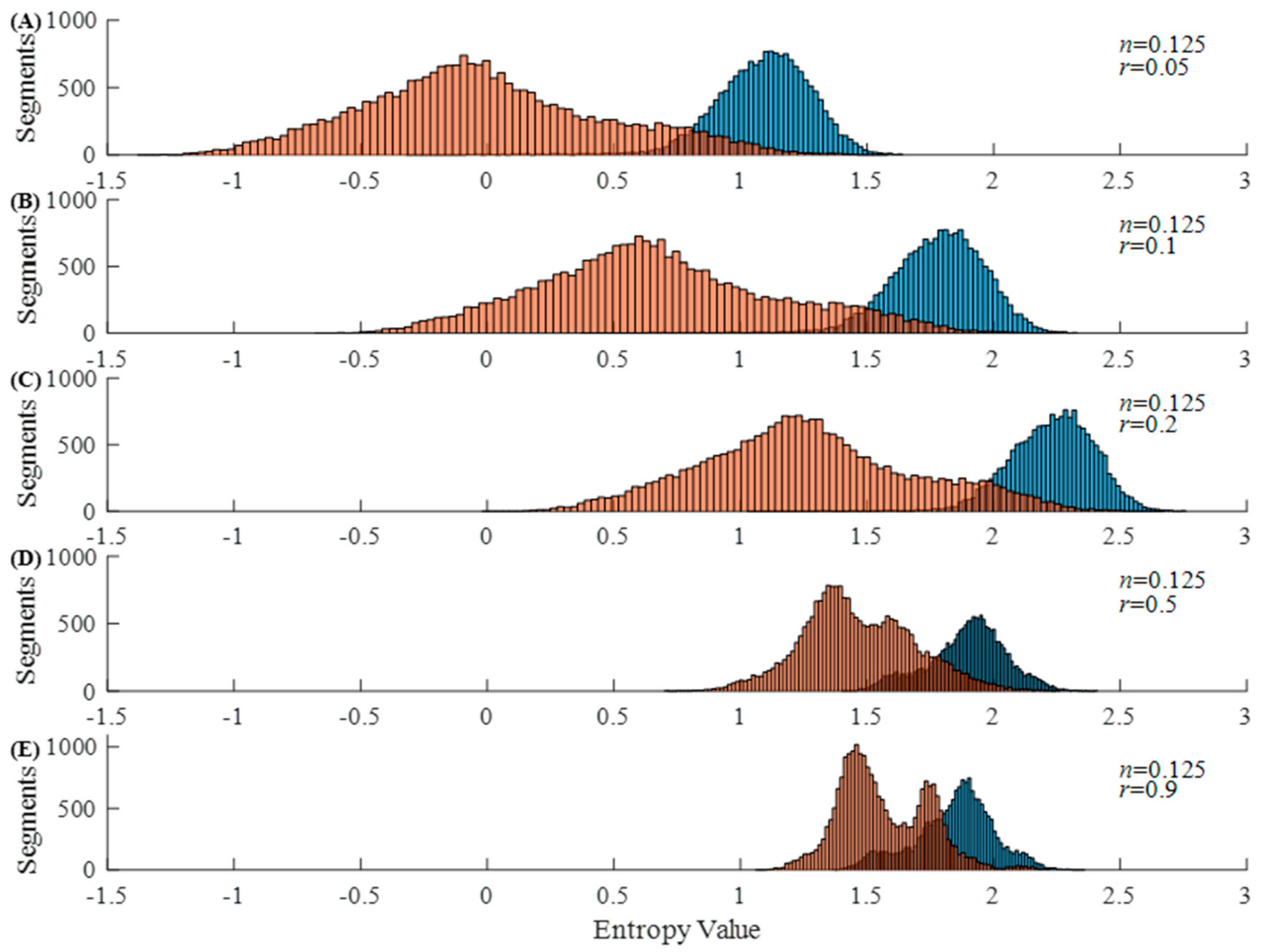
3.1. Classification Results with Different Parameter Combinations
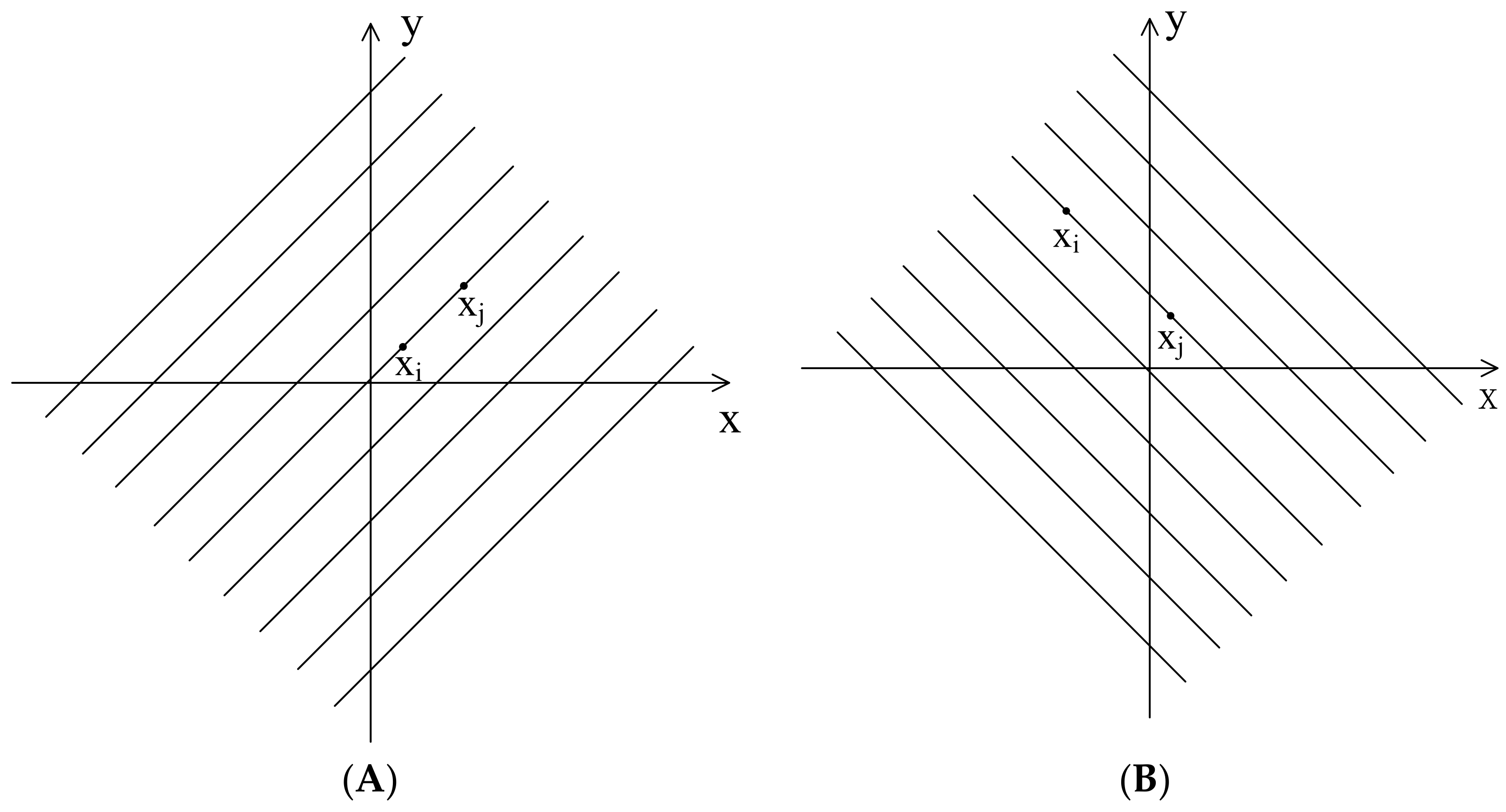
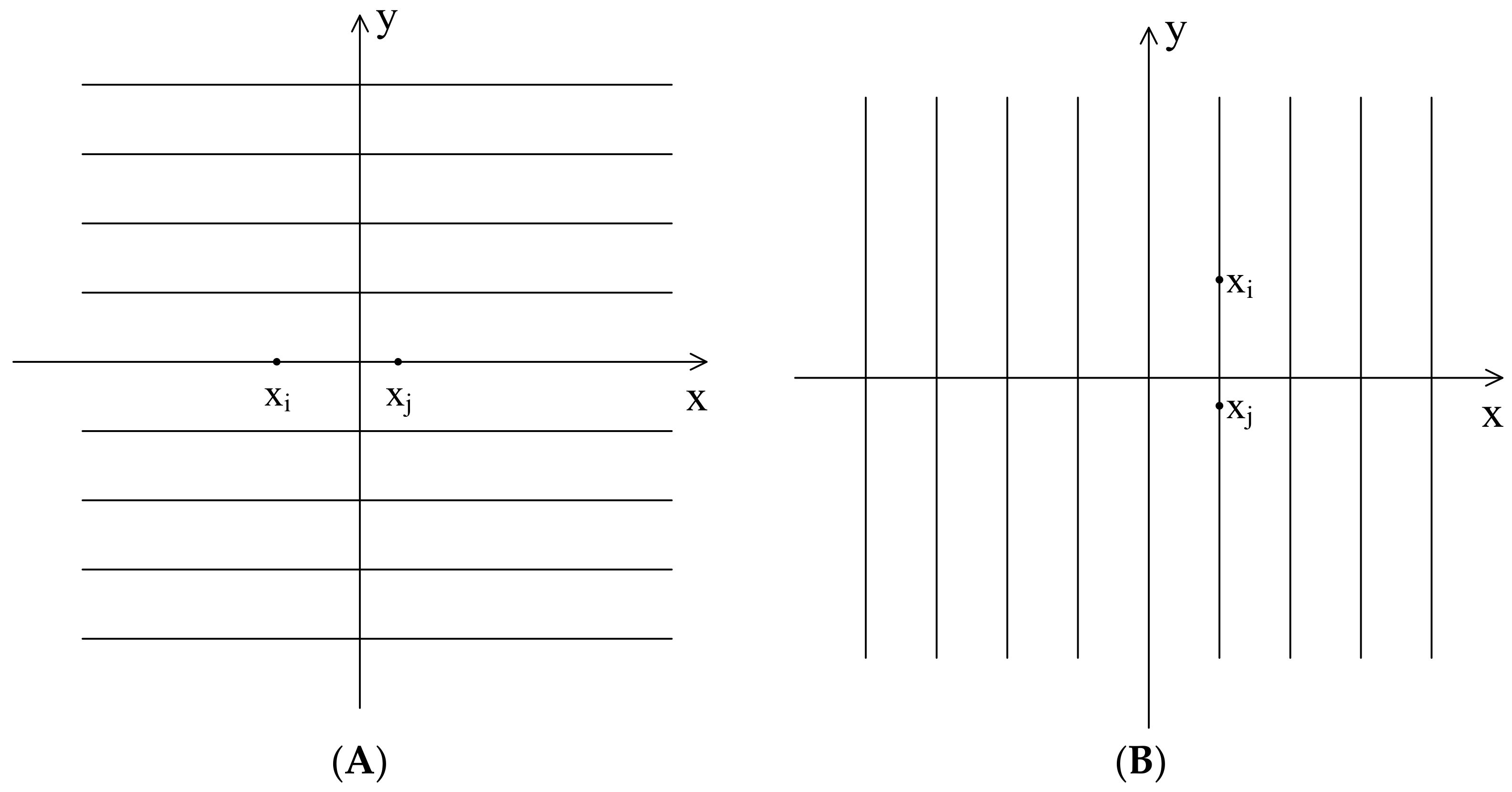
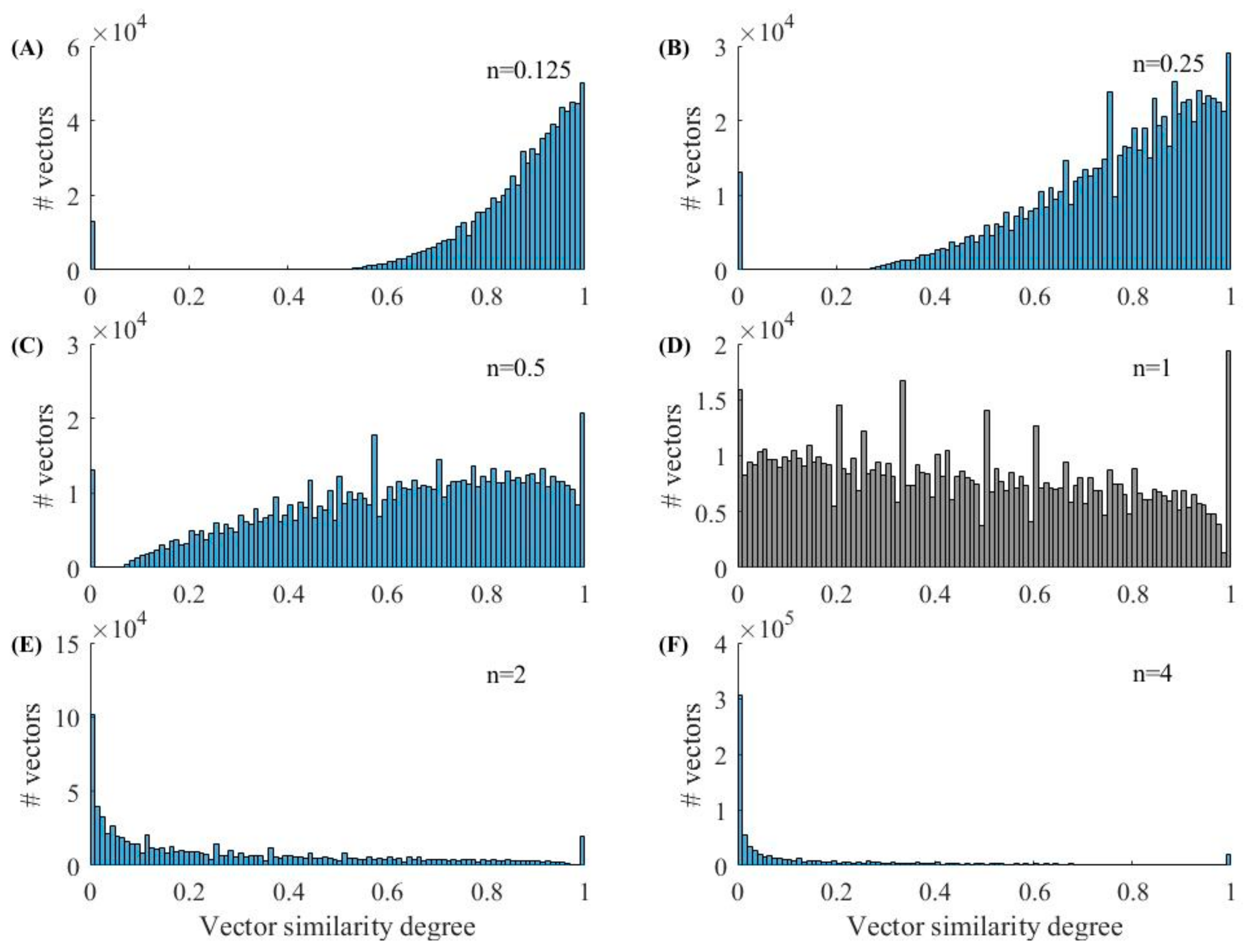
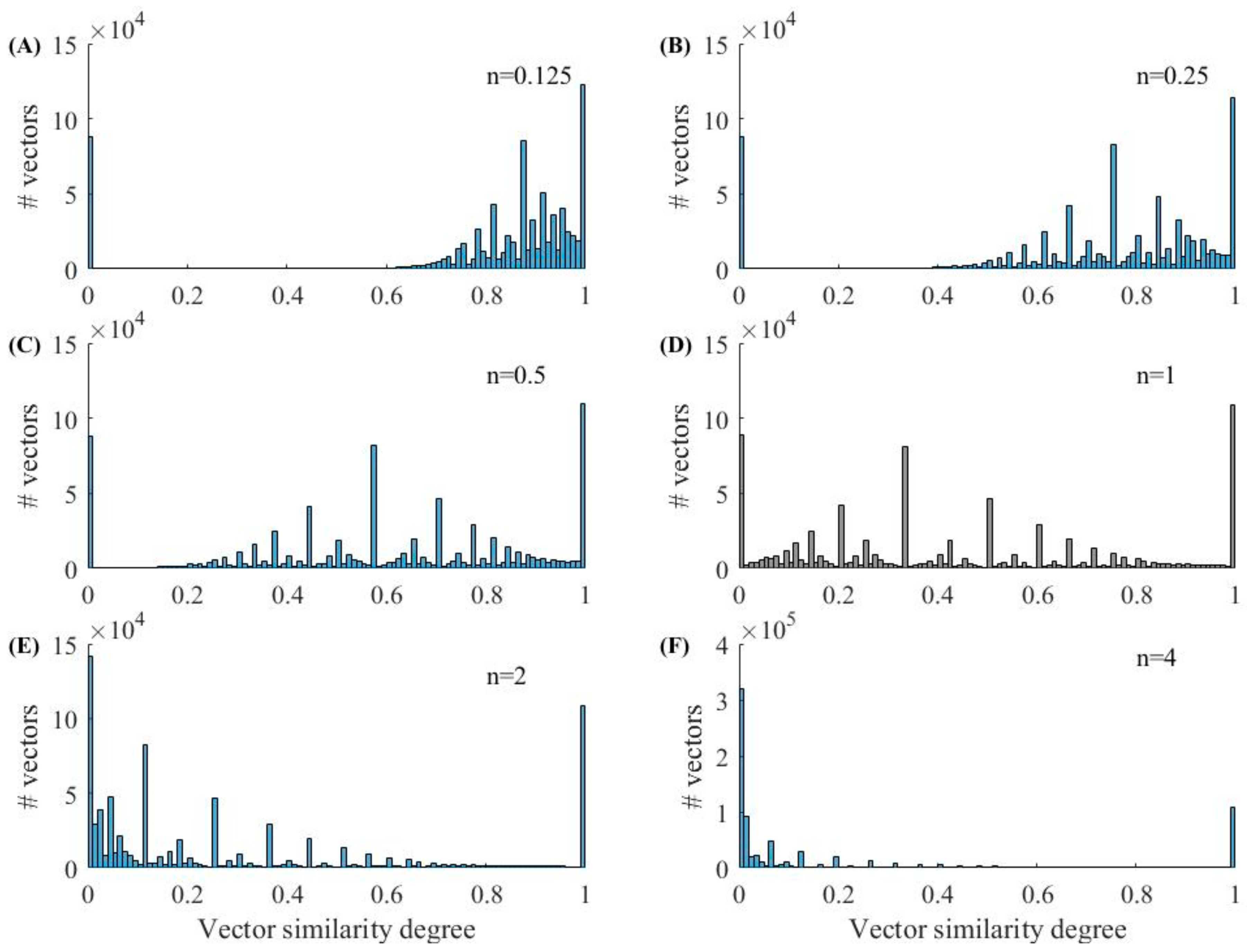
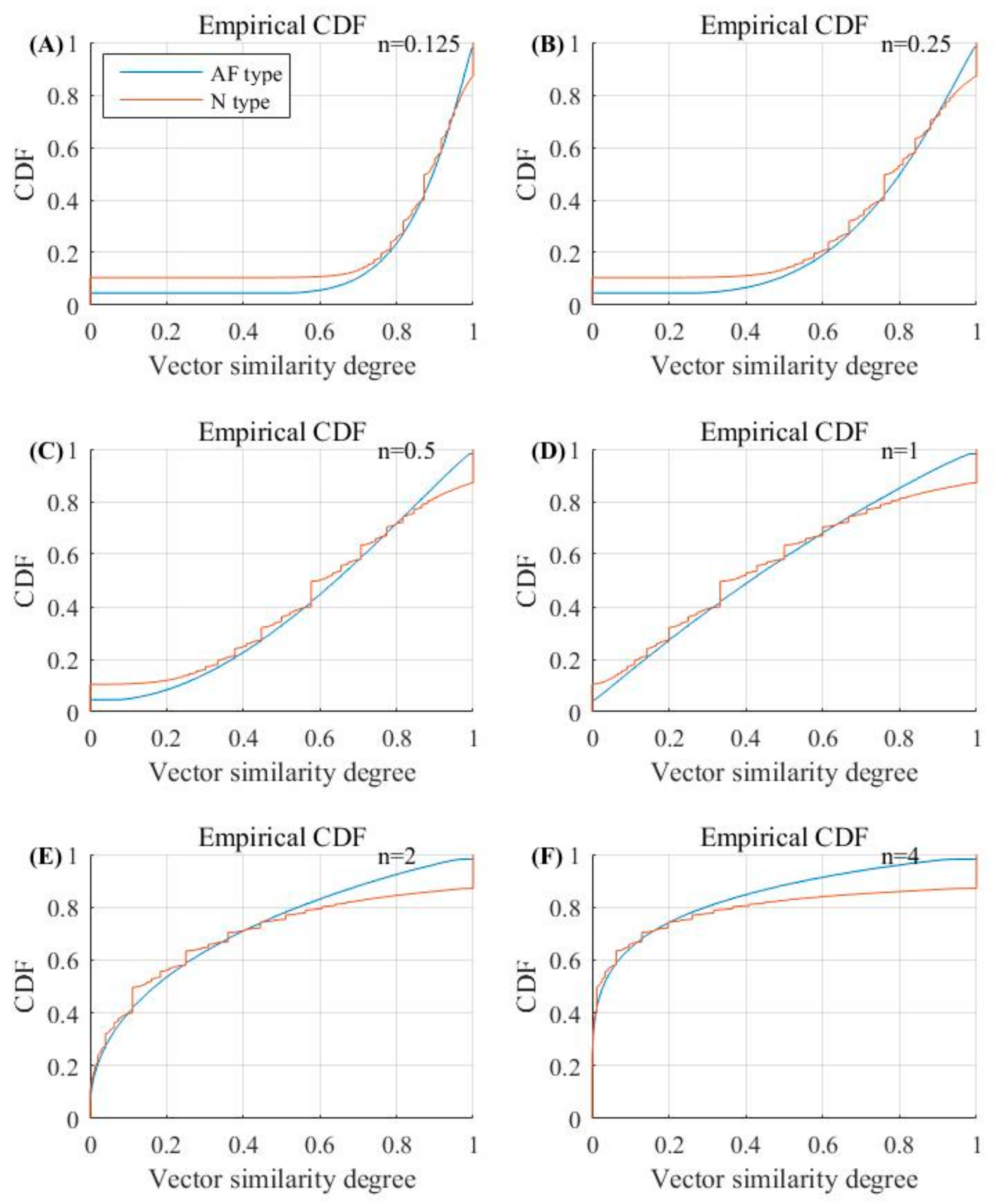
3.2. Inferential Analysis from the Calculation of Vector Distances
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Nattel, S. New ideas about atrial fibrillation 50 years on. Nature 2002, 415, 219–226. [Google Scholar] [CrossRef]
- Lloyd-Jones, D.M.; Wang, T.J.; Leip, E.P.; Larson, M.G.; Levy, D.; Vasan, R.S.; Agostino, R.B.D.; Massaro, J.M.; Beiser, A.; Wolf, P.A. Lifetime risk for development of atrial fibrillation: The Framingham Heart Study. Circulation 2004, 110, 1042–1046. [Google Scholar] [CrossRef]
- Lip, G.Y.; Tse, H. Management of atrial fibrillation. Lancet 2007, 370, 604–618. [Google Scholar] [CrossRef] [Green Version]
- Hindricks, G.; Potpara, T.; Dagres, N.; Arbelo, E.; Bax, J.J.; Blomström-Lundqvist, C.; Boriani, G.; Castella, M.; Dan, G.; Dilaveris, P.E.; et al. ESC Scientific Document Group. 2020 ESC Guidelines for the diagnosis and management of atrial fibrillation developed in collaboration with the European Association for Cardio-Thoracic Surgery (EACTS): The Task Force for the diagnosis and management of atrial fibrillation of the European Society of Cardiology (ESC) Developed with the special contribution of the European Heart Rhythm Association (EHRA) of the ESC. Eur. Heart J. 2021, 42, 373–498. [Google Scholar] [PubMed]
- Rienstra, M.; Lubitz, S.A.; Mahida, S.; Magnani, J.W.; Fontes, J.D.; Sinner, M.F.; Van Gelder, I.C.; Ellinor, P.T.; Benjamin, E.J. Symptoms and functional status of patients with atrial fibrillation: State of the art and future research opportunities. Circulation 2012, 125, 2933–2943. [Google Scholar] [CrossRef] [Green Version]
- Dharmaprani, D.; Dykes, L.; McGavigan, A.D.; Kuklik, P.; Pope, K.; Ganesan, A.N. Information theory and atrial fibrillation (AF): A review. Front. Physiol. 2018, 9, 957. [Google Scholar] [CrossRef]
- Camm, A.J.; Corbucci, G.; Padeletti, L. Usefulness of continuous electrocardiographic monitoring for atrial fibrillation. Am. J. Cardiol. 2012, 110, 270–276. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, X.; Zhao, L.; Liu, F.; Chen, X.; Yao, Y.; Li, J. Signal quality assessment and lightweight QRS detection for wearable ECG SmartVest system. IEEE Internet Things J. 2018, 6, 1363–1374. [Google Scholar] [CrossRef]
- Liu, C.; Yang, M.; Di, J.; Xing, Y.; Li, Y.; Li, J. Wearable ECG: History, Key technologies and future challenges. Chin. J. Biomed. Eng. 2019, 38, 641–652. [Google Scholar]
- Liu, C.; Oster, J.; Reinertsen, E.; Li, Q.; Zhao, L.; Nemati, S.; Clifford, G.D. A comparison of entropy approaches for AF discrimination. Physiol. Meas. 2018, 39, 74002. [Google Scholar] [CrossRef] [PubMed]
- Dilaveris, P.E.; Gialafos, J.E. P--wave dispersion: A novel predictor of paroxysmal atrial fibrillation. Ann. Noninvasive Electrocardiol. 2001, 6, 159–165. [Google Scholar] [CrossRef]
- Guidera, S.A.; Steinberg, J.S. The signal-averaged P wave duration: A rapid and noninvasive marker of risk of atrial fibrillation. J. Am. Coll. Cardiol. 1993, 21, 1645–1651. [Google Scholar] [CrossRef] [Green Version]
- Ladavich, S.; Ghoraani, B. Rate-independent detection of atrial fibrillation by statistical modeling of atrial activity. Biomed. Signal Process. Control 2015, 18, 274–281. [Google Scholar] [CrossRef]
- Colloca, R. Implementation and Testing of Atrial Fibrillation Detectors for a Mobile Phone Application. Master’s Thesis, Politecnico Di Milano, Milan, Italy, 2013. [Google Scholar]
- Tateno, K.; Glass, L. Automatic detection of atrial fibrillation using the coefficient of variation and density histograms of RR and ΔRR intervals. Med. Biol. Eng. Comput. 2001, 39, 664–671. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Lee, S.; Jeon, M. Atrial fibrillation detection by heart rate variability in Poincare plot. Biomed. Eng. Online 2009, 8, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Linker, D.T. Long-Term Monitoring for Detection of Atrial Fibrillation. U.S. Patent 7,630,756, 8 September 2009. [Google Scholar]
- Zhou, X.; Ding, H.; Ung, B.; Pickwell-MacPherson, E.; Zhang, Y. Automatic online detection of atrial fibrillation based on symbolic dynamics and Shannon entropy. Biomed. Eng. Online 2014, 13, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Alcaraz, R.; Rieta, J.J. A review on sample entropy applications for the non-invasive analysis of atrial fibrillation electrocardiograms. Biomed. Signal Process. Control 2010, 5, 1–14. [Google Scholar] [CrossRef]
- Lake, D.E.; Richman, J.S.; Griffin, M.P.; Moorman, J.R. Sample entropy analysis of neonatal heart rate variability. Am. J. Physiol.-Regul. Integr. Comp. Physiol. 2002, 283, R789–R797. [Google Scholar] [CrossRef] [Green Version]
- Lake, D.E.; Moorman, J.R. Accurate estimation of entropy in very short physiological time series: The problem of atrial fibrillation detection in implanted ventricular devices. Am. J. Physiol.-Heart Circ. Physiol. 2011, 300, H319–H325. [Google Scholar] [CrossRef]
- Liu, C.; Li, K.; Zhao, L.; Liu, F.; Zheng, D.; Liu, C.; Liu, S. Analysis of heart rate variability using fuzzy measure entropy. Comput. Biol. Med. 2013, 43, 100–108. [Google Scholar] [CrossRef]
- Omidvarnia, A.; Mesbah, M.; Pedersen, M.; Jackson, G. Range entropy: A bridge between signal complexity and self-similarity. Entropy 2018, 20, 962. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, L.; Liu, C.; Wei, S.; Shen, Q.; Zhou, F.; Li, J. A new entropy-based atrial fibrillation detection method for scanning wearable ecg recordings. Entropy 2018, 20, 904. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, L.; Wei, S.; Zhang, C.; Zhang, Y.; Jiang, X.; Liu, F.; Liu, C. Determination of sample entropy and fuzzy measure entropy parameters for distinguishing congestive heart failure from normal sinus rhythm subjects. Entropy 2015, 17, 6270–6288. [Google Scholar] [CrossRef] [Green Version]
- Pincus, S.M. Assessing serial irregularity and its implications for health. Ann. N. Y. Acad. Sci. 2001, 954, 245–267. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S.M.; Huang, W. Approximate entropy: Statistical properties and applications. Commun. Stat.-Theory Methods 1992, 21, 3061–3077. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [Green Version]
- Aktaruzzaman, M.; Sassi, R. Parametric estimation of sample entropy in heart rate variability analysis. Biomed. Signal Process. Control 2014, 14, 141–147. [Google Scholar] [CrossRef]
- Mayer, C.C.; Bachler, M.; Hörtenhuber, M.; Stocker, C.; Holzinger, A.; Wassertheurer, S. Selection of entropy-measure parameters for knowledge discovery in heart rate variability data. BMC Bioinform. 2014, 15, S2. [Google Scholar] [CrossRef] [Green Version]
- Yentes, J.M.; Hunt, N.; Schmid, K.K.; Kaipust, J.P.; McGrath, D.; Stergiou, N. The appropriate use of approximate entropy and sample entropy with short data sets. Ann. Biomed. Eng. 2013, 41, 349–365. [Google Scholar]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of surface EMG signal based on fuzzy entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef]
- Cao, P.; Ye, B.; Yang, L.; Lu, F.; Fang, L.; Cai, G.; Su, Q.; Ning, G.; Pan, Q. Preprocessing unevenly sampled RR interval signals to enhance estimation of heart rate deceleration and acceleration capacities in discriminating chronic heart failure patients from healthy controls. Comput. Math. Methods Med. 2020, 2020, 9763826. [Google Scholar] [CrossRef]
- Clifford, G.D.; Tarassenko, L. Quantifying errors in spectral estimates of HRV due to beat replacement and resampling. IEEE Trans. Biomed. Eng. 2005, 52, 630–638. [Google Scholar] [CrossRef] [Green Version]
- Kantelhardt, J.W.; Bauer, A.; Schumann, A.Y.; Barthel, P.; Schneider, R.; Malik, M.; Schmidt, G. Phase-rectified signal averaging for the detection of quasi-periodicities and the prediction of cardiovascular risk. Chaos: An Interdiscip. J. Nonlinear Sci. 2007, 17, 015112. [Google Scholar] [CrossRef]

| Variable | AF Rhythm | Non-AF Rhythm | |||
|---|---|---|---|---|---|
| N | AFL | J | Total | ||
| # rhythm episodes | 299 (48.0%) | 292 (46.9%) | 14 (2.2%) | 18 (2.9%) | 324 (52.0%) |
| Total time length (h) | 93.5 (37.5%) | 149.1 (59.8%) | 1.4 (0.6%) | 5.2 (2.1%) | 155.7 (62.5%) |
| # RR intervals | 521,415 (42.6%) | 663,202 (54.2%) | 11,710 (1.0%) | 26,818 (2.2%) | 701,730 (57.4%) |
| # RR segments | 17,247 (42.6%) | 21,968 (54.3%) | 383 (0.9%) | 886 (2.2%) | 23,237 (57.4%) |
| n | 0.0625 | 0.125 | 0.25 | 0.5 | 1 | 2 | 4 | 8 | 16 | |
|---|---|---|---|---|---|---|---|---|---|---|
| r | ||||||||||
| 0.01 | 98.15% | 98.15% | 98.15% | 98.15% | 97.87% | 88.78% | 79.81% | 76.37% | 71.06% | |
| 0.05 | 98.15% | 98.15% | 98.15% | 98.08% | 94.11% | 82.96% | 78.06% | 73.30% | 67.94% | |
| 0.10 | 98.15% | 98.15% | 98.12% | 97.28% | 90.38% | 80.86% | 76.36% | 71.39% | 66.30% | |
| 0.15 | 98.13% | 98.10% | 97.91% | 95.89% | 87.72% | 79.42% | 74.99% | 70.05% | 65.33% | |
| 0.20 | 98.06% | 97.95% | 97.40% | 94.36% | 85.72% | 78.27% | 73.91% | 69.07% | 64.74% | |
| 0.25 | 97.85% | 97.60% | 96.64% | 92.77% | 84.13% | 77.38% | 73.11% | 68.43% | 64.42% | |
| 0.30 | 97.47% | 97.07% | 95.74% | 91.22% | 82.84% | 76.71% | 72.52% | 68.03% | 64.31% | |
| 0.35 | 96.96% | 96.41% | 94.76% | 89.85% | 81.83% | 76.21% | 72.13% | 67.81% | 64.39% | |
| 0.40 | 96.35% | 95.66% | 93.66% | 88.66% | 81.06% | 75.86% | 71.88% | 67.76% | 64.57% | |
| 0.45 | 95.68% | 94.83% | 92.58% | 87.59% | 80.45% | 75.60% | 71.73% | 67.80% | 64.81% | |
| 0.50 | 94.92% | 93.93% | 91.59% | 86.63% | 79.96% | 75.41% | 71.68% | 67.89% | 65.10% | |
| 0.55 | 94.11% | 93.05% | 90.69% | 85.79% | 79.59% | 75.29% | 71.66% | 68.05% | 65.40% | |
| 0.60 | 93.31% | 92.23% | 89.85% | 85.04% | 79.26% | 75.20% | 71.68% | 68.24% | 65.73% | |
| 0.65 | 92.56% | 91.46% | 89.07% | 84.37% | 79.01% | 75.14% | 71.74% | 68.45% | 66.06% | |
| 0.70 | 91.86% | 90.77% | 88.34% | 83.80% | 78.79% | 75.10% | 71.82% | 68.65% | 66.38% | |
| 0.75 | 91.21% | 90.10% | 87.65% | 83.31% | 78.60% | 75.08% | 71.91% | 68.86% | 66.69% | |
| 0.80 | 90.59% | 89.45% | 87.03% | 82.87% | 78.44% | 75.09% | 71.99% | 69.07% | 66.99% | |
| 0.85 | 90.02% | 88.84% | 86.43% | 82.50% | 78.32% | 75.09% | 72.09% | 69.28% | 67.28% | |
| 0.90 | 89.45% | 88.27% | 85.90% | 82.14% | 78.19% | 75.10% | 72.20% | 69.48% | 67.57% | |
| 0.95 | 88.90% | 87.92% | 85.42% | 81.82% | 78.11% | 75.11% | 72.30% | 69.69% | 67.84% | |
| 0.99 | 88.49% | 87.31% | 85.06% | 81.62% | 78.03% | 75.14% | 72.39% | 69.83% | 68.05% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Li, J.; Wan, X.; Wei, S.; Liu, C. Determination of Parameters for an Entropy-Based Atrial Fibrillation Detector. Entropy 2021, 23, 1199. https://doi.org/10.3390/e23091199
Zhao L, Li J, Wan X, Wei S, Liu C. Determination of Parameters for an Entropy-Based Atrial Fibrillation Detector. Entropy. 2021; 23(9):1199. https://doi.org/10.3390/e23091199
Chicago/Turabian StyleZhao, Lina, Jianqing Li, Xiangkui Wan, Shoushui Wei, and Chengyu Liu. 2021. "Determination of Parameters for an Entropy-Based Atrial Fibrillation Detector" Entropy 23, no. 9: 1199. https://doi.org/10.3390/e23091199
APA StyleZhao, L., Li, J., Wan, X., Wei, S., & Liu, C. (2021). Determination of Parameters for an Entropy-Based Atrial Fibrillation Detector. Entropy, 23(9), 1199. https://doi.org/10.3390/e23091199






