Abstract
We study a scheme of thermal management where a three-qubit system assisted with a coherent auxiliary bath (CAB) is employed to implement heat management on a target thermal bath (TTB). We consider the CAB/TTB being ensemble of coherent/thermal two-level atoms (TLAs), and within the framework of collision model investigate the characteristics of steady heat current (also called target heat current (THC)) between the system and the TTB. It demonstrates that with the help of the quantum coherence of ancillae the magnitude and direction of heat current can be controlled only by adjusting the coupling strength of system-CAB. Meanwhile, we also show that the influences of quantum coherence of ancillae on the heat current strongly depend on the coupling strength of system—CAB, and the THC becomes positively/negatively correlated with the coherence magnitude of ancillae when the coupling strength below/over some critical value. Besides, the system with the CAB could serve as a multifunctional device integrating the thermal functions of heat amplifier, suppressor, switcher and refrigerator, while with thermal auxiliary bath it can only work as a thermal suppressor. Our work provides a new perspective for the design of multifunctional thermal device utilizing the resource of quantum coherence from the CAB.
1. Introduction
Quantum thermodynamics mainly studies thermodynamic behaviors emerging in systems that are quantum in nature [1,2,3,4]. Compared with the classical systems dominated by the standard laws of thermodynamics, some novel phenomena can emerge in the quantum systems due to the presence of quantum properties, e.g., quantum coherence [5,6,7,8,9], or entanglement [10,11,12]. For example, the efficiency beyond the Carnot cycle [13], the reversion of heat flowing from the hot system to the colder one [14]. These non-intuitive physical behaviors have become an apparent challenge to the standard laws of thermodynamics [15,16]. The rapid progress of quantum technologies has allowed us to characterize the quantum machine [17,18,19,20] and experimentally realized them in various quantum systems [21,22,23,24,25,26,27,28,29,30]. With the aid of these controllable quantum platforms (systems), some studies focus on the redefinitions of some concepts, such as work and heat [31,32,33,34], and the verification and modification of thermodynamics second law [35] in quantum domain. Others concentrate on heat control/management [36,37,38,39,40,41,42,43] in order to design the quantum thermodynamic process (or quantum thermal machines) that can implement a certain task (or multi-task) using thermal resources [44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59].
Analog to electronic devices of diode and transistors perfectly regulating the electricity in circuit, it is interesting to investigate whether the heat transferring in the quantum system can also be regulated well like the electric current. Some previous studies have been devoted to thermal rectification [60,61,62]. Currently, the quantum thermal transistor [39] to implement heat amplification, and various quantum control devices of heat current with a specific function have been proposed, such as quantum thermal diodes [47,63], quantum heat switch [64], transistors [48,49], thermometers [50,51,52,53], thermal valves [54] and many-body quantum thermal rectification [65]. Most currently, to design a multifunctional quantum thermal device [20,55,56,57,58,59,66], i.e., integrating the multiple functions into a single device, has become an interesting and active subject. Based on some simple quantum systems, such as a qutrit [58], two coupled qubits [66] and three qubits [39,59] the multifunctional devices have been designed, and under the suitable selections of system’s structure and dynamic parameters these thermal devices can implement two or more functions of amplifier, modulator, switcher, valve, stabilizer, and rectifier. These studies further enrich the applications of quantum small systems. However, it is noted that the multifunctional devices designed in previous investigations have a similar structure of electronic-like transistor where three independent thermal baths with different temperatures are connected to the quantum device, and many dynamic parameters are usually involved to carry out the thermal control of a certain function. In addition, the quantum effects influencing the dynamics of thermal system, such as quantum coherence or entanglement completely come from the system itself due to the coherent interactions among subsystems [20,67]. Therefore, of particular interest to us is whether a quantum device can operate as a multifunctional thermal machine with two baths, and execute the flexible switching among multiple functions by fewer controllable parameters or even a single one. Besides, although plenty of studies have contributed to the roles of quantum coherence in work extraction [68,69], heat to work conversion [70,71], thermal transfer [72] and information scrambling, [73] etc. The effects of quantum coherence outside the system on heat management (or design for a multifunctional thermal device) have not been addressed.
Motivated by the quests above, we, in this paper, design a thermal management scheme where a three-qubit system assisted with a coherent auxiliary bath (CAB) can work as a multifunctional thermal device to implement the heat management on a given thermal bath called target thermal bath (TTB), i.e., to control the magnitude and the direction of heat current flowing into/out of the TTB. We, in the framework of collision model (or repeated interaction model), will investigate the behaviors of steady heat current between the system and the TTB (also named target heat current—THC, hereafter) and thermal functions of the system with a CAB. Here, it is pointed out that the collision model has become a convenient and powerful tool for studying the dynamics of open quantum system [74], especially for the situations of non-equilibrium bath with quantum effects [75,76,77]. Thus, so far, the general thermodynamic framework of collision models has been explored deeply and established [35,78,79,80]. Especially, the multipartite collision models protocol [79,81] might provide a promising way in the design of low-dimensional solid-state thermal management devices. Here, it is an interesting question to integrating the multiple functions into a multipartite device to perform the heat management with the help of quantum effects from nonequilibrium bath. In this work, within the framework of collision models we construct a scheme of thermal management of a three-qubit associated with a nonequilibrium CAB. We want to investigate whether the heat current can be controlled effectively with the help of the CAB connected to one side of system. The results show that the quantum coherence in ancillary bath indeed serves as a resource utilized to control the THC for the amplification, suppression or even reverse of THC. Meanwhile, we find that the effects of quantum coherence including the coherence magnitude and relative phase of ancillae strongly depend on the coupling strength of system—CAB (or system-ancillae). Specifically, the coherence of CAB, for a certain value of coupling strength of system—CAB, seems to be frozen to the THC, i.e., quantum coherence almost has no effects on the THC at the critical value. For the coupling strength below/over the critical value the THC increases/decreases monotonically as the coherence magnitude of ancillae increases. Thus, whether the coherence is positive, negative, or not correlated with the THC strongly depends on the coupling strength of system—CAB. Especially, the reversal-THC, in some parametric regime of the coherence of ancillae and the coupling strength of system-CAB, could appear which is impossible for the auxiliary bath being thermal bath without coherence. Therefore, with the aid of CAB the three-qubit system can serve as a multifunctional thermal device integrating the functions of heat amplifier, suppressor, switcher and refrigerator. Of particular interest, the multiple functions can be switched only by adjusting a single controllable coupling strength of system—CAB.
The remainder of this paper is arranged as follows: In Section 2, we introduce the scheme of heat modulation of three-qubit system as a quantum thermal device and its dynamics. In Section 3, we mainly focus on the effects of ancilla’s coherence (including the relative phase and coherence magnitude) of CAB and coupling strength of system-CAB on the THC, and analyze the thermal functions of system with CAB in different parameter regions. We compare the characteristics of THC in CAB with that in thermal auxiliary bath, and demonstrate the role of coherence of CAB as a resource in thermal modulation. In addition, the effects of temperature on the THC are also discussed. We conclude the whole work in Section 4.
2. Model
We design a scheme of heat modulation on a TTB via a tripartite system as quantum machine assisted with an auxiliary bath as shown in Figure 1. In our model, the system is composed of three qubits () with the frequencies . The CAB (TTB) consists of a series of identical and independent two-level atoms (TLAs) () with transition frequency () and density matrix (). We assume that the ancillae of left auxiliary bath and the thermal TLAs of right TTB synchronously pass through the left box and the right box one by one, respectively, and two processes denoted as (interaction process among three subsystems) and (interaction process between the system and the baths) are implemented alternatively with equal time interval . Here, the boxes simulate triggers to control which interaction channels are on/off in the dynamics of system. Specifically, before the atoms reach the boxes, i.e., in process, there are only interactions among the three qubits (). Further, when the atoms entering the boxes, i.e., in process, the interaction channels in are off, and the subsystems () couples to the ancillae (thermal TLA) in the left (right) box. The energy exchange among the CAB, system and TTB occurs in this process. After the repeated implementations of and processes, a steady heat current between the system and the TTB can be established. With the aid of this model, the influences of coherence of CAB on THC and the thermal functions of system assisted with CAB can be exploited at length.
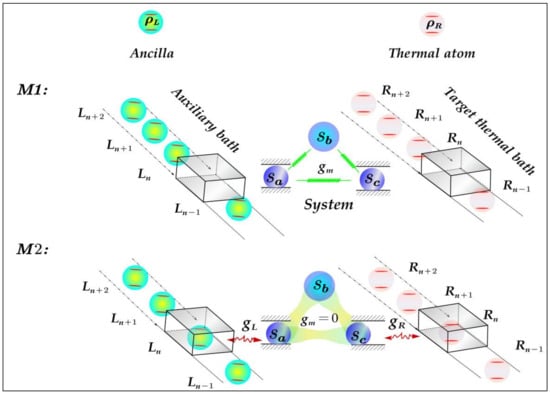
Figure 1.
Schematic of heat modulation on the target thermal bath (TTB). The internal interaction of tripartite system ( ) is first implemented in process; then the subsystems and are coupled to the th ancilla (prepared in ) in coherent auxiliary bath (CAB) and the th thermal atom (prepared in ) in TTB, respectively, in process. After that, the two steps of and are implemented repeatedly, and ancilla (thermal atom) in CAB (TTB) interacting with () are refreshed by the next one in each round. Thus, the steady heat current between the system and TTB, after many rounds, is established.
Next, we focus on the specific dynamics of system in a single round (i.e., to implement the and process once). Here, we denote , ( and ) as the free Hamiltonians of ancillae in CAB and thermal TLAs in TTB and subsystems , and , respectively, where and are independently the transition frequencies and Pauli matrices of the TLAs with subscript , and () describing a TLA in the excited (ground) state. The free Hamilton of system is denoted as . In process, the interaction Hamilton of system is given as:
with is the coupling constant among three subsystems. and ( () being the raising (lowering) operator) representing the off-resonant and the resonant terms, respectively. Here, the XXX-type Hamiltonian as a more likely candidate of three-qubit physical Hamiltonian [82] has been exploited widely in spin system [82,83,84,85], and can be implemented experimentally [59]. Further, its dynamics effectively reduces to that of the resonant coupling on phenomenological grounds [86,87] when the frequencies are resonant and the coupling is weak i.e., the rotating wave approximation applies (the off-resonant term in the interaction Hamiltonian (1) can be omitted). In this paper, we also consider that the condition of resonant frequencies is satisfied. According to the scheme in Figure 1, the dynamics of the system in process for is given as:
where the mapping describes the unitary evolution of system, and the unitary operator is with being the total Hamilton of system. () represents the state of system before (after) the ()th ancilla reaches (leaves) the box, that is, the state of beginning (ending) of system’s internal interaction at time (). One can identify that the free Hamilton of does not commute with the unitary operator for the finite coupling , i.e., which implies that the energy of system is non-preserving in this process due to the off-resonant term introduced. Here, the off-resonant term characterizes the external driven on the system by an external agent (or work source). Any energy changes of system in process are solely due to energy leaving or entering the work external agent. In the process for with (i.e., at the time interval of the th ancillae (TLA in TTB) kept in the left (right) box), the interaction channel in process is switched-off, and the subsystems and are coupled to the ancillae in left box and the thermal TLA in right box, respectively. The interactions are expressed as:
where () and () represent the interaction Hamilton and the coupling constant of - ancillae in the left box (-TLA in the right box), respectively. The dynamics of system and TTB are unitary and can be described as:
where () denotes the state of the system (th thermal TLA of TTB) at time (i.e., the moment of the th thermal TLA in TTB just leaving the right box) the mapping corresponds to a Markov process and with:
Here, it is noted that as usually treated in most works of collision models [35,65,70,71,72,73] we have considered that the state of system after its interaction with two baths is embodied by the stroboscopic map. That ensures the system is being always independent to the particle units (ancillae/thermal-TLAs in CAB/TTB) that have collided, and the dynamics of system a memoryless Markov process. Physically, the collision model protocol is consistent with the inspiration from Boltzmann’s original Stosszahlansatz. For instance, a particle in Brownian motion interacts with only a few water molecules at a time. Moreover, this interaction lasts for an extremely short time, after that the molecule moves on, and never to return [88]. Since the environment is large, the decoherence and dissipation ensure that the next molecule to arrive will be completely uncorrelated from the previous one, so the process repeats anew [35]. The same scenario is also suitable for the multipartite collision models [79,81], and addressing the thermodynamics of engineered reservoirs [37,89,90,91]. In terms 89 of the exchange interaction of given in Equation (3) one can identify that the commutation relation with and holds, which indicates that the total energy of whole system (system plus CAB and TTB) is preserved in this process. Here, it is mentioned that the unitary evolution in Equation (5) above corresponds to a swap gate operation, and we can rewrite it as:
where is the dimensionless coupling strength of system-ancillae in auxiliary bath (system-TLAs in TTB), is the identity operator, and is the two-TLAs swap operator, having for all . Therefore, from Equation (6), the swap strength between two particles is determined by varying with at the period . Further, when the swap strength is zero conrresponding to the weakest swap strength, and for it becomes one characterizing the strongest swap strength (complete swap) between the system and the ancillae in CAB (thermal atoms in TTB). It also means that the energy exchange between the system and the baths (CAB and TTB) will be periodical with the same period as that of swap strength. In our model, only the heat exchange between the system and the TTB occurs in the process due to the energy-persevering evolution. In the same spirit as the definition of heat (or heat flow) in [35,61,78,92,93], the amount of heat exchange between the system and the TTB can be quantified by the energy change of thermal TLAs of TTB in each round. In the arbitrary -th round the amount of heat flowing to TTB reads:
where () is the state of the -th thermal TLA in TTB at the beginning (end) of the subsystem in process. Here, () represents that the system pumps heat into the TTB (the TTB delivers heat to the system). It is pointed out that the state of the -th thermal TLA is initially a thermal state and, the state, after the mapping , remains in a diagonal distribution in the eigenbasis of in our model (i.e., both of them are the mixed states with no coherence), and the energy spectrum of is kept unchanged in the process: . Based on the heat exchange in Equation (7) between the system and the TTB, the average heat current can be defined as:
The positive (negative) current () in Equation (8) indicates the heat flowing into (out of) the TTB, which also means that the system works as a heat pump () (refrigerator ()) to heat (refrigerate) the TTB. In a long-time limit, the steady THC denoted as can be established:
It is well known that when a finite system contacts with an infinite heat/nonequilibrium bath it will relax to (or be thermalized into) a steady state as the time increases, and a dynamical equilibrium can be established among the system and the baths, i.e., the steady heat current emerged. This mechanism is also suitable for our collision model. Specifically, the interaction between the three-qubit system and the two baths in each round is used to mimic the thermal contact process in the conventional model, and the state of system, after each round, can be updated once including the populations and quantum correlation/coherence among qubits. As the collision time increases the system’s state is modified by the baths less and less gradually, and the system, after many rounds, will reach a steady state associated with the steady heat current. In the following subsections, we are mainly concerned about the behaviors of THC and the thermal functions of the system with a thermal/coherent auxiliary bath. For the sake of brevity, the THC mentioned in the following subsections refers to the steady THC.
3. Modulation of Heat Current via Auxiliary Bath
3.1. Initial States of System and Baths
We consider that the CAB, system and TTB are initially uncorrelated, and the initial state of the whole composite system (system plus CAB and TTB) is:
Here is the initial state of system being a thermal product state of three subsystems given as:
where is the partition function with the inverse temperature (set Boltzmann constant ). In Equation (10), represent the initial states of CAB () and TTB () where each bath of CAB and TTB is composed of identical units. Further, the initial state of each thermal TLA in TTB and for the ancillae in CAB are independently given by:
and
where with being the relative phase and with (); () is a weight parameter determining the proportion of two components, thermal state and pure coherent state , in the state . Here, it is noticed that the parameter only appears in the non-diagonal elements of , and the diagonal elements of are the same with the ones of thermal state . According to the coherence measure of -norm, for an arbitrary state the coherence reads [5]
with () the non-diagonal elements of . One can identify that for the state given in Equation (13) the -measure of coherence is proportional to . That is, when fixing the population () of in the energy basis of the coherence of state increases as α increases, and for () the state reduces to a complete mixture state without coherence (pure state with the maximum of coherence in the range of , i.e., ). Thus, the weight can be regarded as an indicator to measure the coherence magnitude of . For simplicity, we, in the next subsections, will take - indicator instead of to measure the coherence magnitude of ancillae of CAB.
3.2. Thermal Modulation with Thermal Auxiliary Bath
First, we consider that the auxiliary bath is a thermal bath without coherence, i.e., each ancilla is in a thermal state, and the situation for CAB is provided in the latter subsections. Here, we focus on the modulation of heat current by the dimensionless coupling strength () between the system and the ancilla with state ( given in Equation (13)) being a thermal state. For simplicity, we set the ancillae of auxiliary bath, subsystems and , and the thermal TLAs of the TTB with the same transition frequencies, and , and the Planck constant , throughout the paper. Though some simplified treatments of parameters have been done in our model it is still hard to get the exact analytical solution of THC given in Equation (9) due to the high dimensions of system. Thus, we will investigate the features of THC numerically below when the auxiliary bath is introduced. By numerical calculations, we find that the THC behaves as a cosine-like periodical function of with the fixed period , and can be fitted with the form:
where the parameters , and have a complex relationship with , , and ( representing the coupling strength among three subsystems).
According to Equation (9) we, in Figure 2, plot the variation of THC with the coupling strength , when fixing the other parameters: , , , and (see the red dotted curve). Further, the blue dotted line corresponds to the fitting function with , and . We can see that numerical results (red curve) of the heat current is basically matched with that of the fitting function (blue curve), i.e., . Thus, the THC can be modulated in cosine-like form of and satisfied as for being zero or positive integer. The maximum (minimum) of THC is () with () corresponding to the minimum (maximum) strength of populations (or energy) exchange between the ancilla and the subsystem via the swap operation given in Equation (6). Physically, the nonzero steady heat current also implies that nonequilibrium steady state of system is reached. For simplicity, to denote the increment of system’s energy as injected by the external work source into system in step of each round, the energy increment of system always equals to the sum of increasing amount of two baths’ energy, (the subscript and represent the left auxiliary bath and the right TTB, respectively), in step, i.e., implying no net energy accumulation in the nonequilibrium steady state dynamics. The stronger the swap strength of system-ancilla (i.e., increasing or decreasing in the range of or , ) is, the larger the energy captured by the auxiliary from the system becomes, and that results in the smaller implying smaller THC , vice versa. Therefore, the variety of the THC in Figure 2 with the coupling strength has an opposite trend with that of swap strength, with fixed period . In addition, we can see that for a finite , , the THC with and . In order to observe how the auxiliary bath influence the THC in our model, it might be appropriate take the value of THC for no interaction (i.e., ) of system-ancilla as a reference THC denoted as , with . Using it, the amplification/suppression of THC can be described intuitively, that is and respectively correspond to the heat amplification and suppression. Here, the refrigeration is indicated by the reversal current . Thus, Figure 2 shows that the quantum machine with the thermal auxiliary bath can only serve as a heat suppressor due to the THC being suppressed for a finite , and zero-current or reversal-current cannot emerge, that is, . Meanwhile, by changing the coupling strength the thermal suppressor can modulate THC in the form of cosine-like function in the range of .
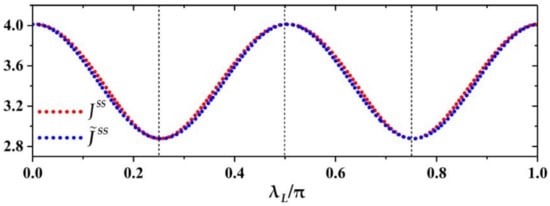
Figure 2.
The heat current as a function of the coupling strength , , in terms of Equation (9) (red dotted curve) and the corresponding curve of fitting function given in Equation (15) with , and (blue dotted curve). The other parameters are chosen as: , , , and .
Here, in order to conveniently describe the capability of quantum machine to modulate the THC by adjusting the controllable coupling strength, we define modulation width of the quantum machine on THC as the difference of the maximum and the minimum of THC, i.e.,
with . As for a thermal control device, one usually expects that it could control the THC varying over a wide range as much as possible. That is, the larger the modulation width of THC is, the better the performance of quantum machine is. In terms of characteristics of THC given in Equation (15), the system with the thermal auxiliary bath can only work as a thermal suppressor with the modulation width .
3.3. Thermal Modulation with CAB
We, in this subsection, mainly focus on the behaviors of THC and the thermal functions of quantum machine assisted with a CAB.
3.3.1. Effects of Relative Phase on THC
Next, we study the effects of the relative phase and the coupling strength of ancillae on the THC numerically for a fixed magnitude of coherence below. From numerical calculations we find that when the thermal auxiliary bath is replaced by the CAB the THC is a periodical function of and , i.e., with and as shown in Figure 3, where each ancilla of CAB is prepared in the same state, given in Equation (13) with the maximum magnitude of coherence . It is noted that the periods and are independent of the other parameters in our model. In order to demonstrate the characteristics of and the thermal functions of quantum machine clearly, the variation of in a single period with and is shown in Figure 4 where all the other parameters are the same as that given in Figure 3. In Figure 4a the multifunctional regions of quantum machine have been shown, and Figure 4b for the corresponding variations of for some fixed , . From Figure 4a it can be seen that the quantum machine could work as a multifunctional thermal device, and the specific function relies on the values of parameters and . Specifically, in terms of the features of in Figure 4a, the whole parametric space of and is divided into several different function regions: switcher region (SR) (the white dotted line for ), refrigeration region (RR) (the region surrounded by the white dotted line for ), heat pump invariable region (HPIR) (the purple dotted line for ), heat pump suppression region (HPSR) (the middle region between the white and purple dotted lines for ) and heat pump amplification region (HPAR) (the left-side region of purple line for ).
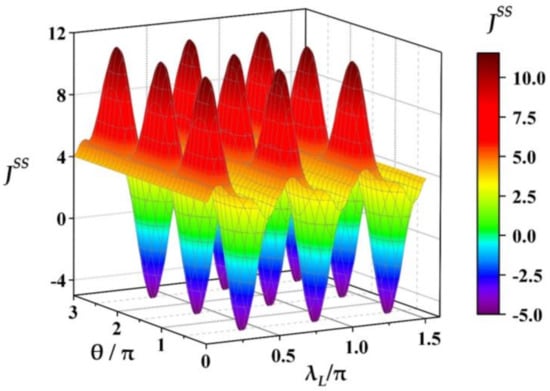
Figure 3.
The THC as a periodical function of and with and . The other parameters are set as: , , , , and .
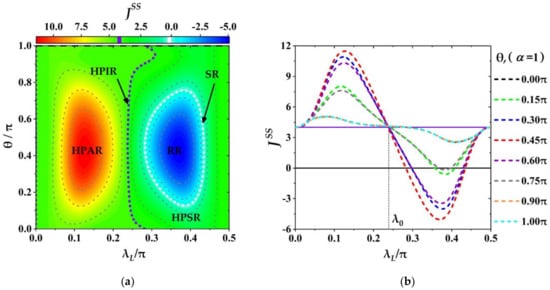
Figure 4.
The variations of THC as and . (a) The phase diagram of the quantum machine working as a multifunctional device in the parametric regimes of and : RR, SR, HPSR, HPIR and HPAR; (b) the variations of with for some fixed relative phases . The other parameters are the same as the ones in Figure 3. The purple (white) dotted line in (a) represents working points with () also corresponding to the purple (black) solid line in (b).
In addition, Figure 4a also demonstrates several obvious features. First, each functional region of HPAR, HPIR, HPSR, SR and RR distributes in a certain continuous parametric space of and . Second, for the convenient descriptions of different functional regions we denote as the coupling strength of HPIR (the purple dotted line at the middle region in Figure 4a), satisfying (note that does not mean the redefinition of the reference current , and only indicates the values of THC at some certain working points on the purple dotted line are the same as reference current as defined before). One can see that the HPAR only lies in the region of below , (i.e., the region of ), and other function regions of HPSR, SR and RR for over , (i.e., the region of ). Further, the SR and RR appear in the middle region of parametric space: and , and the reminder part for the HPSR. Third, for the relative phase taken in RR the quantum machine could perform the different thermal functions in turn: thermal amplifierstabilizationsuppressorswitcherrefrigeratorsuppressor as increases from zero to the maximum in a period.
From Figure 4b, one can see some specific behaviors of varying with and . Firstly, for a finite relative phase the THC always behaves as a sine-like function with respect to . That is, the THC first increases from the initial value to the maximum then decreases to the minimum below , and monotonically returns to its initial value again. Secondly, for the coupling strength being about denoted as the values of with different approach to the same value of , i.e., which means that for the critical coupling strength the THC is almost independent of the relative phase. Thirdly, in the region of (HPAR) and fixing the closer the relative phase is about to denoted as , the larger the THC becomes (except for the larger such as where the three curves of are basically overlap, i.e., the less influence the larger relative phases have), but for the region of the opposite is true (where decreases as closes to , and it can be less than or equal to zero seen the segments below the black solid line with ).
Based on the numerical simulations above, we show that the relative phase of ancillae is related to the THC and could be regarded as a useful resource to modulate the THC well. Meanwhile, at the suitable relative phase of ancillae the quantum machine can integrate multiple functions, such as thermal amplifier, stabilizer, suppressor, switcher and refrigerator, and these functions can be switched only by adjusting the coupling of system-CAB.
3.3.2. Effects of Coherence Magnitude on THC
Next, we mainly concern the influences of coherence magnitude on the THC for a fixed relative phase (here, corresponds to the largest modulation width of (seen in Figure 4a or Figure 4b), i.e., with , where has been given in Equation(16)).
In Figure 5a, we show the different function regions in the parametric space of and , including: SR (the white dotted line for ), HPIR (the purple dotted line for ), HPAR (the left part of the purple dotted line for ), HPSR (the middle regime between the purple and the white dotted lines for ) and RR (the space surrounded by the white dotted line for ). From Figure 5a it can be seen that for small coherence magnitude (about ) the HPAR with becomes very narrow (i.e., for the coupling strength in HPIR is also small), and the rest region of is for the HPSR with . It means that for the small α the quantum machine could serve as a thermal amplifier in the regime of , and the thermal suppressor in the regime of . However, as increases the domain of HPAR/HPSR enlarges/shrinks rapidly, and when is beyond a certain value (about with seen the Figure 5b, the SR and RR can appear in the regime , and both of SR and RR enlarge as increases.
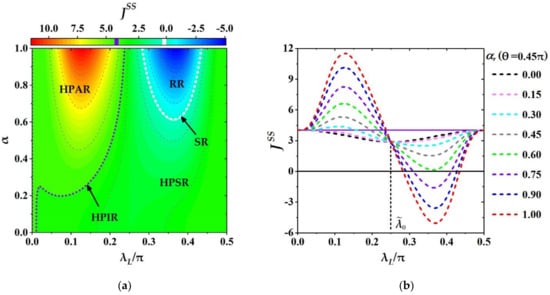
Figure 5.
The variation of with and . (a) The phase diagram of the quantum machine behaving as a multifunctional device in parameter space: and ; (b) the THC as function of for some selected . The other parameters are chosen by , , , and .
To demonstrate the dependence of on and clearly, we, in Figure 5b, plot the variations of with respect to for some selected , . Further, some specific features of have been shown in Figure 5b. Firstly, for a fixed the THC always rises at first, then falls down, and rises up its initial value again. Meanwhile, the modulation width of the THC becomes larger with the increase of . Secondly, we notice that for with , the THCs with different have the same value as the one for thermal auxiliary bath (), i.e., with , which means that at the critical coupling the effects of coherence on THC can be frozen, i.e., the THC is independent of the coherence magnitude of ancillae. For the THC can be amplified by the coherence of CAB, i.e., (seen for all the lines of with different non-zero are above the black solid line with ), and for a fixed the THC always increases monotonously with the increasing of coherence magnitude , which implies that the THC is positively correlated with the coherence magnitude of ancillae. However, for the situation is opposite where the THC is suppressed, (seen all the lines with different are below the one with for ), and the value of with fixed decreases monotonously with increasing , which demonstrates that the THC is negatively correlated with the coherence magnitude of ancillae in the regime of . Especially, for the ancillae with strong coherence () the zero- or reversal-current, , can appear (each curve of with different , (), has one segment below the black solid line with ) which means that for the CAB with strong coherence the quantum machine can also serve as a switcher or a refrigerator.
Based on the analysis above, one can find that the THC is related to not only the coupling of system-ancillae but also the coherence magnitude of ancillae. Meanwhile, the influences of coherence magnitude of ancillae on the THC, such as amplification, suppression and reverse of THC, strongly depend on the coupling strength of system-ancillae. This can be understood that when thermal auxiliary bath is replaced with the CAB the system will reach a new steady state associated with the ancilla’s coherence magnitude and relative phase. Based on some previous researches on the thermalization problem including the thermalization of the TLA/micro-cavity as system by a coherent TLAs/three-level atoms (or atomic-pairs) bath (seen in [94,95,96]) it is known that except for the population of bath units (the coherent TLAs/three-level atoms (or atomic-pairs)) the coherence in bath units and the coupling strength between the system and the units have a nonlinear effect on the coherence and the population of system, and the respective contributions of the coherence (coherence magnitude and relative phase) and the coupling strength to the population of system at steady state cannot be separated though the coherence and the coupling strength are independent parameters. Meanwhile, compared with the thermal bath without coherence the excite populations of system at steady state cannot only increase but also decrease which is determined by the parameters of coherence and coupling strength together. This might be why the THC can exhibit rich behaviours when the TTB is introduced. Thus, based on the characteristics of THC one can see that for a prepared CAB the THC can be modulated well by adjusting the controllable coupling of system-ancilla. Especially, for the ancillae with strong coherence (large ) the THC can go through all the regions: HPAR, HPIR, HPSR, SR and RR orderly only by increasing the coupling strength from zero to .
3.3.3. Maximum and Minimum of THC and Modulation Width
We have shown the characteristics of THC and the thermal functions of quantum machine at fixing coherence magnitude (or relative phase ) before. It demonstrates that quantum machine could behave the different functions in different parametric space of , and . Now, we observe which thermal functions the machine can perform when the coherence parameters, and ( and ), of ancillae are arbitrary.
Due to the continuous variation of THC with the parameters , and , the thermal functions of quantum machine are determined by the maximum and the minimum of THC, i.e., to judge which functional regions of HPAR, HPIR, HPSR, SR and RR are covered in the range of ~. Therefore, we plot the maximum and the minimum of THCs, and , in Figure 6a and the corresponding modulation width of THC, , in Figure 6b in the full parametric space of , and with , and . The lower and upper colorful surfaces in Figure 6a correspond to the variations of and , respectively, and the sliver gray ellipsoid-like surface for the working points of switcher with . It is noticed that the values of are characterized by the colors on surfaces not the height of the surfaces (the height of surface is for the vertical axis ). From Figure 6a, several features of and have been shown. Firstly, it can be seen that the surface of is always above the one of which indicates that for the fixed coherence parameters of (, ) the maximum of THC corresponds to the small being about , and the minimum of THC for the large with . Secondly, and behave as the positive and the negative correlated to the coherence magnitude α, respectively, i.e., the value of () increases (decreases) as increases, which implies that the modulation width, , of THC is an increasing function of as shown in Figure 6b. Thirdly, the maximum (minimum) values of THC are always larger (smaller) than the reference THC, i.e., () with . Therefore, always remains in HPAR, and could distribute into three regions: HPSR (), RR () corresponding the parts outside and inside the gray ellipsoid-like surface, and SR (). In addition, from Figure 6b one can see that the larger of the coherence magnitude and the closer to relative phase is to , the wider the modulation width of THC becomes, and the better the performance of quantum machine is.
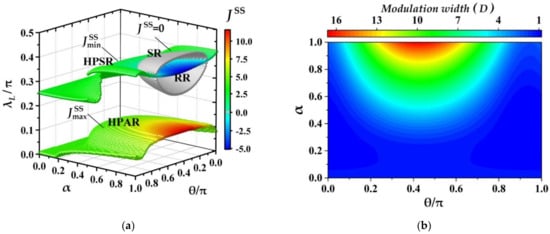
Figure 6.
(a) The maximum and the minimum of THC, and , and function regions of quantum machine; (b) the modulation width of THC, , in in the full parametric space: , and . The other parameters are set as , , , and .
With respect to the characteristics of above, one can infer that the quantum machine assisted with CAB can always work as a heat amplifier or a suppressor by tuning the coupling strength , , due to both regions of HPAR and HPSR being covered in the full parametric space, (, ), of coherence. Meanwhile, for some regimes of (, ) with (or ) the quantum machine can also work as a switcher (a switcher or a refrigerator) due to the SR (or RR) being involved. Especially, in full coherent parametric space of and the maximum (minimum) of () exists at and , i.e., () which also corresponds to the largest modulation width of THC (seen Figure 6b). Thus, the CAB consisting of the ancillae with and can be regarded as the optimal CAB, in which the quantum machine not only integrates all thermal functions as a heat amplifier, suppressor, switcher and refrigerator, but also could perform the strongest capabilities in heat amplification and refrigeration.
3.3.4. Effect of Temperature on THC
From numerical simulation we investigate the effects of temperature on THC. We, in Figure 7, plot the variation of target heat current (THC) with the temperature of TTB, , and the coupling strength, , for fixed . Further, Figure 7a,b respectively depict the behaviors of THC for the auxiliary being the CAB and the thermal auxiliary bath. From Figure 7a one can see that two obvious features of THC have been shown. First, for the fixed the THC always decreases as the temperature increases, and approaches to the steady value for the high enough . Second, for different features of the THC varying with are similar. However, for different the THC can exhibit different behaviors as increases. For example, in the range of the THC always decreases from a relative large positive value to zero, and then increases in the opposite direction. This means that the quantum machine in this coupling region can perform a heat pump ( region outside the white curve), switching ( the working points on the white curve) or refrigerator ( region inside the white curve) which depends on the temperature of TTB. It is noted that for the coupling strength about and the heat always flow into the TTB no matter is higher or lower than . Thus, the machine assisted with the coherent auxiliary bath can also exhibit thermal-diode-like action in the certain parametric regimes. Further, the amplification (refrigeration) of the machine with CAB can be enhanced in the heating (cooling) region with (the left side of black solid line) ( (the right side of black solid line)). That is, the different temperatures could boost the performance of the machine in the certain region of .
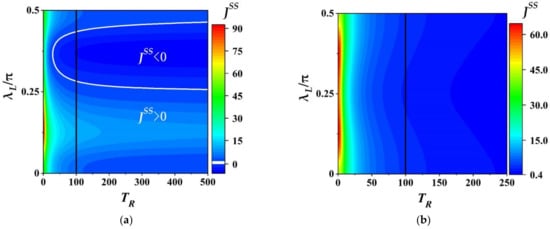
Figure 7.
The heat current as a function of the temperature of TTB and the coupling strength with for the CAB with and in (a), and the thermal auxiliary bath in (b). Here, the white solid line in (a) represents working points with , and the black solid line in (a,b) indicate the position with equal temperatures . The other parameters: , , , and .
Compared with the situation of CAB for the thermal auxiliary bath shown in Figure 7b, though the THC also decreases as the temperature it cannot be less than or equal to zero in whole parametric space of and , which implies that the device assisted with the thermal auxiliary bath cannot work as a thermal switch or refrigerator.
4. Conclusions
In summary, we have proposed a scheme of heat modulation via a three-partite system assisted with a CAB to control the magnitude and the direction of heat current between the system and the TTB. We have analyzed the influences of quantum coherence of ancillae, the coupling strength of system-ancillae and the temperature of two baths on the THC at length. It is shown that for the thermal auxiliary without coherence, the THC behaves as a cosine-like variation with the coupling strength of system-ancillae and a suitable fitting function has been given. Meanwhile, under the thermal auxiliary bath, no matter the high or the low temperature of TTB the heat always flows into the TTB implying the device assisted with the thermal auxiliary bath only working as a heat pump. However, replacing the thermal auxiliary bath with the CAB, due to the influence of coherence (including the coherence magnitude of and the relative phase) of ancillae the THC, in certain parametric regimes of coherence and the coupling of system-ancillae, could exhibit rich behaviors, such as heat amplification, heat suppression, zero- and reversal-current. Therefore, the three-partite system assisted with the CAB could serve as a multifunctional thermal device integrating with heat amplifier, suppressor, switcher and refrigerator. Via the analysis of the maximum and the minimum THC in full coherence parametric space of coherence magnitude and relative phase, the optimal CAB can be suggested, in which the modulation width of THC is largest, and the machine could perform the strongest capabilities in heat amplification and refrigeration. Besides, it has been demonstrated that the different thermal functions can be switched flexibly only by adjusting the coupling strength of system-ancillae, which is convenient for practical application.
Our research might shed some light on the role of resource of quantum coherence outside the system, could boost the deep understanding of thermodynamic properties of quantum coherence, and provide a new perspective for the design of multifunctional thermal management device with the aid of a non-equilibrium auxiliary bath.
Author Contributions
Conceptualization, W.-L.Y., T.L., and H.L.; methodology, H.L.; validation, W.-L.Y., T.L. and H.L.; formal Analysis, Y.Z., H.L., J.Z. and Y.-D.W.; investigation, H.L., and J.Z.; writing—original draft preparation, W.-L.Y., T.L., and H.L.; writing—review and editing, W.-L.Y., T.L., H.L., Y.Z., J.Z., Y.-D.W.; supervision, H.L. and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is financially supported by the National Natural Science Foundation of China, Grant Number 11775019; the National Key R&D Program of China, Grant Number 2017YFA0304503; the Peng Huanwu Theoretical Physics Renovation Center, Grant Number 12047503, and the Shandong Provincial Science and Technology Support Program of Youth Innovation Team in Colleges, Grant Numbers 2019KJN041 and 2020KJN005.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brandner, K.; Seifert, U. Periodic thermodynamics of open quantum systems. Phys. Rev. E 2016, 93, 062134. [Google Scholar] [CrossRef]
- Brandão, F.; Horodecki, M.; Ng, N.; Oppenheim, J.; Wehner, S. The second laws of quantum thermodynamics. Proc. Natl. Acad. Sci. USA 2015, 112, 3275–3279. [Google Scholar] [CrossRef]
- Kosloff, R. Quantum Thermodynamics: A Dynamical Viewpoint. Entropy 2013, 15, 2100–2128. [Google Scholar] [CrossRef]
- Millen, J.; Xuereb, A. Perspective on quantum thermodynamics. New J. Phys. 2016, 18, 011002. [Google Scholar] [CrossRef]
- Winter, A.; Yang, D. Operational Resource Theory of Coherence. Phys. Rev. Lett. 2016, 116, 120404. [Google Scholar] [CrossRef] [PubMed]
- Streltsov, A.; Adesso, G.; Plenio, M.B. Colloquium: Quantum coherence as a resource. Rev. Mod. Phys. 2017, 89, 041003. [Google Scholar] [CrossRef]
- De Vicente, J.I.; Streltsov, A. Genuine quantum coherence. J. Phys. A Math. Theor. 2017, 50, 045301. [Google Scholar] [CrossRef]
- Lostaglio, M.; Korzekwa, K.; Jennings, D.; Rudolph, T. Quantum Coherence, Time-Translation Symmetry, and Thermodynamics. Phys. Rev. X 2015, 5, 021001. [Google Scholar] [CrossRef]
- Misra, A.; Singh, U.; Bhattacharya, S.; Pati, A.K. Energy cost of creating quantum coherence. Phys. Rev. A 2016, 93, 052335. [Google Scholar] [CrossRef]
- Manzano, G.; Plastina, F.; Zambrini, R. Optimal Work Extraction and Thermodynamics of Quantum Measurements and Correlations. Phys. Rev. Lett. 2018, 121, 120602. [Google Scholar] [CrossRef]
- Vedral, V.; Plenio, M.B.; Rippin, M.A.; Knight, P.L. Quantifying Entanglement. Phys. Rev. Lett. 1997, 78, 2275. [Google Scholar] [CrossRef]
- Bruß, D. Characterizing entanglement. J. Math. Phys. 2002, 43, 4237. [Google Scholar] [CrossRef]
- Roßnagel, J.; Abah, O.; Schmidt-Kaler, F.; Singer, K.; Lutz, E. Nanoscale Heat Engine Beyond the Carnot Limit. Phys. Rev. Lett. 2014, 112, 030602. [Google Scholar] [CrossRef] [PubMed]
- Levy, A.; Kosloff, R. The local approach to quantum transport may violate the second law of thermodynamics. EPL 2014, 107, 20004. [Google Scholar] [CrossRef]
- Evans, D.J.; Cohen, E.G.D.; Morriss, G.P. Probability of Second Law Violations in Shearing Steady States. Phys. Rev. Lett. 1993, 71, 2401. [Google Scholar] [CrossRef]
- Ćwikliński, P.; Studziński, M.; Horodecki, M.; Oppenheim, J. Limitations on the Evolution of Quantum Coherences: Towards Fully Quantum Second Laws of Thermodynamics. Phys. Rev. Lett. 2015, 115, 210403. [Google Scholar] [CrossRef]
- Roßnagel, J.; Dawkins, S.T.; Tolazzi, K.N.; Abah, O.; Lutz, E.; Schmidt-Kaler, F.; Singer, K. A single-atom heat engine. Science 2016, 352, 325–329. [Google Scholar] [CrossRef]
- Quan, H.T.; Liu, Y.; Sun, C.P.; Nori, F. Quantum thermodynamic cycles and quantum heat engines. Phys. Rev. E 2007, 76, 031105. [Google Scholar] [CrossRef]
- Haack, G.; Giazotto, F. Efficient and tunable Aharonov-Bohm quantum heat engine. Phys. Rev. B 2019, 100, 235442. [Google Scholar] [CrossRef]
- Du, J.; Shen, W.; Su, S.; Chen, J. Quantum thermal management devices based on strong coupling qubits. Phys. Rev. E 2019, 99, 062123. [Google Scholar] [CrossRef]
- Xu, X.; Choo, K.; Balachandran, V.; Poletti, D. Transport and Energetic Properties of a Ring of Interacting Spins Coupled to Heat Baths. Entropy 2019, 21, 228. [Google Scholar] [CrossRef]
- Werlang, T.; Rigolin, G. Thermal and magnetic quantum discord in Heisenberg models. Phys. Rev. A 2010, 81, 044101. [Google Scholar] [CrossRef]
- Lidar, D.A.; Chuang, I.L.; Whaley, K.B. Decoherence Free Subspaces for Quantum Computation. Phys. Rev. Lett. 1997, 81, 2594–2597. [Google Scholar] [CrossRef]
- Fanchini, F.F.; Castelano, L.K.; Caldeira, A.O. Entanglement versus quantum discord in two coupled double quantum dots. New J. Phys. 2010, 12, 073009. [Google Scholar] [CrossRef]
- Mukherjee, S.; De, B.; Muralidharan, B. Three-terminal vibron-coupled hybrid quantum dot thermoelectric refrigeration. J. Appl. Phy. 2020, 128, 234303. [Google Scholar] [CrossRef]
- Daré, A.M. Comparative study of heat-driven and power-driven refrigerators with Coulomb-coupled quantum dots. Phys. Rev. B 2019, 100, 195427. [Google Scholar] [CrossRef]
- Mitchison, M.T.; Huber, M.; Prior, J.; Woods, M.P.; Plenio, M.B. Realising a quantum absorption refrigerator with an atom-cavity system. Quantum Sci. Technol. 2016, 1, 015001. [Google Scholar] [CrossRef]
- Quan, H.T.; Zhang, P.; Sun, C.P. Quantum heat engine with multilevel quantum systems. Phys. Rev. E 2005, 72, 056110. [Google Scholar] [CrossRef]
- Xu, J.S.; Li, C.F.; Zhang, C.J.; Xu, X.Y.; Zhang, Y.S.; Guo, G.C. Experimental investigation of the non-Markovian dynamics of classical and quantum correlations. Phys. Rev. A 2010, 82, 042328. [Google Scholar] [CrossRef]
- Ashrafi, S.M.; Malekfar, R.; Bahrampour, A.R.; Feist, J. Optomechanical heat transfer between molecules in a nanoplasmonic cavity. Phys. Rev. A 2019, 100, 013826. [Google Scholar] [CrossRef]
- Pereira, E. Heat, work, and energy currents in the boundary-driven XXZ spin chain. Phys. Rev. E 2018, 97, 022115. [Google Scholar] [CrossRef] [PubMed]
- Reis, L.H.; Silva, S.; Pereira, E. Beyond the Lindblad master equation: Heat, work, and energy currents in boundary-driven spin chains. Phys. Rev. E 2020, 101, 062107. [Google Scholar] [CrossRef]
- Esposito, M.; Ochoa, M.A.; Galperin, M. Nature of heat in strongly coupled open quantum systems. Phys. Rev. B 2015, 92, 235440. [Google Scholar] [CrossRef]
- Dorfman, K.E.; Xu, D.; Cao, J. Efficiency at maximum power of a laser quantum heat engine enhanced by noise-induced coherence. Phys. Rev. E 2018, 97, 042120. [Google Scholar] [CrossRef]
- Rodrigues, F.L.S.; Chiara, G.D.; Paternostro, M.; Landi, G.T. Thermodynamics of Weakly Coherent Collisional Models. Phys. Rev. Lett. 2019, 123, 140601. [Google Scholar] [CrossRef]
- Abdallah, P.B.; Biehs, S.A. Near-Field Thermal Transistor. Phys. Rev. Lett. 2014, 112, 044301. [Google Scholar] [CrossRef]
- Landi, G.T.; Novais, E.; de Oliveira, M.J.; Karevski, D. Flux rectification in the quantum XXZ chain. Phys. Rev. E 2014, 90, 042142. [Google Scholar] [CrossRef]
- Schuab, L.; Pereira, E.; Landi, G.T. Energy rectification in quantum graded spin chains: Analysis of the XXZ Model. Phys. Rev. E 2016, 94, 042122. [Google Scholar] [CrossRef]
- Joulain, K.; Drevillon, J.; Ezzahri, Y.; Ordonez-Miranda, J. Quantum Thermal Transistor. Phys. Rev. Lett. 2016, 116, 200601. [Google Scholar] [CrossRef]
- Mascarenhas, E.; Santos, M.F.; Auffèves, A.; Gerace, D. Quantum rectifier in a one-dimensional photonic channel. Phys. Rev. A 2016, 93, 043821. [Google Scholar] [CrossRef]
- Giazotto, F.; Martínez-Pérez, M.J. The Josephson heat interferometer. Nature 2012, 492, 401. [Google Scholar] [CrossRef] [PubMed]
- Ronzani, A.; Karimi, B.; Senior, J.; Chang, Y.; Peltonen, J.T.; Chen, C.; Pekola, J.P. Tunable photonic heat transport in a quantum heat valve. Nat. Phys. 2018, 14, 991–995. [Google Scholar] [CrossRef]
- Wijesekara, R.T.; Gunapala, S.D.; Stockman, M.I.; Premaratne, M. Optically controlled quantum thermal gate. Phys. Rev. B 2020, 101, 245402. [Google Scholar] [CrossRef]
- Scovil, H.E.D.; Schulz-DuBois, E.O. Three-Level Masers as Heat Engines. Phys. Rev. Lett. 1995, 2, 262–263. [Google Scholar] [CrossRef]
- Kosloff, R.; Levy, A. Quantum Heat Engines and Refrigerators: Continuous Devices. Annu. Rev. Phys. Chem. 2014, 65, 365–393. [Google Scholar] [CrossRef]
- Brunner, N.; Huber, M.; Linden, N.; Popescu, S.; Silva, R.; Skrzypczyk, P. Entanglement enhances cooling in microscopic quantum refrigerators. Phys. Rev. E 2014, 89, 032115. [Google Scholar] [CrossRef]
- Balachandran, V.; Benenti, G.; Pereira, E.; Casati, G.; Poletti, D. Perfect Diode in Quantum Spin Chains. Phys. Rev. Lett. 2018, 120, 200603. [Google Scholar] [CrossRef]
- Guo, B.; Liu, T.; Yu, C. Quantum thermal transistor based on qubit-qutrit coupling. Phys. Rev. E 2018, 98, 022118. [Google Scholar] [CrossRef]
- Majland, M.; Christensen, K.S.; Zinner, N.T. Quantum thermal transistor in superconducting circuits. Phys. Rev. B 2020, 101, 184510. [Google Scholar] [CrossRef]
- Yang, J.; Elouard, C.; Splettstoesser, J.; Sothmann, B.; Sánchez, R.; Jordan, A.N. Thermal transistor and thermometer based on Coulomb-coupled conductors. Phys. Rev. B 2019, 100, 045418. [Google Scholar] [CrossRef]
- Correa, L.A.; Mehboudi, M.; Adesso, G.; Sanpera, A. Individual quantum probes for optimal thermometry. Phys. Rev. Lett. 2015, 114, 220405. [Google Scholar] [CrossRef]
- Banerjee, S.; Singha, A. A realistic non-local electrical thermometer based on Coulomb coupled systems. J. Appl. Phys. 2021, 129, 114901. [Google Scholar] [CrossRef]
- Hofer, P.P.; Brask, J.B.; Perarnau-Llobet, M.; Brunner, N. Quantum Thermal Machine as a Thermometer. Phys. Rev. Lett. 2017, 119, 090603. [Google Scholar] [CrossRef]
- Lee, M.H.; Dunietz, B.D. Active control of thermal transport in molecular spin valves. Phys. Rev. B 2013, 88, 045421. [Google Scholar] [CrossRef]
- Huangfu, Y.; Qi, S.; Jing, J. A multifunctional quantum thermal device: With and without inner coupling. Phys. Lett. A 2021, 393, 127172. [Google Scholar] [CrossRef]
- Zhong, W.R.; Zheng, D.Q.; Hu, B. Thermal control in graphene nanoribbons: Thermal valve, thermal switch and thermal amplifier. Nanoscale 2012, 4, 5217. [Google Scholar] [CrossRef]
- Manzano, G.; Sánchez, R.; Silva, R.; Haack, G.; Brask, J.; Brunner, N. Hybrid thermal machines: Generalized thermodynamic resources for multitasking. Phys. Rev. Res. 2020, 2, 043302. [Google Scholar] [CrossRef]
- Wang, C.; Xu, D.; Liu, H.; Gao, X. Thermal rectification and heat amplification in a nonequilibrium V-type three-level system. Phys. Rev. E 2019, 99, 042102. [Google Scholar] [CrossRef]
- Guo, B.; Liu, T.; Yu, C. Multifunctional quantum thermal device utilizing three qubits. Phys. Rev. E 2019, 99, 032112. [Google Scholar] [CrossRef]
- Pereira, E.; Lemos, H.C.F. Symmetry of heat conductivity in inhomogeneous quantum chains. J. Phys. A Math. Theor. 2009, 42, 225006. [Google Scholar] [CrossRef]
- Werlang, T.; Marchiori, M.A.; Cornelio, M.F.; Valente, D. Optimal rectification in the ultrastrong coupling regime. Phys. Rev. E 2014, 89, 062109. [Google Scholar] [CrossRef]
- Chen, T.; Wang, X.B. Thermal rectification in the nonequilibrium quantum-dots-system. Phys. E Low-Dimens. Syst. Nanostruct. 2015, 72, 58–62. [Google Scholar] [CrossRef]
- Ordonez-Miranda, J.; Ezzahri, Y.; Joulain, K. Quantum thermal diode based on two interacting spinlike systems under different excitations. Phys. Rev. E 2017, 95, 022128. [Google Scholar] [CrossRef]
- Karimi, B.; Pekola, J.P.; Campisi, M.; Fazio, R. Coupled qubits as a quantum heat switch. Quantum Sci. Technol. 2017, 2, 044007. [Google Scholar] [CrossRef]
- Pereira, E. Perfect thermal rectification in a many-body quantum Ising model. Phys. Rev. E 2019, 99, 032116. [Google Scholar] [CrossRef]
- Naseem, M.T.; Misra, A.; Müstecaplioglu, Ö.E.; Kurizki, G. Minimal quantum heat manager boosted by bath spectral filtering. Phys. Rev. E 2020, 2, 033285. [Google Scholar]
- Tian, F.; Zou, J.; Li, L.; Li, H.; Shao, B. Effect of Inter-System Coupling on Heat Transport in a Microscopic Collision Model. Entropy 2021, 230, 471. [Google Scholar] [CrossRef]
- Skrzypczyk, P.; Short, A.J.; Popescu, S. Work extraction and thermodynamics for individual quantum systems. Nat. Commun. 2014, 5, 5185. [Google Scholar] [CrossRef]
- Ivan, H.; Serra, R.M. Role of quantum coherence in the thermodynamics of energy transfer. Phys. Rev. E 2018, 97, 062105. [Google Scholar]
- Ghosh, A.; Latune, C.L.; Davidovich, L.; Kurizki, G. Catalysis of heat-to-work conversion in quantum machines. Proc. Natl. Acad. Sci. USA 2017, 114, 12156–12161. [Google Scholar] [CrossRef]
- Ghosh, A.; Gelbwaser-Klimovsky, D.; Niedenzu, W.; Lvovsky, A.I.; Mazets, I.; Scully, M.O.; Kurizki, G. Two-level masers as heat-to-work converters. Proc. Natl. Acad. Sci. USA 2018, 115, 9941–9944. [Google Scholar] [CrossRef]
- Li, L.; Zou, J.; Li, H.; Xu, B.M.; Wang, Y.M.; Shao, B. Effect of coherence of nonthermal reservoirs on heat transport in a microscopic collision model. Phys. Rev. E 2018, 97, 022111. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.; Jin, J. Information scrambling in a collision model. Phys. Rev. A 2020, 101, 042324. [Google Scholar] [CrossRef]
- Campbell, S.; Vacchini, B. Collision models in open system dynamics: A versatile tool for deeper insights? EPL 2021, 133, 60001. [Google Scholar] [CrossRef]
- Bernardes, N.K.; Carvalho, A.; Monken, C.H.; Santos, M.F. Environmental correlations and Markovian to non-Markovian transitions in collisional models. Phys. Rev. A 2014, 90, 032111. [Google Scholar] [CrossRef]
- Guarnieri, G.; Morrone, D.; Çakmak, B.; Plastina, F.; Campbell, S. Non-equilibrium steady-states of memoryless quantum collision models. Phys. Lett. A 2020, 384, 126576. [Google Scholar] [CrossRef]
- Stable, A.L.L.; Noa, C.E.F.; Oropesa, W.G.C.; Fiore, C.E. Thermodynamics of collisional models for Brownian particles: General properties and efficiency. Phys. Rev. Res. 2020, 2, 043016. [Google Scholar] [CrossRef]
- Strasberg, P.; Schaller, G.; Brandes, T.; Esposito, M. Quantum and Information Thermodynamics: A unifying Framework Based on Repeated Interactions. Phys. Rev. X 2017, 7, 021003. [Google Scholar] [CrossRef]
- Cattaneo, M.; Chiara, G.D.; Maniscalco, S.; Zambrini, R.; Giorgi, G.L. Collision models can efficiently simulate any multipartite markovian quantum dynamics. Phys. Rev. Lett. 2021, 126, 130403. [Google Scholar] [CrossRef]
- Seah, S.; Nimmrichter, S.; Scarani, V. Nonequilibrium dynamics with finite-time repeated interactions. Phys. Rev. E 2019, 99, 042103. [Google Scholar] [CrossRef]
- García-Pérez, G.; Rossi, M.A.C.; Maniscalco, S. IBM Q experience as a versatile experimental testbed for simulating open quantum systems. NPJ Quantum Inf. 2020, 6, 1–10. [Google Scholar] [CrossRef]
- Seah, S.; Nimmrichter, S.; Scarani, V. Refrigeration beyond weak internal coupling. Phys. Rev. E 2018, 98, 012131. [Google Scholar] [CrossRef]
- Pachos, J.K.; Plenio, M.B. Three-Spin Interactions in Optical Lattices and Criticality in Cluster Hamiltonians. Phys. Rev. Lett. 2004, 93, 056402. [Google Scholar] [CrossRef]
- Bermudez, A.; Porras, D.; Martin-Delgado, M.A. Competing many-body interactions in systems of trapped ions. Phys. Rev. A 2009, 79, 060303. [Google Scholar] [CrossRef]
- Reiss, T.O.; Khaneja, N.; Glaser, S.J. Broadband geodesic pulses for three spin systems: Time-optimal realization of effective trilinear coupling terms and indirect SWAP gates. J. Magn. Reson. 2003, 165, 95–101. [Google Scholar] [CrossRef][Green Version]
- Linden, N.; Popescu, S.; Skrzypczyk, P. How Small Can Thermal Machines Be? The Smallest Possible Refrigerator. Phys. Rev. Lett. 2010, 105, 130401. [Google Scholar] [CrossRef]
- Skrzypczyk, P.; Brunner, N.; Linden, N.; Popescu, S. The smallest refrigerators can reach maximal efficiency. J. Phys. A Math. Theor. 2011, 44, 492002. [Google Scholar] [CrossRef]
- Wax, N. Selected Papers on Noise and Stochastic Processes; Dover: New York, NY, USA, 1954. [Google Scholar]
- Karevski, D.; Platini, T. Quantum Nonequilibrium Steady States Induced by Repeated Interactions. Phys. Rev. Lett. 2009, 102, 207207. [Google Scholar] [CrossRef]
- Scarani, V.; Ziman, M.; Štelmachovič, P.; Gisin, N.; Bužek, V. Thermalizing Quantum Machines: Dissipation and Entanglement. Phys. Rev. Lett. 2002, 88, 097905. [Google Scholar] [CrossRef] [PubMed]
- Lorenzo, S.; McCloskey, R.; Ciccarello, F.; Paternostro, M.; Palma, G. M. Landauer’s Principle in Multipartite Open Quantum System Dynamics. Phys. Rev. Lett. 2015, 115, 120403. [Google Scholar] [CrossRef] [PubMed]
- Gardas, B.; Deffner, S. Thermodynamic universality of quantum Carnot engines. Phys. Rev. E 2015, 92, 042126. [Google Scholar] [CrossRef] [PubMed]
- Misra, A.; Singh, U.; Bera, M.N.; Rajagopal, A.K. Quantum Renyi relative entropies affirm universality of thermodynamics. Phys. Rev. E 2015, 92, 042161. [Google Scholar] [CrossRef] [PubMed]
- Liao, J.Q.; Dong, H.; Sun, C.P. Single-particle machine for quantum thermalization. Phys. Rev. A 2010, 81, 052121. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S.; Agarwal, G.S.; Walther, H. Extracting Work from a Single Heat Bath via Vanishing Quantum Coherence. Science 2003, 299, 862–864. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Zou, J.; Yu, W.L.; Xu, B.M.; Li, J.G.; Shao, B. Quantum coherence rather than quantum correlations reflect the effects of a reservoir on a system’s work capability. Phys. Rev. E 2014, 89, 052132. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).