Adaptive Extended Kalman Filter with Correntropy Loss for Robust Power System State Estimation
Abstract
:1. Introduction
2. Preliminaries
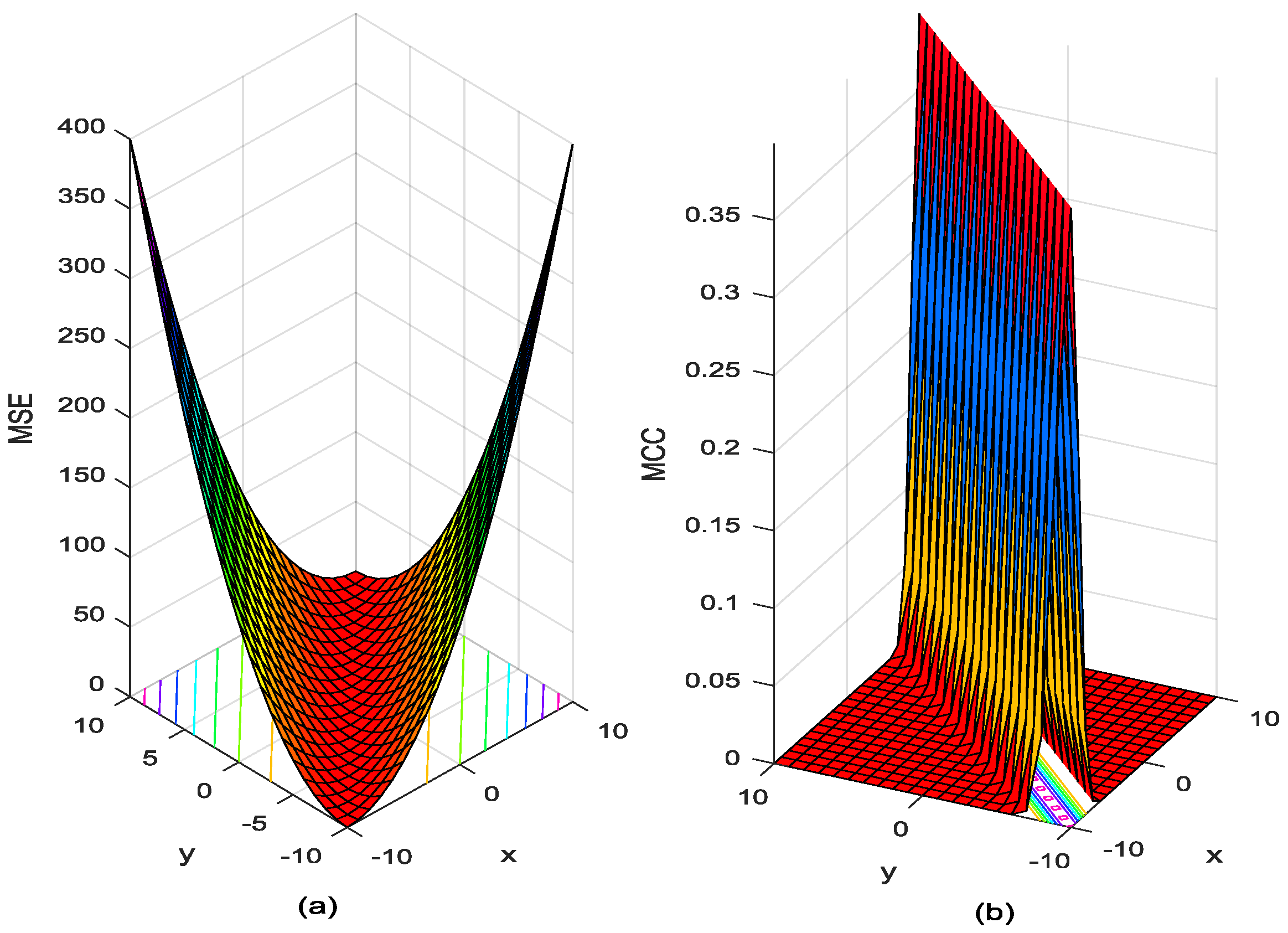
2.1. Maximum Correntropy Criteria
2.2. Review of Extended Kalman Filter
3. Adaptive Extended Kalman Filter With Correntropy Loss
3.1. Extended Kalman Filter with Correntropy Loss
3.2. Adaptive Extended Kalman Filter with Correntropy Loss
4. Adaptive Extended Kalman Filter With Correntropy Loss for PSDSE
4.1. Power System Dynamic Model
4.2. Adaptive Extended Kalman Filter with Correntropy Loss for Power System Forecasting-Aided State Estimation
- 1)
- Select the appropriate initial parameters: a proper kernel bandwidth and a small positive ; Set an initial state value and corresponding covariance matrix ; Let k = 1;
- 2)
- Use Equations (8) and (9) to calculate the and , and obtain the by Cholesky decomposition;
- 3)
- Let k = 1 and , where stands for the estimated state at the fixed-point iteration k;
- 4)
- Calculate the state transition function using (45)–(47) and the Jacobian matrix using (51)–(60);
- 5)
- Get the estimates state by Equations (61)–(69);With
- 6)
- Compare the estimation of the current step and the estimation of the last step. If (70) holds, let and continue to 7). Otherwise, , and go back to 5);
- 7)
- Moreover, the posterior matrix is updated as (71), and go back to 2).
5. Results
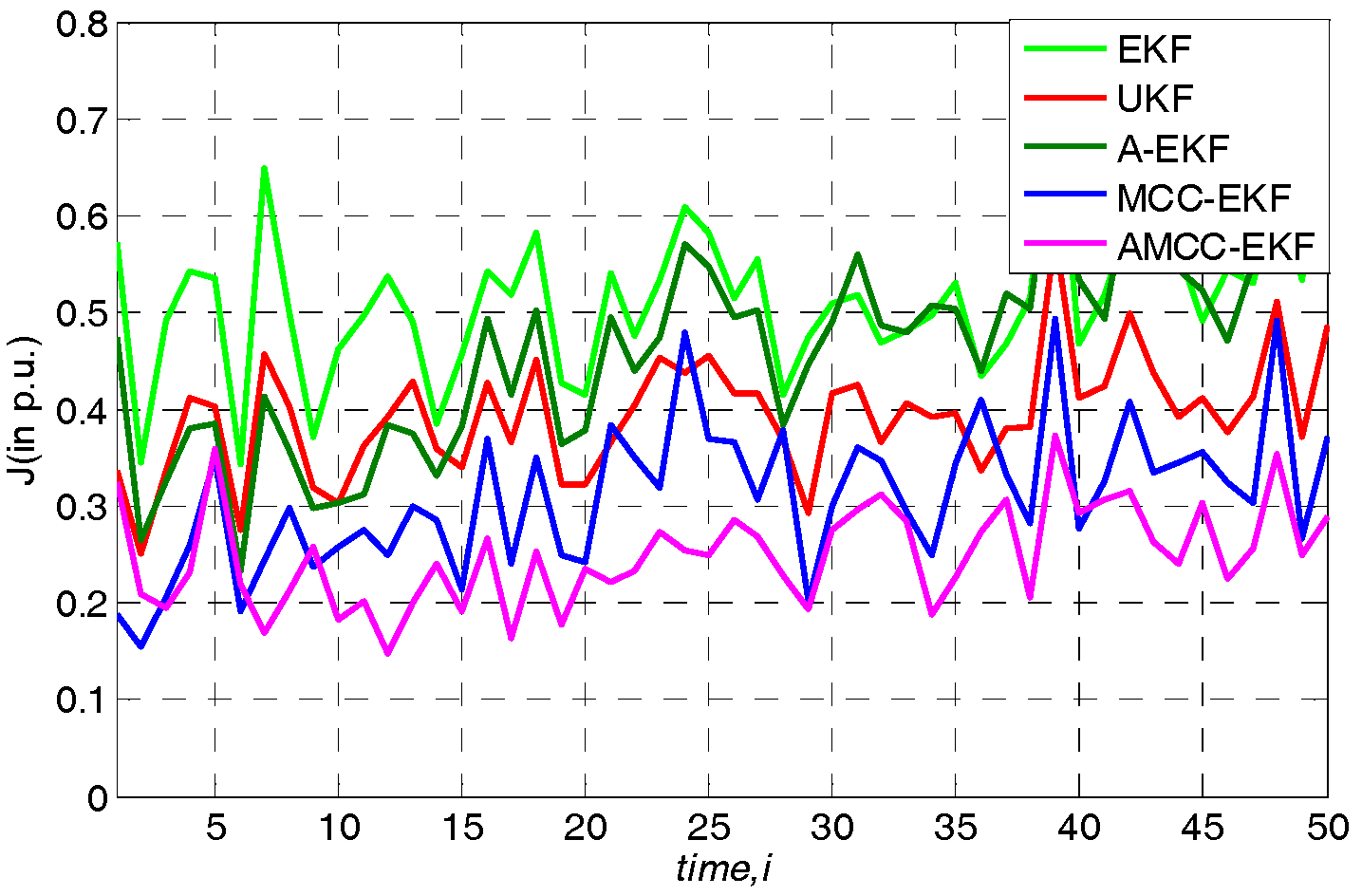
5.1. Case 1: Gaussian Measurement Noise Environment
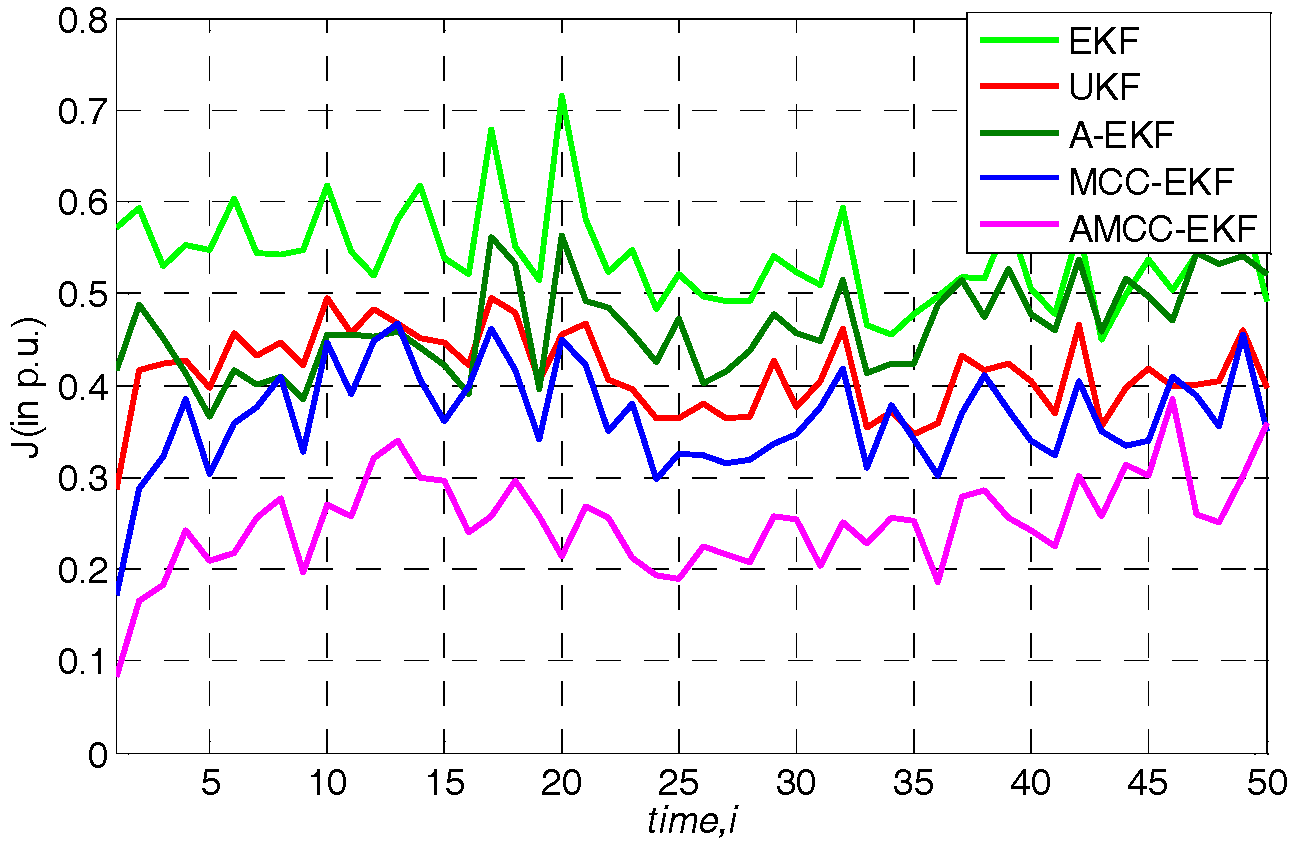
5.2. Case 2: Gaussian Mixture Measurement Noise Environment
5.3. Case 3: Laplace and Gaussian Mixture Measurement Noise Environment
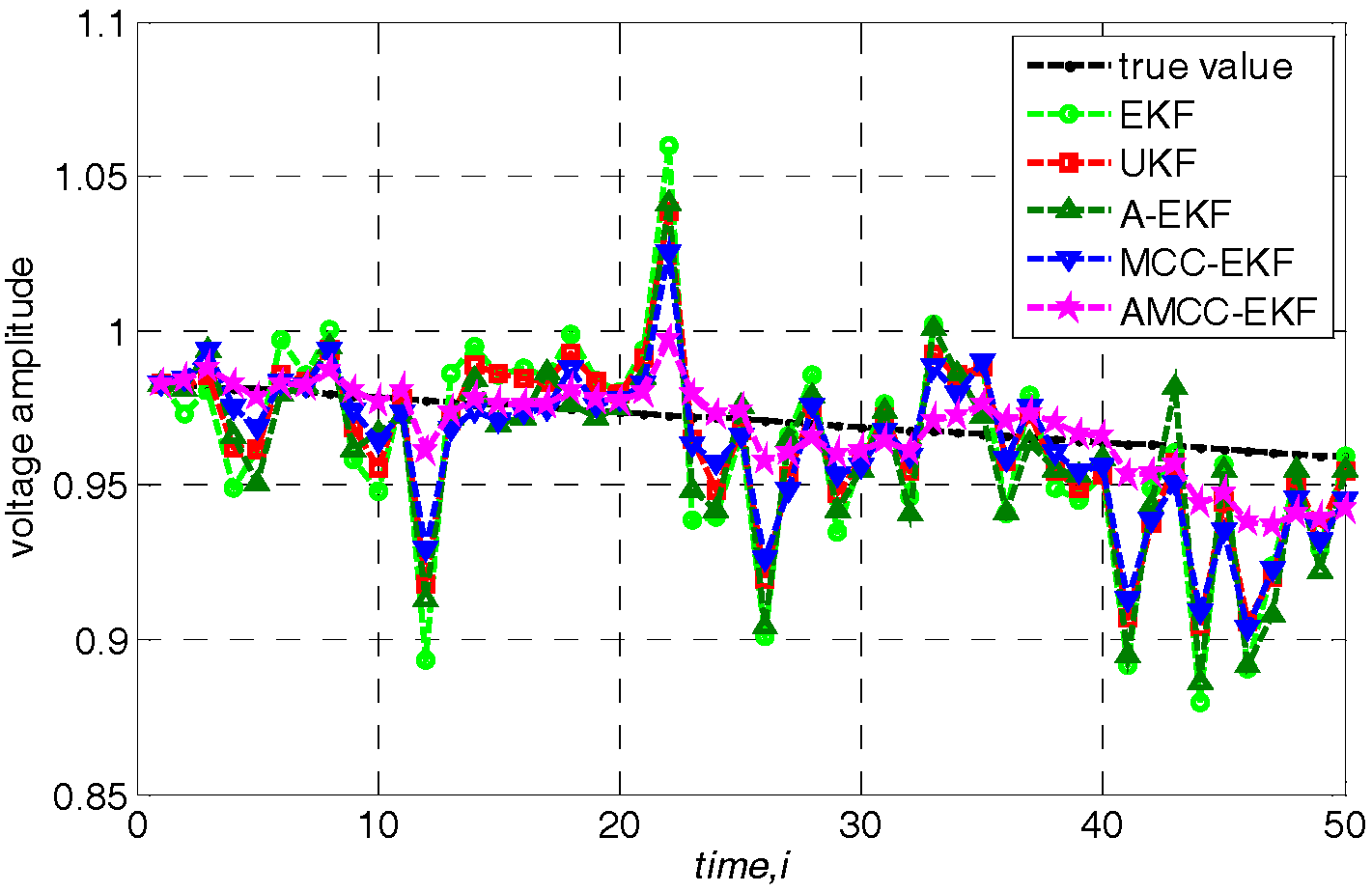
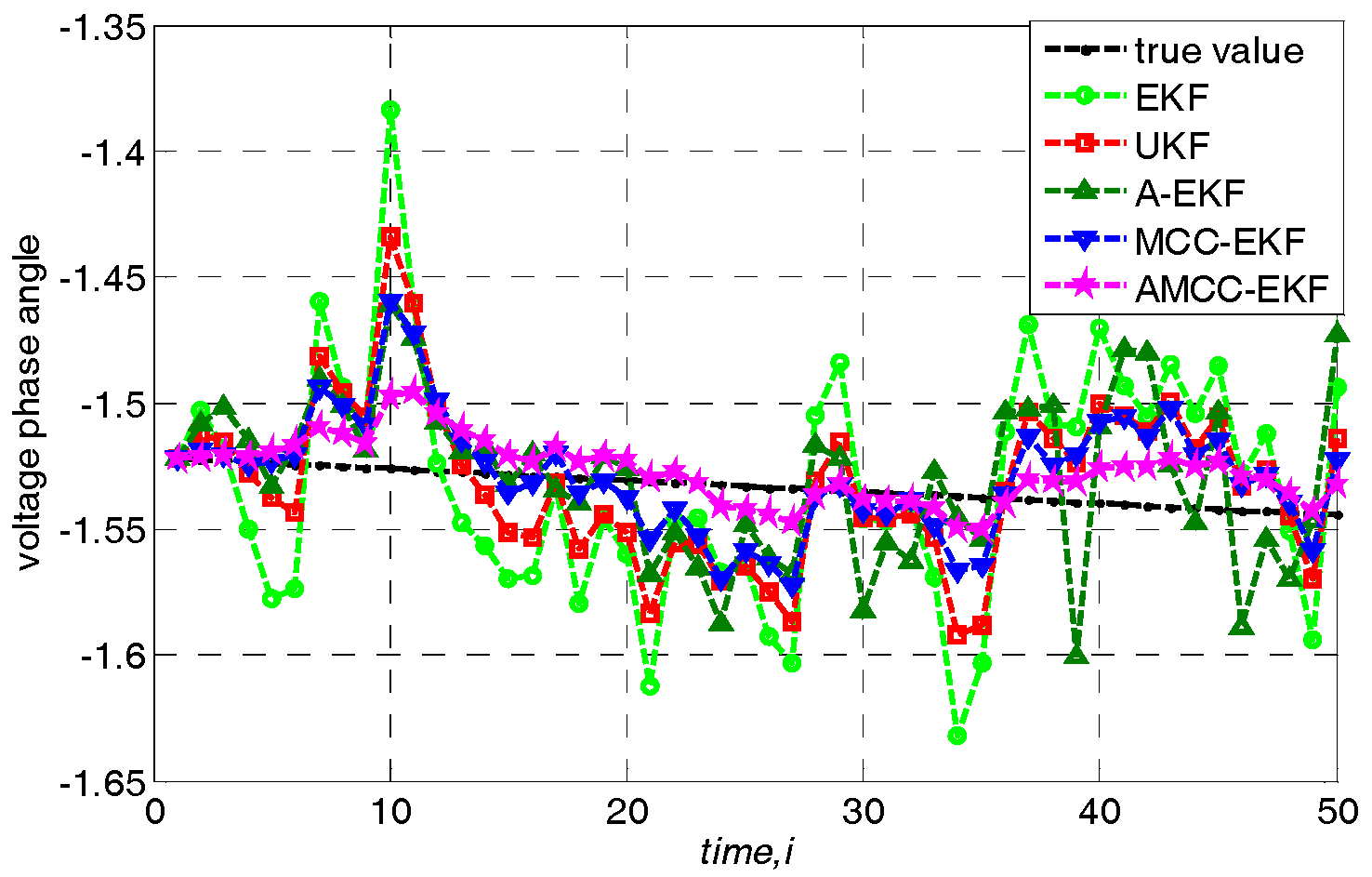
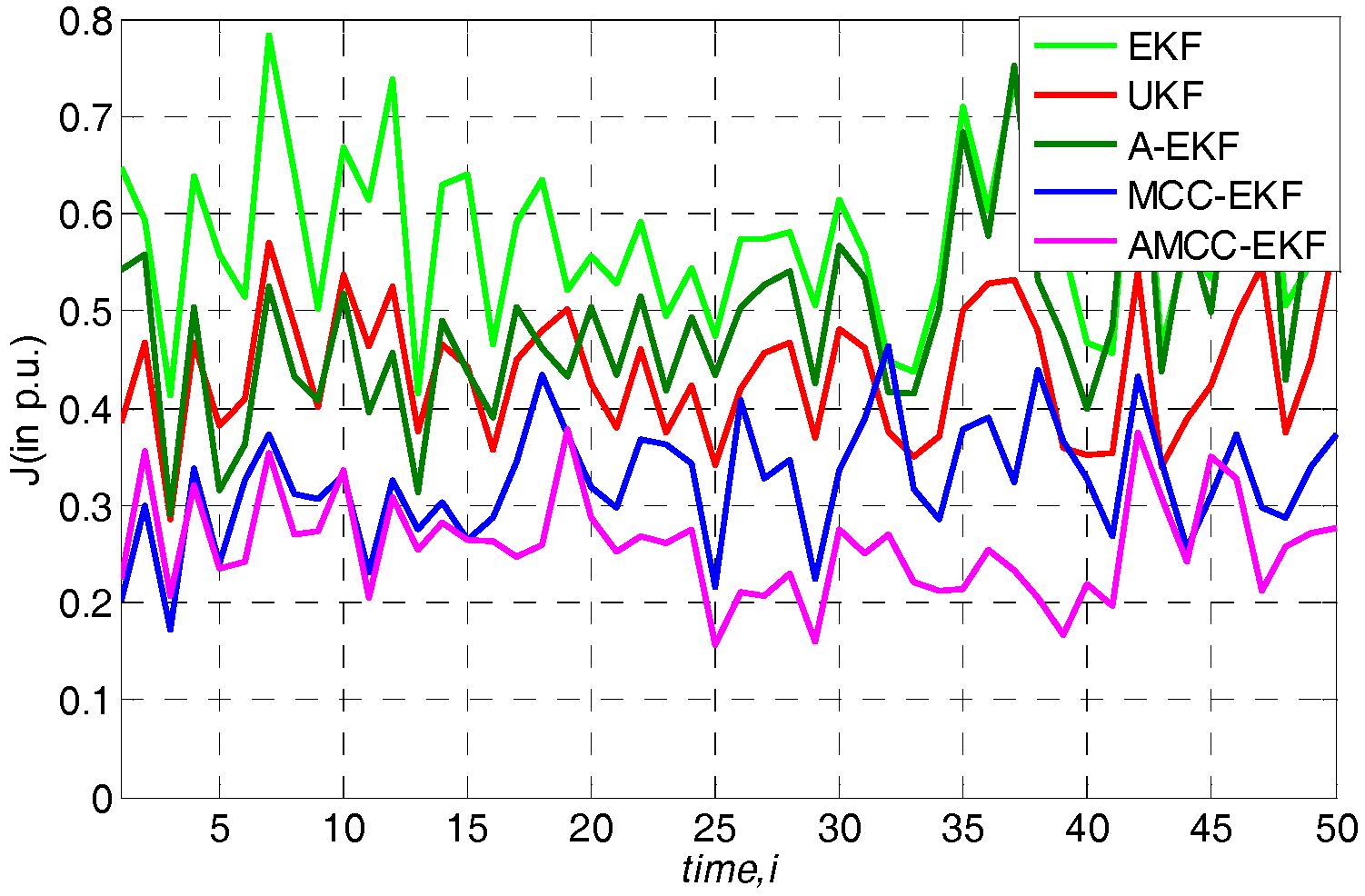
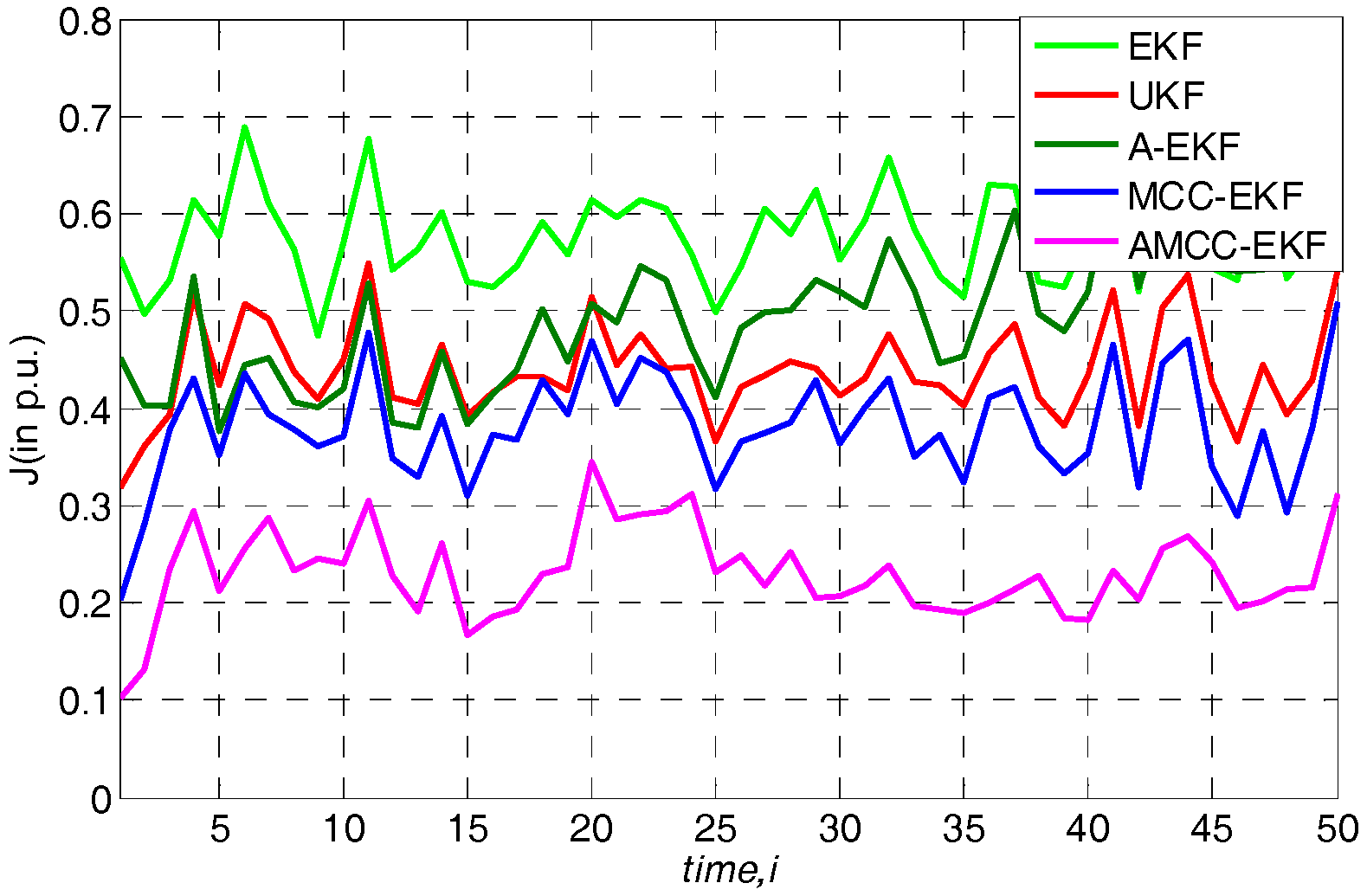
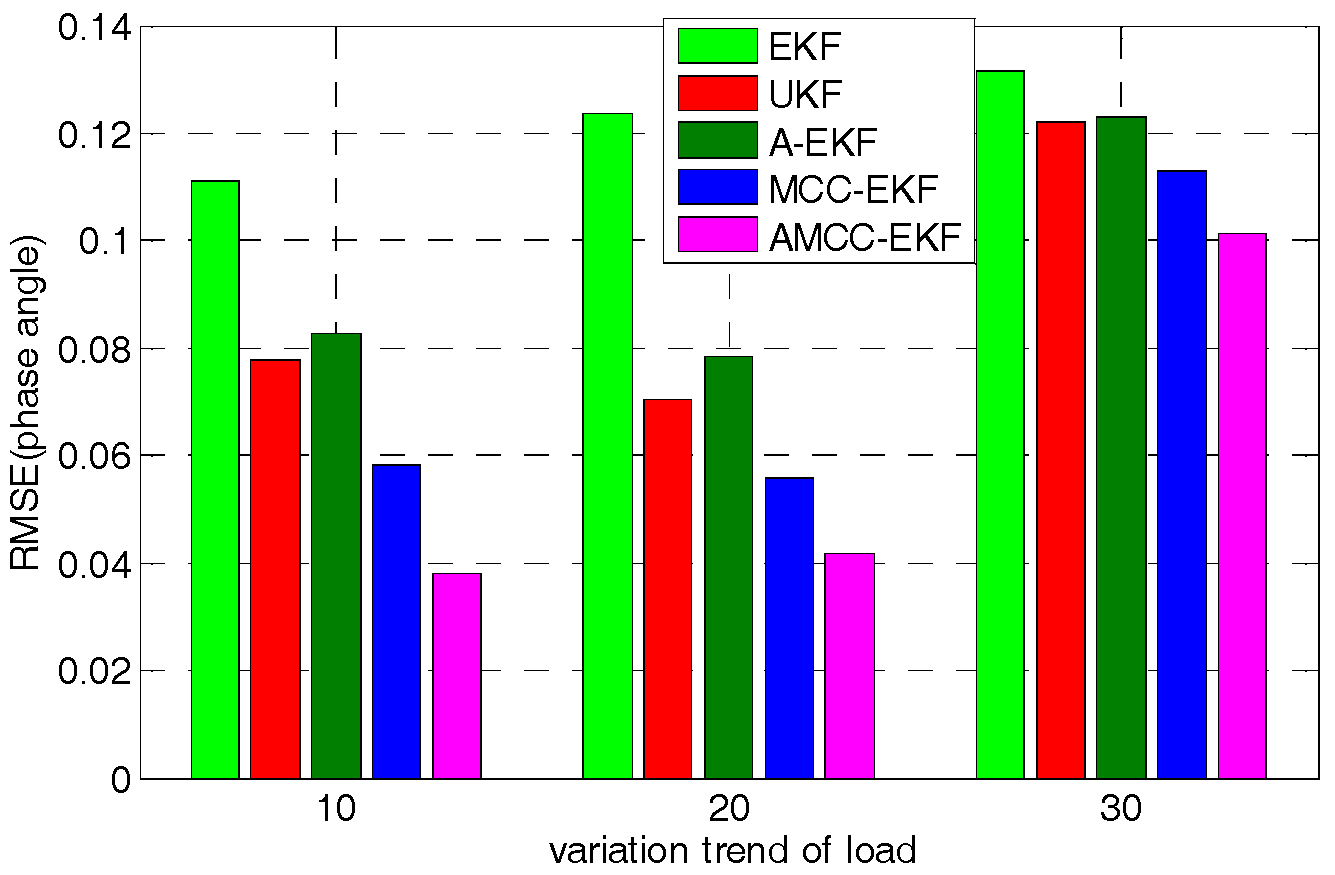
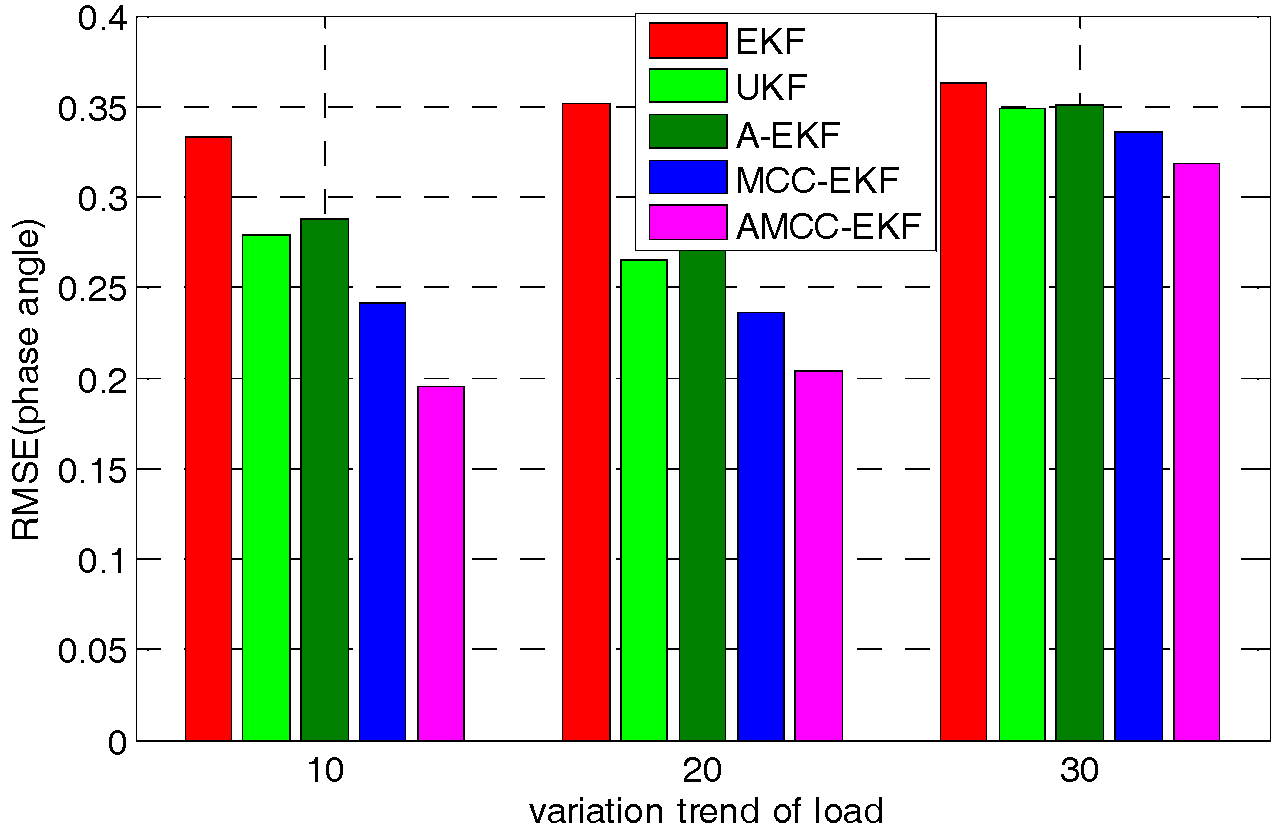
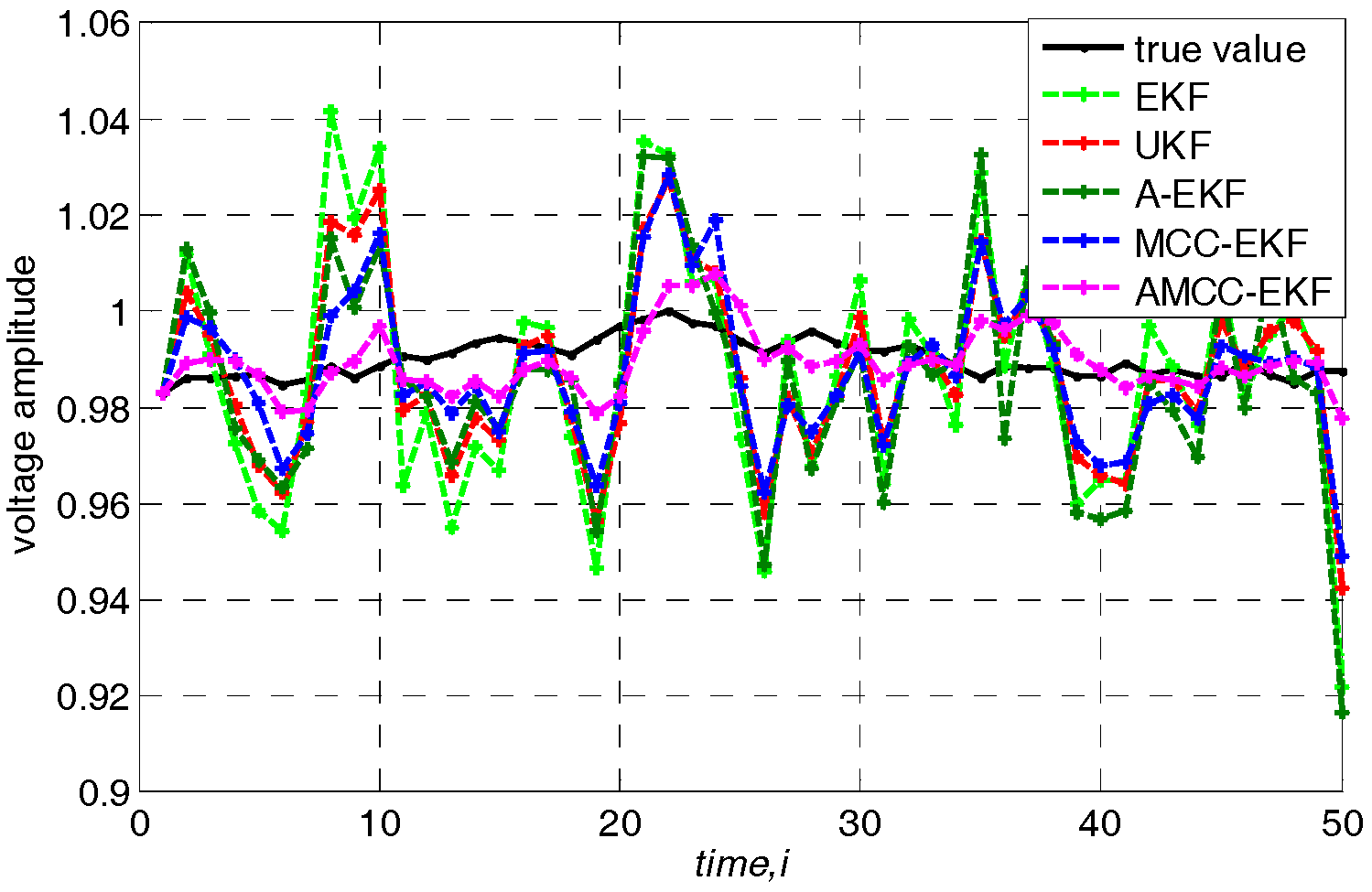
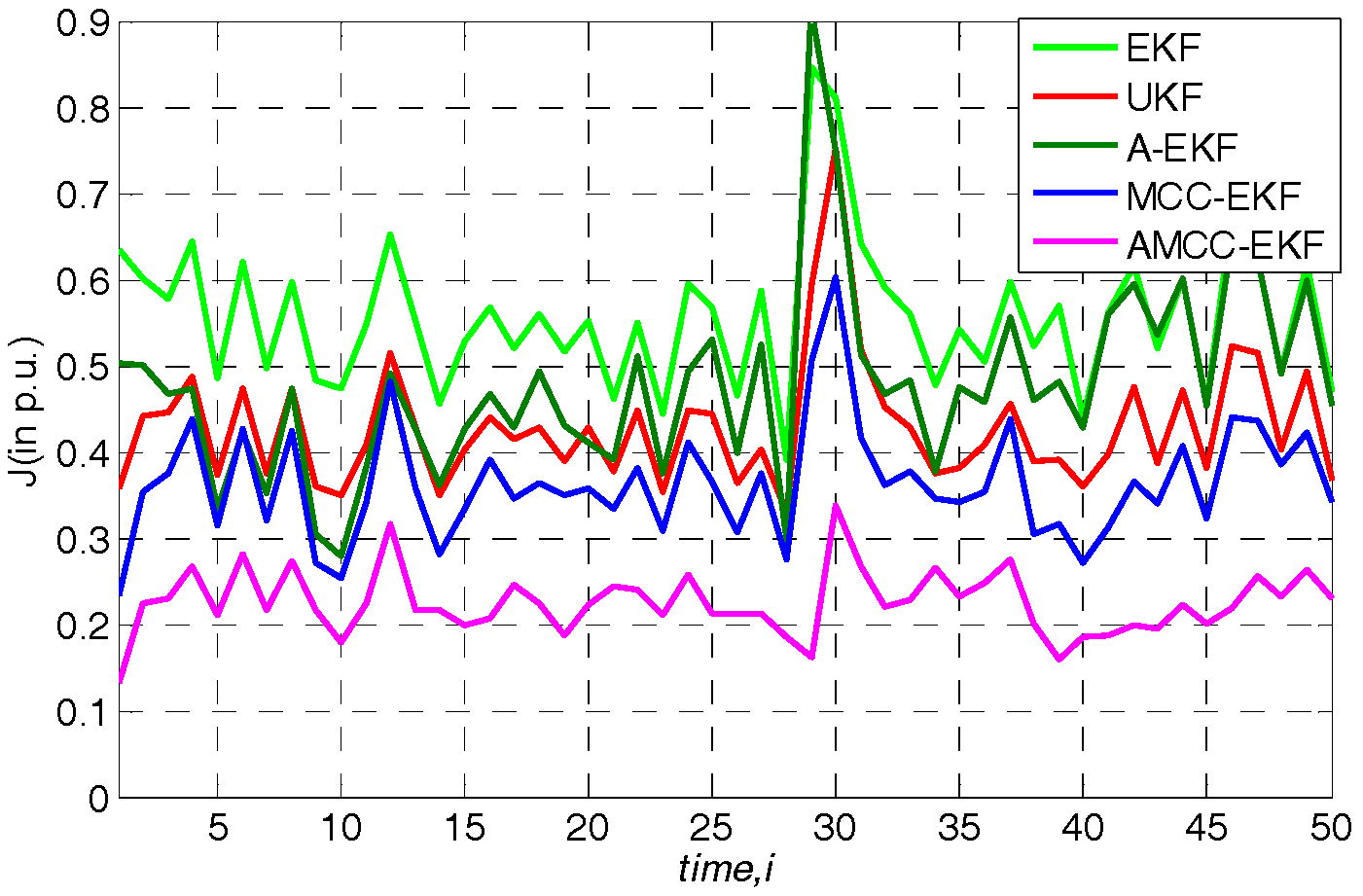
5.4. Case 4: the Nonlinear Variation of Loads
5.5. Case 5: in Presence of Outliers
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stott, B.; Alsac, O.; Monticelli, A.J. Security analysis and optimization. Proc. IEEE 1987, 75, 1623–1644. [Google Scholar] [CrossRef]
- Shivakumar, N.R.; Jain, A. A review of power system dynamic state estimation techniques. In Proceedings of the Joint International Conference on Power System Technology & IEEE Power India Conference, New Delhi, India, 12–15 October 2008; pp. 1–6. [Google Scholar]
- Gomez-Exposito, A.; Conejo, A.J.; Canizares, C. Electric Energy Systems: Analysis and Operation; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Green, R.C.; Wang, L.; Alam, M. Applications and trends of high performance computing for electric power systems: Focusing on smart grid. IEEE Trans. Smart Grid 2013, 4, 922–931. [Google Scholar] [CrossRef]
- Li, W.; Li, J.; Gao, A. Review and research trends on state estimation of electrical power systems. In Proceedings of the Power and Energy Engineering Conference (APPEEC), 2011 Asia-Pacific, New York, NY, USA, 25–28 March 2011; pp. 1–4. [Google Scholar]
- Ljung, L. Asymptotic behavior of the extended Kalman filter as a parameter estimator for linear systems. IEEE Trans. Autom. Control 2013, 24, 36–50. [Google Scholar] [CrossRef]
- Ghahremani, E.; Kamwa, I. Dynamic state estimation in power system by applying the extended Kalman filter with unknown inputs to phasor measurements. IEEE Trans. Power Syst. 2011, 26, 2556–2566. [Google Scholar] [CrossRef]
- Maybeck, P.S.; Jensen, R.L.; Harnly, D.A. An adaptive extended Kalman filter for target image tracking. IEEE Trans. Aerosp. Electron. Syst. 1981, 2, 173–180. [Google Scholar] [CrossRef]
- Netto, M.; Zhao, J.; Mili, L. A robust extended Kalman filter for power system dynamic state estimation using PMU measurements. In Proceedings of the Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Gandhi, M.A.; Mili, L. Robust Kalman filter based on a generalized maximum-likelihood-type estimator. IEEE Trans. Signal Process. 2010, 58, 2509–2520. [Google Scholar] [CrossRef]
- Zhao, J.B.; Netto, M.; Mili, L. A robust iterated extended Kalman filter for power system dynamic state estimation. IEEE Trans. Power Syst. 2017, 32, 3205–3216. [Google Scholar] [CrossRef]
- Zhao, J.B. Dynamic State Estimation With Model Uncertainties Using H∞ Extended Kalman Filter. IEEE Trans. Power Syst. 2018, 33, 1099–1100. [Google Scholar] [CrossRef]
- Wan, E.A.; Van, D.M.R. The unscented Kalman filter for nonlinear estimation. In Proceedings of the Adaptive Systems for Signal Processing, Communications, and Control Symposium, Lake Louise, AB, Canada, 4 October 2000; pp. 153–158. [Google Scholar]
- Valverde, G.; Terzija, V. Unscented Kalman filter for power system dynamic state estimation. IET Gener. Transm. Distrib. 2011, 5, 29–37. [Google Scholar] [CrossRef]
- Liu, W.; Puskal, P.; Jose, C. Principe Correntropy: Properties and Applications in Non-Gaussian Signal Processing. IEEE Trans. Signal Process. 2007, 55, 5286–5298. [Google Scholar] [CrossRef]
- Chen, B.; Xing, L.; Liang, J. Steady-state mean-square error analysis for adaptive filtering under the maximum correntropy criterion. IEEE Signal Process. Lett. 2014, 21, 880–884. [Google Scholar]
- Chen, B.; Wang, J.; Zhao, H.; Zheng, N. Convergence of a Fixed-Point Algorithm under Maximum Correntropy Criterion. IEEE Signal Process. Lett. 2015, 22, 1723–1727. [Google Scholar] [CrossRef]
- Chen, B.; Príncipe, J.C. Maximum correntropy estimation is a smoothed MAP estimation. IEEE Signal Process. Lett. 2012, 19, 491–494. [Google Scholar] [CrossRef]
- Chen, B.; Xing, L.; Zhao, H. Robustness of Maximum Correntropy Estimation Against Large Outliers. arXiv, 2017; arXiv:1703. 08065. [Google Scholar]
- Chen, B.; Liu, X.; Zhao, H. Maximum correntropy Kalman filter. Automatica 2017, 76, 70–77. [Google Scholar] [CrossRef]
- Liu, X.; Qu, H.; Zhao, J. Extended Kalman filter under maximum correntropy criterion. In Proceedings of the International Joint Conference on Neural Networks, Vancouver, BC, Canada, 24–29 July 2016; pp. 1733–1737. [Google Scholar]
- Ma, W.; Chen, B.; Qu, H. Sparse least mean p-power algorithms for channel estimation in the presence of impulsive noise. Signal Image Video Process. 2016, 10, 503–510. [Google Scholar] [CrossRef]
- Wang, S.; Dang, L.; Wang, W.; Qian, G. Kernel adaptive filters with feedback based on maximum correntropy. IEEE Access 2018, 6, 10540–10552. [Google Scholar] [CrossRef]
- Dees, B.S.; Xia, Y.; Douglas, S.C. Correntropy-Based Adaptive Filtering of Noncircular Complex Data. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018. [Google Scholar]
- Wang, G.; Gao, Z.; Zhang, Y. Adaptive Maximum Correntropy Gaussian Filter Based on Variational Bayes. Sensors 2018, 18, 1960. [Google Scholar] [CrossRef]
- Xian, Z.; Hu, X.; Lian, J. Robust innovation-based adaptive Kalman filter for INS/GPS land navigation. In Proceedings of the Chinese Automation Congress IEEE, Changsha, China, 7–8 November 2013; pp. 374–379. [Google Scholar]
- Hide, C.; Moore, T. Adaptive Kalman filtering for low-cost INS/GPS. J. Navig. 2003, 56, 143–152. [Google Scholar] [CrossRef]
- Haykin, S.S. Adaptive Filter Theory; Publishing House of Electronics Industry: Beijing, China, 2002. [Google Scholar]
- Elkeyi, A.; Kirubarajan, T.; Gershman, A.B. Robust adaptive beamforming based on the Kalman filter. IEEE Signal Process Soc. 2005, 53, 3032–3041. [Google Scholar] [CrossRef]
- Conejo, A.J. Power System State Estimation-Theory and Implementations. IEEE Power Energy Mag. 2005, 3, 64–65. [Google Scholar] [CrossRef]
- Leite, A.M.; Silva, M.B.D.; Queiroz, J.F. State forecasting in electric power systems. IEE Proc. C Gener. Transm. Distrib. 1983, 130, 237–244. [Google Scholar] [CrossRef]

| EKF | UKF | A-EKF | MCC-EKF | AMCC-EKF | |
|---|---|---|---|---|---|
| Index J (p.u.) | 0.39 | 0.29 | 0.31 | 0.25 | 0.16 |
| EKF | UKF | A-EKF | MCC-EKF | AMCC-EKF | |
|---|---|---|---|---|---|
| Index J (p.u.) | 0.53 | 0.41 | 0.49 | 0.33 | 0.23 |
| EKF | UKF | A-EKF | MCC-EKF | AMCC-EKF | |
|---|---|---|---|---|---|
| Index J (p.u.) | 0.55 | 0.41 | 0.48 | 0.32 | 0.24 |
| EKF | UKF | A-EKF | MCC-EKF | AMCC-EKF | |
|---|---|---|---|---|---|
| Index J (p.u.) | 0.65 | 0.48 | 0.53 | 0.36 | 0.28 |
| EKF | UKF | A-EKF | MCC-EKF | AMCC-EKF | |
|---|---|---|---|---|---|
| Index J (p.u.) | 0.59 | 0.52 | 0.46 | 0.38 | 0.23 |
| EKF | UKF | A-EKF | MCC-EKF | AMCC-EKF | |
|---|---|---|---|---|---|
| MAE | 0.06 | 0.05 | 0.05 | 0.03 | 0.01 |
| RMSE | 0.25 | 0.21 | 0.23 | 0.18 | 0.12 |
| EKF | UKF | A-EKF | MCC-EKF | AMCC-EKF | |
|---|---|---|---|---|---|
| Index J (p.u.) | 0.56 | 0.46 | 0.48 | 0.36 | 0.24 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Qiu, J.; Ma, W. Adaptive Extended Kalman Filter with Correntropy Loss for Robust Power System State Estimation. Entropy 2019, 21, 293. https://doi.org/10.3390/e21030293
Zhang Z, Qiu J, Ma W. Adaptive Extended Kalman Filter with Correntropy Loss for Robust Power System State Estimation. Entropy. 2019; 21(3):293. https://doi.org/10.3390/e21030293
Chicago/Turabian StyleZhang, Zhiyu, Jinzhe Qiu, and Wentao Ma. 2019. "Adaptive Extended Kalman Filter with Correntropy Loss for Robust Power System State Estimation" Entropy 21, no. 3: 293. https://doi.org/10.3390/e21030293
APA StyleZhang, Z., Qiu, J., & Ma, W. (2019). Adaptive Extended Kalman Filter with Correntropy Loss for Robust Power System State Estimation. Entropy, 21(3), 293. https://doi.org/10.3390/e21030293





