Abstract
Secret sharing is a cryptographic discipline in which the goal is to distribute information about a secret over a set of participants in such a way that only specific authorized combinations of participants together can reconstruct the secret. Thus, secret sharing schemes are systems of variables in which it is very clearly specified which subsets have information about the secret. As such, they provide perfect model systems for information decompositions. However, following this intuition too far leads to an information decomposition with negative partial information terms, which are difficult to interpret. One possible explanation is that the partial information lattice proposed by Williams and Beer is incomplete and has to be extended to incorporate terms corresponding to higher-order redundancy. These results put bounds on information decompositions that follow the partial information framework, and they hint at where the partial information lattice needs to be improved.
Keywords:
information decomposition; partial information lattice; shared information; secret sharing MSC:
94A17; 94A62
1. Introduction
Williams and Beer [1] have proposed a general framework to decompose the multivariate mutual information between a target random variable S and predictor random variables into different terms (called partial information terms) according to different ways in which combinations of the variables provide unique, shared, or synergistic information about S. Williams and Beer argue that such a decomposition can be based on a measure of shared information. The underlying idea is that any information can be classified according to “who knows what”. However, is this true?
A situation where the question “who knows what?” is easy to answer very precisely is secret sharing—a part of cryptography in which the goal is to distribute information (the secret) over a set of participants such that the secret can only be reconstructed if certain authorized combinations of participants join their information (see [2] for a survey). The set of authorized combinations is called the access structure. Formally, the secret is modelled as a random variable S, and a secret sharing scheme assigns a random variable to each participant i in such a way that if is an authorized set of participants, then S is a function of ; that is, ; and, conversely, if is not authorized, then . It is assumed that the participants know the scheme, and so any authorized combination of participants can reconstruct the secret if they join their information. A secret sharing scheme is perfect if non-authorized sets of participants know nothing about the secret; i.e., . Thus, in a perfect secret sharing scheme, it is very clearly specified “who knows what”. In this sense, perfect secret sharing schemes provide model systems for which it should be easy to write down an information decomposition.
One connection between secret sharing and information decompositions is that the set of access structures of secret sharing schemes with n participants is in one-to-one correspondence with the partial information terms of Williams and Beer. This correspondence makes it possible to give another interpretation to all partial information terms: namely, the partial information term is a measure of how similar a given system of random variables is to a secret sharing scheme with a given access structure.
This correspondence also allows the introduction of the secret sharing property that makes the above intuition precise: An information decomposition satisfies this property if and only if any perfect secret sharing scheme has just a single partial information term (which corresponds to its access structure). Lemma 2 states that the secret sharing property is implied by the Williams and Beer axioms, which shows that the secret sharing property plays well together with the ideas of Williams and Beer. Proposition 1 shows that in an information decomposition that satisfies a natural generalization of this property, it is possible to prescribe arbitrary nonnegative values to all partial information terms.
These results suggest that perfect secret sharing schemes fit well together with the ideas of Williams and Beer. However, following this intuition too far leads to inconsistencies. As Theorem 4 shows, extending the secret sharing property to pairs of perfect secret sharing schemes leads to negative partial information terms. While other authors have started to build an intuition for negative partial terms and argue that they may be unavoidable in information decompositions, the concluding section collects arguments against such claims and proposes as another possible solutions that the Williams and Beer framework is incomplete and is missing nodes that represent higher-order redundancy.
Cryptography, where the goal is not only to transport information (as in coding theory) but also to keep it concealed from unauthorized parties, has initiated many interesting developments in information theory; for example, by introducing new information measures and re-interpreting older ones (see, for example, [3,4]). This manuscript focuses on another contribution of cryptography: probabilistic systems with well-defined distribution of information.
The remainder of this article is organized as follows: Section 2 summarizes definitions and results of secret sharing schemes. Section 3 introduces different secret sharing properties that fix the values that a measure of shared information assigns to perfect secret sharing schemes and combinations thereof. The main result of Section 4 is that the pairwise secret sharing property leads to negative partial information terms. Section 5 discusses the implications of this incompatibility result.
2. Perfect Secret Sharing Schemes
We consider n participants among whom we want to distribute information about a secret in such a way that we can control which subsets of participants together can decrypt the secret.
Definition 1.
An access structure is a family of subsets of , closed to taking supersets. Elements of are called authorized sets.
A secret sharing scheme with access structure is a family of random variables S, such that:
- , whenever .
Here, for all subsets . A secret sharing scheme is perfect if
- , whenever .
The condition for perfection is equivalent to . See [2] for a survey on secret sharing.
Theorem 1.
For any access structure and any , there exists a perfect secret sharing scheme with access structure for which the entropy of the secret S equals .
Proof.
Perfect secret sharing schemes for arbitrary access structures were first constructed by Ito et al. [5]. In this construction, the entropy of the secret equals 1 bit. Combining n copies of such a secret sharing scheme gives a secret sharing scheme with a secret of n bit. As explained in [2] (Claim 1), the distribution of the secret may be perturbed arbitrarily (as long as the support of the distribution remains the same). In this way it is possible to prescribe the entropy of the secret in a perfect secret sharing scheme. ☐
Example 1.
Let be independent uniform binary random variables, and let , , , where ⊕ denotes addition modulo 2 (or the XOR operation). Then is a perfect secret sharing scheme with access structure
It may be of little surprise that integer addition modulo k is an important building block in many secret sharing schemes.
While the existence of perfect secret sharing schemes is solved, there remains the problem of finding efficient secret sharing schemes in the sense that the variables should be as small as possible (in the sense of a small entropy), given a fixed entropy of the secret. For instance, in Example 1, for all i (see [2] for a survey).
Since an access structure is closed to taking supersets, it is uniquely determined by its inclusion-minimal elements
For instance, in Example 1, the first three elements belong to . The set has the property that no element of is a subset of another element of . Such a collection of sets is called an antichain. Conversely, any such antichain equals the set of inclusion-minimal elements of a unique access structure.
The antichains have a natural lattice structure, which was used by Williams and Beer to order the different values of shared information and organize them into what they call the partial information lattice. The same lattice also has a description in terms of secret sharing.
Definition 2.
Let and be antichains. Then
The partial information lattice for the case is depicted in Figure 1.
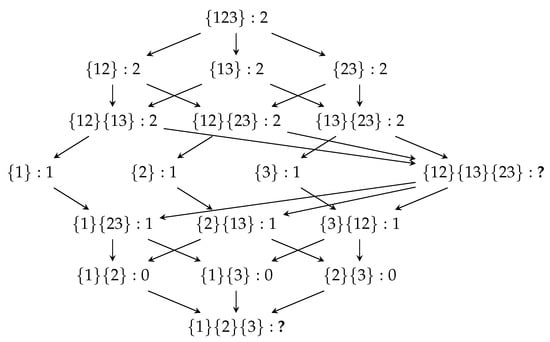
Figure 1.
The partial information lattice for . Each node is indexed by an antichain. The values (in bit) of the shared information in the XOR example from the proof of Theorem 2 according to the pairwise secret sharing property are given after the colon.
Lemma 1.
Let be an access structure on , and let be an antichain. Then are all authorized for if and only if .
Proof.
The statement directly follows from the definitions. ☐
3. Information Decompositions of Secret Sharing Schemes
Williams and Beer [1] proposed to decompose the total mutual information between a target random variable S and predictor random variables according to different ways in which combinations of the variables provide unique, shared, or synergistic information about S. One of their main ideas is to base such a decomposition on a single measure of shared information , which is a function that takes as arguments a list of random variables, of which the first, S, takes a special role. To arrive at a decomposition of , the variables are taken to be combinations of , corresponding to subsets A of . For simplicity, is denoted by for all .
Williams and Beer proposed a list of axioms that such a measure should satisfy. It follows from these axioms that it suffices to consider the function in the case that is an antichain. Moreover, is a monotone function on the partial information lattice (Definition 2).
Thus, it is natural to write each value on the lattice as a sum of local terms corresponding to the antichains that lie below in the lattice:
The terms are called partial information terms. This representation always exists, and the partial information terms are uniquely defined (using a Möbius inversion). However, it is not guaranteed that is always nonnegative. If is nonnegative, then is called locally positive.
Williams and Beer also defined a function denoted by that satisfies their axioms and that is locally positive. While the framework is intriguing and has attracted a lot of further research (as this special issue illustrates), the function has been criticized as not measuring the right thing. The difficulty of finding a reasonable measure of shared information that is locally positive [6,7] has led some to argue that maybe local positivity is not a necessary requirement for an information decomposition. This issue is discussed further in Section 5.
The goal of this section is to present additional natural properties for a measure of shared information that relate secret sharing with the intuition behind information decompositions. In a perfect secret sharing scheme, any combination of participants knows either nothing or everything about S. This motivates the following definition:
Definition 3.
A measure of shared information has the secret sharing property if and only if for any access structure and any perfect secret sharing scheme with access structure , the following holds:
Lemma 2.
The secret sharing property is implied by the Williams and Beer axioms.
Proof.
The Williams and Beer axioms imply that
whenever is not authorized. On the other hand, when are all authorized, then the monotonicity axiom implies
Perfect secret sharing schemes lead to information decompositions with a single nonzero partial information term:
Lemma 3.
If has the secret sharing property and if is a perfect secret sharing scheme with access structure , then
Proof.
Suppose that , and let be the right hand side of Equation (1). We need to show that . Since the Möbius inversion is unique, it suffices to show that , where
By Lemma 1,
for any , from which the claim follows. ☐
What happens when we have several secret sharing schemes involving the same participants? In order to have a clear intuition, assume that the secret sharing schemes satisfy the following definition:
Definition 4.
Let be access structures on . A combination of (perfect) secret sharing schemes with access structures consists of random variables , such that is a (perfect) secret sharing scheme with access structure for and such that
This definition ensures that the secrets are independent in the sense that knowing some of the secrets provides no information about the other secrets. Formally, one can see that the secrets are probabilistically independent as follows: For any (for example, ),
In Definition 4, if two access structures are identical, then we can replace and by a single random variable and obtain a smaller combination of (perfect) secret sharing schemes.
In a combination of perfect secret sharing schemes, it is very clear who knows what: Namely, a group of participants knows all secrets for which it is authorized, while it knows nothing about the remaining secrets. This motivates the following definition:
Definition 5.
A measure of shared information has the combined secret sharing property if and only if for any combination of perfect secret sharing schemes with access structures ,
(the entropy of those secrets for which are all authorized). has the pairwise secret sharing property if and only if the same holds true in the special case .
The combined secret sharing property implies the pairwise secret sharing property. The pairwise secret sharing property does not follow from the Williams and Beer axioms. For example, satisfies the Williams and Beer axioms, but not the pairwise secret sharing property (as will become apparent in Theorem 2). So one can ask whether the pairwise and combined secret sharing properties are compatible with the Williams and Beer axioms. This question is difficult to answer, since currently there are only two proposed measures of shared information that satisfy the Williams and Beer axioms, namely and the minimum of mutual informations [8]:
Both measures do not satisfy the pairwise secret sharing property.
While there has been no further proposal for a function that satisfies the Williams and Beer axioms for arbitrarily many arguments, several measures have been proposed for the “bivariate case” , notably of Harder et al. [9] and of [10]. The appendix shows that at least satisfies the combined secret sharing property “as far as possible”.
Combinations of l perfect secret sharing schemes lead to information decompositions with at most l nonzero partial information terms.
Lemma 4.
Assume that has the combined secret sharing property. If , is a combination of perfect secret sharing schemes with pairwise different access structures , then
for any .
The proof is similar to the proof of Lemma 3 and is omitted.
The combined secret sharing property implies that any combination of nonnegative values can be prescribed as partial information values.
Proposition 1.
Suppose that a nonnegative number is given for any antichain . For any measure of shared information that satisfies the combined secret sharing property, there exist random variables such that the corresponding partial measure satisfies for all antichains .
Proof.
By Theorem 1, for each antichain there exists a perfect secret sharing scheme , with . Combine independent copies of these perfect secret sharing schemes and let
where runs over all antichains. Then is an independent combination of perfect secret sharing schemes, and the statement follows from Lemma 4. ☐
Unfortunately, not every random variable S can be decomposed in such a way as a combination of secret sharing schemes. However, Proposition 1 suggests that, given a measure of shared information that satisfies the combined secret sharing property, can informally be interpreted as a measure that quantifies how much looks like a perfect secret sharing scheme with access structure .
Lemma 5.
Suppose that is a measure of shared information that satisfies the pairwise secret sharing property. If and are independent, then .
In the language of [11], the lemma says that the pairwise secret sharing property implies the independent identity property.
Proof.
Let , . Then is a pair of perfect secret sharing schemes with access structures and . The statement follows from Definition 5, since is not authorized for and is not authorized for . ☐
4. Incompatibility with Local Positivity
Unfortunately, although the combined secret sharing property very much fits the intuition behind the axioms of Williams and Beer, it is incompatible with a nonnegative decomposition according to the partial information lattice:
Theorem 2.
Let be a measure of shared information that satisfies the Williams–Beer axioms and has the pairwise secret sharing property. Then, is not nonnegative.
Proof.
The XOR example, which was already used by Bertschinger et al. [6] and Rauh et al. [7] to prove incompatibility results for properties of information decompositions, can also be used here.
Let be independent binary uniform random variables, let , and let . Observe that the situation is symmetric in . In particular, are also independent, and . The following values of can be computed from the assumptions:
- , since is a function of and by the monotonicity axiom.
- by Lemma 5.
By monotonicity, . Moreover, , since 2 bit is the total entropy in the system. Then, however,
where denotes values of that vanish. Thus, is not nonnegative. ☐
Note that the random variables from the proof of Theorem 2 form three perfect secret sharing schemes that do not satisfy the definition of a combination of perfect secret sharing schemes. The three secrets are not independent, but they are pair-wise independent (and so Lemma 4 does not apply).
Remark 1.
The XOR example from the proof of Theorem 2 (which was already used by Bertschinger et al. [6] and Rauh et al. [7]) was criticized by Chicharro and Panzeri [12] on the grounds that it involves random variables that stand in a deterministic functional relation (in the sense that ). Chicharro and Panzeri argue that in such a case it is not appropriate to use the full partial information lattice. Instead, the functional relationship should be used to eliminate (or identify) nodes from the lattice. Thus, while the monotonicity axiom of Williams and Beer implies (and so is not part of the partial information lattice), the same axiom also implies that in the XOR example, and so should similarly be excluded from the lattice when analyzing this particular example. Note, however, that the first argument is a formal argument that is valid for all joint distributions of , while the second argument takes into account the particular underlying distribution.
It is easy to work around this objection. The deterministic relationship disappears when an arbitrarily small stochastic noise is added to the joint distribution. To be precise, let be independent binary random variables, and let be binary with
for . For , the example from the proof is recovered. Assuming that the partial information terms depend continuously on this joint distribution, the partial information term will still be negative for small . Thus, assuming continuity, the conclusion of Theorem 2 still holds true when the information decomposition according to the full partial information lattice is only considered for random variables that do not satisfy any functional deterministic constraint.
Remark 2.
Analyzing the proof of Theorem 2, one sees that the independent identity axiom (Lemma 5) is the main ingredient to arrive at the contradiction. The same property also arises in the other uses of the XOR example [6,7].
5. Discussion
Perfect secret sharing schemes correspond to systems of random variables in which it is very clearly specified “who knows what”. In such a system, it is easy to assign intuitive values to the shared information nodes in the partial information lattice, and one may conjecture that the intuition behind this assignment is the same intuition that underlies the Williams and Beer axioms, which define the partial information lattice. Moreover, following the same intuition, independent combinations of perfect secret sharing schemes can be used as a tool to construct systems of random variables with prescribable (nonnegative) values of partial information.
Unfortunately, this extension to independent combinations of perfect secret sharing schemes is not without problems: By Theorem 2, it leads to decompositions with negative partial information terms. What does it mean, however, that the examples derived from the same intuition as the Williams and Beer axioms contradict the same axioms in this way? Is this an indication that the whole idea of information decomposition does not work (and that the question posed in the first paragraph of the introduction cannot be answered affirmatively)?
There are several ways out of this dilemma. The first solution is to assign different values to combinations of perfect secret sharing schemes. This solution will not be pursued further in this text, as it would change the interpretation of the information decomposition as measuring “who knows what”.
The second solution is to accept negative partial values in the information decomposition. It has been argued that negative values of information can be given an intuitive interpretation in terms of confusing or misleading information. For event-wise (also called “local”) information quantities, such as the event-wise mutual information , this interpretation goes back to the early days of information theory [13]. Sometimes, this phenomenon is called “misinformation” [11,14]. However, in the usual language, misinformation refers to “false or incorrect information, especially when it is intended to trick someone” [15], which is not the effect that is modelled here. Thus, the word misinformation should be avoided, in order not to mislead the reader into the wrong intuition.
While negative event-wise information quantities are well-understood, the situation is more problematic for average quantities. When an agent receives side-information in the form of the value x of a relevant random variable X, she changes her strategy. While the prior strategy should be based on the prior distribution , the new strategy should be based on the posterior . Clearly, in a probabilistic setting, any change of strategy can lead to a better or worse result in a single instance. On average, though, side-information never hurts (and it is never advantageous on average to ignore side-information), which is why the mutual information is never negative. Similarly, it is natural to expect non-negativity of other information quantities. It is difficult to imagine how correct side-information (or an aspect thereof) can be misleading on average. The situation is different for incorrect information, where the interpretation of a negative value is much easier.
More conceptually, I would suspect that an (averaged) information quantity that may change its sign actually conflates different aspects of information, just as the interaction information (or co-information) conflates synergy and redundancy [1] (and one can argue whether the same should be true for event-wise quantities; cf. [16]).
In any case, allowing negative partial values alters the interpretation of an information decomposition to a point where it is questionable whether the word “decomposition” is still appropriate. When decomposing an object into parts, the parts should in some reasonable way be sub-objects. For example, in a Fourier decomposition of a function, the Fourier components are never larger than the function (in the sense of the -norm), and the sum of the squared -norms of the Fourier coefficients equals the squared -norm of the original function. As another example, given a (positive) amount of money and two investment options, it may indeed be possible to invest a negative share of the total amount into one of the two options in order to increase the funds that can be invested in the second option. However, such short selling is regulated in many countries with much stronger rules than ordinary trading.
I do not claim that an information decomposition with negative partial information terms cannot possibly make sense. However, it has to be made clear precisely how to interpret negative terms, and it is important to distinguish between correct information that leads to a suboptimal decision due to unlikely events happening (“bad luck”) and incorrect information that leads to decisions being based on the wrong posterior probabilities (as opposed to the “correct” conditional probabilities).
A third solution is to change the underlying lattice structure of the decomposition. A first step in this direction was done by Chicharro and Panzeri [12], who propose to decompose mutual information according to subsets of the partial information lattice. However, it is also conceivable that the lattice has to be enlarged.
Williams and Beer derived the partial information lattice from their axioms together with the assumption that everything can be expressed in terms of shared information (that is, according to “who knows what”). Shared information is sometimes equivalently called redundant information, but it may be necessary to distinguish the two. Information that is shared by several random variables is information that is accessible to each single random variable, but redundancy can also arise at higher orders. An example is the infamous XOR example from the proof of Theorem 2: In this example, each pair is independent and contains of two bits, but the total system has only two bits. Therefore, there is one bit of redundancy. However, this redundancy bit is not located anywhere specifically: It is not contained in either of , and thus it is not shared information. Since the redundant bit is not part of , it is not “shared” by in this sense. This phenomenon corresponds to the fact that random variables can be pairwise independent without being independent.
This kind of higher-order redundancy does not have a place in the partial information lattice, so it may be that nodes corresponding to higher-order redundancy have to be added. When the lattice is enlarged in this way, the structure of the Möbius inversion is changed, and it is possible that the resulting lattice leads to nonnegative partial information terms, without changing those cumulative information values that are already present in the original lattice. If this approach succeeds, the answer to the question from the introduction will be negative: Simply classifying information according to “who knows what” (i.e., shared information) does not work, since it does not capture higher-order redundancy. The analysis of extensions of the partial information lattice is the scope of future work.
Acknowledgments
I thank Fero Matúš for teaching me about secret sharing schemes. I thank Guido Montúfar and Pradeep Kr. Banerjee for their remarks about the manuscript. I am grateful to Nils Bertschinger, Jürgen Jost and Eckehard Olbrich for many inspiring discussions on the topic. I thank the reviewers for many comments, in particular concerning the discussion.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Combined Secret Sharing Properties for Small k
This section discusses the defining Equation (2) of the combined secret sharing property for and . The case is incorporated in the definition of a combination of perfect secret sharing schemes: The following lemma implies that any measure of shared information that satisfies self-redundancy satisfies Equation (2) for . Recall that Williams and Beer’s self-redundancy axiom implies that .
Lemma A1.
Let be a combination of perfect secret sharing schemes with access structures . Then
Proof.
Suppose that the secret for which A is authorized are . Then
On the other hand,
By independence (remark after Definition 4), and . Thus,
The next result shows that the bivariate measure of shared information proposed by Bertschinger et al. [10] satisfies Equation (2) for . The reader is referred to loc. cit. for definitions and elementary properties of .
Proposition A1.
Let be a combination of perfect secret sharing schemes with access structures , Then
Proof.
For given , suppose that are the secrets for which at least one of or is authorized and that are the secrets for which neither nor is authorized alone.
Let P be the joint distribution of . Let be the set of alternative joint distributions for that have the same marginal distributions as P on the subsets and . According to the definition of , we need to compare P with the elements of and find the maximum of over , where the subscript to H indicates with respect to which of these joint distributions the conditional entropy is evaluated.
Define a distribution for by
Then . Under P, the secrets are independent of (marginally) and independent of , and so are independent of the pair under . On the other hand, are a function of either or under P, and so is a function of under . Thus,
On the other hand, under any joint distribution , the secrets are functions of , whence
It follows that solves the optimization problem in the definition of .
Suppose that the secrets for which is authorized are and that the secrets for which is authorized are (with ). One computes
whence
References
- Williams, P.; Beer, R. Nonnegative Decomposition of Multivariate Information. arXiv 2010, arXiv:1004.2515v1. [Google Scholar]
- Beimel, A. Secret-Sharing Schemes: A Survey. In Proceedings of the Third International Conference on Coding and Cryptology, Qingdao, China, 30 May– 3 June 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 11–46. [Google Scholar]
- Maurer, U.; Wolf, S. The Intrinsic Conditional Mutual Information and Perfect Secrecy. In Proceedings of the 1997 IEEE International Symposium on Information Theory, Ulm, Germany, 29 June–4 July 1997. [Google Scholar]
- Csiszar, I.; Narayan, P. Secrecy capacities for multiple terminals. IEEE Trans. Inf. Theory 2004, 50, 3047–3061. [Google Scholar] [CrossRef]
- Ito, M.; Saito, A.; Nishizeki, T. Secret Sharing Scheme Realizing General Access Structure. In Proceedings of the IEEE Global Telecommunication Conference, Tokyo, Japan, 15–18 November 1987; pp. 99–102. [Google Scholar]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J. Shared Information—New Insights and Problems in Decomposing Information in Complex Systems. In Proceedings of the European Conference on Complex Systems; Springer: Berlin/Heidelberg, Germany, 2013; pp. 251–269. [Google Scholar]
- Rauh, J.; Bertschinger, N.; Olbrich, E.; Jost, J. Reconsidering Unique Information: Towards a Multivariate Information Decomposition. In Proceedings of the 2014 IEEE International Symposium on 2014 Information Theory (ISIT), Honolulu, HI, USA, 29 June–4 July 2014; pp. 2232–2236. [Google Scholar]
- Barrett, A.B. An exploration of synergistic and redundant information sharing in static and dynamical Gaussian systems. Phys. Rev. E 2014, 91, 52802. [Google Scholar] [CrossRef] [PubMed]
- Harder, M.; Salge, C.; Polani, D. A Bivariate measure of redundant information. Phys. Rev. E 2013, 87, 12130. [Google Scholar] [CrossRef] [PubMed]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying unique information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Ince, R. Measuring multivariate redundant information with pointwise common change in surprisal. Entropy 2017, 19, 38. [Google Scholar] [CrossRef]
- Chicharro, D.; Panzeri, S. Synergy and Redundancy in Dual Decompositions of Mutual Information Gain and Information Loss. Entropy 2017, 19, 71. [Google Scholar] [CrossRef]
- Fano, R.M. Transmission of Information; MIT Press: Cambridge, MA, USA, 1961. [Google Scholar]
- Wibral, M.; Lizier, J.T.; Priesemann, V. Bits from Brains for Biologically Inspired Computing. Front. Robot. AI 2015, 2, 5. [Google Scholar] [CrossRef]
- Macmillan Publishers Limited. Macmillan Dictionary. Available online: http://www.macmillandictionary.com/ (accessed on 15 March 2012).
- Ince, R. The Partial Entropy Decomposition: Decomposing multivariate entropy and mutual information via pointwise common surprisal. arXiv 2017, arXiv:1702.01591. [Google Scholar]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).