Thermoeconomic Coherence: A Methodology for the Analysis and Optimisation of Thermal Systems
Abstract
:1. Introduction
2. Theoretical Background and Conventional Approaches
2.1. General Case: Optimization without Constraints
2.1.1. Minimization of the Generation Cost
2.1.2. Maximization of the Yearly Cash Flow
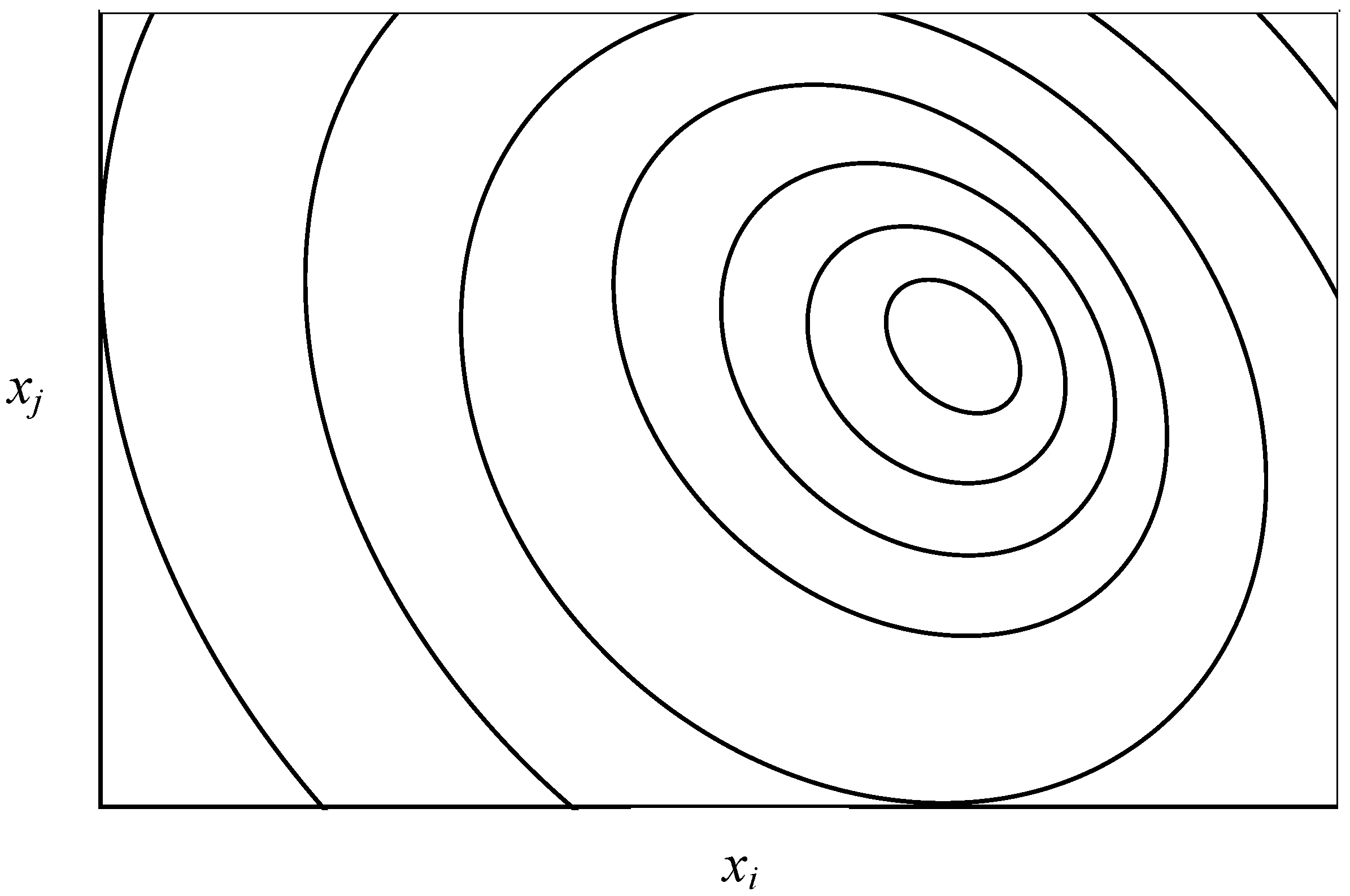
2.2. Optimization Subjected to Constraints
2.2.1. Conventional Approach
2.2.2. Lagrange Multipliers
3. Proposed Methodology: Corrected Standardised Marginal Costs and Divergence from the Coherent Design
3.1. Equivalent Standardised Marginal Costs
3.2. Corrected Standardised Marginal Costs
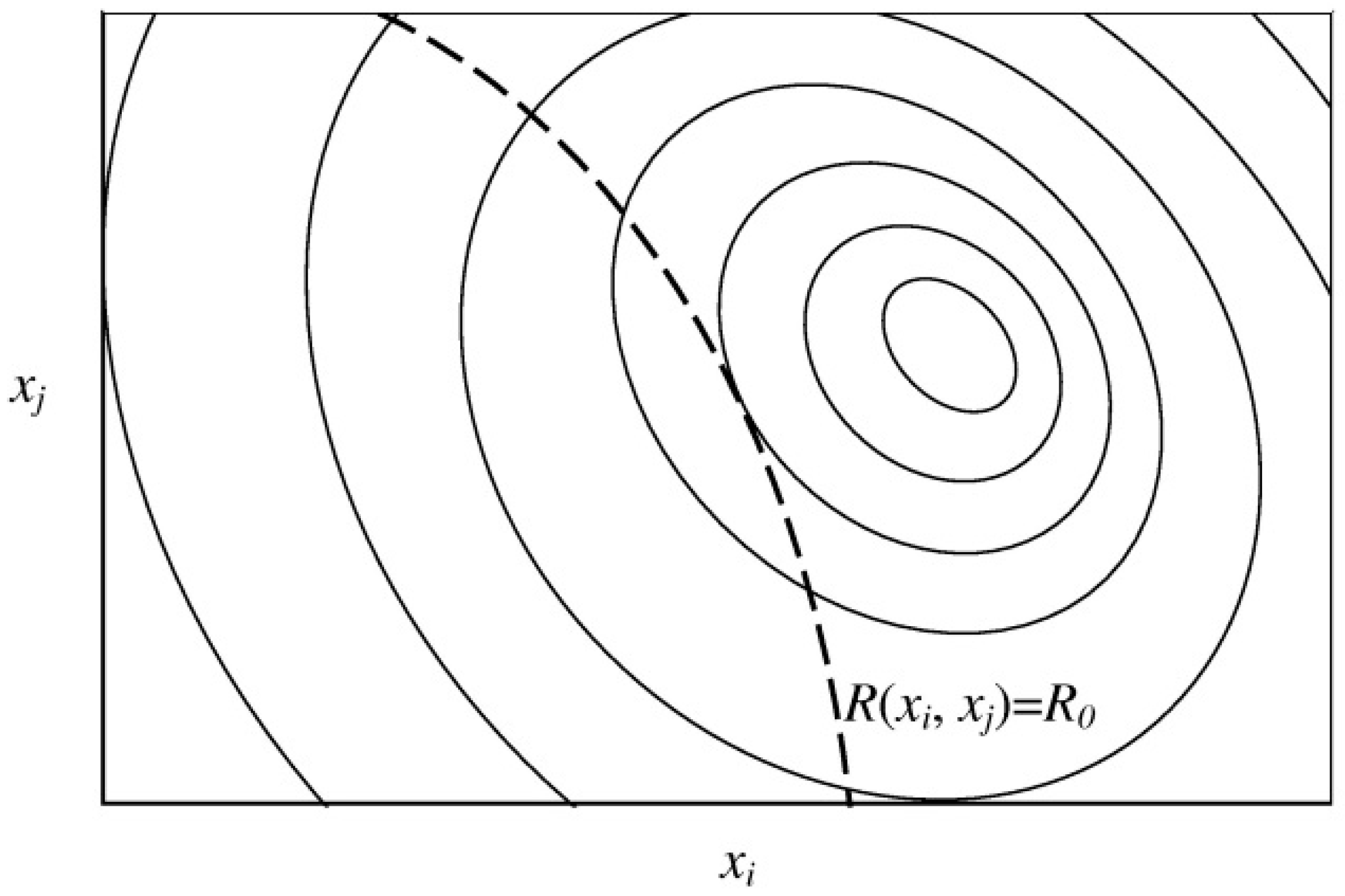
3.3. Divergence from the Coherent Design
- It should be congruent for all the possible sets of design parameters of a system (independence of the coordinate system);
- It should allow the comparison of the coherence of different facilities with independence of the objective function, its value in the optimum and its number of degrees of freedom;
- The divergence should be zero at the optimum.
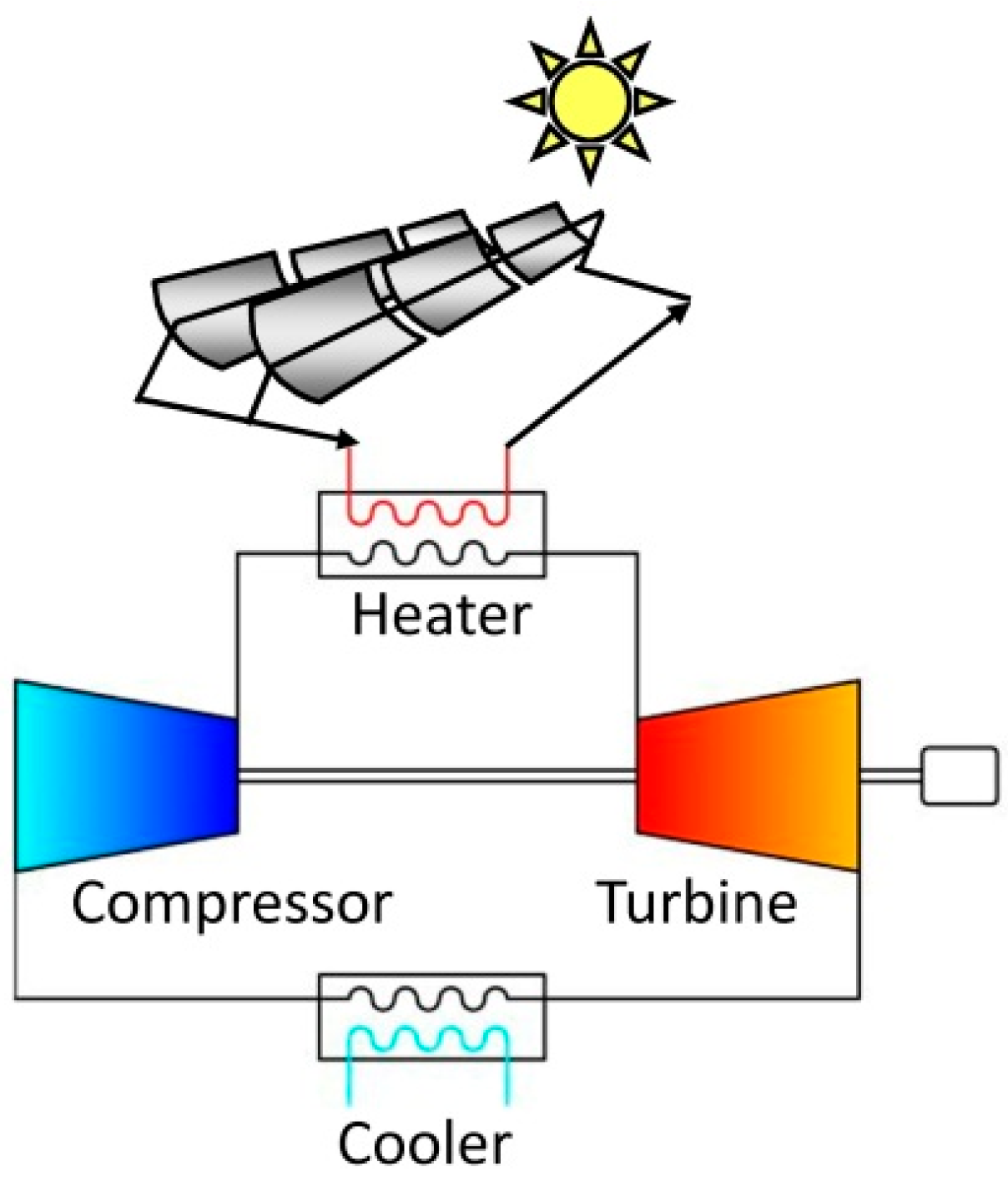
4. Application Example: Coherence in a Solar Gas Turbine
- The pressure ratio (intensive parameter) is replaced by the ratio of the compressor power to the thermal power supplied to the system ().
- The effectiveness (intensive parameter) of the heater and cooler are replaced by the ratio of their irreversibility to the thermal power supplied to the system ().
- The maximum temperature of the solar field (intensive parameter) is replaced by the ratio of the exergy content of the thermal power to the supplied thermal power ().
- The mass flow (the extensive parameter) is replaced by the thermal power supplied to the system ().
5. Extension of the Methodology to Robustness and Uncertainty Analysis and Combined Heat and Power
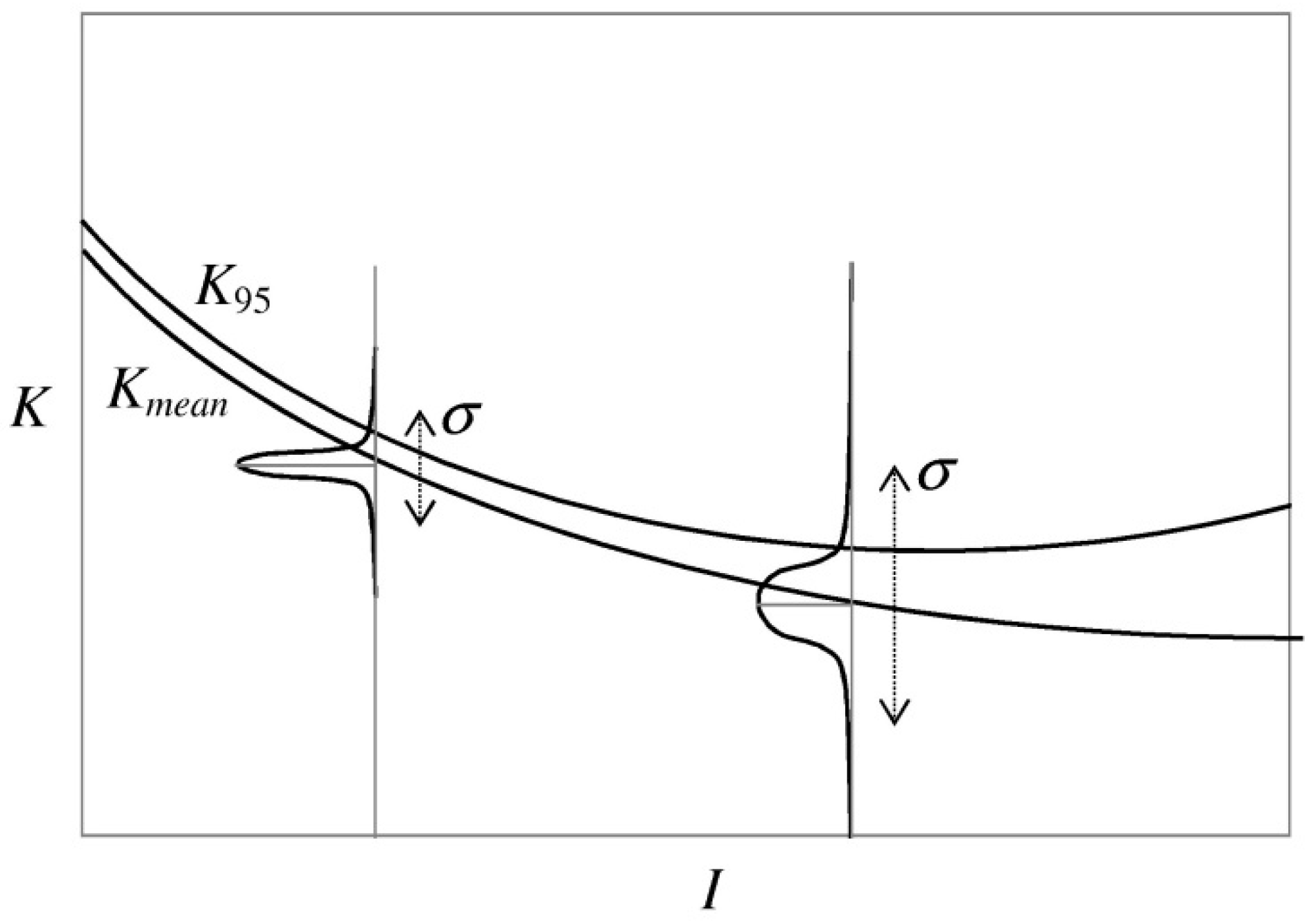
5.1. Robustness and Uncertainty: Optimization in Economy of Scales
5.2. Combined Heat and Power
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Acronyms | |
| CGAM | CHP problem defined in [11] |
| CHP | Combined heat and power |
| LCOE | Levelized cost of energy |
| Mu | Monetary units |
| O&M | Operation & maintenance cost |
| TADEUS | Thermoeconomic Approach to the Diagnosis of Energy Utility System Malfunctions [12] |
| Symbols | |
| A | Amortisation cost (monetary units, mu); Constant of the probability distributions |
| C | Acquisition cost (mu) |
| CF | Cash flow (mu) |
| d | Normalized marginal cost (-) |
| D | Divergence (-) |
| E | Exploitation cost (mu) |
| Exergy content of the thermal power (W) | |
| f | generic function |
| F | Fuel cost (mu) |
| Irreversibility (W) | |
| Itotal | Total investment (mu) |
| K | Generation cost (mu·J−1) |
| m | safety coefficient, number of variables including the economic frame |
| Mass flow rate (kg·s−1) | |
| M | Marginal cost (mu·J−1) |
| n | Number of degrees of freedom |
| P | Yearly production of the plant (J) |
| Thermal power rate at the heat source (W) | |
| R | Restriction |
| Tit | Turbine inlet temperature (K) |
| Texh | Turbine exhaust temperature (K) |
| Tmax | Maximum temperature of the solar field (K) |
| UA | Product of the overall heat transfer coefficient and the heat exchange area (W·K−1) |
| V | Selling price of the product (mu·J−1) |
| Compressor power (W) | |
| x | Original design parameters |
| y | Standardized variables |
| Greek letters | |
| Δ | increment |
| ε | Heat exchanger effectiveness (-) |
| η | thermal efficiency (-) |
| Λ | Lagrange multiplier |
| Π | pressure ratio (-) |
| Σ | Variance |
| Subscripts | |
| cool | Cooler |
| comp | Compressor |
| GT | Gas turbine |
| heat | Heater |
| solar | Solar field |
| turb | Turbine |
Appendix
References
- Bejan, A.; Tsatsaronis, G.; Moran, M. Thermal design and optimization, 1st ed.; John Wiley & sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Attala, L.; Facchini, B.; Ferrara, G. Thermoeconomic Optimization Method as Design Tool in Gas-Steam Combined Plant Realization. Energy Convers. Manag. 2001, 42, 2163–2172. [Google Scholar] [CrossRef]
- Valdés, M.; Durán, M.D.; Rovira, A. Thermoeconomic optimization of combined cycle gas turbine using genetic algorithms. Appl. Therm. Eng. 2003, 23, 2169–2182. [Google Scholar] [CrossRef]
- International Renewable Energy Agency. Available online: http://www.irena.org/documentdownloads/publications/re_technologies_cost_analysis-csp.pdf (assessed on 1 July 2016).
- Energy Information Administration. Available online: https://www.eia.gov/forecasts/aeo/pdf/electricity_generation.pdf (assessed on 1 July 2016).
- Evans, R.B. A Contribution to the Theory of Thermoeconomics. Master’s Thesis, University of California, Los Angeles, CA, USA, 1961. [Google Scholar]
- El-Sayed, Y.M.; Evans, R.B. Thermoeconomics and the Design of Heat Systems. Trans. ASME J. Eng. Power 1970, 92, 27–34. [Google Scholar] [CrossRef]
- Tsatsaronis, G.; Winhold, M. Exergoeconomic Analysis and Evaluation of Energy Conversion Plants—I. A New General Methodology. Energy 1985, 10, 69–80. [Google Scholar] [CrossRef]
- Frangopoulos, C.A. Thermo-Economic Functional Analysis and Optimization. Energy 1987, 12, 563–571. [Google Scholar] [CrossRef]
- Lozano, M.A.; Valero, A. Theory of the Exergetic Cost. Energy 1993, 18, 39–60. [Google Scholar] [CrossRef]
- Valero, A.; Lozano, M.A.; Serra, L.; Tsatsaronis, G.; Pisa, J.; Frangopoulos, C.A.; von Spakovsky, M. CGAM Problem: Definition and Conventional Solution. Energy 1994, 19, 279–286. [Google Scholar] [CrossRef]
- Valero, A.; Correas, L.; Zaleta, A.; Lazzaretto, A.; Verda, V.; Reini, M.; Rangel, V. On the thermoeconomic approach to the diagnosis of energy system malfunctions—Part 1: the TADEUS problem. Energy 2004, 29, 1875–1887. [Google Scholar] [CrossRef]
- Petrakopoulou, F.; Tsatsaronis, G.; Morosuk, T.; Carassai, A. Advanced Exergoeconomic Analysis Applied to a Complex Energy Conversion System. J. Eng. Gas Turbines Power 2012, 134. [Google Scholar] [CrossRef]
- Li, H.; Chen, J.; Sheng, D.; Li, W. The improved distribution method of negentropy and performance evaluation of CCPPs based on the structure theory of thermoeconomics. Appl. Therm. Eng. 2016, 96, 64–75. [Google Scholar] [CrossRef]
- Modi, A.; Kærn, M.R.; Andreasen, J.G.; Haglind, F. Thermoeconomic optimization of a Kalina cycle for a central receiver concentrating solar power plant. Energy Convers. Manage. 2016, 115, 276–287. [Google Scholar] [CrossRef]
- Baral, S.; Kim, D.; Yun, E.; Kim, K.C. Experimental and Thermoeconomic Analysis of Small-Scale Solar Organic Rankine Cycle (SORC) System. Entropy 2015, 17, 2039–2061. [Google Scholar] [CrossRef]
- Ozcan, H.; Dincer, I. Exergoeconomic optimization of a new four-step magnesiumechlorine cycle. Int. J. Hydrog. Energy. in press. [CrossRef]
- Keshavarzian, S.; Gardumi, F.; Rocco, M.V.; Colombo, E. Off-Design Modeling of Natural Gas Combined Cycle Power Plants: An Order Reduction by Means of Thermoeconomic Input–Output Analysis. Entropy 2016, 18. [Google Scholar] [CrossRef]
- Piacentino, A. Application of advanced thermodynamics, thermoeconomics and exergy costing to a Multiple Effect Distillation plant: In-depth analysis of cost formation process. Desalination 2015, 371, 88–103. [Google Scholar] [CrossRef]
- Dechamps, P.J. Incremental cost optimization of Heat Recovery Steam Generators; 95-CTP-101; The American Society of Mechanical Engineers: New York, NY, USA, 1995. [Google Scholar]
- Dechamps, P.J. The optimization of combined cycle HRSGs as a function of the plant load duty. In Proceedings of the ASME 1996 International Gas Turbine and Aeroengine Congress and Exhibition, Birmingham, UK, 10–13 June 1996.
- Kirschen, D.; Strbac, G. Fundamentals of Power System Economics; John Wiley & sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Valdés, M.; Rovira, A.; Durán, M.D. Influence of the heat recovery steam generator design parameters on the thermoeconomic performances of combined cycle gas turbine power plants. Int. J. Energy Res. 2004, 28, 1243–1254. [Google Scholar] [CrossRef]
- Stoecker, W.F. Design of Thermal Systems, 3rd ed.; MacGraw-Hill Book Company: New York, NY, USA, 1989. [Google Scholar]
- Jaluria, Y. Design and Optimization of Thermal Systems, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Shore, J.E.; Johnson, R.W. Axiomatic Derivation of the Principle of Maximum Entropy and the Principle of Minimum Cross-Entropy. IEEE Trans. Inform. 1980, 26, 26–37. [Google Scholar] [CrossRef]
- Zare, V.; Mahmoudi, S.M.S.; Yari, M. An exergoeconomic investigation of waste heat recovery from the Gas Turbine-Modular Helium Reactor (GT-MHR) employing an ammonia—water power/cooling cycle. Energy 2013, 61, 397–409. [Google Scholar] [CrossRef]
- Ghaebi, H.; Amidpour, M.; Karimkashi, S.; Rezayan, O. Energy, exergy and thermoeconomic analysis of a combined cooling, heating and power (CCHP) system with gas turbine prime mover. Int. J. Energy Res. 2011, 35, 697–709. [Google Scholar] [CrossRef]
- Rovira, A.; Barbero, R.; Montes, M.J.; Abbas, R.; Varela, F. Analysis and comparison of Integrated Solar Combined Cycles using parabolic troughs and linear Fresnel reflectors as concentrating systems. Appl. Energy 2016, 162, 990–1000. [Google Scholar] [CrossRef]
| Component | Costing Model | Reference |
|---|---|---|
| Compressor | [27,28] 1 | |
| Turbine | [27,28] 1 | |
| Heat exchangers | [2,28] 1,2 | |
| Solar field | [29] 1,3 |
| Design Parameters | Marginal Cost Regarding Design Parameters | ||
|---|---|---|---|
| π | 8 | Mπ (mu/GWh) | 0.076 |
| εheat | 80% | Mεheat (mu/GWh) | 0.429 |
| εcool | 95% | Mεcool (mu/GWh) | 2.491 |
| (kg/s) | 50 | Mm (mu/GWh) | 0.803 |
| Tmax (K) | 900 | MTmax (mu/GWh) | 0.140 |
| Results | |||
| Compressor cost (mu) | 28.3 | ||
| Turbine cost (mu) | 21.0 | ||
| Heater cost (mu) | 20.8 | ||
| Cooler cost (mu) | 72.3 | ||
| Solar field cost (mu) | 45.5 | ||
| Exploitation cost (mu) | 12.5 | ||
| Yearly production (GWh) | 10.5 | ||
| Generation cost (mu/GWh) | 1.198 | ||
| Base | (1) Constant I | (2) Constant P | (3) Constant P + Texh | (4) Constant P + Tit | |
|---|---|---|---|---|---|
| π | 8 | 4.92 | 4.85 | 7.25 | 4.29 |
| εheat | 80% | 80.9% | 80.3% | 62.2% | 71.4% |
| εcool | 95% | 86.4% | 86.0% | 89.6% | 85.7% |
| (kg/s) | 50 | 64.7 | 38.9 | 64.9 | 46.6 |
| Tmax (K) | 900 | 966.7 | 966.9 | 957.0 | 959.4 |
| Texh (K) | 499.4 | 595.7 | 596.1 | 499.4 | 580.5 |
| Tit (K) | 836.7 | 887.7 | 885.6 | 817.3 | 836.7 |
| Ccomp (mu) | 28.3 | 25.1 | 23.0 | 29.3 | 22.9 |
| Cturb (mu) | 21.0 | 21.0 | 20.6 | 21.3 | 20.7 |
| Cheat (mu) | 20.8 | 26.7 | 17.3 | 12.6 | 13.5 |
| Ccool (mu) | 72.3 | 37.1 | 23.9 | 47.3 | 27.1 |
| Csolar (mu) | 45.5 | 78.1 | 48.1 | 53.7 | 51.9 |
| Itotal (um) | 188.0 | 188.0 | 132.9 | 164.2 | 136.1 |
| E (um/year) | 12.5 | 12.5 | 8.86 | 10.9 | 9.08 |
| P (GWh) | 10.5 | 17.7 | 10.5 | 10.5 | 10.5 |
| K (mu/GWh) | 1.198 | 0.707 | 0.847 | 1.046 | 0.868 |
| ηGT | 20.7% | 20.5% | 20.2% | 17.5% | 18.3% |
| (mu/GWh) | Base | (1) Constant I | (2) Constant P | (3) Constant P + Texh | (4) Constant P + Tit | |
|---|---|---|---|---|---|---|
| Design parameters | Mπ | 0.076 | 0.496 | 0.518 | 0.066 | 0.997 |
| Mεheat | 0.429 | 0.496 | 0.518 | 0.235 | 0.364 | |
| Mεcool | 2.491 | 0.496 | 0.518 | 0.871 | 0.582 | |
| Mm | 0.803 | 0.496 | 0.518 | 0.694 | 0.539 | |
| MTmax | 0.140 | 0.496 | 0.518 | 0.235 | 0.364 | |
| Standardised | MWc | 1.045 | 0.496 | 0.518 | 0.093 | 0.334 |
| MIheater | 0.891 | 0.496 | 0.518 | 0.196 | 0.232 | |
| MIcool | 4.786 | 0.496 | 0.518 | 1.299 | 0.483 | |
| MEQ | 0.063 | 0.496 | 0.518 | 0.196 | 0.232 | |
| MQ | 0.803 | 0.496 | 0.518 | 0.694 | 0.539 | |
| (mu/GWh) | (1) Constant I | (2) Constant P | (3) Constant P + Texh | (4) Constant P + Tit | |
|---|---|---|---|---|---|
| Optimised | cMcomp | 0.707 | 0.847 | 1.046 | 0.868 |
| cMturb | 0.707 | 0.847 | 1.046 | 0.868 | |
| cMheat | 0.707 | 0.847 | 1.046 | 0.868 | |
| cMcool | 0.707 | 0.847 | 1.046 | 0.868 | |
| cMsolar | 0.707 | 0.847 | 1.046 | 0.868 | |
| λr | −1.6 × 10−3 | −3.2 × 10−2 | −3.4 × 10−2 (P) −6.2 × 10−3 (Texh) | −3.1 × 10−2 (P) −7.7 × 10−4 (Tit) | |
| Base case | cMWc | 0.345 | 0.919 | 2.353 | –1.343 |
| cMIheater | 0.294 | 0.765 | 1.603 | 1.617 | |
| cMIcool | 1.578 | 4.660 | 1.203 | 1.251 | |
| cMEQ | 0.021 | –0.063 | 0.775 | 0.789 | |
| cMQ | 0.265 | 0.677 | –0.394 | –3.305 | |
| λr | 4.3 × 10−3 | 1.2 × 10−2 | 0.11 (P) −2.0 × 10−2 (Texh) | 0.39 (P) −1.2 × 10−2 (Tit) | |
| (mu/GWh) | Base | (1) Constant I | (2) Constant P | (3) Constant P + Texh | (4) Constant P + Tit |
|---|---|---|---|---|---|
| DWc | –0.001 | –0.067 | –0.088 | –0.054 | –0.120 |
| DIheater | 0.002 | –0.067 | –0.088 | –0.064 | –0.111 |
| DIcool | 1.405 | –0.067 | –0.088 | 0.121 | –0.120 |
| DEQ | 0.035 | –0.067 | –0.088 | –0.064 | –0.111 |
| DQ | 0.004 | –0.067 | –0.088 | –0.079 | –0.114 |
| D | 1.084 | 0.059 | 0.108 | 0.353 | 0.281 |
| (mu/GWh) | (1) Constant I | (2) Constant P | (3) Constant P + Texh | (4) Constant P + Tit | |
|---|---|---|---|---|---|
| Optimised | DWc | −2.1 × 10−6 | 1.6 × 10−6 | 1.3 × 10−6 | 2.6 × 10−8 |
| DIheater | −2.1 × 10−6 | 1.2 × 10−7 | 9.5 × 10−7 | 1.1 × 10−6 | |
| DIcool | 2.1 × 10−8 | 2.6 × 10−6 | −4.3 × 10−8 | −2.7 × 10−8 | |
| DEQ | 2.1 × 10−6 | −1.9 × 10−6 | −1.0 × 10−6 | −1.2 × 10−6 | |
| DQ | 1.4 × 10−6 | 3.7 × 10−6 | 4.0 × 10−6 | 1.5 × 10−6 | |
| D | 7.6 × 10−11 | 1.1 × 10−10 | 8.3 × 10−11 | 2.4 × 10−11 | |
| Base case | DWc | –0.029 | –0.001 | 0.466 | 0.023 |
| DIheater | –0.025 | 0.002 | 0.105 | 0.062 | |
| DIcool | 0.740 | 1.694 | 0.017 | 0.014 | |
| DEQ | 0.004 | 0.034 | –0.011 | 0.001 | |
| DQ | –0.022 | 0.005 | 0.003 | 0.876 | |
| D | 0.620 | 1.383 | 0.325 | 0.608 | |
| Homogeneous Variance Variation | Variance Variation with Tmax | Homogeneous Variance variation | Variance Variation with Tmax | ||
|---|---|---|---|---|---|
| π | 4.82 | 4.78 | K (mu/GWh) | 0.972 | 0.849 |
| εheat | 80.0% | 80.3% | K95 | 1.192 | 1.247 |
| εcool | 85.7% | 85.9% | ηGT | 20.1% | 20.0% |
| (kg/s) | 28.3 | 39.8 | Mπ | 0.532 | 0.519 |
| Tmax (K) | 967.0 | 960.0 | Mεheat | 0.532 | 0.519 |
| Texh (K) | 596.3 | 594.1 | Mεref | 0.532 | 0.519 |
| Tit (K) | 884.4 | 879.3 | Mm | 0.532 | 0.519 |
| Ccomp (mu) | 22.1 | 23.0 | MTmax | 0.532 | 0.348 |
| Cturb (mu) | 20.4 | 20.6 | Dπ | –0.036 | –0.032 |
| Cheat (mu) | 13.2 | 17.6 | Dεheat | –0.036 | –0.032 |
| Ccool (mu) | 18.3 | 24.3 | Dεref | –0.036 | –0.032 |
| Csolar (mu) | 35.9 | 47.8 | Dm | –0.036 | –0.032 |
| Itotal (mu) | 109.9 | 133.3 | DTmax | –0.036 | –0.035 |
| E (mu/year) | 7.33 | 8.88 | D | 0.153 | 0.140 |
| P (GWh) | 7.54 | 10.5 | m | 0.827 | 0.253 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rovira, A.; Martínez-Val, J.M.; Valdés, M. Thermoeconomic Coherence: A Methodology for the Analysis and Optimisation of Thermal Systems. Entropy 2016, 18, 250. https://doi.org/10.3390/e18070250
Rovira A, Martínez-Val JM, Valdés M. Thermoeconomic Coherence: A Methodology for the Analysis and Optimisation of Thermal Systems. Entropy. 2016; 18(7):250. https://doi.org/10.3390/e18070250
Chicago/Turabian StyleRovira, Antonio, José María Martínez-Val, and Manuel Valdés. 2016. "Thermoeconomic Coherence: A Methodology for the Analysis and Optimisation of Thermal Systems" Entropy 18, no. 7: 250. https://doi.org/10.3390/e18070250
APA StyleRovira, A., Martínez-Val, J. M., & Valdés, M. (2016). Thermoeconomic Coherence: A Methodology for the Analysis and Optimisation of Thermal Systems. Entropy, 18(7), 250. https://doi.org/10.3390/e18070250







