Abstract
Recently a short scale modified black hole metric, known as holographic metric, has been proposed in order to capture the self-complete character of gravity. In this paper we show that such a metric can reproduce some geometric features expected from the quantum N-portrait beyond the semi-classical limit. We show that for a generic N this corresponds to having an effective energy momentum tensor in Einstein equations or, equivalently, non-local terms in the gravity action. We also consider the higher dimensional extension of the metric and the case of an AdS cosmological term. We provide a detailed thermodynamic analysis of both cases, with particular reference to the repercussions on the Hawking-Page phase transition.
1. Introduction
Black holes are among the most fascinating and mysterious objects in Physics and are subject to an intense theoretical and observational research activity. Astrophysical black holes, whose masses typically range from few solar masses to billions of solar masses, are pretty well described by general relativity. There might exist, however, a new breed of black holes with masses below , that have been produced in early Universe epochs due to the extreme matter density fluctuations [1] and/or for quantum mechanical decay of de Sitter space [2,3,4]. Such black holes, one can term microscopic black holes, have sizes of elementary particles and are subject to quantum mechanical effects. Even if the existence of microscopic black holes still needs corroboration from experiments and observations, they are extremely interesting since they represent one of the crucial challenges to our understanding of fundamental physics. In the mid 1970’s, Hawking showed that quantum effects allow black holes for evaporating, i.e., emitting a thermal spectrum of particles like a black body [5]. This fact has supported the idea of black hole thermodynamics. Black holes have a temperature proportional to their surface gravity and an entropy proportional to their horizon area. Such an intriguing scenario is, however, not free of problems. Static, spherically symmetric black holes have a negative heat capacity. This is equivalent to saying that, while emitting particles, they shrink and become hotter and hotter. The process is runaway and the destiny of an evaporating black hole is, in general, still unknown. Another issue concerns the statistical interpretation of the black hole entropy. We still miss a complete understanding of the microscopic degrees of freedom that support the entropy/area law in the thermodynamic limit. A related problem concerns the information loss. This arises already at classical level. The collapsing star microstates become inaccessible when the event horizon forms. The Hawking radiation, however, aggravates the situation. The initial stellar particle pure state would evolve into a mixed state of thermally distributed particles, in marked contrast with one of the principles of quantum mechanics (see [6,7,8,9,10,11] for recent discussions on the topic).
It is believed that the open problems listed above can only be solved by the ultraviolet completion of the gravitational field. In other words, at short scales, i.e., lengths of the order of the Planck length, the spacetime description in terms of general relativity breaks down and a quantum theory of gravity must be invoked. This explains the great interest in new black hole models able to account for quantum gravity effects in place of the classical curvature singularity (see e.g., [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]). It is interesting to note that these models tend to converge towards a unique scenario: the singularity is removed or softened; the evaporating black hole undergoes a phase transition prior the final stages of evaporation, switching from a negative heat capacity warming to a positive heat capacity cooling down. Ultimately the black hole approaches a zero temperature stable black hole remnant configuration. Alternatives to the above scenario are offered by the Planck star [28] and by some models inspired by the generalized uncertainty principle that allow for either the formation of hot remnants [29] or of sub-Planckian black holes [30] (for recent reviews see [31,32,33,34,35]).
Recently there has been a growing conviction that black holes might have an intrinsically new description (known as quantum N-portrait), alternative and complementary to what one can deduce from a semiclassical, geometric arguments. Theoretical evidence is supporting the idea that a black hole is a bound state or better a condensate of N gravitons, whose quantum interaction strength is [36,37]. This conjecture is reminiscent of the fuzzball proposal for black holes, whose entropy is described in terms of a bound (BPS) state of parallel branes [38,39,40,41,42]. The parameter N is related to the pixelization of the event horizon in fundamental qubits, as it emerges from the black hole holographic entropy [43,44]
where is the size of the black hole and is the Planck length. Accordingly one finds and the black holes mass , with the Planck mass. In this picture, the Hawking radiation corresponds to the quantum depletion of the condensate that produces a thermal spectrum with [45]. The black-hole-condensate is supposed to be formed in an extreme energy graviton scattering process [46]. More precisely the black hole is an intermediate state between two asymptotic states, and . Both quantum field theory and string theory calculations in the large N limit confirm that each final state in the reverse process is exponentially suppressed by a factor depending on the black hole entropy . [46]. The above scenario is supposed to affect all black hole formation mechanisms. These also include the gravitational collapse that in its final stages concerns matter and energy interacting at length scales of the order of the Planck length, . As a result, the quantum N-portrait efficiently describes black holes in all mass regimes—black hole macroquantumness [47]—including those one typically encounters in astrophysics.
The quantum N-portrait proposal has generated a considerable follow-up work, most notably in relation to the so called “horizon wave function” (HWF) formalism. The latter is a formulation in which one attributes to any quantum mechanical particle a wave function for the gravitational radius [48,49,50,51,52,53]. In doing so, one obtain probabilistic conditions to distinguish black holes from elementary particles (for a recent review see [54]). As a by-product, the HWF naturally encodes the generalized uncertainty principle for the particle position and the black hole decay rate.
Interestingly, the black hole quantum N-portrait helps to understand the very nature of gravity, that is self-complete in the ultraviolet regime. This means that gravity prevents us from probing length scales shorter than . In a trans-Planckian center of mass energy scattering, , all states “classicalize”, i.e., they conceal to form a classical black hole [55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70]. Both quantum field theory and string theory calculations in the large N limit show that the black hole configuration dominates over other non-black hole classical states [46]. The higher is the energy , the higher is the occupation number N of non-propagating gravitons and the larger are the probed length scales. Accordingly also the problem of gravity bad short distance behavior, i.e., curvature singularities, is ultimately circumvented.
Within the black hole quantum N-portrait paradigm, one recovers, in the large N-limit, the geometric picture of black holes in terms of the Schwarzschild metric [45,71]. On the ground of mere geometric considerations, the Schwarzschild metric is, however, in conflict with the self-complete character of gravity. Solutions of Einstein equations can exist irrespective of any lower bound for the black hole mass. For , there is a scale ambiguity, due to the coexistence of Compton wavelengths and Schwarzschild radii. In principle, a Schwarzschild black hole can probe sub-Planckian length scales by decaying through the Hawking radiation (see Figure 1a). Of course, this scenario cannot be fully trusted due to a breakdown of the semiclassical description at the Planck scale. One expects that in the strong coupling regime, gravity actually deviates from Einstein gravity. To this purpose, an array of formulations have been proposed to consistently modify the Einstein-Hilbert action, e.g.,
where is the covariant D’Alembertian and dots stand for higher derivative terms (for a review see [72]). Accordingly, the geometric picture is also supposed to depart from the Schwarzschild geometry. In the absence of further indications from the quantum N-portrait beyond the large N limit, one can only rely on ultraviolet improved gravity theories to draw scenarios of black holes close to the Planck scale.

Figure 1.
Size vs. Energy relation in Planck units. (a) the size of particles, estimated by the Compton wavelength , compared to the size of black holes, determined by Schwarzschild radius . The shaded area is inaccessible. At sub-Planckian energy scales, a length scale ambiguity arises; (b) the self-complete gravity paradigm proposes a solution.
Given such a background, a new metric, obtained by a process of black hole engineering, has recently been proposed in order to capture all the desiderata of the quantum N-portrait for any N [73]. In a nutshell, such a metric, known as holographic metric, enjoys the following properties:
- (i)
- the metric admits an extremal configuration for a black hole mass and radius ;
- (ii)
- the extremal configuration represents the fundamental qubit of the system; any larger black holes are governed by a unique universal parameter N, which is set via a holographic relation similar to that between voxels and pixels [44];
- (iii)
- the metric coincides with the Schwarzschild metric away from the Planck scale, i.e., in the limit.
Notably the holographic metric fulfils the self-complete gravity paradigm. At the Planck scale one has a single graviton system represented by an extremal black hole configuration. The evaporation stops there and it is no longer possible to probe distances below the Planck length. Accordingly the ambiguity between particles and black holes for is removed (see Figure 1b). At length scales , the geometric picture of the spacetime virtually ceases to exist, being inaccessible both via a particle compression or a black hole decay.
In this paper, we present the higher-dimensional extension of the holographic metric and we address the issue of the presence of a negative cosmological constant term. The paper is organized as follows: in Section 2, we recap the properties of the holographic metric and we provide an alternative derivation based on nonlocal gravity equations [23,25,74]; in Section 3 we extend our findings to the case of large extra-dimensions; in Section 4, we accommodate the metric in a Anti-deSitter (AdS) background and we analyze the related thermodynamics. Finally in Section 5, we draw our conclusions.
2. Holographic Metric in -dimensions
In this section we recap the properties of the holographic metric. Following the lines in [73], we consider the energy density for a point particle in spherical coordinates as
As far as , one does not expect that the spacetime will significantly deviate from Minkowski space. Being particles characterized by a size (as noted in [63], one refers to distances and energies measured in the center of mass reference frame as seen from an ADM observer at spatial infinity), the curvature turns to be at the most . On the other hand, Einstein’s equations allow for gravitational collapse for any M. As a result, one has that Equation (3) can also accommodate black holes for any sub-Planckian mass M.
Before proceeding we recall that Equation (3) can be written in terms of the Heaviside function, being . The sharp step function is, however, believed to be modified by wild quantum disturbances at the Planck scale. This suggests that has to be replaced by a smooth function , accounting for the average of the quantum gravity fluctuations. The exact profile of the is, in general, not known. In the absence of theoretical indications or experimental constraints, we can reduce the class of profiles of only by invoking some guiding principles, e.g., the self-complete character of gravity. In doing so, we aim to remove the particle-black hole ambiguity of the Schwarzschild geometry in the sub-Planckian regime. To reach this goal, we need to derive a metric admitting an extremal configuration, whose size (radius and mass) sets the characteristic scales of gravity.
We proceed by keeping general and we express Equation (3) as
The above energy density is no longer infinitesimally narrow. This means that there exists a non-vanishing energy momentum tensor, whose time-time mixed component, , is determined by Equation (4). All non-classical phenomena are incorporated in such an effective energy momentum tensor. The procedure allows for the derivation of a Schwarzschild-like geometry with a mass profile which collects all deviations from Einstein gravity, i.e.,
Here the function is given by
where the boundary condition as has been used to fix the integration constant. The conservation equation and the “clean black hole condition” univocally determine the effective energy momentum tensor with equation of state and angular pressure . The profile of corresponds to the case of an anisotropic fluid peaked at the origin and leads to a local violation of energy conditions. Energy momentum tensors of this kind have already been employed in a variety of black hole models aiming to improve classical spacetime geometries, such as vacuum nonsingular black holes [75,76,77,78,79,80,81], noncommutative geometry inspired black holes [14,18,19], nonlocal gravity black holes [23,24], generalized uncertainty principle inspired black holes [25], nonlinear electric source black holes [82,83,84,85,86].
From Equation (6), one can see that all metric modifications are now expressed in terms of the function . For consistency there should be a characteristic length scale such that for larger distances the metric in Equation (5) reproduces the standard Schwarzschild solution. Since in gravity there exists just a unique length scale, we conclude that for . The profile of has also to obey the tenets of the self-complete gravity paradigm. To reach this goal, one requires that allows for horizon extremisation when . The net result is a metric that matches the Schwarzschild metric at large distances and admits a Planckian extremal black hole configuration. The most compact profile fulfilling the above requirement is
Accordingly the holographic metric reads [73]
This metric enjoys the property of having a couple of horizons
with and , that coalesce in the extremal configuration, , for . Extremal black holes are zero temperature states, a fact that is evident by analyzing the thermodynamic of Equation (8). By evaluating the black hole surface gravity κ, one obtains
The profile of the temperature (see Figure 2) reveals that the hole undergoes a phase transition from a negative heat capacity warming to a positive heat capacity cooling, also known as black hole SCRAM [18]. At , , the black hole decay virtually halts and for no event horizons form. Interestingly the curvature singularity cannot be probed either by a particle compression or black hole decay, in agreement to what sought within the self-complete gravity paradigm (see Figure 1).
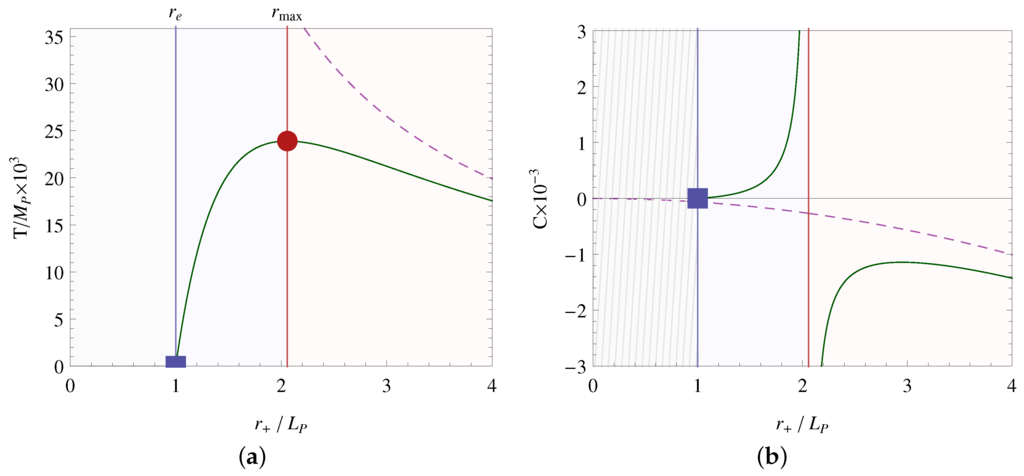
Figure 2.
(a) Temperature of the holographic metric in -dimensions; (b) heat capacity . The shades area is inaccessible . The asymptote in the heat capacity occurs at the maximum temperature. The positive heat capacity phase corresponds to the cool down phase also known as “SCRAM phase”.
The calculation of the black hole entropy
discloses further interesting features of the holographic metric. The non-classical corrections have logarithm dependence as largely expected in all the major approaches to quantum gravity. Furthermore one can use the quantization rule Equation (1) to express the entropy in terms of the parameter N as
In other words the extremal configuration, , represents the basic information capacity of the system, the holographic representation of the black hole quantum constituent, i.e., the graviton. In the large N regime, the black hole entropy is just a multiple of the fundamental area .
Interestingly the parameter N governs all metric corrections. For , we can re-write the line element Equation (5) as
where non-classical corrections die off as in agreement with the quantum N-portrait [45]. We note that the above term also matches the quantum mechanical corrections to the horizon radius obtained by means of the generalized uncertainty principle [30]. Quantum mechanical effects at the horizon are a key feature of the fuzzball proposal too [41,42], a fact that is signalling the convergence towards a model independent scenario.
Derivation in Terms of Non-Local Gravity Actions
In the recent years there has been a lot of interest in modifications of Einstein gravity both in the ultraviolet and infrared regimes [72]. A notable example is offered by the class of non-local gravity deformations, theories that exhibit an infinite number of derivative terms [23,24,25,74,87,88,89,90,91,92,93,94,95].
In order to derive the holographic metric, we consider the following non-local action [90,91,92] in place of the conventional Einstein-Hilbert action
where μ is the non-local gravity scale and is the non-local operator. The above action is a truncation of the action proposed in [74,88,89]. To a first approximation non-local actions lead to the same field equations [23,87,95]
Here is derived from an action describing ordinary matter, where the gravity part is affected by non-local effects. Following the line of reasoning in [23,25,87,95], we neglect higher order corrections and we cast the non-local equations in the following form
where the non-local energy momentum tensor, , is coupled to the standard Einstein tensor.
We can exploit the above equations to reproduce the effective energy momentum tensor we employed for the holographic metric. We start the calculation by considering a static source. We recall that the standard Schwarzschild geometry can be derived by considering a static point-like particle sitting at the origin with energy profile given by Equation (3). As a result, any non-local energy density deformation is of the form
where □ becomes the Laplace operator Δ in case of static sources. Apart from being entire functions in momentum space , there are no additional, theoretical or experimental constraints on the profile of the operators. One can invoke some principles to postulate a specific profile. As a consequence we can select a profile of to reproduce the self-complete character of gravity encoded in the holographic metric. This is equivalent to solving the following equation in term of
with .
Following the procedure in [23,87,95], we can Fourier transform the Equation (18) and algebraically determine the profile of where . The result reads
where
The above function can be expanded in power series and written back into coordinate space by means of the following Schwinger representation for operators
In particular p turns out to be dual to . We note that the function in Equation (19) is an entire function, it admits the inverse function , and can be Taylor expanded for . As a result one finds that the operator in Equation (18) can be written as a power series:
where the logarithm of an operator is defined by . We conclude that the Einstein gravity is consistently recovered in the limit
The procedure can be extended by including higher order corrections in the equations and further terms in the action. Such terms are important only at the Planck scale or beyond, i.e., at energies where the very concept of line element and the geometric description of the black hole actually breaks down. In principle one could exploit forthcoming indications from the quantum N-portrait (possibly away from the large N limit) to get information about such additional terms as well as stricter constraints on . As far as we are concerned of energies below the Planck scale, the first order approximation efficiently works. We also recall that the extremal configuration is an asymptotic state. This means that the presented profile can be safely used for all practical purposes.
3. Higher Dimensional Holographic Metric
In the past two decades there has been a considerable attention on the so called terascale quantum gravity, a phenomenological repercussion of large extra dimensions [96,97,98] and brane-world scenario [99,100]. The later are two paradigms proposed to tackle the hierarchy problem, i.e., the huge discrepancy between the Planck scale, GeV and the electroweak scale GeV. The common feature of such scenarios is the possibility of having a new fundamental scale around the terascale, TeV, by allowing the spacetime to have additional spatial dimensions. A lower fundamental scale is equivalent to having a stronger gravitational interaction and a rich quantum gravity phenomenology in particle collisions or in high energy cosmic ray showers. The latter includes the colliding particle gravitational collapse in microscopic black holes [61,101,102,103,104,105,106] (for reviews on the topics see e.g., [107,108,109,110,111,112,113,114,115,116,117]). Although experimental investigations up to TeV put severe constraints on extradimensional models and black hole production [118,119], extradimensions remain the only viable tool to address the incompleteness of the Standard Model (see [120,121] for some comments about the non-observation of terascale quantum gravity). In addition extradimensions have been proposed in formulations, that being alternative to the large-extradimensions and the brane world scenario, might not suffer from current experimental constraints [122,123,124,125]. This is equivalent to saying, that apart from the mathematical importance, the study of higher dimensional black holes might still have phenomenological repercussions in high energy physics.
On the ground of results in the previous section we present the higher dimensional extension of the holographic metric. For brevity we display the property of the metric in just one set up, the large extradimension model. We introduce the fundamental mass by integrating out the volume of the extra dimensions ,
where n is the number of extra dimensions, is total number of dimensions and is a dimensionless prefactor of the order of unity. In case of toroidal compactification the volume is where is the compactification radius of the extra dimensions.
The system has a length scale defined by , that will be the order of magnitude of the size of any black hole of mass . To neglect boundary effects we assume the fundamental scale be much smaller than the compactification radius . Accordingly an hyperspherical black hole solution consistently describes the spacetime geometry irrespective of brane effects.
We proceed by considering a modified Schwarzschild–Tangherlini energy density as for the four dimensional case, i.e.,
where is the surface of the unit -sphere, given by . From the equation above we can write
where the function is higher dimensional version of the function in Section 2. To solve the D-dimensional Einstein’s equations, we assume a static, neutral metric of the kind
with
The integration of the equations leads to the Newton’s potential expressed in terms of :
From the above line element one can calculate relevant thermodynamic quantities. For instance the black hole temperature reads
while the generic profile of the entropy is
The actual profile of the holographic metric in higher dimensions can be found by means of entropic arguments. By requiring that entropy corrections have a logarithmic dependence in any dimensions, i.e., , we can postulate that the function in higher dimensions has to be:
To check that this is the correct profile we need to verify whether the conditions for a remnant at the fundamental scale are fulfilled. To do this, we calculate the radius of extremal configuration, , i.e., the solution of the following system of equations
We notice that the function for both and . This means that it must admit at least a stationary point for intermediate values of r. From Figure 3 one can see that describes a family of curves labeled by the mass parameter M. For , the curve intersects the r-axis two times, i.e., in . For , the curve never intersects the r-axis and no horizons form. Finally for , the curve has a double zero in .

Figure 3.
The function versus r for . The three curves corresponds to three different values of the mass parameter M.
The horizon extremisation at guarantees the self-complete character of the metric, as it is evident by analyzing the profile of the temperature in Figure 2. As in the four dimensional case, the black hole reaches a maximum temperature before “scramming” down towards a zero temperature thermodynamic limit (see Figure 4). This implies that the holographic horizon is colder with respect to the Schwarzchild black hole of the same size and does not suffer of relevant back reaction. Up to , the temperature/mass ratio is during all the evaporation process (see Table 1). This lets us conclude that, in analogy to what found in [126], the holographic black hole tends to emit softer particles mainly on the brane, i.e., with a reduced bulk emission with respect to Schwarzschild black holes with the same mass. It would be interesting to study the rotating version of the holographic metric and understand how the reduction of its spectrum competes with superradiance effects recently found to take place in the extradimensional scenario (see [127,128]).

Figure 4.
(a) Temperatures of the higher dimensional holographic metric (n is the number of spatial dimensions); (b) ration between the holographic metric temperature and that of the Schwarzschild-Tangherlini temperature black hole, .

Table 1.
Maximum radii and maximum temperatures of the holographic black hole in spatial dimensions.
We notice, however, that by increasing the number of extradimensions n, the holographic horizon becomes relatively hotter. The ratio increases with n (see Table 1), rather than decreasing as found in [126]. This is due to the fact that the temperature of the holographic metric drops to zero at irrespective of n. On the contrary models studied in [126] have smaller remnant radii as n increases and flatter temperature profiles, with a maximum that decreases with n. This is not the case for the holographic metric. We conclude that this might be a peculiar feature of self-completeness.
4. AdS Background and Hawking-Page Phase Transition
The holographic metric in Section 2 showed intriguing thermodynamic properties such as logarithmic corrections to the area law. The pixelization of the event horizon lets us describe the system in terms of a unique parameter N, in the same fashion of what happens within the quantum N-portrait. In the present section, rather than black holes in asymptotically flat space, we consider the case of a non-vanishing cosmological constant. In particular we aim to study the case of a black hole in AdS space, characterized by a negative cosmological constant , where b is the AdS radius. The AdS curvature term can equivalently be described in terms of a fluid-like stress tensor, characterized by negative pressures and tendency to collapse. An AdS background is also a key element of the gauge-gravity duality, a correspondence between some strongly coupled field theories and (weakly curved) gravitational systems [129].
In the conventional Schwarzschild-AdS geometry, the black hole has a minimum Hawking temperature for . This means that black holes have positive specific heat for and can be in stable equilibrium with the thermal radiation at fixed temperature. On the other hand, at temperature below , there is no possibility for the thermal gas to collapse and form an AdS black hole. The thermal gas is thus stable. This suggests that a thermal phase transition should occur at some temperature , with the thermal gas dominating at temperatures below and the large black hole dominating above . This is the so-called Hawking-Page transition [130].
It is therefore natural to ask what would be the impact of a metric encoding the self-complete character of gravity on Hawking-Page transition and the thermodynamics of AdS black holes. A non-vanishing cosmological term, however, requires some revision. The presence of thermal radiation modifies the conditions for Planckian remnants and attaining a ultraviolet self-complete metric. One needs to consider that the class of functions in Section 2 is just the limit of a larger class of functions, i.e., for . Therefore we can postulate that the generic line element reads
with as . The internal energy of the system can be obtained by the equation and reads
The horizon temperature can be calculated by evaluating the surface gravity
and one can check that for , , the above temperature matches the standard Schwarzschild-AdS temperature. To obtain the extremal configuration we need to couple Equation (35) with the equation , i.e.,
and assuming that , one can use Equation (35) in Equation (37) to get
We notice that for any finite b, the extremal mass at the Planck scale reads
and equals the Planck mass only in the limit . The physical reason is due to the fact that our black hole is immersed in a thermal bath. We recall that the cosmological term emerges by coupling Einstein tensor to a energy momentum tensor . The amount of energy related to the cosmological term in a volume V can be estimated by . For one gets , i.e., the additional term on the r.h.s. of Equation (39). As a result we can only require that the remnant radius while only in the limit . Using for , we find that
is a solution of Equation (37). The above profile is a legitimate distribution to replace the Heaviside function. We have the limits as and as . This guarantees that the spacetime is asymptotically AdS-space. Interestingly, for , one has that . This means that, contrary to the Schwarzschild-AdS case, there is no black hole and the spacetime becomes a purely thermal AdS-state. In other words there exists a minimum mass for black hole formation. If the AdS-radius is too small, the black hole cannot fit in. Inserting the profile Equation (40) in Equation (34), one has that the metric coefficient is
From the horizon equation , one finds that there exists a value , depending on b and , such that: for the metric admits two horizons , with and ; for the metric has no horizons; for the metric admits one degenerate horizon .
The extremal horizon guarantees the ultraviolet self-completeness character of the metric. The inner horizon, being smaller than the Planck length, is actually inaccessible. This facts downplays the problem of the Cauchy instability and the related mass inflation [131,132,133,134] much in the same way as the problem of the curvature singularity. The self-complete character allows to hide all kinds of pathologies of the metric behind the Planck barrier.
The temperature plot is given in Figure 5. At large distances the curve coincides with the conventional Schwarzschild-AdS temperature, while at short distances the black hole cools down in the same way as in Figure 4. From the horizon equations one obtains the internal energy, that reads
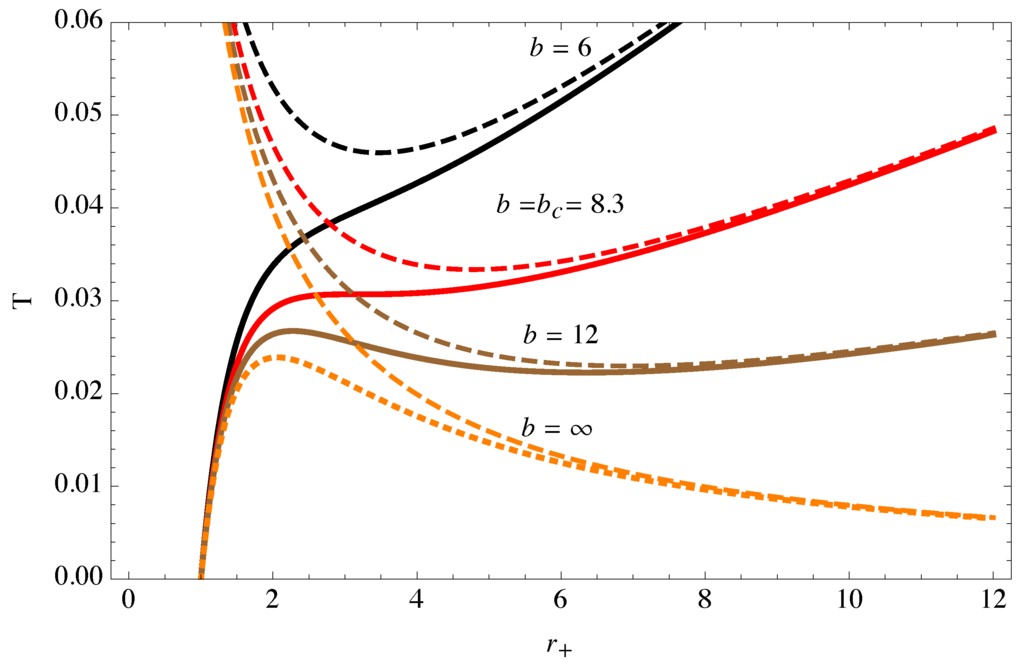
Figure 5.
Plot of the Hawking temperature Equation (42) as function of the horizon radius with . The temperature goes to zero for . The dashed line shows the behaviour of the standard Schwarzschild-AdS temperature. The case corresponds to the temperature of the asymptotically flat holographic metric.
We can also calculate the black hole entropy
We find a logarithmic correction to the area law. Contrary to the standard Scharzschild-AdS case, the entropy depends on the AdS radius b through the logarithmic term. If , the entropy diverges, . From the point of view of black hole pair creation, this is equivalent to saying that no black hole can form since the AdS-space has attained the maximum entropy configuration. Accordingly the black hole mass parameter Equation (43) vanishes in this limit.
By analyzing the temperature profile in Figure 6, one see that there exists a black hole for any temperature. This means that the pure thermal AdS radiation never occurs for . Furthermore one can see that there exists a critical value of the AdS radius parameter such that:
- for , the temperature admits both a minimum value and a maximum value ;
- for , the temperature is a monotonically increasing function of ;
- for , the minimum and the maximum temperature coalesce, , in a point where the curve exhibit an inflection, .

Figure 6.
Black hole temperature for different values of AdS radius b for .
The above thermodynamic quantities let us define the free energy of the system
In Figure 7, one has the free energy F as a function of the horizon radius . We see that above the critical value, , there exists a local minimum of the free energy, while below the critical value , the free energy is monotonically decreasing. In Figure 8, there is the free energy as a function of the temperature. For , the curves exhibit a swallow-tail, a typical signature of non-analytic phase transition with latent heat exchange while for there is a just smooth cross over.

Figure 7.
Free energy vs. horizon radius for .

Figure 8.
Free Energy as function of the temperature for .
A deeper analysis reveals the following. We start from the case and we present the following possibilities:
- (i)
- for , there exist just one horizon radius . The heat capacity of the black hole is positive defined, the systems is locally stable but the free energy is positive. This means that the black hole is a meta-stable state. The AdS-thermal background results the favorable state.
- (ii)
- For , there are three horizon radii, . While at and the heat capacity is positive, this is not the case at that is locally unstable. This corresponds the case of a mixed phase. The configuration in can decay to to or in thermal AdS. From Figure 7, one can see that is always globally unstable since , while may have either positive or negative free energy.
- (iii)
- From Figure 8 we see that there is a value at which the curve intersects itself by forming a cross at the vertex of the swallow tail. The value is the temperature at which the phase transition between small and big black holes occurs [135]. For the pure AdS background is still favorable state, even if small black holes, , and big black holes, , are possible. The smaller black hole is the meta-stable state since it sits in local minimum of the free energy in Figure 7.
- (iv)
- For the AdS thermal state is still favorable state and the bigger black holes are in the meta-stable state since . Here is the Hawking-Page temperature, i.e., . For , bigger black holes are the favorable state while AdS radiation and are meta-stable states. This can be seen by the fact that . For , there exist only one horizon radius and the black hole is the favorable state while the AdS radiation is the meta-stable state. From Figure 6, we see that .
- (v)
- As in the standard Schwarzschild-AdS case there exists a temperature , above which the AdS thermal radiation cannot longer sustain itself. The value of such a temperature is of the order [130]. Accordingly there exist another regime: for , the AdS radiation will inevitably collapse in a black hole. For , the collapse of the AdS radiation occurs above the local maximum temperature, i.e., . A rough estimate of parameters suggests that .
When we are at the critical point. This means that the latent heat goes to zero, corresponding to a second order phase transition. Finally, for one ends up with an analytical cross-over between small and large black holes. In both cases, the bigger black holes are the favorable state. For , AdS is still the favorable state.
In this section we have seen that the phase structure of the solution Equation (41) differs from that of the Schwarzschild-AdS geometry and resembles that of models admitting an extremal horizon (see e.g., the case of charged black holes [136], rotating black holes [137] and neutral static regular black holes [138,139,140]). Finally the current results can pave the way to further developments. At the light of recent proposals about the role of the cosmological constant as a thermodynamical variable analogue to the pressure [137,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155], it would be interesting to extend the holographic metric Equation (41) to the case in which the black hole mass plays the role of the enthalpy of spacetime. We believe this kind of analysis might disclose further insights about the quantum N-portrait proposal.
5. Conclusions
In this paper, we have offered an extensive analysis of the properties of so called holographic metric [73]. We showed that the new line element describes a neutral static black hole and captures the main features of the quantum N-portrait. Specifically the new metric encodes the self-complete character of gravity, i.e., the possibility of masking the curvature singularity with the formation of an extremal horizon at the Planck scale. We also showed that such geometric description uniquely depends on the parameter N, that regulates the pixelization of the event horizon. Interestingly our analysis offers a viable scenario beyond the limit usually considered within the quantum N-portrait. We also showed that having a generic N, corresponds to replacing the Einstein-Hilbert action with a non-local gravity action.
We derived the higher-dimensional holographic metric. We showed that the thermodynamic properties are equivalent to those of the four dimensional solution. During the evaporation the black hole reaches a maximum temperature before cooling down to a terascale remnant. The profile of the temperature suggests that the black hole emission is in marked contrast with that of the higher dimensional Schwarzschild black hole. Within the ADD model one can conclude that the holographic black hole tends to emit softer particle mainly on the brane.
Finally, we devoted our interest to the holographic metric in the presence of AdS cosmological term. After deriving a new line element, that consistently matches the features of the quantum N-portrait with AdS background, we offered a deep analysis of the phase structure of the related thermodynamics. We showed that new metric phase diagram extends the conventional Hawking-Page scenario to a Van der Waals like structure. There exists a critical value of the AdS radius above which the transition from small to large black holes is non-analytical, i.e., with latent heat. In other words, one has a first order transition between small and large black holes. Below the critical value one has just smooth cross-over, while at the critical value the latent heat is vanishing and one ends up with a second order phase transition. We believe that translation of the quantum N-portrait in a geometric model will lead to the identification of further black hole universal characters beyond the semiclassical limit.
Acknowledgments
This work has been supported by the project “Evaporation of the microscopic black holes” of the German Research Foundation (DFG) under the grant NI 1282/2-1, by the HIC for FAIR within the framework of the LOEWE program (Landesoffensive zur Entwicklung Wissenschaftlich-Ökonomischer Exzellenz) launched by the State of Hesse, by the H-QM and partially by the European COST action MP0905 “Black Holes in a Violent Universe”. The authors thank the referees for the constructive comments.
Author Contributions
The paper is the result of a collaborative work in which responsibilities are equally shared among authors. As a result one can assign 33% to each author to the work load for designing the research, writing the manuscript, and drawing pictures. The present paper is in the framework of theoretical physics. Accordingly there is no data analysis phase. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Carr, B.J.; Hawking, S.W. Black holes in the early Universe. Mon. Not. Roy. Astron. Soc. 1974, 168, 399–415. [Google Scholar] [CrossRef]
- Mann, R.B.; Ross, S.F. Cosmological production of charged black hole pairs. Phys. Rev. D 1995, 52, 2254–2265. [Google Scholar] [CrossRef]
- Bousso, R.; Hawking, S.W. Pair creation of black holes during inflation. Phys. Rev. D 1996, 54, 6312–6322. [Google Scholar] [CrossRef]
- Mann, R.B.; Nicolini, P. Cosmological production of noncommutative black holes. Phys. Rev. D 2011, 84, 064014. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Hawking, S.W. Information Preservation and Weather Forecasting for Black Holes. 2014; arxiv:1401.5761. [Google Scholar]
- Hawking, S.W. The Information Paradox for Black Holes. 2015; arXiv:1509.01147. [Google Scholar]
- Hawking, S.W.; Perry, M.J.; Strominger, A. Soft Hair on Black Holes. 2016; arXiv:1601.00921. [Google Scholar]
- Dvali, G. Non-Thermal Corrections to Hawking Radiation Versus the Information Paradox. 2015; arXiv:1509.04645. [Google Scholar]
- Saini, A.; Stojkovic, D. Radiation from a collapsing object is manifestly unitary. Phys. Rev. Lett. 2015, 114, 111301. [Google Scholar] [CrossRef] [PubMed]
- Averin, A.; Dvali, G.; Gomez, C.; Lust, D. Gravitational Black Hole Hair from Event Horizon Supertranslations. 2016; arXiv:1601.03725. [Google Scholar]
- Bonanno, A.; Reuter, M. Renormalization group improved black hole space-times. Phys. Rev. D 2000, 62, 043008. [Google Scholar] [CrossRef]
- Nicolini, P.; Smailagic, A.; Spallucci, E. The fate of radiating black holes in noncommutative geometry. 2005; arXiv:hep-th/0507226. [Google Scholar]
- Nicolini, P.; Smailagic, A.; Spallucci, E. Noncommutative geometry inspired Schwarzschild black hole. Phys. Lett. B 2006, 632, 547–551. [Google Scholar] [CrossRef]
- Rizzo, T.G. Noncommutative inspired black holes in extra dimensions. J. High Energy Phys. 2006, 09, 021. [Google Scholar] [CrossRef]
- Ansoldi, S.; Nicolini, P.; Smailagic, A.; Spallucci, E. Noncommutative geometry inspired charged black holes. Phys. Lett. B 2007, 645, 261–266. [Google Scholar] [CrossRef]
- Spallucci, E.; Smailagic, A.; Nicolini, P. Non-commutative geometry inspired higher-dimensional charged black holes. Phys. Lett. B 2009, 670, 449–454. [Google Scholar] [CrossRef]
- Nicolini, P. Noncommutative black holes, the final appeal to quantum gravity: A review. Int. J. Mod. Phys. A 2009, 24, 1229–1308. [Google Scholar] [CrossRef]
- Nicolini, P.; Spallucci, E. Noncommutative geometry inspired dirty black holes. Class. Quant. Grav. 2010, 27, 015010. [Google Scholar] [CrossRef]
- Smailagic, A.; Spallucci, E. “Kerrr” black hole: the lord of the string. Phys. Lett. B 2010, 688, 82–87. [Google Scholar] [CrossRef]
- Modesto, L.; Nicolini, P. Charged rotating noncommutative black holes. Phys. Rev. D 2010, 82, 104035. [Google Scholar] [CrossRef]
- Modesto, L. Loop quantum black hole. Class. Quant. Grav. 2006, 23, 5587–5602. [Google Scholar] [CrossRef]
- Modesto, L.; Moffat, J.W.; Nicolini, P. Black holes in an ultraviolet complete quantum gravity. Phys. Lett. B 2011, 695, 397–400. [Google Scholar] [CrossRef]
- Nicolini, P. Nonlocal and generalized uncertainty principle black holes. 2012; arXiv:1202.2102. [Google Scholar]
- Isi, M.; Mureika, J.; Nicolini, P. Self-Completeness and the Generalized Uncertainty Principle. J. High Energy Phys. 2013, 1311, 139. [Google Scholar] [CrossRef]
- Greenwood, E.; Stojkovic, D. Quantum gravitational collapse: Non-singularity and non-locality. J. High Energy Phys. 2008, 06, 042. [Google Scholar] [CrossRef]
- Saini, A.; Stojkovic, D. Nonlocal (but also nonsingular) physics at the last stages of gravitational collapse. Phys. Rev. D 2014, 89, 044003. [Google Scholar] [CrossRef]
- De Lorenzo, T.; Pacilio, C.; Rovelli, C.; Speziale, S. On the Effective Metric of a Planck Star. Gen. Rel. Grav. 2015, 47. [Google Scholar] [CrossRef]
- Adler, R.J.; Chen, P.; Santiago, D.I. The generalized uncertainty principle and black hole remnants. Gen. Rel. Grav. 2001, 33, 2101–2108. [Google Scholar] [CrossRef]
- Carr, B.J.; Mureika, J.; Nicolini, P. Sub-Planckian black holes and the Generalized Uncertainty Principle. J. High Energy Phys. 2015, 07, 052. [Google Scholar] [CrossRef]
- DeBenedictis, A. Developments in Black Hole Research: Classical, Semi-Classical, and Quantum. In Classical and Quantum Gravity Research; Nova Science Publishers: New York, NY, USA, 2008; pp. 371–426. [Google Scholar]
- Calmet, X.; Carr, B.; Winstanley, E. Quantum Black Holes. In SpringerBriefs in Physics; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Spallucci, E.; Smailagic, A. Semi-Classical Approach to Quantum Black Holes. In Advances in Black Holes Research; Barton, A., Ed.; Nova Science Publishers: New York, NY, USA, 2014. [Google Scholar]
- Chen, P.; Ong, Y.C.; Yeom, D.-H. Black Hole Remnants and the Information Loss Paradox. Phys. Rept. 2015, 603, 1–45. [Google Scholar] [CrossRef]
- Casadio, R.; Micu, O.; Nicolini, P. Minimum Length Effects in Black Hole Physics. In Quantum Aspects of Black Holes; Springer: Berlin/Heidelberg, Germany, 2015; Volume 178, pp. 293–322. [Google Scholar]
- Dvali, G.; Gomez, C. Black Hole’s Quantum N-Portrait. Fortsch. Phys. 2013, 61, 742–767. [Google Scholar] [CrossRef]
- Dvali, G.; Gomez, C. Black Holes as Critical Point of Quantum Phase Transition. Eur. Phys. J. C 2014, 74, 2752. [Google Scholar] [CrossRef] [PubMed]
- Lunin, O.; Mathur, S.D. Metric of the multiply wound rotating string. Nucl. Phys. B 2001, 610, 49–76. [Google Scholar] [CrossRef]
- Lunin, O.; Mathur, S.D. The Slowly rotating near extremal D1–D5 system as a “hot tube”. Nucl. Phys. B 2001, 615, 285–312. [Google Scholar] [CrossRef]
- Lunin, O.; Mathur, S.D. AdS/CFT duality and the black hole information paradox. Nucl. Phys. B 2002, 623, 342–394. [Google Scholar] [CrossRef]
- Mathur, S.D. The Fuzzball proposal for black holes: An Elementary review. Fortsch. Phys. 2005, 53, 793–827. [Google Scholar] [CrossRef]
- Skenderis, K.; Taylor, M. The fuzzball proposal for black holes. Phys. Rept. 2008, 467, 117–171. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
- Nicolini, P.; Singleton, D. Connecting horizon pixels and interior voxels of a black hole. Phys. Lett. B 2014, 738, 213–217. [Google Scholar] [CrossRef]
- Dvali, G.; Gomez, C. Black Hole’s 1/N Hair. Phys. Lett. B 2013, 719, 419–423. [Google Scholar] [CrossRef]
- Dvali, G.; Gomez, C.; Isermann, R.S.; Luest, D.; Stieberger, S. Black hole formation and classicalization in ultra-Planckian 2 to N scattering. Nucl. Phys. B 2015, 893, 187–235. [Google Scholar] [CrossRef]
- Dvali, G.; Gomez, C. Black Hole Macro-Quantumness. 2012; arXiv:1212.0765. [Google Scholar]
- Casadio, R. Localised particles and fuzzy horizons: A tool for probing Quantum Black Holes. 2013; arXiv:1305.3195. [Google Scholar]
- Casadio, R.; Scardigli, F. Horizon wave-function for single localized particles: GUP and quantum black hole decay. Eur. Phys. J. C 2014, 74, 2685. [Google Scholar] [CrossRef]
- Casadio, R.; Micu, O.; Scardigli, F. Quantum hoop conjecture: Black hole formation by particle collisions. Phys. Lett. B 2014, 732, 105–109. [Google Scholar] [CrossRef]
- Casadio, R.; Micu, O.; Stojkovic, D. Inner horizon of the quantum Reissner-NordstrÃűm black holes. J. High Energy Phys. 2015, 05, 096. [Google Scholar] [CrossRef]
- Casadio, R.; Micu, O.; Stojkovic, D. Horizon Wave-Function and the Quantum Cosmic Censorship. Phys. Lett. B 2015, 747, 68–72. [Google Scholar] [CrossRef]
- Casadio, R.; Cavalcanti, R.T.; Giugno, A.; Mureika, J. Horizon of quantum black holes in various dimensions. 2015; arXiv:1509.09317. [Google Scholar]
- Casadio, R.; Giugno, A.; Micu, O. Horizon Quantum Mechanics: A hitchhiker’s guide to quantum black holes. 2015; arXiv:1512.04071. [Google Scholar]
- Veneziano, G. A stringy nature needs just two constants. Europhys. Lett. 1986, 2, 199. [Google Scholar] [CrossRef]
- Gross, D.J.; Mende, P.F. String Theory Beyond the Planck Scale. Nucl. Phys. B 1988, 303, 407. [Google Scholar] [CrossRef]
- Amati, D.; Ciafaloni, M.; Veneziano, G. Can Space-Time Be Probed Below the String Size? Phys. Lett. B 1989, 216, 41. [Google Scholar] [CrossRef]
- Konishi, K.; Paffuti, G.; Provero, P. Minimum Physical Length and the Generalized Uncertainty Principle in String Theory. Phys. Lett. B 1990, 234, 276. [Google Scholar] [CrossRef]
- Witten, E. Reflections on the fate of space-time. Phys. Today 1996, 49N4, 24–30. [Google Scholar] [CrossRef]
- Susskind, L. Twenty years of debate with Stephen. In Proceedings of the Workshop on Conference on the Future of Theoretical Physics and Cosmology in Honor of Steven Hawking’s 60th Birthday, Cambridge, UK, 7–10 January 2002; pp. 330–347.
- Banks, T.; Fischler, W. A Model for high-energy scattering in quantum gravity. 1999; arXiv:hep-th/9906038. [Google Scholar]
- Banks, T. A Critique of pure string theory: Heterodox opinions of diverse dimensions. 2003; arXiv:hep-th/0306074. [Google Scholar]
- Dvali, G.; Folkerts, S.; Germani, C. Physics of Trans-Planckian Gravity. Phys. Rev. D 2011, 84, 024039. [Google Scholar] [CrossRef]
- Dvali, G.; Gomez, C. Ultra-High Energy Probes of Classicalization. JCAP 2012, 1207, 015. [Google Scholar] [CrossRef] [PubMed]
- Mureika, J.; Nicolini, P. Self-completeness and spontaneous dimensional reduction. Eur. Phys. J. Plus 2013, 128, 78. [Google Scholar] [CrossRef]
- Aurilia, A.; Spallucci, E. Planck’s uncertainty principle and the saturation of Lorentz boosts by Planckian black holes. 2013; arXiv:1309.7186. [Google Scholar]
- Aurilia, A.; Spallucci, E. Why the length of a quantum string cannot be Lorentz contracted. Adv. High Energy Phys. 2013, 2013, 531696. [Google Scholar] [CrossRef]
- Adler, R.J. Six easy roads to the Planck scale. Am. J. Phys. 2010, 78, 925–932. [Google Scholar] [CrossRef]
- Carr, B.J. Primordial Black Holes and Quantum Effects. Springer Proc. Phys. 2016, 170, 23–31. [Google Scholar]
- Lake, M.J.; Carr, B. The Compton-Schwarzschild correspondence from extended de Broglie relations. J. High Energy Phys. 2015, 11, 105. [Google Scholar] [CrossRef]
- Dvali, G.; Gomez, C.; Luest, D. Classical Limit of Black Hole Quantum N-Portrait and BMS Symmetry. 2015; arXiv:1509.02114. [Google Scholar]
- Capozziello, S.; de Laurentis, M. Extended Theories of Gravity. Phys. Rept. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Nicolini, P.; Spallucci, E. Holographic screens in ultraviolet self-complete quantum gravity. Adv. High Energy Phys. 2014, 2014, 805684. [Google Scholar] [CrossRef]
- Modesto, L. Super-renormalizable Quantum Gravity. Phys. Rev. D 2012, 86, 044005. [Google Scholar] [CrossRef]
- Dymnikova, I. Vacuum nonsingular black hole. Gen. Rel. Grav. 1992, 24, 235–242. [Google Scholar] [CrossRef]
- Magli, G. A Simple model of a black hole interior. Rept. Math. Phys. 1999, 44, 407–412. [Google Scholar]
- Giambo, R. Anisotropic generalizations of de Sitter space-time. Class. Quant. Grav. 2002, 19, 4399–4404. [Google Scholar]
- Mbonye, M.R.; Kazanas, D. A Non-singular black hole model as a possible end-product of gravitational collapse. Phys. Rev. D 2005, 72, 024016. [Google Scholar] [CrossRef]
- Hayward, S.A. Formation and evaporation of regular black holes. Phys. Rev. Lett. 2006, 96, 031103. [Google Scholar] [CrossRef] [PubMed]
- Bambi, C.; Malafarina, D.; Modesto, L. Non-singular quantum-inspired gravitational collapse. Phys. Rev. D 2013, 88, 044009. [Google Scholar] [CrossRef]
- Neves, J.C.S. Deforming regular black holes. 2015; arXiv:1508.06701. [Google Scholar]
- Ayon-Beato, E.; Garcia, A. Regular black hole in general relativity coupled to nonlinear electrodynamics. Phys. Rev. Lett. 1998, 80, 5056–5059. [Google Scholar] [CrossRef]
- Ayon-Beato, E.; Garcia, A. Nonsingular charged black hole solution for nonlinear source. Gen. Rel. Grav. 1999, 31, 629–633. [Google Scholar] [CrossRef]
- Ayon-Beato, E.; Garcia, A. New regular black hole solution from nonlinear electrodynamics. Phys. Lett. B 1999, 464, 25. [Google Scholar] [CrossRef]
- Ayon-Beato, E.; Garcia, A. The Bardeen model as a nonlinear magnetic monopole. Phys. Lett. B 2000, 493, 149–152. [Google Scholar] [CrossRef]
- Culetu, H. On a regular charged black hole with a nonlinear electric source. Int. J. Theor. Phys. 2015, 54, 2855–2863. [Google Scholar] [CrossRef]
- Moffat, J.W. Ultraviolet Complete Quantum Gravity. Eur. Phys. J. Plus 2011, 126. [Google Scholar] [CrossRef]
- Krasnikov, N.V. Nonlocal gauge theories. Theor. Math. Phys. 1987, 73, 1184–1190. [Google Scholar] [CrossRef]
- Tomboulis, E.T. Superrenormalizable gauge and gravitational theories. 1997; arXiv:hep-th/9702146. [Google Scholar]
- Barvinsky, A.O. Nonlocal action for long distance modifications of gravity theory. Phys. Lett. B 2003, 572, 109–116. [Google Scholar] [CrossRef]
- Barvinsky, A.O. On covariant long-distance modifications of Einstein theory and strong coupling problem. Phys. Rev. D 2005, 71, 084007. [Google Scholar] [CrossRef]
- Barvinsky, A.O. Dark energy and dark matter from nonlocal ghost-free gravity theory. Phys. Lett. B 2012, 710, 12–16. [Google Scholar] [CrossRef]
- Biswas, T.; Gerwick, E.; Koivisto, T.; Mazumdar, A. Towards singularity and ghost free theories of gravity. Phys. Rev. Lett. 2012, 108, 031101. [Google Scholar] [CrossRef] [PubMed]
- Calcagni, G.; Modesto, L.; Nicolini, P. Super-accelerating bouncing cosmology in asymptotically-free non-local gravity. Eur. Phys. J. C 2014, 74, 2999. [Google Scholar] [CrossRef]
- Gaete, P.; Helayel-Neto, J.A.; Spallucci, E. Un-graviton corrections to the Schwarzschild black hole. Phys. Lett. B 2010, 693, 155–158. [Google Scholar] [CrossRef]
- Antoniadis, I.; Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. New dimensions at a millimeter to a Fermi and superstrings at a TeV. Phys. Lett. B 1998, 436, 257–263. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. The Hierarchy problem and new dimensions at a millimeter. Phys. Lett. B 1998, 429, 263–272. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. Phenomenology, astrophysics and cosmology of theories with submillimeter dimensions and TeV scale quantum gravity. Phys. Rev. D 1999, 59, 086004. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. A large mass hierarchy from a small extra dimension. Phys. Rev. Lett. 1999, 83, 3370–3373. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. An alternative to compactification. Phys. Rev. Lett. 1999, 83, 4690–4693. [Google Scholar] [CrossRef]
- Argyres, P.C.; Dimopoulos, S.; March-Russell, J. Black holes and submillimeter dimensions. Phys. Lett. B 1998, 441, 96–104. [Google Scholar] [CrossRef]
- Dimopoulos, S.; Landsberg, G.L. Black holes at the LHC. Phys. Rev. Lett. 2001, 87, 161602. [Google Scholar] [CrossRef] [PubMed]
- Giddings, S.B.; Thomas, S.D. High-energy colliders as black hole factories: The End of short distance physics. Phys. Rev. D 2002, 65, 056010. [Google Scholar] [CrossRef]
- Feng, J.L.; Shapere, A.D. Black hole production by cosmic rays. Phys. Rev. Lett. 2002, 88, 021303. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Muniz, J.; Feng, J.L.; Halzen, F.; Han, T.; Hooper, D. Detecting microscopic black holes with neutrino telescopes. Phys. Rev. D 2002, 65, 124015. [Google Scholar] [CrossRef]
- Kowalski, M.; Ringwald, A.; Tu, H. Black holes at neutrino telescopes. Phys. Lett. B 2002, 529, 1–9. [Google Scholar] [CrossRef]
- Landsberg, G.L. Black holes at future colliders and beyond: A Review. In Proceedings of the 10th International Conference on Supersymmetry and Unification of Fundamental Interactions (SUSY’02), Hamburg, Germany, 17–23 June 2002; pp. 562–577.
- Cavaglia, M. Black hole and brane production in TeV gravity: A Review. Int. J. Mod. Phys. A 2003, 18, 1843–1882. [Google Scholar] [CrossRef]
- Kanti, P. Black holes in theories with large extra dimensions: A Review. Int. J. Mod. Phys. A 2004, 19, 4899–4951. [Google Scholar] [CrossRef]
- Hossenfelder, S. What black holes can teach us. 2004; arXiv:hep-ph/0412265. [Google Scholar]
- Casanova, A.; Spallucci, E. TeV mini black hole decay at future colliders. Class. Quant. Grav. 2006, 23, R45–R62. [Google Scholar] [CrossRef]
- Bleicher, M. How to Create Black Holes on Earth? Eur. J. Phys. 2007, 28, 509–516. [Google Scholar] [CrossRef]
- Winstanley, E. Hawking Radiation From Rotating Brane Black Holes. In Proceedings of the Conference on Black Holes and Naked Singularities, Milan, Italy, 10–12 May 2007.
- Bleicher, M.; Nicolini, P. Large extra dimensions and small black holes at the LHC. J. Phys. Conf. Ser. 2010, 237, 012008. [Google Scholar] [CrossRef]
- Calmet, X. A Review of Quantum Gravity at the Large Hadron Collider. Mod. Phys. Lett. A 2010, 25, 1553–1579. [Google Scholar] [CrossRef]
- Park, S.C. Black holes and the LHC: A Review. Prog. Part. Nucl. Phys. 2012, 67, 617–650. [Google Scholar] [CrossRef]
- Kanti, P.; Winstanley, E. Hawking Radiation from Higher-Dimensional Black Holes. Fundam. Theor. Phys. 2015, 178, 229–265. [Google Scholar]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Ero, J.; Friedl, M.; Fruehwirth, R.; Ghete, V.M.; et al. Search for resonances and quantum black holes using dijet mass spectra in proton-proton collisions at TeV. Phys. Rev. D 2015, 91, 052009. [Google Scholar] [CrossRef]
- ATLAS Collaboration. Search for new phenomena with photon+jet events in proton-proton collisions at TeV with the ATLAS detector. 2015; arXiv:1512.05910. [Google Scholar]
- Mureika, J.; Nicolini, P.; Spallucci, E. Could any black holes be produced at the LHC? Phys. Rev. D 2012, 85, 106007. [Google Scholar] [CrossRef]
- Bleicher, M.; Nicolini, P. Mini-review on mini-black holes from the mini-Big Bang. Astron. Nachr. 2014, 335, 605. [Google Scholar] [CrossRef]
- Appelquist, T.; Cheng, H.-C.; Dobrescu, B.A. Bounds on universal extra dimensions. Phys. Rev. D 2001, 64, 035002. [Google Scholar] [CrossRef]
- Gogberashvili, M. Four dimensionality in noncompact Kaluza-Klein model. Mod. Phys. Lett. A 1999, 14, 2025–2032. [Google Scholar] [CrossRef]
- Gogberashvili, M. Our world as an expanding shell. Europhys. Lett. 2000, 49, 396–399. [Google Scholar] [CrossRef]
- Gogberashvili, M. Hierarchy problem in the shell universe model. Int. J. Mod. Phys. D 2002, 11, 1635–1638. [Google Scholar] [CrossRef]
- Nicolini, P.; Winstanley, E. Hawking emission from quantum gravity black holes. J. High Energy Phys. 2011, 11, 075. [Google Scholar] [CrossRef]
- Frolov, V.P.; Stojkovic, D. Black hole as a point radiator and recoil effect in the brane world. Phys. Rev. Lett. 2002, 89, 151302. [Google Scholar] [CrossRef] [PubMed]
- Frolov, V.P.; Stojkovic, D. Quantum radiation from a five-dimensional rotating black hole. Phys. Rev. D 2003, 67, 084004. [Google Scholar] [CrossRef]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1113–1133. [Google Scholar] [CrossRef]
- Hawking, S.W.; Page, D.N. Thermodynamics of black holes in anti-deSitter space. Commun. Math. Phys. 1983, 87, 577–588. [Google Scholar] [CrossRef]
- Poisson, E.; Israel, W. Inner-horizon instability and mass inflation in black holes. Phys. Rev. Lett. 1989, 63, 1663–1666. [Google Scholar] [CrossRef] [PubMed]
- Poisson, E.; Israel, W. Internal structure of black holes. Phys. Rev. D 1990, 41, 1796–1809. [Google Scholar] [CrossRef]
- Batic, D.; Nicolini, P. Fuzziness at the horizon. Phys. Lett. B 2010, 692, 32–35. [Google Scholar] [CrossRef]
- Brown, E.; Mann, R.B. Instability of the noncommutative geometry inspired black hole. Phys. Lett. B 2011, 695, 440–445. [Google Scholar] [CrossRef]
- Spallucci, E.; Smailagic, A. Maxwell’s equal area law for charged Anti-deSitter black holes. J. Grav. 2013, 2013, 525696. [Google Scholar]
- Chamblin, A.; Emparan, R.; Johnson, C.V.; Myers, R.C. Charged AdS black holes and catastrophic holography. Phys. Rev. D 1999, 60, 064018. [Google Scholar] [CrossRef]
- Caldarelli, M.M.; Cognola, G.; Klemm, D. Thermodynamics of Kerr-Newman-AdS black holes and conformal field theories. Class. Quant. Grav. 2000, 17, 399–420. [Google Scholar] [CrossRef]
- Nicolini, P.; Torrieri, G. The Hawking-Page crossover in noncommutative anti-deSitter space. J. High Energy Phys. 2011. [Google Scholar] [CrossRef]
- Frassino, A.M. Phase transitions of regular Schwarzschild-Anti-deSitter black holes. Springer Proc. Phys. 2016, 170, 241–247. [Google Scholar]
- Smailagic, A.; Spallucci, E. Thermodynamical phases of a regular SAdS black hole. Int. J. Mod. Phys. D 2013, 22, 1350010. [Google Scholar] [CrossRef]
- Creighton, J.D.E.; Mann, R.B. Quasilocal thermodynamics of dilaton gravity coupled to gauge fields. Phys. Rev. D 1995, 52, 4569–4587. [Google Scholar] [CrossRef]
- Kastor, D.; Ray, S.; Traschen, J. Enthalpy and the Mechanics of AdS Black Holes. Class. Quant. Grav. 2009, 26, 195011. [Google Scholar] [CrossRef]
- Dolan, B.P. The cosmological constant and the black hole equation of state. Class. Quant. Grav. 2011, 28, 125020. [Google Scholar] [CrossRef]
- Dolan, B.P. Pressure and volume in the first law of black hole thermodynamics. Class. Quant. Grav. 2011, 28, 235017. [Google Scholar] [CrossRef]
- Dolan, B.P. Compressibility of rotating black holes. Phys. Rev. D 2011, 84, 127503. [Google Scholar] [CrossRef]
- Dolan, B.P. Where is the PdV term in the fist law of black hole thermodynamics? 2012; arXiv:1209.1272. [Google Scholar]
- Cvetic, M.; Gibbons, G.W.; Kubiznak, D.; Pope, C.N. Black Hole Enthalpy and an Entropy Inequality for the Thermodynamic Volume. Phys. Rev. D 2011, 84, 024037. [Google Scholar] [CrossRef]
- Larranaga, A.; Cardenas, A. Geometric Thermodynamics of Schwarzschild-AdS black hole with a Cosmological Constant as State Variable. J. Korean Phys. Soc. 2012, 60, 987–992. [Google Scholar] [CrossRef]
- Larranaga, A.; Mojica, S. Geometric Thermodynamics of Kerr-AdS black hole with a Cosmological Constant as State Variable. Abraham Zelmanov J. 2012, 5, 68–77. [Google Scholar]
- Gibbons, G.W. What is the Shape of a Black Hole? AIP Conf. Proc. 2012, 1460, 90–100. [Google Scholar]
- Kubiznak, D.; Mann, R.B. P-V criticality of charged AdS black holes. J. High Energy Phys. 2012, 07, 033. [Google Scholar] [CrossRef]
- Gunasekaran, S.; Mann, R.B.; Kubiznak, D. Extended phase space thermodynamics for charged and rotating black holes and Born-Infeld vacuum polarization. J. High Energy Phys. 2012, 11, 110. [Google Scholar] [CrossRef]
- Belhaj, A.; Chabab, M.; El Moumni, H.; Sedra, M.B. On Thermodynamics of AdS Black Holes in Arbitrary Dimensions. Chin. Phys. Lett. 2012, 29, 100401. [Google Scholar] [CrossRef]
- Lu, H.; Pang, Y.; Pope, C.N.; Vazquez-Poritz, J.F. AdS and Lifshitz Black Holes in Conformal and Einstein-Weyl Gravities. Phys. Rev. D 2012, 86, 044011. [Google Scholar] [CrossRef]
- Hendi, S.H.; Vahidinia, M.H. Extended phase space thermodynamics and P-V criticality of black holes with a nonlinear source. Phys. Rev. D 2013, 88, 084045. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).