Abstract
We consider the dynamics of swarms of scalar Brownian agents subject to local imitation mechanisms implemented using mutual rank-based interactions. For appropriate values of the underlying control parameters, the swarm propagates tightly and the distances separating successive agents are iid exponential random variables. Implicitly, the implementation of rank-based mutual interactions, requires that agents have infinite interaction ranges. Using the probabilistic size of the swarm’s support, we analytically estimate the critical interaction range below that flocked swarms cannot survive. In the second part of the paper, we consider the interactions between two flocked swarms of Brownian agents with finite interaction ranges. Both swarms travel with different barycentric velocities, and agents from both swarms indifferently interact with each other. For appropriate initial configurations, both swarms eventually collide (i.e., all agents interact). Depending on the values of the control parameters, one of the following patterns emerges after collision: (i) Both swarms remain essentially flocked, or (ii) the swarms become ultimately quasi-free and recover their nominal barycentric speeds. We derive a set of analytical flocking conditions based on the generalized rank-based Brownian motion. An extensive set of numerical simulations corroborates our analytical findings.
1. Introduction
Elementary models of multi-agents swarms often rely on the assumption that all individuals obey identical dynamical rules. This hypothesis of agents’ homogeneity significantly simplifies the mathematical modeling and its treatment. In particular, for large swarms, homogeneity enables analytical discussions based on the mean-field (MF) approach. In the MF approach, the effects of mutual interactions are aggregated into an external effective force field, driving the dynamic of a single randomly picked agent, whose behavior reflects the whole society’s evolution. Homogeneity is, however, rarely encountered in actual situations. A natural question is to then ask how heterogeneity between agents affects and/or possibly destroys the potential emergence of collective (i.e., flocking) dynamics. In the presence of heterogeneity, analytical approaches are more difficult as, a priori, the MF approach cannot be directly employed. In multi-agent swarms, heterogeneity can manifest itself in many different forms and degrees. It may concern the individual dynamics of each agent and/or the way agents interact with their fellows. An extreme heterogeneous situation is realized when, due to its specificities, a single agent is actually leading the entire swarm [1,2,3,4,5]. In this paper, we focus on comparatively low heterogeneities encountered when only the individual dynamics differ but not the interacting rules. For this case, a paradigmatic and pioneering example is the Kuramoto synchronization of heterogeneous phase oscillators for which the role of heterogeneity can, to a certain extent, be analytically discussed [6,7]. More recently, models based on rank-based drifted Brownian motion (RBM) [8], and, in particular, the so-called Hybrid Atlas Model (HAM) [9], offer another possibility to analytically discuss the heterogeneous swarm dynamics, without relying on the MF approach. In the sequel, we shall basically use the HAM modeling framework to study a new type of global heterogeneity. This is achieved when two sub-swarms are forced to mutually interact. Each sub-swarm, formed by homogeneous agents, is initially tightly flocked and obeys specific collective dynamics. The global society formed by the union of the two sub-swarms is clearly heterogeneous. This example depicts a situation where two distinct sub-swarms (agents of each sub-swarm are different) interact via a local competition mechanism (here, agents systematically try to catch their leaders in a finite observation range). In this paper, we are able to analytically characterize the post-collisional outputs. Depending on external control parameters (individual sub-swarm dynamics, strength of competition), we observe that the post-collisional situation can either be a single tight swarm or a segregation into the nominal sub-swarm.
The paper is organized as follows: In Section 2, we introduce the microscopic agent’s dynamic and link it to RBMs. In Section 3, relying on the HAM theory, we derive the flocking conditions for single swarms composed of scalar agents interacting via imitation. The mutual interactions are effectively of long-range types (i.e., each agent can observe all leaders independent of their distance). For a finite number of tightly flocked agents, the (scalar) inter-distance between successive fellows is a stationary random variable, and, hence, so is the size of the swarm extension. This enables us to define a characteristic stationary swarm extension. In Section 4, we consider a couple of sub-swarms, initially well separated on the real line and with different average barycentric speeds. As the positive barycentric velocity of the leftmost sub-swarm is chosen, larger than the one of the rightmost sub-swarm, collision is unavoidable. For large but finite observation ranges of the sub-swarm (i.e., range larger than the sub-swarm characteristics of each sub-swarm extension derived in Section 3), we study the asymptotic post-collisional behavior of the whole system. The conditions for either the emergence of a global flocking swarm or quasi-freedom of the sub-swarms are approximatively derived. All analytical findings are tested and corroborated by simulation experiments. Concluding remarks, along with perspectives, are finally presented in Section 5.
2. Flocking of Interacting Brownian Agents
We consider a swarm of N Brownian agents , , diffusing on . Agent follows the dynamic:
where and () are independent White Gaussian Noise (WGN) sources. The set of individual drifts for are rank-dependent interactions that are defined as follows:
- (i)
- In real-time, agent counts the (time-dependent) number of leading fellows located within an observation interval U, namely the number of for that are located in with:
- (ii)
- The -rank-based drift in Equation (1) is then determined by:with a velocity scale factor.
According to Equation (1), agent is positively accelerated by its leaders located in but ignores the presence of its followers. These types of dynamics generically model imitation mechanisms; a typical example for the diffusion of innovation is shown in [10].
For very large swarms (i.e., when ), we may define an agent probability density at position x at time t. Adopting a mean-field (MF) approach, obeys a (nonlinear) Fokker–Planck parabolic partial differential equation (pde):
For , the model can be analytically investigated, and its solution behaves as a flocked swarm of agents that propagate like a soliton wave [10,11,12]. Conversely, for small U, a first order expansion of Equation (4) yields Burgers’ equation, that can be analytically solved via the well known Hopf–Cole (logarithmic) transformation [11]. In this small U regime, exhibits a diffusive behavior that asymptotically vanishes with time. Qualitatively, when U is very small, the agents mutual interactions are not strong enough to sustain a cooperative soliton dynamic pattern. By introducing a decreasing distance-dependent modulation on rank-based drifts, it has been showed that a bifurcation point, controlled by the distance decay rate, exists that separates both propagating regimes [10,12].
In general, however, the joint nonlocal and nonlinear characteristics of Equation (4) precludes direct analytical characterization of this bifurcation point. Alternative approaches then have to be found. In the present paper, focusing on Equation (1) with , we shall use available results for rank-based Brownian motions [8,9] to approximately estimate the observation range required to generate a soliton-like propagation.
Rank-Based Brownian Motions (RBMs)
For calculation convenience, we now consider the dynamics of Equation (1) with respect to the swarm’s barycenter. That is to say, Equation (3) becomes:
In other words, agents , counts, in real time, the number of its leaders with . It then updates its drift as given in Equation (5), where γ is the average drift velocity of the swarm. Since the WGN in Equation (1) achieves unbounded realizations, the ability for all ’s to exactly count the number of their leaders effectively requires an infinite observation range U.
By construction, one can verify that the stability conditions:
are verified, meaning that the laggards have a systematic average tendency to catch up with the leaders.
The rank-based drifts effectively implement a stylized gravity model, where the set of conditions for Equation (6) ensures the existence of a stationary probability measure for the RBM. This stationary regime corresponds to a tight propagating swarm that effectively behaves like a soliton propagating wave. Moreover, [8,13] established that in this stationary state, the inter-distances between successive agents are independent, -exponentially distributed random variables with:
Since the swarm’s stationary size is the sum of independent exponentially distributed r.v.’s, it defines a hypoexponential probability distribution with density:
Accordingly, the average size of the swarm and its corresponding variance behave as follows:
The coefficient of variation , which measures the stochasticity of the swarm’s size, vanishes in the mean-field limit (). Observe that, in the mean-field limit, the agents’ density of the RBM directly coincides with Burgers’ dynamics for . This leads to a tight soliton-like propagation density with infinite support. This is consistent with Equation (9), where the swarm’s size slowly diverges for .
3. Heuristic Characterization of the Observation Threshold Leading to Cooperative Dynamics
Consider the nominal dynamics Equation (1) and now assume finite observation ranges (i.e., ). Due to the unboundedness of the WGN, an exact ranking procedure is therefore not strictly possible. A non vanishing probability (decreasing with increasing U’s) exists to find outlying leaders (i.e., located beyond the observation range of some of their followers). While the average swarm size from Equation (9) is valid only when , we postulate that it can still be used to approximately characterize the minimal observation range required to sustain a tight swarm. Indeed, whenever , it is highly probable that some agents cannot determine their respective ranks. These outlying agents will underestimate their instantaneous drifts (from their incomplete observations), ultimately leading to their escape from the bulk. Outlying agents always escape the swarm from the rear, leading with time to an effective “evaporation”.
For consistency, the initial conditions , to be drawn from a probability measure with finite support , namely with and must be restricted. Let us now define a characteristic relaxation time that corresponds to the time needed by the stochastic processes to diffuse over the interval of length . For observation ranges and initial conditions , all N agents mutually interact at time , and, therefore, correctly determine their relative ranks. We assume that this will remain true with high probability, for times . In other words, we expect that the initially tight swarm is likely to remain flocked for , effectively a meta-stable state. For asymptotic times, however (i.e., ), the swarm’s tightness will be destroyed. Indeed, for any finite U, outliers will ultimately escape the attraction generated by the bulk of the remaining swarm. Therefore, our heuristic postulates that the characteristic observation range, separating these two regimes, . The actual validity of these simple heuristics have been tested in several numerical experiments that are reported in Figure 1 and Figure 2.
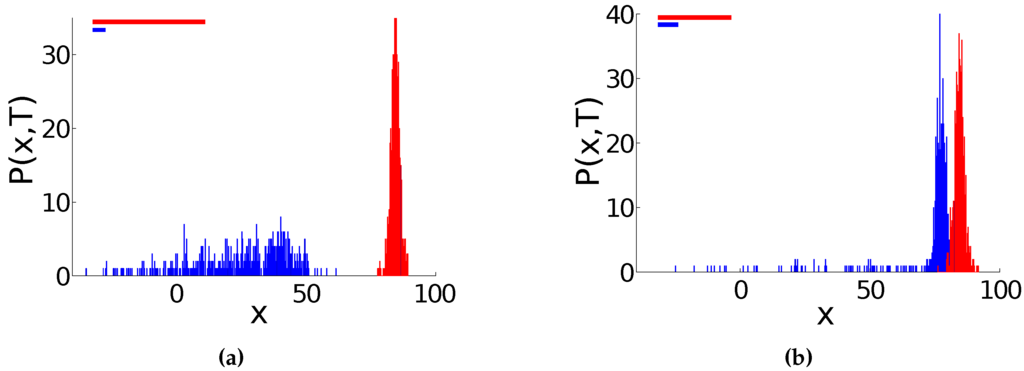
Figure 1.
End probability distribution at time of swarms of agents, with respect to U. Here, all agents initially start at . (a): tight swarm for (red) and “diffusive evaporating” swarm for (blue). (b): tight swarm for (red) and “diffusive evaporating” swarm for (blue). The respective observation ranges U are depicted at the top of each figure.
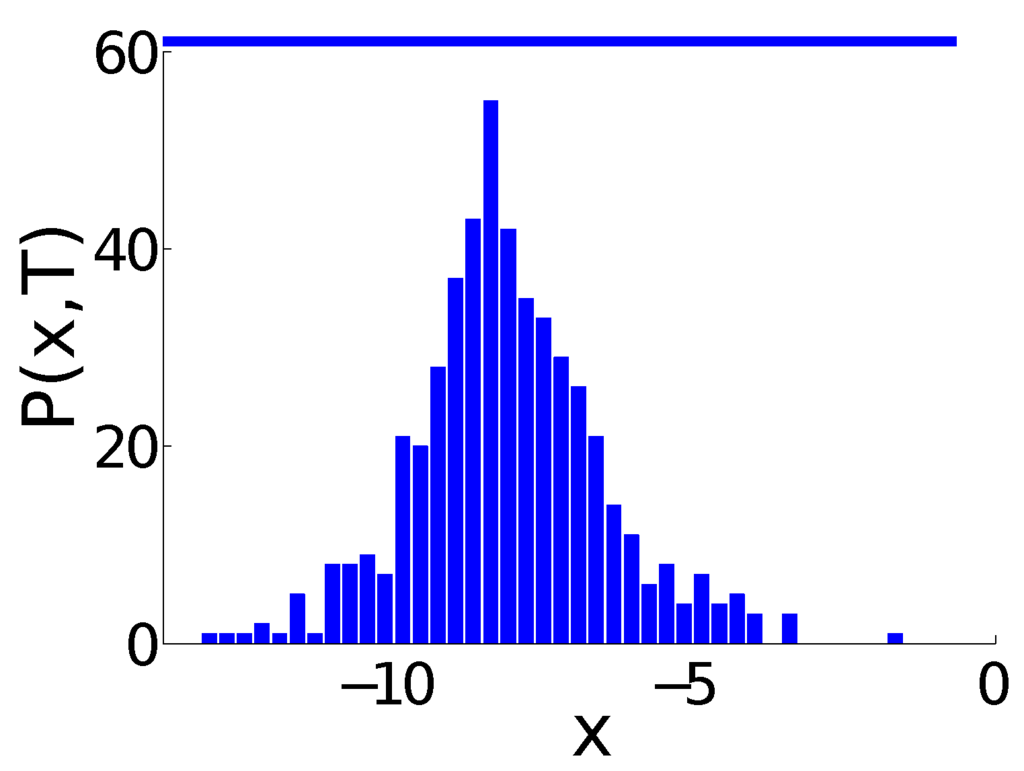
Figure 2.
End probability distribution at time of a swarm of agents, initially starting at . The observation range is depicted at the top of the figure. Notice that the evaporation (i.e., destruction of swarm tightness) does not start before the relaxation time .
4. Interactions between Collinear Colliding Swarms
In this section, we investigate the mutual interactions between two initially distinct swarms and composed of , respectively , agents driven by rank-based interactions. Initially, we let all agents from be randomly positioned with ; similarly, for , we assume that . Assume non-overlapping supports with (interval is located on the left of ) and finite observation ranges U such that ). Accordingly, at time , agents from do not interact with agents from and vice versa. We further assume that initially the swarm with has an average barycentric drift velocity and that . This implies that the -agents will, on average, catch and ultimately overcome their -fellows. Therefore, for large times, the -agents exhibit a net tendency to become -leaders. Qualitatively, after a - collision, the following dynamic features occur:
- (i)
- -agents become leaders and thus are less influenced by (or possibly almost independent from) -agents. This implies that, with time, -agents will exhibit a net tendency to recover their nominal drifts (i.e., the drifts realized before the collision).
- (ii)
- -agents feel the presence of their leaders from and, therefore, have a net tendency to increase their drifts.
Therefore, depending on the values of the population sizes and and drifts and , two alternative situations emerge:
- (a)
- Mutual capture of swarms. After collision, and aggregate into a global tight swarm . The average barycentric drift of is larger than . Thus, in this case, mutual interactions generate an increase in the average velocity of the global population.
- (b)
- Quasi-asymptotic freedom of swarms. After collision, and for asymptotic times, the swarms and evolve almost without interactions (quasi-free swarm evolutions). In the quasi-free regime, and recover their respective initial individual barycentric velocities and .
In the sequel, the implementation of the velocity condition is realized by considering two distinctive rank-based dynamics: (i) The Hybrid-Atlas model (HAM) introduced by T. Ichiba et al. [9] and (ii) a new modified HAM model (MHAM). For both cases, we analytically estimate the threshold values of the relevant control parameters that lead to either outcome (a) or (b).
4.1. Colliding Swarms Driven by Hybrid Atlas Models
In this first situation, we assume that the swarms and are populated by slightly different types of agents. Agents and share a common rank-based drift, given in Equation (1), but we endow the s with an extra systematic constant drift :
with .
This ensures that -agents, on average, initially travel faster than -agents, and, therefore, . Since the initial -support is located on the left of , a --collision is unavoidable. At this point, we emphasize that when , the global heterogeneous society , when subject to the dynamics given by Equation (1), is a special case of HAM dynamics [9]. In [9], the authors derive the set of combinatorial stability conditions that ensure the existence of a tight swarm stationary state. Heuristically speaking, one has to explicitly verify that, in all possible ranking configurations, the agents and are systematically driven by attractive drifts directed toward the barycenter of .
For , the hypotheses in [9] are not strictly realized (since the perfect ranking determination would indeed require ). Along the same lines as in Section 3, we assume that for large enough but finite U, the agents’ ranking in during collision remains approximately unaffected. Accordingly, the HAM tightness conditions also remain approximately valid in , during collision. The average barycentric drift of , during collision and when is ahead of , reads:
Therefore, the recentered rank-based drift of agent from , in this configuration, becomes:
According to [9], the set of combinatorial tightness stability conditions for HAM dynamics, under any permutation of the agents read as:
where expresses the necessary condition.
To check the validity of Equation (13), it is sufficient to focus on the most critical agent configuration. This configuration is realized when all faster agents take the ranks (i.e., when is ahead of ). This corresponds to the choice in Equation (13), under the permutation , where:
To ensure that this sum is negative, one must finally have:
4.2. Colliding Swarms Driven by Modified Hybrid Atlas (MHAM) Dynamics
Here, we assume that the agents from follow the dynamics of Equation (1), with and similarly, is subject to the same dynamics but with . From now on and without loss of generality, we focus only on the and . As before, we initially configure the system so that swarm and do not interact at time (i.e., , , and the common observation range U is such that ). When , we have and we look for a critical ratio under which a tight swarm survives a - collision. To this aim, let us consider a “post-colliding” configuration realized when is completely ahead of . In term of stability, this configuration is the most critical: -agents can only escape from via this configuration. Therefore, the tightness has to be checked under this specific configuration.
Accordingly, whenever the stability conditions from [9] are verified under this critical configuration, they will also be verified under any other configuration. Therefore, the tightness of only depends on this critical configuration. Formally, we now rewrite Equation (5) for and verify whether the stability requirements given by [9] are fulfilled for this critical case. In this case, the recentered dynamics read:
From [9], the stability conditions for read:
The most critical condition is realized for (this condition tests whether the distance between and remains stationary). It reads:
implying that the critical threshold finally reads:
Notice that for , cannot possibly exist (i.e., ). The first agent has no drift, since it never observes any leader. Therefore, a society of one leader cannot possibly drive a swarm. Instead a single leader always remains flocked with . For , Figure 3 shows the critical value . When , asymptotically converges toward . Figure 4 shows the behavior of as a function of the proportion (faster agents in ), for agents. For and , .
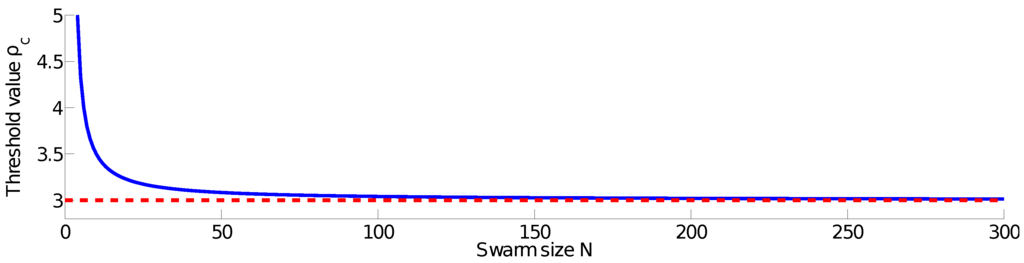
Figure 3.
Value of the critical threshold , with regard to the swarm size N of the HAM, when . The asymptotic value of is depicted in red.
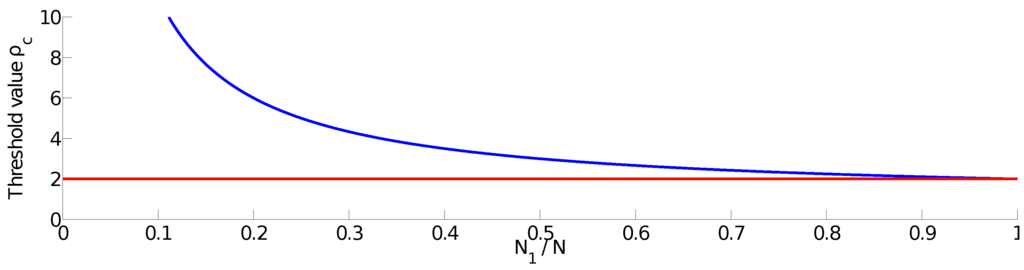
Figure 4.
Value of the critical threshold , with regard to the proportion of fast agents in the HAM, when .
4.3. Numerical Simulations
We consider two different cases, both with agents. In both simulations, the society starts with all agents located at , while agents from start at . The common observation range U is selected large enough (), and . For the experiments, we vary ρ, in order to compare i) a case in which both societies remain flocked together with ii) a case leading to the quasi-freedom behavior.
Figure 5 shows one realization in which , allowing both societies to remain flocked. The left plot shows the final distribution of agents from both societies, as leads . In the right plot of Figure 5, we show the average barycentric speeds of both societies. Notice how is initially accelerated as its agents interact with those from . Later, when has overcome , agents from get an extra drift due to interactions with . This finally enables both societies to evolve at the same average barycentric speed (and therefore to remain flocked).
In Figure 6, we show the same scenario, for one realization with (quasi-freedom regime). In the right plot, we still notice the initial drift gained by as its agents interact with those from . Once has overcome , agents from get an extra drift, that is not large enough to keep both societies flocked together. The extra drift gained by finally vanishes, once exits the observation range of the agents from . Finally, and recover their nominal speeds.
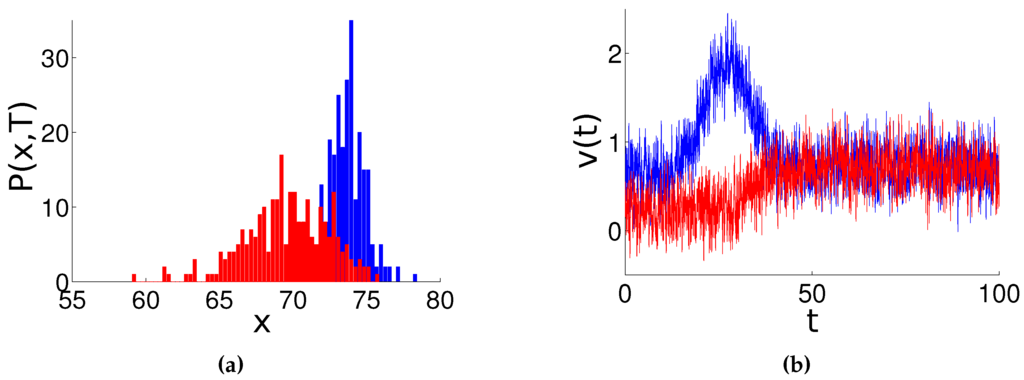
Figure 5.
Final distributions and average barycentric speeds for one realization, in which both societies that start at achieve flocking. Here, , , and agents. (a): distribution of the agents from (blue) and (red), at ending time . (b): average barycentric speed of each society, with respect to time.
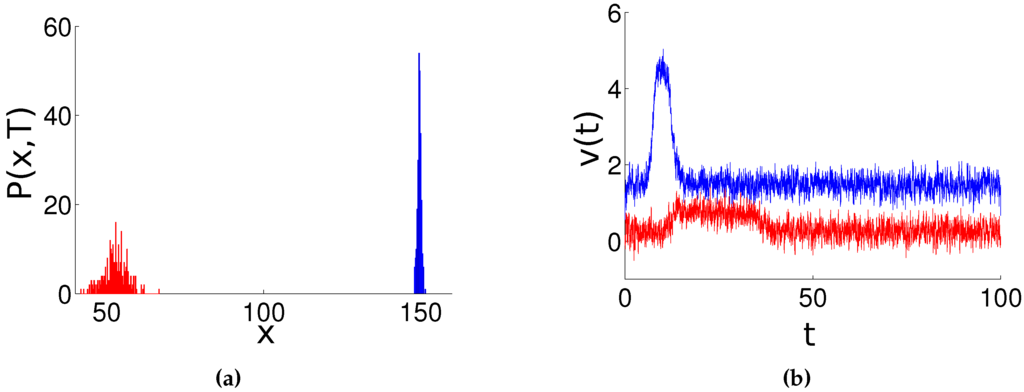
Figure 6.
Final distributions and average barycentric speeds for one realization, in which both societies that start at do not achieve flocking. Here, , , and agents. (a): distribution of the agents from (blue) and (red), at ending time . (b): average barycentric speed of each society, with respect to time.
5. Conclusions and Perspectives
Tightly flocked swarms of agents are externally perceived as plastic (i.e., deformable) macroscopic bodies with dynamics resulting from the compromise between the individual evolutions, and the nature and range of the mutual interactions. Having macroscopic bodies at hand, basic physics naturally suggests the questions: (i) how such do solid bodies mutually interact; (ii) what emerges after collisions, and (iii) what type of information can we get from studying the results of the collisions? The discussion of collisions presents some similarities with the physics of solitons’ interactions where the underlying nonlinearities precludes the superposition principle to be be invoked. We show here that the rank-based Brownian dynamics is one possible approach to explore, in a partly analytical way, some of the challenging questions related to swarm interactions.
Acknowledgments
Detailed comments from anonymous referees strongly contributed to the presentation and quality of this paper. Guillaume Sartoretti is funded by the Swiss National Science Foundation.
Author Contributions
Max-Olivier Hongler came up with the core concept of the paper; Guillaume Sartoretti and Max-Olivier Hongler made the analytical calculations; Guillaume Sartoretti performed the numerical experiments; Max-Olivier Hongler and Guillaume Sartoretti wrote the paper. Both authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Couzin, I.D.; Krause, J.; Franks, N.R.; Levin, S.A. Effective leadership and decision-making in animal groups on the move. Nature 2005, 433, 513–516. [Google Scholar] [CrossRef] [PubMed]
- Sartoretti, G.; Hongler, M.O.; Filliger, R. The Estimation Problem and Heterogenous Swarms of Autonomous Agents. In Proceedings of Stochastic Modeling Techniques and Data Analysis International Conference (SMTDA 2014), Lisbon, Portugal, 11–14 June 2014.
- Han, J.; Li, M.; Guo, L. Soft control on collective behavior of a group of autonomous agents by a shill agent. J. Syst. Sci. Complex. 2006, 19, 54–62. [Google Scholar] [CrossRef]
- Sartoretti, G.A.; Hongler, M.O. Soft Control of Swarms: Analytical Approach. In Proceedings of the 5th International Conference on Agents and Artificial Intelligence (ICAART 2013), Barcelona, Spain, 15–18 February 2013; pp. 147–153.
- Sartoretti, G.; Hongler, M.-O. Soft Control of Self-Organized Locally Interacting Brownian Planar Agents. In Computer Aided Systems Theory - EUROCAST 2013; Moreno-Díaz, R., Pichler, F., Quesada-Arencibia, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 45–52. [Google Scholar]
- Strogatz, S.H. From Kuramoto to Crawford: Exploring the onset of synchronization in populations of coupled oscillators. Physica D 2000, 143, 1–20. [Google Scholar] [CrossRef]
- Acebrón, J.A.; Bonilla, L.L.; Vicente, C.J.P.; Ritort, F.; Spigler, R. The Kuramoto model: A simple paradigm for synchronization phenomena. Rev. Mod. Phys. 2005, 77. [Google Scholar] [CrossRef]
- Pal, S.; Pitman, J. One dimensional Brownian particle systems with rank-dependent drifts. Ann. Appl. Probab. 2008, 18, 2179–2207. [Google Scholar] [CrossRef]
- Ichiba, T.; Papathanakos, V.; Banner, A.; Karatzas, I.; Fernholz, R. Hybrid Atlas Model. Ann. Appl. Probab. 2011, 21, 609–644. [Google Scholar] [CrossRef]
- Hongler, M.O.; Gallay, O.; Hashemi, F. Imitation’s Impact on the Dynamics of Long-Wave Growth. Econ. Model. 2015. submited. [Google Scholar]
- Jourdain, B.; Malrieu, F. Propagation of chaos and Poincaré inequalities for a system of particles interacting through their CDF. Ann. Appl. Probab. 2008, 18, 1706–1736. [Google Scholar] [CrossRef]
- Hongler, M.O.; Filliger, R.; Gallay, O. Local versus nonlocal barycentric interactions in 1D agent dynamics. Math. Biosci. Eng. 2014, 11, 303–315. [Google Scholar] [PubMed]
- Banner, A.D.; Fernholz, R.; Karatzas, I. Atlas Models of Equity Markets. Ann. Appl. Prob. 2005, 15, 2296–2330. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).