Abstract
At present, many cloud services are managed by using open source software, such as OpenStack and Eucalyptus, because of the unification management of data, cost reduction, quick delivery and work savings. The operation phase of cloud computing has a unique feature, such as the provisioning processes, the network-based operation and the diversity of data, because the operation phase of cloud computing changes depending on many external factors. We propose a jump diffusion model with two-dimensional Wiener processes in order to consider the interesting aspects of the network traffic and big data on cloud computing. In particular, we assess the stability of cloud software by using the sample paths obtained from the jump diffusion model with two-dimensional Wiener processes. Moreover, we discuss the optimal maintenance problem based on the proposed jump diffusion model. Furthermore, we analyze actual data to show numerical examples of dependability optimization based on the software maintenance cost considering big data on cloud computing.
1. Introduction
At present, big data and cloud computing are now attracting attention as the next-generation software service paradigm. Cloud software is connected by many types of mobile software. Then, mobile clouds based on the cloud service become known as the next-generation software service paradigm. In the case of such mobile clouds, the installer software developed under third-party developers, indirectly affects the reliability in the area of a mobile device. In particular, OSS (open source software) systems serve as key components of critical infrastructures in society. Open source projects contain special features, so-called software compositions, by which several geographically-dispersed components are developed in all parts of the world. However, the poor handling of the quality problem and customer support has limited the progress of OSS, because the development cycle of OSS has no specific testing phase to detect and remove software faults introduced in the development process. Mobile OSS has been gaining much attention in the embedded system area, i.e., Android [1], BusyBox [2], Firefox OS [3], etc. Therefore, it is difficult for many companies to assess the reliability in mobile clouds, because a mobile OSS includes several software versions, vulnerability issues, open source code, security holes, etc.
Considering the reliability assessment for cloud computing, mobile clouds and OSS, it is difficult to deal with the external factors, such as the results of big data, because the external factors arising from the relationship between big data and cloud computing have an effect on the infrastructure software for mobile clouds. Therefore, it is important for software managers to consider these external factors for big data, mobile clouds and cloud computing.
In this paper, we focus on the method of reliability analysis for cloud computing. Then, we propose a method of software reliability analysis based on a jump diffusion model with a stochastic differential equation for big data on cloud computing. In particular, we estimate several parameters included in the proposed model by using actual software fault data. Furthermore, we formulate the total expected software cost considering big data on cloud computing. Then, we show that the proposed reliability and optimization analysis can assist with the improvement of the quality for big data on a cloud computing environment.
2. Related Research
Many software reliability growth models (SRGMs) [4–7] have been applied to assess the reliability of quality management and testing progress control of software development. On the other hand, only a few effective methods assisting dynamic testing management for a new distributed development paradigm, as typified by the open source projects, have been presented [8–10]. Furthermore, several research works [11–15] are based on the area of cloud computing and mobile clouds. However, these papers focus on security, service optimization, secure control, resource allocation technique, etc. Only a few research papers in terms of reliability for big data and cloud computing have peen presented. When considering the effect of the debugging process on the entire system in the development of a method of reliability assessment for software developed under third-party developers in mobile clouds, it is necessary to grasp the situation of installer software, the network traffic, the installed software, etc. Then, it is very important to consider the status of network traffic in terms of the reliability assessment from the following standpoints:
- ► In the case of a mobile device, the network access devices are frequently used by many types of software installed via the installer software.
- ► By using the installer software, the various types of third-party software are installed via the network.
- ► In the case of open source software, the weakness of reliability and security becomes a significant problem with respect to a computer network.
Furthermore, there are some interesting research papers in terms of cloud hardware, cloud service, mobile clouds and cloud performance evaluation [13,16,17]. However, most of them have focused on case studies of cloud service and cloud data storage technologies. Only a few effective methods of dynamic reliability assessment considering the environment, such as cloud computing and OSS, have been presented. In particular, it is very important to consider the status of fault detection and big data in terms of the reliability assessment for cloud computing from the following standpoints:
- ► Cloud computing has a particular maintenance phase, such as the provisioning processes.
- ► Big data as the result of many and complicated data from using the Internet cause system-wide failures because of the complexity of data management.
- ► The various mobile devices are connected via the network to the cloud service.
- ► The data storage areas for cloud computing are reconfigured via the various mobile devices.
From the above reasons, it is important to consider the indirect influences of big data on reliability. We have proposed several methods of software reliability for cloud computing in the past [18,19]. However, only a few effective methods of reliability assessment considering both the big data factor and the fault factor have been presented, because it is very difficult to describe the indirect influence of big data and fault data as the reliability assessment measures, as shown in Figure 1. Then, we propose a new approach to describe the indirect effect on reliability by using two kinds of Brownian motions and a jump diffusion process.
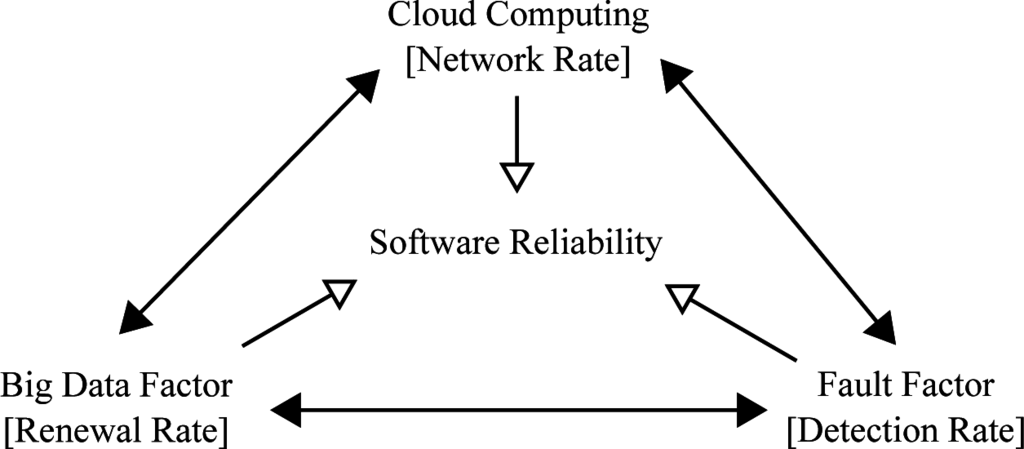
Figure 1.
The relationship among big data, cloud computing, the network and reliability.
From the above discussed points, we consider that all of the factors of big data, cloud computing and network access have an effect on cloud computing, directly and indirectly. In other words, big data and cloud computing have a deeply complex reliability issue. Therefore, it is very important to consider big data from the point of view of the reliability of cloud computing, i.e., it will be able to maintain the stable operation of cloud computing if we can offer several reliability assessment measures considering big data in terms of all of the factors of cloud computing, mobile clouds and open source software.
Moreover, it is very important in terms of software management for us to decide the optimal length of the maintenance period considering the network environment for big data on cloud computing. We propose the optimal maintenance problem based on the jump diffusion model with two Brownian motions. Considering the amount of noise in the sample path as the stability requirement, we find the optimum maintenance time by minimizing the total expected software cost. Furthermore, we analyze actual data to show numerical examples of the dependability optimization considering the network environment for cloud computing.
3. Model Description
3.1. Wiener Process Modeling
Let M(t) be the cumulative number of detected faults latent in the cloud OSS by operational time t (t ≥ 0). Suppose that M(t) takes on continuous real values. Since latent faults in the cloud OSS are detected and eliminated during the operation phase, M(t) gradually increases as the operation procedures go on. Thus, under common assumptions for the software reliability growth modeling [4], the following linear differential equation can be formulated:
where b(t) is the software fault-detection rate at operation time t, and a non-negative function, R(t), means the amount of changes of the requirement specifications [20]. Furthermore, R(t) is defined as follows:
where α is the number of latent faults in the cloud OSS and β the changing rate of requirement specifications. It is assumed that the fault-prone requirement specifications of cloud OSS grow exponentially in terms of t [20]. Thus, the cloud OSS shows a reliability regression trend if β is negative. On the other hand, the cloud OSS shows a reliability growth trend if β is positive. In particular, cloud computing has the unique characteristics of provisioning processes. Then, considering the independence of each noise, we extend Equation (1) to the following stochastic differential equation considering two Brownian motions [21,22]:
where σ1 and σ2 are positive constants representing a magnitude of the irregular fluctuation, v1(t) and v2(t) standardized Gaussian white noise.
We extend Equation (3) to the following stochastic differential equation of an Itô type [23]:
where ωi(t) is the i-th one-dimensional Wiener process, which is formally defined as an integration of the white noise vi(t) with respect to time t. We define the two dimensionprocesses [ω1(t), ω2(t)] as follows [24]:
Then, the compound Wiener process ῶ(t) is a Gaussian process and has the following properties:
where Pr[·] and E[·] represent the probability and expectation, respectively.
By using Itô’s formula [21,22], we can obtain the solution of Equation (4) under the initial condition M(0) = 0 as follows [23]:
Moreover, we define the software fault-detection rate per fault in the case of b(t) defined as:
where I(t) means the mean value functions for the inflectedS-shaped SRGM, based on a nonhomogeneous Poisson process (NHPP) [4], a the expected number of latent faults for SRGM and b the fault detection rate per fault. Generally, the parameter c is defined as
. We define the parameter l as the mean value for the change of rate of network traffic, i.e., we assume that the cloud software is managed under the severe environment when the change rate of network traffic is large.
We can represent the noise-by-noise sample path for each factor as the following equations. First, the sample path in terms of the fault factor is given as:
Second, the sample path in terms of the network factor is given as:
Therefore, the cumulative number of detected faults is obtained as follows:
In the proposed model, we assume that the parameter σ1 depends on the parameter b resulting from the failure occurrence phenomenon. Similarly, we assume that the parameter σ2 depends on the parameter c resulting from the network environment of cloud computing.
In particular, we can use the coefficient of variation as the measure of variation without the effect of mean value. We can derive the following coefficient of variation from Equation (13):
where the variance of the cumulative number of detected faults, Var[M(t)], is given by the following equation.
3.2. Jump-Diffusion Modeling
Generally, the jump diffusion models have been applied to the area of option pricing. In particular, it is difficult to directly apply the idea of the existing option pricing model to the software fault-detection phenomena, because the log-normal distribution is optimized based on the option pricing area. Furthermore, it is unnatural to apply the log-normal distribution based on the option pricing model to the software fault-detection phenomena, because it is usually assumed that the software fault-detection phenomena have a non-biased distribution in the research area of software reliability. For above-mentioned reason, we assume the following normal distribution function as a Gaussian jump diffusion process in order to consider the characteristics of the software fault-detection phenomena.
Then, we assume that the i-th jump range Vi is approximately estimated as the positive values in almost all cases, because the mean value μ keeps a large value.
The jump term can be added to the proposed stochastic differential equation models in order to incorporate the irregular state around the time t by a change in the number of log-in users. Then, the jump diffusion process [25] is given as follows.
where Yt(γ) is a Poisson point process with parameter γ at operation time t. Furthermore, Yt(γ) is the number of jumps that occurred, γ the jump rate. Yt(γ), ω(t) and Vi are assumed to be mutually independent. Moreover, Vi is the i-th jump’s range.
Similarly, we can represent the noise-by-noise sample path for each factor as the following equations. First, the sample path in terms of the fault factor is given as:
Second, the sample path in terms of the network factor is given as:
By using Itô’s formula [21,22], the solution of the former equation can be obtained as follows:
Then, we conclude the noises in terms of the proposed model as follows:
- ► The Brownian motion ω1 represents the results from the failure-occurrence phenomenon.
- ► The Brownian motion ω2 represents the results from cloud computing having the unique characteristics of provisioning processes, the change of the number of log-in users, etc.
- ► The jump term means the indirect effects as a result of the many and complicated data from using the Internet, causing the system-wide failures because of the complexity of data management, i.e., the system failures of DataNodeand NameNodein terms of Hadoop and NoSQLin order to manage big data, etc.
The proposed model in Equation (20) includes the noise with jump term Vi. The software managers can assess several characteristics of cloud computing by using the size and shape of noises with the jump term, because the proposed model can totally comprehend the provisioning process, the change of users, the change of cloud applications, the indirect effects as a result of the many and complicated data in cloud computing, with big data as the noise.
4. Parameter Estimation
4.1. Method of Maximum-Likelihood
In this section, the estimation method of unknown parameters α, β, b and σ1 in Equation (9) is presented. Then, we assume that σ2 and l are the given parameters, because σ2 and l are considered as the network factors. The joint probability distribution function of the process M(t) is denoted as:
The probability density of Equation (21) is denoted as:
Since M(t) takes on continuous values, the likelihood function, λ, for the observed data (tk; yk)(k = 1, 2, ⋯, K) is constructed as follows:
For convenience in mathematical manipulations, the following logarithmic likelihood function is used:
The maximum-likelihood estimates α*, β*, b* and
are the values making Λ in Equation (24) maximal. These can be obtained as the solutions of the following simultaneous likelihood equations [23]:
4.2. Estimation of the Jump Diffusion Parameters
Generally, it is difficult to estimate the jump diffusion parameters of the stochastic differential equation model because of the complicated likelihood function, mixed distribution, etc. The estimation methods of jump diffusion parameters are proposed by several researchers. However, only a few effective methods of estimation have been presented. We focus on the estimation methods performed in two stages [26]. A genetic algorithm (GA) in order to estimate the jump diffusion parameters of the proposed model is used in this section. The procedure of the GA algorithm is given in the following [27].
It is assumed that the proposed jump diffusion model includes the parameters γ, μ and τ. The parameters μ and τ mean the parameters included in the i-th jump’s range Vi.
- Step 1: The initial individuals are randomly generated. Furthermore, the set of initial individuals is converted to the binary digit.
- Step 2: Two parental individuals are selected, and new individuals are produced by the crossover recombination.
- Step 3: The value of fitness is calculated from the evaluated value of each individual. The following value of fitness as the error between the estimated and the actual values is defined in this paper:where Mj(i) is the number of detected faults at operation time i in the proposed jump diffusion model and yi the number of actual detected faults. Furthermore, θ means the set of parameters γ, μ, and τ.
- Step 4: Step 2 and Step 3 are continued until reaching a specific size.
The jump diffusion parameters γ, μ, and τ are estimated by using the above-mentioned steps.
5. Optimal Maintenance Problem
Considering the conventional optimal software release problems [28,29], we define the following cost parameters:
- c1: the fixing cost per fault during the operation,
- c2: the maintenance cost per unit time during the operation,
- c3: the maintenance cost per fault after the maintenance.
Then, the expected software cost in the operation of cloud OSS can be formulated as:
Furthermore, the expected software maintenance cost after the maintenance of cloud OSS is represented as follows:
Consequently, from Equations (27) and (28), the total expected software maintenance cost is given by:
The optimum maintenance time t*is obtained by minimizing C(t) in Equation (29). Then, we consider the optimal maintenance problem as follows:
Then, the optimum maintenance time t*can be estimated numerically by using the optimization algorithms.
Moreover, we can represent the noise-by-noise sample path for each factor as the following equations. First, the sample path in terms of the fault factor is given as:
Second, the sample path in terms of the network factor is given as:
6. Numerical Examples
We focus on OpenStack [30] in order to evaluate the performance of our method. In this paper, we show numerical examples by using the datasets for OpenStack of cloud OSS. The data used in this paper are collected in the bug tracking system on the website of the OpenStack open source project.
6.1. Reliability Assessment
The unknown parameters included in the proposed model are estimated with the following results:
where the changing rate of network traffic l is experientially assumed to be 0:1. Furthermore,
is estimated as 0:00113. Moreover, the estimation results of jump diffusion parameters based on GA are shown as follows:
The estimated sample path of cumulative numbers of detected faults,
, in Equation (20) is shown in Figure 2. From Figure 2, we found that the noise becomes large from 100 to 200 days. Moreover, the estimated sample paths of cumulative numbers of detected faults,
and
in Equations (18) and (19) are shown in Figures 3 and 4. From Figures 3 and 4, we can confirm that the sample path in terms of the fault factor becomes large throughout the whole operation phase. On the other hand, the sample path in terms of the network factor becomes small throughout the whole operation phase. Moreover, Figure 5 shows the estimated sample path of the number of detected faults in terms of fault and network factors. The software managers will be able to comprehend easily the motion of noises by using the cubic graph, such as Figure 5.
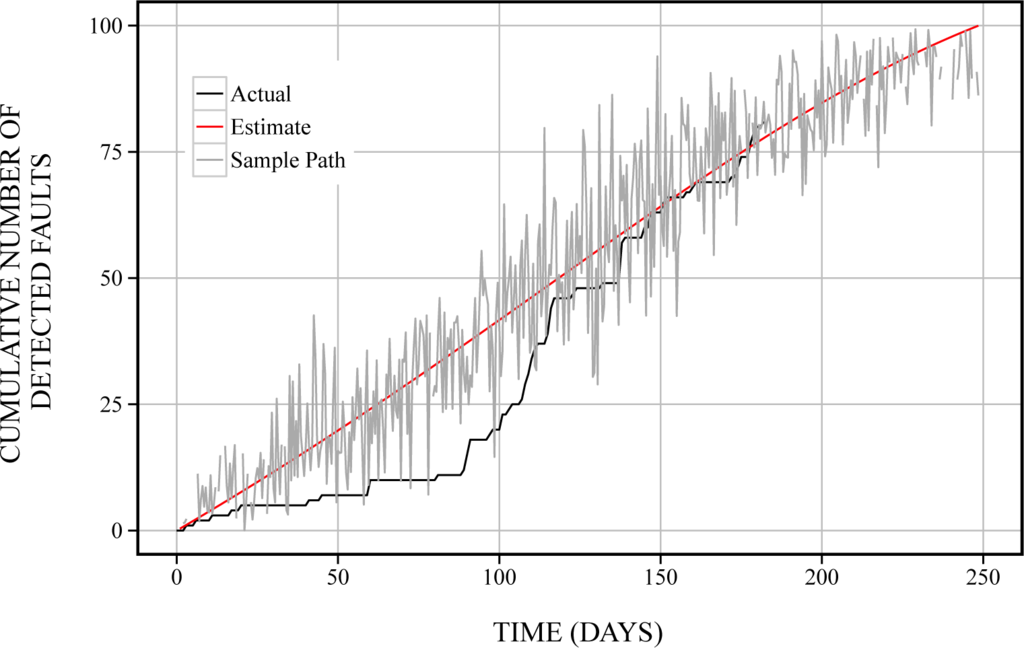
Figure 2.
The estimated sample path of cumulative numbers of detected faults in terms of fault and network factors.
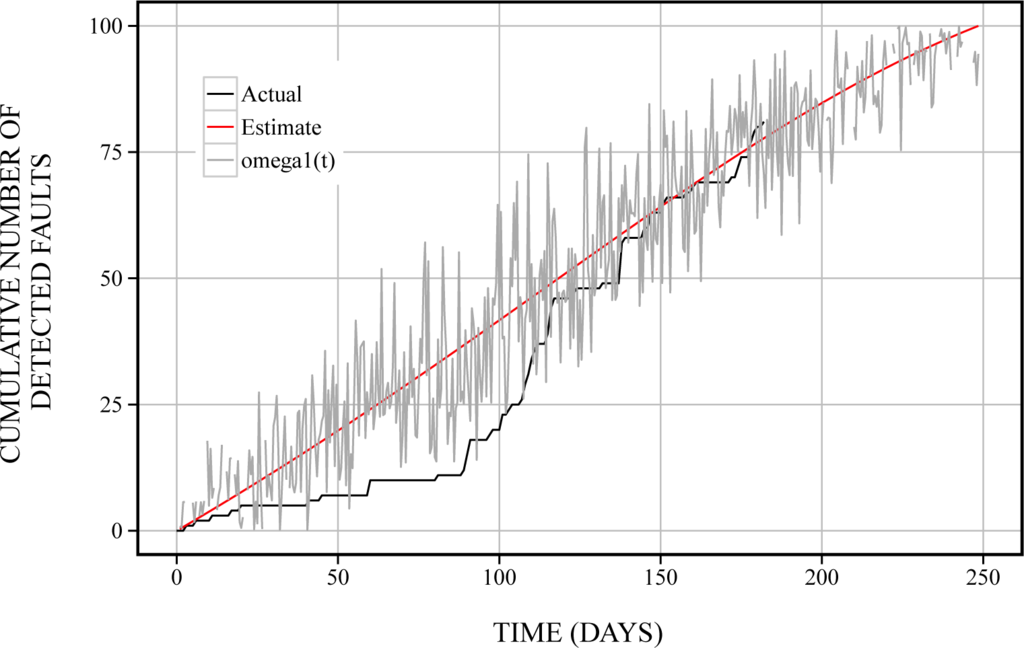
Figure 3.
The estimated sample path of cumulative numbers of detected faults in terms of the fault factor.
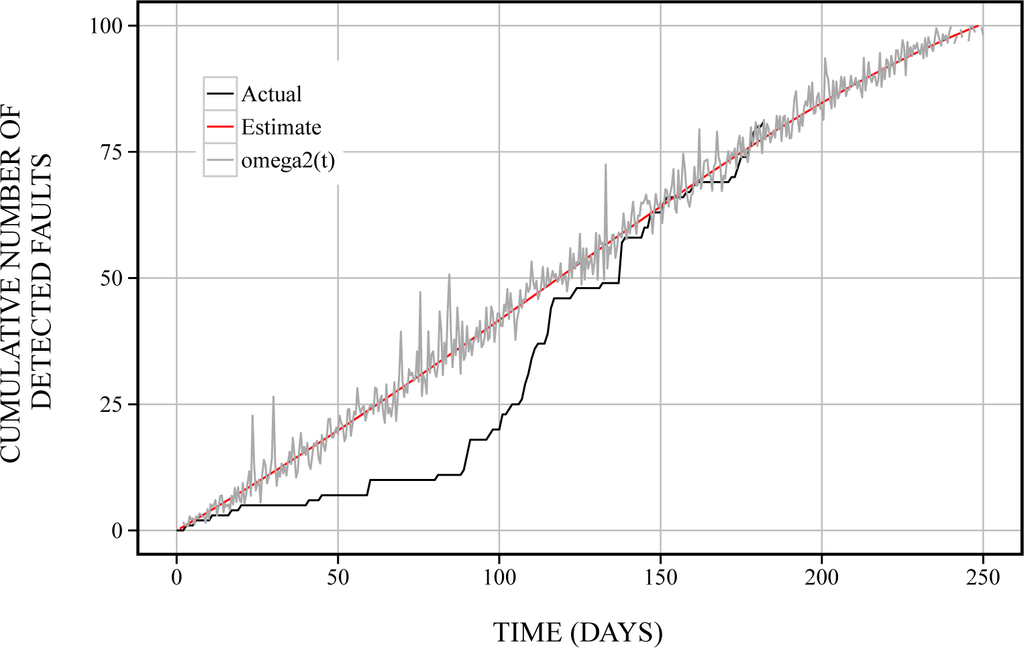
Figure 4.
The estimated sample path of cumulative numbers of detected faults in terms of the network factor.
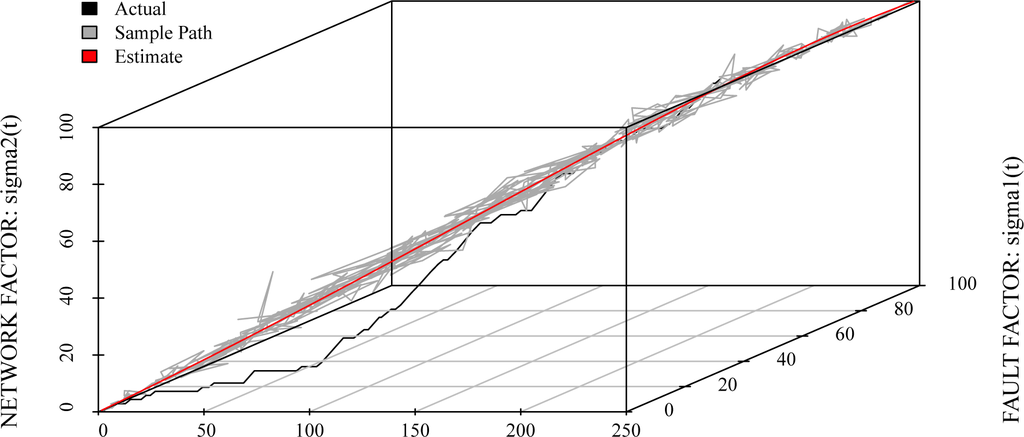
Figure 5.
The estimated sample path of cumulative numbers of detected faults in terms of fault and network factors.
6.2. Optimal Maintenance Time
We show the numerical examples based on the optimal maintenance problems, which are discussed in Section 5. Figure 6 shows the sample path of estimated total software cost. From Figure 6, we find that the optimum maintenance time is derived as t*= 384.17 days. Then, the total software maintenance cost is 677:01. Moreover, we can estimate the optimal maintenance time with stability requirements by using the amount of noise in Figure 6. Then, the estimated total software cost with stability requirements is about 450.
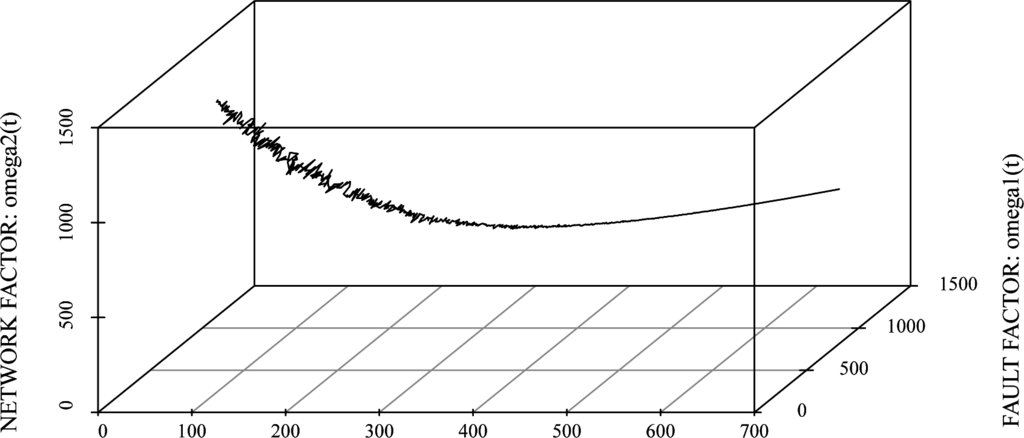
Figure 6.
The estimated total software cost.
7. Concluding Remarks
In this paper, we have discussed a software dependability assessment based on the jump diffusion model with a two-dimensional Wiener processes in order to consider the software management environment of big data on cloud computing. Furthermore, we have assumed that several factors, big data, cloud computing and network access, have an effect on cloud software, indirectly. Then, we have applied several noises to these indirect factors. Moreover, we have formulated and minimized the total software cost considering the network environment of big data on cloud computing. In particular, we have defined the optimal maintenance problems considering the amount of noise in the sample path as the stability requirement. Then, we have found that our method can evaluate the optimum maintenance time considering the operational environment of cloud computing. Furthermore, we have analyzed actual data to show numerical examples of the dependability optimization for cloud computing. Software managers will be able to understand the stability for the environment of big data on cloud computing by using the noises of the proposed jump diffusion model. Our method may be useful as a method of dependability assessment and as an optimal maintenance method for the cloud computing environment.
Acknowledgments
This work was supported in part by the Telecommunications Advancement Foundation in Japan and JSPSKAKENHIGrant No. 15K00102 and No. 25350445 in Japan.
Author Contributions
Both authors have worked equally in this manuscript. Both authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Open Handset Alliance, Android. Available online: http://www.android.com/ accessed on 25 June 2015.
- Andersen, E. BUSYBOX. Available online: http://www.busybox.net/ accessed on 25 June 2015.
- Firefox, O.S. Marketplace, Android–Partners–mozilla.org, Mozilla Foundation. Available online: http://www.mozilla.org/firefoxos/ accessed on 25 June 2015.
- Yamada, S. Software Reliability Modeling: Fundamentals and Applications; Springer: Tokyo, Japan and Heidelberg, Germany, 2013. [Google Scholar]
- Lyu, M.R. Handbook of Software Reliability Engineering; Mcgraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Musa, J.D.; Iannino, A.; Okumoto, K. Software Reliability: Measurement, Prediction, Application; McGraw-Hill: New York, NY, USA, 1987. [Google Scholar]
- Kapur, P.K.; Pham, H.; Gupta, A.; Jha, P.C. Software Reliability Assessment with OR Applications; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Li, X.; Li, Y.F.; Xie, M.; Ng, S.H. Reliability analysis and optimal version-updating for open source software. J. Inf. Softw. Technol. 2011, 53, 929–936. [Google Scholar]
- Ullah, N.; Morisio, M.; Vetro, A. A comparative analysis of software reliability growth models using defects data of closed and open source software, Proceedings of the 35thIEEE Software. Engineering Workshop, Heraclion, Greece, 12–13 October 2012; pp. 187–192.
- Cotroneo, D.; Grottke, M.; Natella, R.; Pietrantuono, R.; Trivedi, K.S. Fault triggers in open-source software: An experience report, Proceedings of the 24th IEEE International Symposium on Software Reliability Engineering, Pasadena, CA, USA, 4–7 November 2013; pp. 178–187.
- Park, J.; Yu, H.C.; Lee, E.Y. Resource allocation techniques based on availability and movement reliability for mobile cloud computing. In Distributed Computing and Internet Technology; Ramanujam, R., Ramaswamy, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 263–264. [Google Scholar]
- Suo, H.; Liu, Z.; Wan, J.; Zhou, K. Security and privacy in mobile cloud computing, Proceedings of the 9th International Wireless Communications and Mobile Computing Conference, Cagliari, Italy, 1–5 July 2013; pp. 655–659.
- Khalifa, A.; Eltoweissy, M. Collaborative autonomic resource management system for mobile cloud computing, Proceedings of the Fourth International Conference on Cloud Computing, GRIDs, and Virtualization, Valencia, Spain, 27 May–1 June 2013; pp. 115–121.
- Gabner, R.; Schwefel, H.P.; Hummel, K.A.; Haring, G. Optimal model-based policies for component migration of mobile cloud services, Proceedings of the 10th IEEE International Symposium on Network Computing and Applications, Cambridge, MA, USA, 25–27 August 2011; pp. 195–202.
- Park, N. Secure data access control scheme using type-based re-encryption in cloud environment. In Semantic Methods for Knowledge Management and Communication; Springer: Berlin/Heidelberg, Germany, 2011; pp. 319–327. [Google Scholar]
- Yang, B.; Tan, F.; Dai, Y.S. Performance evaluation of cloud service considering fault recovery. J. Supercomput. 2013, 65, 426–444. [Google Scholar]
- Iosup, A.; Ostermann, S.; Yigitbasi, M.N.; Prodan, R. Fahringer, T; Epema, D.H.J. Performance analysis of cloud computing services for many-tasks scientific computing. IEEE Trans. Parallel Distrib. Syst. 2011, 22, 931–945. [Google Scholar]
- Tamura, Y.; Miyahara, H.; Yamada, S. Reliability analysis based on jump diffusion models for an open source cloud computing, Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management, Hong Kong Convention and Exhibition Centre, Hong Kong, China, 10–13 December 2012; pp. 752–756.
- Tamura, Y.; Yamada, S. Reliability analysis methods for an embedded open source software. In Mechatronic Systems, Simulation, Modelling and Control; Milella, A., Di Paola, D., Cicirelli, G., Eds.; IN-TECH: Vienna, Austria, 2010; pp. 239–254. [Google Scholar]
- Yamada, S.; Fujiwara, T. Testing-domain dependent software reliability growth models and their comparisons of goodness-of-fit. Int. J. Reliab. Qual. Saf. Eng. 2001, 8, 205–218. [Google Scholar]
- Arnold, L. Stochastic Differential Equations-Theory and Applications; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Wong, E. Stochastic Processes in Information and Systems; McGraw-Hill: New York, NY, USA, 1971. [Google Scholar]
- Yamada, S.; Kimura, M.; Tanaka, H.; Osaki, S. Software reliability measurement and assessment with stochastic differential equations. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 1994, E77–A, 109–116. [Google Scholar]
- Mikosch, T. Elementary Stochastic Calculus with Finance in View; World Scientific: Singapore, Singapore, 1998. [Google Scholar]
- Merton, R.C. Option pricing when underlying stock returns are discontinous. J. Financ. Econ. 1976, 3, 125–144. [Google Scholar]
- Honoré, P. Pitfalls in estimating jump-diffusion models. 1998. Available online: http://papers.ssrn.com/sol3/papers.cfm?abstract_id=61998 accessed on 25 June 2015.
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Yamada, S.; Osaki, S. Cost-reliability optimal software release policies for software systems. IEEE Trans. Reliab 1985, R-34, 422–424. [Google Scholar]
- Yamada, S.; Osaki, S. Optimal software release policies with simultaneous cost and reliability requirements. Eur. J. Oper. Res. 1987, 31, 46–51. [Google Scholar]
- The OpenStack project, OpenStack. Available online: http://www.openstack.org/ accessed on 25 June 2015.
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).