Abstract
The time operator and internal age are intrinsic features of entropy producing innovation processes. The innovation spaces at each stage are the eigenspaces of the time operator. The internal age is the average innovation time, analogous to lifetime computation. Time operators were originally introduced for quantum systems and highly unstable dynamical systems. Extending the time operator theory to regular Markov chains allows one to relate internal age with norm distances from equilibrium. The goal of this work is to express the evolution of internal age in terms of Lyapunov functionals constructed from entropies. We selected the Boltzmann–Gibbs–Shannon entropy and more general entropy functions, namely the Tsallis entropies and the Kaniadakis entropies. Moreover, we compare the evolution of the distance of initial distributions from equilibrium to the evolution of the Lyapunov functionals constructed from norms with the evolution of Lyapunov functionals constructed from entropies. It is remarkable that the entropy functionals evolve, violating the second law of thermodynamics, while the norm functionals evolve thermodynamically.
1. Introduction
The idea to represent time as an operator goes back to Pauli, who remarked that although the time-energy uncertainty relation is analogous to the position-momentum uncertainty relation, there is no self-adjoint time operator
canonically conjugate to the energy operator H (Hamiltonian) of a quantum system, as is the case with the position-momentum operators [1,2]. Time operators, however, can be defined for density matrices describing ensembles in quantum statistical mechanics. Quantum systems admitting time operators include irreversible processes, like resonance scattering, decay, radiation transition and quantum measurement [3–8].
Time operator theory was extended to describe the statistical properties of complex dynamical systems [3,9–13], providing a new representation of non-equilibrium processes and the innovation of non-predictable stationary stochastic processes [14–19]. The time operator is a self-adjoint operator on the space of fluctuations, with eigenvalues the clock times and corresponding eigenspaces the successive innovations. The time operator of Markov chains has been presented in [20] as an extension of the time operator of Bernoulli processes [21]. From the time operator, we can compute the internal age Age(Xt) of some random variable at each clock time t, as the expectation of the time operator (Section 2). The aging of canonical processes (Bernoulli) has been shown to keep step with the clock time t [9,10]:
After extending the time operator theory to more general processes, like Markov chains, we found non-canonical age formulas, where the correction to the canonical formula is proportional to a decaying exponential term [20]:
This rather unexpected new age formula resulted from the need to relate age with mixing time (time to approach equilibrium [22,23]). The internal age also determines the mixing time of Markov chains [20]. Mixing time estimations are useful in non-equilibrium statistical physics, in web analysis and network dynamics, computer science and statistics. More specifically, the mixing time of a Markov chain determines the running time of a Monte Carlo simulation [23], the time needed for a randomized algorithm to find a solution [22,24], so as to quantify the computational cost, the average navigation time within a website [25–27], the average travel time within a road network [28], the time needed for Google’s PageRank algorithm to compute the pageranksand find the right web page [29] and the time of validity of specific Markov models, such as the Markov switching between growth and recession of the U.S. GNP [30]. The internal age is applicable to all of the above models. However, the internal age can also be estimated directly from real data, as illustrated for specific financial applications [21]. For the Athens Stock Market, the internal age was found to take lower values in periods of low uncertainty and greater values in periods of high uncertainty, such as the Greek National Elections of June, 2012. This explicit calculation confirms the intuition underlying the age concept. Age is increasing when innovations appear; therefore, predictability is low.
Moreover, the non-canonical age formula indicates a link of aging with the associated Lyapunov functional, in this case defined by the total variation distance [20]. As entropies were historically the first Lyapunov functionals, we investigate in this work which entropies fit better the age formula and are compatible with the monotonic approach to equilibrium, as stated by the second law of thermodynamics (Section 4). The salient features of time operators and age are presented in Section 2, and the evolution of the selected entropies in Section 3.
2. Time Operator and Age
The time operator associated with the binary (two-value) observations of the stochastic process Xt, t = 1, 2, … is constructed as follows: At each stage t, the observation defines a partition of the sample space Ω into two sets
,
corresponding to the values 0,1. At the next stage t + 1, the sample space Ω is partitioned into the corresponding sets
,
corresponding to the values 0,1. Therefore, the knowledge obtained after all successive observations up to time t is the common refinement of the corresponding partitions. We denote by
the conditional expectation projecting onto the fluctuations observed up to time t. The sequence of conditional expectation projections:
, t = 0, 1, … is a resolution of the identity in , i.e.,:
,
and
. We have omitted the mathematical and technical details, as they are presented elsewhere [19,20], and they are not necessary for the scope of this work.
Definition 1. The self-adjoint operator with spectral projections being the conditional expectations on the space of fluctuations is called the time operator of the stochastic process Xt, t = 1, 2, ….
The internal age of the random variable Z is defined by the Rayleigh quotient [21]:
In the case of the so-called “canonical” time operators [9,10], the internal age keeps step with the clock time t:
In general, however, the age formula is non-linear, as in the case of cosmological models [31]:
The nonlinear function η(t) is the deviation of the age formula from the canonical linear model Equation (5). General analytical formulas for the internal age of Markov chains, Equation (6), are hard to obtain, because the innovation rates of Markov chains have neither been constructed, nor classified.
We estimated the nonlinear function η(t) [20] for classes of Markov chains:
maximizing the total variation distance [23]:
with respect to all initial distributions ρ(0):
Here, ρ(t) is the probability distribution at time t and ρeq is the equilibrium distribution of the process. Formula (7) follows from estimations of Markov chains, verified by a Monte Carlo method [20].
Explicit age formulas may be obtained for Markov chains Xt, t = 1, 2, … [20] with state space S = {0, 1}:
The parameter γ = 1 − w01 − w10, |γ| < 1 is the second largest eigenvalue of the stochastic transition matrix W [32]:
wκλ are the transition probabilities:
The evolution of probability distributions ρ(t) is given by the formula [32,33]:
The equilibrium distribution is [32]:
Using the r-norm distances, instead of the total variation distance, we obtain:
Lemma 1. For any two state Markov chain:
where:
Therefore, the approach to equilibrium is monotonic and faster as r tends to infinity.
Proof. From Equation (12),
We see from Equation (14) that for any initial distribution ρ(0) and for all r ≥ 1, the approach to equilibrium is monotonic. The r-norm is minimized with respect to r as r tends to infinity:
where
, because
, and the function
decreases with r:
It is straightforward from Equation (14) that:
The maximization of the distance ║ρ(t) − ρeq║r with respect to all initial distributions ρ(0) relates the age with any r-norm distance, generalizing Equation (22) as follows:
Formulas (2) and (15) provide the estimation of the age in terms of norm distances for two-state regular Markov chains. These chains are good models of irreversible processes, because every initial distribution converges to the unique equilibrium distribution, which is independent of the initial state. Moreover, regular Markov chains eventually become indistinguishable from stationary Bernoulli process. As indicated in Equation (12), the convergence rate is estimated by the second eigenvalue of the transition matrix [33].
3. Lyapunov Functionals and Entropies
The age formula Equation (7) is an estimation of the “distance” from equilibrium and has been related to entropy [10,34,35]. The total variation distance in the age formula, as well as other distances, like the r-norm distances, had been originally introduced in order to define the so-called “mixing time” estimating the effective duration of the approach to equilibrium [20,22,23]. The approach to equilibrium was historically estimated in terms of entropies and more generally in terms of Lyapunov functionals [10,36] originating in the context of statistical physics. We remind the reader that a Lyapunov functional
satisfies the conditions:
- LF1, for all y.
- LF2 The equation has the unique solution .
- LF3 vanishes as .
- LF4 is monotonically decreasing: , if t2 > t1.
We shall investigate the approach to equilibrium in terms of typical entropy functionals, like the Boltzmann–Gibbs–Shannon entropy, the Tsallis entropies [37] and the Kaniadakis entropies [38–40]. There are several Lyapunov functionals in the literature; see, for example, [41].
Non-monotonic Lyapunov functionals satisfying LF1, LF2, LF3 may serve also to describe the approach to equilibrium. The monotonicity condition is of course necessary when the Lyapunov functional serves as a model of thermodynamic entropy
, where
is the equilibrium entropy and k is Boltzmann’s constant. Monotonicity is not a general property of mixing or regular Markov chains [32], but only of doubly-stochastic Markov chains [42,43].
The evolution of the non-equilibrium entropies
to the equilibrium entropy
is described by the Lyapunov functional:
where
is any entropy, such as:
- Boltzmann–Gibbs–Shannon entropy [43]:
- Tsallis entropies [37]:
- Kaniadakis entropies [38–40]:where:
The mathematical properties of the generalized logarithm lnκ(x), Equation (20) are discussed in [44]. The Boltzmann–Gibbs–Shannon entropy, Equation (17), is a special case of the Tsallis entropies, Equation (18) for q → 1. The limiting case of κ → 0 reduces the Kaniadakis entropy, Equation (19), to the Boltzmann–Gibbs–Shannon entropy, Equation (17). Moreover, Kaniadakis entropies are related to the Tsallis entropies as follows [38]:
The traditional formulation of the second law of thermodynamics requires that entropy increases monotonically to the maximum value, which corresponds and defines equilibrium (Chapter 1 in [10] ; Chapter 3 in [45]). In the case of doubly-stochastic Markov chains, the approach to equilibrium is indeed monotonic [42,43]. However, in more general mixing Markov chains, the approach to equilibrium may be monotonic or not depending on the selected Lyapunov functional
as well as on the initial distribution ρ(0). For example, consider the Markov chain, Equation (10), with w01 = 0.245, w10 = 0.095. The evolution of the Boltzmann–Gibbs–Shannon entropy, Equations (16) and (17), for the initial distribution ρ0(0) = 0, ρ1(0) = 1 is monotonic (Figure 1), while for the initial distribution ρ0(0) = 1, ρ1(0) = 0 is non-monotonic (Figure 2). For both initial conditions, however, the evolution of the total variation distance is monotonic. This is also the case for all r-norm distances, as demonstrated by Lemma 1.
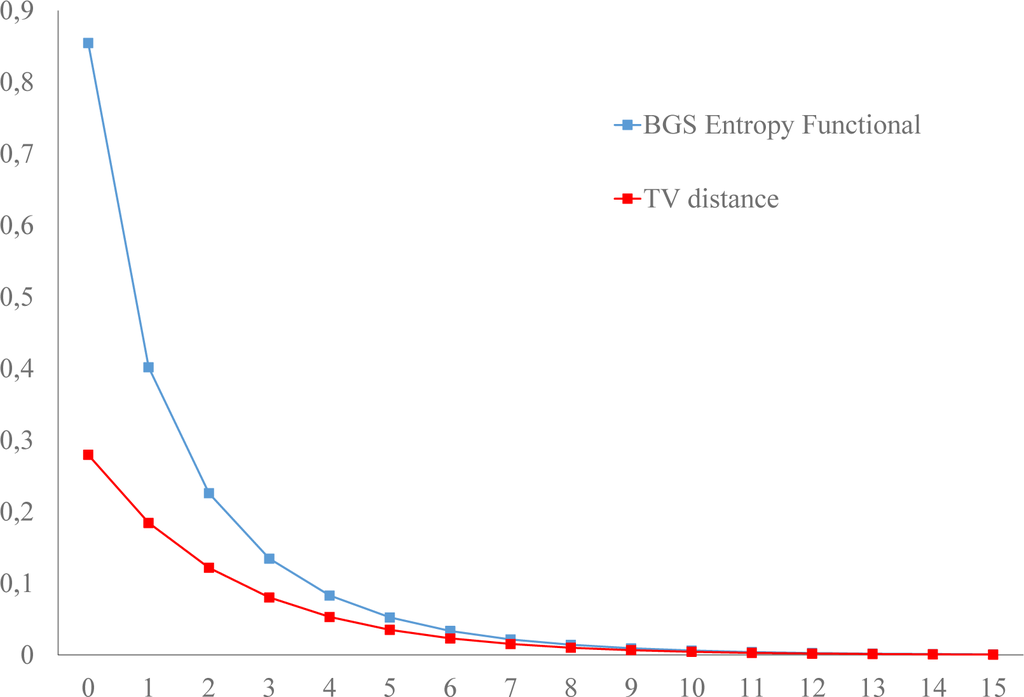
Figure 1.
The evolution of the total variation distance (solid line) from equilibrium and the Boltzmann–Gibbs–Shannon entropy, Equations (16) and (17), for the two-state Markov chain with w01 = 0.245, w10 = 0.095 and initial distribution ρ0(0) = 0, ρ1(0) = 1.
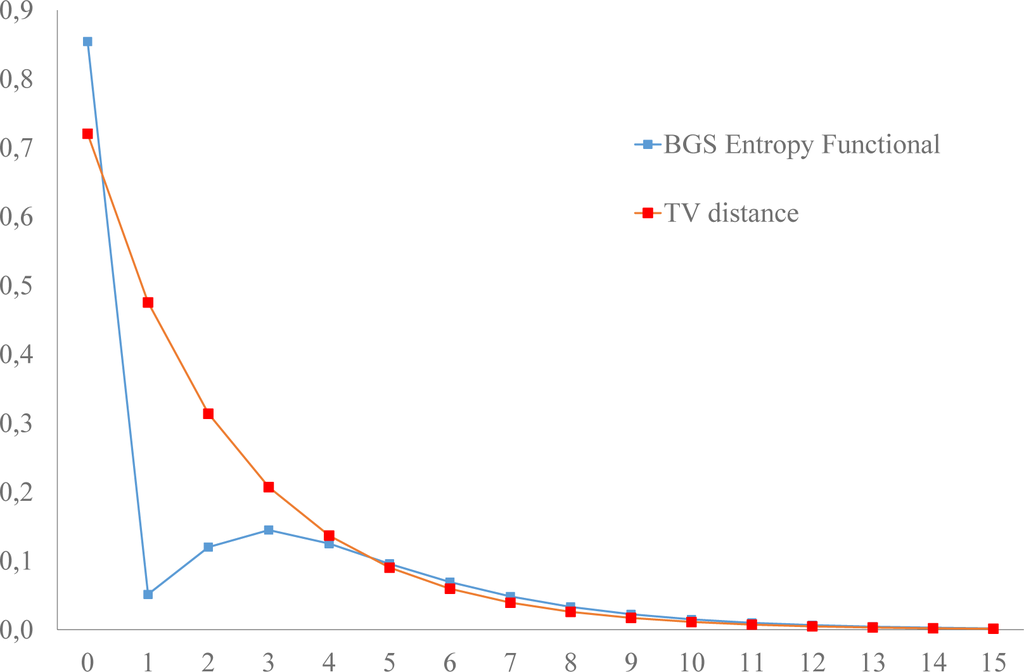
Figure 2.
The evolution of the total variation distance (solid line) from equilibrium and the Boltzmann–Gibbs–Shannon entropy, Equations (16) and (17), for the two-state Markov chain with w01 = 0.245, w10 = 0.095 and initial distribution ρ0(0) = 1, ρ1(0) = 0.
The Boltzmann–Gibbs–Shannon Lyapunov functional deviates significantly from the evolution of total variation Lyapunov functionals (Figures 1 and 2), while eventually, they converge. It is remarkable that for the same Markov chain, the total variation functional is monotonic for all times, in agreement with the second law of thermodynamics, while the Boltzmann–Gibbs–Shannon entropy is not monotonic, (Figure 2), therefore violating the monotonicity assumed in the traditional formulation of the second law of thermodynamics.
The evolutions of Boltzmann–Gibbs–Shannon entropy, the Tsallis and Kaniadakis entropies for the above Markov chain and the same initial distributions, are presented in Figures 3 and 4. We observe that all three entropies approach equilibrium monotonically for the initial distribution ρ0(0) = 0, ρ1(0) = 1 (Figure 4), in accordance with the second law of thermodynamics, while for the initial distribution ρ0(0) = 1, ρ1(0) = 0 (Figure 3), they violate the second law of thermodynamics in threeways: (1) the approach to equilibrium is non-monotonic; (2) the equilibrium distribution is not the maximum entropy distribution; and (3) the system begins with a state with entropy lower than the equilibrium entropy, then evolves to the state ρ0(3) = 0.4866, ρ1(3) = 0.5134 with maximal entropy and then relaxes monotonically to the equilibrium with lower entropy.
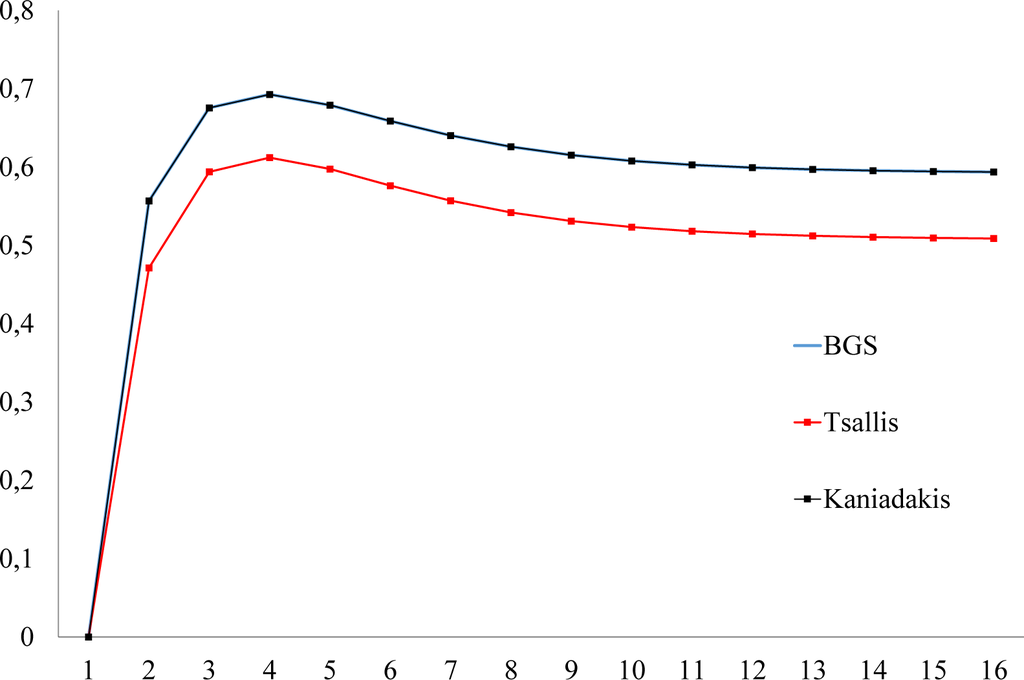
Figure 3.
The evolution of the Boltzmann–Gibbs–Shannon entropy, the Tsallis entropy for q = 1.3648 and the Kaniadakis entropy for κ = 0.0045 for the initial distribution ρ0(0) = 1, ρ1(0) = 0. The Kaniadakis entropy is indistinguishable from the Boltzmann–Gibbs–Shannon entropy, because the value of κ is very close to zero. The values of the entropic indices q, κ were selected so that the difference between the maximum entropy and the equilibrium entropy is maximal. The distribution of maximal entropy is ρ0(3) = 0.4866, ρ1(3) = 0.5134.
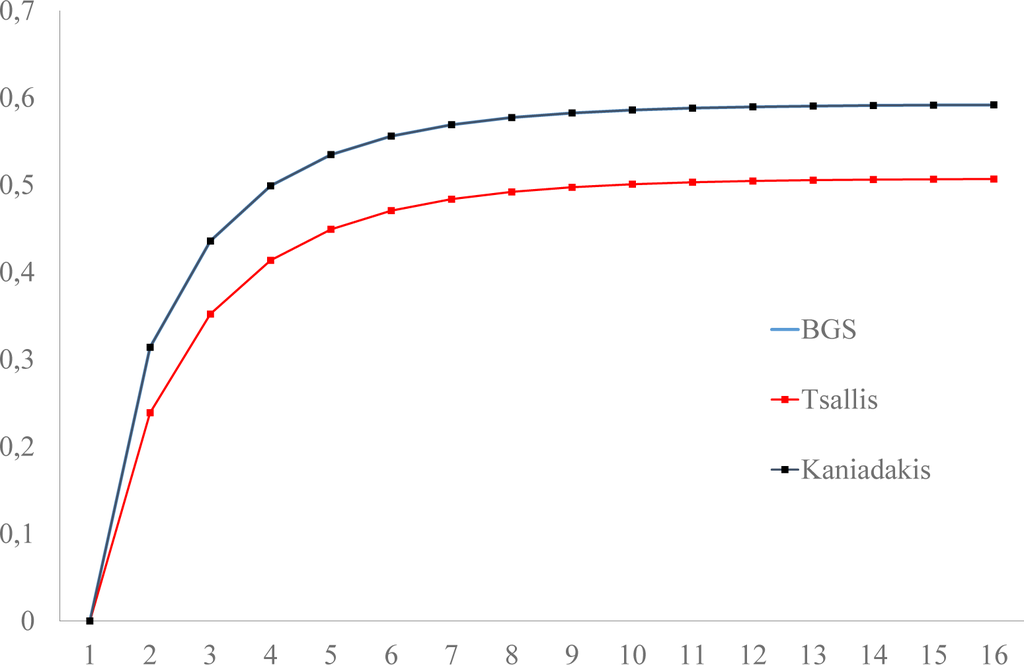
Figure 4.
The evolution of the Boltzmann–Gibbs–Shannon entropy, the Tsallis entropy for q = 1.3648 and the Kaniadakis entropy for κ = 0.0045 for the initial distribution ρ0(0) = 0, ρ1(0) = 1. The three entropies increase monotonically to the equilibrium entropy, which is the maximum entropy.
4. Age in Terms of Entropy
As general analytical formulas for the internal age of a Markov chain are not available, the nonlinear age formula should be computed numerically. An algorithm for the computation of the age of two-state Markov chains is proposed in Appendix C of [20]. We shall examine several examples of doubly-stochastic Markov chains using the total variation distance and related entropies. For each Markov chain, we compare the difference t − Age(Xt) with the evolution of the total variation distance and the evolution of Lyapunov functionals, Equation (16), defined from the Tsallis and Kaniadakis entropies.
The validity of the relation:
where
,
has been tested in [20] for a sample of 1,000 two-state Markov chains.
We investigate whether the age difference t − Age(Xt) can be expressed in terms of entropies, as both distances and entropies estimate the “distance” from equilibrium:
We shall examine whether the classic Boltzmann–Gibbs–Shannon entropy, as well as the non-additive Tsallis and Kaniadakis entropies approximate the age difference t − Age(Xt), for several rates of convergence to equilibrium γ.
Consider the initial distributions with the lowest possible entropy:
and the family of doubly-stochastic Markov chains:
with equilibrium distribution being the uniform distribution:
having the highest possible entropy.
We present in Figure 5 the convergence of the differences t − Age(Xt) to a constant α for n = 8 different doubly-stochastic Markov chains:
with corresponding rates of convergence 2λn − 1. The differences t − Age(Xt) become constant after a time instant t, which depends on the rate of convergence 2λn − 1 (Figure 5).
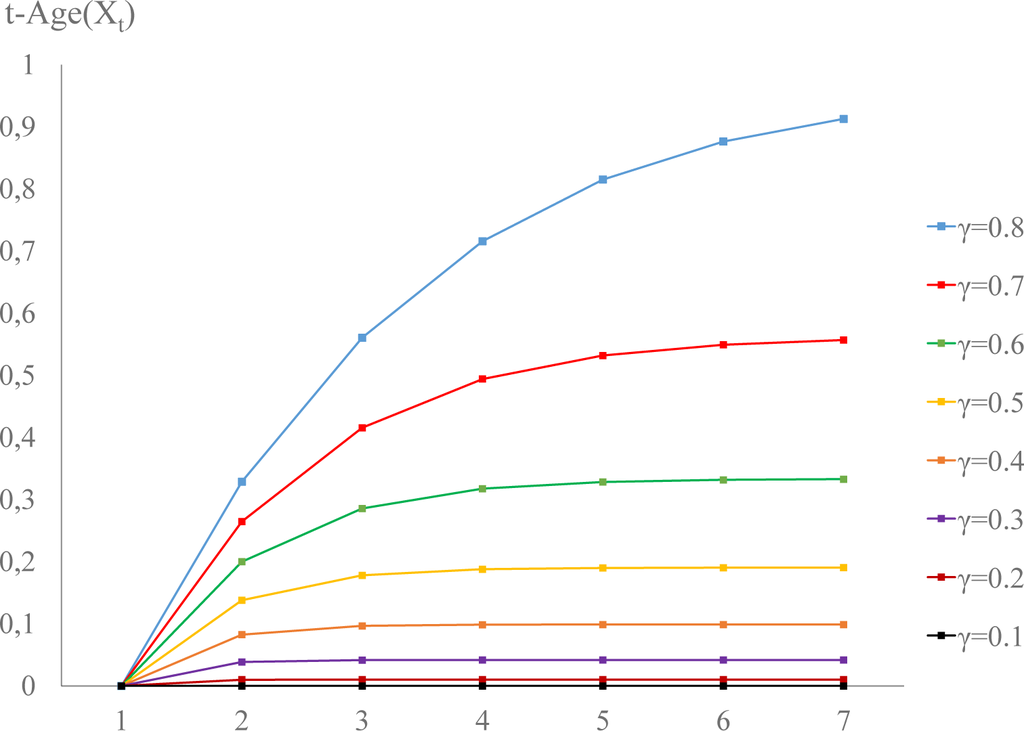
Figure 5.
The differences t − Age(Xt) become eventually constant.
The evolution of the total variation distance of the initial distribution Equation (24) from the equilibrium distribution, Equation (26), of the doubly-stochastic Markov chain of Equation (25) is given by dTV (ρ(t), ρeq) = 0.5(2λn − 1)t, because |ρ0 − ρeq,0| = 0.5 for ρ0 = 0 or ρ0 = 1 and ρeq,0 = 0.5.
Concerning the validity of the linear regression formula Equation (22), we present the linear regression analysis of the variable t − Age(Xt) versus the total variation distance, Equation (8), in Table 1. The objective is to compare the mean square error (MSE) among the estimations of Equation (22) of the total variation distance and the estimations of Equation (23) among the Boltzmann–Gibbs–Shannon entropy, Tsallis entropy and Kaniadakis entropy.

For all rates of convergence γ, the linear relation between the total variation distance dTV(ρ(t), ρeq) and the age differences t − Age(Xt) is statistically significant (Table 1), verifying the results of the Monte Carlo simulation technique that we followed in [20]. Concerning the validity of the linear regression formula Equation (23) for the Boltzmann–Gibbs–Shannon entropy, we repeat the same analysis in Table 2.

Table 2.
Linear regression between t − Age(Xt) and the Lyapunov functional defined in terms of the Boltzmann–Gibbs–Shannon entropy, Equation (23).
The Tsallis and Kaniadakis non-additive entropies fit the evolution of age differences t − Age(Xt) better compared to the Boltzmann–Gibbs–Shannon entropy (Figures 6 and 7). More specifically, in Figure 6, the mean square error (MSE) of the linear regression to the Tsallis-entropy (q = 2.5) Lyapunov functional is less than the MSE of the linear fit to the Boltzmann–Gibbs–Shannon entropy Lyapunov functional. Searching for other entropic indices q > 0, so that the MSE is further reduced, using the Tsallis entropy Lyapunov functional, we found that for q = 2.5, the MSE attains its minimum (Figure 8) for all rates of convergence γ.
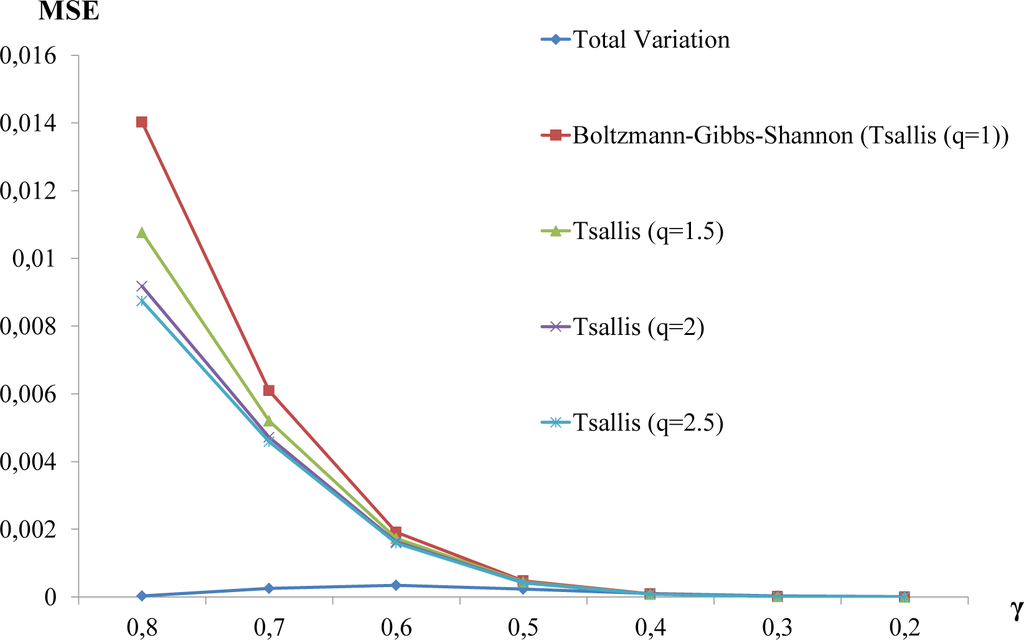
Figure 6.
The mean square error of the linear fit to the total variation distance, the Boltzmann–Gibbs–Shannon entropy and the Tsallis entropy for q = 1.5, q = 2 and q = 2.5.
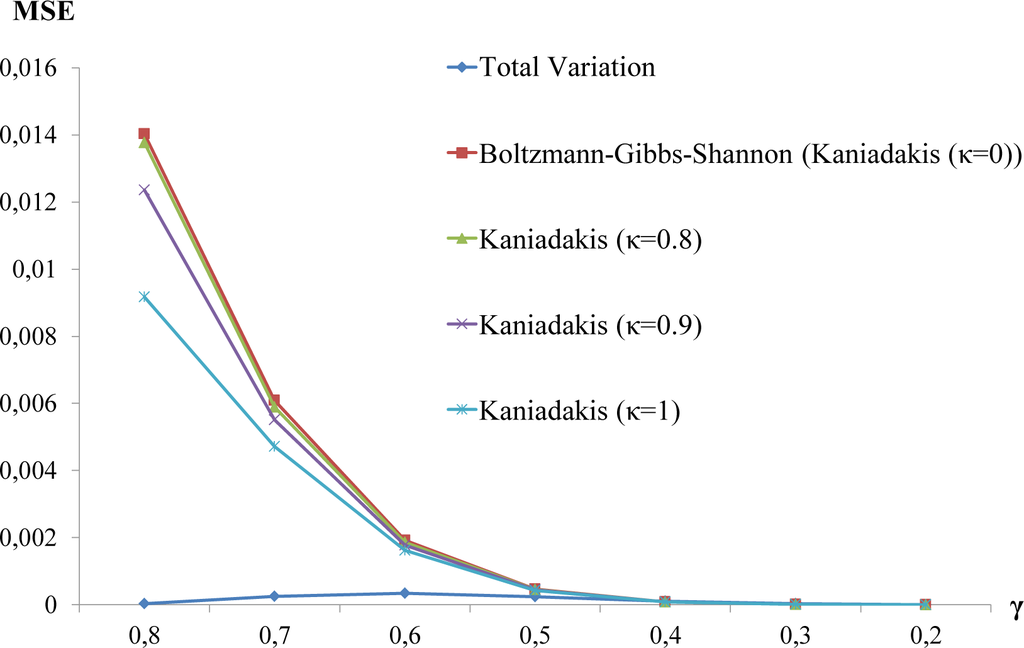
Figure 7.
The mean square error of the linear fit to the total variation distance, the Boltzmann–Gibbs–Shannon entropy and the Kaniadakis entropy for κ = 0.8, κ = 0.9 and κ = 1.
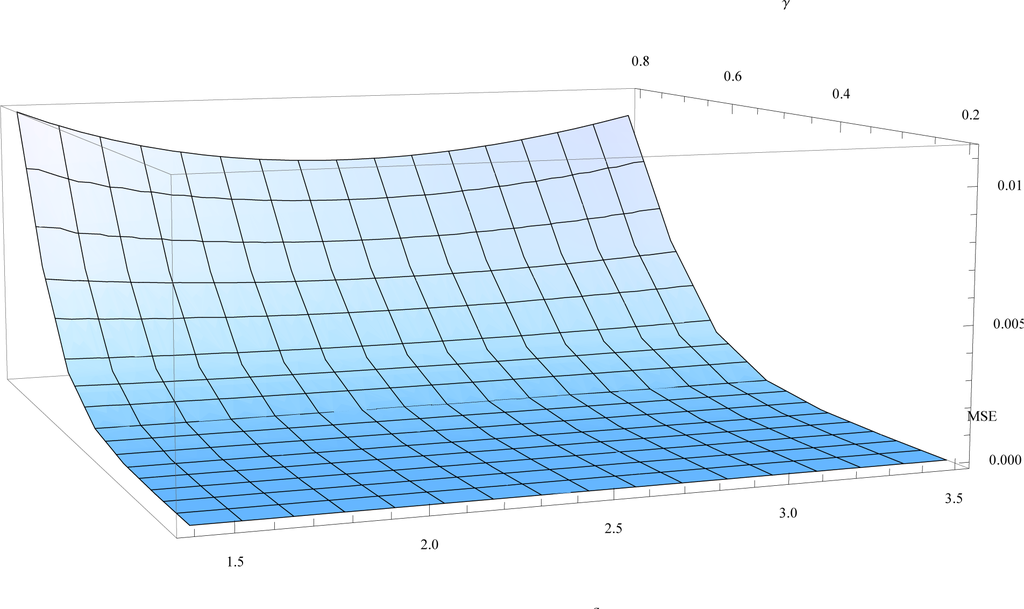
Figure 8.
The mean square error (MSE) as a function of the entropic index q ∈ [1.4, 3.5] for all rates of convergence γ ∈ [0.2, 0.8]. The MSE attains its minimum for q = 2.5.
In Figure 7, it is shown that the linear fit to the age evolution may also be obtained using the functional, Equation (23), from the Kaniadakis entropy. Searching in the region 0 < κ < 1, we found that the best fit is attained at the boarders |κ| → 1 (Figure 9). The desired MSE using the total variation distance, which is the lowest known so far, is not obtained, but the generalizations of Tsallis and Kaniadakis improve the approach to the internal age differences t − Age(Xt) significantly when compared to the Boltzmann–Gibbs–Shannon entropy.
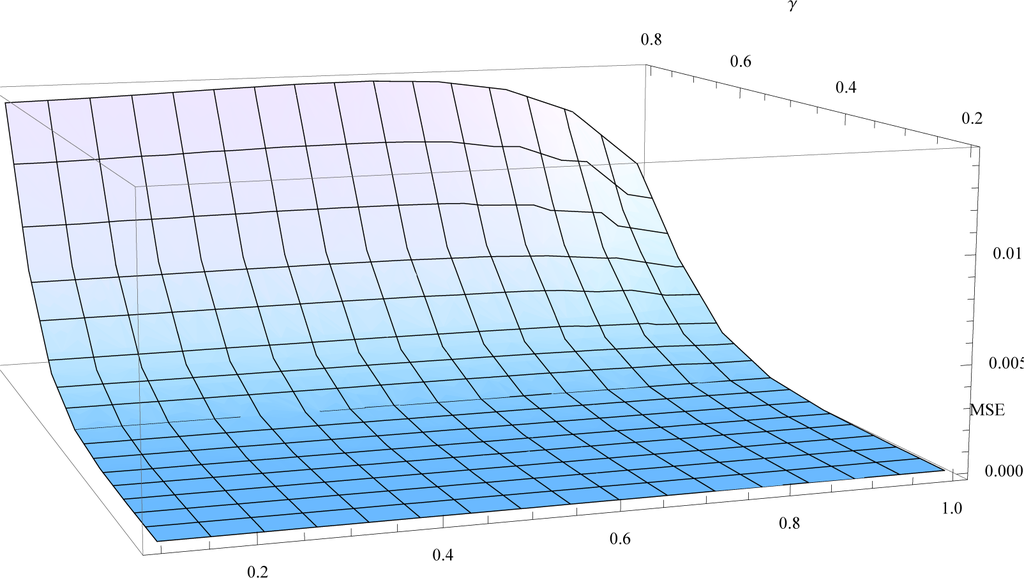
Figure 9.
The mean square error (MSE) as a function of the entropic index κ ∈ (0, 1] for all rates of convergence γ ∈ [0.2, 0.8]. The MSE attains its minimum for κ = 1.
We note that Markov chains with rate γ close to zero are very close to equilibrium, so there are no significant changes in the way we observe the convergence to equilibrium. This is the reason why as the rate γ decreases, the deviations from one functional to another (Boltzmann–Gibbs–Shannon, Tsallis and Kaniadakis Lyapunov functionals) also decrease.
From the above analysis, we obtain the following internal age formulas expressed in terms of entropies:
- Tsallis entropy:
- Kaniadakis entropy:
Comparing Equations (28) and (29) to the age evolution in terms of the Boltzmann–Gibbs–Shannon entropy:
we present the percentage decrease of the mean square error in Figure 10 for all rates of convergence γ.
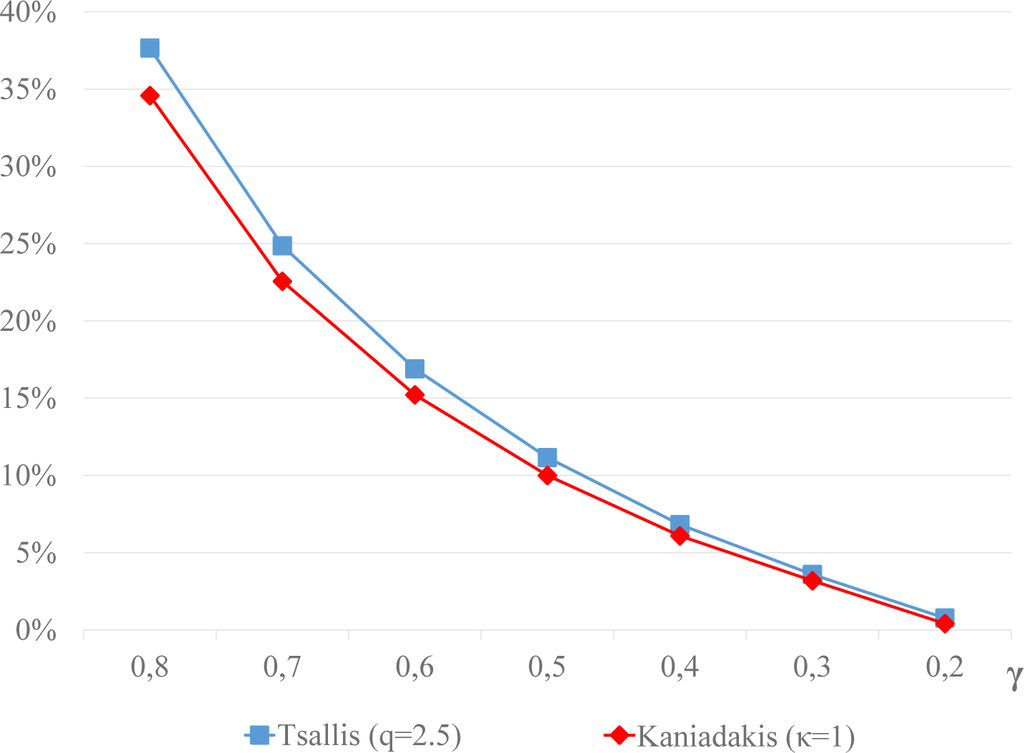
Figure 10.
The percentage decrease in the mean square error using the Lyapunov functionals associated with Tsallis entropy, Equation (28), and Kaniadakis entropy, Equation (29), compared with the MSE of the Boltzmann–Gibbs–Shannon Lyapunov functional, Equation (30).
5. Concluding Remarks
The age of Markov chains evolves closer to non-additive entropies (Tsallis, Kaniadakis) than the additive Boltzmann–Gibbs–Shannon entropy, as indicated in Figures 6 and 7. This result extends and justifies previous use of the quadratic entropy for Markov chains intertwined with Kolmogorov systems [3,9,10]. The distinction between additivity and extensivity is reviewed by Tsallis [46].
We generalized the age formula (22) expressing age in terms of Lyapunov functionals
(LF1–LF4). The minimal requirement for a Lyapunov functional
is positivity and discernibility:
. Monotonicity (LF4) is necessary for models compatible with the second law of thermodynamics. In this case, the Lyapunov functional serves as a model of thermodynamic entropy. Monotonicity is not a general property of mixing or regular Markov chains [32], but only of doubly-stochastic Markov chains [42,43]. Lyapunov functionals are not in general distances, because they do not satisfy symmetry and triangle inequality. However, distances like the total variation distance serve as Lyapunov functionals.
The presence of the Lyapunov functional
in the age formula (31) is a manifestation of the fact that after mixing, Markov chains become indistinguishable from Bernoulli processes, and the age formula (6) becomes indistinguishable from the canonical age formula, Equation (5). The age formulas (28) and (29) are specific examples of non-canonical age formulas. Canonical age formulas actually manifest in the case of Bernoulli processes [21], as has been the case of the original definition of time operators [9,10].
Conversely, now, we may construct Lyapunov functionals from the internal age of the Markov chain Xt, t = 1, 2, …:
The Lyapunov functional (32) satisfies LF1–LF4, because it is a distance:
Concerning the evolution of the Lyapunov functionals considered, we observed that:
- The Lyapunov functionals defined in terms of norms (total variation and r-norms; Equation (29) in [20] and Equation (14), respectively) evolve monotonically towards equilibrium, respecting the second law of thermodynamics; Figures 1 and 2:
- For the same system, the Lyapunov functionals defined in terms of entropies evolve violating the second law of thermodynamics in three ways (Figure 3): (1) the approach to equilibrium is non-monotonic; (2) the equilibrium distribution is not the maximum entropy distribution; and (3) the initial entropy is lower than the equilibrium entropy, then entropy increases above equilibrium and then decreases monotonically to equilibrium. Monotonicity violations (1) have been reported for non-doubly-stochastic regular Markov chains ([42] (Theorem 5, p. 104); p. 81 in [43]). Examples of evolutions where the maximum entropy is not the equilibrium entropy (2), therefore violating Jaynes [47] maximum entropy principle, have also been reported [48] (pp. 82–83 in [43]). We did not find entropy evolutions with the behavior (3) in Figure 3.
We conclude, therefore, that even though the Tsallis, Kaniadakis and the Boltzmann–Gibbs–Shannon entropy violate the second law of thermodynamics, the Lyapunov functionals in terms of norms evolve in accordance with thermodynamics for the same Markov process.
Acknowledgments
The present work was announced in “SigmaPhi2014: International Conference on Statistical Physics, Rhodes, Greece”. We thank several participants of the conference for useful remarks and interesting discussions after the presentation, which contributed to the improvement of the discussion on the significance of our results. Moreover, we appreciate the interest and support of Giorgio Kaniadakis. We are also grateful to Karl Gustafson for useful discussions and remarks. The comments and recommendations of the referees improved the clarity and presentation of this work. We acknowledge the Aristotle University of Thessaloniki and especially the Research Committee for supporting one of us (Ilias Gialampoukidis) by awarding him the Excellence Scholarship 2013.
Author Contributions
Both authors contributed equally in the results of this paper.
Conflicts of Interest
The authors declare no conflict of interest
References
- Pauli, W. Prinzipien der Quantentheorie 1. In Encyclopedia of Physics; Volume 5, Flugge, S., Ed.; Springer-Verlag: Berlin, Germany, 1958; English Translation: General Principles of Quantum Mechanics; Achuthan, P., Venkatesan, K., Translater; Springer: Berlin, Germany, 1980. [Google Scholar]
- Putnam, C.R. Commutation Properties of Hilbert Space Operators and Related Topic; Springer: Berlin, Germany, 1967. [Google Scholar]
- Misra, B. Nonequilibrium entropy, Lyapounov variables, and ergodic properties of classical systems. Proc. Natl. Acad. Sci. USA 1978, 75, 1627–1631. [Google Scholar]
- Misra, B.; Prigogine, I.; Courbage, M. Lyapunov variable: Entropy and measurements in quantum mechanics. Proc. Natl. Acad. Sci. USA 1979, 76, 4768–4772. [Google Scholar]
- Courbage, M. On necessary and sufficient conditions for the existence of Time and Entropy Operators in Quantum Mechanics. Lett. Math. Phys 1980, 4, 425–432. [Google Scholar]
- Lockhart, C.M.; Misra, B. Irreversebility and measurement in quantum mechanics. Physica A 1986, 136, 47–76. [Google Scholar]
- Antoniou, I.; Suchanecki, Z.; Laura, R.; Tasaki, S. Intrinsic irreversibility of quantum systems with diagonal singularity. Physica A 1997, 241, 737–772. [Google Scholar]
- Courbage, M.; Fathi, S. Decay probability distribution of quantum-mechanical unstable systems and time operator. Physica A 2008, 387, 2205–2224. [Google Scholar]
- Misra, B.; Prigogine, I.; Courbage, M. From deterministic dynamics to probabilistic descriptions. Physica A 1979, 98, 1–26. [Google Scholar]
- Prigogine, I. From Being to Becoming; Freeman: New York, NY, USA, 1980. [Google Scholar]
- Courbage, M.; Misra, B. On the equivalence between Bernoulli dynamical systems and stochastic Markov processes. Physica A 1980, 104, 359–377. [Google Scholar]
- Courbage, M. Intrinsic Irreversibility of Kolmogorov Dynamical Systems. Physica A 1983, 122, 459–482. [Google Scholar]
- Antoniou, I. The Time Operator of the Cusp Map. Chaos Soliton Fractal 2001, 12, 1619–1627. [Google Scholar]
- Gustafson, K.; Misra, B. Canonical Commutation Relations of Quantum Mechanics and Stochastic Regularity. Lett. Math. Phys 1976, 1, 275–280. [Google Scholar]
- Gustafson, K.; Goodrich, R. Kolmogorov systems and Haar systems. Colloq. Math. Soc. Janos Bolyai 1987, 49, 401–416. [Google Scholar]
- Gustafson, K. Lectures on Computational Fluid Dynamics, Mathematical Physic and Linear Algebra; Abe, T., Kuwahara, K., Eds.; World Scientific: Singapore, Singapore, 1997. [Google Scholar]
- Antoniou, I.; Gustafson, K. Wavelets and Stochastic Processes. Math. Comput. Simul 1999, 49, 81–104. [Google Scholar]
- Antoniou, I.; Prigogine, I.; Sadovnichii, V.; Shkarin, S. Time Operator for Diffusion. Chaos Soliton Fractal 2000, 11, 465–477. [Google Scholar]
- Antoniou, I.; Christidis, T. Bergson’s Time and the Time Operator. Mind Matter 2010, 8, 185–202. [Google Scholar]
- Gialampoukidis, I.; Gustafson, K.; Antoniou, I. Time Operator of Markov Chains and Mixing Times. Applications to Financial Data. Physica A 2014, 415, 141–155. [Google Scholar]
- Gialampoukidis, I.; Gustafson, K.; Antoniou, I. Financial Time Operator for random walk markets. Chaos Soliton Fractal 2013, 57, 62–72. [Google Scholar]
- Aldous, D.; Fill, J. Reversible Markov Chains and Random Walks on Graphs, 2002. 14 January 2015.
- Levin, D.A.; Peres, Y.; Wilmer, E.L. Markov Chains and Mixing Times; American Mathematical Society: Providence, RI, USA, 2009. [Google Scholar]
- Aldous, D.; Lovász, L.; Winkler, P. Mixing times for uniformly ergodic Markov chains. Stoch Process. Appl 1997, 71, 165–185. [Google Scholar]
- Levene, M.; Loizou, G. Kemeny’s constant and the random surfer. Am. Math. Mon 2002, 741–745. [Google Scholar]
- Jenamani, M.; Mohapatra, P.K.; Ghose, S. A stochastic model of e-customer behavior. Electron. Commer. R. A 2003, 2, 81–94. [Google Scholar]
- Kirkland, S. Fastest expected time to mixing for a Markov chain on a directed graph. Linear Algebra Appl 2010, 433, 1988–1996. [Google Scholar]
- Crisostomi, E.; Kirkland, S.; Shorten, R. A. Google-like model of road network dynamics and its application to regulation and control. Int. J. Control 2011, 84, 633–651. [Google Scholar]
- Brin, S.; Page, L. The anatomy of a large-scale hypertextual Web search engine. Comput. Netw. ISDN 1998, 30, 107–117. [Google Scholar]
- Hamilton, J.D. A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica 1989, 357–384. [Google Scholar]
- Lockhart, C.M.; Misra, B.; Prigogine, I. Geodesic instability and internal time in relativistic cosmology. Phys. Rev. D 1982, 25, 921. [Google Scholar]
- Kemeny, J.G.; Snell, J.L. (Eds.) Finite Markov Chains; D. Van Nostrand: Princeton, NJ, USA, 1960.
- Howard, R.A. Dynamic Probabilistic Systems; Wiley: New York, NY, USA, 1971; Volume I. [Google Scholar]
- De La Llave, R. Rates of convergence to equilibrium in the Prigogine-Misra-Courbage theory of irreversibility. J. Stat. Phys 1982, 29, 17–31. [Google Scholar]
- Atmanspacher, H. Dynamical Entropy in Dynamical Systems; Springer: Berlin, Germany, 1997. [Google Scholar]
- Mackey, M.C. The dynamic origin of increasing entropy. Rev. Mod. Phys 1989, 61, 981. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann–Gibbs statistics. J. Stat. Phys 1988, 52, 479–487. [Google Scholar]
- Kaniadakis, G. Non–linear kinetics underlying generalized statistics. Physica A 2001, 296, 405–425. [Google Scholar]
- Kaniadakis, G. H–theorem and generalized entropies within the framework of nonlinear kinetics. Phys. Lett. A 2001, 288, 283–291. [Google Scholar]
- Kaniadakis, G.; Lissia, M.; Scarfone, A.M. Deformed logarithms and entropies. Physica A 2004, 340, 41–49. [Google Scholar]
- Gorban, A.N. Entropy: The Markov Ordering Approach. Entropy 2010, 12, 1145–1193. [Google Scholar]
- Cover, T.M. Which processes satisfy the second law? In PhysicaL Origins of Time Asymmetry; Halliwell, J.J., Pérez-Mercader, J., Zurek, W.H., Eds.; Cambridge University Press: Cambridge, UK, 1994; pp. 98–107. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Kaniadakis, G. Theoretical foundations and mathematical formalism of the power-law tailed statistical distributions. Entropy 2013, 15, 3983–4010. [Google Scholar]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics, From Heat Engines to Dissipative Structures; Wiley: Chichester, UK, 1998. [Google Scholar]
- Tsallis, C. The Nonadditive Entropy Sq and Its Applications in Physics and Elsewhere: Some Remarks. Entropy 2011, 13, 1765–1804. [Google Scholar]
- Jaynes, E.T. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Landsberg, P.T. Is equilibrium always an entropy maximum? J. Stat. Phys 1984, 35, 159–169. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).